2. 天津市现代机电装备技术重点实验室, 天津 300387
2. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology, Tianjin 300387, China
《第二次全国残疾人抽样调查主要数据公报》显示,我国残疾人口占总人口数量的6.3%。由于活动受限、矫形器使用百分比过低等原因,下肢体残疾人行走能力不能及时恢复,容易引起腿部肌肉萎缩,从而造成神经系统和内分泌系统的损伤。近年来,随着下肢康复外骨骼技术的发展,下肢行动障碍患者通过下肢康复外骨骼进行康复训练,减轻了康复医师的工作负担,提高了康复治疗的效果[1]。
遵循仿生学原理,以人体下肢骨骼刚体模型为参考,将关节运动简化为铰链运动,如Lokomat[2]、ReWalk[3]、Rex[4]、SIAT[5]等下肢康复外骨骼。这类下肢康复外骨骼以人体-外骨骼运动模型为参考,将外骨骼与人体直接固连,形成人机闭合运动链。
现有下肢康复外骨骼的人机接口大多是采用绷带、卡套进行紧固式连接。理想状态下,外骨骼与人体形成平行链,人机尺寸完全匹配,运动协调[6]。然而,在外骨骼实际使用过程中,因外骨骼周期性运动,人机之间产生相对滑动,出现运动偏差。若人机接口处的紧固式连接不足以补偿人机滑动产生的变形和错位,外骨骼会强制人体关节产生相对移动,对人体腿部产生压力,使肢体不适,甚至对肢体造成二次损伤。尽管研究者们已注意到人机相对滑动产生人机运动偏差的现象,但在外骨骼结构设计中,如何调整人机相对滑动,未进行深入探讨。
基于人机偏差变量理论[7]和人机相容理论[6, 8],针对人机相对滑动产生运动偏差的问题,对人机接口处结构进行选型优化,在现有人体-外骨骼运动模型的基础上建立人体-外骨骼调整模型。结合人体-外骨骼运动模型与人体-外骨骼调整模型,设计下肢康复外骨骼,并对外骨骼机构进行运动学建模与仿真。
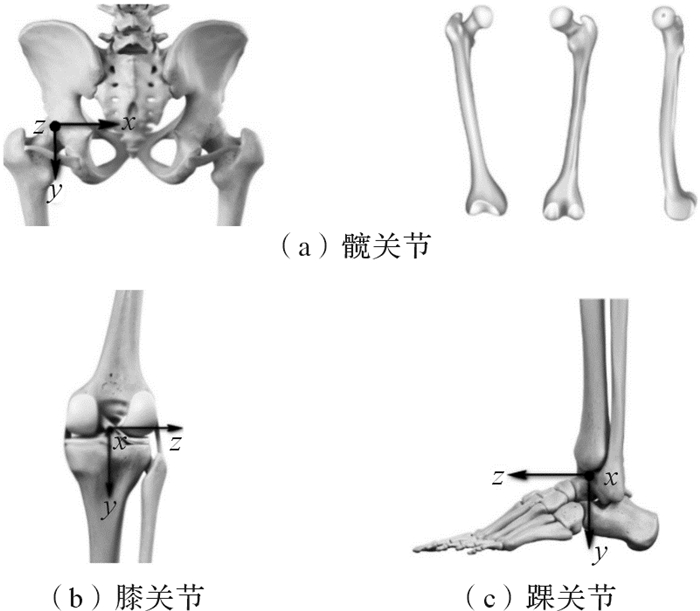
1 人体-外骨骼模型的建立 1.1 人体下肢骨骼模型人体行走是由下肢肌肉群的收缩带动骨骼绕关节转动,由髋关节、膝关节、踝关节实现协同运动。人体下肢骨骼模型如图 1所示,其中:髋关节是球窝关节,具有三自由度,大腿绕髋关节在矢状面内作屈伸运动,在冠状面内作外展内收运动,在水平面内作内外旋运动;膝关节为椭圆滑车关节,大小腿绕膝关节在矢状面内作屈伸运动;踝关节为滑车关节,足部和小腿围绕它在矢状面内作跖屈、背屈运动,在冠状面内作外展内收运动,在水平面内作内外翻运动[9]。
|
| 图 1 人体下肢骨骼模型 Fig.1 Skeleton model of human lower limb |
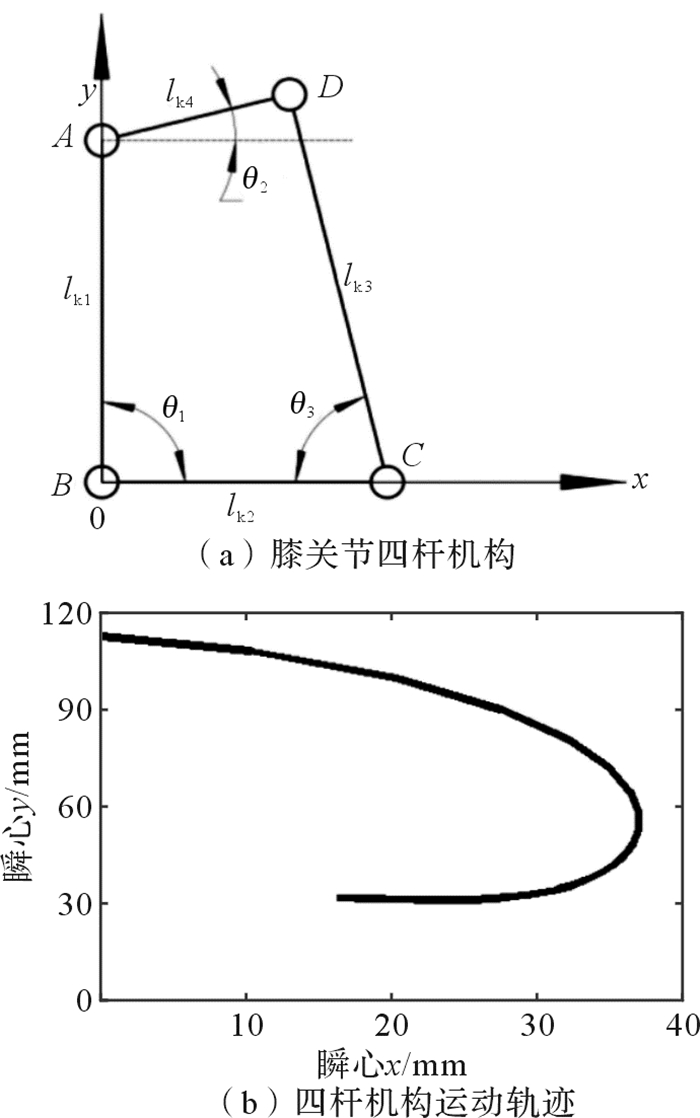
以人体模型中应用广泛的多刚体骨骼模型对下肢模型进行等效替代[10],简化人体下肢运动模型。髋关节为三自由度关节,选择球副等效替代,可沿关节的3个轴线方向转动。膝关节为单自由度关节,目前有普通铰链关节[2-5]和四杆机构[6, 11]两种替代形式。由于膝股胫关节结构的特殊性,膝关节屈伸运动为变瞬心运动,单自由度铰链关节难以反映人体膝关节的真实运动,而四杆机构更接近膝关节的实际运动情况,四杆机构及其运动轨迹如图 2所示。踝关节为三自由度关节,在人体行走过程中,踝关节主要运动形式为跖屈、背屈运动,可选择普通铰链关节替代,满足基本行走需求。
|
| 图 2 膝关节四杆机构及其运动轨迹 Fig.2 Four-bar mechanism of knee joint and its motion trajectory |
基于上述内容,建立人体下肢关节-骨骼刚体模型,如图 3所示。根据《中国成年人人体尺寸》 (GB/T 10000—1988),取身高为180 cm人群的平均参数,大腿长为523 mm,小腿长为419 mm, 踝高为79 mm。
|
| 图 3 人体下肢关节-骨骼刚体模型 Fig.3 Rigid body model of joint-skeleton for human lower limb |
在人体-外骨骼运动模型中,外骨骼与人体直接固连,形成人机平行链,人机尺寸匹配,运动协调。
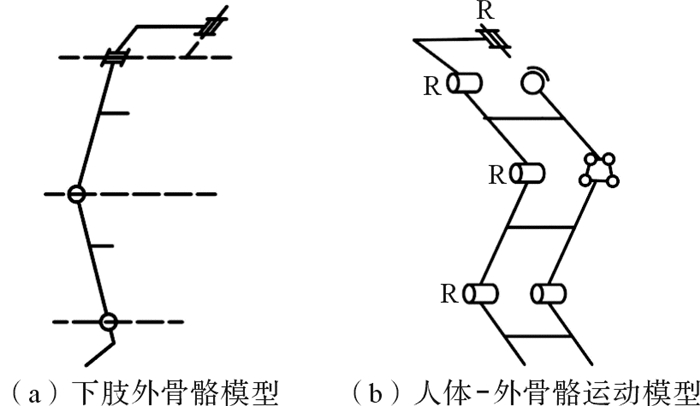
基于人体下肢康复运动机理,以外骨骼机构能在矢状面内实现髋、膝、踝关节屈伸运动,在冠状面内实现髋关节外展内收运动,作为外骨骼模型选择依据。人体-外骨骼运动模型由所选人体模型与外骨骼模型直接连接,形成H型人机闭合运动链,如图 4所示。在运动过程中,由下肢康复外骨骼辅助患者完成行走任务。
|
| 图 4 下肢外骨骼模型及人体-外骨骼运动模型 Fig.4 Exoskeleton model of lower limb and human-exoskeleton movement model |
基于人体-外骨骼运动模型的下肢康复外骨骼在使用中存在因人机之间的相对滑动产生的运动偏差,若人机接口处的活动余量不足以补偿人机滑动产生的变形和错位,外骨骼会强制人体运动,轻则使肢体麻木,重则会造成肢体二次损伤。
针对人体-外骨骼运动模型中的运动偏差,通过增补被动自由度的方式,对人机接口结构进行优化[7, 12],建立人体-外骨骼调整模型,使得当运动偏差对人体造成不适时,能够补偿偏差。
从空间单封闭型机构角度分析[13],各关节闭合运动链应符合:
| $ F = \sum {f - \lambda } $ | (1) |
式中:F为各关节自由度;f为关节各运动副自由度;λ为闭合约束数,一般空间机构中,λ=6。
针对人体-外骨骼调整模型,式(1)可表示为:
| $ F = {f_{\rm{k}}} + {f_{{\rm{uk}}}} - \lambda $ | (2) |
式中:fk为人体-外骨骼调整模型中单封闭链已知自由度,fuk为人体-外骨骼调整模型中单封闭链未知自由度。
基于人体-外骨骼运动模型,可知髋部人机闭合运动链已知自由度fk, H=4,膝部人机闭合运动链已知自由度fk, K=2, 踝部人机闭合运动链已知自由度fk, A=2, 因此通过式(2)分别求解髋部、膝部与踝部人机闭合运动链的未知自由度fuk, H、fuk, K与fuk, A,为:
| $ {f_{{\rm{uk,H}}}} = {F_{\rm{H}}} - {f_{{\rm{k,H}}}} + \lambda = 2 - 4 + 6 = 4 $ | (3) |
| $ {f_{{\rm{uk,K}}}} = {F_{\rm{K}}} - {f_{{\rm{k,K}}}} + \lambda = 1 - 2 + 6 = 5 $ | (4) |
| $ {f_{{\rm{uk,A}}}} = {F_{\rm{A}}} - {f_{{\rm{k,A}}}} + \lambda = 1 - 2 + 6 = 5 $ | (5) |
式中:FH、FK、FA分别为髋关节、膝关节、踝关节的闭合运动链自由度。
由式(3)至(5)可知:髋部人机闭合运动链需增补4个自由度,膝部和踝部人机闭合运动链各需增补5个自由度。
人机运动微偏差主要表现为移动微偏差和旋转微偏差[10],以此作为优化依据,并确定构型优选原则:
1) 尽量使外骨骼机械腿运动平稳;
2) 避免人机接口构型与人体-外骨骼运动模型冲突;
3) 保证人体-外骨骼调整模型有确定运动。
假设在髋部人机闭合运动链处引入1个移动副P和1个球副S,补偿其纵向移动和小范围转动;在膝部人机闭合运动链处引入2个移动副P和1个球副S,补偿其纵向和横向的移动以及小范围转动;在踝部人机闭合运动链处引入2个移动副P和1个球副S,补偿其纵向和横向的移动以及小范围转动。
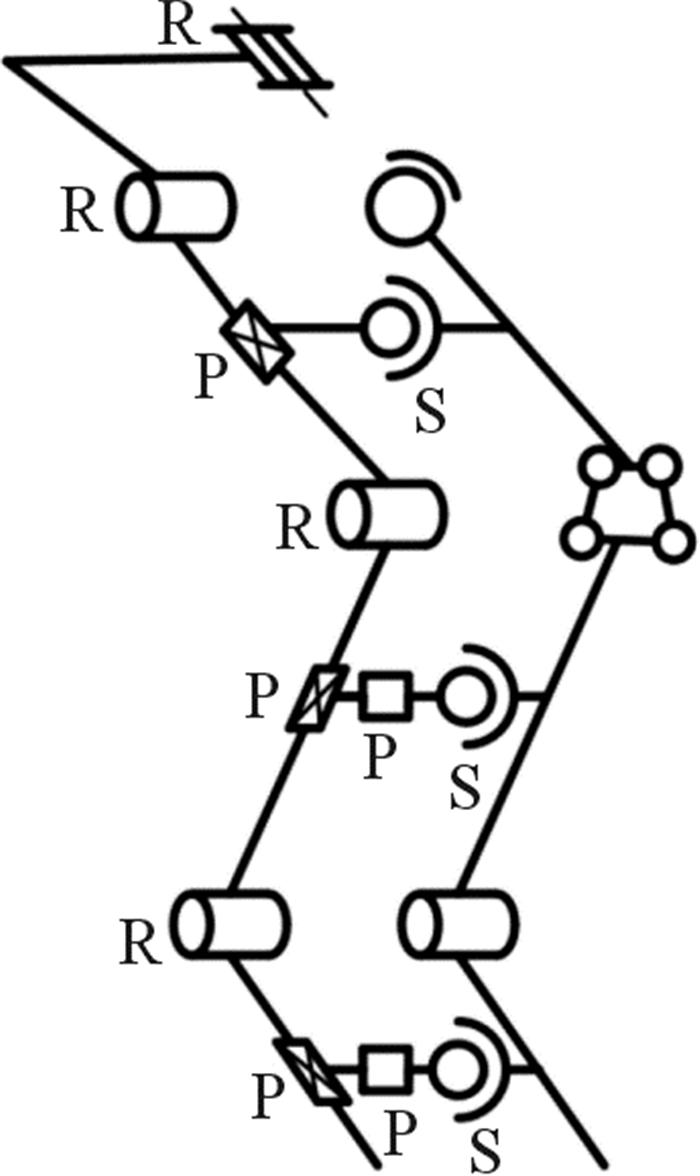
根据上述假设在人机接口处增加连接关节,建立人体-外骨骼调整模型,如图 5所示。人体-外骨骼调整模型由髋部人机闭合运动链、膝部人机闭合运动链、踝部人机闭合运动链共同组成。
|
| 图 5 人体-外骨骼调整模型 Fig.5 Human-exoskeleton adjustment model |
分别对各关节闭合运动链自由度FH、FK、FA进行验证:
| $ {F_{\rm{H}}} = \sum {{f_{\rm{H}}} - \lambda } = 3 + 3 + 2 - 6 = 2 $ | (6) |
| $ {F_{\rm{K}}} = \sum {{f_{\rm{K}}} - \lambda } = 1 \times 4 + 3 - 6 = 1 $ | (7) |
| $ {F_{\rm{A}}} = \sum {{f_{\rm{A}}} - \lambda } = 1 \times 4 + 3 - 6 = 1 $ | (8) |
| $ {F_{\rm{T}}} = {F_{\rm{H}}} + {F_{\rm{K}}} + {F_{\rm{A}}} = 4 $ | (9) |
式中:FT为人体-外骨骼调整模型自由度。
显然,当人体-外骨骼调整模型自由度数FT与原动件个数相等时,所设人体-外骨骼调整模型有确定运动,人机接口处被动自由度能够补偿人机之间相对滑动产生的变形和错位。
2 下肢康复外骨骼结构设计及其运动模式 2.1 下肢康复外骨骼结构设计下肢康复外骨骼通过精密可靠的机械结构发挥作用,结构设计应遵循简单、安全、轻便、易操控的基本原则。
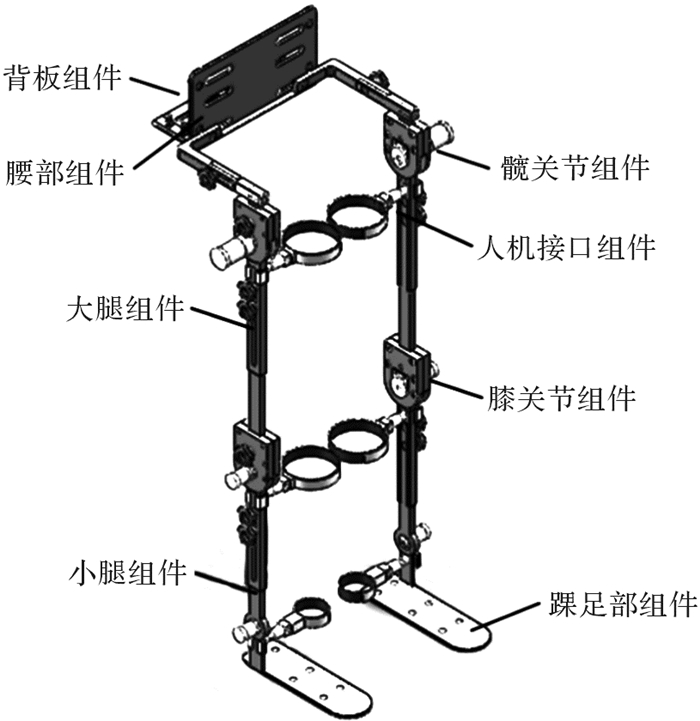
根据上文的2种人体-外骨骼模型,确定下肢康复外骨骼的原动件数和基本结构。设计时,下肢康复外骨骼左右对称,它主要由背板组件、腰部组件、髋关节组件、膝关节组件、踝足部组件、大腿组件、小腿组件以及人机接口组件构成。将髋关节屈伸运动和外展内收运动简化为轴线相交的铰链运动形式,膝关节、踝关节屈伸运动简化为单自由度铰链运动。各关节铰接,并设有角度编码盘,由伺服电机配合谐波减速器为各关节屈伸运动提供动力;髋关节外展内收运动变化范围较小,不设驱动。足部脚底板设有6个压力感应点,用于感应足部对脚底板的压力,结合各关节编码盘共同采集人体步态信息。人机接口的人机接触处材质为橡胶和弹性绷带。下肢康复外骨骼整机结构如图 6所示。
|
| 图 6 下肢康复外骨骼整机结构 Fig.6 Whole structure of lower limb rehabilitation exoskeleton |
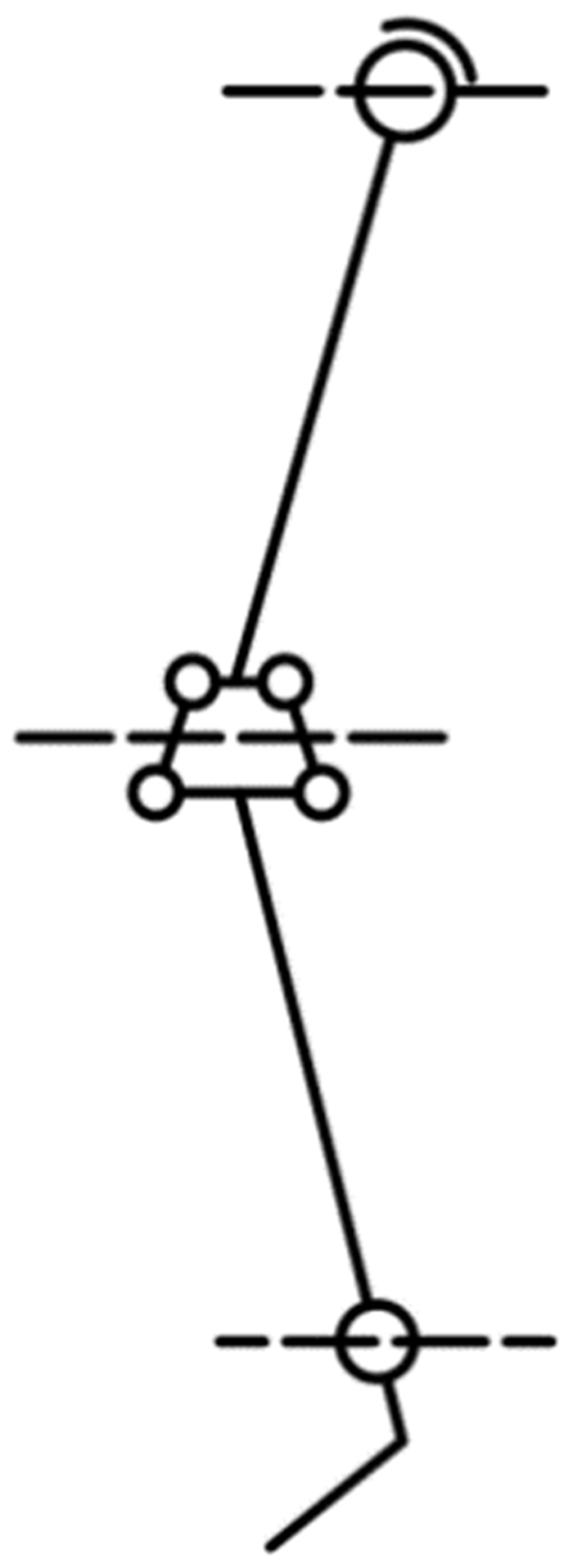
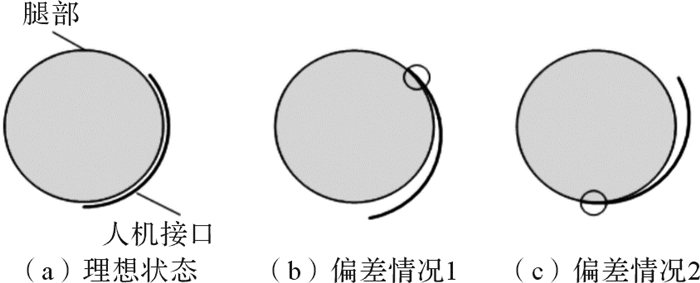
下肢康复外骨骼的人机接口处分别设有2个三维测力传感器,用于感应人机相对滑动对人体产生的压力,当人机滑动产生的压力达到预设值附近时,可通过传感器调控外骨骼系统的使用模式。具体的调控方式为:当人机滑动产生的压力大于或等于预设值时,启用被动自由度;当低于预设值时,关闭被动自由度。图 7为人机滑动偏差检测示意图,图中圆环标记部分为人机接触检测范围。理想状态下腿部与人机接口的相对位置如图 7(a)所示,两者间无相对滑动;运动过程中,腿部前后摆动,肢体与人机接口相对滑动并伴有接触,人机脱离平行状态,传感器检测到运动偏差,如图 7(b)和(c)所示。
|
| 图 7 人机滑动偏差检测示意图 Fig.7 Schematic diagram of human-machine sliding deviation detection |
根据《中国成年人人体尺寸》(GB/T 10000—1988),为满足不同体型人群的使用需求,设置下肢康复外骨骼尺寸可调,其尺寸参数如表 1所示。踝足部作为人体运动执行末端,以结构简单可靠为原则,不作尺寸调节。下肢康复外骨骼机械腿限位范围如表 2所示, 髋关节与膝关节作屈伸运动时,角度变化较大,踝关节作屈伸运动时,角度波动较小,因此主要对髋、膝关节矢状面内的屈伸运动进行限位。
| mm | ||
| 名称 | 长度调节范围 | 长度差 |
| 大腿 | 436~530 | 94 |
| 小腿 | 330~420 | 90 |
| 踝足部 | 79 | 0 |
| (°) | |||
| 运动类型 | 关节 | 姿态限位 | 行走限位 |
| 矢状面屈伸运动 | 髋关节 | -25~90 | -25~30 |
| 膝关节 | 0~90 | 0~70 | |
| 踝关节 | -15~10 | -15~10 | |
| 冠状面外展内收运动 | 髋关节 | -8~8 | -8~8 |
该外骨骼具备坐起和行走两个功能,患者由坐姿穿戴外骨骼后,转换为站姿进行康复运动,坐起过程中髋、膝转角达到90°,而行走过程中各关节的转角变化较小,为使康复训练安全可靠,通过限位块实现姿态限位到行走限位的转变。以髋关节屈伸运动为例,坐姿下髋部转动90°,人站起后,拨动限位块,使得髋关节转角可在-25°~30°范围内调节,以避免行走过程中外骨骼运动幅度超过人体运动范围极限。
2.2 下肢康复外骨骼运动模式基于人体-外骨骼运动模型和人体-外骨骼调整模型,该下肢康复外骨骼运动模式有2种:以人体-外骨骼运动模型为依据的模式1,及以人体-外骨骼调整模型为依据的模式2。
2种运动模式在使用上以降低控制难度,提高系统的安全性、可靠性为原则,运动时模式1与模式2交替使用,模式1为主要运动模式。当使用模式1时,人机接口处的被动自由度处于锁死状态,人体与外骨骼固连,由直流伺服电机为下肢康复外骨骼提供动力;当人机滑动产生的压力超过预设值时,启用模式2,在该模式下,被动自由度启动,待人机位置调节至正常范围后,人机接口处被动自由度再度被锁死,则模式1继续使用,人体进行康复运动。
3 下肢康复外骨骼运动学理论分析人体下肢行走主要发生在矢状面内,取单侧外骨骼机械腿为研究对象,在运动模式下,研究其矢状面内的运动学特性。
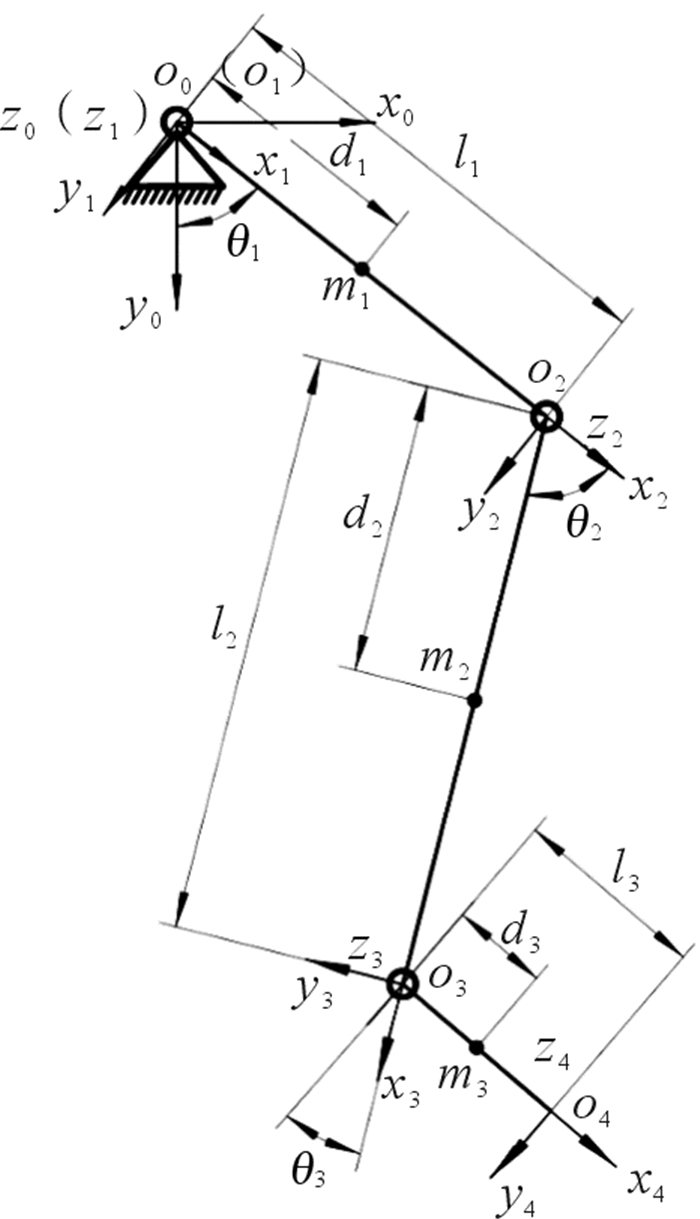
采用D-H法[14]对单侧外骨骼机械腿进行建模,单侧外骨骼机械腿连杆模型包括髋关节、膝关节、踝关节、大腿杆、小腿杆和踝足杆。分别建立符合右手规则的基坐标系和连杆坐标系,如图 8所示,其中,oi-xiyizi表示在某点建立的坐标系,o0-x0y0z0表示基坐标系,θi表示各关节转角,li表示各连杆长度,mi表示各连杆质量,di表示各连杆质心到所在关节i的距离。
|
| 图 8 单侧外骨骼机械腿连杆模型 Fig.8 Linkage model of single lateral exoskeleton mechanical leg |
根据几何法得到外骨骼机构中大腿杆质心的位置和速度为:
| $ \left\{ \begin{array}{l} {x_{o1}} = {d_1}\sin {\theta _1}\\ {y_{o1}} = {d_1}\cos {\theta _1} \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} {{\dot x}_{o1}} = {d_1}{{\dot \theta }_1}\cos {\theta _1}\\ {{\dot y}_{o1}} = - {d_1}{{\dot \theta }_1}\sin {\theta _1} \end{array} \right. $ | (11) |
同理,小腿杆质心的位置和速度为:
| $ \left\{ \begin{array}{l} {x_{o2}} = {d_2}\sin \left( {{\theta _2} - {\theta _1}} \right) + {l_1}\sin {\theta _1}\\ {y_{o2}} = {d_2}\cos \left( {{\theta _2} - {\theta _1}} \right) + {l_1}\cos {\theta _1} \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} {{\dot x}_{o2}} = {d_2}{{\dot \theta }_2}\cos \left( {{\theta _2} - {\theta _1}} \right) + {l_1}{{\dot \theta }_1}\cos {\theta _1}\\ {{\dot y}_{o2}} = - {d_2}{{\dot \theta }_2}\sin \left( {{\theta _2} - {\theta _1}} \right) - {l_1}{{\dot \theta }_1}\sin {\theta _1} \end{array} \right. $ | (13) |
踝足杆质心的位置和速度为:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{x_{o3}} = {d_3}\sin \left[ {\frac{{\rm{ \mathsf{ π} }}}{2} - \left( {{\theta _3} + {\theta _2} - {\theta _1}} \right)} \right] + }\\ {{l_2}\sin \left( {{\theta _2} - {\theta _1}} \right) + {l_1}\sin {\theta _1}} \end{array}\\ \begin{array}{*{20}{c}} {{y_{o3}} = {d_3}\cos \left[ {\frac{{\rm{ \mathsf{ π} }}}{2} - \left( {{\theta _3} + {\theta _2} - {\theta _1}} \right)} \right] + }\\ {{l_2}\cos \left( {{\theta _2} - {\theta _1}} \right) + {l_1}\cos {\theta _1}} \end{array} \end{array} \right. $ | (14) |
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{{\dot x}_{o3}} = {d_3}{{\dot \theta }_3}\cos \left[ {\frac{{\rm{ \mathsf{ π} }}}{2} - \left( {{\theta _3} + {\theta _2} - {\theta _1}} \right)} \right] + }\\ {{l_1}{{\dot \theta }_2}\cos \left( {{\theta _2} - {\theta _1}} \right) + {l_2}{{\dot \theta }_1}\cos {\theta _1}} \end{array}\\ \begin{array}{*{20}{c}} {{{\dot y}_{o3}} = - {d_3}{{\dot \theta }_3}\sin \left[ {\frac{{\rm{ \mathsf{ π} }}}{2} - \left( {{\theta _3} + {\theta _2} - {\theta _1}} \right)} \right] - }\\ {{l_1}{{\dot \theta }_2}\sin \left( {{\theta _2} - {\theta _1}} \right) - {l_2}{{\dot \theta }_1}\sin {\theta _1}} \end{array} \end{array} \right. $ | (15) |
用球面坐标表示下肢康复外骨骼机械腿的运动位置矢量,得到各连杆变换矩阵为:
| $ \mathit{\boldsymbol{T}}_1^0 = \left( {\begin{array}{*{20}{c}} {\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _1}} \right)}&{ - \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _1}} \right)}&0&0\\ {\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _1}} \right)}&{\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _1}} \right)}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right) $ | (16) |
| $ \mathit{\boldsymbol{T}}_2^1 = \left( {\begin{array}{*{20}{c}} 1&0&0&{{l_1}\cos {\theta _1}}\\ 0&1&0&{{l_1}\sin {\theta _1}}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right) $ | (17) |
| $ \mathit{\boldsymbol{T}}_3^2 = \left( {\begin{array}{*{20}{c}} {\cos {\theta _2}}&{ - \sin {\theta _2}}&0&{{l_2}\cos {\theta _2}}\\ {\sin {\theta _2}}&{\cos {\theta _2}}&0&{{l_2}\sin {\theta _2}}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right) $ | (18) |
| $ \mathit{\boldsymbol{T}}_4^3 = \left( {\begin{array}{*{20}{c}} {\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}&{ - \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}&0&{{l_3}\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}\\ {\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}&{\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}&0&{{l_3}\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2} - {\theta _3}} \right)}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right) $ | (19) |
根据末端坐标系相对于基坐标系的位姿变换,得到下肢康复外骨骼机械腿末端位姿矩阵为:
| $ \mathit{\boldsymbol{T}}_4^0 = \mathit{\boldsymbol{T}}_1^0\mathit{\boldsymbol{T}}_2^1\mathit{\boldsymbol{T}}_3^2\mathit{\boldsymbol{T}}_4^3 $ | (20) |
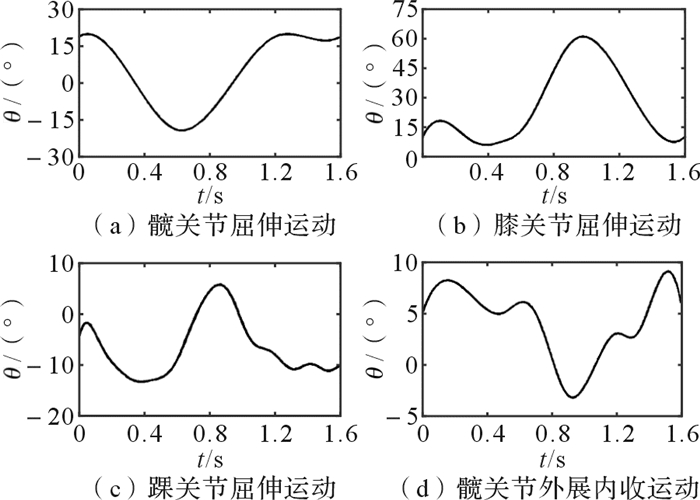
为验证下肢康复外骨骼设计的合理性,取人体一个步态周期运动时长为1.6 s,将图 9所示的外骨骼各关节运动输入数据[15]代入式(10)至(15)中,运用MATLAB对外骨骼进行运动学分析。以人体模型踝关节行走轨迹为参考,验证下肢康复外骨骼踝关节行走区域与人体踝关节行走轨迹的相容性。
|
| 图 9 一个步态周期内下肢康复外骨骼各关节输入数据 Fig.9 Each joint input data of lower limb rehabilitation exoskeleton in a gait cycle |
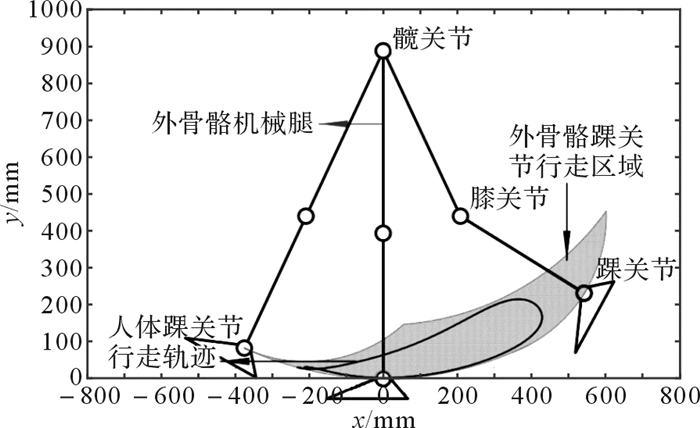
如图 10所示,灰色区域为外骨骼踝关节矢状面内行走区域,黑色曲线为人体踝关节矢状面内行走轨迹[15]。由图 10可知,外骨骼踝关节的运动幅度与人体踝关节的运动幅度类似,这表明所设计的下肢康复外骨骼在矢状面内的行走空间可以覆盖人体踝关节行走轨迹,即外骨骼满足人体运动学要求。
|
| 图 10 人机运动区域相容性检验 Fig.10 Compatibility test of human-machine movement region |
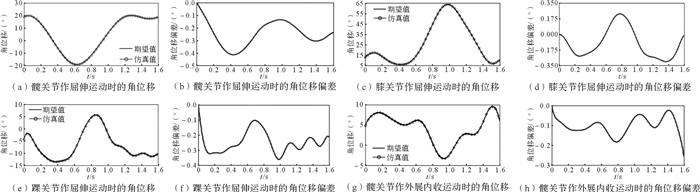
将下肢康复外骨骼简化模型转为Parasolid(*.x_t)格式并导入ADAMS,以图 9中的数据作为驱动数据,施加连接与约束,进行运动学仿真[16]。以理论角位移为期望值,调用ADAMS软件后处理模块,求取外骨骼各个关节的角位移仿真值,并与期望值进行对比分析。图 11为外骨骼髋关节作屈伸运动、膝关节作屈伸运动、踝关节作屈伸运动、髋关节作外展内收运动时各关节的角位移和角位移偏差曲线。由图可见,外骨骼各关节角位移的仿真值与期望值基本一致,但存在角位移偏差,其中,髋关节作屈伸运动时最大偏差为0.413 1°,膝关节作屈伸运动时最大偏差为0.303 9°,踝关节作屈伸运动时最大偏差为0.359 6°,髋关节作外展内收运动时最大偏差为0.244 5°。由此可见,外骨骼各关节运动角位移偏差值在外骨骼行走限位设定范围内,表明所设计的下肢康复外骨骼满足行走需求。
|
| 图 11 下肢康复外骨骼各关节角位移和角位移偏差曲线 Fig.11 Each joint angular displacement and angular displacement deviation curves of lower limb rehabilitation exoskeleton |
为验证人体-外骨骼调整模式对人体-外骨骼运动模式的补偿能力,对运动模式和调整模式设置相同的输入数据,分别进行人体-外骨骼模型运动学仿真。
取模型单侧腿为研究对象,在SolidWorks中建立简化的人体-外骨骼模型,再将模型转为Parasolid(*.x_t)格式并导入ADAMS,进行运动学仿真分析,图 12分别为人体-外骨骼的简化模型和仿真模型。设置各构件材料属性,外骨骼部分添加相应关节连接与约束,人机接触部分添加约束与接触,各关节配置驱动。运动模式下,人机接口处被动自由度锁死;调整模式下,人机接口处被动自由度启动。调用软件后处理模块,求取2种模式下人体各关节的运动曲线。

|
| 图 12 人体-外骨骼的简化模型和仿真模型 Fig.12 Simplification model and simulation model of human-exoskeleton |
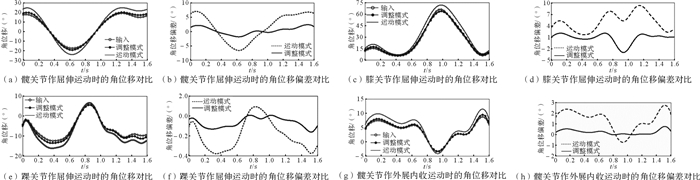
将2种模式下人体各关节的角位移数据与外骨骼各关节的输入数据作对比,同时对比2种模式下人体各关节角位移与角位移偏差仿真曲线,结果如图 13所示。由图可知,当外骨骼端输入数据相同时,调整模式下人体各关节角位移仿真值更接近预设值,调整模式下人体关节的运动规律优于运动模式下人体关节的运动规律。对比2种模式下人体各关节的最大角位移偏差,如表 3所示,调整模式下各关节的最大角位移偏差小于运动模式下的最大角位移偏差。显然,当外骨骼端输入数据相同时,调整模式能对运动模式产生的运动偏差进行一定程度的补偿。
|
| 图 13 人体-外骨骼运动和调整模式下人体各关节角位移与角位移偏差对比 Fig.13 Comparison of angular displacement and angular displacement deviation under human-exoskeleton movement and adjustment mode |
| 关节(运动) | 最大角位移偏差/(°) | ||
| 运动模式 | 调整模式 | ||
| 髋关节(屈伸运动) | 7.102 3 | 2.458 2 | |
| 膝关节(屈伸运动) | 9.342 1 | 3.016 6 | |
| 踝关节(屈伸运动) | 3.772 4 | 1.599 5 | |
| 髋关节(外展内收运动) | 1.982 7 | 0.783 7 | |
1) 针对下肢康复外骨骼因人机相对滑动产生的运动偏差,设计了具有运动模式和调整模式的下肢康复外骨骼。该下肢康复外骨骼结构简单,易于控制,避免了因人机相对滑动引起的人体二次损伤。
2) 在运动模式下,对下肢康复外骨骼进行了运动学建模与仿真,结果表明该外骨骼在矢状面内的运动空间可以包络人体末端运动轨迹,各关节角位移仿真值与期望值的变化趋势一致,各关节角位移偏差在可控范围内。
3) 基于相同的外骨骼端输入数据,分别在运动模式与调整模式下对人体-外骨骼简化模型进行了运动学仿真,并对比了2种模式下人体各关节的角位移与角位移偏差。结果表明,调整模式下人体关节的运动规律优于运动模式下人体关节的运动规律,调整模式能对运动模式产生的运动偏差进行一定程度的补偿,从理论上证实了外骨骼机构设计的合理性。基于人机闭链设计的下肢康复外骨骼机构能够较好地补偿运动偏差,避免人体二次损伤,为外骨骼的实用化设计与研究提供了理论基础。
| [1] | MENG W, LIU Q, ZHOU Z, et al. Recent development of mechanisms and control strategies for robot-assisted lower limb rehabilitation[J]. Mechatronics, 2015, 31: 132–145. DOI:10.1016/j.mechatronics.2015.04.005 |
| [2] | HIDLER J, WISMAN W, NECKEL N. Kinematic trajectories while walking within the Lokomat robotic gait-orthosis[J]. Clinical Biomechanics, 2008, 23(10): 1251–1259. DOI:10.1016/j.clinbiomech.2008.08.004 |
| [3] | TALATY M, ESQUENAZI A, BRICENO J E. Differentiating ability in users of the ReWalkTM powered exoskeleton:an analysis of walking kinematics[J]. Rehabilitation Robotics, 2013, 13(6): 1363–1369. |
| [4] | TAMEZDUQUE J, COBIANUGALDE R, KILICARSLAN A, et al. Real-time strap pressure sensor system for powered exoskeletons[J]. Sensors, 2015, 15(2): 4550–4563. DOI:10.3390/s150204550 |
| [5] | ZHANG S, WANG C, WU X, et al. Real time gait planning for a mobile medical exoskeleton with crutche[C]//Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics, Zhuhai, Dec. 6-9, 2015. |
| [6] |
李剑锋, 吴希瑶, 邓楚慧, 等.
人-机运动相容型下肢康复训练外骨骼机构的构型设计与分析[J]. 中国生物医学工程学报, 2012, 31(5): 720–728.
LI Jian-feng, WU Xi-yao, DENG Chu-hui, et al. Configuration design and analysis of the human-machine kinematically compatible type exoskeleton mechanism for lower limb rehabilitation training[J]. Chinese Journal of Biomedical Engineering, 2012, 31(5): 720–728. DOI:10.3969/j.issn.0258-8021.2012.05.011 |
| [7] | SCHIELE A, VAN FRANS C T D H. Kinematic design to improve ergonomics in human machine interaction[J]. IEEE Transactions on Neural Systems & Rehabilitation Engineering, 2006, 14(4): 456–469. |
| [8] |
李剑锋, 刘钧辉, 张雷雨, 等.
人机相容型肩关节康复外骨骼机构的运动学与灵活性分析[J]. 机械工程学报, 2018, 54(3): 46–54.
LI Jian-feng, LIU Jun-hui, ZHANG Lei-yu, et al. Kinematics and dexterity analysis of the human-machine compatible exoskeleton mechanism for shoulder joint rehabilitation[J]. Journal of Mechanical Engineering, 2018, 54(3): 46–54. |
| [9] | TORTORA Gerard J, DERRICKSON Bryan H. Principles of anatomy and physiology[M]. New Jersey: Wiley, 2011: 631-637. |
| [10] |
邵明旭, 王斐, 殷腾龙, 等.
人体下肢生物力学建模研究进展[J]. 智能系统学报, 2015, 10(4): 518–527.
SHAO Ming-xu, WANG Fei, YIN Teng-long, et al. Research progress on the human lower limb biomechanical modeling[J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 518–527. |
| [11] |
陈殿生, 宁萌, 阮子喆, 等.
电动往复式步态矫形器机构优化设计[J]. 机械工程学报, 2015, 51(21): 33–41.
CHEN Dian-sheng, NING Meng, RUAN Zi-zhe, et al. Mechanism design and optimization for electric reciprocating gait orthoses[J]. Journal of Mechanical Engineering, 2015, 51(21): 33–41. |
| [12] |
李怀仙, 程文明, 张铭奎.
基于人机偏差模型的自对齐髋关节外骨骼解耦设计与计算[J]. 机器人, 2017, 39(5): 627–637.
LI Huai-xian, CHENG Wen-ming, ZHANG Ming-kui. Decoupled design and calculation of the self-aligned hip joint exoskeletons based on the human-robot misalignment model[J]. Robot, 2017, 39(5): 627–637. |
| [13] |
张启先.
空间机构的分析与综合[M]. 北京: 机械工业出版社, 1984: 49-69.
ZHANG Qi-xian. Analysis and synthesis of space institutions[M]. Beijing: China Machine Press, 1984: 49-69. |
| [14] | DENAVIT J, HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics-Transactions of the ASME, 1955, 22: 215–221. |
| [15] | VAUGHAN C L, DAVIS B L, O'CONNOR J C. Dynamics of human gait[M]. Cape Town: Human Kinetics Publishers, 1999: 61-79. |
| [16] |
刘小龙, 赵彦峻, 葛文庆, 等.
医疗助力下肢外骨骼设计及动力学仿真分析[J]. 工程设计学报, 2016, 23(4): 327–332.
LIU Xiao-long, ZHAO Yan-jun, GE Wen-qing, et al. Design and dynamics simulation analysis of medical disabled lower limb exoskeleton[J]. Chinese Journal of Engineering Design, 2016, 23(4): 327–332. DOI:10.3785/j.issn.1006-754X.2016.04.005 |



