2. 南通国盛智能科技集团股份有限公司, 江苏 南通 226003
2. Nantong Guosheng Intelligent Technology Group Co., Ltd., Nantong 226003, China
随着航空航天飞行器、船舶机械以及模具制造等行业的迅猛发展,数控机床被广泛应用于各种大型复杂空间曲面零件的加工中[1-2]。为了满足产品技术革新和产业升级对机床高速度、高精度、高效率的加工要求,桥式龙门铣床采用工作台静止、横梁移动的结构设计方案。在机床加工过程中,横梁作为主要运动部件,不仅要能承受自身和滑枕等关键零部件的重量,还应具有良好的动态性能以实现机床的快速平稳运行。因此,设计合理的横梁结构方案,满足横梁的静动态性能要求,并实现横梁的轻量化设计,对机床整机性能的提高至关重要。
近年来,随着有限元分析技术的不断发展和完善,机床部件的设计已逐步从传统的经验设计转向基于计算机虚拟建模及仿真分析的结构优化设计。孙芹等[3]采用基于变密度法的拓扑优化设计方法,调整横梁筋板布置,提高了横梁的结构刚性,实现了横梁的轻量化设计。庞锦平等[4]采用模糊综合评价法、TOPSIS(technique for order preference by similarity to an ideal solution)法和灰色关联分析法对磨床横梁结构的多种方案进行对比分析,选出了3种评价方法下的最优方案,比较得出采用模糊综合评价法效果最优,采用TOPSIS法效果最差。Liu等[5]建立了4种横梁结构的优选模型,并进行静动态性能参数的有限元分析,并通过灰色关联分析法和层次分析法确定了优选设计方案。这些研究虽然促进了横梁设计与优选理论的发展,但仅仅针对方案优选阶段,并没有进一步对与横梁设计相关的尺寸进行优化,因而研究结果缺乏工程实用性。为此,本文以桥式龙门铣床横梁为研究对象,采用CAD/CAE集成仿真技术对横梁结构进行三维建模和有限元分析。在此基础上设计正交试验并运用改进的模糊综合评价法对有限元仿真数据进行处理,确定横梁优选方案,并对其关键设计尺寸进行灵敏度分析与优化,确定具体的设计尺寸并用于指导机床横梁的制造和生产。
1 横梁结构正交试验设计与有限元分析 1.1 横梁结构正交试验设计 1.1.1 设计因素、水平与评价指标为了提高横梁结构设计与优化效率,本文基于传统的横梁设计理念并结合工程实际应用特点,主要考虑以下因素进行横梁结构设计。
1) 横梁结构布局形式。桥式龙门铣床的横梁结构布局形式决定着横梁上载荷的施加方式,它主要包括2种形式,如图 1(a)和(b)所示。一种是滑座组件安装在横梁一侧导轨上,本文定义为侧挂式;另一种是箱中箱式,采用对称结构,滑座组件安装在横梁中间位置。

|
| 图 1 横梁结构布局形式及导轨类型 Fig.1 Structure layout and guideway type of crossbeam |
2) 导轨类型。如图 1所示的横梁导轨类型分硬轨和线轨两种。硬轨接触面积大,能够承受更大的工作载荷,可使机床运行更加平稳;线轨相较于硬轨而言,承载能力小,但能承受较快的机床运行速度,精度高,装配与更换方便。根据桥式龙门铣床加工对象的要求,主要选取硬轨与全滚柱直线导轨作为设计因素。
3) 筋板结构与厚度。合理地选择筋板结构与厚度是实现横梁轻量化设计的基础,有利于提高横梁静动态性能。根据当前机床制造企业常使用的桥式龙门横梁类型,选定初始参数20 mm和25 mm作为筋板厚度,初步设计了井型、菱型、O型、V型四种筋板结构,如图 2所示。

|
| 图 2 横梁筋板结构 Fig.2 Rib structure of crossbeam |
为了较为准确、全面地反映各因素水平参数组合下横梁结构的优劣,确定横梁优选方案,选择质量和外形体积作为评价指标来反映横梁的轻量化水平;选择最大变形量和最大等效应力作为评价指标来反映横梁的静力学性能;选择一阶固有频率作为评价指标来反映横梁的抗振性。
1.1.2 正交试验方案正交试验设计[6-7]是基于工程经验与专业理论的数理统计方法。利用正交表挑选出具有代表性的因素水平参数组合进行横梁结构设计,可以较为全面地反映多因素多水平条件下横梁所具有的综合性能指标,降低结构设计难度。根据1.1.1节所述,选取横梁的结构布局形式、导轨类型、筋板结构与厚度作为正交试验的因素,设计了如表 1所示的四因素混合水平正交表,并依据确定的因素水平规划横梁结构的正交试验方案,如表 2所示。
| 水平 | 因素 | |||
| 筋板结构 | 筋板厚/mm | 横梁结构布局 | 导轨类型 | |
| 1 | 井型 | 20 | 箱中箱 | 线轨 |
| 2 | 菱型 | 25 | 侧挂式 | 硬轨 |
| 3 | O型 | |||
| 4 | V型 | |||
| 方案 | 因素水平 | |||
| 筋板结构 | 筋板厚 | 横梁结构布局 | 导轨类型 | |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 2 | 1 | 1 | 2 |
| 4 | 2 | 2 | 2 | 1 |
| 5 | 3 | 1 | 2 | 1 |
| 6 | 3 | 2 | 1 | 2 |
| 7 | 4 | 1 | 1 | 2 |
| 8 | 4 | 2 | 2 | 1 |
结合企业对桥式龙门铣床横梁的规格要求,运用SolidWorks建立各横梁结构正交试验方案的三维参数化模型。为提高分析结果的准确性,在建模过程中对横梁结构作适当简化,去除一些不必要的细小特征,再将简化模型导入ANSYS Workbench中进行有限元分析。
分析时,将横梁主体材料设置为灰铸铁(HT300),线轨材料设置为碳素钢(55),并对各材料的密度、弹性模量等属性参数进行设置;根据横梁结构形状特点,采用软件的智能网格划分和人工干预相结合的方式进行网格设置;按照横梁受力最恶劣的极限工况[8],即滑座组件运行到横梁导轨中间位置,滑枕伸出最长时,设置约束与载荷条件,得到如图 3所示的横梁结构有限元分析模型。

|
| 图 3 横梁结构有限元分析模型 Fig.3 Finite element analysis model of crossbeam structure |
在图 3中,仅以横梁结构正交试验设计中的2个方案作为示例进行网格划分,不同结构模型的节点数和单元数略有不同,图 3(a)模型共有874 581个节点、483 914个单元,图 3(b)模型共有568 623个节点、318 502个单元。
施加约束与载荷条件时,其约束和载荷的加载位置以及载荷的大小仅与横梁的结构布局形式相关。施加约束时,考虑到侧挂式横梁左右两侧固定安装在滑板上,由滑板带动它在立柱上沿水平方向运动,因此在横梁与滑板的结合面处施加固定约束;箱中箱式横梁通过滑块与全滚柱直线导轨相连,并由两侧丝杆驱动,因此在横梁与滑块结合面处施加固定约束;两侧与丝杆配合连接处施加圆柱面约束,限制轴向和径向位移。施加载荷时,对于2种结构布局形式的横梁,将相同质量的滑座组件对横梁的作用效果等效为横梁导轨上所受到的力进行载荷的施加;同时为模拟自重对横梁模型分析的影响,在载荷设定时,还应在竖直方向上施加1g的重力加速度。
1.2.2 静动态性能仿真分析根据正交试验设计确定的8种横梁结构方案,分别建立相对应的横梁有限元分析模型,并进行静动态特性分析,最终求解得到横梁的轻量化、静力学性能和抗振性的指标值,结果如表 3所示。
| 方案 | 因素 | 评价指标 | ||||||||
| 筋板结构 | 筋板厚/mm | 横梁结构布局 | 导轨类型 | 质量U1/kg | 外形体积 U2/m3 |
最大变形量 U3/μm |
最大等效 应力U4/MPa |
一阶固有 频率U5/Hz |
||
| 1 | 井型 | 20 | 箱中箱式 | 线轨 | 3 989 | 3.425 | 36.905 | 4.816 7 | 98.45 | |
| 2 | 井型 | 25 | 侧挂式 | 硬轨 | 5 753 | 4.709 | 39.010 | 3.459 6 | 101.52 | |
| 3 | 菱型 | 20 | 箱中箱式 | 硬轨 | 4 760 | 3.644 | 39.199 | 5.480 5 | 100.48 | |
| 4 | 菱型 | 25 | 侧挂式 | 线轨 | 5 797 | 4.202 | 34.309 | 5.273 3 | 121.05 | |
| 5 | O型 | 20 | 侧挂式 | 线轨 | 5 899 | 4.202 | 29.565 | 4.506 7 | 118.95 | |
| 6 | O型 | 25 | 箱中箱式 | 硬轨 | 5 364 | 3.644 | 36.034 | 4.619 3 | 101.03 | |
| 7 | V型 | 20 | 侧挂式 | 硬轨 | 4 940 | 4.709 | 65.740 | 5.355 1 | 86.42 | |
| 8 | V型 | 25 | 箱中箱式 | 线轨 | 4 139 | 3.425 | 39.722 | 6.620 3 | 94.50 | |
由于横梁结构正交试验方案各评价指标的含义和作用不同,且不同指标间具有不同的量纲和数量级,因此,仅对横梁静动态性能仿真结果数据进行简单的直观分析,很难确定各方案的优劣。为了实现横梁结构设计方案的多目标优选,采用改进的模糊综合评价法对仿真数据进行处理。
2.1 评价指标权重的确定评价指标权重的确定是模糊综合评价的关键部分,其值的准确性直接影响优选结果的可靠性。而传统的模糊综合评价法仅采用超标赋权法,具有较强的个人主观性,优选结果有时会存在较大偏差[9-10]。为了保证评价结果的客观性,同时降低仿真数据的误差影响,本文采用基于熵值法与模糊层次分析法的组合赋权法进行评价指标权重赋值,形成优势互补的组合权重。
2.1.1 熵值法权重计算假设S= S1, S2, …, Sn为横梁正交试验设计得到的n个设计方案,U= U1, U2, …, Um为设计方案的m个评价指标,aij表示第i个设计方案的第j个指标的仿真数据,建立评价指标矩阵A =(aij)n×m。
对评价指标矩阵 A 进行无量纲化处理:
| $ {{a'}_{ij}} = \frac{{{a_{ij}}}}{{\sum\limits_{i = 1}^n {{a_{ij}}} }} $ | (1) |
各评价指标熵值法权重W = [w1 w2 … wm],
其中:
| $ {w_j} = \frac{{1 - {e_j}}}{{\sum\limits_{j = 1}^m {\left( {1 - {e_j}} \right)} }} $ | (2) |
式中:
根据模糊层次分析法原理确定各评价指标间的相互优先级关系,并以0.1~0.9标度法[11]作为判断准则对各指标进行两两比较,建立权重判断矩阵 B =(bhj)m×m。
由文献[12]推导的公式求解判断矩阵,得到矩阵 B 的权重 W ′= w′1 w′2 … w′m, 其中:
| $ {{w'}_h} = \frac{{\sum\limits_{j = 1}^m {{b_{hj}}} + \frac{m}{2} - 1}}{{m\left( {m - 1} \right)}} $ | (3) |
对判断矩阵进行相容性检验[13],令:
| $ {{w'}_{hj}} = \frac{{{{w'}_h}}}{{{{w'}_h} + {{w'}_j}}},\;\;\;\;h,j = 1,2, \cdots ,m $ | (4) |
则 S =(w′hj)m×m 为判断矩阵 B 的特征矩阵。
B 和 S 的相容性指标为:
| $ I\left( {\mathit{\boldsymbol{B}},\mathit{\boldsymbol{S}}} \right) = \frac{1}{{{m^2}}}\sum\limits_{h = 1}^m {\sum\limits_{j = 1}^m {\left| {{b_{hj}} + {{w'}_{hj}} - 1} \right|} } $ | (5) |
对于决策者的态度 α,当相容性指标 I(B, S)≤α时,认为该判断矩阵是满意一致的。α越小,矩阵相容性越高,一般取α=0.2。
假设有 t个专家,则有模糊判断矩阵 Bk=(bhjk)m×m,k=1, 2, …, t,对应的权重向量集合为W′k=[W′1W′2 … W′t],特征矩阵Sk=(w′hjk)m×m。若t 个判断矩阵 Bk以及各判断矩阵间符合满意一致性,则模糊层次分析法权重为:
| $ {\mathit{\boldsymbol{W}}^ * } = \left[ {\begin{array}{*{20}{c}} {w_1^ * }&{w_2^ * }& \cdots &{w_m^ * } \end{array}} \right] = \frac{1}{t}\sum\limits_{k = 1}^t {{{\mathit{\boldsymbol{W'}}}_k}} $ | (6) |
利用乘法合成的归一化方法[14]对模糊层次分析法和熵值法确定的主、客观权重进行组合计算,得模糊综合评价法权重为:
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{p_1}}&{{p_2}}& \cdots &{{p_m}} \end{array}} \right] $ | (7) |
式中:
构建模糊关系矩阵时,以单一评价指标对各横梁设计方案进行评价,比较各方案的相对优劣程度。将每一个评价指标Uj对设计方案Si的评级记为rj,则:
| $ {\mathit{\boldsymbol{r}}_j} = {\left[ {\begin{array}{*{20}{c}} {{r_{1j}}}&{{r_{2j}}}& \cdots &{{r_{nj}}} \end{array}} \right]^{\rm{T}}} $ | (8) |
式中:rj为U的模糊子集,j=1, 2, …, m。
对于不同的评价指标,有的是越大越优,如横梁的一阶固有频率,有的则是越小越优,如横梁的质量、外形体积、最大变形量和最大等效应力。在对模糊子集中各方案的优劣等级进行量化取值时,对两类评价指标分别考虑:
| $ {\mathit{\boldsymbol{r}}_j} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{a}}_j} - \min {\mathit{\boldsymbol{a}}_j}}}{{\max {\mathit{\boldsymbol{a}}_j} - \min {\mathit{\boldsymbol{a}}_j}}},}&{越大越优指标}\\ {\frac{{\max {\mathit{\boldsymbol{a}}_j} - {\mathit{\boldsymbol{a}}_j}}}{{\max {\mathit{\boldsymbol{a}}_j} - \min {\mathit{\boldsymbol{a}}_j}}},}&{越小越优指标} \end{array}} \right. $ | (9) |
式中:aj表示第j个评价指标对应的n个横梁设计方案仿真数据集合,aj=(a1j, a2j, …, anj)。
将m个评价指标分别对n个横梁设计方案作出评价,得到每一评价指标对应的各方案优劣等级的单指标评价矩阵,并组合构成模糊关系矩阵R。
| $ \mathit{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}}\\ \vdots & \vdots &{}& \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array}} \right]^{\rm{T}}} $ | (10) |
对模糊算子采用加权平均的运算法则[15],得到模糊综合评价模型为:
| $ \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{P}} \circ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{c_1}}&{{c_2}}& \cdots &{{c_n}} \end{array}} \right] $ | (11) |
式中:
根据ci的大小可对设计方案进行优劣排序,确定横梁结构设计优选方案。
2.3 最优参数组合的确定与讨论根据表 3中的仿真数据及式(1)、(2)计算得到熵值法权重为:
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {0.202}&{0.202}&{0.193}&{0.199}&{0.203} \end{array}} \right] $ |
采用模糊层次分析法计算指标权重时,邀请2位长期从事数控机床开发和应用的专家按照0.1~0.9标度法对各评价指标进行两两比较,得到模糊判断矩阵。为便于矩阵的表达,以表格形式呈现,具体如表 4所示。
| 目标层 | U1 | U2 | U3 | U4 | U5 |
| U1 | (0.5, 0.5) | (0.5, 0.6) | (0.6, 0.6) | (0.7, 0.6) | (0.7, 0.7) |
| U2 | (0.5, 0.4) | (0.5, 0.5) | (0.6, 0.5) | (0.7, 0.7) | (0.7, 0.7) |
| U3 | (0.4, 0.4) | (0.4, 0.5) | (0.5, 0.5) | (0.6, 0.6) | (0.6, 0.6) |
| U4 | (0.3, 0.4) | (0.3, 0.3) | (0.4, 0.4) | (0.5, 0.5) | (0.5, 0.6) |
| U5 | (0.3, 0.3) | (0.3, 0.3) | (0.4, 0.4) | (0.5, 0.4) | (0.5, 0.5) |
根据式(3)至式(5)分别计算出2位专家确定的评价指标权重为:
| $ {{\mathit{\boldsymbol{W'}}}_1} = \left[ {\begin{array}{*{20}{c}} {0.180}&{0.180}&{0.160}&{0.140}&{0.140} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{W'}}}_2} = \left[ {\begin{array}{*{20}{c}} {0.180}&{0.172}&{0.164}&{0.148}&{0.136} \end{array}} \right] $ |
B1与S1的相容性指标为:
| $ I\left( {{\mathit{\boldsymbol{B}}_1},{\mathit{\boldsymbol{S}}_1}} \right) = 0.125 < 0.2 $ |
B2与S2的相容性指标为:
| $ I\left( {{\mathit{\boldsymbol{B}}_2},{\mathit{\boldsymbol{S}}_2}} \right) = 0.124 < 0.2 $ |
故可判断矩阵B1和B2都是满意一致的,其对应的评价指标权重W′1、W′2的分配是合理的。
同时,检验矩阵B1和B2之间的满意相容性为:
| $ I\left( {{\mathit{\boldsymbol{B}}_1},{\mathit{\boldsymbol{B}}_2}} \right) = 0.192 < 0.2 $ |
因而可由公式(6)求得模糊层次分析权重为:
| $ {\mathit{\boldsymbol{W}}^ * } = \left[ {\begin{array}{*{20}{c}} {0.180}&{0.176}&{0.162}&{0.144}&{0.138} \end{array}} \right] $ |
并依据式(7)求得组合权重为:
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.227}&{0.223}&{0.196}&{0.179}&{0.175} \end{array}} \right] $ |
由式(8)至式(10)计算得到的模糊关系矩阵为:
| $ \mathit{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{c}} {1.000}&{1.000}&{0.797}&{0.571}&{0.347}\\ {0.076}&{0.000}&{0.739}&{1.000}&{0.436}\\ {0.596}&{0.829}&{0.734}&{0.361}&{0.406}\\ {0.053}&{0.395}&{0.869}&{0.426}&{1.000}\\ {0.000}&{0.395}&{1.000}&{0.669}&{0.939}\\ {0.280}&{0.829}&{0.821}&{0.633}&{0.422}\\ {0.502}&{0.000}&{0.000}&{0.400}&{0.000}\\ {0.921}&{1.000}&{0.719}&{0.000}&{0.233} \end{array}} \right]^{\rm{T}}} $ |
则由式(11)可得横梁设计方案评价结果为:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {0.769}&{0.418}&{0.599}&{0.522}&{0.568}&{0.597}&{0.186}&{0.613} \end{array}} \right] $ |
从而可确定参数组合为“箱中箱-井型-20 mm-线轨”的横梁结构设计方案1为优选方案。
通过优选方案与表 3中其它方案的性能指标数据对比发现,优选方案的质量、外形体积指标数据在所有方案中为最优,最大变形量和最大等效应力在横梁正交设计方案中排在第4位,而一阶固有频率指标数据排在第6位,且靠近横梁最大激振频率范围[16],在机床运行过程中有可能发生共振。由此可知,改进的模糊综合评价法虽综合考虑了不同评价指标对于优选结果的重要程度以及同一评价指标下各方案的优劣等级,大大提高了优选结果的客观性和可靠性,但该方法所确定的横梁结构方案只是综合属性最优,而非所有指标数据均达到最优,其后续仍具有一定的优化设计空间。为尽量提高横梁的各项指标,继续对横梁优选方案进行进一步的优化。
3 横梁优选方案的关键尺寸优化通过前文所述的正交试验设计及改进的模糊综合评价法确定了横梁的主要结构形式,为后续的优化奠定了基础。由于所选的因素除筋板厚度外皆为定性因素,且筋板厚度的大小是选取了离散变量而未将连续区间上的变量数据纳入试验水平,故在横梁优选方案后续的优化中可针对横梁关键设计尺寸进行优化设计,确定具体数值。
考虑到横梁优选方案与其它方案在静力学性能和抗振性能上偏弱,优先对横梁最大变形量、最大等效应力以及一阶固有频率影响较大的尺寸进行优化设计。同时,由于自重所引起的变形量在总变形量中仍占有一定比重,仍要尽可能地减小横梁质量。而由于机床规格及自身结构形式的限制,外形体积指标优化时要保证整体外形尺寸不变。
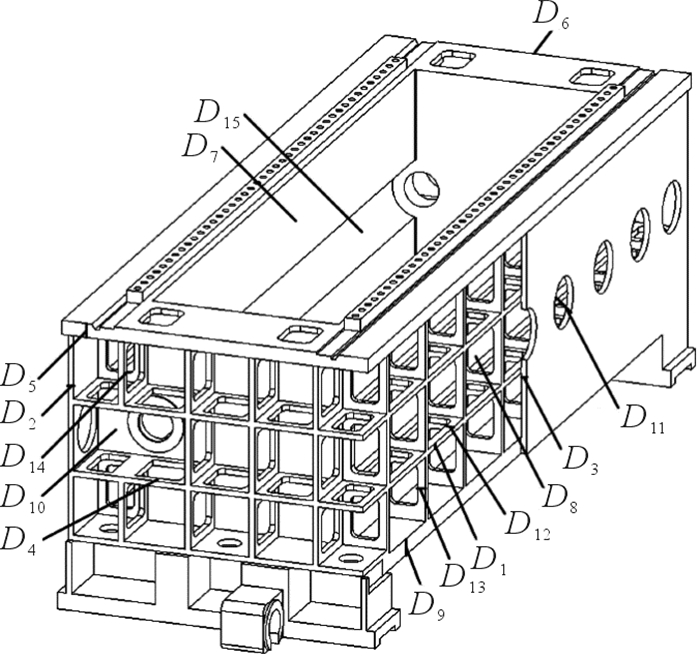
3.1 设计尺寸灵敏度分析与优化针对横梁优选方案的结构特点,初步选取如图 4所示的15个关键尺寸作为待优化尺寸,分别为筋板厚D1、后箱体外壁厚D2、前箱体外壁厚D3、左右箱体水平开孔边距D4、上壁厚D5、左右箱体外壁厚D6、后箱体内壁厚D7、前箱体内壁厚D8、下壁厚D9、左右箱体内壁厚D10、砂孔直径D11、前后箱体水平开孔边距D12、前后箱体竖直开孔边距D13、左右箱体竖直开孔边距D14和弧形槽壁厚D15。
|
| 图 4 横梁关键设计尺寸选择 Fig.4 Selection of key design size for crossbeam |
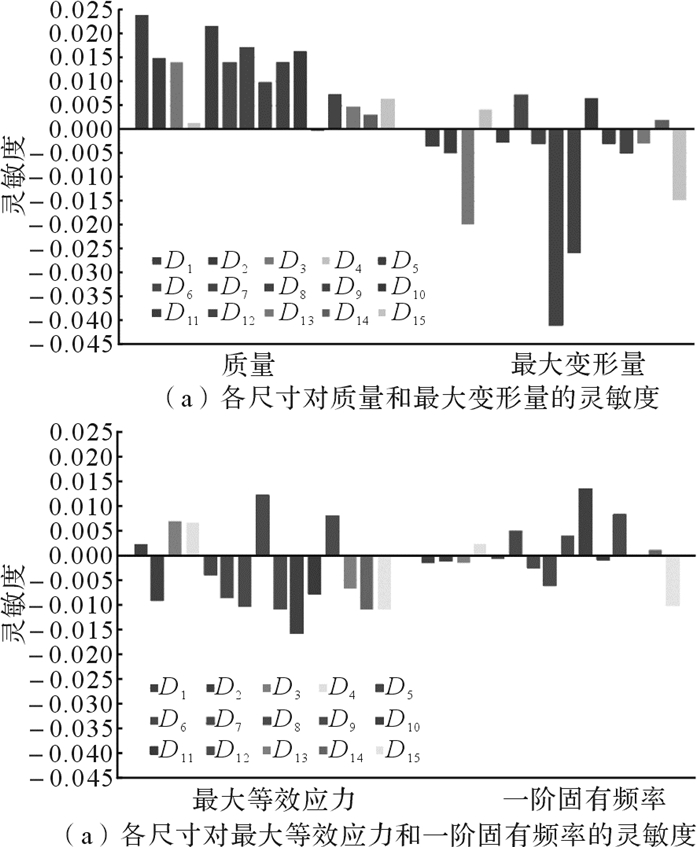
完成设计尺寸定义后,利用ANSYS Workbench优化模块中的中心复合设计自动生成各尺寸取值范围,并建立15个优化设计尺寸与质量、最大变形量、最大等效应力和一阶固有频率这4个优化目标之间的多目标函数关系,得到287组样本点。通过计算每组样本点对应的各优化目标值,获得各尺寸对优化目标的灵敏度,分析结果如图 5所示。
|
| 图 5 横梁各设计尺寸的灵敏度分析结果 Fig.5 Sensitivity analysis result of crossbeam design size |
图 5中,灵敏度为正值,表示设计尺寸增大时优化目标值会相应增大;为负值,表示设计尺寸增大时优化目标值会相应减小。因而灵敏度大小与正负无关,其大小是指绝对值的大小[17-18]。通过灵敏度分析发现,D4、D11、D12和D13对各优化目标的灵敏度非常小,优化时可忽略不计;D1、D2、D5和D6对质量的灵敏度较大,且为正值,但对其它优化目标的灵敏度较小,因而在设定取值范围时,可适当降低其取值下限;D14对最大等效应力的灵敏度较大,且为负值,而对其它优化目标的灵敏度较小,因而在设定取值范围时,可适当提高其取值上限;其余设计尺寸的变化对各优化目标有着不同程度的影响,且均不可忽略,尤其是D3、D8和D9三个对优化目标灵敏度较大的设计尺寸,其取值范围应适当增大。
根据各设计尺寸的灵敏度分析结果并结合企业机床设计数据库资料,对中心复合设计自动生成的设计尺寸的取值范围((90%~110%)初始值)进行调整,得到最终待优化的设计尺寸及其取值范围,如表 5所示。
| mm | ||
| 参数 | 初始值 | 变化范围 |
| D1 | 20 | 12~22 |
| D2 | 20 | 12~22 |
| D3 | 20 | 15~25 |
| D5 | 50 | 35~55 |
| D6 | 20 | 12~22 |
| D7 | 25 | 20~30 |
| D8 | 25 | 15~35 |
| D9 | 50 | 40~60 |
| D10 | 30 | 22~38 |
| D14 | 30 | 27~45 |
| D15 | 25 | 20~30 |
根据横梁结构设计方案优选结果,在对表 5中最终确定的11个关键设计尺寸进行优化时,首先设置尺寸优化的重要级别,将优化目标“最大变形量” “最大等效应力”和“一阶固有频率”设置为重要,“质量”设置为一般,并对各目标设置约束条件,保证优化设计后各目标值均优于优化前。经优化分析后,得到最佳优化设计点。由于最佳优化设计点是根据多组设计点计算结果拟合得到的,其尺寸精度在实际生产过程中很难达到,故需要对优化设计点的尺寸进行圆整,并将圆整后的参数代入验证。设计尺寸圆整结果如表 6所示。
| mm | ||
| 参数 | 优化值 | 实际尺寸 |
| D1 | 18.104 | 18 |
| D2 | 16.853 | 17 |
| D3 | 21.795 | 22 |
| D5 | 48.18 | 48 |
| D6 | 19.295 | 19 |
| D7 | 23.31 | 23 |
| D8 | 33.509 | 34 |
| D9 | 48.554 | 49 |
| D10 | 36.462 | 36 |
| D14 | 34.983 | 35 |
| D15 | 23.081 | 23 |
根据圆整结果对横梁有限元分析模型进行修改,并重新建立横梁有限元分析模型进行验证,分析结果如图 6所示,并与优选出的横梁结构设计方案1(见表 3)的静动态性能仿真分析结果进行对比,如表 7所示。

|
| 图 6 尺寸优化后横梁静动态性能有限元分析结果 Fig.6 Finite element analysis of static and dynamic performance of crossbeam after size optimization |
| 优化目标 | 优化前 | 优化后 | 变化量 | 等级变化 |
| 质量/kg | 3 989 | 3 931 | -58 | 1→1 |
| 外形体积/m3 | 3.425 | 3.425 | 0 | 1→1 |
| 最大变形量/μm | 36.905 | 29.490 | -7.415 | 4→1 |
| 最大等效应力/MPa | 4.816 7 | 2.877 3 | -1.939 4 | 4→1 |
| 一阶固有频率/Hz | 98.45 | 106.63 | 8.18 | 6→3 |
从表 7可知,通过对横梁优选方案的关键设计尺寸进行优化,横梁质量减小了58 kg,优劣等级排序仍保持在第1等级;最大变形量和最大等效应力分别减小了20.1%和40.3%,等级排序由第4等级上升到第1等级;一阶固有频率提高了8.3%,等级排序由第6等级上升到第3等级。因而,尺寸优化后横梁优选方案的静力学性能和抗振性能得到明显改善,并实现了轻量化设计;且除一阶固有频率指标外,其余评价指标优劣等级在8个横梁正交试验设计方案中排在第1位,故所确定的横梁结构设计方案1及其优化的关键设计尺寸可作为横梁结构设计最优方案用于实际的机床横梁制造。按最优方案制造的横梁已投入实际应用,如图 7所示。

|
| 图 7 最优结构横梁在实际中的应用 Fig.7 Application of crossbeam with optimal structure in practice |
1) 本文针对桥式龙门铣床横梁多因素多水平的结构设计特点,采用正交试验设计方法从32种参数组合中挑选出8种具有代表性的参数组合作为横梁结构设计方案,在一定程度上提高了设计效率。通过三维建模和有限元仿真分析获得设计方案的评价指标数据,为横梁设计方案的优选以及后续的优化奠定了基础。
2) 运用改进的模糊综合评价法进行横梁结构设计方案的多目标优选。将熵值法与模糊层次分析法相结合进行评价指标权重赋值,形成优势互补的组合权重;在客观仿真数据的基础上,对各评价指标数据作区分处理,获得同一评价指标下各方案的优劣等级,并建立模糊关系矩阵。综合考虑指标权重与方案优劣等级,确定了“箱中箱式-井型-20 mm-线轨”的横梁结构设计方案作为优选方案,并对其关键设计尺寸进行了灵敏度分析与优化,得到了具体的设计尺寸。优化后,横梁的静动态性能得到明显改善,并实现了轻量化设计,为数控机床其它关键零部件的设计提供了有益参考。
| [1] | YANG J X, ALTINTAS Y. A generalized on-line estimation and control of five-axis contouring errors of CNC machine tools[J]. International Journal of Machine Tools & Manufacture, 2015, 88: 9–23. |
| [2] |
韩振宇, 王瀚, 邵忠喜, 等.
基于有限差分法的重型龙门铣床大跨距横梁重力变形曲线计算方法[J]. 计算机集成制造系统, 2016, 22(6): 1494–1502.
HAN Zhen-yu, WANG Han, SHAO Zhong-xi, et al. Finite difference method based calculation of gravity deformation curve of large span of gantry-type milling machine[J]. Computer Integrated Manufacturing Systems, 2016, 22(6): 1494–1502. |
| [3] |
孙芹, 张进生, 刘伟虔, 等.
基于拓扑优化的龙门加工中心横梁轻量化设计[J]. 组合机床与自动化加工技术, 2016(6): 8–11.
SUN Qin, ZHANG Jin-sheng, LIU Wei-qian, et al. Lightweight design of the gantry machining center beam based on topology optimization[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(6): 8–11. |
| [4] |
庞锦平, 陈永亮, 刘谱, 等.
立式磨床横梁结构优选设计比较研究——基于模糊综合评价法、TOPSIS法和灰色关联分析法[J]. 工程设计学报, 2013, 20(2): 89–96.
PANG Jin-ping, CHEN Yong-liang, LIU Pu, et al. A comparative study on priority design of beam of vertical grinding machine:based on fuzzy comprehensive evaluation method, TOPSIS ang grey correlation method[J]. Chinese Journal of Engineering Design, 2013, 20(2): 89–96. DOI:10.3785/j.issn.1006-754X.2013.02.002 |
| [5] | LIU S H, LI Y, LIAO Y L, et al. Structural optimization of the cross-beam of a gantry machine tool based on grey relational analysis[J]. Structural & Multidisciplinary Optimization, 2014, 50(2): 297–311. |
| [6] |
袁江, 周成一, 沈亚峰, 等.
基于正交设计的主轴径向跳动测试工况研究[J]. 组合机床与自动化加工技术, 2017(3): 21–23, 27.
YUAN Jiang, ZHOU Cheng-yi, SHEN Ya-feng, et al. Research on test condition of spindle radial motion errors based on orthogonal design[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2017(3): 21–23, 27. |
| [7] | MAO H J, SHU M, LI C, et al. Optimization design for beam structures of rail weld CNC fine milling machine based on ANSYS Workbench[J]. Applied Mechanics & Materials, 2015, 716-717(4): 817–824. |
| [8] |
许丹, 刘强, 袁松梅, 等.
一种龙门式加工中心横梁的动力学仿真研究[J]. 振动与冲击, 2008, 27(2): 68–172.
XU Dan, LIU Qiang, YUAN Song-mei, et al. Dynamics simulation for a gantry machine center beam[J]. Journal of Vibration and Shock, 2008, 27(2): 68–172. |
| [9] |
夏红梅, 甄文斌, 曾文.
果蔬采摘机构构型方案的模糊综合评价[J]. 机械科学与技术, 2014, 33(2): 178–182.
XIA Hong-mei, ZHEN Wen-bin, ZENG Wen. Fuzzy comprehensive evaluation for the configuration scheme of fruit and vegetable picking mechanism[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014, 33(2): 178–182. |
| [10] | YANG Z Y, ZHU X C, JIA Y Z, et al. Fuzzy-comprehensive evaluation of use reliability of CNC machine[J]. Key Engineering Materials, 2011, 464: 374–378. DOI:10.4028/www.scientific.net/KEM.464 |
| [11] |
李磊, 汪永超, 唐雨, 等.
基于模糊层次分析法的机械材料选择[J]. 组合机床与自动化加工技术, 2015(11): 8–12.
LI Lei, WANG Yong-chao, TANG Yu, et al. Mechanical material selection based on FAHP[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(11): 8–12. |
| [12] |
徐泽水.
模糊互补判断矩阵排序的一种算法[J]. 系统工程学报, 2001, 16(4): 311–314.
XU Ze-shui. Algorithm for priority of fuzzy complementary judgement matrix[J]. Journal of System Engineering, 2001, 16(4): 311–314. DOI:10.3969/j.issn.1000-5781.2001.04.012 |
| [13] |
王宇, 汪永超, 牛印宝, 等.
基于模糊层次分析法的数控机床设备优化选择[J]. 组合机床与自动化加工技术, 2014(11): 133–136.
WANG Yu, WANG Yong-chao, NIU Yin-bao, et al. Optimization selection of CNC machine tool equipment based on FAHP[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014(11): 133–136. |
| [14] |
鞠家全, 邱自学, 任东, 等.
采用灰色理论和组合赋权法的机床立柱设计与研究[J]. 机械科学与技术, 2017, 36(9): 1388–1395.
JU Jia-quan, QIU Zi-xue, REN Dong, et al. Design and research for column of machining tool using grey theory & combination weight[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(9): 1388–1395. |
| [15] |
王伟, 李晴朝, 康文俊, 等.
基于综合评价体系的五轴数控机床加工性能评价和误差溯源方法[J]. 机械工程学报, 2017, 53(21): 149–157.
WANG Wei, LI Qing-zhao, KANG Wen-jun, et al. Method of machining error tracing and processing performance evaluation for five-axis CNC machine tool based on the comprehensive evaluation system[J]. Journal of Mechanical Engineering, 2017, 53(21): 149–157. |
| [16] |
鞠家全, 邱自学, 崔德友, 等.
基于正交试验的机床移动横梁多目标优化设计[J]. 机械强度, 2018, 40(2): 356–362.
JU Jia-quan, QIU Zi-xue, CUI De-you, et al. Multi-targets optimization design for moving crossbeam of machine tool based on orthogonal experimental method[J]. Journal of Mechanical Strength, 2018, 40(2): 356–362. |
| [17] |
李健, 徐敏, 张宝.
基于模态和灵敏度的主轴箱有限元分析与优化设计[J]. 组合机床与自动化加工技术, 2016(10): 51–54.
LI Jian, XU Min, ZHANG Bao. Finite element analysis and optimal design of the spindle based on modal and sensitivity[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(10): 51–54. |
| [18] |
胡小舟, 林建平, 陈龑, 等.
基于模态应变能及灵敏度分析白车身模态优化[J]. 机械科学与技术, 2015, 34(9): 1415–1418.
HU Xiao-zhou, LIN Jian-ping, CHEN Yan, et al. Modal optimization of body-in-white based on modal strain energy and sensitivity analysis[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(9): 1415–1418. |



