矿井提升机紧急制动系统主要由制动盘和制动器组成,通过液压系统控制盘式制动器的闭合,使闸片与制动盘摩擦制动,完成提升机的紧急制动过程[1]。在制动过程中,制动盘的温度会急剧上升,高温导致由复合材料制作的制动器闸片的摩擦制动性能下降,造成制动性能降低,严重时会影响提升机的安全性能[2-4]。因此针对最大提升速度达到18 m/s的1 500 m超深矿井提升机,进行紧急制动过程中制动盘温度场和应力场的分析及优化研究,对延长制动盘的寿命和提高提升机的安全性能具有重要意义。
国内外学者开展了许多制动盘热性能的相关研究。赵文杰和丁莉芬等[5-6]采用有限元法模拟了不同制动速度下制动盘的瞬态温度场分布,得到了制动盘的温度场和径向温度梯度的变化规律。仲晖[7]研究了不同材料的制动盘在制动过程中的温度场分布及其最高温度。赵海燕等[8]得出制动盘表面瞬时温度呈锯齿状变化的原因。还有学者研究了制动过程中不同的摩擦系数[9-11]、制动压力[12-13]、闸片数量[14]及闸片形状[15]对制动盘温度场和应力场的影响。为优化制动盘热性能,国内一些制动块制造企业生产了以钢纤维和金属氧化物为增强组分的摩擦材料,并将它成功应用于各种型号的车辆中[16]。Andreas和Mesut等[17-18]研究了制动盘冷却通道和不同的通风盘式制动器对制动盘温度的影响,并通过数值模拟和实验进行了验证。Han等[19]通过安装能量收集装置,收集制动过程中制动盘和闸片的热量,使制动盘制动过程中闸片温度不超过150 ℃。
针对制动盘制动过程中温度升高、应力增大等问题,为了提高制动盘热性能,本文建立了制动盘和闸片的直接耦合模型,分析不同闸片数量和排布方式对制动盘温度和应力的影响,并确定制动盘的热性能优化方案。
1 制动盘传热及其有限元模型 1.1 制动盘热传导微分方程及边界条件超深矿井提升机在紧急制动过程中,制动盘表面和内部温度分布随时间变化。在仿真过程中,将制动盘视为无内热源,其材料性能随着温度变化而变化。制动盘的热传导微分方程如下:
| $ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {\lambda r\frac{{\partial T}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{\partial }{{\partial \theta }}\left( {\lambda \frac{{\partial T}}{{\partial \theta }}} \right) + \frac{\partial }{{\partial z}}\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right) = \rho c\frac{{\partial T}}{{\partial t}} $ | (1) |
式中:T为热力学温度,K;ρ为密度,kg/m3;c为比热容,J/(kg·K);λ为导热系数,W/(m·K);t为时间,s;r为制动盘半径,m;z为制动盘侧面垂直方向的位置,m;θ为制动盘半径与轴的夹角,(°)。
在制动盘未制动阶段,制动盘温度与环境温度保持一致。制动开始后,制动盘与闸片发生摩擦,动能转化为热能,大量的热量传递给制动盘使得制动盘温度急剧升高。制动过程中,制动盘通过辐射和对流换热方式将热量向外界传递。
制动盘的热边界条件如下:
| $ T\left( {r, \theta , z} \right) = {T_0}\;\;\;\left( {t = 0} \right) $ | (2) |
式中:T(r, θ, z)为某时刻温度,K;T0为制动盘初始温度,K。
制动盘的对流换热边界条件如下:
| $ - \lambda \frac{{\partial T}}{{\partial z}} = q\left( {t, r} \right){\rm{ }}(t \ge 0) $ | (3) |
1) 制动盘摩擦面位置温度计算。
| $ - \lambda \frac{{\partial T}}{{\partial z}} = \left( {1 - \xi } \right)\left[ {h\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right) + \varepsilon \sigma \left( {T_{\rm{s}}^4 - T_{\rm{f}}^4} \right)} \right] - \xi q $ | (4) |
式中:
| $ \xi = \left\{ \begin{array}{l} 1, 制动盘上该点与闸片接触\\ 0, 制动盘上该点未与闸片接触 \end{array} \right. $ |
q为制动盘吸收的热流密度,W/m2;h为摩擦面的对流换热系数,W/(m2·K);Ts为制动盘温度,K;Tf为外界流体温度,K;ε为制动盘的黑度;σ为斯特芬玻尔兹曼常数,σ=5.67×10-8W/(m2·K4)。
2 )制动盘非摩擦水平方向表面温度计算。
| $ - \lambda \frac{{\partial T}}{{\partial z}} = h\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right) + \varepsilon \sigma \left( {T_{\rm{s}}^4 - T_{\rm{f}}^4} \right) $ | (5) |
3) 制动盘垂直方向表面温度计算。
| $ - \lambda \frac{{\partial T}}{{\partial r}} = h\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right) + \varepsilon \sigma \left( {T_{\rm{s}}^4 - T_{\rm{f}}^4} \right) $ | (6) |
式(4)、(5)和(6)中对流换热系数h与流体的流动状态、物理性质和制动盘表面的几何因素有关,其计算公式为:
| $ h = \frac{{Nu{\lambda _{\rm{f}}}}}{L} $ | (7) |
式中:Nu为努塞尔数;L为制动盘表面的特征尺度,m;λf为流体的导热系数,W/(m·K)。
当制动盘壁面流体的雷诺数为:5×105 < Re < 1×108,边界层的流体处于湍流状态,努塞尔数计算公式为:
| $ Nu = \left( {0.037R{e^{0.8}} - 870} \right)P{r^{\frac{1}{3}}} $ | (8) |
当制动盘壁面流体流动速度较小时,Re < 5×105,壁面边界层的流体处于层流状态,努塞尔数计算公式为:
| $ Nu = 0.664R{e^{\frac{1}{2}}}P{r^{\frac{1}{3}}} $ | (9) |
式(8)和(9)中,Pr为流体的普朗特数,研究中取Pr=0.7。
当提升机制动盘停止旋转,制动盘处于自然对流换热状态时,努塞尔数计算公式为:
| $ Nu = C{\left( {Gr\mathit{Pr}} \right)^n} $ | (10) |
式中:C和n是由实验确定的系数,与换热面的形状、位置、热边界条件以及壁面流体的流动状态有关。
本研究中取制动盘的摩擦界面方向为水平壁面自然换热,制动盘的圆周面方向为竖直壁面自然换热。根据自然对流换热准则,在8×106 < Gr·Pr < 1×1011时,水平壁面系数取C=0.15,n=1/3;在8×109 < Gr·Pr < 1×1013时,竖直壁面的系数取C=0.17,n=1/3。经计算,本研究中Gr·Pr≈5×1010,故水平壁面系数取C=0.15,n=1/3,竖直壁面的系数取C=0.17,n=1/3。
1.2 制动盘热应力计算在制动过程中,制动盘温度升高,制动盘内部不均匀膨胀受到约束而产生应力。制动盘热应力计算公式为:
| $ \delta = \alpha E\Delta T = \alpha E(T - {T_0}) $ | (11) |
式中:δ为热应力,MPa;α为线膨胀系数,K-1;E为弹性模量,MPa。
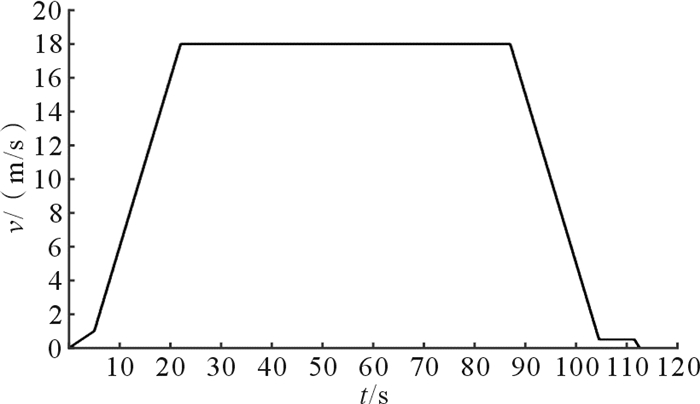
1.3 制动盘分析参数超深矿井提升机提升高度为1 500 m,提升机自重为50 t,载重为50 t。在提升和下放过程中,所设计的提升机运行速度如图 1所示。
|
| 图 1 提升机运行速度曲线 Fig.1 The running speed curve of hoist |
在提升和下放过程中,提升机的最大运行速度达到18 m/s,该阶段运行时间最长。本文以该阶段的运行速度作为紧急制动开始时刻的初速度,设定制动减速度为-3 m/s2,制动时间为6 s。
在提升机正常运行阶段,制动盘与闸片未接触;在紧急制动时,沿闸片垂直方向在闸片上施59 260 N的制动压力,闸片与制动盘表面的摩擦系数为0.4。
制动盘及连接板的尺寸参数如表 1所示。闸片有3种设计,其中模型1为原设计模型,模型2增加了闸片的数量,模型3改变了闸片的排布方式。闸片所在2个区域关于制动盘圆心对称,相邻闸片的圆心角为10.7°,闸片的尺寸参数如表 2所示。
| m | |||
| 部件 | 内径 | 外径 | 厚度 |
| 制动盘 | 3.8 | 4.45 | 0.06 |
| 连接板 | 3.8 | 4.10 | 0.05 |
| m | ||||
| 模型 | 名义摩擦半径 | 长 | 宽 | 高 |
| 模型1 | 4.145 | 0.38 | 0.26 | 0.027 |
| 模型2 | 4.145 | 0.38 | 0.26 | 0.027 |
| 模型3 | 4.007,4.300 | 0.38 | 0.26 | 0.027 |
在制动过程中,制动盘和闸片的材料性能参数随温度的变化而变化。为了在仿真计算中更真实地模拟实际制动状况,需考虑制动盘和闸片的材料性能参数随温度的变化情况。表 3和表 4分别为制动盘和闸片材料性能参数。
| 温度/℃ | 密度/kg·m-3 | 导热系数/(W/(m·K)) | 比热容/(J/(kg·K)) | 线膨胀系数/10-6·K-1 | 弹性模量/GPa | 泊松比 |
| 20 | 7 850 | 53.17 | 460.57 | 8.31 | 206 | 0.3 |
| 100 | 7 850 | 51.08 | 481.51 | 10.99 | 201 | 0.3 |
| 200 | 7 850 | 47.73 | 523.38 | 12.31 | 189 | 0.3 |
| 温度/℃ | 密度/kg·m-3 | 导热系数/(W/(m·K)) | 比热容/(J/(kg·K)) | 线膨胀系数/10-6·K-1 | 弹性模量/GPa | 泊松比 |
| 20 | 1 788 | 1.71 | 980.67 | 15 | 26.65 | 0.3 |
| 100 | 1 788 | 1.60 | 1 171.33 | 15 | 26.65 | 0.3 |
| 200 | 1 788 | 1.50 | 1 285 | 15 | 26.65 | 0.3 |
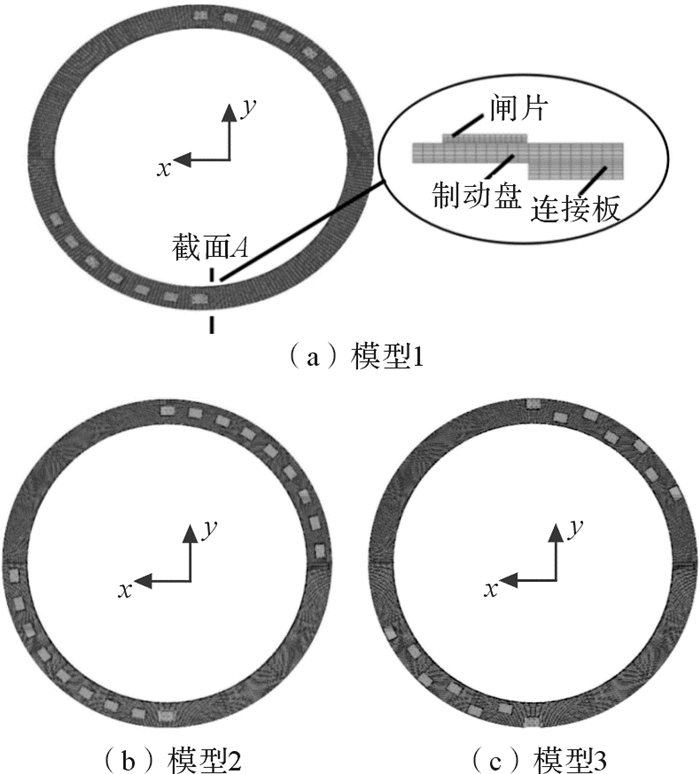
制动盘组件有限元模型1如图 2(a)所示,共划分为100 800个单元、84 000个节点。连接板共划分为39 600个单元、30 000个节点,单个闸片的节点数为2 125个,单元个数为1 536个。为了更加精确地计算摩擦面的温度和热应力并减少计算时间,在摩擦面位置细化网格,远离摩擦面的位置用较粗的网格划分。制动盘横截面如图 2(a)截面A所示。图 2(b)所示的模型2增加了闸片,由原设计的14个增加到18个。图 2(c)所示的模型3为在模型1的基础上优化了闸片的排布方式。模型2与模型3中制动盘和闸片网格划分的大小和数量与模型1相同。模型3中闸片的名义摩擦半径不尽相同,摩擦半径为4.007 m的闸片有6个,摩擦半径为4.300 m的闸片有8个。
|
| 图 2 制动盘组件有限元模型 Fig.2 The brake disc component finite element model |
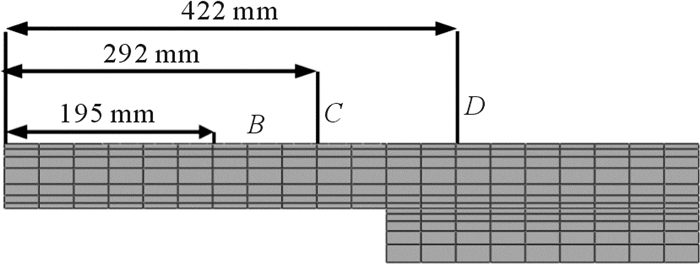
制动过程中由于闸片与制动盘的摩擦,动能转化为热能,制动盘表面温度急剧上升。通过热传导,热量从制动盘表面向内传递。为便于观察制动盘内部径向温度变化,在制动盘上选取如图 2(a)所示A截面位置,在该截面不同半径处选取B、C和D三个参考点,如图 3所示。
|
| 图 3 制动盘截面A上3个参考点的位置示意图 Fig.3 Location diagram of three reference points on section A of brake disc |
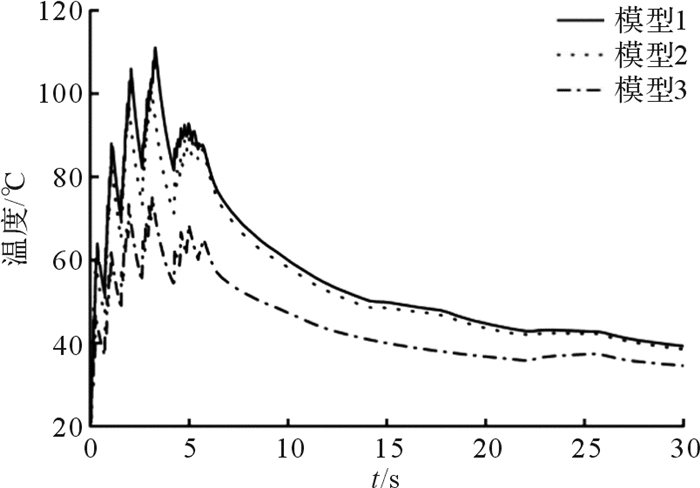
在30 s的制动和冷却过程中,制动盘截面A上B、C和D点处的温度变化如图 4至图 6所示。
|
| 图 4 制动盘截面A上B点处的温度变化曲线 Fig.4 The temperature change curve at B point on section A of brake disc |
|
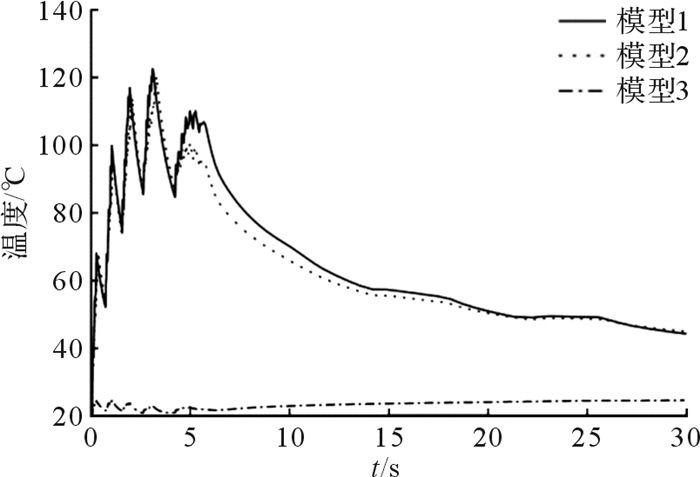
| 图 5 制动盘截面A上C点处的温度变化曲线 Fig.5 The temperature change curve at C point on section A of brake disc |
|
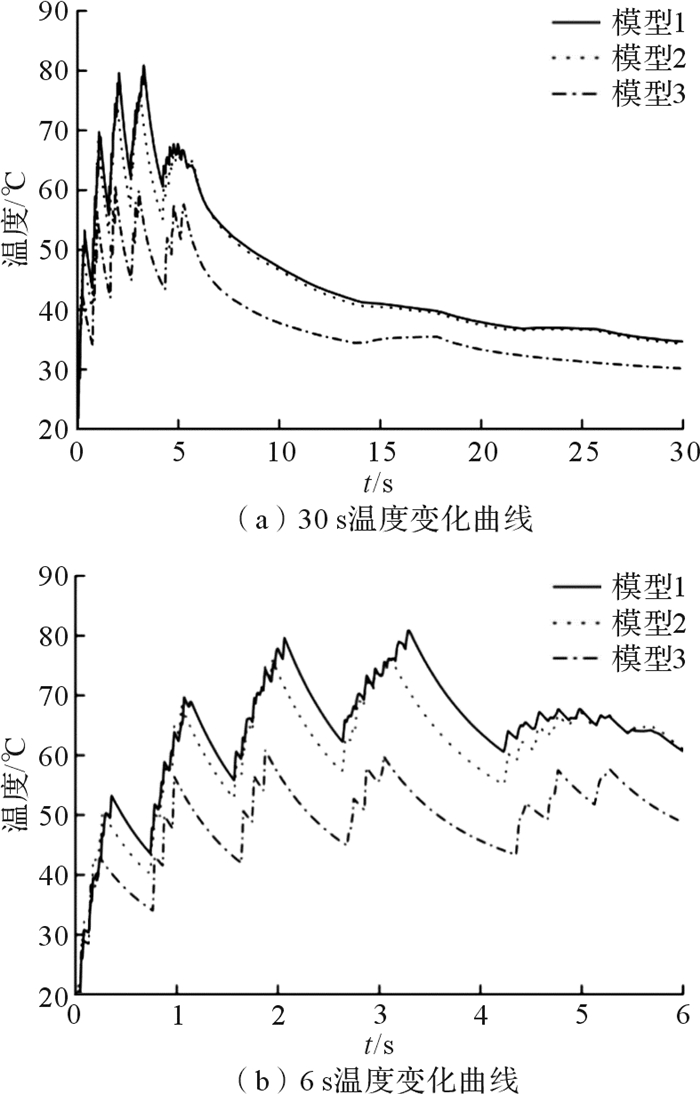
| 图 6 制动盘截面A上D点处的温度变化曲线 Fig.6 The temperature change curve at D point on section A of brake disc |
从图 4至图 6可以看出,制动盘在制动过程中,制动盘表面温度呈锯齿状波动性变化。在制动初期,制动盘摩擦面温度波动性上升,达到最高点后,温度迅速下降。在制动末期,制动盘温度波动性变化加强。这是由于在制动初期制动盘旋转速度很快,制动产生的热流密度大,热量不断积聚在制动盘中,制动盘吸收的热量大于向外传递的热量,因此制动盘温度逐渐上升。如D点处1—1.5 s阶段温度上升曲线,由于在同一摩擦面区域,闸片与制动盘间歇性摩擦,制动盘温度呈现锯齿状上升。在制动后期,制动盘旋转速度减小,制动产生的热流密度降低,制动盘向外传递的热量大于吸收的热量,制动盘温度下降。未摩擦位置处则由于制动盘与空气强制对流换热,温度急剧下降。制动结束后,制动盘与空气自然对流换热,温度逐渐降低。
在制动盘截面A上,模型2的B、C和D处的最高温度比模型1分别降低1.84%,5.9%和9.18%。模型3的B和D处的最高温度比模型1分别降低25.4%和20.1%。在模型3的C点处,制动盘温度变化比较平缓,最高温度为24.82 ℃。由计算可知,模型2和模型3制动盘制动过程中截面A上最高温度有一定幅度降低,但改变闸片排布方式的模型3制动盘,在制动过程中截面温度优化效果更显著。
制动过程中模型1、模型2和模型3制动盘摩擦面上的最高温度分布云图如图 7所示。模型1制动盘在第3.5秒时出现最高温度134.8 ℃,模型2制动盘在第3.6秒时出现最高温度142.4 ℃,模型3制动盘在第3.4秒时出现最高温度86.5 ℃,如图 8所示。模型3制动盘的温度分布较模型1和模型2均匀,制动盘表面温度主要在40~60 ℃之间。

|
| 图 7 制动盘摩擦面最高温度分布 Fig.7 The maximum temperature distribution of brake disc frication surface |
|
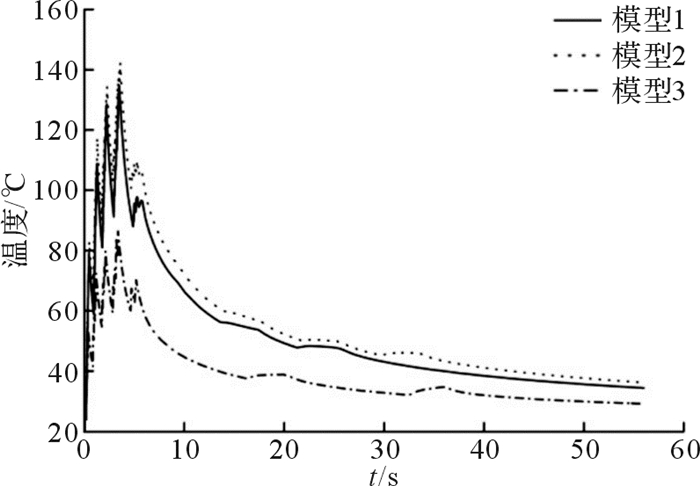
| 图 8 制动盘摩擦面最高温度变化曲线 Fig.8 The maximum temperature change curve of brake disc frication surface |
由图 8所示制动盘摩擦面最高温度变化曲线图可知,模型1、模型2和模型3制动盘摩擦面上最高温度变化趋势相同,但模型3的最高温度最低,并且最早达到峰值。制动结束后,模型3制动盘先于模型1和模型2达到稳定温度,最终冷却温度为29.1 ℃,为三者中最低。
在制动结束时刻制动盘截面A上的温度分布云图如图 9所示。

|
| 图 9 制动结束时刻制动盘截面A上的温度分布云图 Fig.9 Temperature distribution nephogram on section A of brake disc at the end of braking |
由图 9可知,模型3制动盘在制动结束时刻的最高温度低于模型1和模型2制动盘最高温度。模型1、模型2和模型3制动盘截面A上最高温度分别为101.5,107.9和66.5 ℃,模型3制动盘截面温度分布较模型1和模型2均匀,高温分布主要集中在制动盘摩擦表面。
在制动过程中,模型1、模型2和模型3闸片与制动盘摩擦面上的温度分布相似,如图 10所示。闸片温度分布大致沿中心线对称,最高温度分布在与旋转方向相反末端区域两侧。

|
| 图 10 闸片摩擦面最高温度分布 Fig.10 The maximum temperature distribution of brake pad frication surface |
由图 10所示闸片最高温度分布云图可知,模型1、模型2、模型3的闸片最高温度分别为100.7,100.9和71.5 ℃,模型3的闸片温度分布最均匀且最高温度显著低于模型1和模型2。在仿真计算中,由于闸片和制动盘的材料不同,摩擦生成的热量分配不同,闸片的最高温度低于制动盘最高温度。
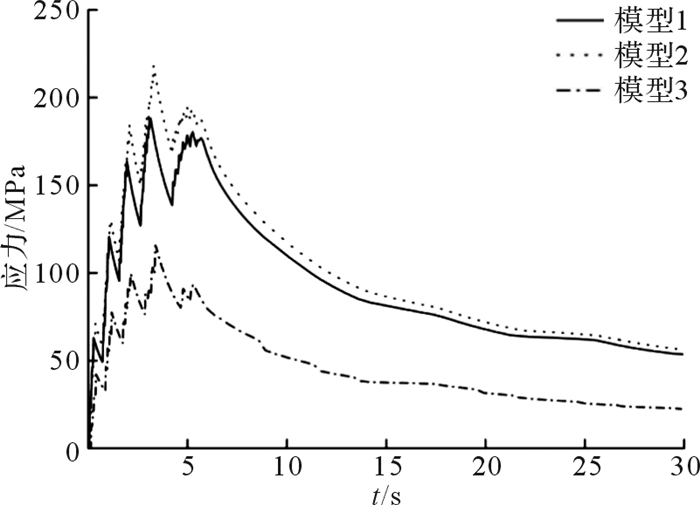
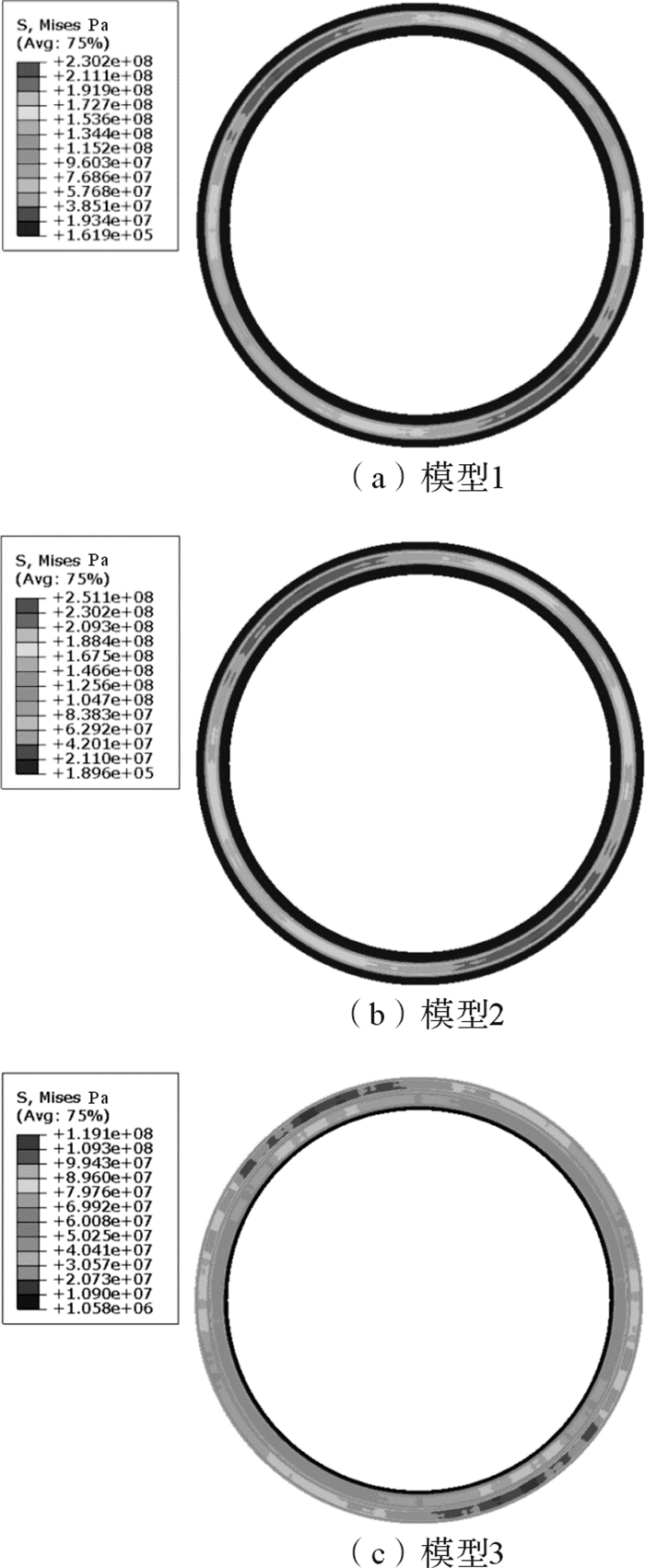
3 制动盘应力场分析制动过程中,由于温度上升,制动盘内部不均匀膨胀受到约束而产生应力。由于摩擦力和施加于闸片上的法向力与产生的热应力不为同一个数量级,因此可忽略摩擦力和法向力对制动盘热应力的影响。如图 11所示,在前6秒的制动过程中,模型1制动盘在第3.48秒产生最大应力,为230.2 MPa;模型2制动盘在第3.58秒产生最大应力,为251.1 MPa;模型3制动盘在第3.37秒产生最大应力,为119.1 MPa。在最大应力时刻,3个模型制动盘摩擦面上应力分布云图如图 12所示。
|
| 图 11 制动盘最大应力变化曲线 Fig.11 The maximum stress change curve of brake disc |
|
| 图 12 最大应力时刻制动盘摩擦面应力分布 Fig.12 The stress distribution of brake disc frication surface under maximum stress |
制动过程中,模型1与模型2制动盘摩擦面最大应力值接近,制动盘摩擦面最大应力时刻应力分布相似。模型3制动盘摩擦面上最大应力小于模型1和模型2的最大应力,最大应力时刻的应力分布相较于模型1与模型2制动盘更均匀,应力值基本在40~90 MPa之间。
由图 11制动盘最大应力值变化曲线可知,制动过程中制动盘最大应力值的变化趋势与最高温度变化趋势相同,呈现锯齿状波动性变化。
4 实验验证为了验证仿真参数设置的正确性,搭建了等比例缩小的卷筒模型力学实验装置,进行制动盘热应力实验,并与仿真结果进行对比。
图 13为实验装置整体布局,由卷筒、制动盘、耐高温应变片、应变仪、电桥盒、温控仪和加热片组成。制动盘热应力测定过程为:在制动盘一面均匀布置加热片,如图 14所示,通过温度控制系统逐步施加相同的热载荷,当制动盘温度达到稳定后,记录应变仪所示的应力值。测试温度由30 ℃上升到140 ℃,每间隔10 ℃选取一个测量点。

|
| 图 13 卷筒模型实验装置 Fig.13 The experimental equipment of reel model |

|
| 图 14 制动盘加热片分布 Fig.14 The heating plate distribution of brake disc |
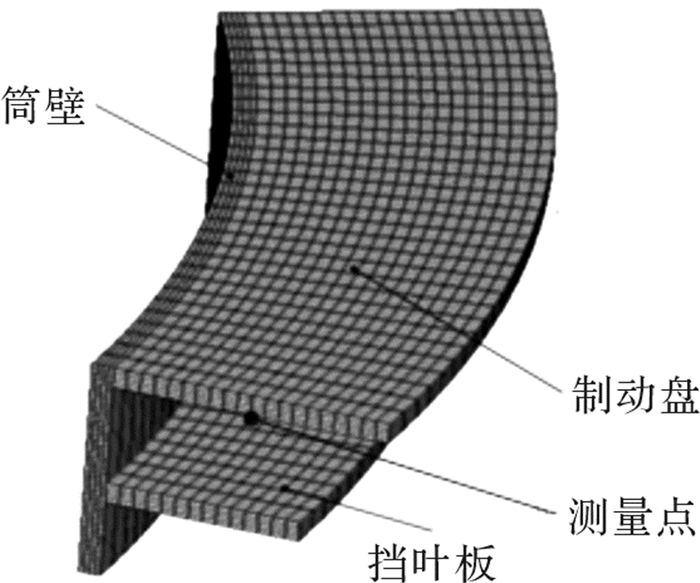
在实验用制动盘上,相邻加热片按照40°的圆心角均匀布置。因此为减少计算时间,在数值仿真中将制动盘两侧面设置为绝热边界条件,以相邻加热片之间的制动盘区域为研究对象,其有限元模型如图 15所示。制动盘的材料为Q235钢,实验装置主要尺寸如表 5所示。
|
| 图 15 研究区域制动盘有限元模型 Fig.15 The finite element model of brake disc in research area |
| mm | |||
| 部位 | 内径 | 外径 | 厚度 |
| 制动盘 | 300 | 350 | 4 |
| 挡叶板 | 300 | 335 | 4 |
| 卷筒 | 296 | 300 | 45 |
仿真中在制动盘表面施加均匀的热载荷,模拟该条件下的应力场,比较相同温度下测量点的应力仿真值和实验值,结果如图 16所示。

|
| 图 16 测量点的应力仿真值和实验值 Fig.16 The stress simulation value and experimental value of measurement point |
由图 16可知,实验值与仿真值较为吻合,且应力变化趋势相同,证明了仿真中制动盘和闸片参数设置的正确性。
5 结论1) 建立了制动盘与闸片三维有限元模型,采取直接耦合方法对制动盘制动过程中的温度场和应力场进行模拟。仿真结果表明,制动盘表面温度和应力的最大值出现在制动盘与闸片接触区域,制动过程中制动盘表面的温度和应力呈现锯齿状波动。
2) 制动过程中,模型1制动盘的温度分布和最高温度与模型2相近,模型3制动盘最高温度显著低于模型1和模型2制动盘的最高温度,且温度和应力分布更均匀。因此增加闸片数量并不能显著提高制动盘热性能,而改变闸片排布方式对制动盘热性能有较大优化作用。
3) 在等比例缩小的卷筒模型力学实验装置上进行热应力实验,验证了仿真中制动盘和闸片参数设置的正确性。
| [1] |
郝用兴.
矿井提升机盘形制动系统工作状态监控与安全[J]. 中国安全科学学报, 2006, 16(5): 126–129.
HAO Yong-xing. Working status monitoring and safety of disk braking system of mine hoisting machine[J]. China Safety Science Journal, 2006, 16(5): 126–129. DOI:10.3969/j.issn.1003-3033.2006.05.025 |
| [2] |
陈德玲, 张建武, 周平.
高速轮轨列车制动盘热应力有限元研究[J]. 铁道学报, 2006, 28(2): 39–43.
CHEN De-ling, ZHANG Jian-wu, ZHOU Ping. FEM thermal stress analysis of high-speed locomotive braking discs[J]. Journal of the China Railway Society, 2006, 28(2): 39–43. DOI:10.3321/j.issn:1001-8360.2006.02.008 |
| [3] | YANG Zhi-yong, HAN Jian-min, LI Wei-jing, et al. Brake test of SiCp/A356 brake disk and interpretation of experimental results[J]. Chinese Journal of Mechanical Engineering, 2007, 20(5): 74–79. |
| [4] | LEE K. Frictionally excited thermoelastic instability in automotive drum brakes[J]. Journal of Tribology, 1993, 122(4): 607–614. |
| [5] |
赵文杰, 吴涛, 徐延海.
基于ANSYS的汽车制动盘温度场仿真分析[J]. 西华大学学报, 2012, 31(2): 31–34.
ZHAO Wen-jie, WU Tao, XU Yan-hai. Thermal field analysis of automobile brake disc based on ANSYS[J]. Journal of Xihua University, 2012, 31(2): 31–34. DOI:10.3969/j.issn.1673-159X.2012.02.007 |
| [6] |
丁莉芬, 张强.
列车制动盘温度场的数值模拟[J]. 装备制造技术, 2010(1): 33–35.
DING Li-fen, ZHANG Qiang. Analysis on fretting fatigue of axle for haul train[J]. Equipment Manufacturing Technology, 2010(1): 33–35. DOI:10.3969/j.issn.1672-545X.2010.01.012 |
| [7] |
仲晖.
两种不同材料的列车制动盘温度场分析[J]. 装备制造技术, 2010(6): 30–31.
ZHONG Hui. Analysis on temperature field of brake disc under two materials[J]. Equipment Manufacturing Technology, 2010(6): 30–31. DOI:10.3969/j.issn.1672-545X.2010.06.012 |
| [8] |
赵海燕, 张海全, 汤晓华.
快速列车盘型制动热过程有限元分析[J]. 清华大学学报, 2005, 45(5): 589–592.
ZHAO Hai-yan, ZHANG Hai-quan, TANG Xiao-hua. Thermal FEM analysis of passenger railway car brake discs[J]. Journal of Tsinghua University, 2005, 45(5): 589–592. DOI:10.3321/j.issn:1000-0054.2005.05.004 |
| [9] | MACKIN T J, NOE S C, BALL K J. Thermal cracking in disc brakes[J]. Engineering Failure Analysis, 2002, 9(1): 63–76. |
| [10] | KIM D J, LEE Y M, PARK J S. Thermal stress analysis for a disk brake of railway vehicles with consideration of the pressure distribution on africtional surface[J]. Materials Science and Engineering A, 2008, 483(1): 456–459. |
| [11] | HWANG P, WU X. Investigation of temperature and thermal stress in ventilated disc brake based on 3D thermo-mechanical coupling model[J]. Journal of Mechanical Science & Technology, 2010, 24(1): 81–84. |
| [12] |
林谢昭, 高诚辉, 黄健萌.
制动工况参数对制动盘摩擦温度场分布的影响[J]. 工程设计学报, 2006, 13(1): 46–48.
LIN Xie-zhao, GAO Cheng-hui, HUANG Jian-meng. Effects of operating condition parameters on distribution of friction temperature field on brake disc[J]. Chinese Journal of Engineering Design, 2006, 13(1): 46–48. |
| [13] |
夏德茂, 奚鹰, 周亚红.
热载荷确定方法对制动盘温度场影响的研究[J]. 中国工程机械学报, 2015, 15(3): 388–393.
XIA De-mao, XI Ying, ZHOU Ya-hong. Impact of thermal loading determination on brake disc temperature field[J]. Chinese Journal of Construction Machinery, 2015, 15(3): 388–393. |
| [14] | CUI Jian-zhong, WANG Cun-tang, XIE Fang-wei, et al. Numerical investigation on transient thermal behavior of multidisk friction pairs in hydro-viscous drive[J]. Applied Thermal Engineering, 2014, 67(1/2): 409–422. |
| [15] |
农万华, 高飞, 符蓉.
摩擦块形状对制动盘摩擦温度及热应力分布的影响[J]. 润滑与密封, 2012, 37(8): 52–56.
NONG Wan-hua, GAO Fei, FU Rong. Influence of brake pad shape on friction temperature and thermal stress of brake disc[J]. Lubrication Engineering, 2012, 37(8): 52–56. |
| [16] |
张扬, 张力孟, 春玲.
汽车摩擦材料用增强纤维的研究现状与发展趋势[J]. 北京工商大学学报, 2006, 24(5): 19–31.
ZHANG Yang, ZHANG Li-meng, CHUN Ling. Development of reinforcing fiber used in automotive friction material[J]. Journal of Beijing Technology and Business University, 2006, 24(5): 19–31. |
| [17] | WAGNER A, GOTTFRIED S K, HAGEDORN P. Structural optimization of an asymmetric automotive brake disc with cooling channels to avoid squeal[J]. Journal of Sound and Vibration, 2014, 333(7): 1888–1898. |
| [18] | DUZGUN M. Investigation of thermo-structural behaviors of different ventilation applications on brake discs[J]. Journal of Mechanical Science & Technology, 2012, 26(1): 235–240. |
| [19] | HAN Chang-bao, DU Wei-ming, ZHANG Chi. Harvesting energy from automobile brake in contact and non-contact mode by conjunction of triboelectrication and electrostatic-induction processes[J]. Nano Energy, 2014, 6: 59–65. |


