2. 河北工业大学 机械工程学院, 天津 300401;
3. 天津工业大学 机械工程学院, 天津 300387
2. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China;
3. School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300387, China
当前,我国现代机械制造业正朝着高精度、高速度、高效率的方向发展。研究表明,对于高速高精度机床,由热变形引起的加工制造误差约占总制造误差的70%[1]。进给系统是机床的主要部件,研究其温升和热变形机理,建立进给系统热致定位误差模型,对于保证和提高机床的精度及其稳定性具有重要意义。
国内外已对滚珠丝杠进给系统热误差开展了相关研究:Min等[2-5]采用有限元方法研究了滚珠丝杠、机床结构的温度场和热变形规律,建立了进给系统热致定位误差模型,研究结果为进给系统热补偿提供了依据;杨军等[6]研究了双驱伺服进给系统热特性对数控机床精度的影响,并建立了二元非线性综合热误差模型;夏军勇等[7]采用杆的一维传热分组显式数值求解方法,提出了基于非线性时序模型与前向神经网络的模型,来辨识热弹性效应;Jin等[8]利用赫兹理论计算了热接触阻力,建立了支撑轴承温升与运行条件之间的关系;Fukada等[9]利用黏弹塑性模型建立了非线性微观行为的仿真模型。除了通过研究丝杠的热伸长来建立机床的热误差模型外,部分学者还研究了其他因素对热致定位误差的影响:Xu等[10]分析了不同冷却液对进给系统热致定位误差的影响;冯文龙等[11-12]提出了基于热特性分析的光栅定位热误差建模理论及补偿方法;Jiang等[13]提出了一种基于机床温升过程可重复性的热致定位误差测量和建模方法,提高了建模的精度和效率。另外还有一些学者通过神经网络的方法研究热误差与影响因素之间的关系:Li等[14]基于有限元法与蒙特卡洛法提出了一种预测滚珠丝杠轴温度瞬态分布和热误差分布的自适应实时模型;王新孟等[15]提出了进给系统热误差的最小二乘支持向量机预测方法;Zhang等[16]对精密机床的热致误差进行了实验研究和理论建模,基于滚珠丝杠轴向热膨胀的实时数据,建立了热误差与丝杠轴向伸长的关系,预测了热误差分布规律。
上述研究主要是针对丝杠本身的热变形,直接建立温度、变形与热误差的预测模型,对进给系统的热致定位误差及其影响进行分析,而机床结构大件(床身、立柱、溜板)热变形对进给系统热致定位误差的影响鲜有涉及。机床在运行时,进给系统(包括导轨滑块运动副)所产生的热量会传导至机床的结构大件上,从而导致结构大件发生热变形,滚珠丝杠是通过电机座/轴承座安装在结构基体上的,结构基体的热变形会加剧丝杠的热变形,从而产生更大的热误差。为了更加准确地得出进给系统的热致定位误差模型,本文建立了综合考虑机床结构大件-进给系统变形的热致定位误差模型,以JIG630精密卧式加工中心为例开展了机床结构大件-进给系统耦合热变形仿真分析,利用多光束激光干涉仪XM-60对机床进给系统的热致定位误差进行了测试实验,实验结果表明,综合考虑机床结构大件-进给系统热致定位误差的分析结果与实验测试结果的吻合度更高。
1 机床结构热变形对热致定位误差的影响机床进给系统中丝杠螺母副的温升取决于其生热与散热的平衡状态,丝杠的热变形则取决于温升值、丝杠材料的热膨胀系数和丝杠的安装方式。丝杠的安装方式主要分为2种:一种为一端固定、一端浮动支撑,按此种方式安装的丝杠可沿浮动支撑端自由热伸长,适用于中速度、低精度的机床丝杠传动系统;另一种为两端固定式,此种安装方式可以限制丝杠的热伸长,适用于高刚度、高精度、高速度的精密机床滚珠丝杠传动系统。本文研究的JIG630精密卧式加工中心进给系统,其滚珠丝杠所采用的安装方式为两端固定式。
两端固定式的安装方式下,丝杠轴承组的轴向刚度会直接影响丝杠的轴向热伸长,所以在有限元仿真分析中要充分考虑轴承组的刚度,需将轴承组作为弹性体来处理。在不同的预紧力下轴承对应的轴向刚度值如表 1所示[17]。本文研究的JIG630精密卧式加工中心进给系统所采用的预紧方式为重预紧。
| 预紧方式 | 预紧力/N | 轴向刚度/(N/μm) |
| 轻预紧(C9) | 2 530 | 1 330 |
| 重预紧(C10) | 5 300 | 1 810 |
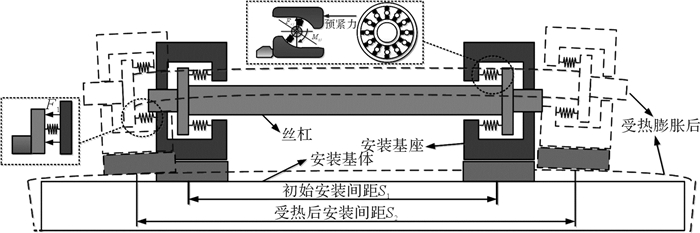
进给系统中各热源产生的热量不仅会使丝杠产生热伸长,还会通过轴承座和电机座传导至进给系统的安装基体(床身、立柱、溜板)上,使安装基体发生结构热变形,从而使轴承座和电机座的安装位置发生变化。如图 1所示,若安装基座的位置固定不动,当丝杠受热膨胀时,由于丝杠是两端固定的,且轴承的轴向刚度较大,所以会在一定程度上限制丝杠的热膨胀。当基体受热变形后,轴承座和电机座在丝杠轴向上的安装间距会发生变化:若间距变大,会给丝杠的热膨胀留有一定空间利于丝杠热膨胀,且间距的变化量若大于丝杠热膨胀量,安装基座还会对丝杠施加一个轴向载荷F1;若间距变小,则会进一步阻碍丝杠的热膨胀。由此可见进给系统安装基体的热变形对丝杠的热膨胀有着重要的影响。
|
| 图 1 机床结构大件-进给系统受热膨胀耦合示意图 Fig.1 Thermal expansion coupling diagram of machine tool large structural component-feed system |
丝杠安装基座间距的变化,从本质上讲是影响了丝杠的受力状态。丝杠受热前由于预拉伸力(轴承预紧力)的作用,丝杠与安装基座之间会有一个初始接触力,此力可以看作阻碍丝杠热伸长的初始力。由于安装基座会阻碍丝杠的伸长,随着丝杠生热后膨胀,接触力会发生改变。若安装基座位置不变,接触力会随着丝杠的热膨胀不断增大,但由于丝杠温升值有限且轴承有一定的刚度,接触力不会无限增大,会达到一种力平衡状态。但当基座安装间距发生改变时,之前的力平衡状态会被打破,丝杠与安装基座之间的接触力会随之发生改变,丝杆的伸长量也会随之发生改变,而达到另一力平衡状态。力、温升和丝杠伸长量的关系为:
| $ F = \Delta l \cdot {K_{\rm{s}}} = \int_0^l {\alpha \Delta T'{\rm{d}}x} \cdot \frac{{EA}}{l} $ | (1) |
式中:F为拉伸力, N;l为丝杠长度,Δl为丝杠伸长量,m;Ks为丝杠轴向刚度;N/m;α为丝杠的线性热膨胀系数,α=12×10-6/℃;E为弹性模量,E=2×1011N/m2;A为丝杠横截面积,m2;ΔT′为丝杠温升值;dx为丝杠轴向微元长度,m。
2 进给系统热致定位误差建模方法 2.1 进给系统热特性仿真分析 2.1.1 生热量与散热量建模机床进给系统的主要热源包括电机、轴承、丝杠-螺母和导轨滑块[18],散热主要是通过自然对流、强制对流以及采用丝杠冷却液散热三种形式。进给系统主要生热、散热计算模型如下[2-3]。
1) 轴承生热率ϕ1。
轴承的生热主要与轴承的摩擦力矩和转速相关,其生热率计算公式为:
| $ {\phi _1} = 0.104\;7n{M_{轴承}} $ | (2) |
式中:n为轴承转速,r/min;M轴承为轴承摩擦力矩,N·m。
轴承摩擦力矩M轴承分为与轴承载荷无关的M0和与轴承载荷有关的M1两部分,即:
| $ {M_{轴承}} = {M_0} + {M_1} $ | (3) |
式中:
| $ \left\{ \begin{array}{l} {M_0} = \left\{ \begin{array}{l} {10^{ - 7}}{f_0}{\left( {vn} \right)^{\frac{2}{3}}}d_{\rm{m}}^3,vn > 120\;000\;{\rm{m}}{{\rm{m}}^2}/{\rm{r}}\\ 160 \times {10^{ - 7}}{f_0}d_{\rm{m}}^3,vn < 120\;000\;{\rm{m}}{{\rm{m}}^2}/{\rm{r}} \end{array} \right.\\ {M_1} = {f_1}{F_\beta }{d_{\rm{m}}} \end{array} \right. $ | (4) |
式中:v为工作温度下润滑剂运动黏度,mm2/s;dm为轴承中径,mm;f0为与轴承类型和润滑方式有关的经验常数;f1为与轴承结构和载荷有关的系数;Fβ为与轴承受力相关的力,N。
2) 丝杠生热率。
滚珠丝杠副的生热率计算方法和轴承相同,为了简化计算过程,对于丝杠摩擦力矩的计算作出如下假设:①由于进给速度变化引起黏性摩擦阻力等因素的变化对丝杠摩擦力矩的影响较小,可以忽略;②加减速阶段的丝杠摩擦力矩变化对丝杠发热影响较小,可以忽略。丝杠摩擦力矩计算公式为:
| $ {M_{丝杠}} = 0.94{M_{\rm{p}}} + {M_{\rm{d}}} $ | (5) |
| $ \left\{ \begin{array}{l} {M_{\rm{d}}} = \frac{{{F_{\rm{t}}}{P_{\rm{h}}}}}{{2{\rm{ \mathsf{ π} }}\eta }}\left( {1 - {\eta ^2}} \right)\\ {M_{\rm{p}}} = \frac{{{F_{\rm{p}}}{P_{\rm{h}}}}}{{2{\rm{ \mathsf{ π} }}\eta }}\left( {1 - {\eta ^2}} \right) \end{array} \right. $ | (6) |
式中:M丝杠为丝杠摩擦力矩,N·m;Mp为滚珠螺旋阻力矩,N·m;Md为驱动力矩,N·m;Ft为丝杠的总轴向载荷,kN;Fp为滚珠丝杠螺母副的轴向预紧力,kN;Ph为丝杠的导程,mm;η为丝杠螺母副传动效率。
3) 导轨生热率Qg。
导轨生热主要源于导轨和滑块之间的摩擦,其生热率计算公式为:
| $ {Q_{\rm{g}}} = {\eta _1}F{v_1} $ | (7) |
式中:Qg是导轨生热率,W;η1是导轨-滑块摩擦系数;F是施加在导轨面上的载荷,N;v1是滑块相对导轨的运动速度,m/s。
4) 电机生热率Q1。
伺服电机的生热量主要包括机械损耗、电损耗、磁损耗和附加损耗转化的热量。其生热率计算公式为:
| $ {Q_1} = \frac{{{M_{\rm{T}}} \cdot n}}{{9\;550}}\left( {1 - {\eta _2}} \right) $ | (8) |
式中:MT为伺服电机的输出扭矩,N·m;η2为伺服电机的机械效率。
5) 对流换热系数h。
滚珠丝杠系统外表面与空气流体接触,因此,会产生热交换。根据努谢尔特准则,换热系数h的计算公式为:
| $ h = \frac{{Nu \cdot \lambda }}{L} $ | (9) |
式中:Nu为努谢尔特数;L为进给系统特征尺寸;λ为流体热传导系数。
6) 冷却液强制散热率Q2。
本文研究的JIG630精密卧式加工中心的进给系统所采用的丝杠是中空丝杠,其冷却液的强制散热率的计算公式为:
| $ {Q_2} = mc\Delta T = \rho {v_2}c\left( {{T_{{\rm{out}}}} - {T_{{\rm{in}}}}} \right) $ | (10) |
式中:ΔT为冷却液进出口温差;ρ为冷却液密度,kg/m3;v2为流量,L/min;Tout为冷却液出口温度;Tin为冷却液进口温度;c为比热容,kJ/kg·℃。其中出口温度需要用ANSYS Fluent进行流体分析。
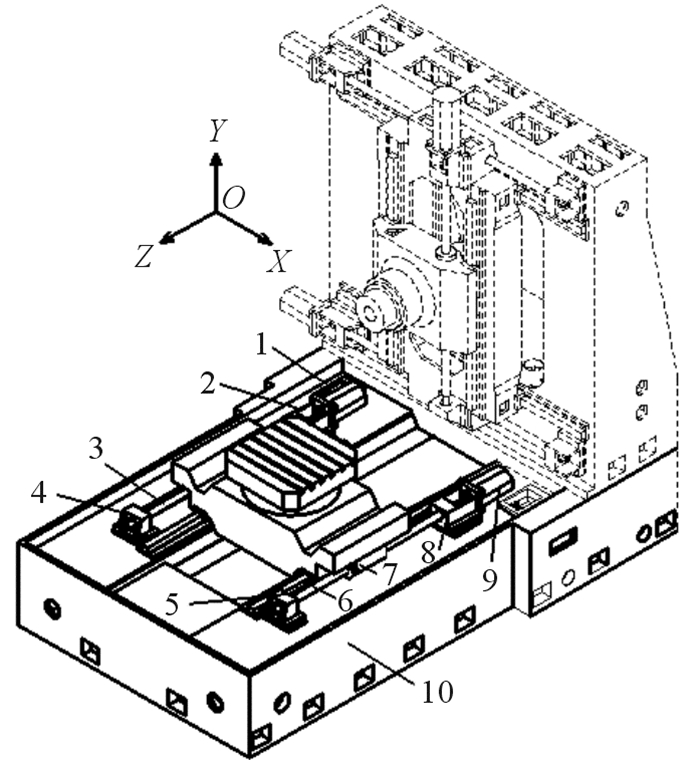
2.1.2 进给系统热-固耦合有限元仿真分析如图 2所示为JIG630精密卧式加工中心简化模型,分别在6,10和15 m/min的进给速度下对其Z向进给系统进行热-固耦合有限元仿真分析。
|
| 1—左电机;2—左电机座;3—左丝杠;4—左轴承座;5—右轴承座;6—右丝杠;7—螺母座;8—右电机座;9—右电机;10—床身 图 2 JIG630精密卧式加工中心简化模型 Fig.2 JIG630 precision horizontal machining center simplified model |
环境温度设置为20 ℃,由上述经验公式,计算出不同进给速度下的主要参数,如表 2和表 3所示。
| 进给速度/(m/min) | n/(r/min) | M1/(N·m) | M0/(N·m) | Md/(N·m) | Mp/(N·m) | Qg/W | Q1/W | ΔT/℃ |
| 6 | 300 | 176 | 82 | 530 | 177 | 9 | 32 | 0.30 |
| 10 | 500 | 176 | 115 | 530 | 177 | 18 | 47 | 0.48 |
| 15 | 750 | 176 | 151 | 530 | 177 | 27 | 60 | 0.70 |
| 进给速度/(m/min) | 轴承热流密度/(W/m2) | 丝杠热流密度/(W/m2) | 电机热流密度/(W/m2) | 导轨热流密度/(W/m2) | 冷却液热流密度/(W/m2) |
| 6 | 1 134 | 106 | 200 | 40 | -118 |
| 10 | 2 132 | 177 | 300 | 80 | -177 |
| 15 | 3 331 | 265 | 380 | 120 | -275 |
将上述参数添入有限元模型中,经热-固耦合计算可得机床的温升及变形仿真结果。
1) 温升仿真结果。
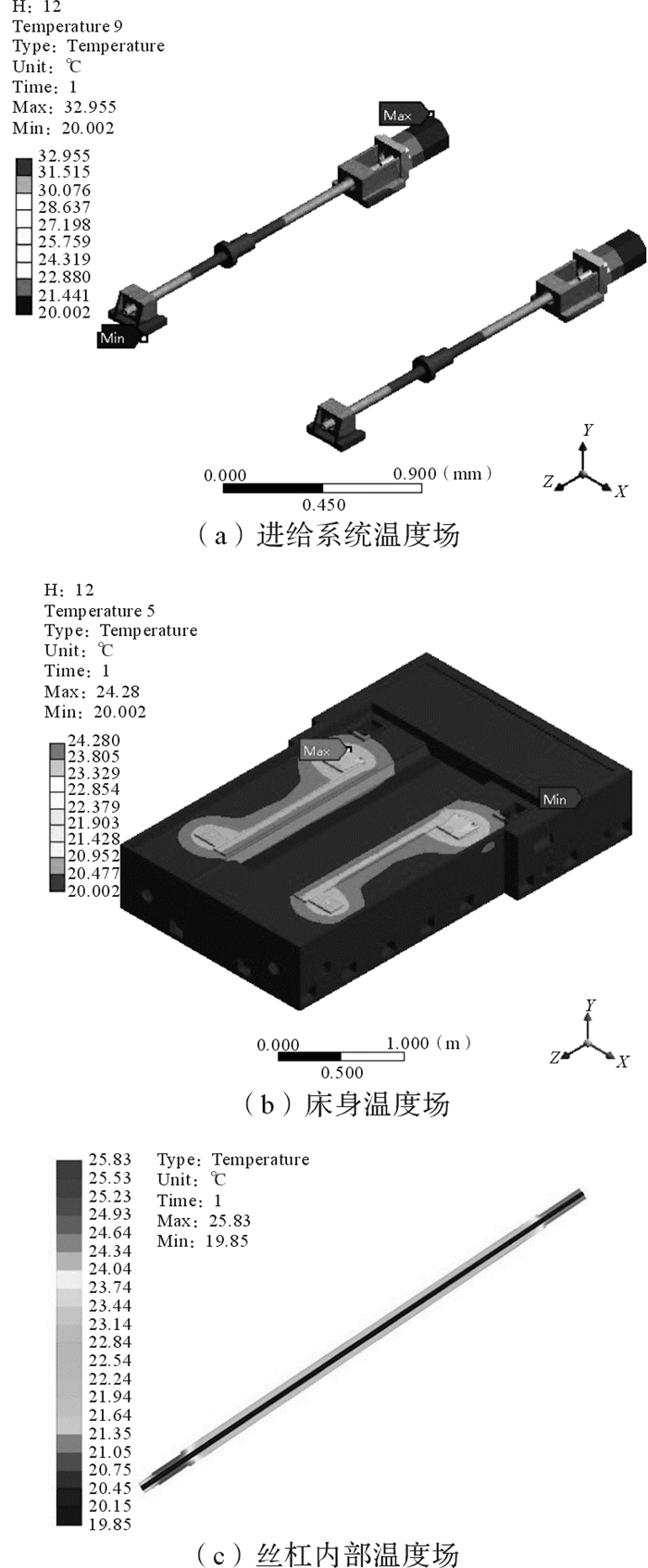
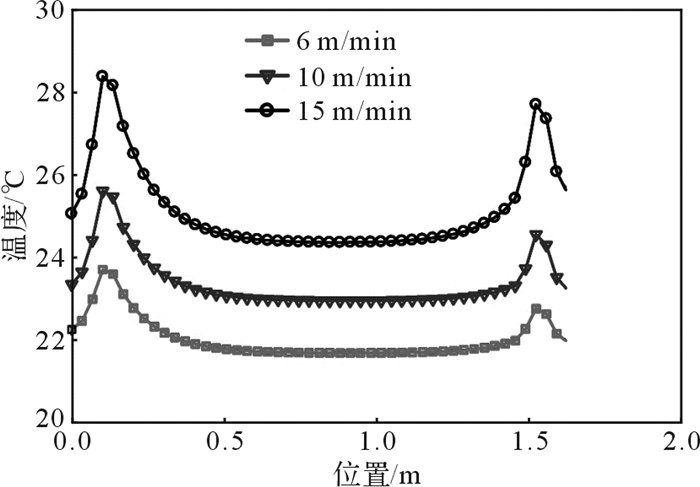
以10 m/min的进给速度为例,JIG630床身和进给系统各部位的稳态温度场分布如图 3所示。因为机床的结构和热源分布都较为对称,所以本文以左丝杠为例研究不同进给速度下丝杠的温度分布规律,沿正Z向提取丝杠全长范围内(1.6 m)的表面温度,如图 4所示。
|
| 图 3 进给速度为10 m/min时JIG630床身和进给系统温度场分布 Fig.3 JIG630 bed and feed system temperature field distribution with feed rate of 10 m/min |
|
| 图 4 不同进给速度下丝杠温度 Fig.4 Screw temperature under different feed rates |
由图 3和4可知:进给系统中电机处温度最高,在JIG630床身上轴承座和电机座附近温度较高;在10 m/min的进给速度下,电机处最高温度达32.96 ℃,床身处最高温度达24.28 ℃;丝杠表面温度分布规律为:靠近轴承处的温度较高,中间部位温度较低。不同进给速度下丝杠中间有螺纹部位的温度分别为21.7,22.96,24.41 ℃。
2) 变形仿真结果。
在不同进给速度下床身Z向(丝杠轴向)变形分布规律不同,分别提取床身左右轴承座、左右电机座在Z向上的变形,如表 4所示。
| 进给速度/(m/min) | Z向变形仿真值/μm | |||
| 左轴承座 | 左电机座 | 右轴承座 | 右电机座 | |
| 6 | 5.19 | -3.34 | 5.17 | -3.31 |
| 10 | 7.09 | -4.75 | 7.06 | -4.73 |
| 15 | 9.08 | -5.81 | 9.06 | -5.79 |
由表 4可得,在6,10,15 m/min的进给速度下,左右丝杠安装间距的平均变化量为分别为8.51,11.82,14.87 μm。在不同进给速度下,丝杠安装基座的间距在变大,机床结构的热变形会引起丝杠热膨胀,即增大机床的热误差。为此,分2种情况研究丝杠的变形规律:考虑安装基体结构热变形和不考虑安装基体结构的热变形。
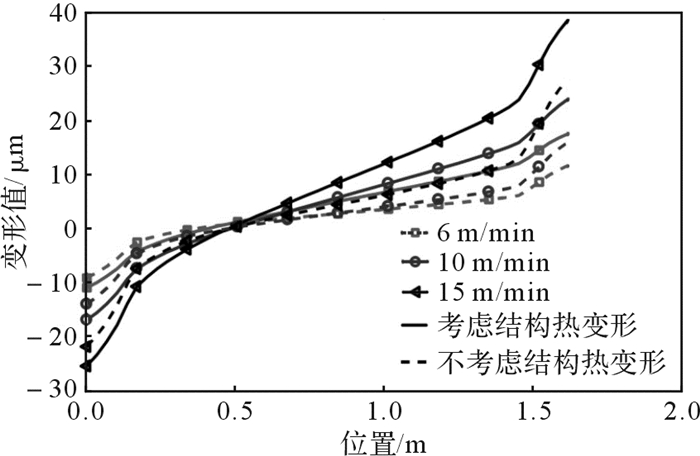
在有限元分析中,考虑结构热变形时将床身底面作为固定约束,不考虑结构热变形时将轴承座和电机座作为固定约束,其他条件不变,对Z向进给系统进行热-固耦合分析。以左丝杠为例研究安装基体结构热变形对丝杠变形的影响,经计算可得丝杠的变形曲线对比,如图 5所示。
|
| 图 5 丝杠变形曲线对比 Fig.5 Comparison of screw deformation curve |
由图 5可得:随着进给速度的增大,滚珠丝杠的生热量增大,丝杠的热变形也越来越大;丝杠变形曲线两端的斜率较大,中间部分斜率较小,这是因为丝杠的安装轴承限制了丝杠中间部分的热伸长,而在安装轴承之外的部分可以自由伸长,并且轴承部位的温度高于丝杠其他部位。
从图 5中还可以看出,当不考虑结构热变形对丝杠的影响时,无论在何种进给速度下,丝杠的热变形都是小于考虑结构热变形时丝杠的热变形。由此可见结构热变形对丝杠热变形的影响不容忽略。
2.2 丝杠内部应力仿真分析由第1节可知,机床结构热变形主要是改变了丝杠的受力状态,同时温度变化还会引起丝杠内部应力变化[19],现对丝杠内部应力分布进行分析。
丝杠的受力与内部应力的关系为:
| $ \sigma = \frac{F}{A} $ | (11) |
式中:σ为丝杠的内部应力,Pa。
当丝杠受热前,由于预拉伸力F0的作用丝杠内部会产生预应力(拉应力);当丝杠受热膨胀后,由于两端固定式的安装方式限制了丝杠的热膨胀,丝杠内部会产生热应力(压应力),且会与之前的预应力部分抵消。当机床结构发生热变形,即安装基座位置发生变化时,丝杠会受到安装基座的额外作用力F1,此时丝杠的内部应力会发生变化。这里假设基座的位置变化量完全转化为丝杠的伸长量Δl,根据丝杠的温升值,由式(1)算得丝杠的受力F,再由式(11)算得丝杠的热应力。丝杠的长度取丝杠两端支撑点间距l=1.2 m,由2.1节丝杠的温升仿真结果可知丝杠中间有螺纹部位的温度分布较为均匀,本文在分析过程中假定丝杠中间有螺纹部位的温升相同。
设初始预应力为σ0;不考虑结构热变形,丝杠热膨胀后的应力为σ1;考虑结构热变形,丝杠热膨胀后的应力为σ2。可得不同进给速度下丝杠的内部应力, 如表 5所示。
| 进给速度/(m/min) | σ0/MPa | σ1/MPa | σ2/MPa |
| 6 | 2.97 | -1.13 | 0.29 |
| 10 | 2.97 | -4.13 | -2.16 |
| 15 | 2.97 | -7.61 | -5.13 |
由表 5可知:若不考虑结构热变形, 丝杠内部的应力全部为压应力,且随着进给速度增大即生热量的增大,压应力也越来越大;当考虑结构热变形时,丝杠内部的应力随着进给速度的增大,由拉应力转化为压应力。2种情况下丝杠内部应力差异较大,表明结构热变形对丝杠的应力分布有着重要的影响。
2.3 热致定位误差建模进给系统热致定位误差是指机床生热后进给轴在进给过程中所产生的位置误差,故可取丝杠有效行程内(Z向行程为0.9 m)的误差作为热致定位误差,由于激光类检测装置默认初始位置误差为0,所以本文将Z向初始位置的误差默认为0。由2.1节分析得到的误差曲线通过多项式拟合可得不同进给速度下Z向的热致定位误差模型。其拟合多项式的最高次幂选取是利用MATLAB的曲线拟合工具箱(Curve Fitting Tool)计算出拟合曲线的相关系数R和方差,结果如表 6所示,然后综合考虑两者得出最高次幂,其中相关系数越接近1、方差越小证明曲线的拟合效果越好。
| 结构热变形 | 进给速度/(m/min) | 1次拟合 R值/方差 |
2次拟合 R值/方差 |
3次拟合 R值/方差 |
4次拟合 R值/方差 |
5次拟合 R值/方差 |
| 6 | 0.998 5/1.444 0 | 0.998 5/1.374 0 | 0.999 8/0.163 5 | 0.999 8/0.143 5 | 1/0.030 6 | |
| 考虑 | 10 | 0.999 3/0.744 1 | 0.999 3/0.711 7 | 0.999 9/0.055 9 | 0.999 9/0.055 4 | 1/0.011 2 |
| 15 | 0.998 7/2.933 0 | 0.998 7/2.890 0 | 0.999 9/0.222 7 | 0.999 9/0.202 5 | 1/0.037 4 | |
| 6 | 0.996 7/0.395 0 | 0.997 4/0.309 5 | 0.999 8/0.029 0 | 0.999 8/0.027 7 | 0.999 9/0.006 7 | |
| 不考虑 | 10 | 0.997 0/0.773 5 | 0.997 2/0.723 2 | 0.999 8/0.059 2 | 0.999 8/0.058 9 | 1.000 0/0.012 7 |
| 15 | 0.995 4/2.979 0 | 0.995 5/2.961 0 | 0.999 6/0.247 1 | 0.999 7/0.222 6 | 0.999 9/0.046 4 |
由表 6的计算结果可知,随着拟合曲线的最高次幂依次提高,方差值不断减小且相关系数不断接近于1。当最高次幂为3次时,方差值明显减小且相关系数接近于1。随着最高次幂的持续提高,方差还会减小,相关系数也还会进一步接近甚至等于1,但是方差的减小幅度和相关系数的增大幅度变小,且最高幂次数越高表达式会越复杂,综合考虑,选取拟合曲线的最高次幂为3次。
热致定位误差模型如式(12)和(13)所示。
考虑结构热变形:
| $ \left\{ \begin{array}{l} {\delta _{{\rm{thermal}}}}\left( {Z,6} \right) = 11.46{z^3} - 18.76{z^2} + 17.71z\\ {\delta _{{\rm{thermal}}}}\left( {Z,10} \right) = 16.16{z^3} - 26.36{z^2} + 27.50z\\ {\delta _{{\rm{thermal}}}}\left( {Z,15} \right) = 25.19{z^3} - 40.08{z^2} + 40.03z \end{array} \right. $ | (12) |
不考虑结构热变形:
| $ \left\{ \begin{array}{l} {\delta _{{\rm{thermal}}}}\left( {Z,6} \right) = 2.87{z^3} - 5.42{z^2} + 8.19z\\ {\delta _{{\rm{thermal}}}}\left( {Z,10} \right) = 4.41{z^3} - 8.98{z^2} + 11.83z\\ {\delta _{{\rm{thermal}}}}\left( {Z,15} \right) = 8.92{z^3} - 15.17{z^2} + 19.31z \end{array} \right. $ | (13) |
式中:δthermal为进给系统在进给速度为i(i=6, 10, 15 m/min)时的热致定位误差,μm;z为工作台Z向位置坐标,m。
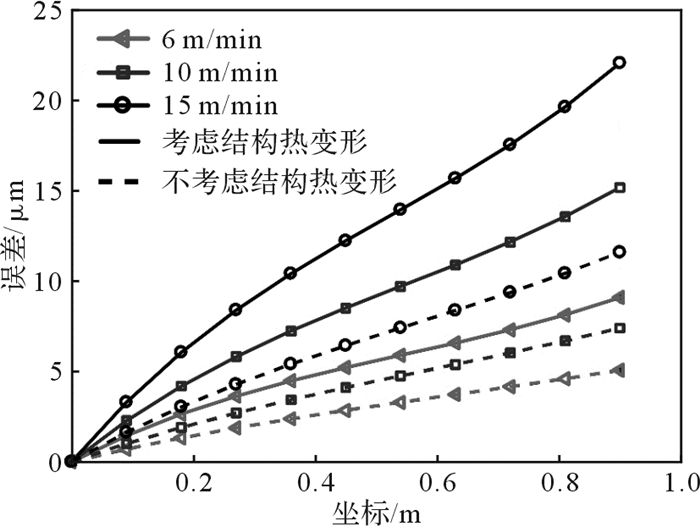
对应的误差曲线对比如图 6所示。
|
| 图 6 不同进给速度下的热致定位误差曲线对比 Fig.6 Comparison of thermal positioning error curve under different feed rates |
为验证所建立的进给系统热致定位误差模型的正确性,对无闭环光栅反馈工况下JIG630精密卧式加工中心的热致定位误差进行测试实验。通过对比实验结果与所建模型仿真分析结果的吻合程度,来验证模型的正确性。
3.1 实验设计本文以JIG630精密卧式加工中心为研究对象,搭建如图 7所示的机床热特性实验平台。该热特性实验平台包括热致定位误差检测装置多光束激光干涉仪XM-60、28通道温度检测系统,可实现机床温度及进给轴热误差测量。温度检测主要是针对进给系统的电机、轴承座、电机座、螺母座、床身、冷却液进出口等附近的关键点温度进行连续测量。

|
| T1—冷却液出口;T2—电机座下;T3—电机座上;T4—电机;T5—冷却液进口;T6—轴承座上;T7—轴承座下;T8—螺母座;T9—床身(靠近电机座);T10—床身(靠近轴承座) 图 7 机床热特性实验平台 Fig.7 Experimental platform for thermal characteristics of the machine tool |
热致定位误差的检测流程为:首先在待机状态下,利用XM-60对机床的Z向进给系统定位误差进行初始测量,然后机床以6 m/min的进给速度进行跑车,每隔1 h对机床的进给系统定位误差进行一次测量,跑车4 h后机床基本达到稳态,然后对进给系统进行最后一次定位误差检测,单轴总共进行5次定位误差检测,然后关机使机床自然冷却。等机床完全冷却后,再分别以10,15 m/min的进给速度分别进行跑车,重复上述检测过程。
热致定位误差是指机床热机后的定位误差相对于冷机时定位误差的变化量,所以热致定位误差也可以定义为:
| $ {\delta _{{\rm{thermal}}}}\left( t \right) = \delta \left( t \right) - \delta \left( 0 \right) $ | (14) |
式中:δthermal(t)是Z向进给系统的热致定位误差;δ(t)是Z向进给系统的定位误差;δ(0)是Z向进给系统初始时刻的定位误差。
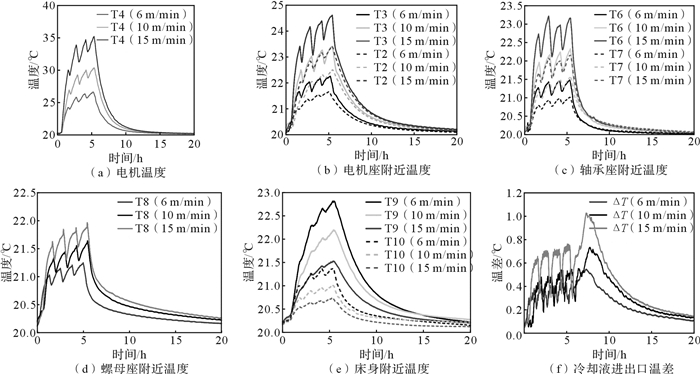
3.2 实验结果及分析 3.2.1 温升实验结果及分析机床在以不同的进给速度运动时,各关键点温度检测结果如图 8所示。其中实验环境为恒温室,环境温度为(20±0.5)℃,在整个实验过程中保持不变。在同一进给速度下每隔1 h进行一次测量, 每次测量时间为10 min左右,完成5次测量后停机,机床自然冷却。
|
| 图 8 不同进给速度下进给系统各关键点温度 Fig.8 Temperature of key positions of feed system under different feed rates |
由图 8可知,随着进给速度的提高,各关键点的温度也不断升高。其中电机温度最高,随后依次是电机座、轴承座、床身、螺母座。另外冷却液进出口温差随着进给速度的增大而增大,这说明随着丝杠温度的升高,冷却液带走的热量也越来越多。温度曲线出现了4个“锯齿状”,这是因为每隔1 h进行一次测量,在测量过程中进给速度会变慢,生热减少,所以温度会有下降趋势。并且第3个“锯齿”和第4个“锯齿”最高温度相差不大,这说明机床在运行4 h后已基本达到稳态。图 8(f)中停机后冷却液进出口温差先升后降是由于停机后冷却系统循环停止所导致。
以进给速度为10 m/min为例,提取进给系统各关键点稳态温度,与仿真结果作对比,如表 7所示。
| ℃ | |||||||
| 对比项 | T3 | T6 | T9 | T10 | T8 | T4 | ΔT |
| 仿真值 | 23.7 | 22.9 | 22.4 | 21.2 | 22.2 | 30.7 | 0.48 |
| 实验值 | 23.2 | 22.2 | 22.2 | 20.9 | 21.6 | 30.2 | 0.52 |
由表 7对比结果可知,仿真值与实验值相差不大,证明本文所建立的有限元模型正确。
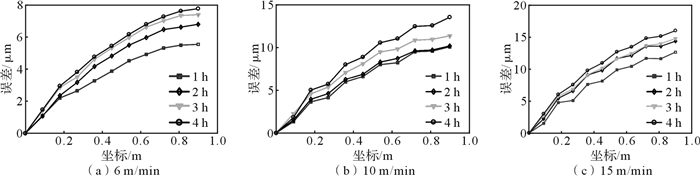
3.2.2 热致定位误差结果及分析当机床分别以6,10,15 m/min的进给速度跑车时,每隔1 h对其定位误差进行一次测量。热致定位误差为热机后测得的定位误差减去初始时刻的定位误差。经计算可得进给系统热致定位误差时变规律,如图 9所示。
|
| 图 9 不同进给速度下进给系统热致定位误差时变规律 Fig.9 Variation rule of thermal positioning error with time under different feed rates |
由图 9可知,随着机床运行时间的增加,进给系统的热致定位误差逐渐增大,并且1 h后热误差的变化幅度较大,2 h及以后的热误差的增幅较小,从图 8的温度曲线可以看出,这是因为第1个小时后进给系统的升温开始变得缓慢。
由上述分析可知,机床在跑车4 h后基本达到稳态,所以可以将4 h后到的热致定位误差作为稳态误差与仿真结果进行对比,结果如图 10所示。
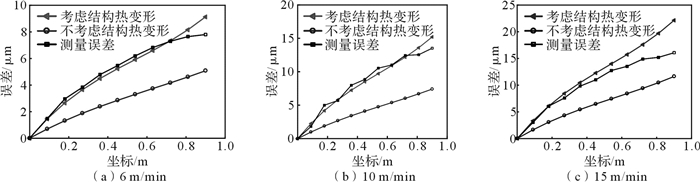
|
| 图 10 不同进给速度下进给系统热致定位误差实验值与仿真值对比 Fig.10 Comparison of experimental and simulated thermal positioning error of feed system under different feed rates |
由图 10可知:考虑了结构变形所建模型的热致定位误差仿真值与实际测量值热重合度更好,整体重合度达90%以上;在进给速度为6 m/min时,仿真值与实测值的最大误差为1.2 μm;在进给速度为10 m/min时,仿真值与实测值的最大误差为1.7 μm;在进给速度为15 m/min时,仿真值与实测值的最大误差为6 μm。若不考虑结构变形,得到的仿真误差曲线与实测误差曲线的整体重合度约为60%,显然误差较大。
4 结论1) 本文提出了一种综合考虑机床结构大件-进给系统热变形的进给系统热致定位误差建模方法,通过建立机床有限元分析模型,对其进行热-固耦合分析,得出机床的温度场和丝杠变形曲线,从而分析得出进给系统的热致定位误差。
2) 为了验证所建立的热致定位误差模型的正确性,以JIG630精密卧式加工中心为例进行了热特性测试实验,利用温度传感器及其采集系统实现了机床温度的检测,利用多光束激光干涉仪XM-60实现了单轴热致定位误差的测量。
3) 通过对比机床关键点温度的实验值与仿真值,验证了有限元模型的准确性。通过对比XM-60测得的热致定位误差与本文所建立的考虑结构热变形及不考虑结构热变形的热致定位误差模型的仿真值,表明本文所建立的考虑结构热变形的热致定位误差模型正确,仿真值与实验值的整体重合度达90%以上。
本文所提出的综合考虑结构热变形的进给系统热致定位误差建模方法,为精密机床进给系统热平衡设计、热致定位误差的控制与补偿提供了参考。
| [1] | BRYAN J. International status of thermal error research[J]. CIRP Annals-Manufacturing Technology, 1990, 39(2): 645–656. DOI:10.1016/S0007-8506(07)63001-7 |
| [2] | MIN X, JIANG S. A thermal model of a ball screw feed drive system for a machine tool[J]. Journal of Mechanical Engineering Science, 2011, 225(1): 186–193. DOI:10.1177/09544062JMES2148 |
| [3] | WU C H, KUNG Y T. Thermal analysis for the feed drive system of a CNC machine center[J]. International Journal of Machine Tools & Manufacture, 2003, 43(15): 1521–1528. |
| [4] | WANG S, YANG Y, LI X, et al. Research on thermal deformation of large-scale computer numerical control gear hobbing machines[J]. Journal of Mechanical Science & Technology, 2013, 27(5): 1393–1405. |
| [5] | SUN L, REN M, HONG H, et al. Thermal error reduction based on thermodynamics structure optimization method for an ultra-precision machine tool[J]. International Journal of Advanced Manufacturing Technology, 2017, 88(5/8): 1267–1277. |
| [6] |
杨军, 施虎, 梅雪松, 等.
双驱伺服进给系统热误差的试验测量与预测模型构建[J]. 西安交通大学学报, 2013, 47(11): 53–59.
YANG Jun, SHI Hu, MEI Xue-song, et al. Measurement and modeling of thermal errors in dual-drive servo feed system[J]. Journal of Xi'an Jiaotong University, 2013, 47(11): 53–59. DOI:10.7652/xjtuxb201311010 |
| [7] |
夏军勇, 胡友民, 吴波, 等.
热弹性效应分析与机床进给系统热动态特性建模[J]. 机械工程学报, 2010, 46(15): 191–198.
XIA Jun-yong, HU You-min, WU Bo, et al. Analysis on thermoelastic domino effect and modeling on thermal dynamic characteristic of machine tools feed system[J]. Journal of Mechanical Engineering, 2010, 46(15): 191–198. |
| [8] | JIN C, WU B, HU Y, et al. Thermal characteristics of a CNC feed system under varying operating conditions[J]. Precision Engineering, 2015, 42: 151–164. DOI:10.1016/j.precisioneng.2015.04.010 |
| [9] | FUKADA S, FANG B, SHIGENO A. Experimental analysis and simulation of nonlinear microscopic behavior of ball screw mechanism for ultra-precision positioning[J]. Precision Engineering, 2011, 35(4): 650–668. DOI:10.1016/j.precisioneng.2011.05.006 |
| [10] | XU Z Z, LIU X J, CHOI C H, et al. A study on improvement of ball screw system positioning error with liquid-cooling[J]. International Journal of Precision Engineering & Manufacturing, 2012, 13(12): 2173–2181. |
| [11] |
冯文龙, 黄奕乔, 拓占宇, 等.
基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿[J]. 上海交通大学学报, 2016, 50(5): 710–715.
FENG Wen-long, HUANG Yi-qiao, TUO Zhan-yu, et al. Modeling of thermal induced grating positioning error of large machine tools based on temperature integral method and real-time compensation[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 710–715. |
| [12] | FENG W, LI Z, GU Q, et al. Thermally induced positioning error modelling and compensation based on thermal characteristic analysis[J]. International Journal of Machine Tools & Manufacture, 2015, 93(6): 26–36. |
| [13] | JIANG H, FAN K, YANG J. An improved method for thermally induced positioning errors measurement, modeling, and compensation[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75(9/12): 1279–1289. |
| [14] | LI T J, ZHAO C Y, ZHANG Y M. Adaptive real-time model on thermal error of ball screw feed drive systems of CNC machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(9/12): 3853–3861. |
| [15] |
王新孟, 杨军, 梅雪松, 等.
精密坐标镗床进给系统热误差分析与预测[J]. 西安交通大学学报, 2015, 49(10): 22–28.
WANG Xin-meng, YANG Jun, MEI Xue-song, et al. Analysis and prediction for thermal error of precision coordinate boring machine[J]. Journal of Xi'an Jiaotong University, 2015, 49(10): 22–28. DOI:10.7652/xjtuxb201510004 |
| [16] | ZHANG D, YANG J, MA C, et al. Experiment-based thermal error modeling method for dual ball screw feed system of precision machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(9/12): 1693–1705. |
| [17] |
日本精工株式会社.日本精工株式会社精密滚动轴承样本[EB/OL].(2009-07-20)[2018-07-01] http://www.nsk.com.cn.
NSK Ltd. Sample of precision rolling bearing of NSK Ltd[EB/OL]. (2009-07-20)[2018-07-01] http://www.nsk.com.cn. |
| [18] |
张大卫, 杨金玉, 高卫国, 等.
基于CAE机床结构工作空间热误差建模[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(2): 111–119.
ZHANG Da-wei, YANG Jin-yu, GAO Wei-guo, et al. Structural thermal error modeling of machine tools in working space based on CAE thermal analysis[J]. Journal of Tianjin University (Science and Technology), 2016, 49(2): 111–119. |
| [19] |
胡俊峰, 郝亚洲, 徐贵阳, 等.
考虑温度效应的微操作平台的建模与性能分析[J]. 工程设计学报, 2015, 22(2): 143–149.
HU Jun-feng, HAO Ya-zhou, XU Gui-yang, et al. Modeling and performance analysis of a micromanipulation stage considering temperature effects[J]. Chinese Journal of Engineering Design, 2015, 22(2): 143–149. DOI:10.3785/j.issn.1006-754X.2015.02.007 |



