逃生管道结构优化,一般是针对其结构的设计参数进行,并依靠相关经验,确定设计的基本方案,然后根据有限元仿真分析和实验来比较设计方案的安全性能[1-2]。然而,传统设计方法仅考虑了设计变量对逃生管道性能的影响,而忽略了噪声因素对逃生管道性能的影响[3-5]。在设计过程中因受到噪声因素影响,如材料特性存在波动或试验条件改变等,优化目标存在超出边界约束的可能性,从而导致产品设计失效[6-7]。
其中,以正交试验设计为基础的田口稳健性设计方法能够有效降低产品性能对噪声因素波动的灵敏度,从而提高其稳健性[8-12]。当落石与新型逃生管道发生碰撞时,往往存在一些不确定性因素,比如落石质量以及碰撞速度等[13]。在优化新型逃生管道的参数时,若不考虑这些不确定因素的影响,管道的安全性可能会随外界环境变化出现较大的波动,严重时可能造成逃生管道安全防护特性失效。在对新型逃生管道进行稳健性设计时,其优化目标需要同时满足结构轻量化和变形量最小的要求。田口稳健性设计方法虽然能够很好地解决单目标的稳健性设计问题,但对于解决新型逃生管道多目标的稳健性设计问题却并不是一种有效的方法。
因此,笔者结合田口稳健性设计方法和满意度函数[14],提出了一种基于满意度函数的多目标稳健性设计方法,将满意度函数方法引入新型逃生管道的参数优化设计中,以降低新型逃生管道结构对噪声因素随机波动的敏感性,提高新型逃生管道设计参数和目标函数的稳健性。
1 新型逃生管道有限元模型的建立和验证 1.1 新型逃生管道有限元模型建立结合传统圆钢式逃生管道在使用过程中遭受落石冲击破坏的情况,设计了一种新型逃生管道,其基本结构见图 1所示,该逃生管道上部区域的吸能空腔结构用以吸收落石的碰撞能量,达到保护逃生管道结构的目的。

|
| 图 1 新型逃生管道几何模型 Fig.1 New escape pipeline geometry model |
利用Hypermesh和LS-DYNA建立新型逃生管道和落石的有限元模型, 其中:新型逃生管道有限元模型采用B-T的四节点壳单元划分,网格单元大小为20 mm×20 mm,如图 2所示;落石有限元模型采用八节点的实体单元划分,网格单元大小为20 mm×20 mm×20 mm,如图 3所示。

|
| 图 2 新型逃生管道有限元模型 Fig.2 New escape pipeline finite element model |

|
| 图 3 落石有限元模型 Fig.3 Falling rock finite element model |
落石碰撞新型逃生管道时,两者之间存在接触。为了防止各接触部分间相互穿透,新型逃生管道和落石各自采用“Automatic single surface”接触定义,落石与新型逃生管道之间采用“Automatic surface to surface”接触定义,并设定动、静摩擦系数分别为0.3和0.2[15]。
仿真分析时,新型逃生管道采用各向同性的硬化材料进行模拟,其中材料硬化系数为1;落石采用非等质量的刚体模型进行模拟。落石与新型逃生管道的材料参数见表 1。
| 材料 | 密度/(kg/m3) | 弹性模量/MPa | 泊松比 | 屈服强度/MPa | 切线模量/MPa |
| 落石 | 2 500 | 0.4×105 | 0.2 | — | — |
| 逃生管道 | 7 800 | 2.1×105 | 0.25 | 235 | 1 000 |
在逃生管道遭受落石冲击过程中,采用Cowper-Symonds本构模型考虑应变率效应,即:
| $ \mathit{\sigma }=\left[ 1+{{\left( \frac{{\dot{\in }}}{C} \right)}^{\frac{1}{p}}} \right]{{\mathit{\sigma }}_{\text{o}}} $ | (1) |
式中:σ为单轴塑性应变率
为了验证所建有限元模型和所设材料参数的正确性,利用相关文献中落石和逃生管道的碰撞实验结果来验证[9, 17]。在实验以及计算中规定落石撞击逃生管道的速度v=11.7 m/s,落石质量m=0.30 t。当逃生管道的端部和中间位置遭受落石碰撞作用时,其接触碰撞区域将会发生凹陷变形,如图 4和图 5所示,结果表明,仿真试验的变形模式与碰撞实验的变形模式吻合良好。如图 6所示,当逃生管道变形稳定后所测得的仿真最大凹陷变形值为221.5 mm,理论计算的最大凹陷变形值为221.0 mm,误差很小。因此,有限元建模方法足够准确,其材料参数和建模方法可用于后续的新型逃生管道仿真分析。

|
| 图 4 碰撞位置位于端部时逃生管道凹陷变形模式对比 Fig.4 Comparison of sunken deformation mode of the escape pipeline with impact position at the end |

|
| 图 5 碰撞位置位于中部时逃生管道凹陷变形模式对比 Fig.5 Comparison of sunken deformation mode of the escape pipeline with impact position in the middle |

|
| 图 6 新型逃生管道凹陷变形值的仿真时程曲线 Fig.6 The simulation time-distance curve of the new escape pipeline sunken deformation value |
信噪比(signal-to-noise ratio)是用来衡量产品稳健性的评价指标,信噪比越大表示质量损失越小,产品稳健性越好。田口稳健性设计方法将质量特性分为3类:望小特性、望大特性和望目特性[18]。
假设产品的质量特性测量值分别为y1,y2,…,yn,T为目标值,则输出响应值的信噪比η可表示为:
| $ \eta =\left\{ \begin{align} & -10\lg \left( \frac{1}{n}\sum\limits_{\mu =1}^{n}{y_{\mu }^{2}} \right), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 望小特性 \\ & -10\lg \left( \frac{1}{n}\sum\limits_{\mu =1}^{n}{{{(\frac{1}{{{y}_{\mu }}})}^{2}}} \right), \ \ \ \ \ \ \ \ \ \ \ 望大特性 \\ & -10\lg \left( \frac{1}{n}\sum\limits_{\mu =1}^{n}{{{\left( {{y}_{\mu }}-T \right)}^{2}}} \right), \ \ \ \ \ 望目特性 \\ \end{align} \right. $ | (2) |
满意度函数法是将每次试验获得的响应函数Yi(i=1, 2, …, l)转换为一个特定的满意度函数di,其中0≤di≤1。结合产品质量特性响应,对于望小特性的满意度函数可表示为:
| $ {{d}_{i}}\left( {{Y}_{i}} \right)=\left\{ \begin{align} & 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{Y}_{i}}\le {{Y}_{i\ \min }} \\ & {{\left( \frac{{{Y}_{i}}-{{U}_{i}}}{{{Y}_{i\ \min }}-{{U}_{i}}} \right)}^{r}}, \ {{Y}_{i\ \min }}\le {{Y}_{i}}\le {{U}_{i}}r\ge 0 \\ & 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{Y}_{i}}\ge {{U}_{i}} \\ \end{align} \right. $ | (3) |
对于望大特性的满意度函数表示为:
| $ {{d}_{i}}\left( {{Y}_{i}} \right)=\left\{ \begin{align} & 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{Y}_{i}}\le {{L}_{i}} \\ & {{\left( \frac{{{Y}_{i}}-{{L}_{i}}}{{{Y}_{i\ \max }}-{{L}_{i}}} \right)}^{r}}, \ {{L}_{i}}\le {{Y}_{i}}\le {{Y}_{i\ \max }}r\ge 0 \\ & 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{Y}_{i}}\ge {{Y}_{i\ \max }} \\ \end{align} \right. $ | (4) |
对于望目特性的满意度函数表示为:
| $ {{d}_{i}}\left( {{Y}_{i}} \right)=\left\{ \begin{align} & {{\left( \frac{{{Y}_{i}}-{{L}_{i}}}{{{T}_{i}}-{{L}_{i}}} \right)}^{s}}, \ {{L}_{i}}\le {{Y}_{i}}\le {{T}_{i}} \\ & {{\left( \frac{{{Y}_{i}}-{{U}_{i}}}{{{T}_{i}}-{{U}_{i}}} \right)}^{t}}, \ {{T}_{i}}\le {{Y}_{i}}\le {{U}_{i}} \\ & 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{Y}_{i}}<{{L}_{i}}或{{Y}_{i}}\ge {{U}_{i}} \\ \end{align} \right. $ | (5) |
式中:r、s、t分别为各满意度函数的权重因子,Ui、Li分别为输出响应值的上、下限。
2.3 基于信噪比与满意度函数的多目标稳健性设计模型结合信噪比以及满意度函数,建立一种新的多目标稳健性设计模型。将各产品质量特性的信噪比转换为满意度,同时满意度又具有田口稳健性设计的望大特性,因此可通过望大特性的满意度函数进行转换,其表达式可定义为:
| $ {{d}_{i}}\left( \eta \right)=\left\{ \begin{align} & 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \eta \le {{\eta }_{\min }} \\ & {{\left( \frac{\eta -{{\eta }_{\min }}}{{{\eta }_{\max }}-{{\eta }_{\min }}} \right)}^{r}}, {{\eta }_{\min }}<\eta <{{\eta }_{\max }} \\ & 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\eta }_{\max }}\le \eta \\ \end{align} \right. $ | (6) |
式中:di(η)为输出响应函数Yi的满意度,0≤di(η)≤1,0≤r≤1,ηmax和ηmin为输出响应值对应的信噪比的上、下限值,其值可根据实际情况以及相关资料进行确定。
当针对多目标的满意度评价时,就需要将多个单目标的满意度函数转换成一个总的满意度函数进行评估,则总体满意度函数D(x)∈(0, 1)可表示为:
| $ D\left( x \right)={{\left( {{d}_{1}}\times {{d}_{2}}\times \ldots \times {{d}_{k}} \right)}^{1/k}} $ | (7) |
式中:dj为第j个子响应的满意度,其中j=1,2, …,k。
3 新型逃生管道参数优化设计 3.1 优化目标定义新型逃生管道因落石碰撞而产生凹陷变形,其最大凹陷变形值Δδ越小,则管道的残余逃生空间越大,越利于人员爬行通过。同时,当新型逃生管道的最大凹陷变形值越小时,其质量m越大,这说明管道安全性与轻量化存在矛盾。为了统一评价指标,可将最大凹陷变形值Δδ与质量m进行无量纲化处理(根据新型逃生管道人员爬行通过的安全性及结构轻量化原则,规定当最大凹陷变形值Δδ>140 mm、质量m>1.1 t时,输出响应的满意度值为0),统一转换为总体满意度作为评价指标来评价优化设计结果的优劣。
3.2 正交试验因素与水平的确定在保证新型逃生管道的圆管直径Φ=720 mm不变的前提下,初步确定新型逃生管道截面构型的设计因素——圆管壁厚A、薄壁外壳壁厚B、支撑板厚C、两支撑板之间的夹角D和圆管与薄壁外壳之间的间距E,为正交试验的试验因素,如图 7所示。

|
| 图 7 新型逃生管道截面构型 Fig.7 New escape pipeline section configuration |
在进行新型逃生管道正交试验分析时,每个因素选取4个水平,且各因素的水平范围为:7≤A≤10 mm;1≤B≤4 mm;1≤C≤4 mm;10°≤D≤40°;70≤E≤100 mm。按照正交试验的等间距取值原则,选取的新型逃生管道各因素及水平见表 2。
| 水平 | 因素 | ||||
| A/mm | B/mm | C/mm | D/(°) | E/mm | |
| 1 | 7 | 1 | 1 | 10° | 70 |
| 2 | 8 | 2 | 2 | 20° | 80 |
| 3 | 9 | 3 | 3 | 30° | 90 |
| 4 | 10 | 4 | 4 | 40° | 100 |
本次试验确定了新型逃生管道的5个重要因素为研究对象,并且每个因素有4个水平值,故选取L16(45)正交表进行正交试验,通过SPSS(statistical product and service solutions,统计产品与服务解决方案)软件生成正交表来安排试验,并对试验结果进行采集,如表 3所示。
| 试验序号 | 因素水平 | 评价指标 | |||||||
| A | B | C | D | E | 最大凹陷变形值Δδ/mm | 质量m/t | 总体满意度 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 248.44 | 0.726 | 0 | |
| 2 | 1 | 2 | 3 | 4 | 2 | 110.03 | 0.832 | 0.229 | |
| 3 | 1 | 3 | 4 | 2 | 3 | 27.41 | 0.906 | 0.38 | |
| 4 | 1 | 4 | 2 | 3 | 4 | 82.45 | 0.928 | 0.253 | |
| 5 | 2 | 1 | 4 | 3 | 2 | 59.22 | 0.898 | 0.326 | |
| 6 | 2 | 2 | 2 | 2 | 1 | 134.43 | 0.910 | 0.083 | |
| 7 | 2 | 3 | 1 | 4 | 4 | 130.57 | 0.964 | 0.091 | |
| 8 | 2 | 4 | 3 | 1 | 3 | 45.39 | 1.001 | 0.247 | |
| 9 | 3 | 1 | 2 | 4 | 3 | 130.40 | 0.972 | 0.089 | |
| 10 | 3 | 2 | 4 | 1 | 4 | 30.20 | 1.066 | 0.156 | |
| 11 | 3 | 3 | 3 | 3 | 1 | 72.66 | 1.067 | 0.120 | |
| 12 | 3 | 4 | 1 | 2 | 2 | 123.44 | 1.094 | 0.024 | |
| 13 | 4 | 1 | 3 | 2 | 4 | 73.62 | 1.096 | 0.044 | |
| 14 | 4 | 2 | 1 | 3 | 3 | 116.15 | 1.102 | 0 | |
| 15 | 4 | 3 | 2 | 1 | 2 | 92.50 | 1.161 | 0 | |
| 16 | 4 | 4 | 4 | 4 | 1 | 38.61 | 1.225 | 0 | |
根据试验结果进行极差分析,可以计算出新型逃生管道各设计因素对应的最大凹陷变形值Δδ和质量m的总体满意度的平均响应值,如图 8所示。

|
| 图 8 新型逃生管道各因素水平对应的总体满意度平均响应值 Fig.8 Overall satisfaction degree mean response value of each factor level of new escape pipeline |
根据总体满意度值越大越满意的原则,确定新型逃生管道正交试验的最优组合为A1B3C4D3E3, 即:圆管壁厚为7 mm、薄壁外壳壁厚为3 mm、支撑板厚为4 mm、两支撑板之间的夹角为30°和圆管与薄壁外壳之间的间距为90 mm。
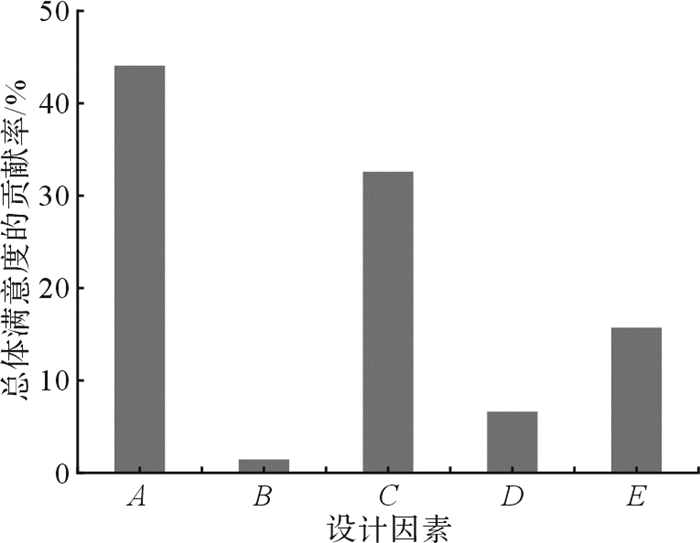
为确定各设计因素对总体满意度的影响程度,在极差分析的基础上,进行了方差分析。通过方差分析可计算出新型逃生管道各设计因素对应的总体满意度的贡献率,从而确定各设计因素的主次关系。由图 9可知,因素A对应的总体满意度的贡献率最大,各设计因素按对应的总体满意度的贡献率从大到小排序,依次为A、C、E、D和B。
|
| 图 9 新型逃生管道各设计因素对应的总体满意度的贡献率 Fig.9 Contribution rate of overall satisfaction degree corresponding to each design factor of the new escape pipeline |
一般性的参数优化设计并未考虑噪声因子对试验结果的影响,为了提高新型逃生管道结构的稳健性,根据正交试验的方差分析结果,选择对试验结果影响较大的3个因素(A、C、E)作为稳健性设计的可控因素,落石的质量以及碰撞速度为噪声因素进行多目标稳健性设计。
选取可控因素水平时,水平间隔范围过大可能导致结果不理想。因此,在正交试验所得最优参数值上下范围各取一个水平,以确定可控因素水平取值,结果如表 5所示。
| mm | |||
| 水平 | 因素 | ||
| A | C | E | |
| 1 | 6 | 3 | 80 |
| 2 | 7 | 4 | 90 |
| 3 | 8 | 5 | 100 |
在进行落石碰撞新型逃生管道正交试验分析时,碰撞条件为:速度v=11.7 m/s,落石质量m=0.30 t。噪声因素的水平范围选择过大也可能导致结果不理想。参考文献[15], 确定噪声因素水平取值在初始值上下浮动10%,如表 6所示。
| 水平 | 因素 | |
| F(落石质量容许误差)/t | G(碰撞速度容许误差)/(m/s) | |
| 1 | 0.27 | 10.53 |
| 2 | 0.30 | 11.70 |
| 3 | 0.33 | 12.87 |
结合田口稳健性设计方法,经过多目标稳健性设计后得到新型逃生管道多响应试验观测值的均值、信噪比以及满意度,见表 7所示。
| 试验序号 | 最大凹陷变形值 | 质量 | 总体满意度 | ||||||
| Δ |
η1 | d1(η1) | η2 | d2(η2) | D | ||||
| 1 | 36.016 | -30.065 | 0.95 | 0.819 | 1.734 | 0.81 | 0.88 | ||
| 2 | 68.302 | -36.684 | 0.19 | 0.824 | 1.681 | 0.79 | 0.39 | ||
| 3 | 82.268 | -38.373 | 0.00 | 0.780 | 2.158 | 1 | 0 | ||
| 4 | 29.663 | -29.662 | 1.00 | 0.937 | 0.056 | 0.06 | 0.24 | ||
| 5 | 57.405 | -36.109 | 0.26 | 0.894 | 0.973 | 0.47 | 0.35 | ||
| 6 | 71.113 | -37.528 | 0.10 | 0.889 | 1.022 | 0.49 | 0.22 | ||
| 7 | 49.911 | -34.718 | 0.42 | 1.008 | -0.069 | 0 | 0 | ||
| 8 | 59.254 | -36.104 | 0.26 | 0.997 | 0.026 | 0.043 | 0.11 | ||
新型逃生管道最大凹陷变形值和质量的总满意度的极差分析结果如表 8所示,经过多目标稳健性设计后各可控因素水平的最优组合为:A1C2E3, 即新型逃生管道的圆管壁厚为6 mm,支撑板厚度为4 mm,圆管与薄壁外壳之间的间距为100 mm。
| 水平 | 因素 | ||
| A | C | E | |
| 1 | 0.423 | 0.110 | 0.117 |
| 2 | 0.270 | 0.460 | 0.253 |
| 3 | 0.087 | 0.210 | 0.410 |
| 极差 | 0.336 | 0.35 | 0.293 |
同时,通过方差分析可计算出新型逃生管道稳健性设计各可控因素对应的总体满意度响应的贡献率(见图 10),从而确定出各因素的主次关系。由图 10可知,可控因素C对应的总体满意度的贡献率最大,各可控因素按对应的总体满意度的贡献率从大到小排序,依次为C、A和E。对于次要的可控因素,根据正交试验结果确定,最终得到稳健性最优的设计方案为:圆管壁厚为6 mm、薄壁外壳壁厚为3 mm、支撑板厚为4 mm、两支撑板之间的夹角为30°和圆管与薄壁外壳之间的间距为100 mm。

|
| 图 10 新型逃生管道稳健性设计中各可控因素对应的总体满意度的贡献率 Fig.10 Contribution rate of overall satisfaction degree corresponding to each controllable factor of the new escape pipeline |
为了验证多目标稳健性设计结果的准确性,将它与正交试验的最优结果进行对比分析,以落石的质量以及碰撞速度为变量,分别对稳健性优化设计前后的结果进行二因素三水平的正交试验,然后计算相应的响应平均值和响应值的标准差,最后对稳健性设计前后的响应均值和响应值的标准差进行对比分析,从而判断多目标稳健性设计结果的准确性。
根据表 6所示因素水平值,选用L9(23)的正交表分别对稳健性设计前后的新型逃生管道进行9组仿真试验,结果如表 9所示。
| 试验序号 | 因素水平 | 最大凹陷变形值Δδ/mm | 质量m/t | |||||
| F | G | 优化前 | 优化后 | 优化前 | 优化后 | |||
| 1 | 1 | 2 | 16.178 | 18.906 | 0.906 | 0.819 | ||
| 2 | 3 | 1 | 31.750 | 30.335 | 0.906 | 0.819 | ||
| 3 | 2 | 2 | 30.584 | 34.147 | 0.906 | 0.819 | ||
| 4 | 2 | 3 | 47.679 | 53.939 | 0.906 | 0.819 | ||
| 5 | 1 | 3 | 24.519 | 24.388 | 0.906 | 0.819 | ||
| 6 | 2 | 1 | 27.603 | 20.432 | 0.906 | 0.819 | ||
| 7 | 1 | 1 | 15.776 | 18.639 | 0.906 | 0.819 | ||
| 8 | 3 | 2 | 59.412 | 52.754 | 0.906 | 0.819 | ||
| 9 | 3 | 3 | 72.678 | 70.602 | 0.906 | 0.819 | ||
| 响应平均值μ | 36.242 | 36.016 | 0.906 | 0.819 | ||||
| 响应值标准差σ | 18.502 | 17.658 | 0 | 0 | ||||
由表 10结果可知,经过多目标稳健性设计后,在噪声因素的影响下,新型逃生管道的最大凹陷变形值Δδ的响应平均值由原来的36.242 mm减小到36.016 mm,减小了0.6%;响应值标准差σ由原来的18.502 mm降低到17.658 mm,降低了4.6%;信噪比由原来的-31.733增大到-30.065,提高了5.3%;新型逃生管道的质量由原来的0.906 t减小到0.819 t,减小了9.6%。上述结果说明,采用基于满意度函数的多目标稳健性设计方法对新型逃生管道进行稳健性设计后,其最大凹陷变形值对落石质量以及碰撞速度波动的敏感性降低,说明碰撞安全的稳健性得到了一定程度的提高,抗干扰能力增强。同时,稳健性设计后实现了新型逃生管道轻量化的目的。
| 对比项 | 最大凹陷变形值 | 质量m/t | ||
| 响应平均值μ/mm | 响应值标准差σ/mm | 信噪比η | ||
| 稳健性设计前 | 36.242 | 18.502 | -31.733 | 0.906 |
| 稳健性设计后 | 36.016 | 17.658 | -30.065 | 0.819 |
人体测量学研究表明[19],人体能够爬行通过的圆形管道的最小直径为585 mm。因此,遭受落石撞击产生凹陷变形后逃生管道的内径必须大于585 mm,才能保证施工人员安全地爬行通过。
5.2 新型逃生管道与传统逃生管道安全性能对比满足要求的传统逃生管道基本几何参数:直径为800 mm,壁厚为10 mm,管道长为5.6 m,质量为1.1 t。根据文献[17]的分析结果可知,当逃生管道遭受落石的冲击时,在其端部位置的顶部产生的凹陷变形最大。图 11给出了2种不同类型逃生管道的最大凹陷变形值,由图 11可知,新型逃生管道的最大凹陷变形值要小于传统逃生管道的。

|
| 图 11 新型逃生管道与传统逃生管道最大凹陷变形值对比 Fig.11 Comparison of maximum sunken deformation value between new escape pipeline and traditional escape pipeline |
1) 结合信噪比与满意度函数,建立了一种新的多目标稳健性设计模型,提出了一种基于满意度函数的多目标稳健性设计方法。
2) 运用提出的基于满意度函数的多目标稳健性设计方法对新型逃生管道进行多目标稳健性设计。稳健性设计后新型逃生管道的响应平均值和响应值标准差均减小、信噪比增大,这说明新型逃生管道结构更加稳健。
| [1] |
杨飚, 庄富盛.
新型隧道逃生管道设计模拟及现场试验研究[J]. 公路交通技术, 2013(2): 111–114.
YANG Biao, ZHUANG Fu-sheng. Simulation and on-site experimental research of new escape pipeline design in tunnels[J]. Technology of Highway and Transport, 2013(2): 111–114. DOI:10.3969/j.issn.1009-6477.2013.02.027 |
| [2] |
李祝龙, 李鹏飞, 梁养辉, 等.
波纹钢管用作隧道逃生管道时的模拟分析[J]. 公路交通科技, 2017, 34(8): 105–113.
LI Zhu-long, LI Peng-fei, LIANG Yang-hui, et al. Simulation analysis of corrugated steel pipe used as tunnel escape pipe[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 105–113. |
| [3] | HUANG M L, HUNG Y H, YANG Z S. Validation of a method using Taguchi, response surface, neural network, and genetic algorithm[J]. Measurement, 2016, 94: 284–294. |
| [4] | SUN B Y, XIAO J B, LI Z B, et al. An analysis of soil detachment capacity under freeze-thaw conditions using the Taguchi method[J]. Catena, 2018, 162: 100–107. DOI:10.1016/j.catena.2017.11.025 |
| [5] | SHETTY S, NILSSON L. Multiobjective reliability-based and robust design optimisation for crashworthiness of a vehicle side impact[J]. International Journal of Vehicle Design, 2015, 67(4): 347–367. DOI:10.1504/IJVD.2015.070410 |
| [6] |
陈永亮, 刘双, 韩瑶, 等.
造船液压机压头锁紧碟簧疲劳寿命稳健优化设计[J]. 工程设计学报, 2012, 19(3): 161–165.
CHEN Yong-liang, LIU Shuang, HAN Yao, et al. Fatigue life robust design of clamping disc springs for a shipbuilding hydraulic press head[J]. Chinese Journal of Engineering Design, 2012, 19(3): 161–165. DOI:10.3785/j.issn.1006-754X.2012.03.001 |
| [7] |
苗怡然, 高良田, 刘峰, 等.
基于参数化的水下航行器外形稳健性优化[J]. 哈尔滨工程大学学报, 2018, 39(4): 622–628.
MIAO Yi-ran, GAO Liang-tian, LIU Feng, et al. Robust optimization design of underwater vehicle shape based on parameterization[J]. Journal of Harbin Engineering University, 2018, 39(4): 622–628. |
| [8] |
胡俊峰, 杨展宏, 徐贵阳.
基于响应面法的微操作平台可靠性稳健设计[J]. 振动与冲击, 2017, 36(15): 245–252.
HU Jun-feng, YANG Zhan-hong, XU Gui-yang. Reliability-based robust design of a micro-manipulation stage with response surface method[J]. Journal of Vibration and Shock, 2017, 36(15): 245–252. |
| [9] |
朱茂桃, 朱彩帆, 郭佳欢, 等.
基于6σ稳健性的轧制差厚板车门优化设计[J]. 中国机械工程, 2017, 28(8): 996–1001.
ZHU Mao-tao, ZHU Cai-fan, GUO Jia-huan, et al. Optimization design of TRB car doors based on 6σ robustness[J]. China Mechanical Engineering, 2017, 28(8): 996–1001. DOI:10.3969/j.issn.1004-132X.2017.08.020 |
| [10] | ABHIRAM D R, GANGULI R, HARURSAMPATH D, et al. Robust design of small unmanned helicopter for hover performance using Taguchi method[J]. Journal of Aircraft, 2018, 55(4): 1746–1753. DOI:10.2514/1.C034539 |
| [11] | LEE S, KIM K, Cho S, et al. Optimal design of interior permanent magnet synchronous motor considering the manufacturing tolerances using Taguchi robust design[J]. IET Electric Power Applications, 2014, 8(1): 23–28. |
| [12] | CHATSIRIRUNGRUANG P. Application of genetic algorithm and Taguchi method in dynamic robust parameter design for unknown problems[J]. International Journal of Advanced Manufacturing Technology, 2010, 47(9/12): 993–1002. |
| [13] |
胡浩军, 狄先均, 李家泰, 等.
隧道逃生管道设计中的圆管冲击计算[J]. 现代隧道技术, 2008, 45(S1): 272–274.
HU Hao-jun, DI Xian-jun, LI Jia-tai, et al. Calculation of pipe impact in tunnel escape pipeline design[J]. Modern Tunnelling Technology, 2008, 45(S1): 272–274. |
| [14] | DERRINGER G, SUICH R. Simultaneous optimization of several response variables[J]. Journal of Quality Technology, 1980, 12(4): 214–219. DOI:10.1080/00224065.1980.11980968 |
| [15] | YIN H, XIAO Y, WEN G, et al. Multi-objective robust optimization of foam-filled bionic thin-walled structures[J]. Thin-Walled Structures, 2016, 109: 332–343. |
| [16] | PENG Y, DENG W, XU P, et al. Study on the collision performance of a composite energy-absorbing structure for subway vehicles[J]. Thin-Walled Structures, 2015, 94: 663–672. |
| [17] |
张瑜, 丁庆荣, 狄先均, 等.
隧道逃生管道的冲击实验与仿真模拟[J]. 华中科技大学学报(城市科学版), 2010, 27(2): 87–89, 94.
ZHANG Yu, DING Qing-rong, DI Xian-jun, et al. Impact experiment and computer simulation of tube for design of escape passage in tunnel construction[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2010, 27(2): 87–89, 94. DOI:10.3969/j.issn.2095-0985.2010.02.020 |
| [18] | VINING G G, MYERS R H. Combining Taguchi and response surface philosophies:a dual response approach[J]. Journal of Quality Technology, 1990, 22(1): 38–45. |
| [19] |
阿尔文·R·蒂利.人体工程学图解: 设计中的人体因素[M].宋涛, 译.北京: 中国建筑工业出版社, 1998: 32-334.
ALVINR Tilley. The measure of man & woman: human factors in design[M]. Translated by SONG Tao. Beijing: China Architecture & Building Press, 1998: 32-334. |



