引用本文
李玉龙, 孙付春.
泵用齿轮副困油卸荷的H型侧隙结构研究[J]. 工程设计学报, 2019, 26(1): 15-19, 28.
LI Yu-long, SUN Fu-chun. Research on H-shaped backlash structure on gear pairs for relief of trapped-oil in pumps[J]. Chinese Journal of Engineering Design, 2019, 26(1): 15-19, 28.
泵用齿轮副困油卸荷的H型侧隙结构研究
1.
宿迁学院 机电工程学院, 江苏 宿迁 223800;
2. 成都大学 机械工程学院, 四川 成都 610106
2. 成都大学 机械工程学院, 四川 成都 610106
摘要:
为满足齿侧间隙在外啮合齿轮泵传动性能和困油性能上的不同需要，提出了一种位于从动齿轮非工作面上的"大-小-大"H型侧隙结构。首先，通过对齿轮泵困油过程的分析，从双齿啮合区内两困油区的连通和单齿啮合区内困油性能的完善两方面出发，建立了连通用和卸荷用侧隙的面积计算公式；然后，根据所确定的最小侧隙面积，计算出H型侧隙结构的几何尺寸；最后，提出一种双微圆贯通型卸荷槽，实现双齿啮合区的困油卸荷。实例分析结果表明：无论侧隙大小如何变化，都不存在绝对连通和绝对卸荷，只有在一定许可压差下的相对连通和相对卸荷；即使侧隙连通区实现了真正的连通，该区内的困油问题仍没有得到解决，需辅以额外的卸荷槽加以卸荷；"大-小-大"H型侧隙结构，既满足了齿轮传动的性能要求，也极大地提高了泵的困油性能；齿轮齿槽根部的两端面圆形除料和双微圆对称贯通型卸荷槽能提供足够的卸荷面积。研究结果表明H型侧隙结构、齿槽根部的两端面圆形除料和双微圆对称贯通型卸荷槽的组合充分满足了齿轮传动性能和困油性能的要求，且具有结构简单、易加工等特点，为消除外啮合齿轮泵困油的危害提供了一种新的卸荷结构。
关键词:
齿轮泵
连通侧隙
卸荷侧隙
H型侧隙
侧隙面积
困油性能
卸荷槽
基金项目: 四川省教育厅自然科学重点资助项目（16ZA0382）；北京卫星制造厂资助项目（20804）
Research on H-shaped backlash structure on gear pairs for relief of trapped-oil in pumps
1. School of Mechanical and Electrical Engineering, Suqian College, Suqian 223800, China;
2. School of Mechanical Engineering, Chengdu University, Chengdu 610106, China
2. School of Mechanical Engineering, Chengdu University, Chengdu 610106, China
Abstract:
In order to meet different requirements of backlash in gear transmission performance and trapped-oil performance of external gear pumps, an H-shaped backlash structure with large-small-large gap on the non-working surface of driven gear is put forward. Firstly, after analyzing the trapped-oil process of gear pumps, two kinds of area formulas necessary for connection and relief backlash were derived under the connection condition of two different trapped-oil volumes in double teeth meshed range and the relief condition of trapped-oil performance in single tooth meshed range. Secondly, through the derived minimum backlash area, the geometric size of the H-shaped backlash structure was calculated. Finally, a feed-through relief groove with asymmetric micro circular profile was invented for trapped-oil relief in double teeth meshed range. It was showed that whatever the backlash size was, the absolute connection and the absolute trapped-oil relief were not existed, but only the relative connection and relative relief under a certain permission pressure difference. Even if the connection was really satisfied in the backlash connection range, the trapped-oil phenomenon in this range was still not solved, and it must be unloaded by supplemented relief groove. On the premise of keeping transmission performance of gear pairs, the trapped-oil performance of pumps was greatly improved by the H-shaped backlash structure, combined with the circular material removal near the root circle on double gear end faces, larger relief area was built by the feed-through relief groove with double micro circular profiles symmetrical about pitch circle node. It is concluded that the combination of the H-shaped backlash structure and the circular material removal structure and the feed-through relief groove structure can fully meet the requirements of gear transmission performance and trapped-oil performance, and it has the characteristics of simple structure and easy processing. It provides a new relief structure for eliminating the hazards of trapped-oil in external meshing gear pump.
Key words:
gear pump
connection backlash
relief backlash
H-shaped backlash
backlash area
trapped-oil performance
relief groove
渐开线外啮合直齿轮泵是一种结构最简单、成本最低、应用最广泛的回转容积泵，简称为齿轮泵[1]，其核心部件为一副同尺寸的主、从动齿轮。该齿轮副因常规的传动要求，多采用0.03 mm左右的小侧隙[2]；但考虑泵容积率[3-5]、振动性能[6-8]、困油性能[9-12]等综合要求，尤其在高困油性能要求下，该齿轮副多采用0.2 mm的大侧隙[2, 13]。因此在传动性能所要求的小侧隙与高困油性能所要求的大侧隙之间，存在选择性矛盾，文献[14]给出了解决方案，但其侧隙结构的加工较复杂。为此，本文提出易加工的H型侧隙结构，以期实现齿轮泵的高传动性能高困油性能。
1 齿轮泵困油过程及其侧隙用途图 1所示为齿轮泵困油过程及其侧隙的用途。图中：o1、o2分别为主、从齿轮的轮心，V1、V2分别为主、从齿轮侧困油区内的困油容积，mm3；p1、p2分别为主、从齿轮侧困油区内的困油压力，MPa；主齿轮啮合点到啮合线端点的距离为s，mm；“■”表示啮合点，“●”表示侧隙点。文献[2]对图 1给出了详细定义：(a)—(e)、(d)—(f)—(b)分别为主、从齿轮的困油子过程；(a)—(f)—(a)为齿轮泵一个完整的困油过程。为便于描述，图 1中均以轴向截面上的啮合点和侧隙点表示实际的轴向啮合线和轴向侧隙线，下同。
|
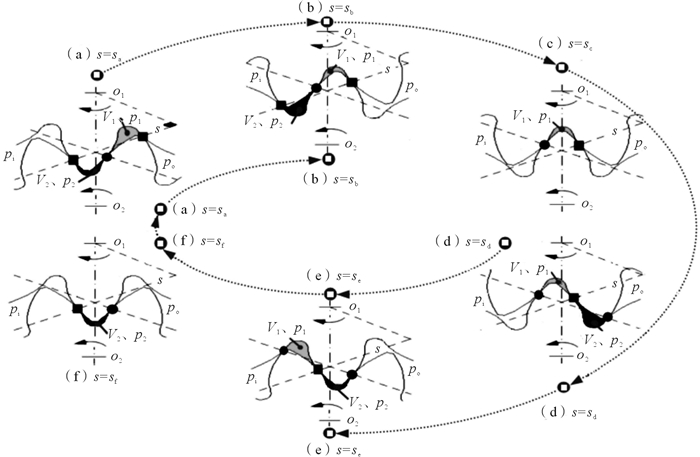
| 图 1 齿轮泵困油过程及其侧隙的用途 Fig.1 Trapped-oil process and different applications of backlash in gear pumps |
设基节、啮合线长度为Lb、L，根切重合度为εw[15-16]，可得：
| $ \left\{ \begin{array}{l} {s_{\rm{a}}} = 0.5\left( {L - {L_{\rm{b}}}{\varepsilon _{\rm{w}}}} \right)\\ {s_{\rm{b}}} = {s_{\rm{a}}} + {L_{\rm{b}}}\left( {{\varepsilon _{\rm{w}}} - 1} \right)\\ {s_{\rm{c}}} = 0.5L - 0.25{L_{\rm{b}}}\\ {s_{\rm{d}}} = 2{s_{\rm{c}}} - {s_{\rm{b}}}\\ {s_{\rm{e}}} = 2{s_{\rm{c}}} - {s_{\rm{a}}}\\ {s_{\rm{f}}} = {s_{\rm{c}}} + 0.5{L_{\rm{b}}} \end{array} \right. $ |
其中：[sa, sb]表示2个困油区通过侧隙连通的区间，简称为连通用侧隙区；[sb, sf]和[sf, sa]表示困油区通过侧隙连通出油口或进油口侧卸荷槽的区间，简称为卸荷用侧隙区。
2 许可压差下最小侧隙面积 2.1 卸荷用最小侧隙面积图 1(b)—(f)—(a)所示的卸荷用侧隙区内，单一困油区均由1个啮合点和1个侧隙点围成。其中，V1、V2的变化率(简称为困油流量)为：
| $ \left\{ \begin{array}{l} {Q_1} = {\rm{d}}{V_1}/{\rm{d}}t = \omega b{L_{\rm{b}}}\left( {s - {s_{\rm{c}}}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s \in \left[ {{s_{\rm{b}}},{s_{\rm{c}}}} \right]\\ {Q_2} = {\rm{d}}{V_2}/{\rm{d}}t = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \omega b{L_{\rm{b}}}\left( {s + {L_{\rm{b}}} - {s_{\rm{f}}}} \right),\\ \omega b{L_{\rm{b}}}\left( {s - {s_{\rm{f}}}} \right), \end{array}&\begin{array}{l} s \in \left[ {{s_{\rm{f}}} - {L_{\rm{b}}},{s_{\rm{a}}}} \right]\\ s \in \left[ {{s_{\rm{d}}},{s_{\rm{f}}}} \right] \end{array} \end{array}} \right. \end{array} \right. $ |
式中：ω为角速度，rad/s；b为齿宽，mm。
Q1、Q2的峰值均为：
| $ {Q_{{\rm{ts}}}} = \omega b{L_{\rm{b}}}\left( {{s_{\rm{c}}} - {s_{\rm{a}}}} \right) = 0.25\omega bL_{\rm{b}}^2\left( {2{\varepsilon _{\rm{w}}} - 1} \right) $ | (1) |
式中：Qts为卸荷用侧隙区内的最大困油流量[1]，mm3/s。
要使侧隙能实现困油的充分卸荷，根据侧隙内最大困油流量Qts等于通过侧隙的交换流量(简称为侧隙流量)Qhd，可得卸荷用最小侧隙面积Acs为：
| $ {A_{{\rm{cs}}}} = {Q_{{\rm{ts}}}}/\left| {C\sqrt {2\Delta p/\rho } \times {{10}^3} - U} \right|,U = {r_{\rm{b}}}\omega \tan \alpha ' $ | (2) |
式中：α′为压力角，rad；rb为基圆半径，mm；Δp为被许可的困油压力差，简称为许可压差，Pa；C为流量系数；U为等效卷吸速度，mm/s；ρ为介质密度，kg/m3。
2.2 连通用最小侧隙面积图 1(a)—(b)所示的连通用侧隙区内，2个困油区由2个啮合点形成一体化的密闭容积V。区间内任一位置上，Q1、Q2始终分别与侧隙流量Qhd处于各自的平衡状态。
假设困油区膨胀时Q1、Q2为正，Qhd以流出为正；那么，联立Q1+Qhd=0和Q2-Qhd=0，可得连通用最小侧隙面积Acd为：
| $ {A_{{\rm{cd}}}} = 0.25\omega bL_{\rm{b}}^2\left| {C\sqrt {2\Delta p/\rho } \times {{10}^3} + U} \right| $ | (3) |
此时，连通区的困油流量Q及其峰值Qtd分别为：
| $ \left\{ \begin{array}{l} Q = {Q_1} + {Q_1} = \omega b{L_{\rm{b}}}\left[ {\left( {s - {s_c}} \right) + \left( {s + {L_{\rm{b}}} - {s_{\rm{f}}}} \right)} \right]\\ {Q_{{\rm{td}}}} = \omega bL_{\rm{b}}^2\left( {{\varepsilon _{\rm{w}}} - 1} \right) \end{array} \right. $ |
由式(1)至(3)和εw>1可知，Acd>Acs。故在许可压差Δp下，既要实现困油的充分卸荷，又要实现2个困油区的真正连通，所需侧隙的面积为：
| $ {A_{\rm{c}}} = \max \left( {{A_{{\rm{cd}}}},{A_{{\rm{cs}}}}} \right) = {A_{{\rm{cd}}}} $ |
如图 2所示，在从动齿轮非工作齿面的两端分别挖去一块深度为cb的除料。其中，除料截面轮廓的外侧直接采用齿面轮廓，内侧为过齿顶点且与过渡曲线相切的直线段，这样形成的最小侧隙为ch，此时并没有破坏齿轮的传动强度和传动关系。如此，将从动齿轮非工作面上的形成侧隙在齿宽方向上分成“大侧隙-小侧隙-大侧隙”三部分：两端为cb宽度的大侧隙ch，实现困油卸荷；中间为(b-2cb)宽度的小侧隙co，实现传动要求。因此，形成所谓的H型侧隙结构，所需除料深度cb为：
| $ {c_{\rm{b}}} = \left( {{A_{\rm{c}}} - b{c_{\rm{o}}}} \right)/\left( {2{c_{\rm{h}}}} \right) $ |
|
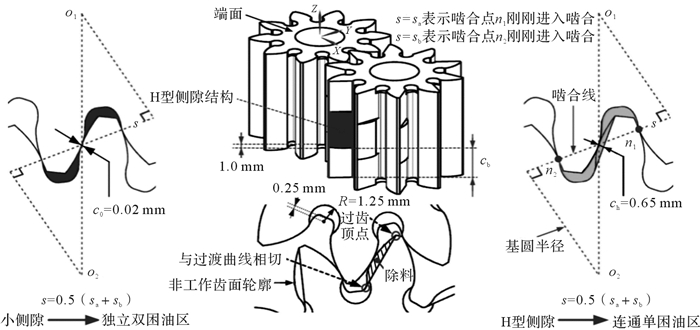
| 图 2 从动齿轮非工作面上的H型侧隙结构 Fig.2 H-shaped backlash structure on the non-working surface of driven gear |
在侧隙连通区内，对于连通困油容积V，除通过卸荷槽的卸荷流量(简称为卸荷槽流量)外，不考虑其它流量，如轴向间隙流量、啮合间隙流量等。其实，这些流量相对卸荷槽流量而言，要小2~4个数量级[1]，忽略其影响是合理的。在任一位置处，困油流量与卸荷槽流量始终处于平衡状态，则有：
| $ {Q_{\rm{t}}} + Q = 0 $ |
式中：Qt卸荷槽流量，mm3/s。
卸荷槽流量Qt可表示为[2]：
| $ {Q_{\rm{t}}} = \left\{ \begin{array}{l} C{S_{\rm{t}}}S\left( {\Delta p} \right)\sqrt {2\left| {\Delta p} \right|/\rho } \Delta p = p - {p_{\rm{o}}},s \in \left[ {{s_{\rm{a}}},\left( {{s_{\rm{a}}} + {s_{\rm{b}}}} \right)/2} \right]\\ C{S_{\rm{t}}}S\left( {\Delta p} \right)\sqrt {2\left| {\Delta p} \right|/\rho } \Delta p = p - {p_{\rm{i}}},s \in \left[ {\left. {{s_{\rm{a}}} + {s_{\rm{b}}}} \right)/2,{s_{\rm{b}}}} \right] \end{array} \right. $ | (4) |
| $ S\left( {\Delta p} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\Delta p \ge 0\\ - 1,\;\;\;\;\Delta p < 0 \end{array} \right. $ | (5) |
式中：St为Δp下所需要的卸荷面积，mm2；p为连通困油区的困油压力，Pa。
联立公式(4)和(5)可得所需的卸荷面积、所允许的压差及连通困油区的困油压力为：
| $ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} {S_{\rm{t}}} = \sqrt {\rho {Q^2}/\left( {2{C^2}\left| {\Delta p} \right|} \right)} \\ \left| {\Delta p} \right| = \rho {Q^2}/\left( {2{C^2}S_{\rm{t}}^2} \right) \end{array} \right.}\\ {p = \left\{ \begin{array}{l} {p_{\rm{o}}} + S\left( {\Delta p} \right)\left| {\Delta p} \right|,s \in \left[ {{s_{\rm{a}}},0.5\left( {{s_{\rm{a}}} + {s_{\rm{b}}}} \right)} \right]\\ {p_{\rm{i}}} + S\left( {\Delta p} \right)\left| {\Delta p} \right|,s \in \left[ {0.5\left( {{s_{\rm{a}}} + {s_{\rm{b}}}} \right),{s_{\rm{b}}}} \right] \end{array} \right.} \end{array} $ |
为了获得更大的卸荷面积，在主、从动齿轮两侧端面上每个齿槽的根部位置均挖去一定形位尺寸的圆形除料，如图 2所示。该圆形除料的特征为：1)在齿槽内左右对称；2)半径R=1.25 mm，除料深度为1.0 mm；3)圆形除料的圆心到根圆的距离为0.125m mm，其中m为模数。挖去圆形除料的目的在于扩大齿顶间隙以获得更大的卸荷面积和使得卸荷槽加工刀具的尺寸标准化。经过这样的处理，原0.25m mm顶隙扩大到0.75m mm。
采用双微圆对称贯通型卸荷槽，如图 3所示。贯通表示该卸荷槽贯通两侧的浮动侧板，从而将内侧的困油与外侧的补偿油连通起来。
|
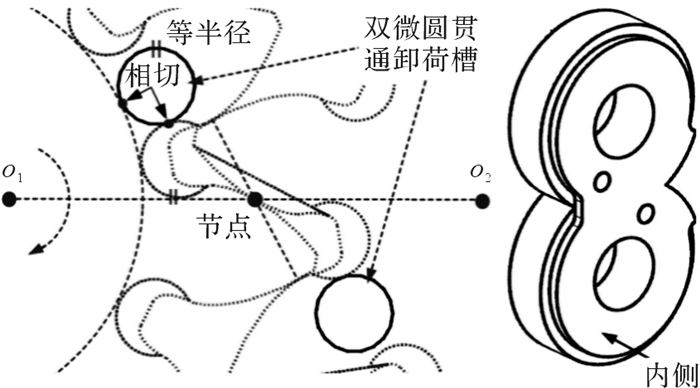
| 图 3 双微圆对称贯通型卸荷槽 Fig.3 Feed-through relief groove with double micro circular profiles symmetrical about pitch circle node |
在图 2所示的s=0.5(sa+sb)位置，采用图 3所示的两点相切和等半径的约束条件，确定卸荷槽的形位尺寸。该型卸荷槽属于微型卸荷槽，相对于常规的矩形、圆形卸荷槽而言，它更利于保护进、出口腔的密封路径和提高泵的容积效率。
5 实例运算及分析实例运算时原始参数为：po=3 MPa，pi=0.1 MPa，额定转速n=3 000 r/min，ω=314.16 rad/s，m=2 mm，齿数z=10，齿顶高系数为1.16，顶隙系数为0.25，压力角为20°，α′=29.6°，变位系数为0.493，εw=1.15，b=21.7 mm，co=0.02 mm，由齿轮副三维模型测得ch=0.65 mm，ρ=870 kg/m3，μ=0.09 Pa·s，C=0.62。
由三维模型测量不同位置(即不同s)下的卸荷面积，并拟合出的卸荷面积St(s)曲线，如图 4(a)所示；不同许可压差下大侧隙的宽度变化如图 4(b)所示；不同位置下困油压力的变化如图 4(c)所示。图 4(c)中，p的峰值为3.38 MPa，相对于进口压力，其变化率仅为(3.38-po)/po=12.7%，加上这一位置处的困油流量接近于0 mm3/s，其它流量再小，也将发挥较大的卸荷作用，故实际变化率小于12.7%，符合设计要求。另峰值发生在最小困油容积的位置附近，与文献结果一致[3, 17-18]。p的谷值为-0.28 MPa，基于上述原因，实际的困油压力最小值高于该谷值，且适量的真空度也利于提高泵的自吸能力，符合设计要求。
|
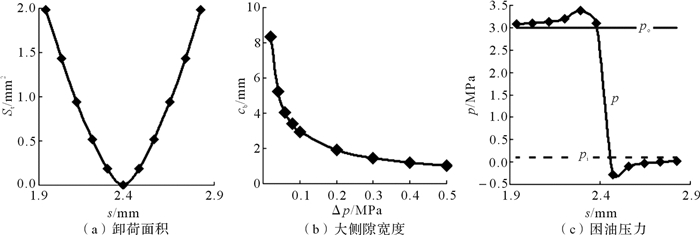
| 图 4 H型侧隙结构齿轮泵的卸荷面积、大侧隙宽度和困油压力变化曲线 Fig.4 Variation curves of relief area, wide backlash width and oil trapping pressure curve of gear pump with H-shaped backlash |
1) 无论侧隙的大小如何，侧隙连通区内的绝对连通和侧隙卸荷区的绝对卸荷并不存在，只有在一定许可压差下的相对连通和相对卸荷。
2) 即使侧隙满足了侧隙连通区内的连通要求，但该区间内的困油问题仍没有得到解决，必须辅以卸荷槽加以卸荷，以缓解困油现象。
3) 从动轮上“大-小-大”的H型侧隙结构，保证了齿轮的传动关系和传动性能，提高了泵的困油性能。
4) 两端除料和卸荷槽的形状均为圆形，相较于传统卸荷槽，加工更简单。
参考文献
| [1] |
李玉龙.外啮合齿轮泵困油机理、模型及试验研究[D].合肥: 合肥工业大学机械工程学院, 2009: 1-5.
LI Yu-long. Mechanism, modeling and experiment investigation of trapped oil in external gear pump[D]. Hefei: Hefei University of Technology, School of Mechanical Engineering, 2009: 1-5. |
| [2] |
孙付春, 李玉龙, 文昌明, 等.
齿轮泵侧隙卸荷的界定标准与验证[J]. 农业工程学报, 2017, 33(20): 61–66.
SUN Fu-chun, LI Yu-long, WEN Chang-ming, et al. Demarcated standard and verification of backlash off-load in external gear pumps[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(20): 61–66. DOI:10.11975/j.issn.1002-6819.2017.20.008 |
| [3] | YANADA H, ICHIKAWA T, ITSUJI Y. Study of the trapping of fluid in a gear pump[J]. Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power & Energy, 1987, 201(11): 39–45. |
| [4] | EATON M, KEOGH P S, EDGE K A. The modeling, prediction and experimental evaluation of gear pump meshing pressures with particular reference to aero-engine fuel pumps[J]. Proceedings of the Institution of Mechanical Engineers Part Ⅰ-Journal of Systems and Control Engineering, 2008, 220(5): 365–379. |
| [5] |
李玉龙, 刘春艳, 王生.
大侧隙外啮合齿轮泵的困油特性和流量特性[J]. 机械科学与技术, 2015, 34(3): 454–458.
LI Yu-long, LIU Chun-yan, WANG Sheng. The trapped oil characteristics and flow characteristics with large backlash gap in external gear pumps[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(3): 454–458. |
| [6] | MUCCHI E, RIVOLA A, DALPIAZ G. Modelling dynamic behaviour and noise generation in gear pumps:procedure and validation[J]. Applied Acoustics, 2014, 77: 99–111. DOI:10.1016/j.apacoust.2013.10.007 |
| [7] | MUCCHI E, DALPIAZ G. Elasto-dynamic analysis of a gear pump-Part Ⅲ:Experimental validation procedure and model extension to helical gears[J]. Mechanical Systems & Signal Processing, 2015, 50-51(9): 174–192. |
| [8] | BORGHI M, MILANI M, PALTRINIERI F. The influence of the notch shape and number on proportional directional control valve metering characteristics[C]//SAE Commercial Vehicle Engineering Congress & Exhibition, Chicago, Lllinois, Oct. 26-28, 2004. |
| [9] |
李玉龙, 孙付春.
齿轮泵齿侧间隙与卸荷槽间距关系的定量分析[J]. 农业工程学报, 2012, 28(22): 63–68.
LI Yu-long, SUN Fu-chun. Quantitative analysis of relationship between backlash value and distance of two relief grooves in external gear pump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(22): 63–68. DOI:10.3969/j.issn.1002-6819.2012.22.010 |
| [10] |
李玉龙, 孙付春.
齿轮泵困油的分析模型及侧隙计算[J]. 排灌机械工程学报, 2011, 29(2): 118–122.
LI Yu-long, SUN Fu-chun. Analysis model on trapped oil and backlash calculation in external gear pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(2): 118–122. DOI:10.3969/j.issn.1674-8530.2011.02.006 |
| [11] |
李玉龙.
外啮合齿轮泵侧隙流量的精确计算[J]. 排灌机械工程学报, 2013, 31(8): 656–661.
LI Yu-long. Accurate calculation of backlash flow in external gear pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(8): 656–661. |
| [12] |
李玉龙, 唐茂.
困油压力对齿轮泵流量脉动的影响分析[J]. 农业工程学报, 2013, 29(20): 60–66.
LI Yu-long, TANG Mao. Influence analysis of trapped oil pressure on flow pulsation in external gear pumps[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(20): 60–66. DOI:10.3969/j.issn.1002-6819.2013.20.009 |
| [13] |
何存兴.
液压元件[M]. 北京: 机械工业出版社, 1985: 45.
HE Cun-xing. Hydraulic components[M]. Beijing: China Machine Press, 1985: 45. |
| [14] |
臧克江, 周欣, 顾立志, 等.
降低齿轮泵困油压力新方法的研究[J]. 中国机械工程, 2004, 15(7): 579–582.
ZANG Ke-jiang, ZHOU Xin, GU Li-zhi, et al. Study on new method of reducing the trap pressure of gear pump[J]. China Mechanical Engineering, 2004, 15(7): 579–582. |
| [15] |
李玉龙, 孙付春, 姚旗, 等.
航天器用超低黏度齿轮泵轻量化设计[J]. 农业工程学报, 2016, 32(21): 109–114.
LI Yu-long, SUN Fu-chun, YAO Qi, et al. Lightweight design of gear pumps with ultra low viscosity medium used in spacecraft[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(21): 109–114. DOI:10.11975/j.issn.1002-6819.2016.21.015 |
| [16] |
李玉龙, 袁影, 吴柏强, 等.
泵用齿轮副根切重合度的公式创建[J]. 机床与液压, 2017, 45(1): 84–88.
LI Yu-long, YUAN Ying, WU Bo-qiang, et al. A new contact ratio formula created for gear pairs with undercut in external gear pumps[J]. Machine Tool & Hydraulics, 2017, 45(1): 84–88. DOI:10.3969/j.issn.1001-3881.2017.01.020 |
| [17] |
李玉龙.
外啮合齿轮泵困油膨胀区的最小压力[J]. 排灌机械工程学报, 2013, 31(12): 1049–1055.
LI Yu-long. The minimal trapped-oil pressure of expansion stage in external gear pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(12): 1049–1055. DOI:10.3969/j.issn.1674-8530.2013.12.008 |
| [18] |
李玉龙.
齿轮泵最大困油压力解析式的建立与验证[J]. 农业工程学报, 2013, 29(11): 71–77.
LI Yu-long. Establishment and verification of analytic formula for maximum trapped-oil pressure in external gear pump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(11): 71–77. |