可控震源是一种绿色环保、安全高效、可控性强的地震勘探装备[1-3]。可控震源振动器作为可控震源的关键部件,在工作过程中通过平板与大地表面的接触传递能量。因此,振动器平板与大地之间的接触面接触性质会影响可控震源振动器输出信号的精度以及振动器的能量传递。
目前,针对振动器-大地接触系统的研究大都将大地表面简化为平面,忽略了大地表面形貌对系统接触性质的影响。Wei等建立了振动器-大地系统有限元模型,研究了可控震源振动器的动力学特性[4-5]。Huang等利用有限元方法分析了激发频率对振动器平板响应特性的影响[6]。由于平板与大地之间为非线性接触,Lebedev等建立了振动器-大地非线性接触模型,研究了非线性接触对系统输出信号精度的影响[7]。李振春等指出振动器平板与大地之间的不均匀接触是可控震源输出信号产生谐波的原因之一[8]。此外,庄娟和Liu等基于土动力学的相关理论,建立了可控震源振动器-大地耦合动力学模型,研究了平板以及大地的材料参数对振动器动力学响应的影响[9-10]。由于大地表面并非绝对平面,大地的表面形貌会影响平板与大地之间接触的均匀性,平板与大地间存在非线性接触,从而影响可控震源振动器输出信号的精度以及振动器的能量传递。此外,大地表面的材料参数也是影响平板与大地之间接触性质的因素之一。因此有必要建立更符合实际的可控震源振动器平板-大地接触模型,研究大地表面形貌及材料参数对平板与大地之间接触刚度及能量传递的影响规律。
本文基于分形理论建立振动器平板-大地接触模型,研究大地表面形貌及材料参数对振动器平板与大地之间接触面的接触力-变形曲线的影响;建立振动器平板-大地接触振动系统的动力学方程,计算具有不同大地表面形貌和材料参数的接触模型的振动响应,并研究振动器平板每一周期的能量传递随时间变化的规律。
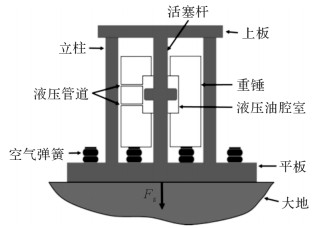
1 可控震源振动器平板-大地接触模型的建立 1.1 振动器平板-大地接触动力学模型如图 1所示,可控震源振动器由上板、立柱、活塞杆、平板和重锤等组成。重锤通过2个空气弹簧与平板连接在一起,空气弹簧用于平衡重锤自身的重力。在工作过程中,可控震源振动器液压系统产生的高压液压油交替进入重锤的上下腔室,推动重锤上下运动,同时由液压油产生的液压力通过活塞杆、上板以及立柱结构传递给平板,最后通过平板与大地的接触传递给大地[11]。
|
| 图 1 可控震源振动器结构示意图 Fig.1 Structure sketch of the vibrator |
为了避免平板与大地在振动器工作过程中发生接触分离,将整个震源车车身的重量作为压重作用在振动器上,平板在压重作用下产生静变形。图 2所示为可控震源振动器平板-大地接触系统在静平衡位置的动力学简化模型。

|
| 图 2 可控震源振动器平板-大地接触系统动力学简化模型 Fig.2 The simplified dynamics model of vibrator baseplate-ground contact system |
由图 2可得可控震源振动器平板-大地接触系统的动力学方程为:
| $ m\ddot{z}+c\dot{z}+f\left( z \right)-{{F}_{\text{t}}}=Q\left( t \right) $ | (1) |
式中:m为平板的质量,c为阻尼系数,z为平板的位移,f(z)为非线性弹性恢复力,Ft为压重,Q(t)为液压力。
可控震源的激发信号为频率线性增加的扫描信号,可表示为:
| $ Q\left( t \right)=A\sin \left[ 2\text{ }\!\!\pi\!\!\text{ }\left( {{f}_{\text{s}}}+\frac{{{f}_{\text{e}}}-{{f}_{\text{s}}}}{2T}t \right)t \right] $ | (2) |
式中:A为液压力振幅,fs为起始频率,fe为终止频率,t为扫描时间,T为扫描长度。
1.2 振动器平板-大地接触有限元模型振动器平板与大地之间的真实接触情况如图 3所示。由于大地表面形貌具有自相似性和尺度独立性,可以采用三维分形模型构建粗糙大地表面形貌[12-13]。

|
| 图 3 振动器平板与大地接触示意图 Fig.3 Sketch of contact between vibrator baseplate and ground |
修正的两参数Weierstrass-Mandelbrot分形函数为[14]:
| $ \begin{align} & z\left( x, y \right)=L{{\left( \frac{G}{L} \right)}^{\left( D-2 \right)}}\left( \frac{\ln \gamma }{M} \right)\sum\limits_{m=1}^{M}{\sum\limits_{n=0}^{^{n}\max }{{{\gamma }^{\left( D-3 \right)n}}}}\cdot \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left\{ \cos {{\varphi }_{m, n}}-\cos \left[ \frac{2\text{ }\!\!\pi\!\!\text{ }{{\gamma }^{n}}\sqrt{{{x}^{2}}+{{y}^{2}}}}{L}\cdot \right. \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left. \left. \cos \left[ {{\tan }^{-1}}\left( \frac{y}{x} \right)-\frac{\text{ }\!\!\pi\!\!\text{ }\mathit{m}}{M} \right]+{{\varphi }_{m, n}} \right] \right\} \\ \end{align} $ | (3) |
式中:z(x, y)表示大地表面高度函数; L为样本长度; G为分形粗糙度; D为分形维度; γ为频率密度参数, γ>1;m为构造表面重叠隆起的个数; n为频率因子,φm, n=[0, 2π],为随机相位。
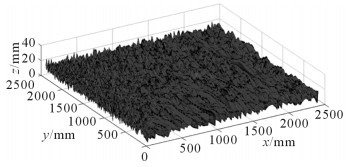
根据分形理论可知,大地的表面形貌由分形粗糙度G和分形维度D决定,且随着G值增大或D值减小,大地表面粗糙度增大。因此,通过改变分形参数G和D,可以构造出不同的大地表面形貌,建立具有不同接触表面形貌的平板-大地接触模型,从而研究大地表面形貌对平板与大地之间接触性质的影响。根据式(3),利用MATLAB建立三维粗糙大地表面,如图 4所示,其中G=6×10-4 mm,D=2.4,γ=1.5。
|
| 图 4 大地表面形貌 Fig.4 Surface topography of ground |
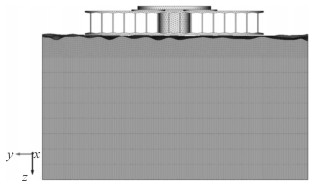
利用ABAQUS建立振动器平板-大地接触有限元模型,如图 5所示。由于振动器平板结构比较复杂,采用四面体单元划分网格,单元尺寸为10 mm。大地模型采用六面体单元划分网格,为了保持大地的表面形貌,网格单元尺寸为5 mm。平板与大地之间采用面-面接触定义,其中平板底面定义为主面,大地表面定义为从面。在振动器工作过程中,大地整体几乎不发生位移,因此约束大地底面3个平动自由度和3个转动自由度。
|
| 图 5 振动器平板-大地接触有限元模型 Fig.5 Finite element model of the baseplate-ground contact |
根据接触分形理论可知,2个粗糙表面的接触可以简化为1个刚性光滑平面与1个等价的粗糙表面的接触。因此将平板设置为刚体,选取平板的质心为参考点,将Z方向的位移载荷施加到参考点上,通过求取平板底面上的反力,获得平板与大地表面之间的接触力。
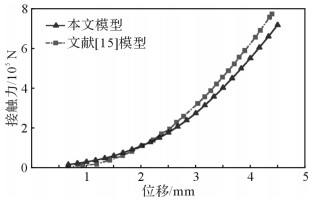
为了验证上述有限元模型的准确性,利用文献[15]的参数计算振动器平板与大地之间的接触力-变形曲线,并与文献[15]的计算结果进行对比。其中所取的大地表面形貌参数D=2.32,G=6×10-4 mm,等价弹性模量为363 MPa,泊松比为0.45。计算结果如图 6所示,根据图 6可知,本文建立的有限元模型的计算结果与文献[15]的计算结果基本一致,最大误差为7%。
|
| 图 6 平板与大地之间接触力-变形曲线对比 Fig.6 Comparison of the baseplate-ground contact force-deflection curves |
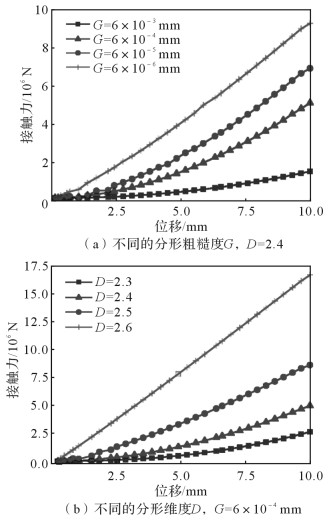
为了研究粗糙大地的表面形貌对振动器平板与大地之间的接触力-变形曲线的影响,通过改变分形参数G和D获得具有不同大地表面形貌的接触模型,并求解不同接触模型在位移载荷作用下的接触力-变形曲线,结果如图 7所示。其中图 7(a)表示保持分形维度D=2.4不变,分形粗糙度G分别取6×10-3,6×10-4,6×10-5,6×10-6 mm时的接触力-变形曲线,图 7(b)表示保持分形粗糙度G=6×10-4 mm不变,分形维度D分别取2.3,2.4,2.5,2.6时的接触力-变形曲线。从图 7可以看出,随着G值的增大或D值减小,振动器平板与大地之间的接触力减小。这是因为大地表面的粗糙度随G值的增大或D值的减小而增大,而振动器平板与大地之间的接触力随大地表面粗糙度的增大而减小。此外,接触力-变形曲线的斜率随着大地表面粗糙度的增大而增大,这说明振动器平板与大地之间接触的非线性随大地表面粗糙度的增大而增强。
|
| 图 7 不同大地表面形貌下振动器平板与大地之间的接触力-变形曲线 Fig.7 Vibrator baseplate-ground contact force-deflection curves under different ground surface topography |
振动器平板与大地之间的接触力-变形的关系可以采用幂函数形式表示[16]:
| $ f\left( z \right)=k{{x}^{a}} $ | (4) |
式中:k和α为与大地表面形貌参数有关的参数。
通过拟合不同表面形貌下振动器平板与大地之间的接触力-变形曲线可得式(4)中k和α的值,如表 1所示。从表 1可以看出,大地表面形貌越粗糙,对应的α值越大,则系统的非线性越强。
| D | G/mm | k/(N/mm) | α |
| 2.3 | 6×10-4 | 1.343×104 | 2.299 |
| 2.4 | 6×10-4 | 6.885×104 | 1.868 |
| 2.5 | 6×10-4 | 4.076×105 | 1.338 |
| 2.6 | 6×10-4 | 1.534×106 | 1.046 |
| 2.4 | 6×10-3 | 5.121×103 | 2.333 |
| 2.4 | 6×10-5 | 1.564×105 | 1.663 |
| 2.4 | 6×10-6 | 5.498×105 | 1.233 |
由于大地表面主要由土壤、岩石等构成,振动器平板在与大地接触过程中,土壤和岩石等材料的非线性会影响平板与大地之间的相互作用。本文采用Drucker-Prager弹塑性模型描述土壤和岩石等材料的非线性,其屈服准则为[17-18]:
| $ \left\{ \begin{align} & F=s-p\tan \beta -d=0 \\ & s=\frac{1}{2}q\left[ 1+\frac{1}{K}-\left( 1-\frac{1}{K} \right){{\left( \frac{r}{q} \right)}^{3}} \right] \\ \end{align} \right. $ | (5) |
式中:s为偏应力参数,β为屈服面倾斜角,K为屈服应力比,d为材料的黏结力;p、q、r分别为等效压应力、Miese等效应力和应力偏张量的第三不变量。
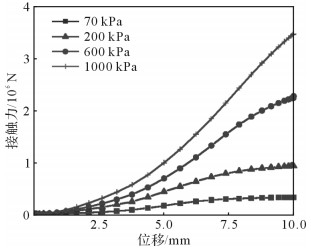
为了研究大地表面材料的非线性对振动器平板与大地之间接触性质的影响,保持大地表面形貌的分形参数G=6×10-4 mm和D=2.4不变以及材料的弹性模量不变,改变大地表面材料的屈服强度σs,分别取70,200,600,1 000 kPa,获得材料参数对接触力-变形曲线的影响规律,结果如图 8所示。
|
| 图 8 不同屈服强度下振动器平板与大地之间的接触力-变形曲线 Fig.8 Vibrator baseplate-ground contact force-deflection curves under different yield strength |
不同材料参数下振动器平板-大地接触模型的接触力-变形的关系式可以看作在幂函数项的基础上增加了因材料非线性引起的非线性项,如式(6)所示:
| $ f\left( z \right)=k{{x}^{a}}+{{k}_{1}}{{x}^{2}}+{{k}_{2}}{{x}^{3}} $ | (6) |
式中:k1、k2与大地表面材料参数有关。
通过拟合不同屈服强度下振动器平板与大地之间的接触力-变形曲线,得到式(6)中参数的取值, 如表 2所示。
| σs/kPa | k/ (N/mm) | α | k1/ (N/mm2) | k2/ (N/mm3) |
| 70 | -1.734×104 | 1.582 | 21 310 | -1 147 |
| 200 | -3.132×104 | 1.658 | 48 230 | -2 468 |
| 600 | -1.068×105 | 1.681 | 113 500 | -3 945 |
| 1 000 | -6.418×104 | 1.723 | 96 150 | -2 702 |
根据可控震源振动器的工作原理可知,在液压力作用的上半周期,平板向大地施加压力,使大地表面压缩,从而传递能量。在压重的作用下,大地表面在静平衡状态时处于压缩状态。因此,在液压力作用的上半周期,平板向大地实际传递的能量为:
| $ {{E}_{\text{传递}}}=\int{_{x1}^{x2}\left| f\left( z \right)-f\left( {{z}_{\text{s}}} \right) \right|\dot{x}\text{d}\mathit{x}} $ | (7) |
式中:x1、x2为相邻波谷与波峰对应的时间,zs为平板在静平衡位置的位移。
3.2 能量传递计算结果为获得振动器平板的响应特性,本文采用四阶龙格-库塔法对式(1)进行求解。计算时各参数值为:m=0.758 5 t,c=1 200,Ft=274 400 N,A=246 960 N,fs=5 Hz,fe=125 Hz,T=12 s。在实际工作过程中,振动器平板和大地之间存在局部脱耦情况,从而导致接触力减小。为了模拟平板与大地之间的局部脱耦情况,平板与大地之间的接触力采用分段函数形式表示:
| $ f\left( z \right)=\left\{ \begin{align} & k\left( z+{{z}_{\text{s}}} \right)\alpha , \ \ \ \ \ \ \ \ \ z\ge -{{z}_{\text{s}}} \\ & 0.5{{k}_{\text{s}}}\left( z+{{z}_{\text{s}}} \right), \ \ \ \ \ \ \ z<-{{z}_{\text{s}}} \\ \end{align} \right. $ | (8) |
式中:ks=nk(zs)α-1。
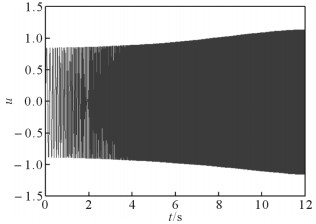
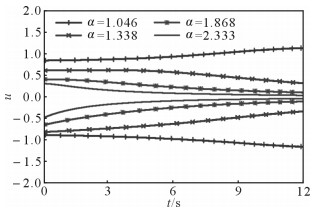
假设振动器平板的无量纲位移u=z/zs,图 9所示为α=1.046时平板的无量纲位移响应曲线。为了对比不同大地表面形貌下振动器-平板接触系统中平板的无量纲位移响应规律,提取位移响应的包络线,如图 10所示。由图 10可知,随着时间的增加(频率增大),较光滑表面(α=1.046)接触模型中振动器平板的位移响应逐渐增大,而粗糙表面(α=2.333)接触模型中振动器平板的位移响应则减小。这是因为粗糙大地表面形貌影响了平板与大地之间接触面的接触刚度,从而影响了接触系统的固有频率。从图 10中可知,系统的固有频率随着接触表面粗糙度的增加而减小。
|
| 图 9 α=1.046时振动器平板的无量纲位移响应曲线 Fig.9 Dimensionless displacement response curve of vibrator baseplate with α=1.046 |
|
| 图 10 不同大地表面形貌下振动器平板无量纲位移响应包络线 Fig.10 Envelope curves of vibrator baseplate dimensionless displacement response under different ground surface topography |
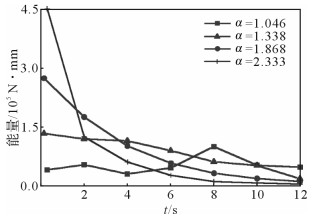
根据不同大地表面形貌接触模型中振动器平板的位移响应曲线,利用式(7)计算得到平板在1个周期内向大地传递的能量随时间变化(扫描频率变化)的曲线,结果如图 11所示。从图 11可知,对于较光滑表面的接触模型,1个周期内平板向大地传递的能量随时间变化的曲线较为平稳,说明在整个扫描时间段,平板的输出能量较为稳定。当α=1.046时,平板-大地接触系统的固有频率在110 Hz左右,系统在高频阶段的输出能量有所增加。然而当激发频率接近共振频率时,平板振动位移的增大导致平板与大地之间出现局部脱耦情况,使得系统传递的能量有所减小。粗糙表面(α≥1.338)接触模型中振动器平板在1个周期内向大地传递的能量随着时间的增加(扫描频率增大)而减小,且表面粗糙度越大能量衰减得越快。由于粗糙表面形貌接触模型的固有频率在中低频段,因此,平板在高频段的输出能量明显不足,这将影响复杂地层的成像精度,同时也不利于可控震源向高频段拓展。
|
| 图 11 不同大地表面形貌下振动器平板能量传递随时间的变化曲线 Fig.11 Energy transfer change curves with time under different ground surface topography |
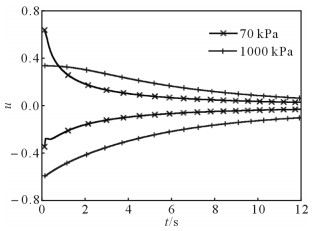
材料不同屈服强度下接触模型中振动器平板的无量纲位移响应包络线如图 12所示。从图 12可以看出,随着时间增加(频率增大),振动器平板位移均减小,且屈服强度较小的接触模型中振动器平板的位移小于屈服强度较大的接触模型的平板位移。同时,由于材料非线性的影响,上半周期和下半周期的平板位移不对称程度提高,在实际工作过程中,这将加剧平板与大地之间局部脱耦情况,影响振动器的输出性能。
|
| 图 12 不同屈服强度下振动器平板无量纲位移响应包络线 Fig.12 Envelope curves of vibrator baseplate dimensionless displacement response under different yield strength |
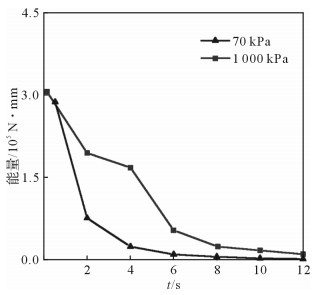
不同屈服强度下振动器平板在1个周期内向大地传递的能量随时间的变化曲线如图 13所示。随着时间的增加,平板向大地传递的能量均减小。材料屈服强度较大的接触模型的平板传递的能量比屈服强度小的传递的能量大,且随时间减小的速率相对较慢。因此,振动器平板-大地接触面材料的非线性会影响系统的位移响应和能量传递,导致平板在高频段的输出能量不足,且接触面材料的屈服强度越小,材料非线性对系统的影响越显著。
|
| 图 13 不同屈服强度下振动器平板能量传递随时间的变化曲线 Fig.13 Energy transfer change curves with time under different yield strength |
本文建立了不同大地表面形貌及材料参数的振动器平板-大地接触模型,研究了表面形貌及材料参数对振动器平板与大地之间的接触力-变形曲线的影响规律,计算了不同振动器平板-大地接触模型的振动响应和能量传递,主要结论如下:
1) 大地表面形貌与材料参数均会导致振动器平板与大地之间的非线性接触,影响振动器平板-大地接触系统的振动响应与能量传递。
2) 不同大地表面形貌的振动器平板-大地接触模型的接触力-变形关系可以用幂函数形式表示,且随着大地表面粗糙度的增大,幂函数的幂增大。不同材料参数的振动器平板-大地接触模型的接触力-变形关系式由幂函数和多项式组成,关系式的系数由表面形貌和材料参数共同决定。
3) 光滑大地表面的接触模型中振动器平板的位移响应随时间的增加而增大,粗糙大地表面的接触模型中振动器平板的位移响应随时间的增加而减小。这是因为振动器平板-大地接触系统的固有频率随大地表面粗糙度的增大而减小。
4) 材料的非线性会加剧振动器平板位移响应减小,且材料的屈服强度越小,平板在上下半周期的位移响应不对称程度越高。
5) 大地表面的粗糙度以及材料的非线性都是造成振动器平板在高频段输出能量不足的原因。
| [1] |
刘金中, 马铁荣.
可控震源的发展状况[J]. 石油科技论坛, 2008, 27(5): 38–42.
LIU Jin-zhong, MA Tie-rong. Development of the vibrosies[J]. Oil Forum, 2008, 27(5): 38–42. DOI:10.3969/j.issn.1002-302X.2008.05.007 |
| [2] | WEI Z, PHILLIPS T F, HALL M A. Fundamental discussions on seismic vibrators[J]. Geophysics, 2010, 75(6): W13–W25. |
| [3] |
陶知非.
改善可控震源高频信号输出品质的探讨[J]. 物探装备, 2008, 18(2): 71–77.
TAO Zhi-fei. Study on improving quality of high-frequency output signal in vibroseis[J]. Equipment for Geophysical Prospecting, 2008, 18(2): 71–77. DOI:10.3969/j.issn.1671-0657.2008.02.001 |
| [4] | WEI Z. Modelling and modal analysis of seismic vibrator baseplate[J]. Geophysical Prospecting, 2010, 58(1): 19–32. DOI:10.1111/gpr.2010.58.issue-1 |
| [5] | WEI Z H, PHILLIPS T F. Characterizing the vibrator captured ground mass system using finite element analysis[C]//SEG Technical Program Expanded Abstracts 2013, Tulsa: SEG, 2013: 126-130. |
| [6] | HUANG Z, LI G, HAO L. Study on dynamics of vibrator baseplate at low and high frequencies[J]. Journal of Vibroengineering, 2017, 19(4): 2413–2426. DOI:10.21595/jve.2017.18170 |
| [7] | LEBEDEV A, BERESNEV I. Nonlinear distortion of signals radiated by vibroseis sources[J]. Geophysics, 2004, 69(4): 968–977. |
| [8] |
李振春, 曲英铭, 韩文功, 等.
可控震源两种谐波产生机理与特征研究[J]. 石油物探, 2016, 55(2): 159–172.
LI Zhen-chun, QU Ying-ming, HAN Wen-gong, et al. Generation mechanism and characteristics of two kinds of harmonic waves for vibroseis[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 159–172. DOI:10.3969/j.issn.1000-1441.2016.02.001 |
| [9] |
庄娟, 林君, 吴东江, 等.
高频可控震源与大地振动耦合过程幅频特性分析[J]. 长春科技大学学报, 1999, 29(2): 184–187.
ZHUANG Juan, LIN Jun, WU Dong-jiang, et al. Analyzing coupling process of the earth-high frequency vibrator[J]. Journal of Changchun University of Science and Technology, 1999, 29(2): 184–187. DOI:10.3969/j.issn.1671-5888.1999.02.019 |
| [10] | LIU J, HUANG Z Q, LI G, et al. Dynamic characteristics analysis of a seismic vibrator-ground coupling system[J]. Shock and Vibration, 2017(6): 1–12. |
| [11] |
丁雅萍, 黄志强, 李刚.
基于有限元法的KZ-28型振动器平板结构优化与性能研究[J]. 机械设计与制造, 2016(11): 205–208.
DING Ya-ping, HUANG Zhi-qiang, LI Gang. Research and structural optimization on the performance of flat plate of KZ-28 type vibrator based on finite element method[J]. Machinery Design & Manufacture, 2016(11): 205–208. DOI:10.3969/j.issn.1001-3997.2016.11.052 |
| [12] |
侯占峰, 薛晶, 闫建国, 等.
土壤地面不平度及接触分形模型[J]. 中国农机化学报, 2015, 36(4): 279–281.
HOU Zhan-feng, XUE Jing, YAN Jian-guo, et al. Soil surface roughness and fractal contact model[J]. Journal of Chinese Agriculture Mechanization, 2015, 36(4): 279–281. |
| [13] |
任新成, 田炜, 刘鹏, 等.
分形大地土壤表面与部分埋藏目标复合散射特性[J]. 强激光与粒子束, 2017, 29(2): 40–46.
REN Xin-cheng, TIAN Wei, LIU Peng, et al. Fractal soil surface and composite scattering characteristic of buried targets[J]. High Power Laser and Particle Beams, 2017, 29(2): 40–46. |
| [14] | MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces[J]. Journal of Tribology, 1991, 113(1): 1–11. |
| [15] | NOORLANDT R, DRIJKONINGEN G. On the mechanical vibrator-earth contact geometry and its dynamics[J]. Geophysics, 2016, 81(3): 37–45. |
| [16] | YAN W, KOMVOPOULO K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics, 1998, 84(7): 3617–3624. DOI:10.1063/1.368536 |
| [17] |
王满生, 周锡元, 胡聿贤.
桩土动力分析中接触模型的研究[J]. 岩土工程学报, 2005, 27(6): 616–620.
WANG Man-sheng, ZHOU Xi-yuan, HU Yu-xian. Studies on contact model of soil-pile dynamic interaction[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 616–620. DOI:10.3321/j.issn:1000-4548.2005.06.002 |
| [18] |
袁凡凡, 栾茂田, 闫澍旺.
筏板-桩-土相互作用的三维弹塑性有限元分析[J]. 岩石力学与工程学报, 2005, 24(18): 3332–3336.
YUAN Fan-fan, LUAN Mao-tian, YAN Shu-wang. 3D elastoplastic finite element analysis of bearing capacity behavior of interaction of raft-pile and soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3332–3336. DOI:10.3321/j.issn:1000-6915.2005.18.023 |


