2. 浙江大学 应用力学研究所, 浙江 杭州 310027
2. Institute of Applied Mechanics, Zhejiang University, Hangzhou 310027, China
封头是承压设备必不可少的零件。椭圆形封头由于应力分布比较均匀且易于加工成形,广泛应用于石油、化工和核电等行业的承压设备。例如中国在建大型先进压水堆核电站,其钢安全壳采用直径约为39.6 m、壁厚约为41.3 mm的超大直径超薄椭圆形封头[1],其主要功能是承受由失水事故导致的压力和温度,防止放射性物质外泄至大气环境中。
由胡金伯格(Huggenberger)推导的椭圆薄膜应力方程式可知,内压作用下的椭圆形封头(凹面受压),其顶部区的经向和环向均受拉伸应力,过渡区的经向也受拉伸应力;当椭圆形封头径高比大于2时,过渡区的环向受压缩应力,可能会发生局部屈曲,尤其是超大直径超薄椭圆形封头[2]。故内压椭圆形封头会出现多种失效模式:强度失效(爆破和轴对称屈服)和局部屈曲失效。如图 1所示,内压作用下超大直径超薄椭圆形封头出现了顶部区爆破和过渡区局部屈曲的失效模式。因此设计内压椭圆形封头时,除了要考虑强度失效,还需注意过渡区局部屈曲失效。

|
| 图 1 内压椭圆形封头失效模式(爆破和局部屈曲) Fig.1 Failure modes of an internally pressurized ellipsoidal head (burst and local buckling) |
内压椭圆形封头设计用规范标准主要有:中国标准GB/T 150—2011《压力容器》(下文简称GB/T 150)[3]和JB 4732—1995《钢制压力容器——分析设计标准》(下文简称JB 4732)[4],美国规范ASME BPVC.Ⅲ.1-NE《核设施MC级部件的建造规则》(下文简称ASME Ⅲ.1-NE)[5]、规范案例N-284《金属安全壳体屈曲设计方法》(下文简称ASME N-284)[6]、ASME BPVC Ⅷ-1《压力容器建造规则》(下文简称ASME Ⅷ-1)[7]、ASME BPVC Ⅷ-2《压力容器建造另一规则》(下文简称ASME Ⅷ-2)[8]以及欧盟标准EN 13445《非火焰接触压力容器》(下文简称EN 13445)[9]。ASME规范和欧盟标准EN 13445均提出了基于失效模式的先进设计理念,而我国标准GB/T 150自1989年版、JB 4732自1995年版后,内压椭圆形封头设计方法基本没有变化,目前我国内压椭圆形封头的设计主要参考ASME Ⅷ-1和ASME Ⅷ-2早期版本的设计方法。为此全国锅炉压力容器标准化技术委员会已于2015年启动了JB 4732的修订工作,内压椭圆形封头设计方法也亟待修订。
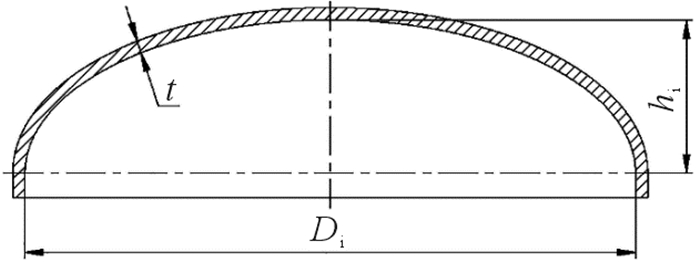
1 椭圆形封头设计方法 1.1 中国标准 1.1.1 GB/T 150椭圆形封头的结构如图 2所示。其设计公式为:
| $ p=\frac{2\left[ \sigma \right]\varphi t}{K{{D}_{\text{i}}}+0.5t} $ | (1) |
| $ K = \frac{1}{6}\left[ {2 + {{\left( {{K_1}} \right)}^2}} \right] $ | (2) |
|
| 图 2 椭圆形封头结构示意图 Fig.2 Schematic diagram of an ellipsoidal head structure |
式中:p为允许工作压力,MPa;[σ]为许用应力,MPa;φ为焊接接头系数;t为封头厚度,mm;K为形状系数;Di为封头内直径,mm;hi为封头内高度,mm;K1=Di/2hi,为径高比。
为防止过渡区局部屈曲失效,规定:K1≤2.0的椭圆形封头,t/Di≥0.001 5;K1>2.0的椭圆形封头,t/Di≥0.003。
1.1.2 JB 4732对标准椭圆形封头(K1=2.0),按照图 3中参数r/Di=0.17的曲线进行设计,其中r为过渡区内半径,mm。对K1≠2.0的椭圆形封头,应看作形状相当的碟形封头,见图 3[4], 其中:k为载荷组合系数;Sm为设计应力强度,MPa;L为顶部区内半径,mm。或按照JB 4732附录A“基本部件、组合部件的应力分析”或附录B“实验应力分析”进行设计。

|
| 图 3 碟形封头设计曲线 Fig.3 Design curves for torispherical head |
JB 4732中碟形封头的设计方法:
1) 当t/L < 0.002时,按JB 4732的附录A或附录B进行设计。必要时应校核稳定性。
2) 当t/L≥0.002且p/kSm≤0.08时,按图 3进行设计。
3) 当p/kSm>0.08时,按式(3)进行设计计算:
| $ t = \frac{{{D_{\rm{i}}}}}{2}\left( {{{\rm{e}}^{p/k{S_{\rm{m}}}}} - 1} \right) $ | (3) |
ASME Ⅲ.1-NE中防止椭圆形封头强度失效的设计公式为:
| $ p=\frac{2\left[ \sigma \right]t}{K{{D}_{\text{i}}}+0.2t} $ | (4) |
对于屈曲失效,ASME N-284给出了屈曲评定方法:一般先进行特征值屈曲分析得到最小特征值系数,再确定承载力折减系数、塑性折减系数和安全系数,从而完成屈曲评定。文献[10]给出了钢制安全壳内压椭圆形封头屈曲评定实例。但ASME N-284未给出防止屈曲失效的设计公式。
1.2.2 ASME Ⅷ-1ASME Ⅷ-1中防止强度失效的设计公式与ASME Ⅲ.1-NE中的相同,但考虑了焊接接头系数的影响。对t/L < 0.002的封头,补充了防止过渡区失效的设计公式,见式(5)至式(9)。
| $ {p_{\rm{e}}} = \frac{{{S_{\rm{e}}}t}}{{{C_2}{R_{\rm{e}}}\left[ {\left( {0.5{R_{{\rm{e}}}}/r} \right) - 1} \right]}} $ | (5) |
| $ {S_{\rm{e}}} = {C_1}Et/r $ | (6) |
式中:pe为弹性屈曲临界压力,MPa;Se为弹性屈曲临界应力,MPa;E为杨氏弹性模量,MPa;Re为等效半径,mm;C1、C2均为几何相关系数;Re、C1、C2的计算式详见文献[7]。
| $ {p_{\rm{y}}} = \frac{{{S_{\rm{y}}}t}}{{{C_2}{R_{\rm{e}}}\left[ {\left( {0.5{R_{\rm{e}}}/r} \right) - 1} \right]}} $ | (7) |
式中:py为屈服压力,MPa;Sy为屈服强度,MPa。
| $ {p_{\rm{f}}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0.6{p_{\rm{e}}},\\ 0.408{p_{\rm{y}}} + 0.192{p_{\rm{e}}},\\ 2.0{p_{\rm{y}}}, \end{array}&\begin{array}{l} G \le 1.0\\ 1.0 < G \le 8.29\\ G > 8.29 \end{array} \end{array}} \right. $ | (8) |
式中:pf为过渡区失效压力,MPa;G=pe/py。
| $ {p_{\rm{k}}} = {p_{\rm{f}}}/1.5 $ | (9) |
式中:pk为过渡区允许工作压力,MPa。
1.2.3 ASME Ⅷ-2ASME Ⅷ-2中椭圆形封头的允许工作压力p取pc和pk的较小值。
防止封头顶部区爆破失效的设计公式为:
| $ {p_{\rm{c}}} = \frac{{2\left[ \sigma \right]\varphi t}}{{L + 0.5t}} $ | (10) |
式中:pc为防止爆破失效的允许工作压力,MPa。
防止封头过渡区失效的设计方法同ASME Ⅷ-1。但当G>1.0时,过渡区失效压力的计算式不同于ASME Ⅷ-1的式(8),为[11-12]:
| $ {p_{\rm{f}}} = \left( {\frac{{0.77508G - 0.20354{G^2} + 0.019274{G^3}}}{{1 + 0.19014G - 0.089534{G^2} + 0.0093965{G^3}}}} \right){p_{\rm{y}}} $ | (11) |
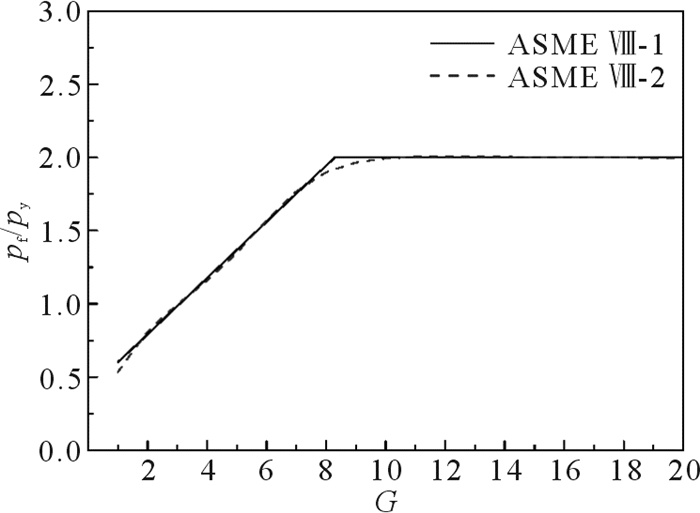
绘制ASME Ⅷ-1和ASME Ⅷ-2的pf/py与G关系曲线,见图 4,可以看出,两者的吻合度很高。
|
| 图 4 pf/py与G关系曲线 Fig.4 The relation curves between pf/py and G |
EN 13445中椭圆形封头的允许工作压力p取pc、ps和pb的最小值。
为防止封头顶部区强度失效,限制封头顶部区薄膜应力,采用式(10)进行设计,与ASME Ⅷ-2相同。
防止封头过渡区轴对称屈服失效的设计公式为:
| $ {p_{\rm{s}}} = \frac{{\left[ \sigma \right]t}}{{\beta \left( {0.75L + 0.2{D_{\rm{i}}}} \right)}} $ | (12) |
式中:ps为防止轴对称屈服失效的允许工作压力,MPa;参数β的确定参见文献[9]。
防止封头过渡区局部屈曲失效的设计公式为:
| $ {p_{\rm{b}}} = 111\left[ \sigma \right]{\left( {\frac{t}{{0.75L + 0.2{D_{\rm{i}}}}}} \right)^{1.5}}{\left( {\frac{r}{{{D_{\rm{i}}}}}} \right)^{0.825}}\left( {t \le 0.005{D_{\rm{i}}}} \right) $ | (13) |
式中:pb为防止局部屈曲失效的允许压力,MPa。
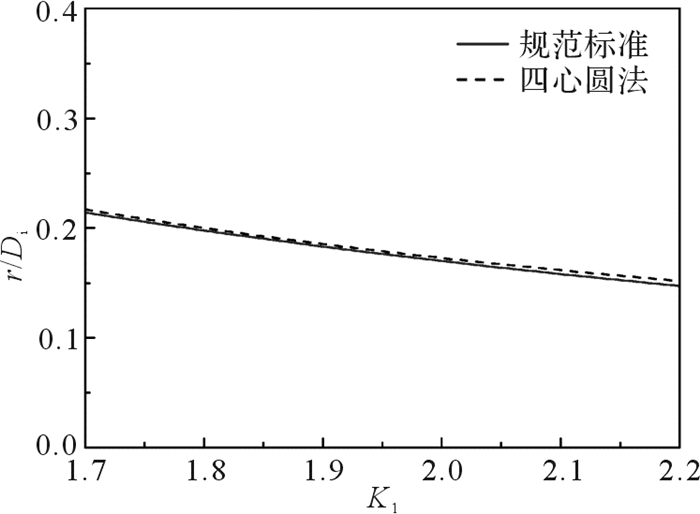
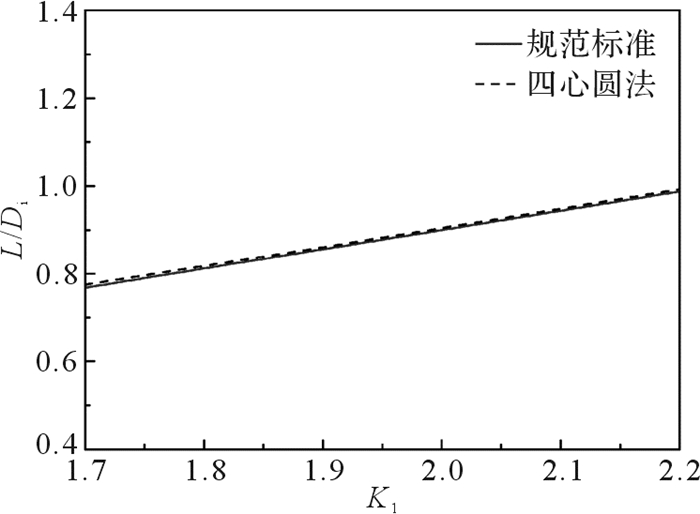
2 比较分析 2.1 椭圆形封头与碟形封头JB 4732以及ASME Ⅷ-1(t/L < 0.002)、ASME Ⅷ-2、EN 13445中椭圆形封头设计均按照形状相当的碟形封头进行。椭圆形封头与碟形封头结构尺寸等效的基本原理是四心圆法,由四心圆法绘制的碟形近似为椭圆形[13],并得到r/Di与K1、L/Di与K1的关系,分别见式(14)和式(15)。ASME Ⅷ-2和EN 13445给出了椭圆形封头与碟形封头的结构尺寸转换关系,见式(16)和式(17),是由式(14)和式(15)转换而来。ASME Ⅷ-1根据式(16)和式(17)给出了椭圆形封头与碟形封头结构尺寸转换关系的表格。绘制r/Di与K1、L/Di与K1关系曲线,分别见图 5和图 6,可以看出式(14)与式(16)、式(15)与式(17)在规范标准规定的1.7≤K1≤2.2范围内吻合度很高,说明由四心圆法得到的式(14)和式(15)可分别转换为形式简单的式(16)和式(17),便于工程计算。JB 4732仅给出标准椭圆形封头的等效说明,对其它径高比未作说明。
| $ r/{D_{\rm{i}}} = \frac{{K_1^2 + 1 - \left( {{K_1} - 1} \right)\sqrt {K_1^2 + 1} }}{{4K_1^2}} $ | (14) |
| $ L/{D_{\rm{i}}} = \frac{{K_1^2 + 1 + \left( {{K_1} - 1} \right)\sqrt {K_1^2 + 1} }}{{4{K_1}}} $ | (15) |
| $ r = {D_{\rm{i}}}\left( {0.5/{K_1} - 0.08} \right) $ | (16) |
| $ L = {D_{\rm{i}}}\left( {0.44/{K_1} + 0.02} \right) $ | (17) |
|
| 图 5 r/Di与K1关系曲线 Fig.5 The relation curves between r/Di and K1 |
|
| 图 6 L/Di与K1关系曲线 Fig.6 The relation curves between L/Di and K1 |
内压椭圆形封头设计方法和设计理念的比较见表 1。可以看出,中国标准GB/T 150和JB 4732分别采用基于最大应力和极限压力的设计思想,防止强度失效,但两者均未给出防止过渡区局部屈曲失效的设计公式,不适用于超大直径超薄椭圆形封头的设计。国外规范标准ASME Ⅲ.1-NE、ASME N-284、ASME Ⅷ-1、ASME Ⅷ-2和EN 13445全面考虑了椭圆形封头的失效模式:强度失效和局部屈曲失效,并给出了相应的设计方法。
| 规范标准 | 设计方法 | 设计方法来源 | 设计理念 |
| GB/T 150 | 为防止强度失效, 采用式(1)设计 | 基于GB/T 150的等径球壳中径公式(式(18)), 考虑形状系数的影响[14-15], 设计准则为最大拉应力理论 | 基于最大应力的设计 |
| 为防止局部屈曲失效, 限制封头厚径比, 但未给出相应设计公式 | |||
| JB 4732 | 为防止强度失效, 1)当t/L < 0.002时, 按该标准的附录A和附录B设计, 但附录A未给出椭圆形封头的计算公式; 2)当t/L≥0.002且p/kSm≤0.08时, 采用图 3设计; 3)当p/kSm>0.08时, 采用式(3)设计 | 1)附录B是以实验方法进行应力分析设计:采用应变电测试验等方法确定控制应力或极限载荷 2)源自Shield和Drucker的工作[16]:按照极限分析的上限定理和下限定理, 在理想塑性材料模型和小变形假设的条件下, 计算并拟合出极限压力预测公式(式(19))。由式(19)可转换为图 3[17], 以防止过渡区过度塑性变形 3)将封头作为等径厚壁圆筒[17] 。基于厚壁筒体Lamè公式和理想弹塑性材料假设, 按照Tresca屈服失效判据, 推导出圆筒的极限压力计算公式(式(20)[18] |
基于极限压力的设计 |
| 未给出防止局部屈曲失效的设计方法, 仅强调"必要时应校核稳定性" | 基于实验方法的设计 | ||
| ASME Ⅲ.1-NE | 为防止强度失效, 采用式(4)设计 | 与GB/T 150类似, 考虑形状系数的影响。考虑沿壁厚方向应力非线性分布特点, ASME Ⅲ.1-NE采用基于Lamè公式的球壳壁厚计算公式(式(21)) | 基于失效模式的设计 |
| ASME N-284 | 给出屈曲评定方法, 但未给出设计公式 | 基于线性特征值屈曲分析, 考虑承载力折减系数和塑性折减系数的影响, 2种折减系数考虑了几何非线性、材料非线性等影响, 均是基于试验结果给出[19] | |
| ASME Ⅷ-1 | 为防止强度失效, 采用式(4)设计 | 同ASME Ⅲ.1-NE | |
| 为防止过渡区失效(轴对称屈服和局部屈曲), 采用式(5)至式(9)设计 | 源自Miller公式[20-21]:由薄壳理论得到过渡区最大薄膜应力计算式(式(22)), 确定最大薄膜应力等于材料屈服强度的封头内压计算式(式(7))、及最大薄膜应力等于弹性屈曲临界应力的封头内压计算式(式(5)), 再通过封头试验结果考虑几何非线性和材料非线性的影响, 从而得到过渡区失效压力的计算式(式(8)) | ||
| ASME Ⅷ-2 | 为防止顶部区爆破失效, 采用式(10)设计 | 按照式(17)将封头顶部区等效为球壳, 采用球壳的中径公式, 也是基于最大应力的设计理念。该设计方法是基于等效球壳的爆破压力预测公式(式(23))[22], 认为封头顶部区薄膜应力等于材料抗拉强度时爆破。但式(23)是基于薄壳理论得到, 未考虑材料应变硬化和大变形的双重影响, 其预测值低于椭圆形封头的实测爆破压力[23], 给出了保守的预测结果 | |
| 为防止过渡区失效, 采用式(5)至式(8)、式(9)和式(11)设计 | 同ASME Ⅷ-1, 源自Miller公式 | ||
| EN 13445 | 为防止顶部区强度失效, 限制顶部区薄膜应力, 采用式(10)设计 | 同ASME Ⅷ-2, 采用等效球壳的中径公式 | |
| 为防止过渡区轴对称屈服失效, 采用式(12)设计 | 源自Kalnins和Updike的工作[24]:理论基础为理想弹塑性材料假设和大变形理论, 由两倍弹性斜率法确定失效压力, 再考虑欧盟的工程经验, 形成设计公式[25] | ||
| 为防止过渡区局部屈曲失效(t≤0.005Di), 采用式(13)设计 | 源自Galletly[26]公式(式(24)):在理想弹塑性材料模型和大变形的条件下, 利用计算机程序BOSOR-5[27]计算并拟合成屈曲压力预测公式[28], 再基于试验结果进行安全裕度分析[29], 形成设计公式[25] |
从表 1也可看出:GB/T 150和ASME Ⅲ.1-NE防止强度失效的设计公式,及ASME Ⅷ-2和EN 13445防止顶部区强度失效的设计公式,均是基于最大应力的设计思想,其理论基础是考虑形状系数的薄壳理论。JB4732采用基于极限压力的设计思想,其理论基础是理想塑性材料模型和小变形假设。对于防止过渡区轴对称屈服失效的设计方法,ASME Ⅷ-1和ASME Ⅷ-2的理论基础是薄壳理论,EN 13445的理论基础是理想弹塑性材料模型和大变形理论。对于防止局部屈曲失效的设计方法,ASME N-284的理论基础是线性特征值屈曲分析方法,ASME Ⅷ-1和ASME Ⅷ-2的理论基础是薄壳理论和弹性屈曲理论,EN 13445的理论基础是理想弹塑性材料模型和大变形理论。可见,现有设计方法在理论上未考虑材料应变硬化和大变形的双重影响。
| $ t = \frac{{{p_{\rm{d}}}{D_{\rm{i}}}}}{{4\left[ \sigma \right]\varphi - {p_{\rm{d}}}}} $ | (18) |
| $ \begin{array}{l} \frac{{{p_{\rm{L}}}}}{{{S_{\rm{y}}}}} = \left( {0.33 + 5.5\frac{r}{{{D_{\rm{i}}}}}} \right)\frac{t}{L} + 28\left( {1 - 2.2\frac{r}{{{D_{\rm{i}}}}}} \right)\\ \;\;\;\;\;\;\;\;{\left( {\frac{t}{L}} \right)^2} - 0.000\;6 \end{array} $ | (19) |
式中:pL为极限压力,MPa; pd为计算压力,MPa。
| $ {p_{\rm{L}}} = {S_{\rm{y}}}\ln \frac{{{D_{\rm{i}}} + 2t}}{{{D_{\rm{i}}}}} $ | (20) |
| $ t = \frac{{{p_{\rm{d}}}{D_{\rm{i}}}}}{{4\left[ \sigma \right]\varphi - 0.4{p_{\rm{d}}}}} $ | (21) |
| $ {S_{\rm{k}}} = {C_2}\left( {1 - 0.5\frac{{{R_{\rm{e}}}}}{r}} \right){p_{\rm{n}}}\frac{{{R_{\rm{e}}}}}{t} $ | (22) |
式中:Sk为过渡区最大薄膜应力,MPa, pn为封头所受内压,MPa。
| $ {p_{\rm{u}}} = \frac{{2t{S_{\rm{u}}}}}{L} $ | (23) |
式中:pu为爆破压力,MPa;Su为抗拉强度,MPa。
| $ \frac{{{p_{\rm{d}}}}}{{\gamma {S_{\rm{y}}}}} = \frac{{80{{\left( {r/{D_{\rm{i}}}} \right)}^{0.825}}}}{{{{\left( {{D_{\rm{i}}}/t} \right)}^{1.5}}{{\left( {L/{D_{\rm{i}}}} \right)}^{1.15}}}} $ | (24) |
式中:γ为制造相关系数。对于分瓣加工封头,γ=1.0;对于冷旋压封头,γ=1.6。
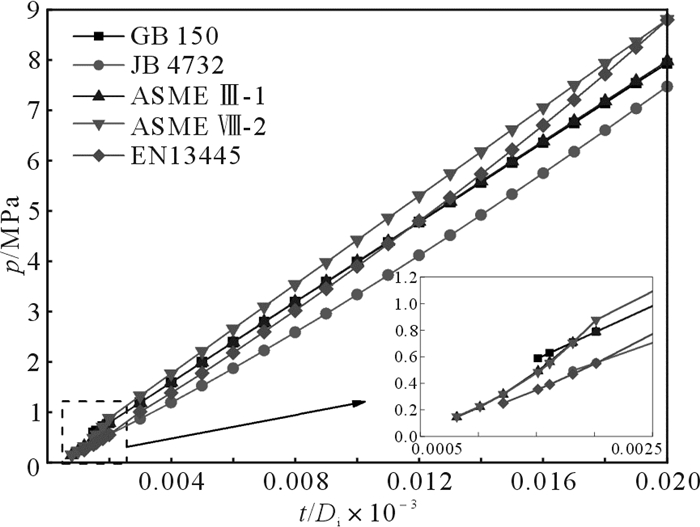
2.3 算例分析为了充分比较各规范标准在椭圆形封头设计上的差异性,选取工程中常用的标准椭圆形封头(0.000 8≤t/Di≤0.02)为例进行设计计算。假定封头内直径Di=5 000 mm,材料为杨氏弹性模量E=2.0×105 MPa、屈服强度Sy=300 MPa的碳素钢,且许用应力相同(排除安全系数的影响),计算得到封头允许工作压力p与t/Di关系曲线,见图 7。
|
| 图 7 p与t/Di关系曲线 Fig.7 The relation curves between p and t/Di |
当t/Di≤0.001 6时,ASME Ⅷ-1的允许工作压力主要由式(5)至式(9)确定;当t/Di≤0.001 8时,ASME Ⅷ-2的允许工作压力主要由式(5)至式(8)、式(9)和式(11)确定;当t/Di≤0.002时,EN 13445的允许工作压力由式(13)确定。以上均为过渡区局部屈曲失效控制,此种情况下ASME Ⅷ-1和ASME Ⅷ-2的允许屈曲压力很接近,且高于EN 13445的允许屈曲压力,此外ASME Ⅷ-1和ASME Ⅷ-2适用的厚径比相对EN 13445要小。当t/Di < 0.001 5时,GB/T 150未给出允许工作压力值,因为GB/T 150规定标准椭圆形封头的t/Di≥0.001 5。当t/Di < 0.001 8时,JB 4732未给出允许工作压力值,JB 4732的附录A未给出椭圆形封头的计算公式,且附录B的实验方法成本高,实施困难。此外,JB 4732也未给出防止局部屈曲失效的设计方法。GB/T 150和JB 4732未给出防止过渡区局部屈曲失效的设计公式,不适用于较小厚径比(超大直径超薄)的封头。
当0.001 8≤t/Di≤0.02时,JB 4732的允许工作压力由图 3确定;当0.003≤t/Di≤0.02时,EN 13445的允许工作压力由式(12)确定。以上均为过渡区屈服失效控制,此种情况下EN 13445的允许工作压力高于JB 4732的。
当0.001 5≤t/Di≤0.02时,GB/T 150的允许工作压力由式(1)确定;当0.001 8≤t/Di≤0.02时,ASME Ⅷ-1的允许工作压力由式(4)确定,与ASME Ⅲ.NE-1相同;当0.002≤t/Di≤0.02时,ASME Ⅷ-2的允许工作压力由式(10)确定。以上均为防止强度失效控制,是基于最大应力的设计,此种情况下对于标准椭圆形封头(K=1.0),在许用应力相同条件下,GB/T 150、ASME Ⅷ-1和ASME Ⅷ-2的允许工作压力大小关系可表示为:1/(Di/t+0.5) < 1/(Di/t+0.2) < 1/(0.9Di/t+0.5),即GB/T150的允许工作压力最小,ASME Ⅷ-2的最大。
当0.001 5≤t/Di≤0.001 6时,允许工作压力的由小到大的关系:pEN 13445 < pASME Ⅷ-2 < pASME Ⅷ-1 < pGB/T 150。EN 13445、ASME Ⅷ-2和ASME Ⅷ-1考虑了过渡区局部屈曲失效控制,而GB/T 150是基于最大应力的设计,未考虑屈曲失效。
当0.001 8≤t/Di≤0.002时,EN 13445的允许工作压力比JB 4732的低0.6%~5.0%,EN 13445考虑了过渡区局部屈曲失效控制,而JB 4732考虑了过渡区屈服失效控制,未考虑屈曲失效。GB/T 150的允许工作压力比JB 4732的平均高41.8%,ASME Ⅷ-1的允许工作压力比JB 4732的平均高41.9%,ASME Ⅷ-2的允许工作压力比JB 4732的高41.2%~57.0%。
当0.003≤t/Di≤0.02时,JB 4732的允许工作压力最低,ASME Ⅷ-2的允许工作压力最高。EN 13445的允许工作压力比JB 4732的平均高16.6%。GB/T 150的允许工作压力比JB 4732的高6.1%~37.0%,ASME Ⅷ-1的允许工作压力比JB 4732的高6.8%~37.1%,ASME Ⅷ-2的允许工作压力比JB 4732的高17.8%~52.2%,并且t/Di越小,差异越明显。总的来说,JB 4732的设计计算结果最保守。
3 结论本文对国内外规范标准中内压椭圆形封头设计方法进行了总结与比较。ASME规范和欧盟标准EN 13445全面考虑了椭圆形封头的失效模式:强度失效和局部屈曲失效,并给出了基于失效模式的设计方法。而中国标准GB/T 150和JB 4732尚未给出防止过渡区局部屈曲失效的设计公式,不适用于超大直径超薄椭圆形封头的设计。算例分析表明:对于0.003≤t/Di≤0.02的标准椭圆形封头,在许用应力相同条件下,按照JB 4732设计的计算结果相对EN 13445、GB/T 150、ASME Ⅷ-1和ASME Ⅷ-2更保守,经济性较差。此外,现有设计方法在理论上未考虑材料应变硬化和大变形的双重影响。因此,建议在理论上考虑材料应变硬化和大变形的双重影响,建立基于失效模式的设计方法,修订中国标准的内压椭圆形封头设计方法。
| [1] |
赵旭, 李会永.
大型压水堆钢制安全壳顶封头现场组装工艺[J]. 压力容器, 2013, 30(3): 67–80.
ZHAO Xu, LI Hui-yong. Field assembling process of steel containment vessel top head in a large pressure water reactor[J]. Pressure Vessel Technology, 2013, 30(3): 67–80. DOI:10.3969/j.issn.1001-4837.2013.03.012 |
| [2] |
郑津洋, 桑芝富.
过程设备设计[M]. 北京: 化学工业出版社, 2015: 29-31.
ZHENG Jin-yang, SANG Zhi-fu. Process equipment design[M]. Beijing: Chemical Industry Press, 2015: 29-31. |
| [3] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.压力容器: GB/T 150-2011[S].北京: 中国标准出版社, 2012: 116-118.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Pressure vessels: GB/T 150-2011[S]. Beijing: Standards Press of China, 2012: 116-118. |
| [4] |
中华人民共和国国家发展和改革委员会, 全国锅炉压力容器标准化技术委员会.钢制压力容器-分析设计标准: JB 4732-1995(2005年确认)[S].北京: 新华出版社, 2007: 38-40.
National Development and Reform Commission of the People's Republic of China, China Standardization Committee on Boillers and Pressure Vessels. Steel pressure vessels-design by analysis: JB 4732-1995(R2005)[S]. Beijing: Xinhua Publishing House, 2007: 38-40. |
| [5] | American National Standards Committee. ASME boiler and pressure vessel code, Section Ⅲ, rules for construction of nuclear facility components: ASME BPVC.Ⅲ.1. NE-2015[S]. New York: The American Society of Mechanical Engineering, 2015: 61-62. |
| [6] | American National Standards Committe. ASME boiler and pressure vessel code, code cases: nuclear components: ASME BPVC.CC. NE-2015[S]. New York: The American Society of Mechanical Engineering, 2015: 1-24. |
| [7] | American National Standards Committe. ASME boiler and pressure vessel code, Section Ⅷ, rules for construction of pressure vessels, division 1: ASME BPVC.Ⅷ.1-2017[S]. New York: The American Society of Mechanical Engineering, 2017: 360-363. |
| [8] | American National Standards Committe. ASME boiler and pressure vessel code, Section Ⅷ, rules for construction of pressure vessels, division 2, alternative rules: ASME BPVC.Ⅷ.2-2017[S]. New York: The American Society of Mechanical Engineering, 2017: 208-210. |
| [9] | CEN National Members. Unfired pressure vessels-Part 3: design: BS EN 13445-3: 2014[S]. London: BSI Standards Limited, 2014: 31-35. |
| [10] |
陈来云, 葛鸿辉, 柳胜华.
核电站钢制安全壳封头屈曲评价方法简介及应用[J]. 压力容器, 2013, 30(7): 56–71.
CHEN Lai-yun, GE Hong-hui, LIU Sheng-hua. Introduction and application of buckling evaluation for steel containment vessel head of nuclear power plant[J]. Pressure Vessel Technology, 2013, 30(7): 56–71. DOI:10.3969/j.issn.1001-4837.2013.07.009 |
| [11] | MOKHTARIAN K, OSAGE D A, JANELLE J L, et al. Design of torispherical and ellipsoidal heads subjected to internal pressure[R]. New York: The Welding Research Council, Inc., 2005. |
| [12] | DAVID A, OSAGE P E. ASME section Ⅷ-division 2 criteria and commentary[M]. New York: The American Society of Mechanical Engineers, 2014: 85-88. |
| [13] |
王林鸿, 陈永辉.
用四心圆法作近似椭圆的偏差分析[J]. 机械工程师, 2002(8): 59–60.
WANG Lin-hong, CHEN Yong-hui. Error analysis of the approximate ellipse made by four-arcs method[J]. Mechanical Engineer, 2002(8): 59–60. DOI:10.3969/j.issn.1002-2333.2002.08.031 |
| [14] | BROWNELL L E, YOUNG E H. Process equipment design-vessel design[M]. New York: John Wiley & Sons, Inc, 1959: 120-140. |
| [15] |
寿比南, 杨国义, 徐峰, 等.
GB 150-2011《压力容器》标准释义[M]. 北京: 新华出版社, 2012: 118-121.
SHOU Bi-nan, YANG Guo-yi, XU Feng, et al. GB 150-2011 Pressure vessels criteria and commentary[M]. Beijing: Xinhua Publishing House, 2012: 118-121. |
| [16] | SHIELD R T, DRUCKER D C. Design of thin-walled torispherical and toriconical pressure-vessel heads[J]. Journal of Applied Mechanics, 1961, 28(2): 292–297. DOI:10.1115/1.3641671 |
| [17] |
全国压力容器标准化技术委员会.《钢制压力容器——分析设计标准》标准释义: JB4732-95[S].北京: 中国标准出版社, 1995: 49-52.
China Standardization Committeeon Pressure Vessels. Steel Pressure vessels-design by analysis criteria and commentary: JB 4732-95[S]. Beijing: Standards Press of China, 1995: 49-52. |
| [18] | KALNINS A, UPDIKE D P. Limit pressures of cylindrical and spherical shells[J]. Journal of Pressure Vessel Technology, 2001, 123(3): 288–292. DOI:10.1115/1.1367273 |
| [19] | MILLER C D. Research related to buckling design of nuclear containment[J]. Nuclear Engineering and Design, 1984, 79(2): 217–227. DOI:10.1016/0029-5493(84)90240-1 |
| [20] | MILLER C D. Buckling criteria for torispherical heads under internal pressure[R]. New York: The Welding Research Council, Inc., 1999. |
| [21] | MILLER C D. Buckling criteria for torispherical heads under internal pressure[J]. Journal of Pressure Vessel Technology, 2001, 123(3): 318–323. DOI:10.1115/1.1360692 |
| [22] | KALNINS A, RANA M D. A new design criterion based on pressure testing of torispherical heads[R]. New York: The Welding Research Council, Inc., 1996. |
| [23] | RANA M D, KALNINS A. Technical basis for code cases on design of ellipsoidal and torispherical heads for ASME section Ⅷ vessels[J]. Journal of Pressure Vessel Technology, 2000, 122(1): 55–59. DOI:10.1115/1.556150 |
| [24] | KALNINS A, UPDIKE D P. New design curves for torispherical heads[R]. New York: The Welding Research Council, Inc., 1991. |
| [25] | BAYLAC G, KOPLEWICZ D. EN 13445 "Unfired pressure vessels" background to the rules in part 3 design[M]. Paris: Standardization Office of the French Standardization System in the Field of Mechanical Engineering and Rubber Industries, 2004: 13-17. |
| [26] | GALLETLY G D. Design equations for preventing buckling in fabricated torispherical shells subjected to internal pressure[J]. Proceedings of the Institution of Mechanical Engineers, 1986, 200: 127–139. DOI:10.1243/PIME_PROC_1986_200_018_02 |
| [27] | BUSHNELL D. BOSOR 5-program for buckling of elastic-plastic complex shells of revolution including large deflections and creep[J]. Computers and Structures, 1976, 6(3): 221–239. DOI:10.1016/0045-7949(76)90034-1 |
| [28] | GALLETLY G D. Plastic buckling of torispherical and ellipsoidal shells subjected to internal pressure[J]. Proceedings of the Institution of Mechanical Engineers, 1981, 195(12): 329–345. |
| [29] | GALLETLY G D. A simple design equation for preventing buckling in fabricated torispherical shells under internal pressure[J]. Journal of Pressure Vessel Technology, 1986, 108(4): 521–526. DOI:10.1115/1.3264824 |



