2. 安徽理工大学 机械工程博士后科研流动站, 安徽 淮南 232001;
3. 广西省制造系统与先进制造技术重点实验室, 广西 桂林 530003;
4. 安徽理工大学 电气与信息工程学院, 安徽 淮南 232001
2. Postdoctoral Research Station of Mechanical Engineering, Anhui University of Science and Technology, Huainan 232001, China;
3. Guangxi Key Lab of Manufacturing System and Advanced Manufacturing Technology, Guilin 530003, China;
4. School of Electrical and information Engineering, Anhui University of Science and Technology, Huainan 232001, China
工业产品的发展趋向于微型化、精密化,各种微型元器件产品越来越多。精密测量机被广泛应用于微型元器的精密测量,它对微型器件的三维形貌、质量等的精确控制具有重要作用。微纳测头是精密测量机的关键零部件,其性能直接影响坐标测量设备的整体性能,因此,新型微纳测头研究成为精密测量领域的关注重点[1-3]。
微纳测头刚度是微纳米测量系统的关键属性,它影响着测头的接触力、稳定性、工艺性、测量精度和动态响应等特性[4]。对于接触式微纳测头,其刚度特性直接影响测头的稳定性、灵敏度、测量精度、动态响应等性能指标,进而影响测头的整体性能。
目前多数研究集中于具有固定刚度特性的微纳测头[5-7]。然而,若微纳测头刚度过高,测量过程中易划伤工件表面;若微纳测头刚度过低,容易造成谐振频率低、动态响应慢、稳定性差和误触发等[8]。微纳测头的约束支撑机构是测头机械结构的主体,其刚度特性直接决定测头的整体刚度。因此,通过研究使得微纳测头在使用过程中具有最优的刚度特性,对测头性能的提升具有非常重要的理论意义与实际价值。
鉴于固定刚度微纳测头存在的诸多不足,Alblalaihid等[9]提出一种基于三角悬臂梁支撑机构的微纳测头,利用压杆失稳原理实现支撑机构的变刚度,但未给出准确的刚度计算方法及临界屈曲载荷模型。Kim等[10]提出用施加额外载荷力的方式放大测头位移以改变其刚度。Bonello等[11]提出通过改变梁与框架的安装点来改变梁的有效长度,进而改变刚度。但是,文献[10-11]所提方法增大了测头结构的复杂性。
笔者设计了一种十字交叉型悬臂梁约束支撑微纳测头。基于压杆失稳原理,利用压电装置改变悬臂梁的轴向受力以改变其刚度,进而改变约束支撑机构的整体刚度。基于最小势能原理建立约束支撑机构的刚度模型,为计算变刚度控制过程所需压电驱动力提供重要的理论依据,并通过有限元仿真验证理论模型的准确性和变刚度调节的可行性。
1 变刚度微纳测头构型与测量过程图 1所示为基于十字交叉压缩悬臂梁的变刚度微纳测头,它主要由测球、测杆、中心体、支撑梁、基座、H型柔顺机构、位移传感器及压电驱动装置等组成。
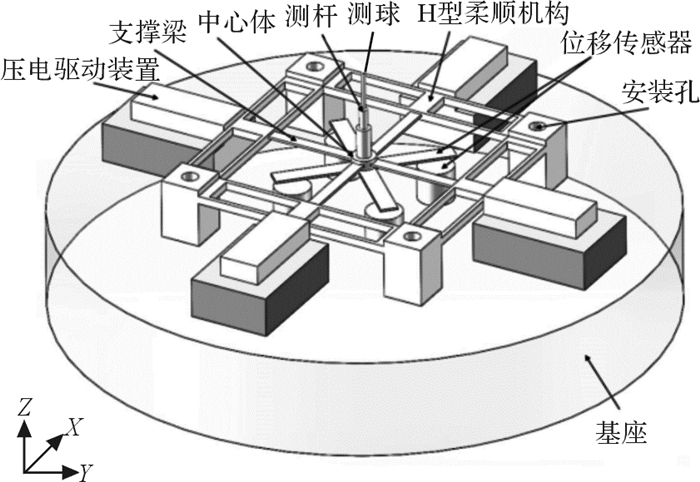
|
| 图 1 变刚度微纳测头结构示意图 Fig.1 Structure diagram of variable stiffness micro-nano probe |
微纳测头测量过程中的刚度变化过程如图 2所示[12]。图 2(a)所示为微纳测头主轴从远处快速接近被测工件的过程,为避免惯性力导致中心体及位移传感器位姿改变而造成误触发,压电装置不提供驱动力,此时,微纳测头刚度较大。图 2(b)所示为微纳测头接触到被测工件的过程,测球与工件表面发生接触,接触力通过测杆传递至中心体并使其位姿发生变化,通过位移传感器及其信号采集装置获取被测点的三维坐标。为了避免测球划伤工件表面,压电装置提供驱动力,使得测头支撑梁受压,从而降低测头刚度。图 2(c)所示为微纳测头测量完后离开被测工件的过程,为克服工件表面与测球之间的吸附力,压电装置不提供驱动力,此时,微纳测头具有较大的刚度。
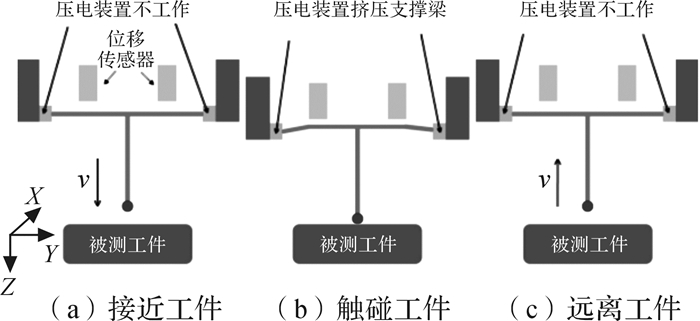
|
| 图 2 变刚度微纳测头测量过程 Fig.2 Measurement process of variable stiffness micro-nano probe |
由前述可知,微纳测头的刚度主要取决于约束支撑机构的刚度, 故有必要建立微纳测头支撑机构的整体刚度模型,为变刚度控制提供理论基础。
在构建微纳测头支撑机构的整体刚度模型时,假设除支撑梁以外的其他部件皆为刚性构件,支撑梁的变形处于弹性变形范围内,支撑梁是薄壁梁,不考虑横截面剪应力的影响,故可采用Euler-Bernoulli梁模型[13]。
2.1 Z向刚度分析微纳测头支撑机构的主要参数如图 3所示,l、wb、tb分别为支撑梁长度、宽度和厚度, ls为测杆长度,wi为中心体半径。其中:Z向为轴向,Y向为横向。

|
| 图 3 微纳测头支撑机构主要参数 Fig.3 Main parameters of the micro-nano probe supporting mechanism |
如图 4所示,当微纳测头受Z向力时,每根梁的受力情况相同,单根梁受力FB=F/4。单根梁与柔顺机构的连接端可看作固定约束端。
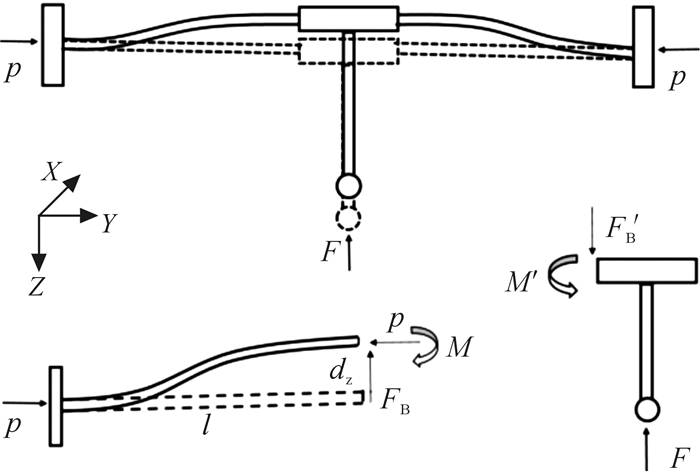
|
| 图 4 微纳测头支撑机构Z向受力示意图 Fig.4 Schematic diagram of Z-direction force of micro-nano probe supporting mechanism |
由图 4可知,支撑梁处主要存在弯曲和轴向压缩变形,建立支撑梁弯曲时的试函数[14]:
| $ \hat u\left( x \right) = {c_1}{x^2} + {c_2}{x^3} $ | (1) |
式中:c1、c2为待定系数,其大小由边界条件和势能泛函确定。
根据最小势能原理,该试函数应满足如下位移边界条件:
| $ \left\{ \begin{array}{l} \hat u\left( 0 \right) = 0\\ \hat u'\left( 0 \right) = 0\\ \hat u'\left( l \right) = 0 \end{array} \right. $ | (2) |
由边界条件可得:
| $ 2{c_1}l + 3{c_2}{l^2} = 0 $ | (3) |
则该梁的总势能泛函为:
| $ \begin{array}{l} \mathit{\Pi } = \int\limits_0^l {\frac{1}{2}EI{{\left( {\hat u''} \right)}^2}{\rm{d}}x} - \int\limits_0^l {\frac{1}{2}p{{\left( {\hat u'} \right)}^2}{\rm{d}}x} - \\ \;\;\;\;\;\;\;{F_{\rm{B}}}\hat u\left( l \right) - M \cdot \hat u'\left( l \right) \end{array} $ | (4) |
式中:E为弹性模量,M为单根梁所受力矩,p为压电驱动力,I为惯性矩,
联立方程(1)至(4)可得:
| $ \mathit{\Pi } = \frac{3}{2}c_2^2EI{l^3} - \frac{3}{{20}}c_2^2p{l^5} - \frac{1}{2}{c_2}{F_{\rm{B}}}{l^3} $ | (5) |
由
| $ {c_2} = \frac{{{F_{\rm{B}}}}}{{6EI - \left( {3/5} \right)p{l^2}}} $ | (6) |
由方程(1)、(3)和(6)可得微纳测头的Z向刚度Kz为:
| $ {K_z} = \frac{F}{{{d_z}}} = \frac{{4E{w_{\rm{b}}}t_{\rm{b}}^3}}{{{l^3}}} - \frac{{24}}{{5l}}p $ | (7) |
令Kz=0,得支撑梁的屈曲临界载荷为:
| $ {p_{{\rm{cr}}z}} = \frac{{10EI}}{{{l^2}}} $ | (8) |
如图 5所示,当微纳测头受Y向负载时,中心体会发生微小的Y向移动和转动。由于梁的长度远远大于其厚度,故可以忽略Y向移动,只考虑平面内的弯曲和绕梁中心轴线的转动[15]。
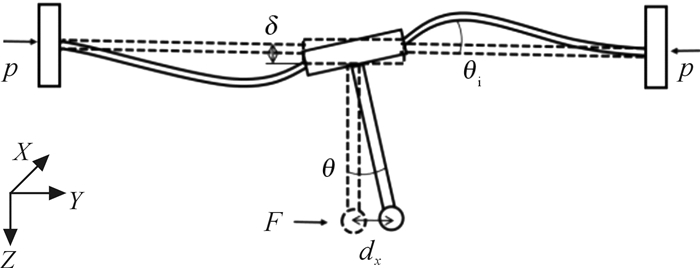
|
| 图 5 微纳测头支撑机构Y向受力示意图 Fig.5 Schematic diagram of Y-directional force of micro-nano probe supporting mechanism |
由于微纳测头是中心对称结构,该测头约束支撑机构在受Y向力时的变形可以分解为弯曲变形和扭转变形,与之相对应的梁分别为弯曲梁和扭转梁,则微纳测头的横向刚度Ky由弯曲刚度Kb与扭转刚度Kt组成。
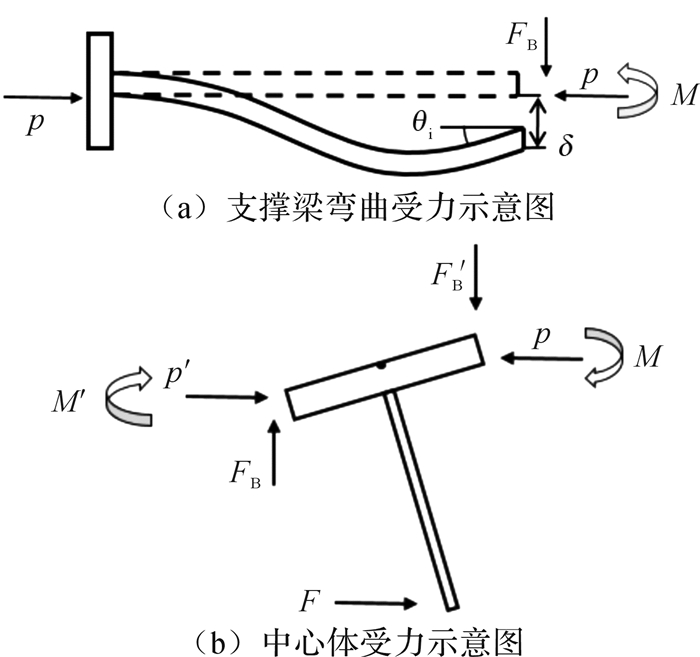
2.2.1 弯曲刚度分析图 6所示为微纳测头支撑机构弯曲受力示意图。
|
| 图 6 微纳测头支撑机构弯曲受力示意图 Fig.6 Schematic diagram of bending force of micro-nano probe supporting mechanism |
由图 6(a)可知, 弯曲梁的受力情况与微纳测头受Z向载荷时支撑梁的受力情况是一致的,故支撑梁弯曲时试函数与式(1)相同。
由几何关系θi=θ≈tanθ可得:
| $ {\theta _{\rm{i}}} \cdot {w_{\rm{i}}} = \delta $ | (9) |
式中:δ为梁末端Z向位移,
由式(9)得边界条件为:
| $ \left\{ \begin{array}{l} \hat u\left( 0 \right) = 0\\ \hat u'\left( 0 \right) = 0\\ {w_{\rm{i}}} \cdot \hat u'\left( l \right) = \hat u\left( l \right) \end{array} \right. $ | (10) |
由式(10)可得:
| $ {c_1} = - \frac{{3l{w_{\rm{i}}} + {l^2}}}{{l + 2{w_{\rm{i}}}}}{c_2} $ | (11) |
支撑梁弯曲时的势能泛函为:
| $ \begin{array}{l} {\mathit{\Pi }_{\rm{b}}} = \int\limits_0^l {\frac{1}{2}EI{{\left( {\hat u''} \right)}^2}{\rm{d}}x} - \int\limits_0^l {\frac{1}{2}p{{\left( {\hat u'} \right)}^2}{\rm{d}}x} - \\ \;\;\;\;\;\;\;{F_{\rm{B}}}\delta - \frac{1}{2}M{\theta _{\rm{i}}} \end{array} $ | (12) |
由
| $ {c_2} = \frac{{F{l_{\rm{s}}}\left( {l + 2{w_{\rm{i}}}} \right)}}{{8EI\left( {{l^2} + 3w_{\rm{i}}^2 + 3l{w_{\rm{i}}}} \right) - 2p{l^2}\left( {\frac{2}{{15}}{l^2} + \frac{6}{5}w_{\rm{i}}^2 + \frac{6}{5}l{w_{\rm{i}}}} \right)}} $ | (13) |
由图 6(b)得中心体力矩平衡方程:
| $ \frac{1}{2}F{l_{\rm{s}}} + p\delta = M + {F_{\rm{B}}}{w_{\rm{i}}} $ | (14) |
由几何关系dx=θls,得:
| $ {K_{\rm{b}}} = \frac{F}{{{d_x}}} = \frac{F}{{\hat u'\left( l \right) \cdot {l_{\rm{s}}}}} $ | (15) |
由方程(10)至(15)可得:
| $ \begin{array}{l} {K_{\rm{b}}} = \frac{{E{w_{\rm{b}}}t_{\rm{b}}^3}}{{l_{\rm{s}}^2l}}\left( {\frac{2}{3} + \frac{{2w_i^2}}{{{l^2}}} + \frac{{2{w_{\rm{i}}}}}{l}} \right) - \frac{p}{{5l \cdot l_{\rm{s}}^2}}\\ \;\;\;\;\;\;\;\left( {\frac{{4{l^2}}}{3} + 12w_{\rm{i}}^2 + 12l{w_{\rm{i}}}} \right) \end{array} $ | (16) |
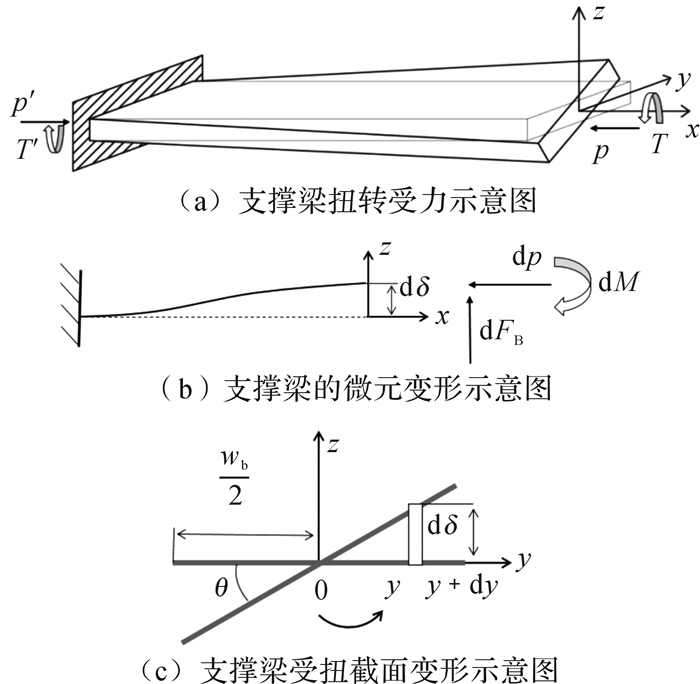
图 7所示为微纳测头支撑机构扭转受力示意图。
|
| 图 7 微纳测头支撑机构扭转受力示意图 Fig.7 Schematic diagram of torsional force of micro-nano probe supporting mechanism |
如图 7(a)所示,支撑梁受绕x轴的扭转力矩T和沿x轴的轴向压力p。梁为狭长矩形截面薄壁梁,可忽略翘曲影响。选取三角级数的前2项作为转角函数的试函数[16],为:
| $ \theta \left( x \right) = \sum\limits_{i = 3,4} {{c_i}\left( {1 - \cos \frac{{{\rm{i \mathsf{ π} }}x}}{{2l}}} \right)} $ | (17) |
式中:c3、c4为待定系数。
转角函数θ(x)应满足如下边界条件:
| $ \theta \left( 0 \right) = \theta '\left( 0 \right) = \theta ''\left( l \right) = 0 $ | (18) |
| $ \hat u\left( x \right) = \theta \left( x \right) \cdot y $ | (19) |
支撑梁扭转的势能泛函为:
| $ \begin{array}{l} {\mathit{\Pi }_{\rm{t}}} = \frac{1}{2}\int\limits_0^l {GJ{{\left( {\theta '} \right)}^2}d} - \int\limits_0^{\frac{{{w_{\rm{b}}}}}{2}} {\int\limits_0^l {{{\left( {\hat u'} \right)}^2}\frac{p}{{{w_{\rm{b}}}}}{\rm{d}}x{\rm{d}}y} } - \\ \;\;\;\;\;\;\;\;T \cdot \theta \left( l \right) \end{array} $ | (20) |
式中:G为抗剪切模量,J为截面极惯性矩。
对于矩形截面[17],其截面极惯性矩为:
| $ J = G{w_{\rm{b}}}t_{\rm{b}}^3\left[ {\frac{1}{3} - 0.21\frac{{{t_{\rm{b}}}}}{{{w_{\rm{b}}}}}\left( {1 - \frac{{t_{\rm{b}}^4}}{{12w_{\rm{b}}^4}}} \right)} \right] $ | (21) |
由中心体力矩平衡得:
| $ T = \frac{1}{2}F{l_{\rm{s}}} $ | (22) |
由
| $ {c_3} = 9{c_4} = \frac{{48F{l_{\rm{s}}}l}}{{12GJ{{\rm{ \mathsf{ π} }}^2} + pw_{\rm{b}}^2{{\rm{ \mathsf{ π} }}^2}}} $ | (23) |
由方程(17)和(23)可得扭转刚度为:
| $ {K_{\rm{t}}} = \frac{F}{{\theta \cdot {l_{\rm{s}}}}} = \frac{{9{{\rm{ \mathsf{ π} }}^2}GJ}}{{40l_{\rm{s}}^2l}} - \frac{{3pw_{\rm{b}}^2{{\rm{ \mathsf{ π} }}^2}}}{{160l_{\rm{s}}^2l}} \approx \frac{{2Gl}}{{l_{\rm{s}}^2l}} - \frac{{pw_{\rm{b}}^2}}{{5l_{\rm{s}}^2l}} $ | (25) |
结合上述支撑梁的弯曲刚度Kb和扭转刚度Kt,可得测头支撑机构Y向刚度Ky为:
| $ \begin{array}{*{20}{c}} {{K_y} = {K_{\rm{b}}} + {K_{\rm{t}}} = \frac{{E{w_{\rm{b}}}t_{\rm{b}}^3}}{{l_{\rm{s}}^2l}}\left( {\frac{2}{3} + \frac{{2{w_{\rm{i}}}}}{l} + \frac{{2w_{\rm{i}}^2}}{{{l^2}}}} \right) + \frac{{2Gl}}{{l_{\rm{s}}^2l}} - }\\ {\frac{p}{{5l \cdot l_{\rm{s}}^2}}\left( {\frac{{4{l^2}}}{3} + 12l{w_{\rm{i}}} + 12lw_{\rm{i}}^2 + w_{\rm{b}}^2} \right)} \end{array} $ | (25) |
令Ky=0,得支撑梁屈曲临界载荷pcry为:
| $ {p_{{\rm{cry}}}} = \frac{{10EI}}{{{l^2}}}\left( {\frac{{12{l^2} + 36l{w_{\rm{i}}} + 36w_{\rm{i}}^2 + \frac{{3GJ}}{{EI}}{l^2}}}{{4{l^2} + 36l{w_{\rm{i}}} + 36w_{\rm{i}}^2 + 3w_{\rm{b}}^2}}} \right) $ | (26) |
由于l远大于wi、wb,故有:
| $ {p_{{\rm{cry}}}} > {p_{{\rm{crz}}}} \ge p \ge 0 $ | (27) |
令Kz=Ky,得:
| $ {p_{{\rm{iso}}}} = \frac{{10EI}}{{{l^2}}}\left( {\frac{{12{l^2} + 36l{w_{\rm{i}}} + 36w_{\rm{i}}^2 + \frac{{3GJ}}{{EI}}{l^2} - 72l_{\rm{s}}^2}}{{4{l^2} + 36l{w_{\rm{i}}} + 36w_{\rm{i}}^2 + 3w_{\rm{b}}^2 - 72l_{\rm{s}}^2}}} \right) $ | (28) |
当p=piso时,微纳测头在测量过程中的刚度具有较好的各向同性。
3 数值验证为验证上述微纳测头刚度模型的正确性,利用有限元分析加以验证。
微纳测头的材料属性和结构参数如表 1和表 2所示,其中,支撑梁选用铍青铜,测杆选用碳化钨,测球选用红宝石[18]。
| 材料 | 弹性模量/GPa | 密度/(kg/m3) | 泊松比 |
| 铍青铜 | 130 | 8 300 | 0.34 |
| 碳化钨 | 345 | 19 300 | 0.31 |
| 红宝石 | 375 | 3 890 | 0.22 |
| mm | |||||
| 参数 | ls | wi | l | wb | tb |
| 数值 | 4.85 | 0.6 | 4.4 | 0.6 | 0.1 |
根据表 2所示的微纳测头的结构参数,建立微纳测头约束支撑机构的三维模型并进行有限元仿真,对支撑梁末端施加固定约束。对测球表面的Z向与Y向分别施加大小为1 mN的力,得到位移云图,如图 8与图 9所示。
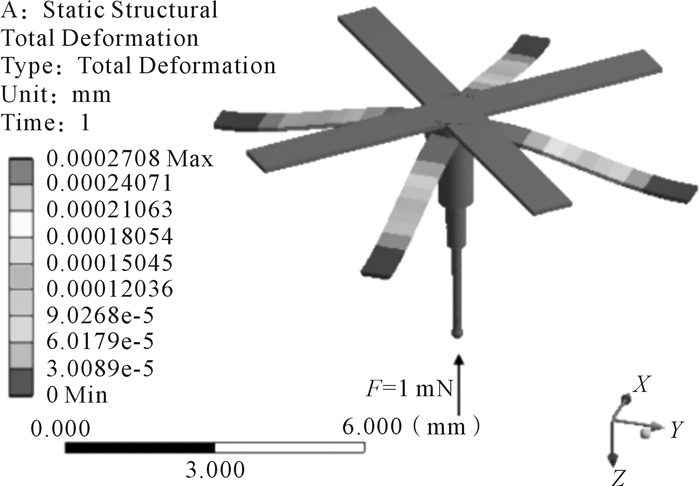
|
| 图 8 p=0 N,Z向力为1 mN时微纳测头位移云图 Fig.8 Displacement nephogram of micro-nano probe with P=0 N, Z-directional force of 1 mN |
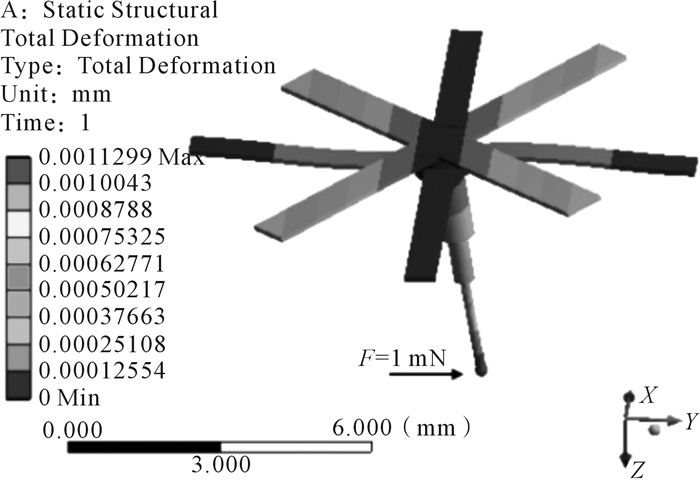
|
| 图 9 p=0 N, Y向力为1 mN时微纳测头位移云图 Fig.9 Displacement nephogram of micro-nano probe with p=0 N, Y-directional force of 1 mN |
由图 8与图 9可知,当微纳测头受到压电驱动力p=0 N时,测头的Z向刚度与Y向刚度分别为3.694 mN/μm与0.885 mN/μm。
通过有限元仿真和理论计算分别得到压电驱动力p与测头刚度K的关系曲线,如图 10所示。
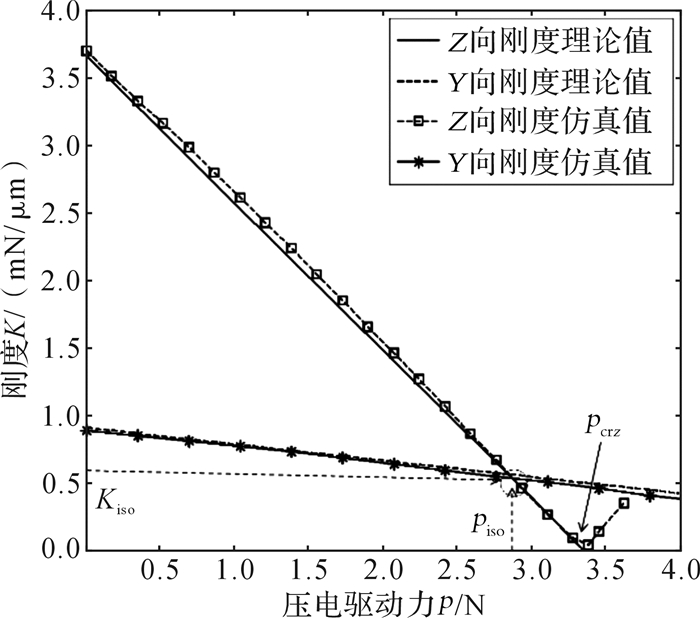
|
| 图 10 压电驱动力与微纳测头刚度的关系曲线 Fig.10 Relationship curves of piezoelectric drive force and micro-nano probe stiffness |
由图 10可知,微纳测头刚度随着压电驱动力的增加而减小,当压电驱动力的范围为0≤p≤pcrz时,压电驱动力p与测头刚度K呈线性关系。仿真表明,当p≥pcrz时,支撑梁在任意微小扰动下发生弯曲失稳,此时微纳测头不具有测量稳定性,说明压电驱动力p必须小于屈曲临界载荷pcrz。通过式(8)、(29)计算得到pcrz、piso,并将piso代入式(7)可得Kiso,所得计算结果与有限元仿真结果如表 3所示。
| 比较项 | pcrz/N | piso/N | Kiso/(mN/μm) |
| 理论值 | 3.36 | 2.71 | 0.559 |
| 仿真值 | 3.42 | 2.84 | 0.530 |
通过式(29)可计算表 3中理论计算结果与仿真结果的相对误差。
| $ S = \frac{1}{n}\sum\limits_{j = 1}^n {\frac{{\left| {{X_j} - {Y_j}} \right|}}{{{X_j}}}} $ | (29) |
式中:S为相对误差,Xj为仿真值,Yj为理论值,n为取值点数。
当0≤p≤pcrz,n=10时,由式(7)与式(25)分别计算得微纳测头的Z向刚度Kz和横向刚度Ky。结合仿真结果,利用式(29)算得计算值与仿真值的平均相对误差分别为2.94%,3.03%。
上述结果表明,理论计算值和有限元仿真结果较为一致,表明了本文所建立的微纳测头刚度模型及临界屈曲载荷模型具有较高的准确性。
4 结论1) 利用压杆失稳原理,设计了一种基于十字交叉型悬臂梁约束支撑的变刚度微纳测头。
2) 利用最小势能原理,构建了微纳测头柔性约束支撑刚度模型,基于该模型进一步得到了约束梁的临界屈曲载荷。
3) 给定微纳测头结构参数,得到了微纳测头具有各向同性刚度特性时所应具有的压电驱动力大小。
4) 有限元仿真分析说明,本文构建的各个理论模型具有较高的准确性,为新型变刚度测头样机研制和变刚度控制试验研究奠定了坚实的理论基础。
| [1] | CLAVERLEY J D, LEACH R K. Development of a three-dimensional vibrating tactile probe for miniature CMMs[J]. Precision Engineering, 2013, 37(2): 491–499. DOI:10.1016/j.precisioneng.2012.12.008 |
| [2] |
黄强先, 余惠娟, 黄帅, 等.
微纳米三坐标测量机测头的研究进展[J]. 中国机械工程, 2013, 24(9): 1264–1272.
HUANG Qiang-xian, YU Hui-juan, HUANG Shuai, et al. Advances in probes of micro-nano coordinating measuring machine[J]. China Mechanical Engineering, 2013, 24(9): 1264–1272. DOI:10.3969/j.issn.1004-132X.2013.09.026 |
| [3] | LI R J, FAN K C, HUANG Q X, et al. A long-stroke 3D contact scanning probe for micro/nano coordinate measuring machine[J]. Precision Engineering, 2016, 43: 220–229. DOI:10.1016/j.precisioneng.2015.08.001 |
| [4] | BOS E J C. Aspects of tactile probing on the micro scale[J]. Precision Engineering, 2011, 35(2): 228–240. DOI:10.1016/j.precisioneng.2010.09.010 |
| [5] |
刘芳芳, 费业泰, 夏豪杰.
纳米坐标测量机的三维接触式测头机构[J]. 纳米技术与精密工程, 2011, 9(3): 249–252.
LIU Fang-fang, FEI Ye-tai, XIA Hao-jie. Research on the 3D touch probe mechanism of nano-CMM[J]. Nanotechnology and Precision Engineering, 2011, 9(3): 249–252. DOI:10.3969/j.issn.1672-6030.2011.03.012 |
| [6] | ALBLALAIHID K, KIRK T, LAWES S, et al. Fabrication of a smart suspension structure of micro tactile probing[J]. Procedia Engineering, 2014, 87: 1164–1167. DOI:10.1016/j.proeng.2014.11.373 |
| [7] |
陈晓怀, 陈贺, 王珊, 等.
微纳测量机测头弹性结构的参数设计[J]. 光学精密工程, 2013, 21(10): 2587–2593.
CHEN Xiao-huai, CHEN He, WANG Shan, et al. Design of elastic structure parameters of probe in micro-nano CMM[J]. Optics and Precision Engineering, 2013, 21(10): 2587–2593. |
| [8] | ALBLALAIHID K, KINNELL P, LAWES S. Fabrication and characterisation of a novel smart suspension for micro-CMM probes[J]. Sensors and Actuators A:Physical, 2015, 232: 368–375. DOI:10.1016/j.sna.2015.04.029 |
| [9] | ALBLALAIHID K, KINNELL P, LAWES S, et al. Performance assessment of a new variable stiffness probing system for micro-CMMs[J]. Sensors, 2016, 16(4): 492. DOI:10.3390/s16040492 |
| [10] | KIM K, LIU X, ZHANG Y, et al. Nanonewton force-controlled manipulation of biological cells using a monolithic MEMS microgripper with two-axis force feedback[J]. Journal of Micromechanics & Microengineering, 2008, 18(5): 055013. |
| [11] | BONELLO P, BRENNAN M J, ELLIOTT S J, et al. Designs for an adaptive tuned vibration absorber with variable shape stiffness element[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society, 2005: 3955-3976. |
| [12] | ALBLALAIHID K, LAWES S, KINNELL P. Variable stiffness probing systems for micro-coordinate measuring machines[J]. Precision Engineering, 2016, 43: 262–269. DOI:10.1016/j.precisioneng.2015.08.004 |
| [13] | PRIL W. Development of high precision mechanical probes for coordinate measuring machines[J]. Technische Universiteit Eindhoven, 2002, 25(2): 100–102. |
| [14] |
曾攀.
有限元分析及应用[M]. 北京: 清华大学出版社, 2004: 51-87.
ZENG Pan. Finite element analysis and application[M]. Beijing: Tsinghua University Press, 2004: 51-87. |
| [15] |
李源.MEMS压阻式三维微触觉测头及其在纳米测量机上的应用研究[D].天津: 天津大学精密仪器与光电子工程学院, 2007: 29-30.
LI Yuan. Study on MEMS piezo-resistance 3D micro tactile probe and application in NMM[D]. Tianjin: Tianjin University, School of Precision Instruments & Optoelectronics Engineering, 2007: 29-30. http://cdmd.cnki.com.cn/article/cdmd-10056-2008185236.htm |
| [16] |
刘迎春, 邓世林, 张文福, 等.
集中荷载作用下扭转支撑悬臂梁弯扭屈曲分析[J]. 东北石油大学学报, 2017, 41(3): 103–110.
LIU Ying-chun, DENG Shi-lin, ZHANG Wen-fu, et al. Flexural-torsional buckling analysis for cantilever beam with torsional bracing under concentrated load[J]. Journal of Northeast Petroleum University, 2017, 41(3): 103–110. DOI:10.3969/j.issn.2095-4107.2017.03.011 |
| [17] |
范钦珊.
材料力学[M]. 北京: 清华大学出版社, 2008: 20-40.
FAN Qin-shan. Materials mechanics[M]. Beijing: Tsinghua University Press, 2008: 20-40. |
| [18] | HE M, LIU R, LI Y, et al. Tactile probing system based on micro-fabricated capacitive sensor[J]. Sensors and Actuators A:Physical, 2013, 194: 128–134. DOI:10.1016/j.sna.2013.01.030 |



