2. 中信重工机械股份有限公司, 河南 洛阳 471039
2. CITIC(China International Trust and Investment Corporation) Heavy Industries Co., Ltd., Luoyang 471039, China
超深矿井提升机卷筒是提升系统的关键部件,它承受着提升过程中全部有效载荷。仅对卷筒结构进行静强度分析,通过分析几种典型计算工况得出卷筒最大应力值,无法准确得到提升系统在上提、下放全过程中卷筒结构的应力动态变化情况。因此针对目前我国正在创新设计的1 500 m超深矿井多层缠绕式提升机卷筒的设计需要,有必要对作业过程中卷筒结构进行强度分析,得到卷筒作业过程中关键部位的动态载荷与应力分布,从而对卷筒结构的疲劳寿命作出较准确的预测。
卷筒结构主要受到钢丝绳的缠绕力,因此准确计算钢丝绳在上提、下放过程中的张力变化对于卷筒结构的动态应力研究具有重要作用。Wang等[1-2]建立了矿井提升钢丝绳两端张力的微分方程,运用Simulink仿真分析了在上提和下放重载过程中钢丝绳的动态张力随有效载荷和加速度的变化情况;韩仕豪等[3]分析了不同运行阶段钢丝绳的张力和钢丝绳对提升机主轴的作用力,得出了提升系统主轴在正常动载荷和非正常动载荷作用下的应力分布。为准确地分析钢丝绳在超深、高速、重载的复杂情况下对提升机卷筒的作用力,Dietz[4]在研究多层缠绕情况下钢丝绳对卷筒的作用力时,讨论了钢丝绳张力随层数的变化过程,Otto等[5]分析了提升系统在提升重载过程中钢丝绳对卷筒的径向压力以及对挡绳板的轴向推力。由于钢丝绳对卷筒的作用力是循环载荷,大多数的零部件在循环载荷作用下都会产生疲劳破坏,所以对提升机卷筒结构进行疲劳寿命研究具有重要意义。有限元法对于疲劳寿命分析具有限制条件少、适用性好及不需确定疲劳缺口系数等优势,所以国内外许多研究学者用有限元数值仿真分析方法进行筒状结构的疲劳寿命研究:Peng等[6]利用ANSYS软件对矿井提升机卷筒进行了应力分析和模态分析,并对卷筒上薄弱位置进行了疲劳寿命分析,得到了卷筒薄弱位置的寿命;Ahmet等[7]对回旋式干燥机筒壳法兰接头和改进后筒壳的对接焊缝进行了有限元分析和疲劳计算;Li等[8]在有限元分析基础上,建立了一个实时动态加载模型,提出了带式输送机滚筒疲劳寿命可靠性分析方法;Li等[9]通过有限元数值模拟得出了焦炭塔裙座与筒体连接区域最大等效应变幅,并把该应变值代入根据实验结果回归分析得到的寿命表达式中,得出疲劳裂纹产生的时间和焦炭塔的疲劳寿命值;熊伟红等[10]通过有限元法计算了钢丝绳从自由状态至承受额定负载时的疲劳寿命值,并与用局部应力应变法算得的钢丝绳的疲劳寿命值进行比较,验证了局部应力应变法的准确性。
本文基于矿井提升动力学原理,结合提升系统在满载上提和空载下放时钢丝绳张力的变化情况,采用数值模拟的方法,分析1 500 m超深矿井提升机卷筒在满载上提和空载下放两种工况下的应力分布和应力-时间历程。利用提升机卷筒作业过程动态应力的分析结果对卷筒的疲劳寿命进行预测,分析在给定的存活率下不同负载对卷筒疲劳寿命的影响。
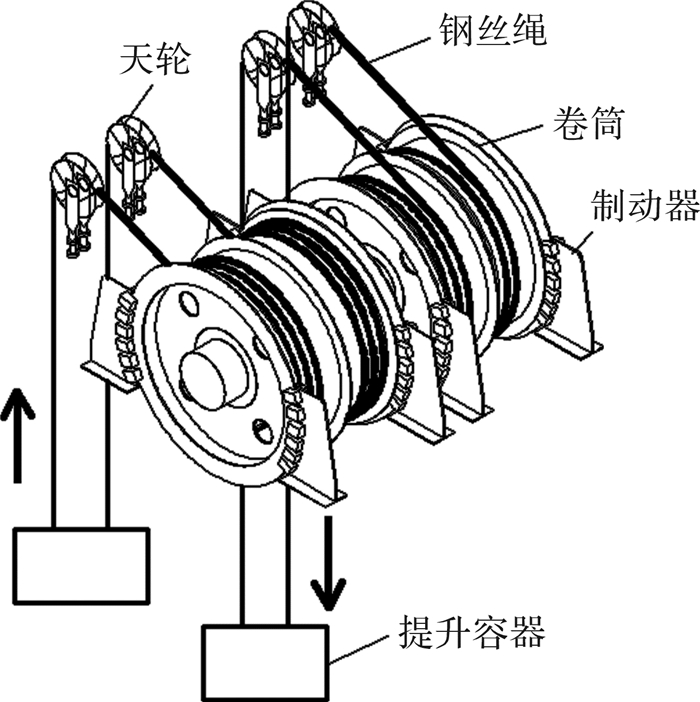
1 提升机卷筒工作载荷分析 1.1 提升系统工作原理1 500 m超深矿井提升机采用多绳缠绕式提升系统。它是由多根钢丝绳卷绕在同一个分段卷筒上,利用钢丝绳在卷筒上卷入或绕出,实现提升容器的上提或下放。其中,每个分段滚筒上卷绕2根钢丝绳,钢丝绳其中一端绕过天轮,通过张力平衡装置与提升容器相连接,其中一个提升容器处于上升状态,而另一个处于下放状态。提升钢丝绳在不同分段卷筒上的缠绕方向相反,如图 1所示,由于电机带动卷筒运转,当改变电机的运转方向时即可实现重物的上升或下降。
|
| 图 1 双卷筒提升系统示意图 Fig.1 Schematic diagram of double-drum lifting system |
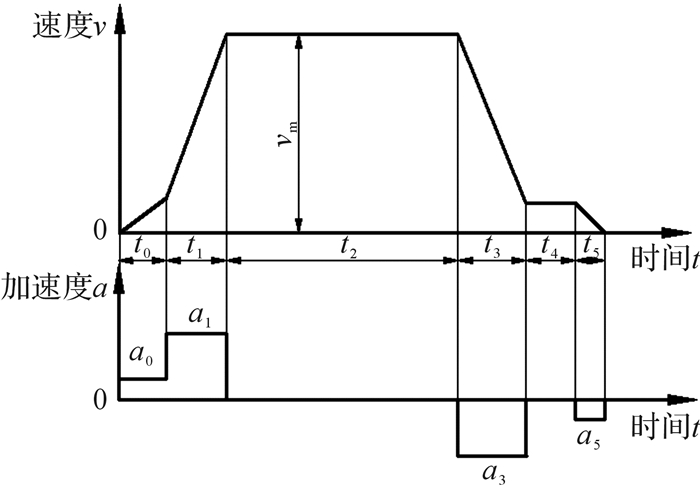
基于提升机运动学原理,采用六阶段速度图研究提升系统各个阶段相关运动参数(速度、加速度、位移、时间等)之间的关系,六阶段速度图包含初加速阶段、主加速阶段、等速阶段、减速阶段、爬行阶段和停车阶段,如图 2所示,表达了提升机在一个提升周期内的速度、加速度变化规律。根据曲线图可计算得出第2阶段也就是主加速度阶段的加速度最大,同时负载所产生的惯性力也最大。
|
| 图 2 六阶段速度图 Fig.2 The six stage velocity diagram |
当提升系统处于静止状态和等速运行阶段时,钢丝绳上任意位置的拉力是由绳端负载和该位置以下的绳重构成的[11]。当提升系统在加、减速运行阶段时,钢丝绳上任意位置的拉力不仅包含绳端负载和该位置以下的绳重,还需加上由于加速而产生的附加拉力或减去由于减速而产生的附加拉力。
1) 满载上提时钢丝绳的动态张力。
整个提升过程中卷筒侧钢丝绳的张力为:
| $ {F_{\rm{s}}} = \frac{{K(mg + {m_{\rm{z}}}g) + N{m_{\rm{p}}}g\left( {H - x} \right) + \sum {m_1}{a_t}}}{N} $ | (1) |
式中:K为矿井阻尼系数;m为提升货载质量,kg;mz为容器自身质量,kg;mp为提升钢丝绳每米质量,kg/m;H为钢丝绳悬垂高度,m;at为各个运行阶段的加速度,m/s2;∑m1为满载提升时提升系统的变位质量,kg; N为钢丝绳根数;x为提升容器运行距离,m。
满载上提时提升系统的变位质量为:
| $ \sum {m_1} = m + {m_{\rm{z}}} + {m_{\rm{j}}} + {m_{\rm{t}}} + {m_{\rm{d}}} + N{m_{\rm{p}}}\left( {H - x} \right) $ | (2) |
| $ x = {v_{0t}}\cdot t + \frac{1}{2}{a_t}\cdot{t^2} $ | (3) |
式中:mj为提升主机不包括天轮和电动机的变位质量,kg;v0t为各个阶段的初始速度,m/s;t为各个阶段运行时间,s;mt为天轮变位质量,kg;md为电动机变位质量,kg。
2) 空载下放时钢丝绳的动态张力。
整个下放过程中卷筒侧钢丝绳的张力为:
| $ {F_{\rm{x}}} = \frac{{K{m_{\rm{z}}}g + N{m_{\rm{p}}}gx + \sum {m_2}a}}{N} $ | (4) |
| $ \sum {m_2} = {m_{\rm{z}}} + {m_{\rm{j}}} + {m_{\rm{t}}} + {m_{\rm{d}}} + N{m_{\rm{p}}}x $ | (5) |
式中:∑m2为空载下放时提升系统的变位质量,kg。
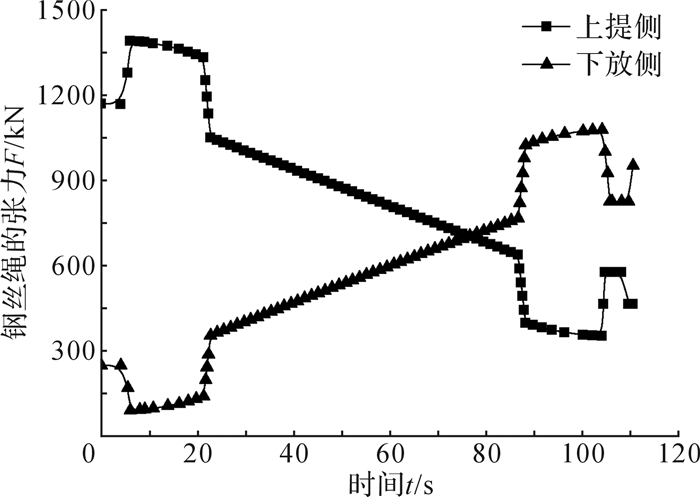
根据提升机卷筒的设计参数,结合式(1)至式(5), 可得卷筒侧钢丝绳张力随时间变化曲线,如图 3所示。由图 3可知,满载上提时钢丝绳的最大张力出现在第9秒, 即主加速阶段;空载下放时钢丝绳的最大张力出现在第104秒,即减速阶段。
|
| 图 3 卷筒侧钢丝绳张力随时间的变化曲线 Fig.3 The variation curves of the tension of steel wire rope on the drum side with time |
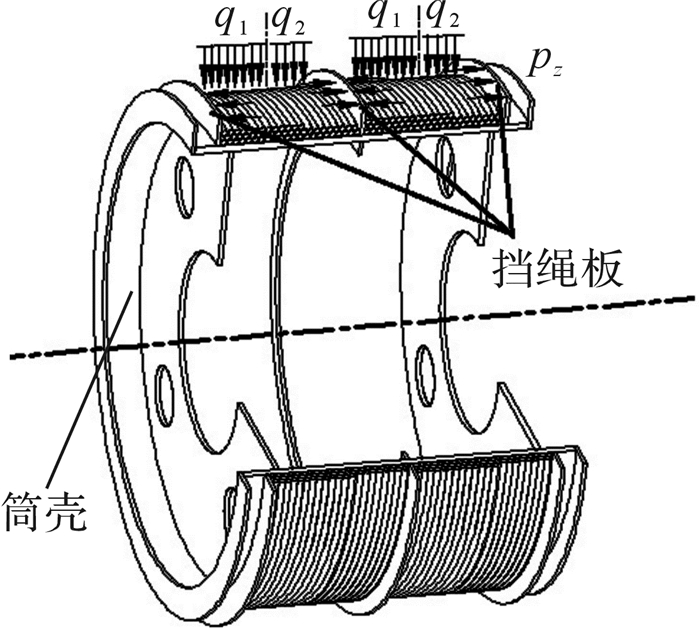
为便于对超深矿井提升机卷筒结构进行受力分析,将卷筒分为筒壳和挡绳板两个主要部分,如图 4所示。由于钢丝绳在缠绕过程中对筒壳的作用位置不同,所以以q1、q2表示不同层数钢丝绳作用在卷筒上的载荷集度,S表示钢丝绳对挡绳板的轴向作用力。
|
| 图 4 提升机卷筒结构示意图 Fig.4 Schematic diagram of hoist drum structure |
一般情况下,已缠绕到提升机卷筒上的钢丝绳仍对两端的端侧板产生轴向作用力,以pz表示钢丝绳对挡绳板的轴向作用力,因此需从卷筒所受的径向载荷集度和轴向作用力两方面来分析钢丝绳多层缠绕时卷筒的受力情况。
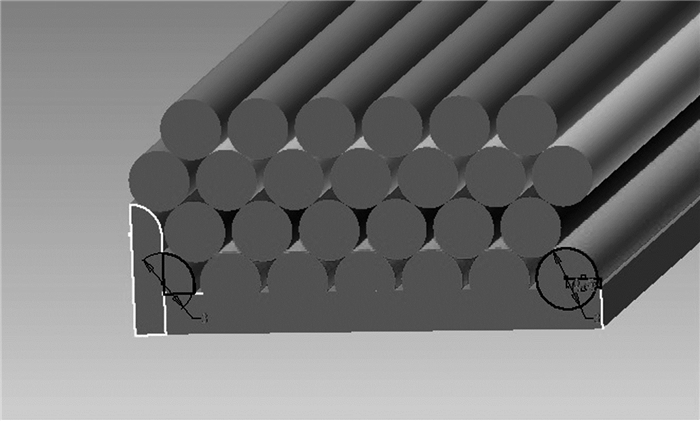
1) 钢丝绳缠绕到卷筒上时,对筒壳产生了箍紧力。在多层缠绕过程中,外部钢丝绳缠绕于里层相邻两圈钢丝绳间隙所形成的绳槽里,如图 5所示。
|
| 图 5 钢丝绳堆叠在卷筒上的断面图 Fig.5 Cross-section diagram of the wire rope stacked over the drum |
基于弹性板壳理论,将钢丝绳缠绕在卷筒上所形成的绳圈简化为质地均匀的圆环,每个圆环对筒壳的径向压力是均布的。由于卷筒结构的均匀对称性,在对薄壳圆筒进行受力分析时,可以截取任一单位长度的筒壳,并把它看作单元梁来进行研究,整个筒壳可视为由很多单元梁构成。钢丝绳在缠入或绕出卷筒时,钢丝绳对卷筒的作用面积是随时间而变化的,而钢丝绳的张力也是随时间变化的,所以钢丝绳对卷筒的径向压力也在不断变化。如图 6所示,截取任意时刻、任一单位长度的筒壳进行研究,卷筒受到钢丝绳对它的径向作用力是均匀的且不承受钢丝绳对它的轴向作用力。

|
| 图 6 提升机卷筒受力分析 Fig.6 Force analysis of hoist drum |
在任意时刻,钢丝绳以张力F缠绕至卷筒时,由平衡条件可知,钢丝绳对筒壳的径向作用力为:
| $ {\rm{d}}{F_{\rm{N}}} = 2F{\rm{sin}}\frac{{{\rm{d}}\theta }}{2} = 2F\frac{{{\rm{d}}\theta }}{2} = F{\rm{d}}\theta $ | (6) |
由于dθ极小,一般近似有sin (dθ/2)≈dθ/2。
钢丝绳在卷筒上的作用面积为
| $ q = \frac{{F{\rm{d}}\theta }}{{ru{\rm{d}}\theta }} = \frac{F}{{ru}} $ | (7) |
在进行多层缠绕时,随着缠绕层数的增加,筒壳所受到钢丝绳对它的作用力也随之增加。内层钢丝绳由于受到外层钢丝绳的挤压而产生形变,导致钢丝绳圈的拉力降低,对筒壳的径向压力随之降低。在多层缠绕过程中,底层钢丝绳对卷筒的径向均布载荷为qC,其中C为钢丝绳的拉力降低系数。随着缠绕层数的增多,里层钢丝绳因为挤压变形导致其拉力小于初始张力F,而卷绕在最外面钢丝绳的拉力即为初始张力F。多层缠绕时钢丝绳对卷筒的径向载荷集度为CqCn,Cn为n层钢丝绳缠绕时的缠绕系数。
2) 在实际作业过程中,提升机卷筒上布置的是双过渡的平行折线绳槽,该绳槽在每2个过渡区内每次过渡半个绳径。这样在层间过渡的时候,第1层钢丝绳向第2层过渡时,实际上是爬升到第1层钢丝绳和过渡块组成的绳槽之内,爬升时钢丝绳对挡绳板并不产生轴向作用力(即钢丝绳对挡绳板的作用力为零),第2层钢丝绳爬升到第3层时也是如此。提升机卷筒上的过渡块位置及钢丝绳过渡示意图如图 7所示。

|
| 图 7 提升机卷筒上的过渡块位置及钢丝绳过渡示意图 Fig.7 Sketch of position of transition block and wire rope transition on hoist drum |
提升机在上提或下放重载过程,钢丝绳对卷筒结构的作用力是随时变化的,运用有限元数值模拟可以求得提升机卷筒结构在瞬态载荷作用下的应力随时间变化的曲线。研究提升机卷筒作业过程的动态应力,既对钢丝绳的研制和使用非常重要,又对提升机卷筒结构的设计、改进及延长其使用寿命等有重要的意义[12]。
2.1 卷筒结构约束与载荷施加提升机在实际作业中,作用在卷筒上的载荷较为复杂,且易受外界因素影响,在对卷筒结构进行载荷计算时需对较为复杂的载荷作适当简化。
由于提升机卷筒所承受的外部载荷主要是钢丝绳对它的径向作用力,在满载上提和空载下放时,可将每一绳圈对卷筒的径向作用力视为均匀分布, 则多层缠绕钢丝绳对卷筒筒壳的径向载荷集度为:
| $ {q_n} = Cq{C_n} = \frac{{C{C_n}F}}{{ru}} $ | (8) |
卷筒多层缠绕系数Cn随着钢丝绳缠绕层数的增加而增大,当达到一定的缠绕层数时,多层缠绕系数Cn趋于某一定值[13],如图 8所示。

|
| 图 8 卷筒多层缠绕系数变化曲线 Fig.8 The variation curve of drum multi-layer winding coefficient |
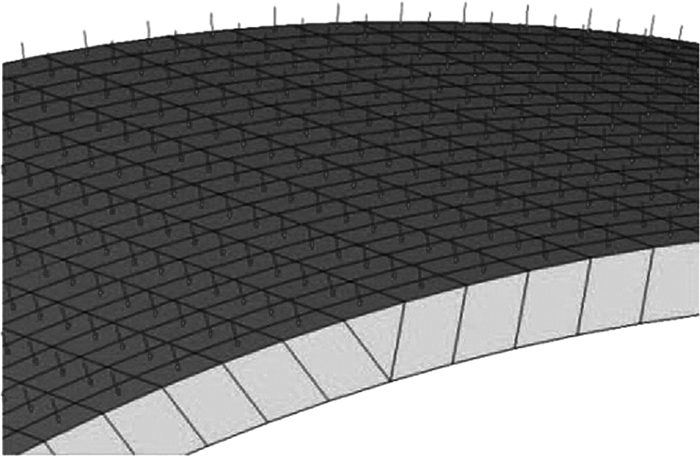
根据提升机卷筒的结构特点及受载情况,钢丝绳缠到卷筒上时由于其张力及其作用在筒壳上位置不断变化,在对筒壳进行加载时需对卷筒模型进行分割处理,根据钢丝绳直径大小把筒壳分割为若干绳径宽度的筒壳环,在每一筒壳环上施加不同的径向均布载荷。筒壳载荷施加见图 9所示。
|
| 图 9 卷筒筒壳载荷施加示意图 Fig.9 Schematic diagram of load exertion on drum shell |
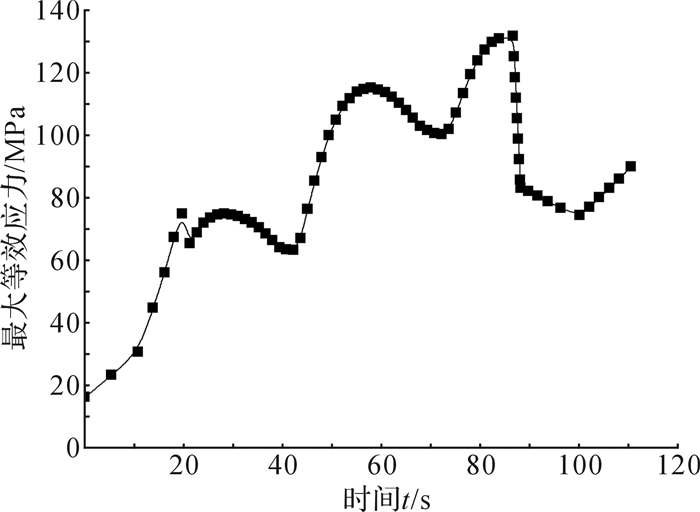
通过对满载上提和空载下放两种工况下钢丝绳对卷筒结构作用力的分析,得出卷筒结构在不同运行阶段的应力图,可以精确找到卷筒受力最大的时刻,并得出应力-时间响应曲线。通过分析可得出,卷筒的最大等效应力出现在内壁上,这是由于卷筒内侧支轮、支环和卷筒内壁连接处存在应力集中。卷筒内、外壁上的应力并非均匀分布,而是沿着轴向波动起伏,最大等效应力出现的部位不是卷筒筒壳中间位置,而是支轮与支环的中间部位,并且此部位筒壳的变形也最大。提取满载上提和空载下放两种工况下卷筒的最大等效应力图,如图 10所示。图 11和图 12为卷筒内壁上等效应力最大部位在不同运行阶段的应力-时间历程曲线。

|
| 图 10 满载上提和空载下放两种工况下卷筒最大等效应力 Fig.10 Maximum equivalent stress of the drum under two conditions of full load lifting and no-load descent |
|
| 图 11 满载上提过程中卷筒内壁最大等效应力变化曲线 Fig.11 The maximum stress variation curve of inner wall of the drum in the process of full load lifting |

|
| 图 12 空载下放过程中卷筒内壁最大等效应力变化曲线 Fig.12 The maximum stress variation curve of inner wall of the drum in the process of no-load descent |
由图 3、图 11、图 12可知,卷筒侧钢丝绳的张力最大时,卷筒结构上的最大等效应力并非是该运行阶段内最大的。因为卷筒结构上的最大等效应力不仅与卷筒侧钢丝绳的张力有关,还与钢丝绳的缠绕系数有关。在满载上提过程中,卷筒结构的最大等效应力为131.6 MPa,低于材料的屈服极限,达到最大等效应力的时间为87 s,即为钢丝绳缠绕卷筒第3层且等速阶段结束的时刻;空载下放时,卷筒结构的最大等效应力为75.12 MPa,时间在第52秒,即发生在等速阶段。
3 卷筒结构疲劳寿命估算通过对提升机卷筒结构作业过程的动态应力分析,得到了卷筒结构的动态载荷。然后定义材料的S-N特性曲线,输入整个工作循环中的载荷谱,根据相关的疲劳累积损伤理论对每一个载荷事件进行寿命计算。卷筒结构疲劳寿命计算流程如图 13所示。

|
| 图 13 卷筒结构疲劳寿命计算流程 Fig.13 The fatigue life calculation process of drum structure |
任一超过材料或结构疲劳极限的应力的循环作用均会对材料或结构造成不同程度的损伤,而造成的损伤是累积的,当损伤累积达到材料或结构疲劳失效的临界值时材料或结构就会出现疲劳损坏。
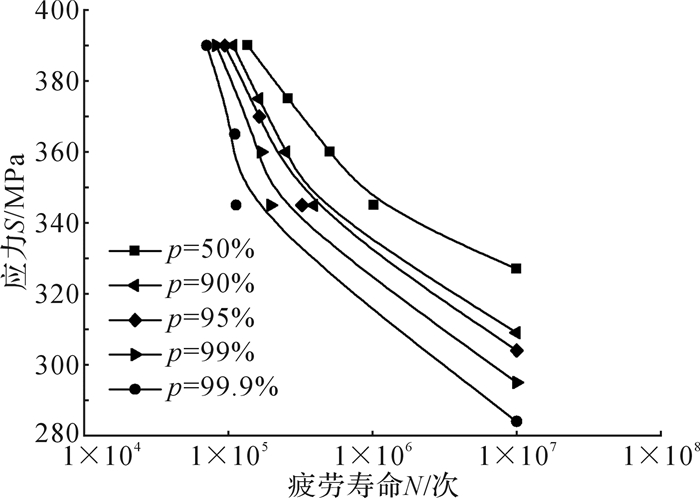
考虑S-N曲线的存活率及提升系统的安全性,参考文献[14]引入16Mn的p-S-N曲线,p-S-N曲线表示不同存活率下的应力-寿命曲线,与S-N曲线相比具有更广泛的应用。绘制不同存活率下16Mn的S-N曲线,如图 14所示。在设计中应根据可靠性和经济性要求来选择具体曲线。一般规定:若试样经107次循环仍不失效,则认为它能够承受无限次循环载荷的作用。
|
| 图 14 不同存活率下16Mn的S-N曲线 Fig.14 The S-N curve of 16Mn under different survival rate |
作用在卷筒上的循环动态载荷如图 15所示,由于该载荷谱的平均应力不等于零,一般需要将该载荷谱转换为对称循环(使其平均应力等于零),这样便可以利用标准试样的S-N曲线预测卷筒结构的疲劳寿命。而Goodman曲线为简单的直线形式,且其计算结果偏于保守,所以本文采用Goodman来修正具有不同平均载荷的载荷谱[15],交变载荷修正公式为:
| $ {S_{\rm{a}}} = {S_{ - 1}}(1 - {S_{\rm{m}}}/{S_{\rm{b}}}) $ | (9) |

|
| 图 15 提升机卷筒的设计载荷谱 Fig.15 Design load spectrum of hoist drum |
式中:Sa为应力幅,MPa;S-1为材料疲劳极限,MPa;Sb为强度极限,MPa;Sm为平均应力,MPa。
3.2 疲劳寿命计算结果分析若卷筒结构在作业过程中的最大等效应力比S-N曲线所定义的最小交变应力小,那么卷筒结构的疲劳寿命即为S-N曲线所定义的最大寿命值(一般为107次循环)。由图 10可知,卷筒结构的最大等效应力为131.6 MPa,小于S-N曲线所定义的最小交变应力,所以卷筒结构的疲劳寿命高于107次循环,即可承受无限次循环。在ANSYS中设置相应的疲劳分析参数和不同存活率下的S-N曲线,输入整个工作循环的载荷谱,对提升机卷筒结构进行疲劳寿命计算,得出卷筒结构的疲劳寿命为1.1×108次循环。施加载荷不同,卷筒疲劳寿命也不同,由于提升机在满载上提过程的第87秒时卷筒结构的应力值达到最大,故用γ表示施加在卷筒结构上的载荷与满载上提第87秒时对卷筒结构所施加载荷的比值,分析得出在有限寿命范围内,卷筒结构在上提和下放全过程中的疲劳寿命与存活率、载荷比的关系,如图 16所示。

|
| 图 16 卷筒疲劳寿命与存活率、载荷比的关系曲线 Fig.16 The relation curve of between drum fatigue life and survival rate, load ratio |
由图 16可知,在一定的加载范围内,施加的载荷相同时,给定的存活率越高,对应的安全寿命越短;对于相同的安全寿命,给定的存活率越高,对应的应力水平越低,经济性越差。所以在疲劳设计中,选择合适的存活率p对于提高提升机卷筒结构的安全性和可靠性具有重要意义。
4 结论1) 根据矿井提升系统动力学分析得出了卷筒侧钢丝绳在不同运行阶段的张力数学模型,确定了卷筒结构的动态载荷。满载上提时钢丝绳的最大张力出现在主加速阶段,空载下放时钢丝绳的最大张力出现在减速阶段。
2) 在对卷筒结构作业过程动态应力分析中综合考虑了在不同运行阶段钢丝绳张力和多层缠绕系数对卷筒受力的影响。通过动力学仿真分析确定了卷筒结构上的最大等效应力发生在卷筒的内壁支轮与支环的中间部位,得到了卷筒内壁上应力最大部位在不同运行阶段的应力-时间历程曲线。
3) 运用有限元法对卷筒结构在整个工作循环中的疲劳寿命进行分析,计算得出其疲劳寿命为1.1×108次循环。同时研究了不同存活率下卷筒结构的疲劳寿命,并给出了不同负载对疲劳寿命估算的影响。
| [1] | WANG Da-gang, LI Xiao-wu, WANG Xiang-ru, et al. Effects of hoisting parameters on dynamic contact characteristics between the rope and friction lining in a deep coal mine[J]. Tribology International, 2016, 96: 31–42. DOI:10.1016/j.triboint.2015.12.019 |
| [2] | WANG Da-gang, ZHANG De-kun, MAO Xian-biao, et al. Dynamic friction transmission and creep characteristics between hoisting rope and friction lining[J]. Engineering Failure Analysis, 2015, 57: 499–510. DOI:10.1016/j.engfailanal.2015.08.010 |
| [3] |
韩仕豪, 杨兆建, 任芳.
JK型提升机主轴的瞬态动力学分析[J]. 中国农机化学报, 2015, 36(5): 73–78.
HAN Shi-hao, YANG Zhao-jian, REN Fang. Transient analysis of the main shaft of JK mine hoist[J]. Journal of Chinese Agricultural Mechanization, 2015, 36(5): 73–78. |
| [4] | DETIZ P. Design criteria for multilayer wound winch drums following lightweight design principles[C]//Proceeding of the 8th International Design Conference, Dubrovnik, May 18-21, 2004. |
| [5] | OTTO S, MUPENDE I, DETIZ P. Influence of the hoisting drum winding system on the end plates loads[C]//Proceeding of the 7th International Design Conference, Dubrovnik, May 14-17, 2002. |
| [6] | PENG Xia, GONG Xian-sheng. Fatigue life analysis of mine hoist drum[J]. Advanced Materials Research, 2014, 940: 81–85. DOI:10.4028/www.scientific.net/AMR.940 |
| [7] | AHMET Yapici, GOKSEL Saracoglu. Fatigue analysis of bolted flange joints of a rotary dryer[J]. Engineering Failure Analysis, 2016, 63: 182–190. DOI:10.1016/j.engfailanal.2016.02.011 |
| [8] | LI Jia, WANG Lei, WANG Xin. Fatigue life reliability analysis of belt conveyor driving drums based on FEM[J]. Advanced Materials Research, 2010, 118-120: 492–496. DOI:10.4028/www.scientific.net/AMR.118-120 |
| [9] | LI Zhen, XUE Zhou, WANG Xu, et al. Safe life estimation of coke drum in service environment[J]. Journal of Pressure Vessel Technology-Transactions of the ASME, 2012, 134(3): 1–4. |
| [10] |
熊伟红, 向晓东, 喻青.
基于局部应力应变法的桥式起重机用钢丝绳疲劳寿命估算[J]. 机械科学与技术, 2015, 34(1): 47–50.
XIONG Wei-hong, XIANG Xiao-dong, YU Qing. Fatigue life prediction of bridge crane wire rope based on local stress-strain method[J]. Mechanical Science and Technology, 2015, 34(1): 47–50. |
| [11] |
潘英.
提升钢丝绳中最大动张力的计算公式[J]. 煤炭学报, 2000, 25(Supplement 1): 138–141.
PAN Ying. The formula for calculating the maximum dynamic tension of hoisting rope[J]. Journal of China Coal Society, 2000, 25(Supplement 1): 138–141. |
| [12] |
严世榕, 闻邦椿.
竖井提升钢丝绳容器系统在提升过程中的动力学仿真[J]. 中国有色金属学报, 1998, 8(Supplement 2): 618–622.
YAN Shi-rong, WEN Bang-chun. Dynamic simulation of shaft hoisting steel wire rope container system in hoisting process[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(Supplement 2): 618–622. |
| [13] |
胡勇, 许学三, 胡吉全.
基于MATLAB的双折线式多层缠绕卷筒的受力分析研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(2): 297–300.
HU Yong, XU Xue-san, HU Ji-quan. Force analysis of lebus drum wound by multi-layer wire rope based on MATLAB[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2015, 39(2): 297–300. |
| [14] |
机械工程材料性能数据手册编委会.
机械工程材料性能数据手册[M]. 北京: 机械工业出版社, 1995: 99-105.
The Editorial Committee of Handbook of Mechanical Engineering Materials Performance Data. Handbook of mechanical engineering material performance data[M]. Beijing: Machinery Industry Press, 1995: 99-105. |
| [15] |
穆志韬, 曾本银.
直升机结构疲劳[M]. 北京: 国防工业出版社, 2009: 31-38.
MU Zhi-tao, ZENG Ben-yin. Fatigue of helicopter structures[M]. Beijing: National Defence Industry Press, 2009: 31-38. |


