工业装配领域存在快节奏、高度重复以及费力的手部工作,装配工人往往需要以非中性的身体姿势去操纵工具,其肌肉骨骼会受到一些来自外部的机械压力和振动冲击,这些都是诱发与工作相关肌肉骨骼系统疾病(work-related muscular skeleton disorder,WMSDs)的重要因素[1-3]。随着社会进步和劳动力成本的上升,装配工人的健康问题越来越受到重视,因此工业装配外骨骼作为解决工人肌肉骨骼损伤问题的主要辅助工具,已成为装配领域的一个研究热点。工业装配外骨骼与传统负重外骨骼不同,它主要应用于工业流水线,用于减轻装配工人的工作负荷,保护装配工人肌肉骨骼,减少装配工人肌肉骨骼累积损伤,从而减小装配工人患WMSDs的风险[4]。
目前,工业装配外骨骼主要类型有3种:第1种是以瑞士NOONEE公司[5]研发的Chairless chair为代表的椅子型工业外骨骼,它主要用于生产装配车间,为工人提供长时间静态支撑;第2种是以法国RB3D公司[6]研发的HERCULE V3为代表的力量辅助型外骨骼,它主要用于力量辅助、重物搬运和工具操控;第3种是以美国洛克希德马丁公司[7]推出的FORTIS为代表的工具支撑型外骨骼,它应用范围广,可以辅助支撑多种类型工具。
对于工具支撑型工业装配外骨骼,机械臂是非常重要的组成部分,其性能直接影响此类外骨骼的使用性能。由于装配工人在工作时动作具有不确定性、高度复杂性以及个体差异性等特性,工业装配外骨骼机械臂必须具备足够的自由度与可操作性。因此,笨重的带动力型机械臂在工业装配领域被舍弃,取而代之的是基于弹簧连杆机构的机械臂。基于弹簧连杆机构的机械臂通过重力势能与弹性势能的相互转换,可以在任何位置都保持平衡。因此,此类机械臂在机器人或外骨骼领域有很广泛的应用,其中包括辅助康复训练的机器人及外骨骼、宇航员的阻力训练器、辅助承重的机械臂以及一些无动力的外骨骼[8-10]。
本文提出一种基于弹簧连杆机构的工具支撑型工业装配外骨骼机械臂,其核心为平行四边形弹簧连杆机构,它不仅能够支撑工具,还具有稳定工具的功能。该机械臂安装在工业装配外骨骼上,在额定载荷内,无论是有人操纵还是无人操纵,机械臂及其所支撑的工具都能达到平衡。本文结合ADAMS仿真软件,来研究此机械臂的相关性能。
1 基于弹簧连杆机构的机械臂人的手臂在生物结构以及运动机理上都十分复杂,通过神经系统的控制,手臂各组成结构能够协同完成各种复杂的操作。为了让外骨骼机械臂更好地配合工人工作,其设计准则应该符合人体工程学[11]。不考虑手掌以及手指对手臂运动的影响,Morecki指出人的手臂具有3个肩关节自由度、1个肘关节自由度和3个腕关节自由度等7个自由度[12]。国内外很多学者在研究仿人机械臂时,采用较多的为七自由度机械臂模型[13-15]。笔者以我国成年男性手臂尺寸(如表 1)为参考[16],基于弹簧连杆机构设计了一款工业装配外骨骼机械臂,它安装于外骨骼腰部,如图 1所示。在不考虑云台(腕关节)的基础上,本文设计的机械臂为具有6个自由度的弹簧连杆机械臂,其原理简图如图 2所示。
| mm | |||||||
| 测量目标 | 百分位数1) | ||||||
| 1 | 5 | 10 | 50 | 90 | 95 | 99 | |
| 身高 | 1 543 | 1 583 | 1 604 | 1 678 | 1 754 | 1 775 | 1 814 |
| 上臂 | 279 | 289 | 294 | 313 | 333 | 338 | 349 |
| 下臂 | 206 | 216 | 220 | 237 | 253 | 258 | 268 |
| 注:1)百分位数为统计学术语,如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数。 | |||||||
|
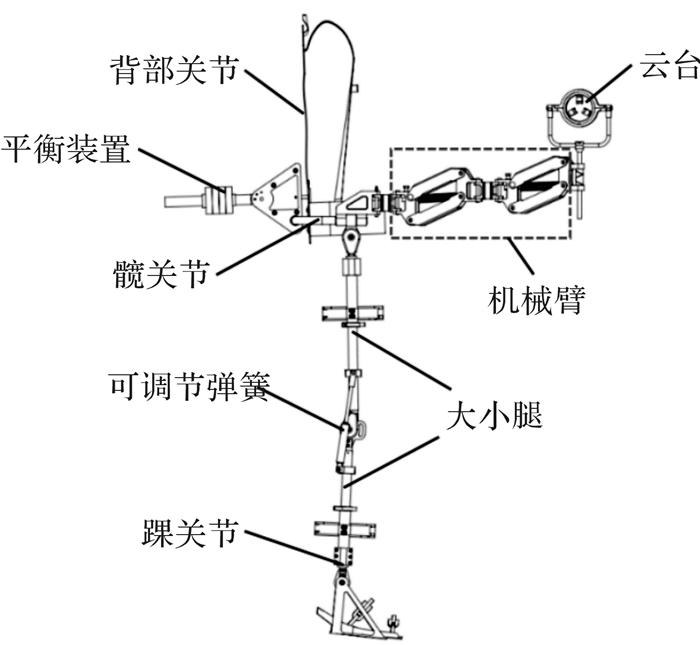
| 图 1 工业装配外骨骼三维模型 Fig.1 Three dimensional model of industrial assembly exoskeleton |
|
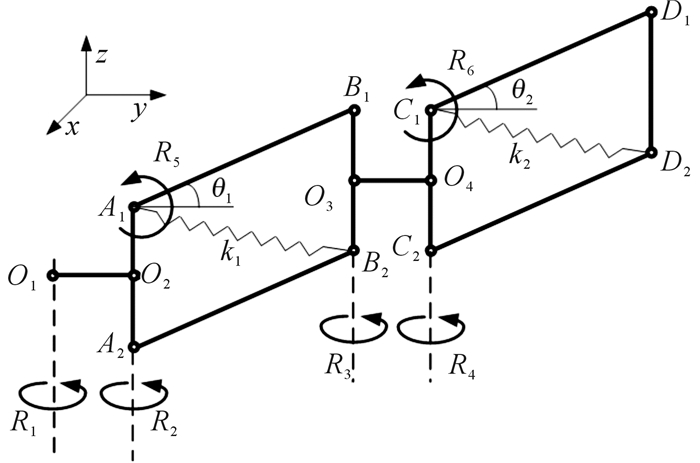
| 图 2 基于弹簧连杆机构的机械臂原理简图 Fig.2 Principle diagram of manipulator based on spring-linkage mechanism |
由图 2可知,整个机械臂具有6个转动自由度,其中R1、R2、R3、R4绕z轴方向转动,R5、R6绕x轴方向转动。从表 1能得出,我国成年男性手臂的上臂一般要比下臂长80 mm左右,本文所设计的机械臂需适配于身高为1 600~1 780 mm的工人,因此设置的主要设计参数为:
| $ \begin{array}{l} {L_1} = {A_1}{B_1} = {A_2}{B_2} = {C_1}{D_1} = {C_2}{D_2} = 220\;\;{\rm{mm}}\\ {L_2} = {O_1}{O_2} = {O_3}{O_4} = 80\;\;{\rm{mm}} \end{array} $ |
不同身高成年男性的上臂与下臂差值的平均值为78 mm,身高为1 775 mm成年男性的臂长比身高为1 604 mm的臂长要长82 mm,因此取冗余块长度为80 mm。冗余块O1O2用于补偿机械臂整体长度,以适应不同臂长的工人;冗余块O3O4用于补偿上臂与下臂差值,以适应不同上下臂比例的工人。从图 2可以看出,使用不同长度的弹簧可以得到不同初始角度θ1、θ2的机械臂,本文主要研究初始角度θ1、θ2对机械臂承重性能的影响。
2 弹簧连杆机械臂力学性能本文所设计的机械臂是基于弹簧连杆机构的静平衡原理,如图 3所示。机械臂整体结构由2个弹簧连杆机构串联而成[17]。在弹簧弹性范围内,通过机械臂,工人可以毫无负重感地支撑重型工具。

|
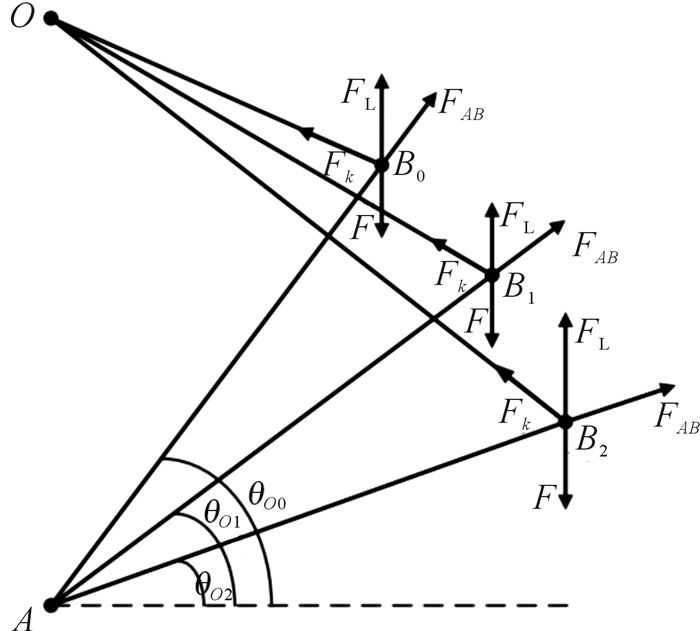
| 图 3 弹簧连杆机构静平衡原理 Fig.3 Static balance principle of spring-linkage mechanism |
由图 3可知,忽略连杆AB的质量,将连杆AB看作二力杆,则连杆AB在B点的受力可以分解为连杆方向的力FAB、弹簧拉力Fk以及外负载F,它们之间的相互关系为:
| $ \begin{array}{l} {F_k}{\rm{cos}}\left( {\alpha - \theta } \right) = {F_{AB}}{\rm{cos}}\theta \\ F = {F_k}{\rm{sin}}\left( {\alpha - \theta } \right) + {F_{AB}}{\rm{sin}}\theta \\ {F_k} = \frac{F}{{{\rm{sin}}\left( {\alpha - \theta } \right) + {\rm{cos}}(\alpha - \theta ){\rm{tan}}}} \end{array} $ |
在保证弹簧原长l0不变的情况下,可以通过改变O点的位置(即改变l1的长度)来改变连杆AB的初始角度θ0,同时弹簧与连杆之间的初始角度α0也随之改变。初始角度可由以下关系式求得:
| $ \begin{array}{l} {\rm{cos}}{\alpha _0} = \frac{{{l_0}^2 + {l_2}^2 - {l_1}^2}}{{2{l_0}{l_2}}}\\ {\rm{cos}}(90^\circ - {\theta _0}) = \frac{{{l_1}^2 + {l_2}^2 - {l_0}^2}}{{2{l_1}{l_2}}} \end{array} $ |
当O点位置固定不变时,由于负载的作用,弹簧伸长,角度α、θ都相应减小,其中θ的减小量为:
| $ \left\{ \begin{array}{l} \Delta \theta = {\rm{arcsin}}\left( {\frac{{l_1^2 + l_2^2 - l_0^2}}{{2{l_1}{l_2}}}} \right) - \\ {\rm{arcsin}}\left( {\frac{{l_1^2 + l_2^2 - {{({l_0} + \Delta l)}^2}}}{{2{l_1}{l_2}}}} \right)\\ \Delta l = \frac{{{F_k}}}{k} \end{array} \right. $ | (1) |
从式(1)可以看出,当弹簧弹性系数k确定时,Δθ会随着O点位置(l1的大小)和负载的变化而变化。在负载以及O点位置确定时,负载大小决定Δθ的大小,则可将Δθ定义为整个系统能够承受负载的有效范围。在O点位置固定的情况下,弹簧长度不同时弹簧机构受力分析简图如图 4所示。在外负载F的作用下,当θ=θO2时弹簧机构达到静平衡,此时外负载完全由弹簧和连杆承受,需要的举升力FL=0;当θ=θO0时,弹簧处于初始状态,Fk=0且FAB=0,外负载完全由人承受,所需的举升力FL=F;当
|
| 图 4 弹簧长度不同时弹簧机构受力分析示意图 Fig.4 Force analysis diagram of spring mechanism with different spring length |
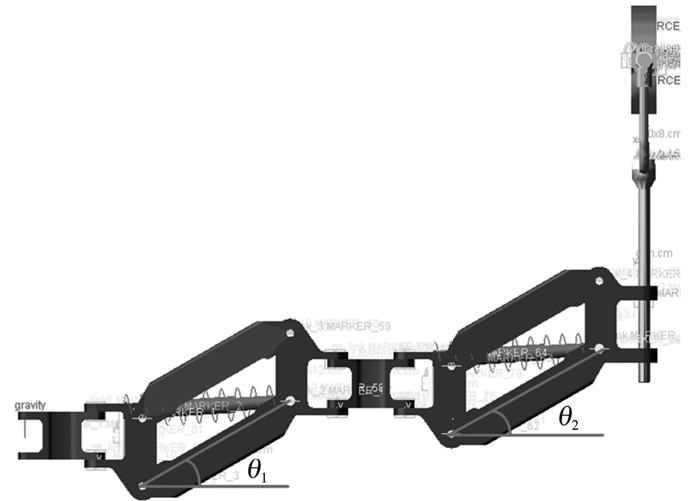
从上述分析可知,机械臂的承重性能与弹簧刚度、弹簧固定位置以及连杆的初始角度有关。为研究验证机械臂的静力学性能,利用ADAMS软件对机械臂进行仿真试验。将机械臂三维模型进行相应简化,导入ADAMS软件进行仿真研究。弹簧连杆机械臂仿真模型如图 5所示。
|
| 图 5 弹簧连杆机械臂仿真模型 Fig.5 Simulation model of spring-linkage manipulator |
保持两弹簧刚度k相同且不变,弹簧固定点位置不变,通过改变弹簧长度来改变连杆初始角度θ1、θ2的大小。由于工作时工具的运动可以近似看作处于平衡状态(静止或以很小的速度匀速运动),因此可以用ADAMS软件进行静力学仿真来研究机械臂的承重性能,同时不考虑动力学因素,即工具的惯性力不再考虑,此时在机械臂云台工具固定处施加一个等效力FG,FG大小不随机械臂移动而改变,其方向始终竖直向下。按照实际工作情况添加机械臂相关约束。
为了研究两弹簧连杆初始角度θ1、θ2对机械臂性能的影响,本文设置了不同θ1、θ2的9组仿真试验。考虑到机械臂实用性,θ1、θ2不宜过大,θ1、θ2过大会使得机械臂整体高度过高以及机械臂有效长度过短,影响其实际使用性能,为此θ1、θ2的取值范围规定在(0°, 45°]内。仿真试验相关参数如表 2所示。
| 组别 | θ1/(°) | θ2/(°) | k/(N/mm) |
| 1 | 45 | 45 | 10 |
| 2 | 45 | 30 | 10 |
| 3 | 45 | 15 | 10 |
| 4 | 30 | 45 | 10 |
| 5 | 30 | 30 | 10 |
| 6 | 30 | 15 | 10 |
| 7 | 15 | 45 | 10 |
| 8 | 15 | 30 | 10 |
| 9 | 15 | 15 | 10 |
机械臂在自重和外负载的作用下达到平衡,其连杆角度从θ1、θ2变成θ′1、θ′2。当机械臂处于平衡位置时,所需举升力FL=0。从平衡位置出发,慢慢举升工具,并测得举升高度与举升力的关系,从而评价机械臂的省力范围。在ADAMS仿真中,一般是从模型的原始位置出发,到平衡位置截止;而本文需从平衡位置出发,则需要预先设置平衡位置的相应参数,这使得仿真变得异常复杂且会降低仿真的准确性。因此,本文提出一种逆向仿真方法。
首先,求得弹簧伸长量为0 mm时整个系统所需最小举升力FL min(方向为竖直向上),当FL=FL min时,机械臂不会起到承受负载的作用。在ADAMS静力学仿真中通过逐步减小FL,可以得到机械臂保持静平衡的具体位置[18]。设FL为随时间变化的函数,通过ADAMS静力学仿真,得出举升高度随时间变化的曲线,经过相应的处理就可以得到举升力与举升高度的关系。本文所测量的弹簧伸长量为0 mm、外负载为10 kg时的最小举升力为118 N左右,为方便测量,将最小举升力设为120 N,则FL=120-20×t,仿真时间为6 s。
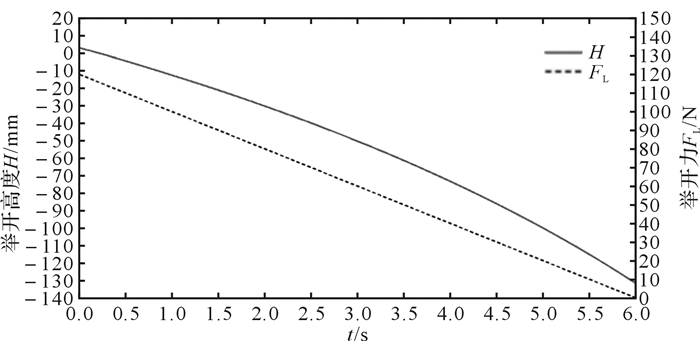
通过ADAMS静力学仿真可以得到θ1=30°、θ2=30°时机械臂的举升力、举升高度与时间的关系曲线,如图 6所示。通过处理得到如图 7所示的机械臂举升高度与举升力的关系曲线。为了更好地研究机械臂承重性能,引入“有效举升高度”这一概念,定义为弹簧长度为原始长度时(机械臂完全由举升力平衡)机械臂举升高度与举升力均为零时(机械臂完全由弹簧平衡)机械臂举升高度的高度差。通过仿真可以得到不同初始角度下机械臂有效举升高度,如表 3所示。
|
| 图 6 θ1=30°、θ2=30°时机械臂举升力、举升高度与时间的关系曲线 Fig.6 Relationship curves between lift force, lift height of manipulator and time with θ1 =30°、θ2=30° |
| mm | |||
| θ2 | θ1 | ||
| 45° | 30° | 15° | |
| 45° | 105.5 | 110.6 | 156.9 |
| 30° | 108.6 | 134.9 | 181.2 |
| 15° | 146.9 | 173.2 | 219.5 |
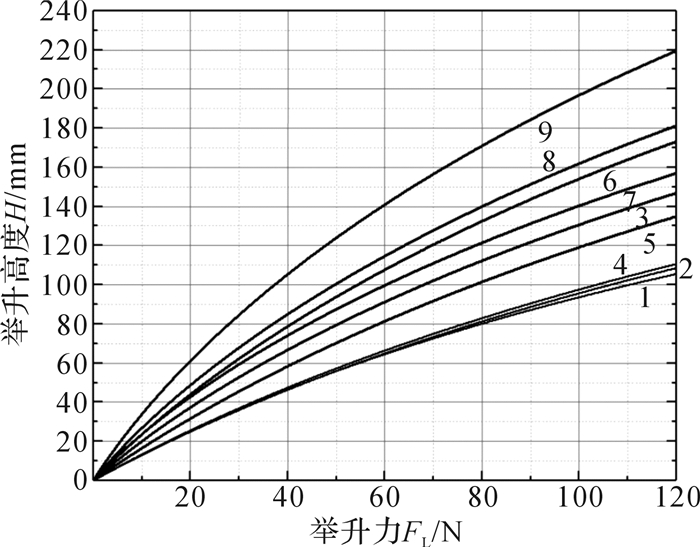
由图 7和表 3可知,举升高度与举升力在不同初始角度下的整体变化情况相似。对比多条曲线可以得出,减小初始角度值能增大关系曲线曲率,即在达到相同有效举升高度时,减小机械臂初始角度则能减小相应的举升力。换言之,减小机械臂初始角度,可以获得更大的有效举升高度区间;较大的初始角有较强的稳定工具的作用。此外,从表 3还可以发现,初始角度θ1、θ2对机械臂承重性能的影响程度不同,θ1的变化更能影响有效举升高度的变化。
|
| 图 7 9组仿真试验所得机械臂举升高度与举升力关系曲线 Fig.7 7 Relationship curve between lift height and lift force for manipulator obtained from nine groups of simulation experiments |
由于机械臂为双弹簧连杆机构串联而成,此结构决定了机械臂前后两节所受的负载不相同,机械臂后一节受到负载以及自身重力的作用,而前一节除了受负载以及自身重力外还承受后一节的重力。因此前一节提供的支撑力要略大于后一节,所以θ1对机械臂性能的影响要略大于θ2,这与仿真试验结果吻合。
由上述分析可知:在进行此类机械臂设计时,如果负载工具质量大,在不改变弹簧弹性系数的情况下,增大初始角度可以极大地稳定工具,增强安全性能;如果负载工具质量较小,在不改变弹性系数的情况下,减小初始角度可以极大地增大有效举升高度,提高机械臂的灵活性。
4 结论1) 结合现有仿人机械臂设计方法,参考中国成年男子手臂尺寸参数,基于弹簧连杆机构设计了一套用于工业装配外骨骼的具有支撑工具功能的弹簧连杆机械臂,并证明了该机械臂能够很好地应用于工业装配外骨骼。
2) 结合机械臂实际工作情况,提出了一种针对所设计机械臂举升过程的ADAMS逆向仿真方法;并提出了有效承重区间概念,为后续此类问题的研究提供了一种思路。
3) 通过相关仿真试验得到了机械臂举升高度与举升力的关系曲线;从仿真结果可以知道,初始角度对机械臂有效举升高度有重要影响,其中θ1对有效举升高度的影响大于θ2。研究结果为此类机械臂的设计提供一定的参考依据。
| [1] |
贾宁, 凌瑞杰, 王伟, 等.
汽车装配工人工效学负荷与工作相关肌肉骨骼损伤的相关性研究[J]. 环境与职业医学, 2017, 34(10): 858–863.
JIA Ning, LING Rui-jie, WANG Wei, et al. Correlation between ergonomic load and work-related musculoskeletal disorders among automobile assembly workers[J]. Journal of Environmental & Occupational Medicine, 2017, 34(10): 858–863. |
| [2] |
李玉珍, 李珏, 李刚, 等.
汽车装配作业工人肌肉骨骼损伤与工效学负荷水平的相关性[J]. 环境与职业医学, 2015, 32(5): 393–398.
LI Yu-zhen, LI Jue, LI Gang, et al. Correlation between musculoskeletal disorders and ergonomic load levels among automobile assembly workers[J]. Journal of Environmental & Occupational Medicine, 2015, 32(5): 393–398. |
| [3] |
郭智屏, 刘新霞, 刘浩中, 等.
制造行业生产工人职业性肌肉骨骼疾患影响因素[J]. 中国职业医学, 2017, 44(4): 459–462.
GUO Zhi-ping, LIU Xin-xia, LIU Hao-zhong, et al. Influencing factors of occupational musculoskeletal disorders in workers of manufacturing industry[J]. China Occupational Medicine, 2017, 44(4): 459–462. |
| [4] | SPADA S, GHIBAUDO L, GILOTTA S, et al. Analysis of exoskeleton introduction in industrial reality: main issues and EAWS risk assessment[C]//Advances in Physical Ergonomics and Human Factors. AHFE 2017. Advances in Intelligent Systems and Computing, Los Angeles, Jul.17-21, 2017. |
| [5] | NOONEE. The chairless chair[EB/OL]. (2014-06-20)[2018-05-18]. http://robohub.org/noonee-the-chairless-chair/ |
| [6] | RB3D. Exoskeletons for heavy loads[EB/OL].[2018-05-18]. https://www.rb3d.com/produits/exosquelettes/ |
| [7] | Lockheed Martin Space Systems Company. Exoskeleton technologies[EB/OL].[2018-05-18]. http//www.lockheedmartin.com/us/products/exoskeleton/FORTIS.html. |
| [8] |
叶平, 宋爽, 何雷, 等.
基于弹簧机构的宇航员抗阻力训练器[J]. 机械工程学报, 2014, 50(23): 1–7.
YE Ping, SONG Shuang, HE Lei, et al. Resistive exercise device based on spring mechanism for astronauts[J]. Journal of Mechanical Engineering, 2014, 50(23): 1–7. |
| [9] | BANALA S K, AGRAWAL S K, FATTAH A, et al. Gravity-balancing leg orthosis and its performance evaluation[J]. IEEE Transaction on Robotics, 2006, 22(6): 110–119. |
| [10] | ALTENBURGER R, SCHERLY D, STADLER K S. Design of a passive, iso-elastic upper limb exoskeleton for gravity compensation[J]. Robomech Journal, 2016, 3(1): 12. DOI:10.1186/s40648-016-0051-5 |
| [11] |
赵京, 宋春雨, 杜滨.
基于人体工程学的仿人机械臂构型[J]. 机械工程学报, 2013, 49(11): 16–21.
ZHAO Jing, SONG Chun-yu, DU Bin. Configuration of humanoid robotic arm based on human engineering[J]. Journal of Mechanical Engineering, 2013, 49(11): 16–21. |
| [12] | MORECKI A. Biomechanics of engineering:modelling, simulation, control[M]. Wien: Springer Verlag, 1987: 1-83. |
| [13] | ZACHARIAS F, HOWARD I S, HULIN T, et al. Workspace comparisons of setup configurations for human-robot interaction[C]//Proceedings of 23rd IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, IROS 2010, Taiwan, China, Oct.18-22, 2010. |
| [14] | PERRY J C, ROSEN J. Design of a 7 degree offreedom upper-limb powered exoskeleton[C]//IEEE/RAS-Embs International Conference on Biomedical Robotics and Biomechatronics, Pisa: IEEE, 2006: 805-810. |
| [15] | NAIDU D, STOPFORTH R, BRIGHT G, et al. A 7 DOF exoskeleton arm: shoulder, elbow, wrist and hand mechanism for assistance to upper limb disabled individuals[C]//Africon, Livingstone, IEEE, 2011: 1-6. |
| [16] |
中国标准化与信息分类编码研究院.中国成年人人体尺寸: GB 10000-1988[S].北京: 国家技术监督局, 1989: 1-5.
China National Institute of Standardization. Human dimensions of Chinese adults: GB10000-1988[S]. Beijing: Inspection and Quarantine of the People's Republic of China, 1989: 1-5. |
| [17] | HERDER J L. Energy-free systems, theory, conception and design of statically balanced spring mechanisms[D]. Delft: Delft University of Technology, 2001 |
| [18] |
苏欣平, 周京京, 郭爱东, 等.
基于ADAMS的叉车静态稳定性分析与仿真[J]. 中国工程机械学报, 2012, 10(1): 77–80.
SU Xin-ping, ZHOU Jing-jing, GUO Ai-dong, et al. ADAMS-based static stability analysis and simulation on forklifts[J]. Chinese Journal of Construction Machinery, 2012, 10(1): 77–80. DOI:10.3969/j.issn.1672-5581.2012.01.016 |



