欠驱动夹持器是一种对物体形状适应能力强、控制简单的机器人末端执行器,能够实现对小物体的精确抓取以及对大体积物体的包络抓取,它在机器人领域得到广泛应用。欠驱动夹持器表现为平面或空间多指构型,并具有多种工作模式[1-8]。其中,夹持力是夹持器输出性能的重要表征。通过对夹持器结构参数进行优化设计,可以实现根据不同工作模式的特点合理分配夹持力,这对提升夹持器抓取稳定性和扩大抓取操作应用范围具有重要意义。
Birglen[1]设计了一种平动夹持器,通过对比多组参数对夹持力的影响进行参数优选。王杰等[9]研制了一种手指康复外骨骼机器人,从工作空间角度优化机构性能。金波和林龙贤[10]研制了一种欠驱动水果夹持器,通过遗传算法实现夹持性能的优化,但优化结果仅适用于特定的水果形状尺寸。针对欠驱动夹持器,Birglen等[11-12]研究了多组特定的阻尼弹簧位置或不同的手指指骨架构对夹持力的影响。Stavenuiter等[13]提出了一种欠驱动夹持器,从提高鲁棒性角度优化夹持力控制。但是,上述研究并未针对适用于一般操作对象的欠驱动夹持器进行系统的参数优化设计。欠驱动夹持器优化设计的难点主要体现在:因其抓取方式具有多样性并表现为欠驱动连杆机构的运动,建立目标函数较为困难。
机构优化设计中常用的算法有梯度优化算法[14]和进化算法[15-17]。梯度优化算法收敛速度快,但容易导致局部最优解;遗传算法、蚁群算法属于进化算法,能有效规避局部最优解,但搜索到满足点距准则、函数值变化准则或梯度准则的最优解需要较长的迭代时间。
本文针对典型的平面阻尼型欠驱动夹持器提出一种多模式参数优化设计方法。首先,对平面阻尼型欠驱动夹持器的工作模式进行分析;然后,分别对各种工作模式进行优化,并分析优化方向的共性;最后,利用ADAMS对优化结果进行仿真验证。
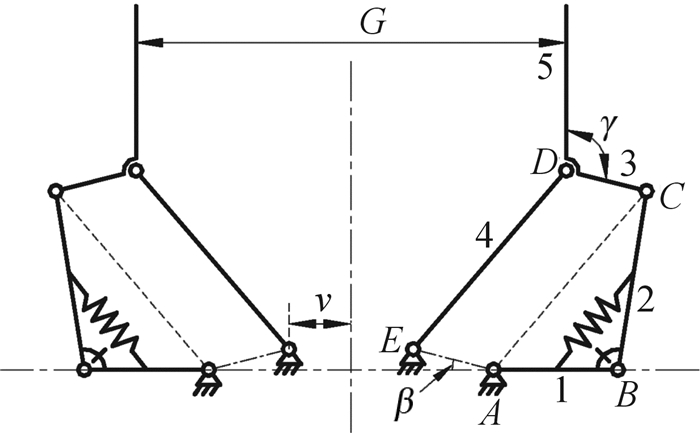
1 平面阻尼型欠驱动夹持器工作模式分析由于在平面阻尼型欠驱动夹持器连杆间添加了弹簧力,使得该机构满足最小阻尼定律[18],即沿最小阻尼方向运动时,尽管其自由度数目大于驱动数目,也不会呈现运动状态不确定的现象。图 1为典型的二自由度平面阻尼型欠驱动夹持器,其中:β为EA与水平方向的夹角,γ为杆3和杆5之间的夹角;v为点E到夹持器对称轴的距离,G为夹持器最大开口范围。夹持器左右对称,以右侧结构为例,弱弹簧安装于驱动杆1、推动杆2之间,可在运动过程中对铰链B添加阻尼。由于弹簧刚度很小,在建立夹持力模型时弱弹簧力可以忽略不计。
|
| 图 1 二自由度平面阻尼型欠驱动夹持器 Fig.1 Two degree of freedom planar damped underactuated gripper |
图 1所示的欠驱动夹持器的工作模式可以分为两点夹持与包络抓取。两点夹持是指只使用杆5抓取物体,并且当远指节接触到物体时,通过添加限位销来限制驱动杆1与推动杆2夹角减小的趋势,从而保证夹持稳定性。包络夹持分为4步:1)初始状态时,运动杆4向物体靠近;2)运动杆4接触到物体时,产生约束作用;3)驱动杆1继续推动杆2,弹簧被拉伸;4)杆5完全与物体接触,实现包络整个物体的夹持动作。
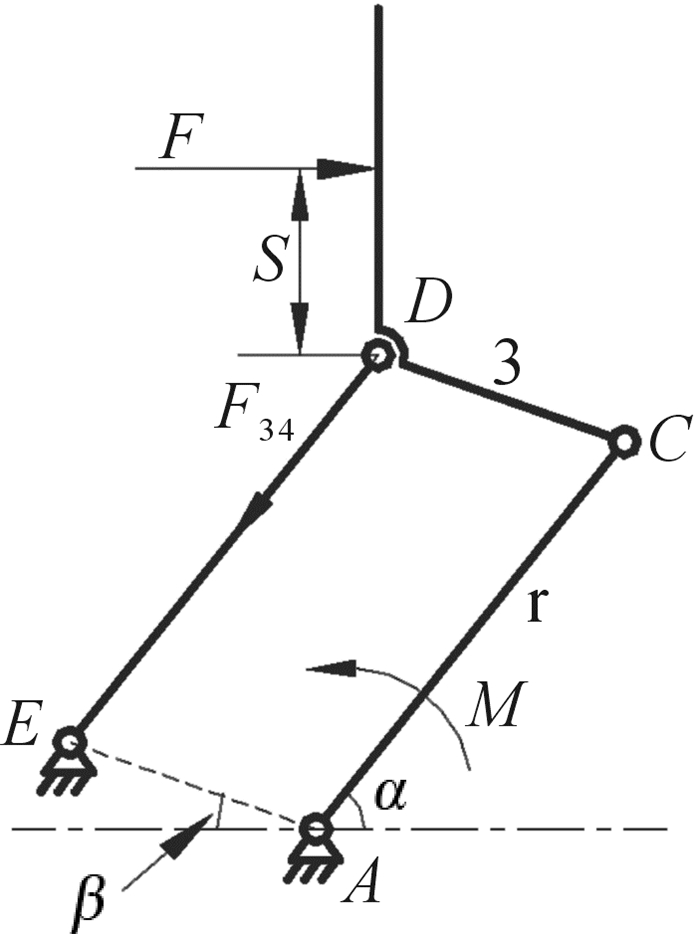
2 夹持器两点夹持模式优化两点夹持模式下驱动杆1与推动杆2的夹角呈减小趋势,位于驱动杆1与推动杆2之间的铰链上的限位销起限位作用,则可以将夹持器右侧机构进行简化,如图 2所示。
|
| 图 2 两点夹持模式下夹持器右侧机构的简化示意图 Fig.2 Simplified schematic diagram of right side mechanism of gripper under two-point grasping mode |
这里用杆r代表杆1和杆2。在静力学分析过程中,摩擦力忽略不计。取杆r、杆3整体作为研究对象,对A点取矩,得:
| $ - F\left( {S + {l_3}\sin \beta + {l_{\rm{r}}}\sin \alpha } \right) - {F_{34}}{l_3}\sin \left( {\beta + \alpha } \right) + M = 0 $ | (1) |
取杆3为研究对象,对C点取矩,得:
| $ - F\left( {S + {l_3}\sin \beta } \right) - {F_{34}}{l_3}\sin \left( {\alpha + \beta } \right) = 0 $ | (2) |
式中:l3为杆3的长度,lr为点A、C间的距离,S为夹持力作用点到D点的距离,α为杆r与水平方向的夹角,M为A点输入扭矩,F34为D点处杆3对杆4的作用力。
联立式(1)和式(2),得F与M的关系式为:
| $ F = \frac{M}{{{l_{\rm{r}}}\sin \alpha }} $ | (3) |
由式(3)可看出输入扭矩、输出夹持力只与lr、α有关。而在夹持状态下,α被夹持物体限制为特定的值。设lr的下限为lrl,即lr取值范围是[lrl, +∞]。由式(3)可知,当优化参数lr=lrl时,F取得最大值。
平面阻尼型欠驱动夹持器各结构参数的含义及初始值如表 1所示。其中,为了使杆5在两点夹持状态时于任意时刻均保持垂直状态,需满足:l0=l3,l4=lr,γ=90°+β。因四边形ACDE是平行四边形,根据几何关系,l2可由其余结构参数确定,如式(4)所示:
| $ {l_2} = \sqrt {l_1^2 + l_4^2 - 2{l_1}{l_4}\frac{{\left( {G/2} \right) - v}}{{{l_4}}}} $ | (4) |
| 参数 | 含义 | 初始值 |
| l1 | 杆1长度 | 40 mm |
| l2 | 杆2长度 | 49 mm |
| l3 | 杆3长度 | 28 mm |
| l4 | 杆4长度 | 60 mm |
| l5 | 杆5长度 | 40 mm |
| lr | 点A、C间的距离 | 60 mm |
| l0 | 基座点E、A间的距离 | 28 mm |
| β | EA与水平方向夹角 | 20° |
| v | E到夹持器对称轴距离 | 20 mm |
| γ | 杆3、杆5的夹角 | 110° |
| G | 夹持器最大开口范围 | 110 mm |
| M | 输入扭矩 | 200 N·mm |
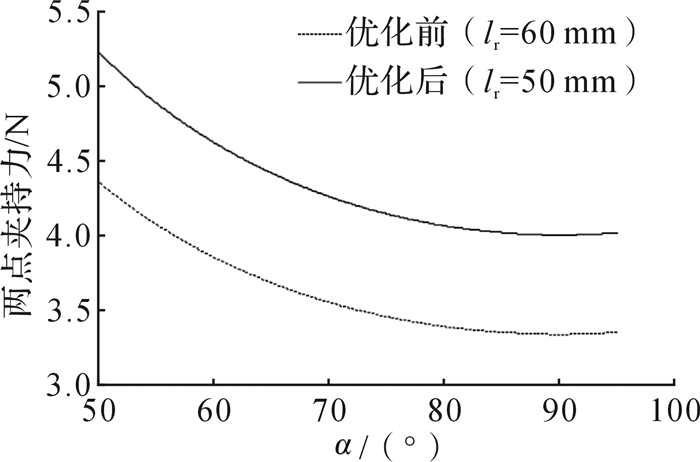
两点夹持模式下夹持器结构参数的优化结果如表 2所示。图 3为结构参数优化前后夹持力的对比。可见优化后,在夹持不同尺寸物体时,夹持力平均提升幅度为20.00%。
| 参数 | l1/mm | l2/mm | l3/mm | l4/mm | β/(°) |
| 数值 | 40.00 | 36.06 | 28.00 | 50.00 | 20.00 |
|
| 图 3 两点夹持模式下夹持器优化前后夹持力对比 Fig.3 Comparison of the grasping force before and after optimization of gripper under two-point grasping mode |
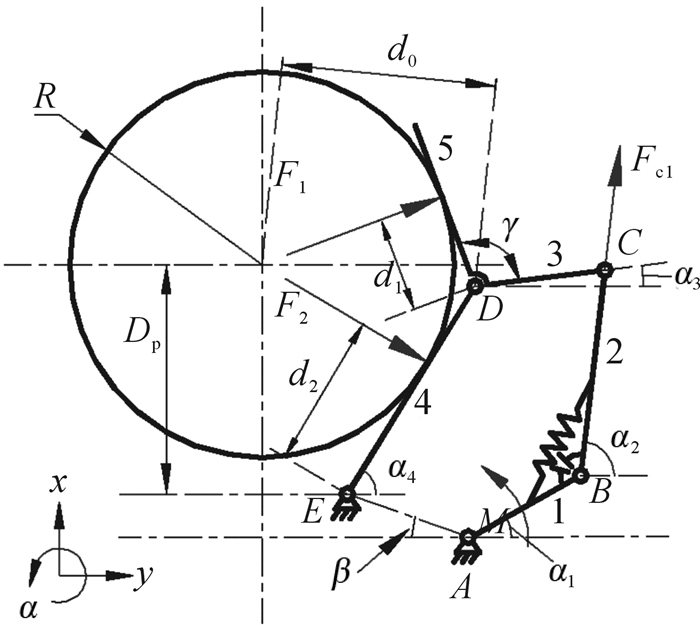
包络夹持模式下静平衡位置较难确定,待优化参数较多,建立目标函数的过程较为复杂,难以直接优化求解。圆柱体是包络夹持对象的常见形状,包络夹持模式下夹持器的受力分析如图 4所示。假设被抓取物体为底面半径为R的圆柱体,对R进行一系列取值,可近似获得运动杆4、杆5的位置约束,从而保证外部约束引入的一般性。其中,由于静平衡位置较难借助静力学分析确定,通过ADAMS对表 1所示的夹持器结构参数初始值进行仿真可以获得不同R对应的静平衡位置参数Dp的值,结果如表 3所示。
|
| 图 4 包络夹持模式下夹持器的受力分析 Fig.4 Force analysis of gripper under enveloped grasping mode |
| R/mm | 50 | 45 | 40 | 35 |
| Dp/mm | 53.66 | 47.96 | 43.56 | 37.83 |
如图 4所示,以杆3、杆1为研究对象,分别对D点、A点取矩,可得:
| $ {F_1}{d_1} = {F_{c1}}{l_3}\sin \left( {{\alpha _2} - {\alpha _3}} \right) $ | (5) |
| $ - {F_{c1}}{l_1}\sin \left( {{\alpha _2} - {\alpha _1}} \right) + M = 0 $ | (6) |
联立式(5)和(6),解得:
| $ {F_1} = \frac{{M{l_3}\sin \left( {{\alpha _2} - {\alpha _3}} \right)}}{{{d_1}{l_1}\sin \left( {{\alpha _2} - {\alpha _1}} \right)}} $ | (7) |
以圆柱体为对象,可得:
| $ \sum {{F_y}} = {F_{1y}} - {F_{2y}} = 0 $ | (8) |
| $ {F_{1y}} = {F_1}\sin \left[ {{{90}^ \circ } - \left( {{{180}^ \circ } - {\alpha _3} - \gamma } \right)} \right] $ | (9) |
| $ {F_2} = {F_{2y}}/\cos {\alpha _4} $ | (10) |
联立式(8)至(10),可得:
| $ {F_2} = \frac{{M{l_3}\sin \left( {{\alpha _2} - {\alpha _3}} \right)\sin \left[ {{{90}^ \circ } - \left( {{{180}^ \circ } - {\alpha _3} - \gamma } \right)} \right]}}{{{d_1}{l_1}\sin \left( {{\alpha _2} - {\alpha _1}} \right)\cos {\alpha _4}}} $ | (11) |
根据夹持器组成的封闭五边形向量的投影关系,得出l1、l2、l3、l4与α1、α2、α3、α4之间的关系,用于确定α1、α2:
| $ - {l_0}\cos \beta + {l_4}\cos {\alpha _4} = {l_1}\cos {\alpha _1} + {l_2}\cos {\alpha _2} - {l_3}\cos {\alpha _3} $ | (12) |
| $ {l_0}\sin \beta + {l_4}\sin {\alpha _4} = {l_1}\sin {\alpha _1} + {l_2}\sin {\alpha _2} - {l_3}\sin {\alpha _3} $ | (13) |
外部约束的其它几何参数均是关于R的函数, 即:
| $ \cos {\alpha _4} = \frac{R}{{{D_{\rm{p}}} + v\tan {\alpha _4}}} $ | (14) |
| $ {d_0} = \sqrt {{j^2} + {k^2} - 2jk\cos \left( {{{90}^ \circ } - {\alpha _4}} \right)} $ | (15) |
| $ {\alpha _3} = {180^ \circ } - \gamma - \left( {2\arcsin \frac{R}{{{d_0}}} - {\alpha _4}} \right) $ | (16) |
| $ {d_1} = \sqrt {d_0^2 + {R^2}} $ | (17) |
其中,式(15)中参数j、k的表达式为:
| $ j = {l_4} + \frac{v}{{\cos {\alpha _4}}} $ | (18) |
| $ k = {D_{\rm{p}}} + v\tan {\alpha _4} $ | (19) |
设置参数取值范围时需考虑3个方面:避免机械干涉、避免优化过程出现畸形结构、保持基座紧凑性。在实际应用中,铰链具有一定尺寸,为避免铰链间发生干涉,连杆长度应具有下限。其中,l1的下限还需略微提高以预留位置用来添加限位销。夹持器的最大开口范围G=110 mm。为保证夹持器在优化过程中不出现畸形结构,需分别对各连杆长度设定上限及下限。角度β与基座尺寸大小正相关,为避免基座尺寸过大,应给予上限限制。综上分析并结合实际经验,夹持器各设计变量取值范围如表 4所示。
| 参数 | 取值范围 |
| l1/mm | [30, 45] |
| l3/mm | [25, 45] |
| l4/mm | [50, 70] |
| β/(°) | [10, 30] |
使用MATLAB工具包中的非线性约束优化函数fmincon对与R相关的设计变量进行优化求解,即求得目标函数[-(F=F1+F2)]的最小值,其中:其几何约束为式(4)、(12)和(13),外部约束为式(14)至式(19);设计变量取值范围参考表 4。
夹持器各结构参数的优化结果如表 5所示,对于不同的R值,各结构参数优化结果均相同。当R=35 mm时,在约束Dp作用下运动杆4、杆5无法贴合圆柱以致无法包络夹持,需舍弃。优化前后夹持器夹持力对比如表 6所示。其中,Foe为优化后夹持器的总输出力,Fce为优化前夹持器的总输出力。表 6显示,包络夹持模式下优化后夹持力提升幅度随R增大而减少,但不低于10%,总体优化效果明显。
| 参数 | R/mm | |||
| 50 | 45 | 40 | 35 | |
| l1/mm | 30.00 | 30.00 | 30.00 | 30.00 |
| l2/mm | 36.06 | 36.06 | 36.06 | 36.06 |
| l3/mm | 25.00 | 25.00 | 25.00 | 25.00 |
| l4/mm | 50.00 | 50.00 | 50.00 | 50.00 |
| β/(°) | 30.00 | 30.00 | 30.00 | 30.00 |
| 参数 | R/mm | ||||
| 40 | 42 | 44 | 48 | 52 | |
| Foe/N | 28.09 | 15.48 | 12.28 | 9.43 | 7.77 |
| Fce/N | 11.14 | 10.15 | 9.04 | 7.87 | 6.94 |
| 提升幅度/% | 152.15 | 52.51 | 35.84 | 19.82 | 11.96 |
由第2节两点夹持模式下的优化结果可知,两点夹持力仅与lr(即l4)有关,且与包络夹持优化方向相同。若在2种模式下l4取值范围相同,则夹持器各结构参数取包络夹持模式下的优化结果时,2种模式的夹持力均可达到最大, 因此选取包络夹持模式下的优化结果作为最终的优化值。
4 仿真验证 4.1 ADAMS仿真模型的建立假设实际加工中夹持器杆件宽度为10 mm(如图 5),选取长度L=20~90 mm的长方体作为两点夹持对象(相应的理论值为30~100 mm),选取R=35~47 mm的圆柱作为包络抓取对象(相应的理论值为40~52 mm)。为与理论分析直观对比,下述分析以夹持对象理论尺寸作为其仿真模型中的尺寸。夹持器2种工作模式的ADAMS建模如图 5所示,其中,在进行包络夹持仿真时,对夹持对象添加一个沿夹持器对称轴方向的滑动副约束,使得仿真时机构能自动寻找静平衡位置。
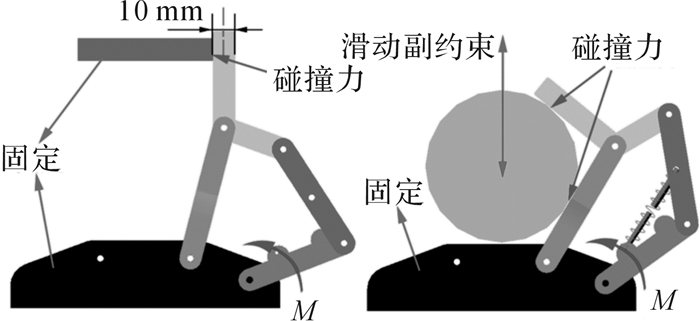
|
| 图 5 夹持器2种工作模式的ADAMS建模 Fig.5 ADAMS modeling of two working modes for gripper |
两点夹持模式下夹持器优化前后夹持力的仿真结果如图 6所示。对比夹持力平均提升幅度的理论分析值和表 7所示的仿真值可知,两者误差为3.89% < 5%,这说明两点夹持模式下的优化结果具备正确性。
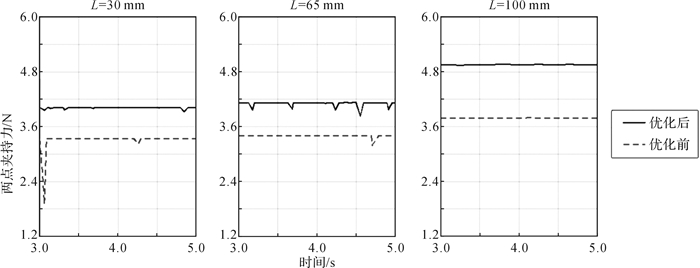
|
| 图 6 两点夹持模式下夹持器优化前后夹持力仿真结果 Fig.6 Simulation results of grasping force before and after optimization of gripper under two-point grasping mode |
| 夹持对象长度/mm | 优化前夹持力/N | 优化后夹持力/N | 夹持力提升幅度/% | 夹持力平均提升幅度/% |
| 30 | 3.35 | 4.02 | 20.00 | 23.89 |
| 65 | 3.40 | 4.11 | 20.88 | |
| 100 | 3.80 | 4.97 | 30.79 |
包络夹持下夹持器优化前后夹持力的对比如图 7所示和表 8所示,包络夹持力提升幅度仿真值与理论值对比如图 8所示,两者误差为4.68% < 5%,这说明包络夹持力建模及最终优化结果具备正确性。
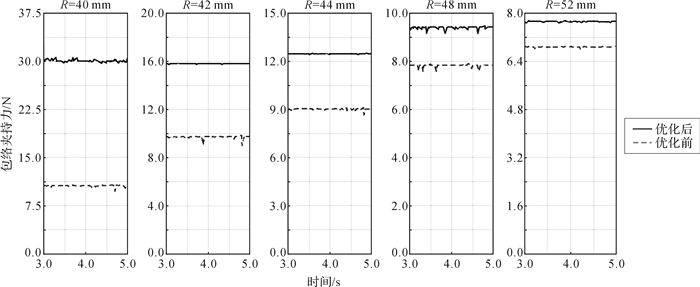
|
| 图 7 包络夹持模式下夹持器优化前后夹持力仿真结果 Fig.7 Simulation results of grasping force before and after optimization of gripper under enveloped grasping mode |
| 夹持对象半径/mm | 优化前夹持力/N | 优化后夹持力/N | 夹持力提升幅度/% | 夹持力平均提升幅度/% |
| 40 | 10.62 | 30.11 | 183.52 | 63.33 |
| 42 | 9.72 | 15.83 | 62.86 | |
| 44 | 9.04 | 12.49 | 38.16 | |
| 48 | 7.84 | 9.40 | 19.90 | |
| 52 | 6.89 | 7.73 | 12.19 |
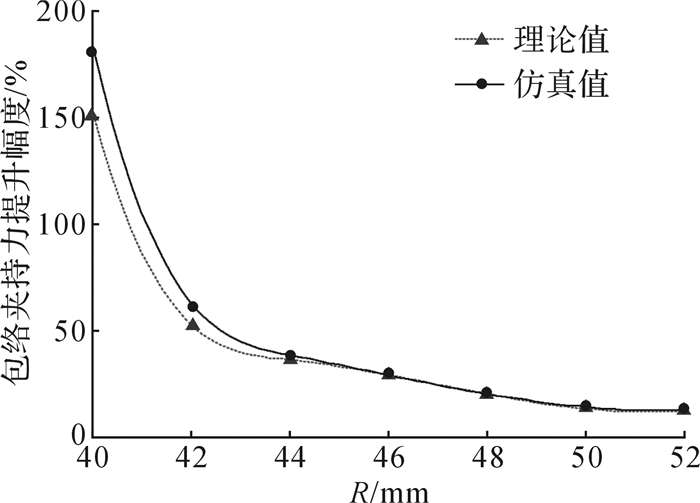
|
| 图 8 包络夹持力提升幅度对比 Fig.8 Comparison of the enveloped grasping force |
此外,图 9展示了包络夹持优化机构、两点夹持优化机构在两点夹持模式下的仿真结果。对比2组优化参数结果可知,除l4外,部分参数数值不同,但两优化机构的两点夹持力仿真值几乎相同,再次验证了两点夹持力建模的正确性。
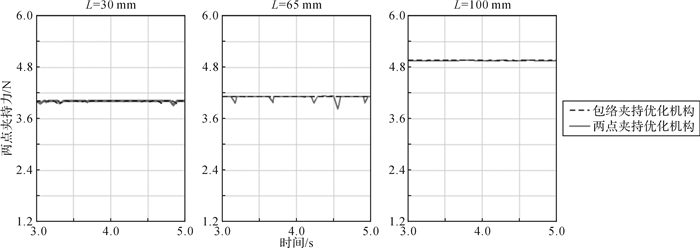
|
| 图 9 两点夹持模式下2种优化机构的夹持力对比 Fig.9 Comparison of grasping force of two optimal mechanisms under two-point grasping mode |
本文针对典型的平面阻尼型欠驱动夹持器提出一种多模式参数优化设计方法。平面阻尼型欠驱动夹持器具有两点夹持与包络夹持两种工作模式。基于静力学建模和外部约束法,对不同工作模式下的夹持器进行优化设计。优化结果表明,相比于优化前,两点夹持力平均提升20.00%以上,包络夹持力提升幅度随夹持对象尺寸的增大而减小,但不低于10%,总体优化效果明显。进一步分析优化结果的共性可知,当夹持器结构参数取包络夹持模式下的优化结果时,2种模式的夹持力均可达到最大。通过ADAMS仿真验证了静力学建模、优化结果的正确性。
| [1] | BIRGLEN L. Enhancing versatility and safety of industrial grippers with adaptive robotic fingers[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Sep.28-Oct.2, 2015. |
| [2] | DEMERS L A A, LEFRANÇOIS S, JOBIN J P. Gripper having a two degree of freedom underactuated mechanical finger for encompassing and pinch grasping: US 8973958 B2[P]. 2015-03-10. |
| [3] | LALIBERTÉ T, BIRGLEN L, GOSSELIN C. Underactuation in robotic grasping hands[J]. Machine Intelligence & Robotic Control, 2002, 4(3): 1–11. |
| [4] |
梁达尧, 张文增.
平夹自适应欠驱动手的参数优化与稳定性分析[J]. 机器人, 2017, 39(3): 282–291.
LIANG Da-yao, ZHANG Wen-zeng. Parameters optimization and stability analysis for a parallel and self-adaptive underactuated hand[J]. Robot, 2017, 39(3): 282–291. |
| [5] | DECHEV N, CLEGHORN W L, NAUMANN S. Multiple finger, passive adaptive grasp prosthetic hand[J]. Mechanism & Machine Theory, 2001, 36(10): 1157–1173. |
| [6] | LI G X, LIU H B, ZHANG W Z. Development of multi-fingered robotic hand with coupled and directly self-adaptive grasp[J]. International Journal of Humanoid Robotics, 2012, 9(4): 1–18. |
| [7] |
张祥, 苏衍宇, 王伟东, 等.
一种平面混合驱动夹持器的结构优化设计[J]. 机器人, 2016, 38(3): 343–351.
ZHANG Xiang, SU Yan-yu, WANG Wei-dong, et al. A structural optimization design method of planar hybrid gripper[J]. Robot, 2016, 38(3): 343–351. |
| [8] | LI G, ZHANG C, ZHANG W, et al. Coupled and self-adaptive under-actuated finger with a novel s-coupled and secondly self-adaptive mechanism[J]. Journal of Mechanisms & Robotics, 2014, 6(4): 041010. |
| [9] |
王杰, 管声启, 夏齐霄.
手指康复外骨骼机器人的结构优化设计[J]. 中国机械工程, 2018, 29(2): 224–229.
WANG Jie, GUAN Sheng-qi, XIA Qi-xiao. Structural design of finger rehabilitation exoskeleton robots[J]. China Mechanical Engineering, 2018, 29(2): 224–229. DOI:10.3969/j.issn.1004-132X.2018.02.015 |
| [10] |
金波, 林龙贤.
果蔬采摘欠驱动机械手爪设计及其力控制[J]. 机械工程学报, 2014, 50(19): 1–8.
JIN Bo, LIN Long-xian. Design and force control of an underactuated robotic hand for fruit and vegetable picking[J]. Journal of Mechanical Engineering, 2014, 50(19): 1–8. |
| [11] | BIRGLEN L. The kinematic preshaping of triggered self-adaptive linkage-driven robotic fingers[J]. Mechanical Sciences, 2011, 2(1): 41–49. DOI:10.5194/ms-2-41-2011 |
| [12] | LAROUCHE L, BIRGLEN L. Assisted design of linkage-driven adaptive soft fingers[J]. Industrial Robot, 2013, 40(4): 337–346. DOI:10.1108/01439911311320840 |
| [13] | STAVENUITER R A J, BIRGLEN L, HERDER J L. A planar underactuated grasper with adjustable compliance[J]. Mechanism & Machine Theory, 2017, 112: 295–306. |
| [14] | CHEN W, ZHANG X, LI H, et al. Nonlinear analysis and optimal design of a novel piezoelectric-driven compliant microgripper[J]. Mechanism & Machine Theory, 2017, 118: 32–52. |
| [15] | BOUCHER J M, BIRGLEN L. Underactuated finger closing motion control using dual drive actuation[C]//ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, Aug.2-5, 2015. |
| [16] | WANG R, ZHANG X. Optimal design of a planar parallel 3-DOF nanopositioner with multi-objective[J]. Mechanism & Machine Theory, 2017, 112: 61–83. |
| [17] |
苏华礼, 秦保军.
基于遗传算法的散热器优化设计[J]. 工程设计学报, 2007, 14(1): 31–34.
SU Hua-li, QIN Bao-jun. Optimal design of heat sinks based on genetic algorithms[J]. Chinese Journal of Engineering Design, 2007, 14(1): 31–34. DOI:10.3785/j.issn.1006-754X.2007.01.007 |
| [18] |
李香山, 任海川.
欠驱动机构的运动学分析及应用研究[J]. 机械研究与应用, 2010, 23(2): 29–31.
LI Xiang-shan, REN Hai-chuan. Motion analysis and application research on the under-actuated mechanism[J]. Mechanical Research & Application, 2010, 23(2): 29–31. DOI:10.3969/j.issn.1007-4414.2010.02.010 |


