割草车按自动化程度的高低可分成手动式割草车和乘骑式割草车^[1-3]。本文研究对象是某型号乘骑式割草车，它为园林机械，但从其结构与操作方式来看，也属于车辆范畴。到目前为止，无论国内还是国外，对割草车刀盘或刀片的研究相对较多，这是因为其刀盘或刀片关系到割草车能否可以高效、高质量地进行割草操作。Clijmans等^[4]结合试验数据对割草车的模态、地面特性等进行了分析。Johnson等^[5]作了有关刀片的研究。Skinner和Burroughs^[6]以割草车为目标物体，研究了它在工作过程中的噪声。马晓春^[7]从动力学模型入手，对刀片进行了受力与运动分析，并研究了刀片工作时的振动状态。周宁^[8]对刀片的转速、切割效率以及刀盘高度的调节进行了研究。

割草车在农业、园林等领域应用广泛，而节能优化设计可以使割草车在同样能耗下行驶更长距离，进行更长时间的割草工作。割草车的主要工作部件是割刀，因此刀片的节能优化设计对降低能耗具有重要的意义^[8-9]。本文应用Fluent软件对某割草车刀盘和刀片进行模拟计算，分析刀片在刀盘中的运动情况，并在此基础上，对刀盘角区和刀片的形状进行优化。

1 割草车刀盘流场控制方程及刀盘与刀片几何模型建立 1.1 刀盘流场的控制方程

本文选取的割草车割台包含3个刀片以及1个刀盘，由此组成了单刀盘三刀片结构。刀片用于割草，刀盘起构造流场流动的气室的作用。本文主要模拟刀片旋转引起的空气在割草机刀盘中的流动情况，以及断草随空气经出口流入大气的过程。

不可压缩流体的连续性方程在空间直角坐标系中的表达式为：

$ \frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_y}}}{{\partial y}} + \frac{{\partial {v_z}}}{{\partial z}} = 0 $

(1)

式中：v_x、v_y、v_z分别表示某点在x、y、z方向上的速度分量。

不可压缩黏性流体的N-S方程在空间直角坐标系中的表达式为：

$ \left\{ \begin{array}{l} {m_x} - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \eta \left( {\frac{{{\partial ^2}{v_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_z}}}{{\partial {z^2}}}} \right) = \frac{{{\rm{d}}{v_x}}}{{{\rm{d}}t}}\\ {m_y} - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \eta \left( {\frac{{{\partial ^2}{v_x}}}{{\partial {x^2}}}} + \frac{{{\partial ^2}{v_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_z}}}{{\partial {z^2}}}\right) = \frac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}}\\ {m_z} - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + \eta \left( {\frac{{{\partial ^2}{v_x}}}{{\partial {x^2}}}} + \frac{{{\partial ^2}{v_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_z}}}{{\partial {z^2}}}\right) = \frac{{{\rm{d}}{v_z}}}{{{\rm{d}}t}} \end{array} \right. $

(2)

式中：m_x、m_y、m_z分别表示某点在x、y、z方向上的质量分量，ρ表示流体密度，p表示流体某点处压强。

理论上，联立方程(1)和(2)就可以求得不可压缩黏性流体流场的解。但由于N-S方程中有速度的二阶导数，只有在某些特殊情况下才能使方程得到充分简化，求得近似解。

本文模拟的流场处于湍流状态，因此采用标准的k-ε模型作为其控制方程^[10-13]。标准k-ε模型中的湍流黏性系数可表示为：

$ {\mu _{\rm{t}}} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon } $

(3)

式中：C_μ表示经验常数，k表示湍流动能，ε表示湍流耗散率。

湍流动能k的方程为：

$ \begin{array}{l} \rho \frac{{\partial k}}{{\partial t}} + \rho {V_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ {\mu _{\rm{t}}}\frac{{\partial {V_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {V_i}}}{{\partial {x_j}}} + \frac{{\partial {V_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon \end{array} $

(4)

式中：$ \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_j}}}} \right]$为扩散项，$ {\mu _{\rm{t}}}\frac{{\partial {V_i}}}{{\partial {x_j}}}(\frac{{\partial {V_i}}}{{\partial {x_j}}} + \frac{{\partial {V_j}}}{{\partial {x_i}}})$为生成项，ρε为耗散项，σ_k为经验常数。

湍流耗散率ε的方程为：

$ \begin{array}{l} \rho \frac{{\partial \varepsilon }}{{\partial t}} + \rho {V_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ {C_{\varepsilon 1}}\frac{\varepsilon }{k}{\mu _{\rm{t}}}\frac{{\partial {V_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {V_i}}}{{\partial {x_j}}} + \frac{{\partial {V_j}}}{{\partial {x_i}}}} \right) - \frac{{{C_{\varepsilon 2}}\rho {\varepsilon ^2}}}{k} \end{array} $

(5)

式中：$ \rho \frac{{\partial \varepsilon }}{{\partial t}}$表示非稳定项，$ \rho {V_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}}$表示对流项，$ \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right]$表示扩散项，${C_{{\varepsilon _1}}}\frac{\varepsilon }{k}{\mu _{\rm{t}}}\frac{{\partial {V_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {V_i}}}{{\partial {x_j}}} + \frac{{\partial {V_j}}}{{\partial {x_i}}}} \right) $表示生成项，$\frac{{{C_{{\varepsilon _2}}}\rho {\varepsilon ^2}}}{k} $表示耗散项，$ {\sigma _\varepsilon }、{C_{{\varepsilon _1}}}、{C_{{\varepsilon _2}}}$表示经验常数。

在Fluent中，k-ε模型中经验常数的默认取值如表 1所示。

1.2 刀盘与刀片几何模型与网格划分

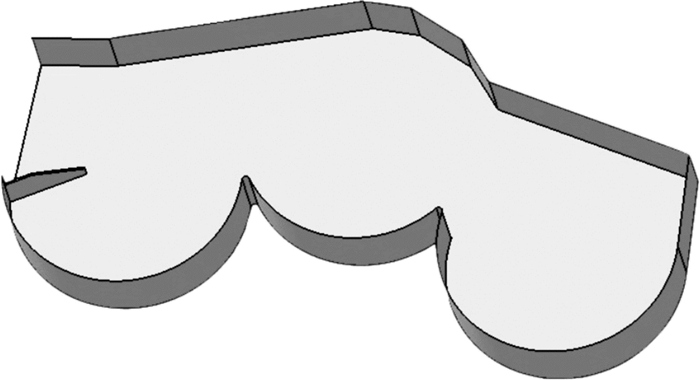
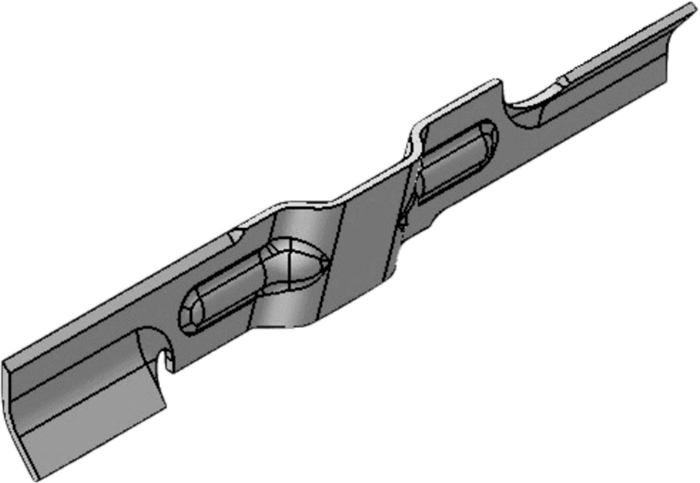
在Solidworks中分别建立刀盘与刀片的三维几何模型，且为了更好地进行网格划分，适当将模型进行简化。建立的刀盘及刀片几何模型分别如图 1和图 2所示。

由于在Solidworks中构建的刀片模型非常不规则，将刀盘和刀片几何模型导入ICEM中进行非结构网格划分^[14-16]，单元尺寸为5 mm，其中壁面、进出口处的网格都进行了加密，刀盘内导流板壁面以及刀片壁面处的最小单元尺寸为2 mm^[17]。刀片共划分为675 504个单元、119 104个节点，刀盘共划分为1 235 684个单元、209 723个节点。刀片网格模型如图 3所示。

2 割草车原始刀盘与刀片仿真分析

由于刀盘中的流体是低速流动的，设置流体是稳态不可压缩的空气。设置所有刀片的旋转速度为3 200 r/min。

入口边界：割草机入口设置为pressure-inlet，压力边界值p=1.3×10⁵ Pa，即表压设为0 Pa，湍流强度为5%，水力直径为2 500 mm。

出口边界：割草机出口设置为pressure-outlet，压力边界值p=1.3×10⁵ Pa，即表压设为0 Pa，湍流强度为5%，水力直径为500 mm。

壁面条件：固体壁面及刀片表面上采用无滑移条件^[18]。

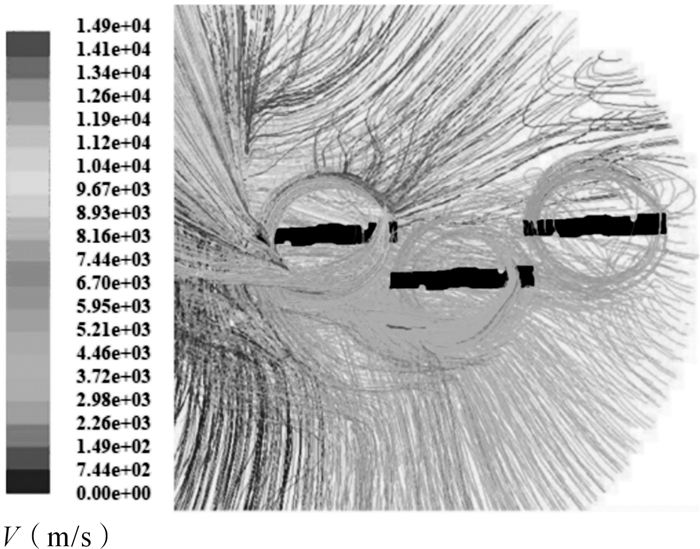
2.1 刀盘流场内流线分析

首先对刀盘整个流场内的流线分布情况进行分析，为刀盘及刀片的改进提供依据。得到刀盘流场内流线分布如图 4所示。由图可以看出，刀片的高速旋转带动入口处的空气与刀片一同旋转，气流在入口处变得不稳定，湍流增加；刀片刀尖处存在泄露流，因此刀尖处的流线较为混乱；在刀盘壁面拐角处也存在大量小尺度涡流，会造成能量损耗。

2.2 刀片及刀盘表面压强分布

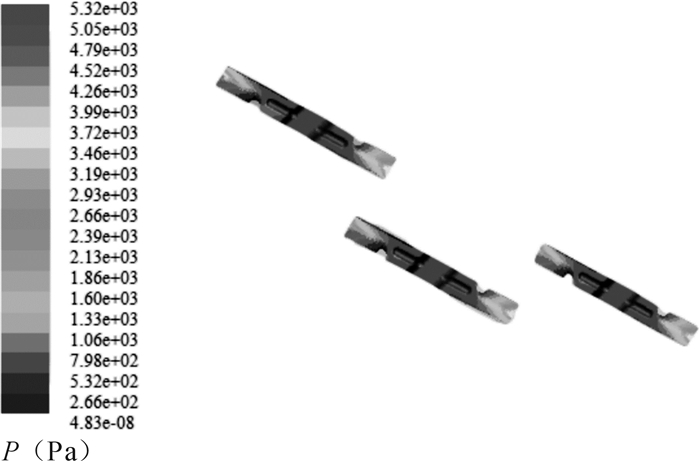
图 5为刀片表面的压强分布。刀片吸力面压强波动较大，尾缘部分压强最大，刀尖靠近尾缘部分和靠近主轴部分前缘处的压强最小；刀片压力面压强波动小于其吸力面的，主轴处下表面压强最小，压力面刀尖靠近尾缘处的压强最大，靠近主轴部分前缘处压强逐渐减小。

由图 5可知，刀片吸力面和压力面靠近尾缘处的压强波动较大，尤其是靠近刀尖部分，波动达到最大，这正是刀尖处泄流涡产生的原因。此外，压强波动不仅引起总压损失，而且也会引起噪声，这说明了可通过改变刀片形状以达到节能的目的。

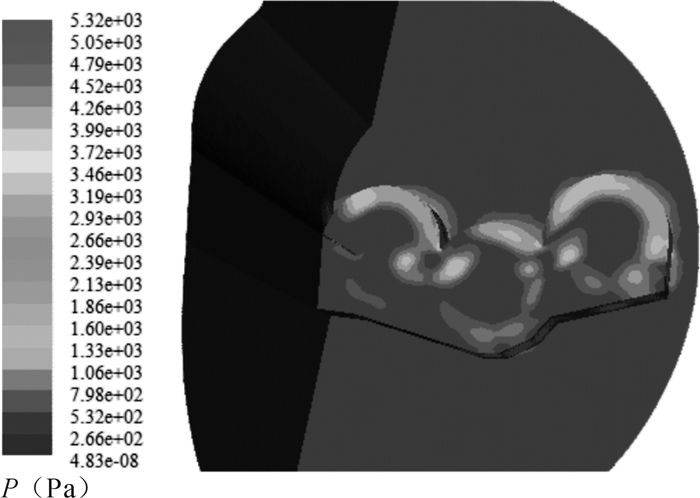
图 6显示了刀盘表面的压强分布。整个刀盘表面的压强随刀片的位置呈周期性变化，其中左侧(封闭侧)和中间表面的压强较大，其中左侧拐角处压强最大，右侧(出口侧)表面的压强较小。

2.3 刀片切割速度云图

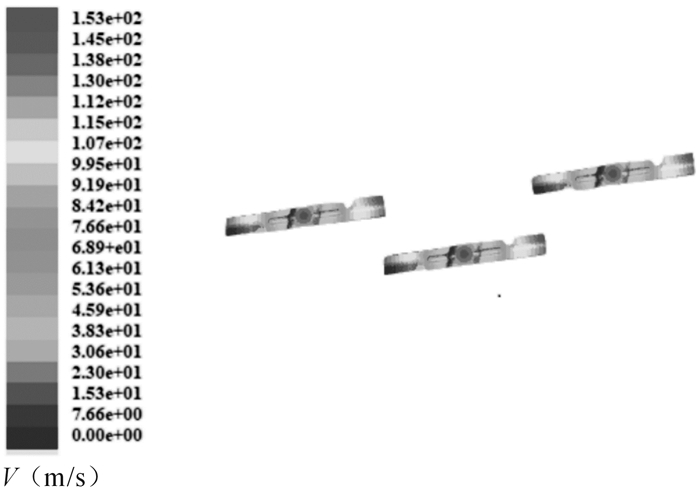
图 7所示为刀片的切割速度云图。从图中可以看出，刀片切割速度从主轴向外逐渐增大，两端边缘处最大，这与实际情况是比较符合的，说明分析结果是相对比较合理的。刀片在刃口及两端边缘处大部分区域切割速度都较大，对于切削，需要刀刃处速度快，这样可以保证切割的顺畅性，而其余部分速度的快慢对于切割效果实际上并没有太大影响。从这点上看，刀片形状有一定的优化空间，即尽量降低其余部分的速度而保持刀刃处有较高速度。

2.4 刀片扭矩

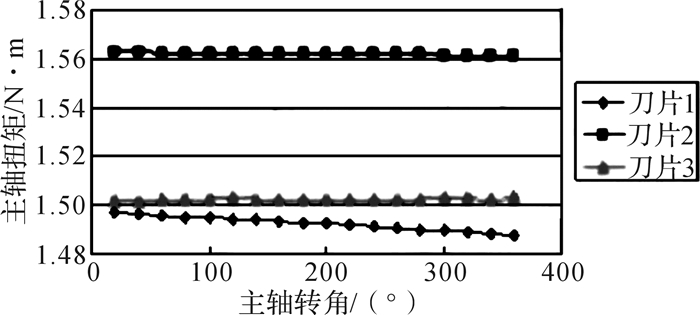
对割草机进行节能优化前，首先需要知道优化前刀片的消耗功率。采用Fluent对割草机的流场进行了分析，设置刀片的旋转速度为3 200 r/min，流场稳定后一个旋转周期内刀片上的扭矩如图 8所示。刀片2(中间刀片)上的扭矩较大，扭矩约为1.56 N·m，且呈较明显的周期性变化；刀片1(出口侧)和刀片3(封闭侧)上的扭矩较小；刀片3上的扭矩在1.5 N·m附近变动，刀片1上的扭矩在1.48~1.5 N·m之间变动。

3 优化方案

图 6的结果显示刀盘流场比较合理，仅在流场壁面、出口和拐角处有较大压力波动，图 5的结果显示刀片的表面有较大的压力变化梯度。考虑到整车的布置和挡板对断草的导流，故仅对刀盘角区和刀片的形状进行优化。

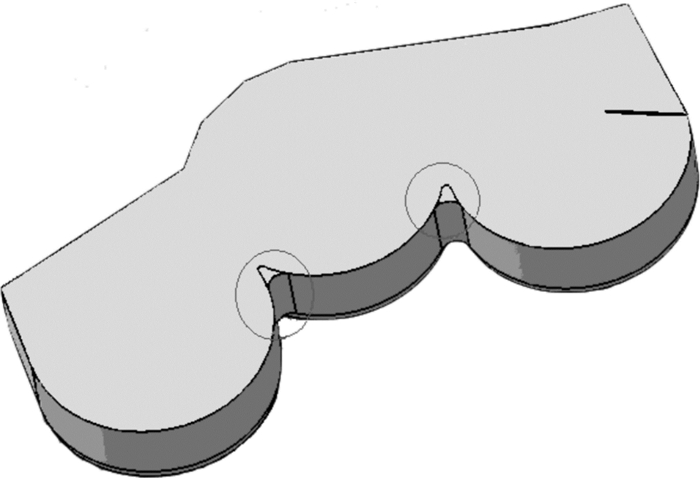
3.1 刀盘优化

因刀盘角区处流场压力变化较快，因此首先对此处进行优化，将原壳体的圆角半径从10 mm改为30 mm，如图 9所示。

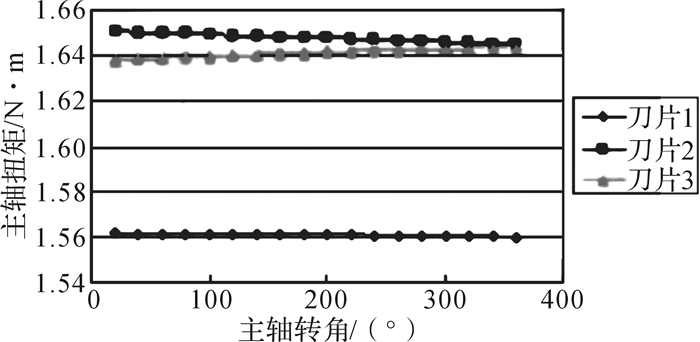
为了与原方案对比，仍采用原来的刀片，用原先的单元尺寸对刀盘重新划分网格，并和刀片旋转区域网格模型组合后形成优化方案1的CFD(computational fluid dynamics，计算流体动力学)模型。设置相同的边界条件，待流场稳定后测得一个旋转周期内刀片上的扭矩, 如图 10所示。

图 10结果显示，优化后刀片1上的扭矩为1.56 N·m；刀片2上的扭矩为1.65 N·m；刀片3上的扭矩约为1.64 N·m。由此可见，刀盘优化后各刀片上的扭矩均比原方案的大，进而使耗能增加, 无法达到节能效果，这可能是因为刀盘拐角半径的增大导致刀片之间的相互作用增大。

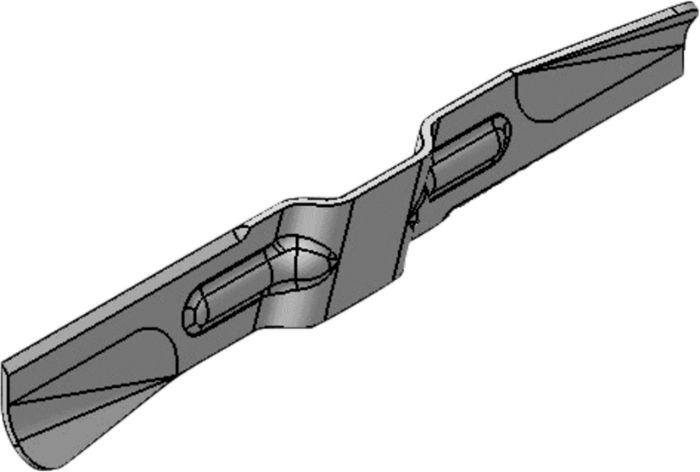
3.2 刀片优化 3.2.1 弯曲刀片

关于刀片的优化方案，主要是通过参考割草机上常用的、工艺性良好的刀片确定的。市面上常见的割草机刀片大概有弯曲刀片、异形刀片和平直刀片(原方案)三种，故优化方案2采用原刀盘和图 11所示的弯曲刀片。

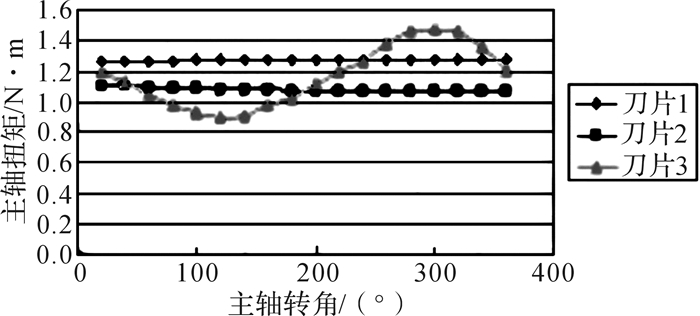
为了与原方案对比，采用原来的刀盘网格模型，用原先的单元尺寸对弯曲刀片重新划分网格，并和刀盘网格模型组合后形成优化方案2的CFD模型。设置相同的边界条件，待流场稳定后测得一个旋转周期内刀片上的扭矩，如图 12所示。

图 12结果显示，优化后刀片1上的扭矩为1.24 N·m；刀片2上的扭矩为1.1 N·m；刀片3上的扭矩为0.95~1.45 N·m。可见，采用方案2进行优化后，刀片上的扭矩均比原方案有较大幅度的降低，达到了节能的效果。但是，可能是优化后流场出口处的速度波动较大，或者产生了较大尺度的涡流，使得靠近出口处的刀片3上的扭矩波动较大, 严重时甚至可能引起整车的振动。

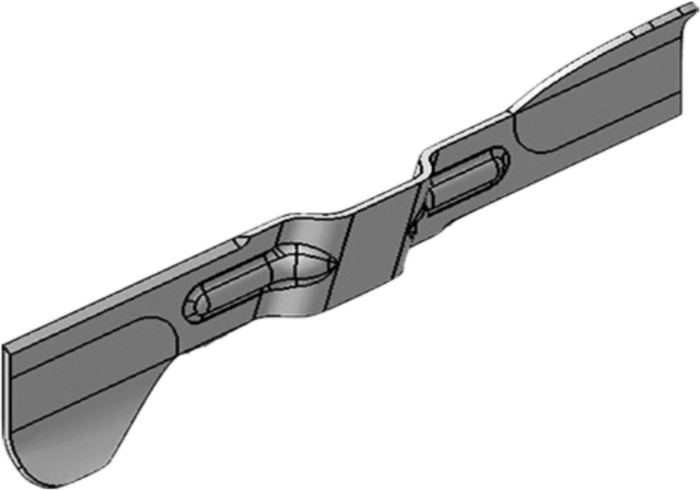
3.2.2 异形刀片

优化方案3仍然是对刀片形状进行优化，异形刀片也是割草机上常用的刀片之一，故优化方案3采用原刀盘和图 13所示异形刀片。

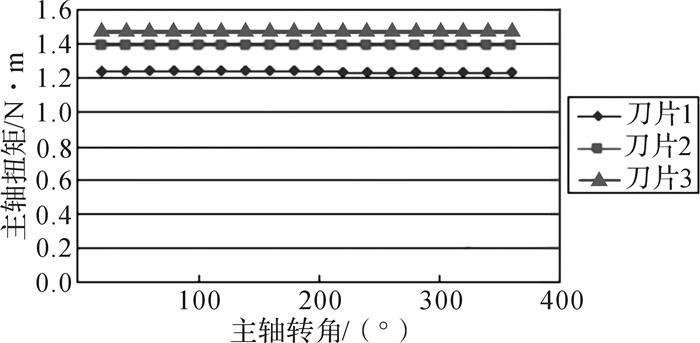
为了与原方案对比，仍采用原来的刀盘网格模型，用原先的单元尺寸对异形刀片重新划分网格，并和刀盘网格模型组合后形成优化方案3的CFD模型。设置相同的边界条件，待流场稳定后测得一个旋转周期内刀片上的扭矩，如图 14所示。

图 13结果显示，优化后的刀片1上的扭矩为1.22 N·m；刀片2上的扭矩为1.4 N·m；刀片3上的扭矩为1.45 N·m。可见，采用方案3(异形刀片)进行优化后, 刀片上的扭矩均比原方案小，达到了节能的效果，但是相比优化方案2(弯曲刀片)，方案3中的3片刀片上的扭矩变化平稳，均未出现波动情况。

在一个旋转周期中，3片刀片上的扭矩会有所波动，为对比分析优化方案的节能效果，对一个旋转周期内刀片上的扭矩取平均值，并对比3个优化方案与原方案中3片刀片上的扭矩，结果如表 2所示。

4 试验验证

将异形刀片加工成形，安装到实际割草车上开展试验研究，验证其割草效果。虽刀片扭矩有一定下降，但刀口的切割速度依然很高，实际割草效果仍能达到要求。经试验测试结果表明，优化后刀片上的扭矩减小了18%左右，与仿真计算的误差小于5%，证明仿真结果有效。另外刀片功率减小了216 W，节能约8.5%，达到了满意的节能效果。图 15(a)是试验用割草车, 图 15(b)是优化后的异形刀片。

5 结论

本文为了提高某割草车的工作效率，降低其长时间工作时的能源损耗，对刀盘和刀片进行建模与仿真分析，通过对刀盘角区和刀片的优化设计，达到节能的效果。主要得出以下结论：

1) 通过增大了刀盘拐角半径，刀片上的扭矩均出现了不同程度的增大，说明改变刀盘角区形状并不能起到很好的节能效果。

2) 采用弯曲刀片时，分析结果显示3片刀片上的扭矩均出现了不同程度的减小，其中扭矩最大减小了29.58%，有很好的节能效果。但出口处的刀片了上会出现扭矩波动增大的情况，严重时甚至可能引起整车振动。

3) 试验结果表明，采用异形刀片时，其扭矩能降低18%左右，与仿真结果的误差在5%以内，且刀片上的扭矩平稳少波动，表明该优化方案具有不错的节能效果。

综上所述，刀盘形状和刀片形状对割草机工作过程中流场及扭矩等有重要影响，刀尾一侧以一定角度上扬的异形刀片在节能提效上有较明显优势，在实际割草机节能优化工作中可优先考虑。