2. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122;
3. 江南大学 物联网工程学院, 江苏 无锡 214122
2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Wuxi 214122, China;
3. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China
在圆弧类工件轮廓测量过程中,空间圆弧拟合是至关重要的一步[1-3]。在通过轮廓特征提取及匹配,获得轮廓点空间三维坐标后,需进一步通过空间圆弧拟合得出圆弧半径、圆心坐标等相关信息。空间圆弧拟合的精度将对最终测量结果产生重要影响。
传统的空间圆弧拟合方法可以分为3种:第1种是将三维坐标点投影到该点所在的平面,将三维问题转化为二维问题,进而在二维平面上进行圆弧拟合并求得二维平面上的圆弧圆心坐标和半径,最后通过投影变换反算出空间圆的圆心坐标和半径[4];第2种是利用几何知识,将三维圆理解为球体与过球心平面的交点集合,进而通过几何知识推导出中垂面方程和空间平面方程,最后得出空间圆的圆心坐标和半径[5];第3种较为复杂,运用较少,其基本原理是将空间圆看作由空间球壳与二维平面相交而成,根据几何关系联立方程组求得球心坐标,进而计算出空间圆的圆心三维坐标[6-7]。
圆弧的拟合多以二维问题进行,空间圆弧拟合方法较少,且传统的空间圆弧拟合方法存在鲁棒性差、拟合精度易受噪声影响等缺点。Sung等人提出利用迭代的方法来增强空间圆弧拟合的鲁棒性及抗噪性,但该方法计算量大,实用性较低[8]。因此,有必要提出一种鲁棒性更强的空间圆弧拟合优化方法。
1 基于拉格朗日乘子法的空间圆弧拟合 1.1 拉格朗日乘子法简介拉格朗日乘子法(Lagrange multiplier method)又称为拉格朗日乘数法,用来求解函数f(x1, x2, ...)在g(x1, x2, ...)=0的约束条件下的极值[9-11]。拉格朗日乘子法一般分为3个步骤:首先,引入一个新的参数λ(称为拉格朗日乘子);其次,联立约束条件及原函数,使得变量数量与方程数量相同;最后,求出方程中各个变量的解。拉格朗日乘子法在微分几何、数学物理方程中有着重要应用,同时在经济学及工程学等实际领域中也有着广泛的应用。本文提出的空间圆弧拟合方法将以拉格朗日乘子法为基础。
关于单约束条件下二元函数的极值问题[12],相关定理如下:
针对z=f(x, y)在约束条件φ(x, y)=0下的极值问题,其中f与φ在区域D上连续可微,若(xo, yo)∈int D是上述函数的极值点,且
| $ \left\{ \begin{array}{l} {L_x} = \frac{{\partial f}}{{\partial x}} + \lambda \frac{{\partial \varphi }}{{\partial x}} = 0\\ {L_y} = \frac{{\partial f}}{{\partial y}} + \lambda \frac{{\partial \varphi }}{{\partial y}} = 0\\ {L_\lambda } = \varphi \left( {x,y} \right) = 0 \end{array} \right. $ | (1) |
式中:Lx、Ly、Lλ是指L(x, y, λ)分别对x、y、λ求导。
1.2 空间圆弧拟合方法传统方法并非直接对空间圆弧进行拟合,其拟合精度易受噪声影响且鲁棒性差。因此,本文拟在拉格朗日乘子法的基础上,基于平面条件约束建立目标函数,进而推导出空间圆弧拟合方程。
基于拉格朗日乘子法的空间圆弧拟合步骤如下:
1) 建立空间圆方程。
首先,建立三维空间圆方程:
| $ \left\{ \begin{array}{l} Ax + By + Cz + D = 0\\ {\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {R^2} \end{array} \right. $ | (2) |
式中:Ax+By+Cz+D=0表示一个法向量为(A, B, C)的平面方程;(x-x0)2+(y-y0)2+(z-z0)2=R2(x-x0)2+(y-y0)2+(z-z0)2=R2表示球心坐标为(x0,y0,z0)、半径为R的球面方程。
然后,通过三维数据点建立空间平面方程:
| $ \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&{{z_1}}&1\\ {{x_2}}&{{y_2}}&{{z_2}}&1\\ \vdots&\vdots&\vdots&\vdots \\ {{x_n}}&{{y_n}}&{{z_n}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} A\\ B\\ C\\ D \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ 0 \end{array}} \right] $ | (3) |
式中:(x1, y1, z1)、(x2, y2, z2)、…、(xn, yn, zn)为匹配后得到的三维数据点。
根据式(3),利用最小二乘法拟合得到平面方程的系数A、B、C和D,进而可得出空间圆所在空间的平面方程。将全部点云数据(xi, yi, zi)投影到平面Ax+By+Cz+D=0上,得到投影点(xi′, yi′, zi′), 各点投影公式为:
| $ \left\{ \begin{array}{l} {{x'}_i} = A \cdot k + {x_i}\\ {{y'}_i} = A \cdot k + {y_i}\\ {{z'}_i} = A \cdot k + {z_i} \end{array} \right. $ | (4) |
式中:
2) 构建Lagrange目标函数。
由解析几何知识可得,投影点(x′i, y′i, z′i)定是平面与球面的相交点,可利用最小二乘法进行求解。将空间圆方程组当作一个多元函数条件极值问题,引入新的参数λ(拉格朗日乘子),构建Lagrange目标函数:
| $ \begin{array}{l} F\left( {{x_0},{y_0},R,\lambda } \right) = \sum\limits_{i = 1}^n {\left[ {{{\left( {{{x'}_i} - {x_0}} \right)}^2} + {{\left( {{{y'}_i} - {y_0}} \right)}^2} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {{{\left( {{{z'}_i} - {z_0}} \right)}^2} - {R^2}} \right]^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {A{x_0} + B{y_0} + C{z_0} + D} \right) \end{array} $ | (5) |
进而根据极值条件建立方程组:
| $ {{F'}_{{x_0}}} = {{F'}_{{y_0}}} = {{F'}_{{z_0}}} = {{F'}_R} = {{F'}_\lambda } = 0 $ | (6) |
联立方程进行求解。
在解方程组过程中假设式(7)成立:
| $ \left[ {{{\left( {{{x'}_i} - {x_0}} \right)}^2} + {{\left( {{{y'}_i} - {y_0}} \right)}^2} + {{\left( {{{z'}_i} - {z_0}} \right)}^2} - {R^2}} \right] \approx 0 $ | (7) |
然后消去多项式中的高次项,从而获得计算圆心坐标与半径的参数方程,如式(8)所示:
| $ \left[ {\begin{array}{*{20}{c}} {8\mathit{\boldsymbol{M}}}&{ - 4{\mathit{\boldsymbol{N}}^{\rm{T}}}}&{{{\bf{0}}^{\rm{T}}}}\\ {2\mathit{\boldsymbol{N}}}&U&0\\ 0&0&0 \end{array}} \right]\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{T}} $ | (8) |
式中:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {x{'}_i^2} }&{\sum\limits_{i = 1}^n {{{x'}_i}{{y'}_i}} }&{\sum\limits_{i = 1}^n {{{x'}_i}{{z'}_i}} }\\ {\sum\limits_{i = 1}^n {{{x'}_i}{{y'}_i}} }&{\sum\limits_{i = 1}^n {y{'}_i^2} }&{\sum\limits_{i = 1}^n {{{y'}_i}{{z'}_i}} }\\ {\sum\limits_{i = 1}^n {{{x'}_i}{{z'}_i}} }&{\sum\limits_{i = 1}^n {{{y'}_i}{{z'}_i}} }&{\sum\limits_{i = 1}^n {z{'}_i^2} } \end{array}} \right] $ |
| $ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {{{x'}_i}} }&{\sum\limits_{i = 1}^n {{{y'}_i}} }&{\sum\limits_{i = 1}^n {{{z'}_i}} } \end{array}} \right] $ |
| $ \mathit{\boldsymbol{O}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n A }&{\sum\limits_{i = 1}^n B }&{\sum\limits_{i = 1}^n C } \end{array}} \right] $ |
| $ U = \sum\limits_{i = 1}^n {\left( { - 1} \right)} $ |
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} {{x_0}}&{{y_0}}&{{z_0}}&l&\lambda \end{array}} \right]^{\rm{T}}} $ |
| $ l = x_0^2 + y_0^2 + z_0^2 - {R^2} $ |
| $ \mathit{\boldsymbol{T}} = \left[ \begin{array}{l} 4\sum\limits_{i = 1}^n {\left( {x{'}_i^3 + {{x'}_i}y{'}_i^2 + {{x'}_i}z{'}_i^2} \right)} \\ 4\sum\limits_{i = 1}^n {\left( {{{y'}_i}x{'}_i^2 + y{'}_i^3 + {{y'}_i}z{'}_i^2} \right)} \\ 4\sum\limits_{i = 1}^n {\left( {{{z'}_i}x{'}_i^2 + {{z'}_i}y{'}_i^2 + z{'}_i^3} \right)} \\ \sum\limits_{i = 1}^n {\left( {x{'}_i^2 + y{'}_i^2 + z{'}_i^2} \right)} \\ \sum\limits_{i = 1}^n {\left( { - D} \right)} \end{array} \right] $ |
3) 求解圆心和半径。
将式(4)中的投影点(x′i, y′i, z′i)代入方程(8),进而得到空间圆的圆心坐标和l值,将圆心坐标代入l=x02+y02+z02-R2即可解出空间圆的半径R。
2 基于RANSAC算法的空间圆弧拟合优化方法本文将利用RANSAC(random sample consensus,随机抽样一致)算法对上述空间圆弧拟合方法的拟合精度进行提升。
2.1 RANSAC算法简介RANSAC算法于1981年由Fischler和Bolles率先提出,其本质是带有自适应去除干扰能力的最小二乘法。RANSAC算法能够从异常的噪声点中提取有效的空间圆弧数学模型[13-17]。
RANSAC算法有以下基本假设:1)局内点为正确的并且符合给定数学模型的数据;2)噪声点和局外点均为不符合该数学模型的数据,而局外点一般产生于错误的数据假设或者错误的测量方法等情况;3)排除局内点和局外点,余下的数据都属于噪声点。
RANSAC算法的输入是一组包含局内点、局外点和噪声点的样本数据,一个给定的空间圆弧数学模型和一些预设的参数阈值。首先假设样本数据中的一个随机子集为局内点,然后通过相关方法验证及排除,最后确定最优模型。
RANSAC算法的具体步骤:
1) 用假设的局内点估计出一个模型,即可以用这些局内点解出上述数学模型的所有未知参数;
2) 验证样本数据中其他数据是否满足步骤1)中的模型,如果满足,则认为它是局内点;
3) 如果有足够多的局内点支持估计的模型,那么估计的模型就是符合要求的;
4) 用步骤2)中得到的局内点集合重新估计模型,因为随着后续局内点的加入,步骤1)中的估计模型已经不是最优模型;
5) 利用上述步骤,找到一个拥有最多局内点支撑的空间圆弧数学模型。
由上述步骤得到的数学模型即为通过RANSAC算法提取的最优模型,该模型拥有最多的局内点。
RANSAC算法的缺点在于它的迭代次数没有上限,从而导致计算量大。但如果设置的迭代次数过少,可能得不到最优的模型,甚至可能得到错误的模型。RANSAC算法的另一个缺点是它需要设定相关参数的阈值,不同的阈值设置可能会得到截然不同的结果。一个RANSAC程序只能计算出一个模型。
2.2 基于RANSAC算法的三维拟合由于RANSAC算法稳定性较高,且能够剔除错误样本点,故将该算法应用到空间圆弧拟合的点云筛选及优化中。
设初始点为(xi, yi, zi),i=0, 1, 2, …n,采用RANSAC算法剔除错误跟踪点,优化步骤如下:
1) 首先随机从样本点中取3个点,然后进行空间圆拟合。参考上述的方法,得到平面方程系数A、B、C和D,空间圆的圆心坐标及半径。
2) 求出初始点集中所有点到拟合的空间平面的距离,以及点到圆心(x0, y0, z0)的距离与半径的差值,分别记为Fi、Di(i=0, 1, 2, …n):
| $ \left\{ \begin{array}{l} {F_i} = \sqrt {{{\left( {A{x_i} + B{y_i} + C{z_i} + D} \right)}^2}} \\ {D_i} = \sqrt {{{\left( {{x_i} - {x_0}} \right)}^2} + {{\left( {{y_i} - {y_0}} \right)}^2} + {{\left( {{z_i} - {z_0}} \right)}^2}} - R \end{array} \right. $ | (9) |
3) 分别设置点到平面距离的阈值T1以及点到圆心距离与半径差值的阈值T2。扫描所有样本数据点,若Fi、Di都在设定的阈值范围内时,则可认为该点为是局内点。在遍历结束后,计算出所有局内点的数目,若局内点的数目大于总数的80%,则认为该模型为可靠模型。
4) 重复上述步骤,统计出可靠模型的数量,直到达到最大循环次数m,最后确定最优模型。
由文献[18]可知,在置信度为η0的条件下,应至少存在一次采样,使得选择出的b个点均为局内点。因此,可以得出最大循环次数m应该满足如下条件:
| $ m \ge \frac{{\log \left( {1 - {\eta _0}} \right)}}{{\log \left( {1 - {\varepsilon ^b}} \right)}} $ | (10) |
式中:置信度η0一般设置在[0.95, 0.99]的范围内; b表示局内点总数;ε表示局内点在所有样本点中所占的比例,然而通常情况下,ε未知,所以ε取最坏条件下局内点的比例。
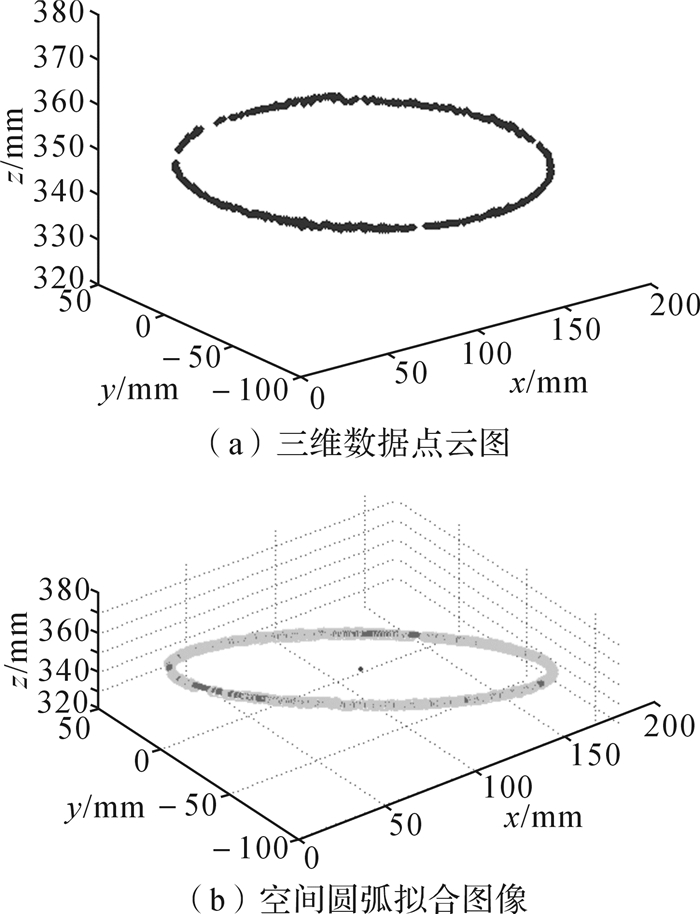
3 空间圆弧拟合实验及其拟合精度分析如图 1所示,取直径为170 mm,直径偏差范围为0~0.8 mm的带轮进行实验。对带轮边缘轮廓进行测量,通过双目视觉圆弧轮廓特征提取和匹配之后,得出边缘外轮廓点的空间三维坐标。图 2所示为求得的带轮边缘外轮廓点云图及空间圆弧拟合图,共获得266个边缘外轮廓点的三维坐标。利用本文拟合优化方法,对上述点云进行8次拟合,平均迭代数为6 895次。拟合结果如表 1所示。

|
| 图 1 带轮实物图 Fig.1 Physical map of belt wheel |
|
| 图 2 带轮边缘外轮廓点云图及空间圆弧拟合图 Fig.2 Point cloud diagram of outer contour of belt wheel edge and its spatial arc fitting image |
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 拟合直径值/mm | 170.624 | 170.614 | 170.756 | 170.676 | 170.738 | 170.538 | 170.576 | 170.762 |
| 直径偏差值/mm | 0.624 | 0.614 | 0.756 | 0.676 | 0.738 | 0.538 | 0.576 | 0.762 |
从表 1的拟合结果可以发现,带轮边缘外轮廓拟合实验中,直径的绝对误差平均值为0.661 mm,在偏差允许范围内,说明本文拟合优化方法针对普通空间圆弧拟合具有一定有效性及实用性。
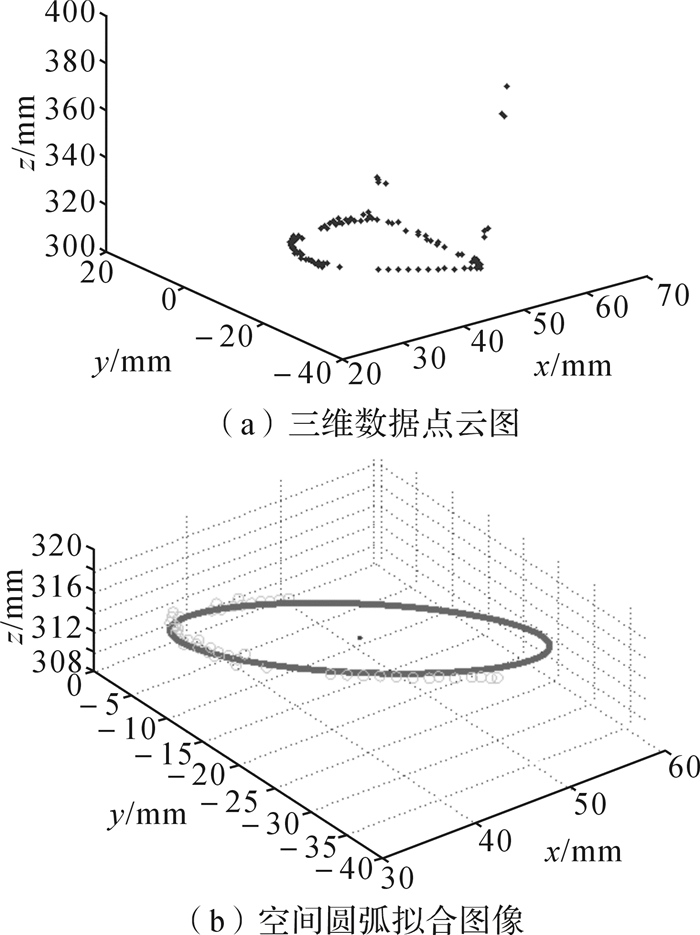
同时本文对复杂圆弧点云进行了拟合。取直径为38 mm,直径偏差范围为0~0.5 mm的半段圆弧工件进行实验,如图 3(a)所示为半段圆弧工件边缘外轮廓点云图,共包含98个边缘轮廓点。复杂圆弧点云中,噪声点较多且存在误差较大的点,同时点云并没有覆盖整个圆弧。如图 3(b)所示为半段圆弧工件边缘外轮廓空间圆弧拟合图像。利用本文拟合优化法,对上述点云进行8次拟合,平均迭代数为3 026次,拟合结果如表 2所示。
|
| 图 3 半段圆弧工件边缘外轮廓点云图及其空间圆弧拟合图 Fig.3 Point cloud diagram of outer contour of half-section arc workpiece edge and its spatial arc fitting image |
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 拟合直径值/mm | 37.587 | 37.598 | 37.590 | 37.606 | 37.576 | 37.618 | 37.584 | 37.622 |
| 直径偏差值/mm | 0.413 | 0.402 | 0.410 | 0.394 | 0.424 | 0.382 | 0.416 | 0.378 |
从表 2的结果可以发现,半段圆弧拟合直径的绝对误差平均值为0.402 mm,说明本文拟合优化方法针对复杂空间圆弧拟合也具有一定的可行性。
实验结果表明:普通圆弧点云拟合的相对精度在0.003左右,复杂圆弧点云拟合的相对精度在0.01左右,这说明基于拉格朗日乘子法的空间圆弧拟合优化方法有较强的理论研究意义和工程实践价值。
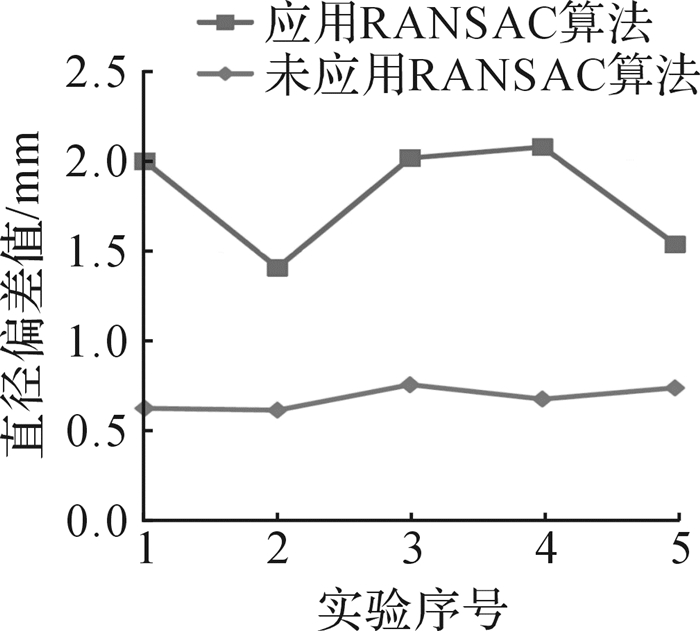
为验证本文提出的空间圆弧拟合优化方法的准确性,对图 2中的数据点云,用基于拉格朗日乘子法的空间圆弧拟合方法进行拟合。分别进行2组各5次拟合实验,其中一组应用了RANSAN算法剔除错误点,拟合结果如表 3所示,分析结果如图 4所示。同时,将本文优化方法与传统空间圆弧拟合方法进行比较,拟合结果如表 4所示,分析结果如图 5所示。
|
| 图 4 基于拉格朗日乘子法的空间圆弧拟合偏差对比 Fig.4 Comparison of spatial arc fitting deviation based on Lagrangian multiplier method |

|
| 图 5 本文优化方法与传统方法的空间圆弧拟合偏差对比 Fig.5 Comparison of spatial arc fitting deviation between the optimization method of this paper and traditional method |
| 实验序号 | 拟合直径/mm | 直径偏差值/mm | |||
| 应用RANSAN算法 | 未应用RANSAN算法 | 应用RANSAN算法 | 未应用RANSAN算法 | ||
| 1 | 170.624 | 171.378 | 0.624 | 1.378 | |
| 2 | 170.614 | 170.794 | 0.614 | 0.794 | |
| 3 | 170.756 | 171.264 | 0.756 | 1.264 | |
| 4 | 170.676 | 171.406 | 0.676 | 1.406 | |
| 5 | 170.738 | 170.802 | 0.738 | 0.802 | |
| 实验序号 | 拟合直径/mm | 直径偏差值/mm | 平均运行时间/ms | |||||
| 本文方法 | 传统方法 | 本文方法 | 传统方法 | 本文方法 | 传统方法 | |||
| 1 | 170.624 | 171.378 | 0.624 | 1.378 | ||||
| 2 | 170.614 | 171.706 | 0.614 | 1.706 | ||||
| 3 | 170.756 | 171.464 | 0.756 | 1.264 | ||||
| 4 | 170.676 | 171.406 | 0.676 | 1.406 | 1 868 | 1 726 | ||
| 5 | 170.738 | 171.102 | 0.738 | 1.102 | ||||
| 6 | 170.538 | 171.348 | 0.538 | 1.348 | ||||
| 7 | 170.576 | 171.422 | 0.576 | 1.422 | ||||
| 8 | 170.762 | 171.806 | 0.762 | 1.806 | ||||
分析表 3和图 4可以得出,应用了RANSAC算法后,拟合结果与理论值更加接近,且稳定性亦有所提高,验证了本文方法的准确性。从表 4及图 5中可以看出,运用本文方法与传统方法拟合耗时相当,但本文方法的鲁棒性较强且拟合精度更高。
4 结论本文提出了一种鲁棒性较强的空间圆弧拟合方法。首先,在拉格朗日乘子法的基础上,建立平面条件约束目标函数,从而推导出空间圆弧拟合方程;其次,由于RANSAC算法稳定性高且具有剔除错误点的功能,本文将它应用到空间圆拟合的点云筛选及优化中,从而提高拟合精度。实验结果表明:普通圆弧点云拟合的相对精度在0.003左右,复杂圆弧点云拟合的相对精度在0.01左右,该空间圆弧拟合优化方法有较强的理论研究意义和工程实践价值。
| [1] |
田艳荣.精密回转型工件的偏心倾斜调整测控技术[D].北京: 北京理工大学光电学院, 2016: 1-30.
TIAN Yan-rong. Measurement and control technology of eccentric tilt adjustment for precision rotary workpieces[D]. Beijing: Beijing Institute of Technology, School of Optics and Photonics, 2016: 1-30. http://cdmd.cnki.com.cn/Article/CDMD-10007-1016716562.htm |
| [2] |
赵阳.高显现力三目视觉测量关键技术[D].天津: 天津大学精密仪器与光电子工程学院, 2011: 15-50.
ZHAO Yang. Key technologies for high-visualization trinocular vision measurement[D].Tianjin: Tianjin University, College of Precision Instruments and Photoelectronics Engineering, 2011: 15-50. http://cdmd.cnki.com.cn/Article/CDMD-10056-1012007442.htm |
| [3] |
丁晓晖.圆柱轮廓精密测量中的滤波与调心调倾技术研究[D].哈尔滨: 哈尔滨工业大学电气工程及自动化学院, 2010: 38-60.
DING Xiao-hui. Research on filtering and centering tilting technology in precision measurement of cylindrical profile[D]. Harbin: Harbin Institute of Technology, School of Electrical Engineering and Automation, 2010: 38-60. http://cdmd.cnki.com.cn/Article/CDMD-10213-1011259668.htm |
| [4] |
杨伟, 陈家新, 李济顺.
基于投影的二阶段空间圆线拟合算法[J]. 工程设计学报, 2009, 16(2): 117–121.
YANG Wei, CHEN Jia-xin, LI Ji-shun. Projection-based two-stage space circular line fitting algorithm[J]. Chinese Journal of Engineering Design, 2009, 16(2): 117–121. |
| [5] |
邹进贵, 陈健.
基于空间向量的空间圆拟合算法研究及其应用[J]. 测绘地理信息, 2013, 37(6): 3–5.
ZOU Jin-gui, CHEN Jian. Research and application of the arithmetic based on space vectorin 3D circle fitting[J]. Journal of Geomatics, 2013, 37(6): 3–5. |
| [6] |
张晶, 黄琴, 兰红军, 等.
工程测量中空间圆的拟合方法研究[J]. 计量与测试技术, 2011, 38(9): 31–32.
ZHANG Jing, HUANG Qin, LAN Hong-jun, et al. Fitting method of 3D circular object in engineering surveying[J]. Metrology and Measurement Technique, 2011, 38(9): 31–32. DOI:10.3969/j.issn.1004-6941.2011.09.015 |
| [7] |
潘国荣, 陈晓龙.
空间圆形物体数据拟合新方法[J]. 大地测量与地球动力学, 2008, 28(2): 92–94.
PAN Guo-rong, CHEN Xiao-long. A new method for 3D circular object fitting[J]. Journal of Geodesy and Geodynamics, 2008, 28(2): 92–94. |
| [8] | AHN Sung Joon, RAUH Wolfgang, WARNECKE Hans-Jürgen. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola[J]. Pattern Recognition, 2001, 34(12): 2283–2303. DOI:10.1016/S0031-3203(00)00152-7 |
| [9] |
田猛, 王先培, 董政呈, 等.
基于拉格朗日乘子法的虚假数据攻击策略[J]. 电力系统自动化, 2017, 41(11): 26–32.
TIAN Meng, WANG Xian-pei, DONG Zheng-cheng, et al. Fake data attack strategy based on Lagrangian multiplier method[J]. Automation of Electric Power Systems, 2017, 41(11): 26–32. DOI:10.7500/AEPS20161225004 |
| [10] |
郭志军.
拉格朗日乘子法在有约束条件的最优化问题研究[J]. 邢台学院学报, 2013, 28(4): 170–171.
GUO Zhi-jun. Study on the optimization problem of Lagrange multiplier method with constraints[J]. Journal of Xingtai University, 2013, 28(4): 170–171. |
| [11] |
陈敬华.
拉格朗日乘子法及其推广[J]. 湖北师范学院学报(自然科学版), 2010, 30(4): 108–111.
CHEN Jing-hua. Lagrange multiplier method and its extension[J]. Journal of Hubei Normal University (Natural Science Edition), 2010, 30(4): 108–111. DOI:10.3969/j.issn.1009-2714.2010.04.029 |
| [12] |
华东师范大学数学系.
数学分析[M]. 北京: 高等教育出版社, 2010: 70-80.
Department of Mathematics, East China Normal University. Mathematical analysis[M]. Beijing: Higher Education Press, 2010: 70-80. |
| [13] |
曲天伟, 安波, 陈桂兰.
改进的RANSAC算法在图像配准中的应用[J]. 计算机应用, 2010, 30(7): 1849–1851.
QU Tian-wei, AN Bo, CHEN Gui-lan. Application of improved RANSAC algorithm in image registration[J]. Journal of Computer Applications, 2010, 30(7): 1849–1851. |
| [14] |
许烨璋, 王鑫森, 郑德华, 等.
一种改进的RANSAC算法提取多模型圆弧特征点云[J]. 测绘工程, 2015, 24(1): 28–32.
XU Ye-zhang, WANG Xin-sen, ZHENG De-hua, et al. An improved RANSAC algorithm for extracting multi-model arc feature point cloud[J]. Geographic Engineering, 2015, 24(1): 28–32. DOI:10.3969/j.issn.1006-7949.2015.01.006 |
| [15] |
赵烨, 蒋建国, 洪日昌.
基于RANSAC的SIFT匹配优化[J]. 光电工程, 2014, 41(8): 58–65.
ZHAO Ye, JIANG Jian-guo, HONG Ri-chang. SIFT matching optimization based on RANSAC[J]. Opto-Electronic Engineering, 2014, 41(8): 58–65. DOI:10.3969/j.issn.1003-501X.2014.08.010 |
| [16] |
甄艳, 刘学军, 王美珍.
一种改进RANSAC的基础矩阵估计方法[J]. 测绘通报, 2014(4): 39–43.
ZHEN Yan, LIU Xue-jun, WANG Mei-zhen. An improved RANSAC based fundamental matrix estimation method[J]. Bulletin of Surveying and Mapping, 2014(4): 39–43. |
| [17] |
李宝, 程志全, 党岗, 等.
一种基于RANSAC的点云特征线提取算法[J]. 计算机工程与科学, 2013, 35(2): 147–153.
LI Bao, CHENG Zhi-quan, DANG Gang, et al. An algorithm of point cloud feature extraction based on RANSAC[J]. Computer Engineering & Science, 2013, 35(2): 147–153. DOI:10.3969/j.issn.1007-130X.2013.02.026 |
| [18] | FISCHLER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Readings in Computer Vision, 1981, 24(6): 381–395. |



