2. 长江勘测规划设计研究院, 湖北 武汉 430010
2. Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430010, China
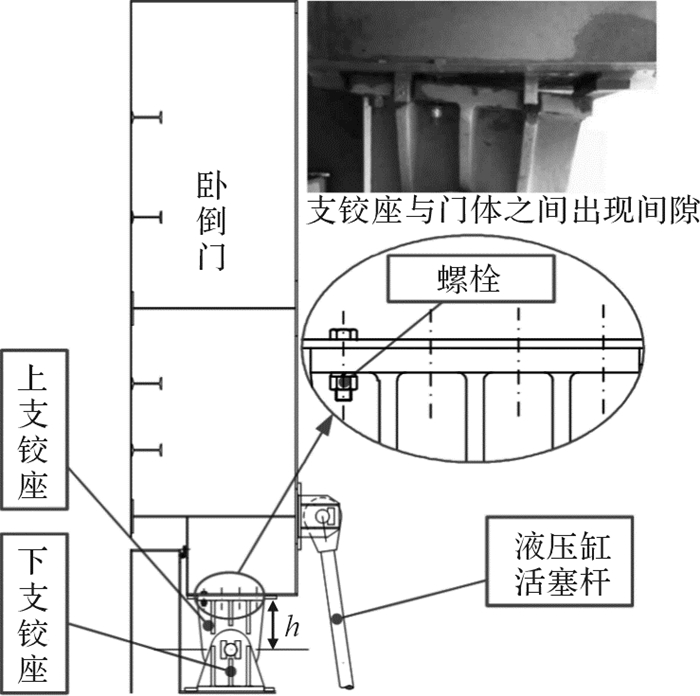
三峡升船机下闸首卧倒门支铰座采用A2-70-M36螺栓,预紧力矩为1 233 N·m,它在试运行过程中曾发生断裂故障,左侧上支铰座的8根螺栓断了7根,右侧上支铰座的8根螺栓断裂了3根。所有螺栓断裂部位均发生在螺栓头部(螺帽与光杆的结合部位),部分螺栓断口呈现典型的疲劳断口宏观形貌特征,部分螺栓断口呈现颈缩特征,支铰座与门体之间出现间隙, 如图 1所示。
|
| 图 1 三峡升船机卧倒门支铰座螺栓联结示意图 Fig.1 Sketch map of joint bolts of support pivots of tumble gate of ship lift in the Three Gorges |
目前国内学者对卧倒门的研究主要是采用数值模拟方法来分析卧倒门的结构强度和进行相关的优化设计。文献[1-3]利用有限元软件建立卧倒门仿真模型,并计算了其结构强度,但是针对卧倒门载荷只考虑了卧倒门的重力和静水压力。文献[4]对气控式卧倒门在静水压力作用下处于最不利水位时的结构强度进行分析,卧倒门载荷考虑了重力、静水压力和固定浮力舱的浮力。文献[5-6]研究了卧倒门运动时所受的动水阻力对卧倒门结构强度的影响,但忽略了卧倒门运动水位差造成的壅水阻力。文献[7]考虑了壅水阻力,并研究了卧倒闸门运行方式对水体阻力、液压缸启闭力以及闸门支铰反力等的影响,但未得到明确的壅水阻力数值。
本文通过分析卧倒门的4种工况(无水关门、无水开门、有水关门和有水开门),来得出实际工况下的壅水高和水位降;同时考虑液压缸启闭力、重力、浮力、风阻力、支铰反力、动水阻力和壅水阻力等7种载荷,计算出卧倒门支铰座螺栓所受载荷,并对支铰座螺栓联结进行强度设计,以期为三峡升船机下闸首卧倒门安全运行提供技术依据。
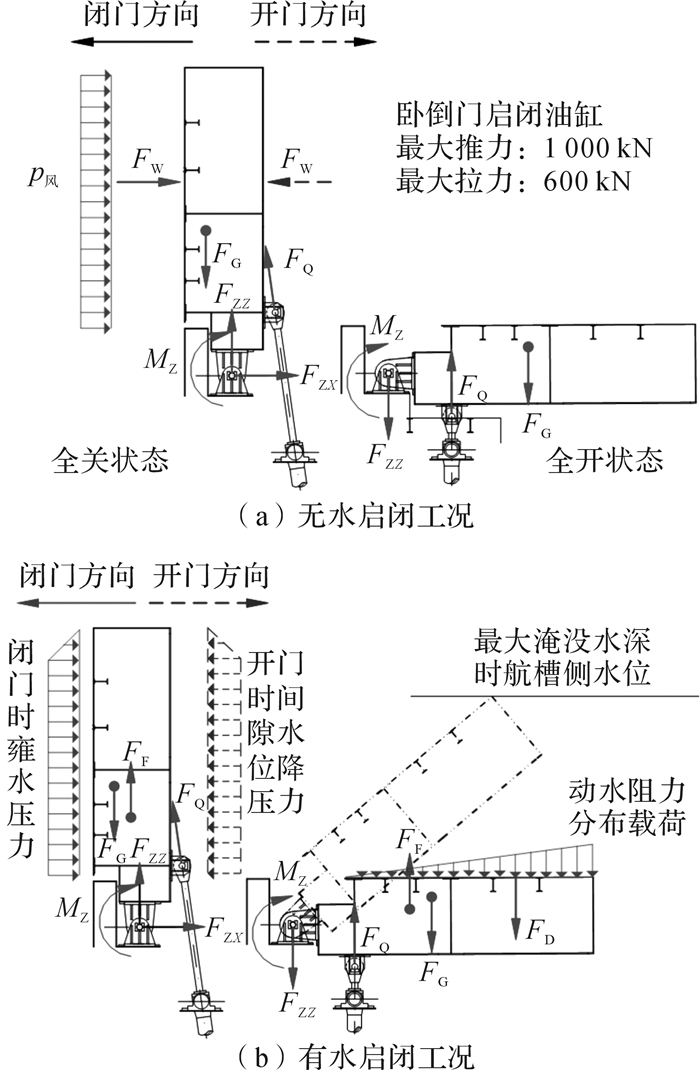
1 卧倒门液压缸启闭力分析 1.1 卧倒门受力分析与运行工况图 2为卧倒门在不同运行工况下的受力分析示意图,其中:FQ、FG、FF、FW、FZZ、FZX、FD和FY分别为液压缸启闭力、重力、浮力、风阻力、支铰座铅垂方向力、支铰座水平方向力、动水阻力和壅水阻力;FX和FZ为任意力F沿水流方向(垂直门体)和铅垂方向分力;MQ、MG、MF、MW、MZ、MD和MY分别代表各力对应的力矩。临近关门终了时(开度θ=84°)重力矩方向发生变化。无水工况下不考虑浮力、动水阻力和壅水阻力,有水工况下忽略风阻力。
|
| 图 2 不同运行工况下卧倒门受力分析示意图 Fig.2 Sketch map of force analysis of tumble gate under different working conditions |
卧倒门为实腹式双主梁对称结构。闸门运行转速相对较低(卧倒门启闭时间为90 s),可将它近似为一刚体平面运动系统[7],根据M动力=M阻力,该系统平衡方程为:
| $ {M_{\rm{Q}}} + {M_{\rm{G}}} + {M_{\rm{F}}} + {M_{\rm{W}}} + {M_{\rm{Z}}} + {M_{\rm{D}}} + {M_{\rm{Y}}} = 0 $ | (1) |
| $ {F_{{\rm{Q}}Z}} + {F_{\rm{G}}} + {F_{\rm{F}}} + {F_{{\rm{Z}}Z}} + {F_{{\rm{D}}Z}} + {F_{{\rm{Y}}Z}} = 0 $ | (2) |
| $ {F_{{\rm{Q}}X}} + {F_W} + {F_{{\rm{Z}}X}} + {F_{{\rm{D}}X}} + {F_{{\rm{Y}}X}} = 0 $ | (3) |
式中:液压缸启闭力矩MQ=FQ×l1,l1为液压缸启闭力臂;重力矩MG=FG×l2,l2为门重力臂;浮力矩MF=FF×l4,l4为浮力臂;风阻力矩MW=FW×l3,l3为风载荷力臂;支铰座摩阻力矩
在闸门的开度范围(90°)内,每10°取一状态点,分别计算4种工况下单支液压缸启闭力:1)无水关门,闸门由全开至全关;2)无水开门,闸门由全关至全开;3)有水关门,闸门由全开至全关;4)有水开门,闸门由全关至全开。
1.2 卧倒门液压缸启闭力额定值卧倒门液压缸额定启闭力为:推力, 2×1 000 kN; 拉力,2×600 kN。在实际运行过程中,液压缸无杆腔输出的最大推力约为1 100 kN,有杆腔输出的最大拉力约为660 kN,同时启闭机液压系统设有安全阀,启闭机的输出力理论上不超过额定启闭力。本文以1 100 kN推力、660 kN拉力作为启闭机启闭力的控制条件。
1.3 实际运行工况下卧倒门液压缸启闭力 1.3.1 无水关门工况无水关门工况下卧倒门的力矩平衡方程为:
| $ {F_{\rm{Q}}} \times {l_1} + {F_{\rm{G}}} \times {l_2} + {F_{\rm{W}}} \times {l_3} + {M_{\rm{Z}}} = 0 $ | (4) |
由公式(4)可得卧倒门液压缸启闭力FQ,其中风阻力FW简化为集中载荷,水平作用于门体,风压方向分顺风和逆风两种情况。无水关门工况下卧倒门液压缸的启闭力如表 1所示, 其中:FQ为正表示输出推力,FQ为负表示输出拉力。
| 开度/(°) | MG | MW | MZ/(kN·m) | MQ | |||||
| FG/kN | l2/m | FW/kN | l3/m | FQ/kN | l1/m | ||||
| 逆风 | 顺风 | ||||||||
| 0 | 577 | 3.90 | 0 | 0 | 12.5 | 707.1 | 707.1 | 1.60 | |
| 10 | 577 | 3.76 | 12.5 | 1.87 | 12.5 | 589.7 | 577.2 | 1.87 | |
| 20 | 577 | 3.50 | 24.3 | 2.50 | 12.5 | 539.4 | 508.1 | 1.94 | |
| 30 | 577 | 3.13 | 35.0 | 3.07 | 12.5 | 498.9 | 443.3 | 1.93 | |
| 40 | 577 | 2.67 | 44.2 | 3.57 | 12.5 | 455.0 | 371.1 | 1.88 | |
| 50 | 577 | 2.13 | 51.9 | 3.98 | 12.5 | 402.1 | 287.6 | 1.80 | |
| 60 | 577 | 1.53 | 57.5 | 4.28 | 12.5 | 335.6 | 191.1 | 1.70 | |
| 70 | 577 | 0.87 | 61.1 | 4.47 | 12.5 | 247.7 | 75.9 | 1.59 | |
| 80 | 577 | 0.19 | 62.5 | 4.55 | 12.5 | 139.1 | -55.5 | 1.46 | |
| 90 | 577 | -0.49 | 61.7 | 4.50 | 12.5 | 2.8 | -209.1 | 1.31 | |
由表 1可知,无水关门工况下单缸启闭机最大推力为707.1 kN,出现在无水关门初始时;最大拉力为209.1 kN,出现在顺风无水关门终了时。
1.3.2 无水开门工况无水开门过程与无水关门过程中卧倒门受到载荷基本相同,其力矩平衡方程亦为式(4)所示。同样考虑2种风压情况。由于篇幅限制,不再详细列出。无水开门工况下单缸启闭机最大推力699.3 kN,出现在无水开门终了时;最大拉力为218.7 kN,出现在逆风无水开门初始时。
1.3.3 有水关门工况有水工况下卧倒门液压缸启闭力的计算是卧倒门处于最大淹没水深时进行的。此工况下卧倒门的力矩平衡方程为:
| $ {F_{\rm{Q}}} \times {l_1} + {M_{\rm{G}}} + {F_{\rm{F}}} \times {l_4} + {M_{\rm{D}}} + {M_{\rm{Z}}} + {M_{\rm{Y}}} = 0 $ | (5) |
忽略闸门门顶出水后动水阻力和浮力的变化。待门顶出水后,考虑壅水阻力,初出水面时壅水高度按壅水与实际门顶齐平计算。通过现场观察,卧倒门启闭时,雍水高不超过0.8 m。雍水载荷作用在闸门面板上,顶部为三角形水体,下部为矩形水体。临近全关状态时,最大壅水高分别按照0.8,0.7,0.5 m进行试算。由公式(5)可得FQ=-(MG+FF×l4+MD+MZ+FY三角形×l6+FY矩形×l′6)/l1,表 2为有水关门工况下卧倒门液压缸的启闭力(卧倒门在不同工况、相同开度时重力臂和液压启闭力臂不变,同表 1)。由表 2可以看出,封闭腔的浮力与卧倒门自重基本抵消,对液压缸单缸启闭力影响最大的是卧倒门在全关位附近作用于门叶的水压,即壅水高。
| 开度/(°) | MG/ kN·m |
MD/ kN·m |
MZ/ kN·m |
MF | MY | 单缸启闭力 FQ/kN |
壅水高/m | |||||
| FF/kN | l4/m | FY三角形/kN | l6/m | FY矩形/kN | l′6/m | |||||||
| 0 | 2 250.3 | 3.1 | 12.5 | 523 | 2.98 | 221.1 | ||||||
| 20 | 2 019.5 | 3.1 | 12.5 | 523 | 2.73 | 156.5 | ||||||
| 40 | 1 540.6 | 3.1 | 12.5 | 523 | 2.15 | 114.8 | ||||||
| 60 | 882.8 | 3.1 | 12.5 | 523 | 1.32 | 31.0 | 6.97 | 598.0 | 3.95 | 820.0 | 0.585 | |
| 80 | 109.6 | 3.1 | 12.5 | 523 | 0.32 | 58.0 | 7.04 | 817.8 | 3.95 | 1 232.5 | 0.8 | |
| 80 | 109.6 | 3.1 | 12.5 | 523 | 0.32 | 44.4 | 7.00 | 715.5 | 3.95 | 1 060.8 | 0.7 | |
| 80 | 109.6 | 3.1 | 12.5 | 523 | 0.32 | 22.7 | 6.94 | 511.1 | 3.95 | 731.3 | 0.5 | |
| 90 | -282.7 | 3.1 | 12.5 | 523 | -0.20 | 58.0 | 7.04 | 817.8 | 3.95 | 1 327.7 | 0.8 | |
| 90 | -282.7 | 3.1 | 12.5 | 523 | -0.20 | 44.4 | 7.00 | 715.5 | 3.95 | 1 136.4 | 0.7 | |
| 90 | -282.7 | 3.1 | 12.5 | 523 | -0.20 | 22.7 | 6.94 | 511.1 | 3.95 | 769.1 | 0.5 | |
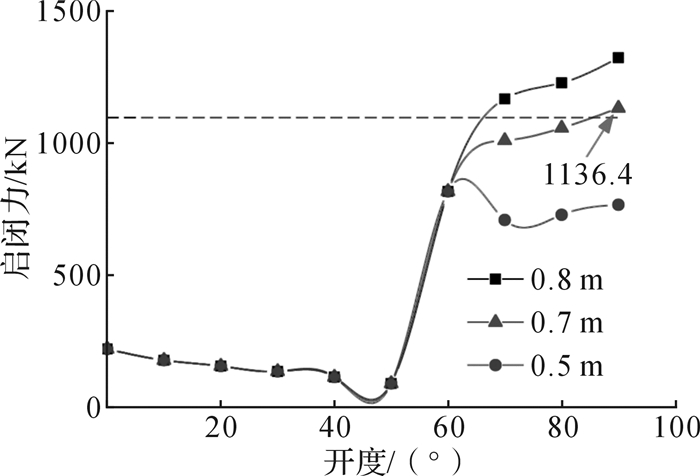
图 3为不同壅水高时有水关门工况下卧倒门液压缸启闭力变化曲线。由图 3可知,在有水关门过程中,液压缸仅输出推力,最大推力出现在关门终了时,壅水高为0.8,0.7,0.5 m时对应的液压缸最大推力分别为1 327.7,1 136.4,769.1 kN。在实际运行过程中,闸门每次启闭时启闭机均未超载,在壅水高为0.7 m时,液压缸的最大推力已超过1 100 kN,可以认为,实际启闭过程中壅水高不超过0.7m。
|
| 图 3 不同壅水高时有水关门工况下卧倒门液压缸启闭力变化曲线 Fig.3 Change curves of hoisting force of tumble gate hydraulic cylinder with different backwater height under the condition of gate closing with water |
有水开门与有水关门工况下卧倒门受到的载荷基本相同,因此有水开门工况下卧倒门的力矩平衡方程亦为式(5)所示。开门初始时分别按最大水位降为0.8,0.5,0.3 m进行试算。因篇幅限制,亦不再详细列出。
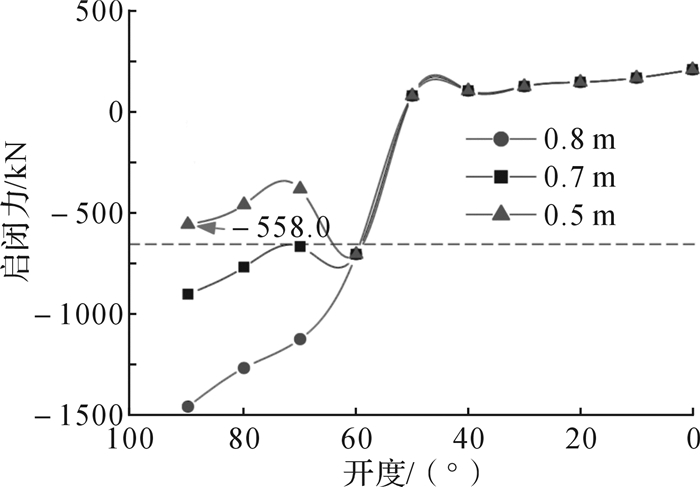
图 4为不同水位降时有水开门工况下卧倒门液压缸启闭力变化曲线。从图中可以看出,在有水开门过程中,液压缸在开门初期闸门门顶未入水前(90°~50°开度范围内)其启闭力为拉力,最大拉力出现在开门初始,水位降为0.8,0.5,0.3 m时对应的最大拉力分别为:1 463.7,905.1,558.0 kN;液压缸在门顶入水后开始输出推力,最大推力出现在开门终了时,为211.3 kN。在实际运行过程中,闸门每次启闭时启闭机均未超载,在水位降为0.3 m情况下,液压缸的最大拉力已接近660 kN,可以认为,实际启闭过程中水位降不超过0.3 m。
|
| 图 4 不同水位降时有水开门工况下卧倒门液压缸启闭力变化曲线 Fig.4 Change curves of hoisting force of tumble gate hydraulic cylinder with different water level drop under the condition of gate closing with water |
在卧倒门最大淹没水深时,以启闭过程壅水高为0.7 m、水位降为0.3 m作为计算条件。根据静力平衡方程,分别计算4种工况下卧倒门支铰座载荷,结果如表 3所示。翻转力矩MFZ=FZh,其中h为螺栓群所在平面到卧倒门支铰座联结轴轴心距离,h=650 mm。在有水关门终了时,卧倒门支铰座出现最大轴力,为1 098.3 kN(受拉),且随着壅水高降低支铰座载荷也减小;在无水开门初始时,卧倒门支铰座联结面出现最大翻转力矩,为200.3 kN·m。
| 工况 | FZZ1)/kN | FZX2)/kN |
| 无水关门初始 | 418.6 | 0 |
| 无水关门终了 | -495.6 | -306.8(顺风) |
| 无水开门初始 | -505.1 | -308.1(逆风) |
| 无水开门终了 | 410.8 | 0 |
| 有水关门初始 | 194.4 | 0 |
| 有水关门终了 | 1098.3 | -222.0 |
| 有水开门初始 | -579.6 | -80.0 |
| 有水开门终了 | 184.6 | 0 |
| 注:1)FZZ为正代表支铰座受拉,为负代表受压; 2)FZX为正代表水平方向力指向上游,为负代表指向下游。 |
||
螺栓紧联结或采用了顶紧块(抗剪板)的松螺栓组联结[9-10],支铰座的联结螺栓组既承受轴向载荷FZZ,又承受翻转力矩MFZ,离中和轴距离最远的螺栓所受最大拉力为:
| $ {F_{\max }} = {F_1} + {F_2} = \frac{{{F_{{\rm{Z}}Z}}}}{n} + \frac{{{M_{{\rm{FZ}}}} \cdot {y_{\max }}}}{{\sum\limits_{i = 1}^n {y_i^2} }} $ | (6) |
式中:n为支铰座联结螺栓数量;yi(i=1, 2, …, n)为计算螺栓到中和轴的距离,ymax为螺栓到中和轴的最远距离。
不同工况下单个螺栓受到最大工作载荷如表 4所示。由式(6)可知降低雍水高能够减小螺栓的最大工作载荷。出于安全考虑,卧倒门上支铰座联结螺栓的最大工作载荷选用243.0 kN。
| 工况 | Fmax/kN | |
| 紧联结 | 松联结 | |
| 无水开门初始 | 209.9 | 168.4 |
| 有水关门终了 | 243.0 | 213.1 |
考虑到工作载荷不稳定,取残余预紧力系数K1=0.6[9],根据所需残余预紧力F′P=K1Fmax,得F′P=145.8 kN。取螺栓联结相对刚度λ=0.2[9],根据FP=F′P+(1-λ)Fmax,得所需预紧力为340.2 kN。由F0=F′P+Fmax,得单个螺栓总载荷为388.8 kN。
在施工安装过程中,闸首卧倒门支铰座螺栓联结采用A2-70-M36螺栓,预紧力矩为1 233 N·m[11]。根据T=K2FPd,取K2=0.2,则预紧力为171.25 kN。显然,该预紧力小于实际计算所需的预紧力,不能满足要求,这也是卧倒门支铰座螺栓联结松动的原因之一。
为此,采用预紧力矩T=2 400 N·m进行计算,可得预紧力为333.3 kN。此时,根据F0=FP+0.2×Fmax得到实际单个螺栓总载荷F0=381.9 kN,可以达到螺栓联结的预紧要求。由
如果选用8.8级螺栓(屈服强度为640 MPa,抗拉强度为800 MPa),考虑到拧紧力矩控制预紧力的±25%的偏差,螺栓受到的实际应力可能达到640 MPa,超过螺栓的屈服强度。为此,选用10.9级M36高强度螺栓(屈服强度达900 MPa,抗拉强度达1 000 MPa),能满足强度要求。
将三峡升船机下闸首卧倒门支铰座联结螺栓更换为10.9级M36高强度螺栓,预紧力矩设为2 400 N·m,维修后的卧倒门运行良好。
4 结论1) 原卧倒门支铰座螺栓联结的预紧力矩过小、A2-70-M36螺栓强度不够,是造成联结松动、螺栓断裂的主要原因。
2) 采用有水关门工况下壅水高为0.7 m、有水开门工况下水位降为0.3 m来计算液压启闭机油缸的作用力,并验证支铰座联结螺栓最大工作载荷的计算方法是合理的。
3) 关门终了时雍水高对螺栓的最大工作载荷影响较大,在运行过程需控制卧倒门运行速度以降低雍水高,从而保证卧倒门安全运行。
4) 在不对支铰座结构进行修改的情况下采用10.9级M36高强度螺栓并施加2 400 N·m预紧力矩,可以使支铰座结构强度满足要求。
| [1] |
赵铁柱, 石端伟.
基于ANSYS Workbench的升船机承船厢卧倒门优化设计[J]. 武汉大学学报(工学版), 2014, 47(3): 378–382.
ZHAO Tie-zhu, SHI Duan-wei. Optimum design of horizontal type gate of shiplift chamber based on ANSYS Workbench[J]. Engineering Journal of Wuhan University, 2014, 47(3): 378–382. |
| [2] |
仇强.撑卧式平板钢闸门静动力特性研究与优化设计[D].山东: 山东农业大学水利土木工程学院, 2009: 9-12.
QIU Qiang. Research and optimal design on static and dynamic property of support-horizontal plane steel gate[D]. Shandong: Shandong Agricultural University, College of Water Conservancy and Civil Engineering, 2009: 9-12. http://cdmd.cnki.com.cn/Article/CDMD-10434-2009234518.htm |
| [3] |
田永军.
大跨度液压下翻转式卧倒门三维结构分析[J]. 山西建筑, 2014, 40(21): 242–243.
TIAN Yong-jun. Three-dimensional structuralanalysis in large-span downflap hydraulic gate[J]. Shanxi Architecture, 2014, 40(21): 242–243. |
| [4] |
张丽.船坞气控式卧倒门结构的有限元分析[D].天津: 天津大学建筑工程学院, 2010: 7-9.
ZHANG Li. The finite element analysis of the pneumatic control dockgate[D]. Tianjin: Tianjin University, School of Civil Engineering, 2010: 7-9. http://cdmd.cnki.com.cn/Article/CDMD-10056-1011267506.htm |
| [5] |
张久锋, 沈丽民.
基于ADAMS的干船坞气控卧倒门的建模和仿真[J]. 机械工程师, 2012(1): 50–52.
ZHANG Jiu-feng, SHEN Li-min. Kinematics modeling and simulation of dry dock gate based on ADAMS[J]. Mechanical Engineer, 2012(1): 50–52. DOI:10.3969/j.issn.1002-2333.2012.01.019 |
| [6] |
习和忠, 习文.
干船坞卧倒门的舱格设计计算[J]. 港工技术, 1998(3): 10–17.
XI He-zhong, XI Wen. The calculation for the design of flap gate of dry dock[J]. Port Engineering Technology, 1998(3): 10–17. |
| [7] |
周赤, 刘敦煌, 杨淳.
三峡升船机卧倒门水动力特性试验研究[J]. 长江科学院院报, 1996, 13(4): 1–5.
ZHOU Chi, LIU Dun-huang, YANG Chun. Studies on hydrodynamical character of horizontal type gate of Three Gorges Project's ship lift[J]. Journal of Yangtze River Scientific Research Institute, 1996, 13(4): 1–5. |
| [8] |
中交第一航务工程勘察设计院, 中交第二航务工程勘察设计院.港口工程荷载规范: JTS 144-1-2010[S].北京: 人民交通出版社, 2010: 34-35.
CCCC First Harbor Consultants Co., Ltd., CCCC Second Harbor Consultants Co., Ltd.. Load code for port engineering: JTS 144-1-2010[S]. Beijing: China Communications Press, 2010: 34-35. |
| [9] |
闻邦椿.
机械设计手册:第2卷[M]. 5版. 北京: 机械工业出版社, 2010: (5-31)-(5-36).
WEN Bang-chun. Mechanical design handbook:Vol 2[M]. 5th ed. Beijing: Machinery Industry Press, 2010: (5-31)-(5-36). |
| [10] |
刘声扬, 王汝恒.
钢结构-原理与设计[M]. 武汉: 武汉理工大学出版社, 2010: 93-95.
LIU Sheng-yang, WANG Ru-heng. Steel structure-principles and design[M]. Beijing: Wuhan University of Technology Press, 2010: 93-95. |
| [11] |
国家机械工业局.重型机械通用技术条件装配: JB/T5000.10-2007[S].北京: 机械工业出版社, 2007: 11.
State Bureau of Machine-Building Industry. The heavy mechanical general techniques and standards assembly: JB/T5000.10-2007[S]. Beijing: Machinery Industry Press, 2007: 11. |



