2. 上海工程技术大学 智能机器人研发中心, 上海 201620
2. Intelligent Robot Research and Development Center, Shanghai University of Engineering Science, Shanghai 201620, China
预应力钢筒混凝土管以其高密封性、高强度和高抗渗的特性,在水利工程、工业供水等领域得到广泛应用[1]。为了满足后续喷涂防腐材料的要求以及保证管道承、插口的尺寸精度[2],改善传统打磨方法存在的效率低、打磨质量难以保证等问题,需要设计一种打磨精度高、效率高的机器人化装备来提高预应力钢筒混凝土管端口打磨的质量与效率以及降低工人劳动强度[3]。
目前,国内外针对PCCP的打磨方法主要有2种:大型起重机辅助打磨和管内移动机器人打磨。前者是采用大型门式起重机配合承、插口打磨机构到指定打磨位置对PCCP端口进行打磨[4],该方法所需设备体型大,不满足在施工现场易携带、占地少的使用要求,而且端口表面清理不彻底,还需要用砂轮手工打磨;后者是利用基于不同驱动方式设计的一类管内爬行移动机器人来实现管道端口的打磨和检测[5],但该方法要求机器人系统有一定的刚度和运动精度,且易造成非加工区钢板的磨损和破坏。
文献[6-9]针对几种较大口径管道的打磨机器人进行了结构设计,实现利用行走机构完成管道内部的打磨工作;文献[10-11]提出了适用于小口径管道工作的小型机器人,它可携带特殊设备,完成对小口径管道内部的打磨、检测等工作;文献[12-14]分别针对V形刚构桥、扭杆结构和直线导轨建立了可靠性设计模型并进行了动态可靠性分析;文献[15-17]利用随机摄动方法完成了对机械零部件或机构的可靠度和灵敏度分析,为机械构件的设计奠定了基础。但很少有采用随机摄动方法对打磨机器人进行可靠性分析的研究。
本文通过对打磨任务的分析,创新设计了一种针对PCCP承、插口两端口打磨的机器人自动化装备。首先,对该端口打磨机器人进行了结构设计,并根据打磨机器人克服摩擦力环绕承、插口钢圈作周向转动以完成打磨工作的特点,利用现场试验分析它在转动过程中产生的打滑失效现象。为了保证打磨机器人能够高效可靠地完成绕端口的转动打磨工作,建立打磨机器人压紧力模型及其可靠度模型,采用随机摄动方法讨论其可靠性问题,分析该端口打磨机器人的动态可靠度,并找出影响打磨机器人可靠性灵敏度的因素,为下一步的结构优化设计及提高其工作可靠性作准备。
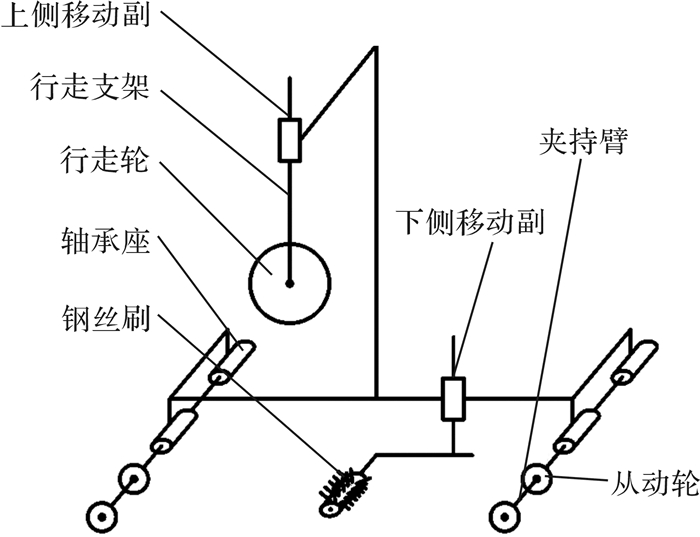
1 预应力钢筒混凝土管端口打磨机器人结构设计根据对PCCP端口打磨的功能需求分析,该类打磨装备需要实现绕端口的自行式转动[6],同时自主完成打磨工作,且还应满足管道及现场施工参数的要求。图 1所示为PCCP插口打磨机器人结构示意图。首先,通过调节上侧移动副使行走轮配合夹持支架的2个夹持臂夹紧管壁,然后,通过调整下侧移动副使得钢丝刷与管道打磨面保持正常的打磨距离,最后,由电机分别驱动行走轮绕管道行进配合钢丝刷对插口端进行打磨。
|
| 图 1 预应力钢筒混凝土管插口打磨机器人结构示意图 Fig.1 Structure diagram of PCCP spigot grinding robot |
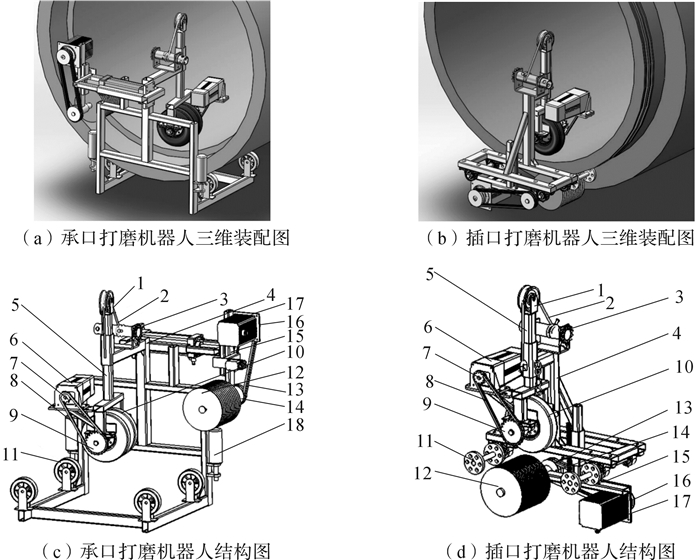
如图 2所示,针对PCCP承、插口两端结构特点,基于所需自动化装备的功能分析和构型设计,分别设计了应用于PCCP承口和插口的边绕管口旋转边完成打磨工作的自行走式高效端口打磨机器人装备[7]。PCCP承口和插口打磨机器人装备都由压紧机构、支撑机构和打磨机构三部分组成,其中:压紧机构主要由压紧架、主动轮及驱动电机组成;打磨机构由打磨架、钢丝刷和伺服电机组成;承口端打磨机器人支撑机构主要由支撑架、从动轮、限制轮和拉紧器组成,插口端打磨机器人支撑机构主要由支撑架、从动轮和拉紧器组成。该端口打磨机器人需要满足的工作参数如表 1所示。
|
| 1—滑轮;2—钢丝绳;3—拉紧器;4—支撑架;5—压紧架;6—驱动电机;7—小链轮;8—链条;9—大链轮;10—主动轮;11—从动轮;12—钢丝刷;13—V型带;14—小带轮;15—打磨架;16—大带轮;17—伺服电机;18—限制轮 图 2 预应力钢筒混凝土管端口打磨机器人三维装配图及结构组成 Fig.2 3D assembly diagram and structure composition of PCCP port grinding robot |
| 参数 | 数值 |
| 打磨管道直径/m | 1.4~4 |
| 质量/kg | ≤50 |
| 整体离地高度/mm | ≤300 |
| 每根管打磨时间/min | ≤10 |
本文设计的机器人化端口打磨装备具有易便携、体积小、自动化程度高、适应多种管径的特点[8]。该装备通过机械式夹紧方式使整机沿端口作周向转动,需要具有一定的预紧力。为了验证该打磨机器人的工作可靠性,制作了一台样机并进行现场试验。在施加预紧力的作用下,配合主动轮和从动轮将打磨机器人固定在管道上[9-10],开启驱动电机和伺服电机进行打磨试验[8, 11]。
如图 3所示,经过多次试验发现,该打磨机器人从端口最低点出发,在沿端口周向转动进行打磨的过程中会发生打滑失效,尤其在π~

|
| 图 3 预应力钢筒混凝土管端口打磨机器人试验现场图 Fig.3 Test site diagram of PCCP port grinding robot |
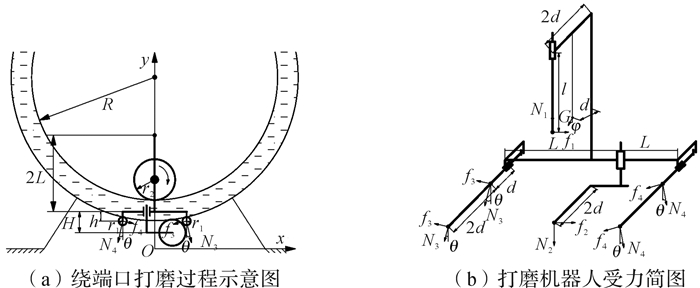
因承、插口打磨机器人具有相同的工作原理和受力特点,本文仅对插口打磨机器人进行受力分析和可靠性分析。插口打磨机器人绕端口的周向转动可以近似为匀速圆周运动,且由于行进速度较慢,忽略向心加速度。如图 4所示为插口打磨机器人绕端口打磨过程中的受力情况。
|
| 图 4 打磨过程中插口打磨机器人受力分析 Fig.4 Force analysis of spigot grinding robot in the process of grinding |
图 4中插口打磨机器人尺寸参数:l=0.3 m,L=0.3 m,h=0.03 m,H=0.12 m,d=0.138 m。根据图 4所示受力关系得出打磨机器人的空间力系平衡方程:
| $ \left\{ \begin{array}{l} {F_{\rm{N}}} = {N_1} - G\cos \varphi \\ {N_1} = G\cos \varphi + {N_2} + 2\left( {{N_3} + {N_4}} \right)\cos \theta + 2\left( {{f_4} - {f_3}} \right)\sin \theta \\ {f_1} + {f_2} = G\sin \varphi + 2\left( {{f_3} + {f_4}} \right)\cos \theta + 2\left( {{N_3} - {N_4}} \right)\sin \theta \\ {\delta _1}{f_2} = 2\left( {{N_4} - {N_3}} \right)\left[ {\left( {R + {r_1}} \right)\cos \theta - {\delta _2}} \right]\sin \theta + 2\left( {{f_3} - {f_4}} \right)\left\{ {R - \left[ {\left( {R + {r_1}} \right)\cos \theta - {\delta _2}} \right]} \right\}\cos \theta \\ - T\\ \left( {{N_2} - {N_1}} \right)d = 2\left( {{N_3} + {N_4}d\cos \theta } \right) + 2\left( {{f_4} - {f_3}} \right)d\sin \theta \\ \left( {{f_1} + {f_2}} \right)d = 2\left( {{N_4} - {N_3}} \right)d\sin \theta - 2\left( {{f_3} + {f_4}} \right)d\cos \theta \end{array} \right. $ | (1) |
其中:
| $ \begin{array}{l} G = {G_1} + {G_2},\theta = \arcsin \frac{{0.3}}{{2 + {r_1}}},{\delta _1} = 2L - l + H = \\ 0.42\;{\rm{m}},{\delta _2} = 2L - l + h = 0.33\;{\rm{m}} \end{array} $ |
| $ \begin{array}{l} {f_i} = \mu {N_i} = 0.2{N_i}\left( {i = 3,4} \right),T = 34.38{r_2}P,\\ {f_2} = 9\;550\frac{{{P_1}}}{{nr}} \end{array} $ |
式中:r表示钢丝刷半径;r1表示从动轮半径;R表示打磨管道的半径;φ表示打磨过程中重力与竖直方向之间的角度;P表示驱动电机功率;P1表示伺服电机功率;G表示打磨机器人总重;G1表示已知材料和零部件的总重;G2表示主动轮和从动轮的重量之和;FN表示施加的预紧力;μ表示从动轮与打磨钢圈的摩擦系数;N1、N2、N3、N4分别表示主动轮与管道内壁、钢丝刷与打磨钢圈、右侧两个从动轮和左侧两个从动轮与管道外壁之间的支持力;f1、f2、f3、f4分别表示主动轮与管道内壁、钢丝刷与打磨钢圈、右侧两个从动轮和左侧两个从动轮与管道外壁之间的摩擦力;θ为从动轮所受支持力与竖直方向间的夹角;T表示驱动电机施加于主动轮的扭矩。
通过方程组(1)可解得:
| $ \begin{array}{l} {f_1} = \left( {{G_1} + {G_2}} \right)\sin \varphi - {f_2} + \mu {F_{\rm{N}}} - \mu {N_2} + \\ \;\;\;\;\;\;\frac{{\left( {{\delta _1}{f_2} + 1.04T} \right)\sin \theta }}{{0.4\cos \theta - \left[ {\left( {R + {r_1}} \right)\cos \theta - {\delta _2}} \right]\left( {\sin \theta + 0.2\cos \theta } \right)}} \end{array} $ | (2) |
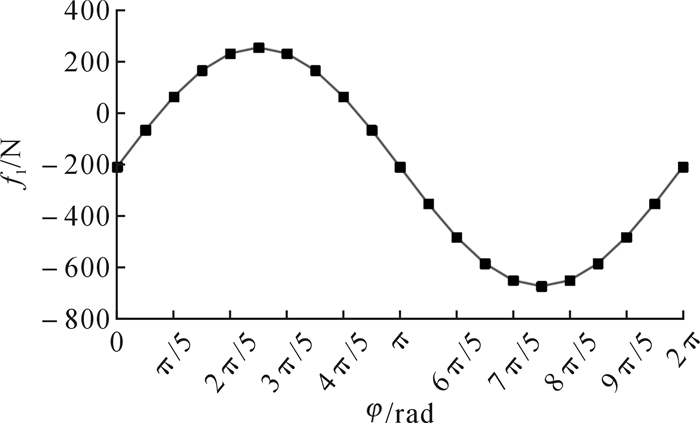
依据公式(2)对运动过程进行受力仿真分析,得到摩擦力f1随角度φ(φ∈[0, 2π] rad)的变化曲线,如图 5所示。
|
| 图 5 主动轮与管道内壁之间摩擦力随角度φ的变化曲线 Fig.5 Variation curve of friction between driving wheel and pipe inner wall with angle φ |
由图 5可知,打磨机器人在[0,237π/1570]与[6669π/7850,2π]区间内摩擦力的值为负,即摩擦力与打磨机器人运动方向相同;而在[237π/1570,6669π/7850]区间内摩擦力的值为正,即摩擦力与打磨机器人运动方向相反[12]。
2.3 压紧力模型在上述受力分析的基础上,保证打磨机器人不发生打滑首先应满足条件:
| $ \lambda {N_1} \ge \left| {{f_1}} \right| $ | (3) |
式中:λ为行走轮与管口内侧管壁的滑动摩擦系数。
由方程组(1)和式(2)、(3)可求得机器人正常工作时的压紧力模型为:
| $ \left\{ \begin{array}{l} {F_{Y1}} = {F_{\rm{N}}} - \frac{{ - \left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi + \lambda {\rm{c}}\varphi } \right) + {f_2} + \mu {N_2}}}{{0.8}} + \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{1.6{\rm{c}}\theta - 4\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}} > 0,\;\;\;\;0 \le \varphi < \frac{{237{\rm{ \mathsf{ π} }}}}{{1570}}\\ {F_{Y2}} = {F_{\rm{N}}} - \frac{{\left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi - \lambda {\rm{c}}\varphi } \right) - {f_2} - \mu {N_2}}}{{0.4}} - \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{0.8{\rm{c}}\theta - 2\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}} > 0,\;\;\;\;\frac{{237{\rm{ \mathsf{ π} }}}}{{1570}} \le \varphi < \frac{{6669{\rm{ \mathsf{ π} }}}}{{7850}}\\ {F_{Y3}} = {F_{\rm{N}}} - \frac{{ - \left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi + 0.6{\rm{c}}\varphi } \right) + {f_2} + \mu {N_2}}}{{0.8}} + \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{1.6{\rm{c}}\theta - 4\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}} > 0,\frac{{6669{\rm{ \mathsf{ π} }}}}{{7850}} \le \varphi \le 2{\rm{ \mathsf{ π} }} \end{array} \right. $ | (4) |
式中:s表示sin,c表示cos;FY表示压紧力,r2表示主动轮半径。
为了简化计算,只对打磨管道半径最大为2 m的端口打磨机器人进行可靠性分析[13],这是因为管道内径越大越容易看出各参数对端口打磨机器人可靠性的影响程度。
3 打磨机器人压紧力可靠性模型 3.1 可靠性摄动理论依据状态函数g(X)的定义、表达式和可靠性设计的摄动法,利用向量值和矩阵值函数的Taylor展开式,将随机变量X和状态函数g(X)在E(X)=X附近展开,并经过推导整理可得状态函数g(X)的均值和方差为:
| $ {\mu _g} = E\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right] = \bar g \approx g\left( {\mathit{\boldsymbol{\bar X}}} \right) $ | (5) |
| $ \sigma _g^2 = {\rm{Var}}\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right] \approx {\left[ {\frac{{\partial {g_d}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial {\mathit{\boldsymbol{X}}^{\rm{T}}}}}} \right]^{\left[ 2 \right]}}{\rm{Var}}\left( \mathit{\boldsymbol{X}} \right) $ | (6) |
式中:g(X)和Var(X)分别表示随机参数的均值和方差向量; (·)[2]=(·)
把状态函数g(X)对基本随机变量X求偏导数,得:
| $ \frac{{\partial {g_d}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial {\mathit{\boldsymbol{X}}^{\rm{T}}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial g}}{{\partial {X_1}}}}&{\frac{{\partial g}}{{\partial {X_2}}}}& \cdots &{\frac{{\partial g}}{{\partial {X_n}}}} \end{array}} \right] $ | (7) |
将式(7)代入状态函数g(X)的方差表达式,则可以得到端口打磨机器人极限状态函数的方差表达式。
当基本随机变量X服从正态分布时,可将可靠性指标定义为:
| $ {\beta _{{\rm{SM}}}} = \frac{{{\mu _g}}}{{{\sigma _g}}} = \frac{{E\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right]}}{{\sqrt {{\rm{Var}}\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right]} }} $ | (8) |
用失效点处状态表面的切平面近似地模拟极限状态表面,可以获得可靠度的一阶估计量:
| $ {R_{{\rm{SM}}}} = \mathit{\Phi }\left( {{\beta _{{\rm{SM}}}}} \right) $ | (9) |
当基本随机变量服从正态分布时,端口打磨机器人的可靠度对基本随机变量X=(X1, X2, …, Xn)T均值的灵敏度为:
| $ \frac{{{\rm{d}}{R_{{\rm{SM}}}}}}{{{\rm{d}}{{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}} = \frac{{\partial {R_{{\rm{SM}}}}}}{{\partial {\beta _{{\rm{SM}}}}}}\frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\mu _g}}}\frac{{\partial {\mu _g}}}{{\partial {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}} $ | (10) |
式中:
| $ \frac{{\partial {R_{{\rm{SM}}}}}}{{\partial {\beta _{{\rm{SM}}}}}} = \varphi \left( {{\beta _{{\rm{SM}}}}} \right) $ | (11) |
| $ \frac{{\partial {\beta _{{\rm{SM}}}}}}{{\partial {\mu _g}}} = \frac{1}{{{\sigma _g}}} $ | (12) |
| $ \frac{{\partial {\mu _g}}}{{\partial {{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial \bar g}}{{\partial {X_1}}}}&{\frac{{\partial \bar g}}{{\partial {X_2}}}}& \cdots &{\frac{{\partial \bar g}}{{\partial {X_n}}}} \end{array}} \right] $ | (13) |
式中:φ(βSM)为标准正态分布函数的概率密度函数。
把已知条件和可靠性计算结果代入式(10),就可以获得可靠性灵敏度dRSM/dXT。
3.3 极限状态函数和设计变量的确定根据端口打磨机器人的工作状况,得出机器人正常工作时其压紧力的极限状态函数:
| $ g\left( \mathit{\boldsymbol{X}} \right) = \left\{ \begin{array}{l} {F_{\rm{N}}} - \frac{{ - \left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi + \lambda {\rm{c}}\varphi } \right) + {f_2} + \mu {N_2}}}{{0.8}} + \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{1.6{\rm{c}}\theta - 4\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}},0 \le \varphi < \frac{{237{\rm{ \mathsf{ π} }}}}{{1570}}\\ {F_{\rm{N}}} - \frac{{\left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi - \lambda {\rm{c}}\varphi } \right) - {f_2} - \mu {N_2}}}{{0.4}} - \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{0.8{\rm{c}}\theta - 2\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}},\frac{{237{\rm{ \mathsf{ π} }}}}{{1570}} \le \varphi < \frac{{6669{\rm{ \mathsf{ π} }}}}{{7850}}\\ {F_{\rm{N}}} - \frac{{ - \left( {{G_1} + {G_2}} \right)\left( {{\rm{s}}\varphi + \lambda {\rm{c}}\varphi } \right) + {f_2} + \mu {N_2}}}{{0.8}} + \frac{{5\left( {{\delta _1}{f_2} + 1.04T} \right){\rm{s}}\theta }}{{1.6{\rm{c}}\theta - 4\left[ {\left( {R + {r_1}} \right){\rm{c}}\theta - {\delta _2}} \right]\left( {{\rm{s}}\theta + 0.2{\rm{c}}\theta } \right)}},\frac{{6669{\rm{ \mathsf{ π} }}}}{{7850}} \le \varphi \le 2{\rm{ \mathsf{ π} }} \end{array} \right. $ | (14) |
由式(14)可得,本文基本随机变量X=(r1,r2,P,FN)T,φ在[0,2π]rad之间变化,故可将它看作常量[15]。这里基本随机变量X的均值E(X)、方差Var(X)是已知的,且这些随机变量是服从正态分布的相互独立的随机变量[14, 16]。
| $ \left\{ \begin{array}{l} g\left( \mathit{\boldsymbol{X}} \right) \le 0,\;\;\;失败状态\\ g\left( \mathit{\boldsymbol{X}} \right) > 0,\;\;\;安全状态 \end{array} \right. $ | (15) |
参照上文试验,端口打磨机器人的主要性能参数如表 2所示。
| 参数 | 数值 |
| 打磨机器人总重G/N | 464.125 |
| 从动轮半径r1/m | 0.05 |
| 主动轮半径r2/m | 0.11 |
| 驱动电机功率P/kW | 0.25 |
| 驱动电机输出转速n/(r/min) | 10 |
| 伺服电机功率P1/kW | 3.5 |
| 伺服电机输出转速n1/(r/min) | 1 000 |
| 预紧力FN/N | 1 300 |
| 支持力N2/N | 100 |
根据经验可知,从动轮半径r1、主动轮半径r2、驱动电机功率P和施加预紧力FN的均值可根据实际数值来确定。其中:从动轮和主动轮半径的标准差分别取为其均值的0.005倍;电机功率和预紧力的标准差分别取为其均值的0.08倍[19]。
随着φ在[0, 2π]rad之间变化,端口打磨机器人的可靠性指标和可靠度也随之变化,在[0, 2π]rad内取不同φ值,分别计算极限状态函数的均值和方差[14-15],结果如表 3所示。
| 角度φ/rad | 均值 | 方差 |
| 0 | 1 062.8 | 10 816.157 13 |
| π/18 | 1 158.2 | 10 816.175 55 |
| 237π/1570 | 2 560.1 | 10 816.447 83 |
| 2π/9 | 2 258.1 | 10 816.493 91 |
| 4π9 | 1 448.8 | 10 816.761 35 |
| 7π/9 | 1 191.5 | 10 816.890 33 |
| 6669π/7850 | 668.825 5 | 10 816.111 90 |
| 19π/18 | 271.153 3 | 10 816.116 65 |
| 23π/18 | 46.511 2 | 10 816.141 71 |
| 4π/3 | 38.203 2 | 10 816.142 95 |
| 5π/3 | 386.305 6 | 10 816.110 06 |
| 17π/9 | 843.375 7 | 10 816.125 81 |
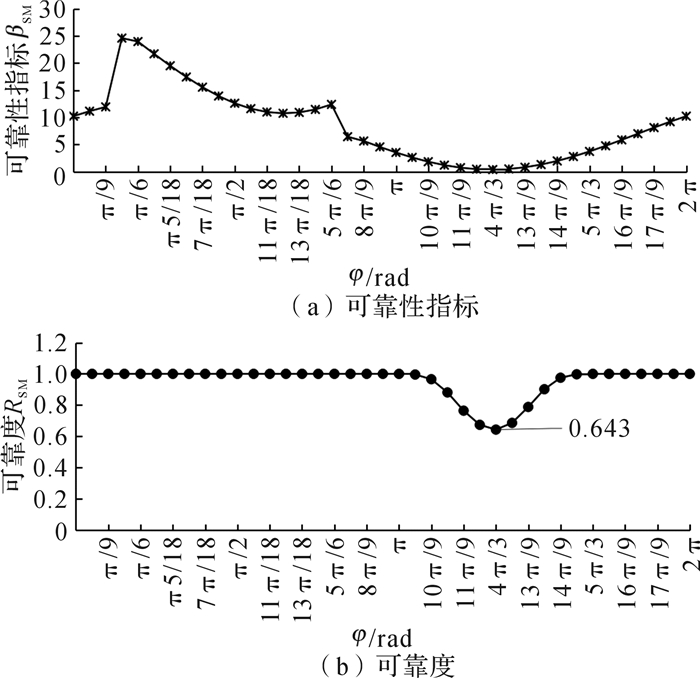
为了更清晰观察端口打磨机器人打磨过程中可靠性指标和可靠度的变化,取π/18为间隔对可靠性指标和可靠度进行计算,并单独对临界点进行计算,得端口打磨机器人的可靠性指标和可靠度随角度φ的变化曲线,如图 6所示。
|
| 图 6 端口打磨机器人打磨过程中可靠性指标和可靠度的变化曲线 Fig.6 Reliability index and reliability variation curve of port grinding robot during grinding process |
由图 6可以看出,整个打磨过程可以分为2个阶段:
1) 第1阶段:随着φ从0 rad增大至237π/1570 rad,可靠性指标随之增大且在φ=237π/1570 rad处取得最大值;随着φ从237π/1570 rad增大至2π/3 rad,可靠性指标随之减小且在φ=2π/3 rad处取得最小值;随着φ从2π/3 rad增大至6669π/7850 rad,可靠性指标随之增大且在φ=6669π/7850 rad处再次取得最大值。由此看出,这一阶段打磨机器人可靠性指标表现为先逐渐增大然后逐渐减小再逐渐增大。而可靠度远远高于实际要求的可靠度,其值均近似为1.0,即不易发生失效。
2) 第2阶段:随着φ从6669π/7850 rad增大至4π/3 rad,可靠性指标随之减小,可靠度也从1.0逐渐减小至最小值0.643,在φ=4π/3 rad处,可靠性指标和可靠度达到整个打磨过程中的最小值;随着φ从4π/3 rad增大至2π rad,可靠性指标随之增大,在φ=2π rad处达到最大且回到初始值,可靠度从最小值(0.643)逐渐增大至1.0并保持到整个打磨过程结束。由此看出,这一阶段打磨机器人可靠性指标表现为先逐渐减小然后逐渐增大。在φ=4π/3 rad处可靠度无法达到实际要求的原因是压紧力的均值仅为38.203 2 N,方差变化可以忽略不计,在惯性的作用下机器人发生打滑失效,随着压紧力的逐渐增加,打磨机器人也逐渐趋于平稳而正常运行。
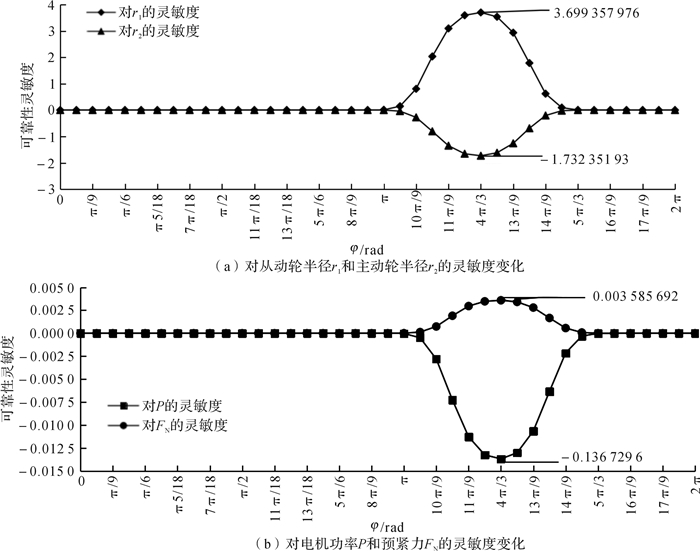
4.2 端口打磨机器人可靠性灵敏度分析端口打磨机器人正常工作时,其可靠度对各参数的灵敏度随φ的变化情况如图 7所示。
|
| 图 7 端口打磨机器人可靠度对各参数的灵敏度随角度φ的变化曲线 Fig.7 Variation curve of the sensitivity of port grinding robot reliability to each working parameter with angle φ |
由图 7可知,在打滑失效区,若打磨机器人从动轮半径r1和预紧力FN的均值增大,可使端口打磨机器人趋于可靠,而主动轮半径r2和驱动电机功率P的均值增大[16-17],则会使端口打磨机器人趋于不可靠(即失效);使端口打磨机器人最快趋向可靠的参数是从动轮半径,其次为主动轮半径、电机功率和预紧力。该灵敏度分析结果可以很好地指导工程人员在打磨机器人的设计、制造、使用和评估中要严格控制从动轮半径、主动轮半径、驱动电机功率和预紧力的变化[14, 18-19]。
5 结论1) 本文创新设计了一种PCCP端口打磨机器人,对该端口打磨机器人进行了结构设计与样机制作,通过现场试验研究其打滑失效问题,并分析了发生打滑失效的原因与影响因素。
2) 根据打磨机器人克服摩擦力环绕承、插口作周向转动的打磨过程,对端口打磨过程进行了受力分析,建立了其压紧力力学模型及可靠度模型,并利用随机摄动法分析了整个打磨过程的动态可靠度,确定了容易打滑失效的关键位置。研究表明,压紧力均值过小会使打磨机器人可靠度较低,在惯性的作用下而发生打滑失效。
3) 对影响端口打磨机器人可靠性的参数进行了灵敏度分析,结果表明使得该管口打磨机器人最快趋向可靠的参数为从动轮半径。研究结果为分析和修改端口打磨机器人的可靠性水平提供了理论依据。
| [1] |
胡少伟, 沈捷, 王东黎, 等.
超大口径预存裂缝的预应力钢筒混凝土管结构分析与试验研究[J]. 水利学报, 2010, 41(7): 876–882.
HU Shao-wei, SHEN Jie, WANG Dong-li, et al. Experiment and numerical analysis on super caliber prestressed concrete cylinder pipes with cracks[J]. Journal of Hydraulic Engineering, 2010, 41(7): 876–882. |
| [2] |
彭寿海.超大口径预应力钢筒混凝土管(PCCP)结构分析[D].北京: 清华大学水利水电工程系, 2009: 1-12.
PENG Shou-hai. Structural analysis of PCCP with super-large diameter prestressed cylinder concrete pipe[D]. Beijing: Tsinghua University, Department of Water Resources and Hydropower Engineering, 2009: 1-12. |
| [3] |
窦铁生, 程冰清, 胡赫, 等.
预应力钢筒混凝土管结构变形规律的原型试验研究Ⅰ:内压[J]. 水利学报, 2017, 48(12): 1438–1446.
DOU Tie-sheng, CHENG Bing-qing, HU He, et al. The prototype test study of prestressed concrete cylinder pipe structure deformation law Ⅰ:the internal pressure[J]. Journal of Hydraulic Engineering, 2017, 48(12): 1438–1446. |
| [4] |
乔俊宏, 马祥, 徐建忠, 等.一种PCCP管打磨装置: CN104227541A[P].2014-12-24.
QIAO Jun-hong, MA Xiang, XU Jian-zhong, et al. A PCCP pipe grinding device: CN104227541A[P]. 2014-12-24. |
| [5] |
严家琛.大口径金属螺旋管内壁焊缝自动跟踪打磨机器人的研制[D].上海: 东华大学机电工程系, 2017: 4-58.
YAN Jia-Chen. Development of automatic tracking and grinding robot for inner wall weld of large caliber metal spiral pipe[D]. Shanghai: Donghua University, Department of Mechanical Engineering, 2017: 4-58. http://cdmd.cnki.com.cn/Article/CDMD-10255-1017710659.htm |
| [6] | PEI Yu. Research and application of piping inside grinding robots in nuclear power plant[J]. Energy Procedia, 2017, 127: 54–59. DOI:10.1016/j.egypro.2017.08.066 |
| [7] |
唐德威, 李庆凯, 姜生元, 等.
具有差动运动功能的管道机器人设计与分析[J]. 机械工程学报, 2011, 47(13): 1–8.
TANG De-wei, LI Qing-kai, JIANG Sheng-yuan, et al. Design and analysis of a pipeline robot with the function of differential movement[J]. Journal of Mechanical Engineering, 2011, 47(13): 1–8. |
| [8] | NAYAK Ankit, PRADHAN S K. Design of a new in-pipe inspection robot[J]. Procedia Engineering, 2014, 97: 2081–2091. DOI:10.1016/j.proeng.2014.12.451 |
| [9] | MATEOS Luis A, VINCZE Markus. DeWaLoP in-pipe robot embedded system[J]. IFAC Proceedings Volumes, 2012, 45(22): 842–847. DOI:10.3182/20120905-3-HR-2030.00122 |
| [10] | ZHU C. In-pipe robot for inspection and sampling tasks[J]. Industrial Robot-An International Journal, 2007, 34(1): 39–45. DOI:10.1108/01439910710718432 |
| [11] | ZINM R A M, SAHARI K S M, SAAD J M, et al. Development of a low cost small sized in-pipe robot[J]. Procedia Engineering, 2012, 41: 1469–1475. DOI:10.1016/j.proeng.2012.07.337 |
| [12] |
孙传智, 李爱群, 缪长青, 等.
大跨V形刚构桥标高控制动态可靠性及灵敏度研究[J]. 应用基础与工程科学学报, 2012, 20(5): 886–894.
SUN Chuan-zhi, LI Ai-qun, MIU Chang-qing, et al. Research on dynamic reliability and reliability sensitivity of elevation control for long span V-shaped rigid frame bridge[J]. Journal of Basic Science and Engineering, 2012, 20(5): 886–894. DOI:10.3969/j.issn.1005-0930.2012.05.014 |
| [13] |
王新刚, 张义民, 王宝艳.
机械零部件的动态可靠性灵敏度分析[J]. 机械工程学报, 2010, 46(10): 188–193.
WANG Xin-gang, ZHANG Yi-min, WANG Bao-yan. Dynamic reliability sensitivity analysis of mechanical parts[J]. Journal of Mechanical Engineering, 2010, 46(10): 188–193. |
| [14] | WANG Wei, ZHANG Yi-min, LI Chang-you. Dynamic reliability analysis of linear guides in positioning precision[J]. Mechanism and Machine Theory, 2017, 116: 451–464. DOI:10.1016/j.mechmachtheory.2017.06.011 |
| [15] |
张义民, 贺向东, 刘巧伶.
螺旋管簧的可靠性鲁棒设计[J]. 应用基础与工程科学学报, 2003, 11(4): 419–424.
ZHANG Yi-min, HE Xiang-dong, LIU Qiao-ling. Reliability-based robust design for coil tube-spring[J]. Journal of Basic Science and Engineering, 2003, 11(4): 419–424. DOI:10.3969/j.issn.1005-0930.2003.04.012 |
| [16] |
杨周.非正态分布参数的机械构件的可靠性灵敏度和可靠性稳健设计[D].沈阳: 东北大学机械工程系, 2010: 11-41.
YANG Zhou. Reliability-based sensitivity and reliability-based robust design of mechanical components with non-normal random variables[D]. Shenyang: Northeastern University, Department of Mechanical Engineering, 2010: 11-41. http://cdmd.cnki.com.cn/Article/CDMD-10145-1013117121.htm |
| [17] |
张义民, 刘仁云, 贺向东.
非正态分布参数的机械联接件的可靠性灵敏度设计[J]. 机械设计与研究, 2005, 21(1): 4–7.
ZHANG Yi-min, LIU Ren-yun, HE Xiang-dong. Reliability sensitivity of mechanical joints with non-normal distribution parameters[J]. Machine Design and Research, 2005, 21(1): 4–7. DOI:10.3969/j.issn.1006-2343.2005.01.001 |
| [18] | WANG Pan, LU Zhen-zhou, HU Ji-xiang, et al. Sensitivity analysis of the variance contributions with respect to the distribution parameters by the kernel function[J]. Computers & Mathematics with Applications, 2014, 67(10): 1756–1771. |
| [19] | WANG Wen-xuan, GAO Hang-shan, ZHOU Chang-cong, et al. Reliability analysis of motion mechanism under three types of hybrid uncertainties[J]. Mechanism and Machine Theory, 2018, 121: 769–784. DOI:10.1016/j.mechmachtheory.2017.12.010 |



