2. 华南理工大学 自主系统与网络控制教育部重点实验室, 广东 广州 510641
2. Ministerial Key laboratory of Autonomous Systems and Network Control, South China University of Technology, Guangzhou 510640, China
近年来,各类伺服控制系统广泛应用于智能制造、工业机器人、精密数控装备等领域。在高性能伺服系统中,电机速度反馈的实时性和精度是影响伺服系统控制性能的决定性因素。在当前的工程应用中,因受限于测速传感器成本和分辨率以及无传感器控制技术依赖于复杂、高阶的电机模型和负载特性,再加上环境扰动、复杂工况等因素的影响,宽范围、高精度电机转速测量问题仍是学术界和工程界具有挑战性的研究重点。
基于各类测速传感器的测速性能优化研究有很多[1-8]。针对基于光电编码器测速系统,结合M法(频率法)和T法(周期法)分别适用于高速区和低速区测速的特点,文献[1]提出了一种宽范围同步测速方法(S法),提高了测速精度,但是仅对脉冲无序变化问题进行了简单弱化处理,系统抗干扰能力不足;文献[2]提出了扩展M/T法(频率周期法),在超低速时采用改进的T法具有较快的速度响应,但是增大了软硬件的复杂性,实时性差。针对磁编码器,文献[3]采用二维查表法提高了系统测速精度;文献[4]基于CORDIC(coordinate rotation digital computer,坐标旋转数字计算)算法提高了磁编码器的分辨率;文献[5]采用锁相环方法对电机旋转角速度进行估计,提高了系统抗干扰能力;文献[6]为磁编码器设计了一种基于二阶和三阶观测器的转速实时解调算法,其性能优于常规的查表法、反正切法和锁相环方法。但是,文献[3-6]并没有解决系统信号频率快速变化时估计误差较大的问题。文献[7]基于霍尔传感元件提出了一种基于普通精度增量式编码器的永磁伺服电机低速检测与控制优化方法,提高了系统的低速性能和抗干扰能力,但是增大了计算的复杂性,不能有效移植至单片机或以DSP (digital signal processor,数字信号处理器)为核心的嵌入式系统中,硬件实现困难。文献[8-15]系统地研究了基于无传感器控制技术的电机低速运行时转速的估计方法:文献[8-9]采用高频信号注入法,文献[10-11]采用反电动势法,文献[12-15]采用滑模观测器方法。上述文献所采用的无传感器测速技术虽然取得了进步,但由于都受限于各型电机精确的模型参数及系统环境,与基于传感器的测速方法相比,这些测速技术精度较低,抗干扰能力较差,仅可应用于对空间、密封性、环境工况等有苛刻要求的特定场景。
目前,综合考虑性价比、可靠性和测速性能,基于传感器的测速方法仍是普通环境下测速应用的首选方法。由于测速传感器的精度与价格成正比,高精度、高性能测速传感器高昂的价格让普通用户望而却步。因此针对常规精度测速传感器,设计一种能保证高、中转速区测速精度,并能有效改善低速区测速精度的宽范围、实时滤波测速算法,对拓宽普通测速传感器的应用范围具有重要的工程意义。
本文针对爪极永磁式交流测速电机,设计了一种宽范围实时滤波测速算法。首先,阐述了该型测速电机的机械结构和工作原理;其次,针对结构不对称条件下测速电机的特性,建立了测速模型;然后,针对基于测速电机的传统测速电路得到的转速测量值是1个或多个感应电动势半波的平均有效值,无法准确反映实时转速值,以及存在低速测速盲区的问题,提出了一种交互双模自适应降阶无迹卡尔曼滤波算法,以期能够实时、宽范围估计被测转速,提高测速的精度和鲁棒性;最后,通过仿真验证了本文所提测速方法的有效性。
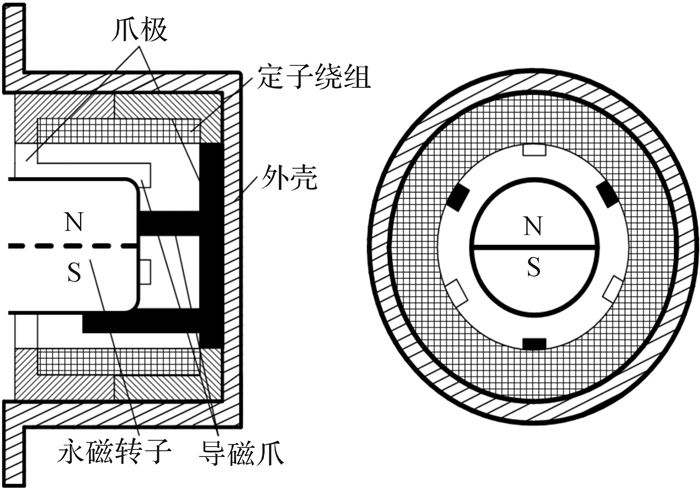
1 爪极永磁式交流测速电机机械结构和工作原理 1.1 机械结构爪极永磁式交流测速电机的机械结构如图 1所示,主要包括外壳、定子绕组、爪极、导磁爪、永磁转子等部件。
|
| 图 1 爪极永磁式交流测速电机的机械结构 Fig.1 Mechanical structure of claw pole permanent magnet AC tachogenerator |
爪极永磁式交流测速电机外壳内的一个定子绕组夹嵌在一对圆筒形的爪极之间;圆筒形爪极中心放置了可以旋转的永磁转子;上(白色)、下(黑色)爪极上的导磁爪围绕永磁转子交错均匀分布。
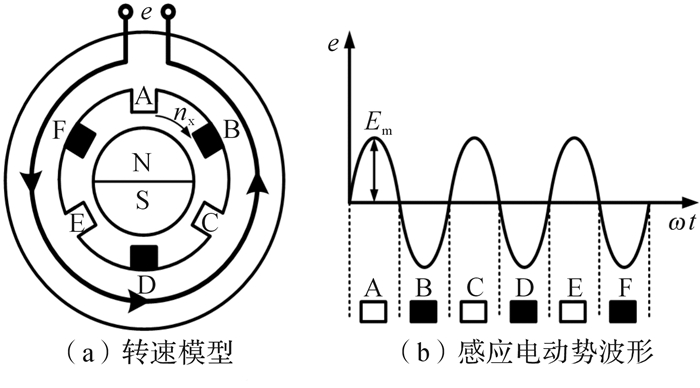
1.2 工作原理爪极永磁式交流测速电机的永磁转子轴向充磁,磁极的极性用N和S表示;导磁爪有6个:上爪极(白色)A、C、E和下爪极(黑色)B、D、F。永磁转子N极、导磁爪A、导磁爪D、永磁转子S极构成磁回路,如图 2(a)所示,磁场方向垂直于纸面;生成的感应电动势按照正弦规律变化,如图 2(b)所示。
|
| 图 2 结构对称型爪极永磁式交流测速电机转速模型及其感应电动势波形 Fig.2 Rotation speed model of structural symmetry claw pole permanent magnet AC tachogenerator and its induction electromotive force waveform |
电动机驱动永磁转子以恒定转速nx(单位为r/min)相对于定子绕组顺时针旋转,与定子绕组之间产生相对运动。根据电磁感应定律,定子绕组中会产生感应电动势e,其瞬时值为:
| $ e = {e_{\rm{N}}} - {e_{\rm{S}}} = {E_{\rm{m}}}\sin \omega t $ | (1) |
其中:
| $ {E_{\rm{m}}} = {\rm{ \mathsf{ π} }}f\varphi = \omega \varphi /2 $ | (2) |
式中:eN和eS分别为N极和S极的电动势,它们大小相等,方向相反,即在时间相位上彼此相差π rad电角度;ω为空间电角速度,rad/s,Em为e的最大值,V;f=2π/ω,为感应电动势e的频率,Hz;φ为气隙每极磁通量,Wb。
若已知ω和导磁爪对数p,则永磁转子沿顺时针方向旋转时的转速nx可以表示为:
| $ {n_{\rm{x}}} = \frac{{60\omega }}{{2{\rm{ \mathsf{ π} }}p}} = \frac{{60{E_{\rm{m}}}}}{{{\rm{ \mathsf{ π} }}p\varphi }} = \frac{{60\sqrt 2 E}}{{{\rm{ \mathsf{ π} }}p\varphi }} $ | (3) |
式中:E为感应电动势e的有效值,V。
根据上述对爪极永磁式交流测速电机的分析及方程(2)和(3)可知,在理想的情况下,当φ为定值时,永磁转子(被测电机)的转速nx与感应电动势e的有效值E成正比。
2 结构不对称条件下测速电机转速模型考虑到在实际工程中应用的爪极永磁式交流测速电机常在结构不对称条件下运行,感应电动势e将发生畸变,不再具有标准的正弦特性,转速nx与感应电动势有效值E不再呈简单的正比关系,则需要重新建立新的测速模型。
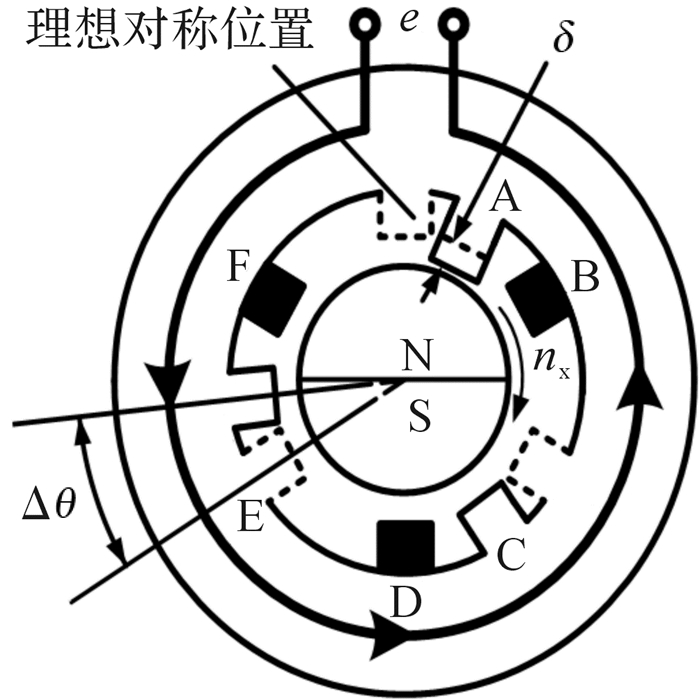
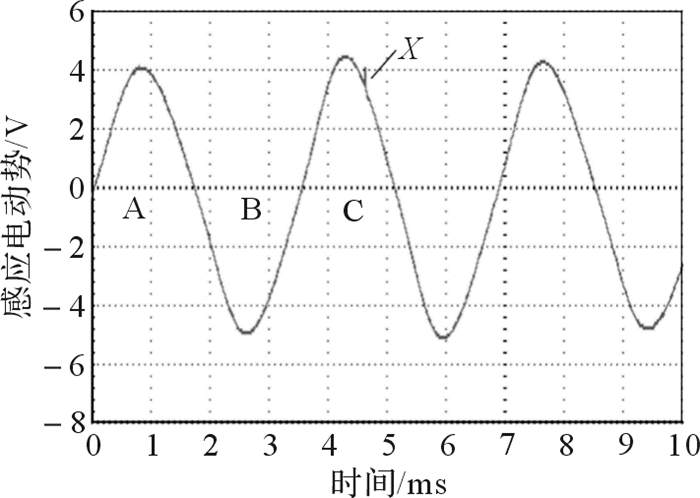
结构不对称条件下爪极永磁式交流测速电机转速模型如图 3所示。当上爪极与下爪极偏差的电角度为θ时,则在导磁爪D与永磁转子S极对齐时,导磁爪A、C、E分别与它们各自在对称条件下的位置偏差电机械角度Δθ,这会导致永磁转子N极和S极产生的电动势eN和eS不对称;若导磁爪A的长度与标准长度相差δ,则气隙磁通量φA将随之变化。结构不对称因子Δθ、δ,转速波动及干扰噪声等随机因素的存在是使定子绕组的感应电动势e产生不对称畸变问题的重要原因。如图 4所示,例如永磁转子在经过导磁爪A、B、C时产生的感应电动势半波的周期和幅值均不一致,在导磁爪C产生的感应电动势半波的X处还产生了毛刺(由导磁爪C的结构瑕疵引起)。建立结构不对称条件下爪极永磁式交流测速电机数学模型,并在其基础上采用滤波方法估计对称电角速度ω,将有助于提高永磁转子(原动机)转速nx的测量精度和鲁棒性。
|
| 图 3 结构不对称型爪极永磁式交流测速电机转速模型 Fig.3 Rotation speed model of structural asymmetry claw pole permanent magnet AC tachogenerator |
|
| 图 4 结构不对称型爪极永磁式交流测速电机感应电动势波形图 Fig.4 Induction electromotive force waveform diagram of structural asymmetry claw pole permanent magnet AC tachogenerator |
由图 3可知,结构不对称参数Δθ的存在,使得6个导磁爪距呈不均匀分布,即出现3段长导磁爪距(其机械弧度
| $ \left\{ \begin{array}{l} \mathit{\Theta }_k^ + = \frac{{\rm{ \mathsf{ π} }}}{{{\rm{ \mathsf{ π} }} + \Delta \theta _k^p}}{\mathit{\Theta }_k},\omega _k^ + = \frac{{\rm{ \mathsf{ π} }}}{{{\rm{ \mathsf{ π} }} + \Delta \theta _k^p}}{\omega _k}\\ \mathit{\Theta }_k^ - = \frac{{\rm{ \mathsf{ π} }}}{{{\rm{ \mathsf{ π} }} - \Delta \theta _k^p}}{\mathit{\Theta }_k},\omega _k^ - = \frac{{\rm{ \mathsf{ π} }}}{{{\rm{ \mathsf{ π} }} - \Delta \theta _k^p}}{\omega _k} \end{array} \right. $ | (4) |
式中:Θk=Θk-1+ωkT,T为采样周期;Δθkp=Δθkp,为导磁爪偏差电角度。
永磁转子的N极或S极每经过1对相邻的
| $ \begin{array}{l} {e_k} = h\left( {{\mathit{\boldsymbol{x}}_k},{\upsilon _k}} \right) = {e_{{\rm{N}}k}} - {e_{{\rm{S}}k}} + {\upsilon _k} = \\ \left\{ \begin{array}{l} {\left( { - 1} \right)^n}\left[ {\frac{{\omega _k^ + {\varphi _{u,k}}}}{2}\cos \mathit{\Theta }_k^ + + \frac{{\omega _k^ + {\varphi _{v,k}}}}{2}\cos \left( {\mathit{\Theta }_k^ + + \Delta \theta _k^p} \right)} \right] + {\upsilon _k}\\ 其中:\forall {\mathit{\Theta }_k} \in \left[ {n{\rm{ \mathsf{ π} }} + 2m{\rm{ \mathsf{ π} }},n{\rm{ \mathsf{ π} }} + \Delta \theta _k^p + 2m{\rm{ \mathsf{ π} }}} \right]\\ \;\;\;\;\;\;\;n = 0,1,m = 1,2, \cdots ,p\\ \;\;\;\;\;\;\;u = n + 2\left( {m - 1} \right)\\ \;\;\;\;\;\;\;v = \bmod \left[ {2 + n + 2\left( {m - 1} \right),2p} \right]\\ {\left( { - 1} \right)^n}\left[ {\frac{{\omega _k^ + {\varphi _{u,k}}}}{2}\cos \mathit{\Theta }_k^ + + \frac{{\omega _k^ - {\varphi _{v,k}}}}{2}\cos \left( {\mathit{\Theta }_k^ - - \Delta \theta _k^p} \right)} \right] + {\upsilon _k}\\ 其中:\forall {\mathit{\Theta }_k} \in \left[ {n{\rm{ \mathsf{ π} }} + \Delta \theta _k^p + 2m{\rm{ \mathsf{ π} }},n{\rm{ \mathsf{ π} }} + {\rm{ \mathsf{ π} }} + 2m{\rm{ \mathsf{ π} }}} \right]\\ \;\;\;\;\;\;\;n = 0,1,m = 1,2, \cdots ,p\\ \;\;\;\;\;\;\;u = n + 2\left( {m - 1} \right)\\ \;\;\;\;\;\;\;v = \bmod \left[ {3 + n + 2\left( {m - 1} \right),2p} \right] \end{array} \right. \end{array} $ | (5) |
式中:φu, k、φv, k∈Φk,vk为零均值白噪声序列,R(协方差矩阵)为vk的属性。
在利用式(5)描述的离散测速方程估计目标转速时,为了避免电角度数据累加溢出,依据eNk或eSk的周期性,将Θk的值域限定在一个周期内,即在算法运行过程中,当Θk从零递增至2πp时就将它清零,使得0≤Θk≤2πp。
3 交互双模自适应无迹卡尔曼滤波算法考虑到测速电机永磁转子的转动状态一般为恒速或变速运动的组合,因此本文将测速电机永磁转子(被测电机)的运动状态对应为2个运动模型M1(恒速)和M2(变速),设Mj(j=1, 2)的离散状态方程为:
| $ {\mathit{\boldsymbol{x}}_{j,k + 1}} = f\left( {{\mathit{\boldsymbol{x}}_{j,k}},{w_{j,k}}} \right) $ | (6) |
式中:
wj, k为方差为Q的零均值白噪声序列;ζk为变速因子;Φk为气隙磁量;φu, k∈Φk,为第u个导磁爪与磁极间的气隙磁通量。
模型M1和M2的马尔可夫概率转移矩阵为:
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}\\ {{p_{21}}}&{{p_{22}}} \end{array}} \right] $ |
式中:pij为第i个模型向第j个模型转移的概率,pij=P{Mj, k|Mi, k-1}。
3.1 无迹卡尔曼滤波算法根据方程(5)可知测速电机模型是非线性方程,无迹卡尔曼滤波(unscented Kalman filter,UKF)的具体计算过程如下:
1) 根据UT变换[16-18],基于τ阶模型Mj计算由2τ+1个sigma点组成的采样点集χk|k:
| $ \begin{array}{l} {\chi _{k\left| k \right.}} = \left\{ {{\mathit{\boldsymbol{x}}_{j,k\left| k \right.}},{\mathit{\boldsymbol{x}}_{j,k\left| k \right.}} + {{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k\left| k \right.}}} } \right]}_1}, \cdots ,{\mathit{\boldsymbol{x}}_{j,k\left| k \right.}} + } \right.\\ \;\;\;\;\;\;\;\;\;{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k\left| k \right.}}} } \right]_\tau },{\mathit{\boldsymbol{x}}_{j,k\left| k \right.}} - {\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k\left| k \right.}}} } \right]_{\tau + 1}}, \cdots ,\\ \;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_{j,k\left| k \right.}} - {{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k\left| k \right.}}} } \right]}_{2\tau }}} \right\} \end{array} $ | (7) |
式中:λ=α2(τ+κ)-τ,为比例因子,α和κ都是正常数,α决定x估值周围sigma点的分布状态,通常0≤α≤1;适当调节α、κ可以提高估计均值的精度;
2) 将2τ+1个sigma点(χk|k)r(χk|k的第r列,r∈[1, 2τ])依次代入永磁转子离散状态方程(6), 计算采样点集χk|k的预测值χk+1|k=f(χk|k)。
3) 通过对χk+1|k加权求均值,计算模型Mj的预测值
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} = {W_{\rm{m}}}{\chi _{k + 1\left| k \right.}}\\ {\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}} = \left( {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} - {\chi _{k + 1\left| k \right.}}} \right){W_{\rm{c}}}{\left( {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} - {\chi _{k + 1\left| k \right.}}} \right)^{\rm{T}}} + \left. \mathit{\boldsymbol{Q}} \right) \end{array} \right. $ | (8) |
式中:
| $ \left\{ \begin{array}{l} {W_{\rm{m}}} = \left[ {\frac{\lambda }{{\tau + \lambda }},\overbrace {\frac{\lambda }{{2\left( {\tau + \lambda } \right)}}, \cdots ,\frac{\lambda }{{2\left( {\tau + \lambda } \right)}}}^{2\tau 个}} \right]\\ {W_{\rm{c}}} = {\rm{diag}}\left( {\frac{\lambda }{{\tau + \lambda }} + \left( {1 - {\alpha ^2} + \beta } \right),\underbrace {\frac{\lambda }{{2\left( {\tau + \lambda } \right)}}, \cdots ,\frac{\lambda }{{2\left( {\tau + \lambda } \right)}}}_{2\tau 个}} \right) \end{array} \right. $ |
式中:Wm、Wc分别为均值和方差加权值; β为正常数,调节β可以提高方差的精度。
4) 根据UT变换和式(8),预测估计采样点集:
| $ \begin{array}{l} {\chi _{k + 1\left| k \right.}} = \left\{ {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}},{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} + {{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}}} } \right]}_1}, \cdots ,} \right.\\ \;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} + {\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}}} } \right]_\tau },{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} - \\ \;\;\;\;\;\;\;\;\;{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}}} } \right]_{\tau + 1}}, \cdots ,\\ \;\;\;\;\;\;\;\;\;\left. {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} - {{\left[ {\sqrt {\left( {\tau + \lambda } \right){\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}}} } \right]}_{2\tau }}} \right\} \end{array} $ | (9) |
5) 将2τ+1个sigma点(χk+1|k)r(χk+1|k的第r列,r∈[1, 2τ])依次代入转速观测方程(5)来预测观测值ek+1|k,进而计算测量均值ek+1|k、协方差Pekek、状态协方差Pxkek和卡尔曼增益矩阵Kk+1,计算方法如下:
| $ \left\{ \begin{array}{l} {e_{k + 1\left| k \right.}} = h\left( {{\chi _{k + 1\left| k \right.}}} \right)\\ {{\bar e}_{k + 1\left| k \right.}} = {W_{\rm{m}}}{e_{k + 1\left| k \right.}}\\ {\mathit{\boldsymbol{P}}_{{e_k}{e_k}}} = \left( {{e_{k + 1\left| k \right.}} - {{\bar e}_{k + 1\left| k \right.}}} \right){W_{\rm{c}}}{\left( {{e_{k + 1\left| k \right.}} - {{\bar e}_{k + 1\left| k \right.}}} \right)^{\rm{T}}} + \mathit{\boldsymbol{R}}\\ {\mathit{\boldsymbol{P}}_{{x_k}{e_k}}} = \left( {{\chi _{k + 1\left| k \right.}} - {{\bar e}_{k + 1\left| k \right.}}} \right){W_{\rm{c}}}{\left( {{\chi _{k + 1\left| k \right.}} - {{\bar e}_{k + 1\left| k \right.}}} \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{K}}_{k + 1}} = {\mathit{\boldsymbol{P}}_{{x_k}{e_k}}}\mathit{\boldsymbol{P}}_{{e_k}{e_k}}^{ - 1} \end{array} \right. $ | (10) |
6) 更新模型Mj的估计和方差:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| {k + 1} \right.}} = {{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| k \right.}} + {\mathit{\boldsymbol{K}}_{k + 1}}\left[ {{e_{k + 1}} - {e_{k + 1\left| k \right.}}} \right]\\ {\mathit{\boldsymbol{P}}_{j,k + 1\left| {k + 1} \right.}} = {\mathit{\boldsymbol{P}}_{j,k + 1\left| k \right.}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{P}}_{{e_k}{e_k}}}\mathit{\boldsymbol{K}}_{k + 1}^{\rm{T}} \end{array} \right. $ | (11) |
1) 模型交互。定义模型Mj匹配的先验初始概率μj, k=P{Mj, k},则测速电机模型M1和M2的混合概率为:
| $ {\mu _{ij,k\left| k \right.}} = \frac{{{p_{ij}}{\mu _{i,k}}}}{{\sum\limits_{i = 1}^2 {{p_{ij}}{\mu _{i,k}}} }},i,j \in \left\{ {1,2} \right\} $ | (12) |
式中:μi, k是k时刻模型Mi的概率。
接下来计算每个模型滤波器的混合输入(估计和方差):
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{j,k\left| k \right.}} = \sum\limits_{i = 1}^2 {{{\mathit{\boldsymbol{\hat x}}}_{i,k\left| k \right.}}{\mu _{ij,k\left| k \right.}}} \\ {\mathit{\boldsymbol{P}}_{j,k\left| k \right.}} = \sum\limits_{i = 1}^2 {{\mu _{ij,k\left| k \right.}}\left[ {{\mathit{\boldsymbol{P}}_{i,k\left| k \right.}} + \left( {{\mathit{\boldsymbol{x}}_{i,k\left| k \right.}} - {{\mathit{\boldsymbol{\hat x}}}_{j,k\left| k \right.}}} \right)} \right.} \\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left( {{\mathit{\boldsymbol{x}}_{i,k\left| k \right.}} - {{\mathit{\boldsymbol{\hat x}}}_{j,k\left| k \right.}}} \right)}^{\rm{T}}}} \right] \end{array} \right. $ | (13) |
2) 滤波。将
3) 更新模型概率。根据贝叶斯(Bayes)公式, 模型Mj在k+1时刻的概率为:
| $ {\mu _{j,k + 1}} = \frac{{\left( {\sum\limits_{i = 1}^2 {{p_{ij}}{\mu _{i,k}}} } \right){\mathit{\Lambda }_{j,k}}}}{{\sum\limits_{j = 1}^2 {{\mathit{\Lambda }_{j,k}}} \left( {\sum\limits_{i = 1}^2 {{p_{ij}}{\mu _{i,k}}} } \right)}} $ | (14) |
其中:似然函数Λi, k的计算方法见文献[10]。
4) 联合估计。根据模型概率,加权合并计算所有模型的滤波值,可得联合估计和方差:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.}} = \sum\limits_{j = 1}^2 {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| {k + 1} \right.}}{\mu _{j,k + 1}}} \\ {\mathit{\boldsymbol{P}}_{k + 1\left| {k + 1} \right.}} = \sum\limits_{j = 1}^2 {{\mu _{j,k + 1}}\left[ {{\mathit{\boldsymbol{P}}_{j,k + 1\left| {k + 1} \right.}} + \left( {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| {k + 1} \right.}} - } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.}}} \right) \times {{\left( {{{\mathit{\boldsymbol{\hat x}}}_{j,k + 1\left| {k + 1} \right.}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.}}} \right)}^{\rm{T}}}} \right] \end{array} \right. $ | (15) |
5) 更新自适应估计转移概率矩阵(transition probability matrix, TPM)。根据文献[10]介绍的方法,在线自适应更新TPM。
6) 自适应降阶。定义滤波误差的标准差为:
| $ {\sigma _{\hat x}} = \sqrt {\frac{1}{M}\sum\limits_{g = 1}^M {{{\left( {{\mathit{\boldsymbol{x}}_{k + 1,g}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.,g}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_{k + 1,g}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.,g}}} \right)} } $ | (16) |
式中:M为采样次数。
定义降阶运行模式为:在系统运行平稳后(
自适应降阶运行策略的步骤为:
步骤1:设定自适应交互双模算法中各变量的初始值以及ε,进入步骤2。
步骤2:运行降阶自适应交互双模算法,并计算
步骤3:并行运行降阶和全阶自适应交互双模算法。当采用降阶估计值保障系统实时性时,在计算耗时较长的全阶算法运行完成一次后修正一次降阶估计值,以提高测速精度。若
为了验证提出的交互双模自适应降阶无迹卡尔曼滤波算法的有效性,采用MATLAB软件进行仿真验证。将式(6)表述为:
| $ {\mathit{\boldsymbol{x}}_{j,k + 1}} = f\left( {{\mathit{\boldsymbol{x}}_{j,k}},{w_{j,k}}} \right) = {\mathit{\boldsymbol{A}}_j}{\mathit{\boldsymbol{x}}_{j,k}} + {\mathit{\boldsymbol{G}}_j}{w_{j,k}} $ | (17) |
首先验证单模情况下自适应降阶无迹卡尔曼滤波算法的性能。设:α=0.01,β=2,κ=0,Qk=Rk=0.1,Δθ0p=0.2 rad,p=3,采样周期T=0.2 ms,Φk中的元素为0~1间的随机数。本文采用恒速模型M1和匀加速模型M2组合的测速电机运动模型,为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_{1,k}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\Theta }_k}}&{{\omega _k}}&{\Delta \theta _k^p}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&T&0\\ 0&1&0\\ 0&0&1 \end{array}}&{{\mathit{\boldsymbol{O}}_{3 \times 2p}}}\\ {{\mathit{\boldsymbol{O}}_{2p \times 3}}}&{{\mathit{\boldsymbol{I}}_{2p}}} \end{array}} \right],{\mathit{\boldsymbol{G}}_1} = \left[ {\begin{array}{*{20}{c}} 0\\ 1\\ 0\\ 0 \end{array}} \right]\\ {\mathit{\boldsymbol{x}}_{2,k}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\Theta }_k}}&{{\omega _k}}&{{\zeta _k}}&{\Delta \theta _k^p}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} 1&T&0&0\\ 0&1&T&0\\ 0&0&1&0\\ 0&0&0&1\\ {}&{{\mathit{\boldsymbol{O}}_{2p \times 3}}}&{}&{{\mathit{\boldsymbol{I}}_{2p}}} \end{array}} \right],{\mathit{\boldsymbol{G}}_2} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1\\ 0\\ 0 \end{array}} \right] \end{array} \right. $ | (18) |
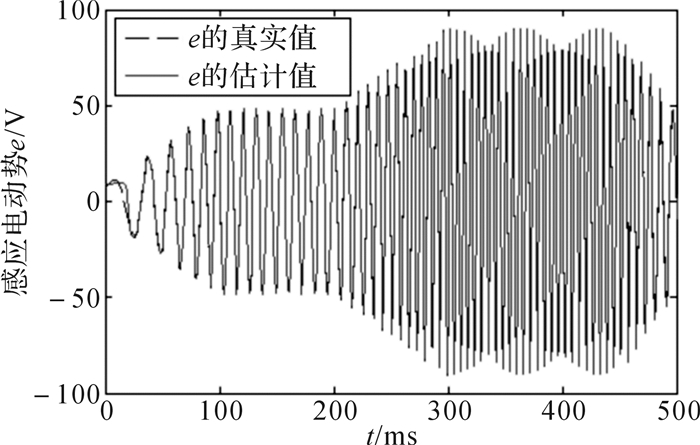
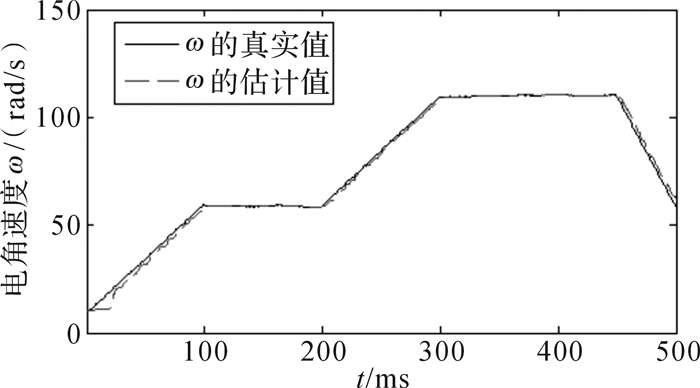
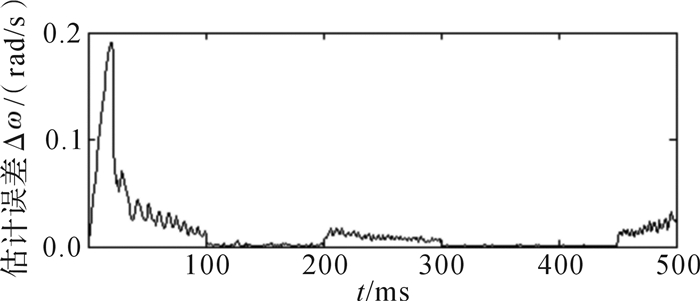
在仿真过程中,测速电机永磁转子以100步为单位在恒速和匀加/减速状态中交替切换,采用蒙特卡洛方法仿真500 ms,仿真结果见图 5至图 7。从图 5可以看出,仿真所得感应电动势的正弦曲线能够较好地跟踪实际测速电机模型输出的电动势曲线。由于仿真时是基于单一的恒速模型运行自适应降阶无迹卡尔曼滤波算法,从图 6和图 7中可以看出单模无迹卡尔曼滤波算法在测速电机永磁转子恒速状态下的估计精度较高,而在加速状态下的估计精度较低。
|
| 图 5 恒速单模无迹卡尔曼滤波条件下的感应电动势曲线 Fig.5 Induction electromotive force curve under the condition of constant speed single-mode UKF |
|
| 图 6 恒速单模无迹卡尔曼滤波条件下的电角速度曲线 Fig.6 Electrical angular velocity curve under the condition of constant speed single-mode UKF |
|
| 图 7 恒速单模无迹卡尔曼滤波条件下的电角速度估计误差曲线 Fig.7 Estimation error curve of electrical angular velocity under the condition of constant speed single-mode UKF |
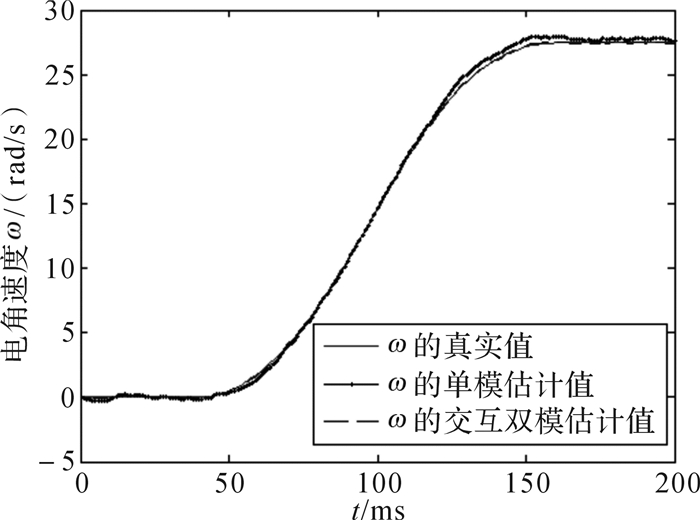
为了进一步验证交互双模自适应无迹卡尔曼滤波算法的性能,测速电机主轴的运动状态采用式(19)表示的机动性更强的变速模型M2和恒速模型M1交替的形式,采用蒙特卡洛方法仿真200 ms(其中,41-90 ms以及111-160 ms采用变速模型,变速因子ζ分别为1和-1,其余步采用恒速模型。仿真结果如图 8至图 10所示。
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} 1&{\frac{{\sin \left( {{\zeta _k}k} \right)}}{{{\zeta _k}}}}&1&0&{}\\ 0&{\cos \left( {{\zeta _k}k} \right)}&{ - \sin \left( {{\zeta _k}k} \right)}&0&{{\mathit{\boldsymbol{O}}_{4 \times 2p}}}\\ 0&0&1&0&{}\\ 0&0&0&1&{}\\ {}&{{\mathit{\boldsymbol{O}}_{2p \times 4}}}&{}&{}&{{\mathit{\boldsymbol{I}}_{2p}}} \end{array}} \right]\\ {\mathit{\boldsymbol{G}}_2} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1\\ 0\\ 0 \end{array}} \right] \end{array} \right. $ | (19) |
|
| 图 8 交互双模自适应无迹卡尔曼滤波条件下的电角速度曲线 Fig.8 Electrical angular velocity curve under the condition of interactive dual-mode adaptive UKF |
|
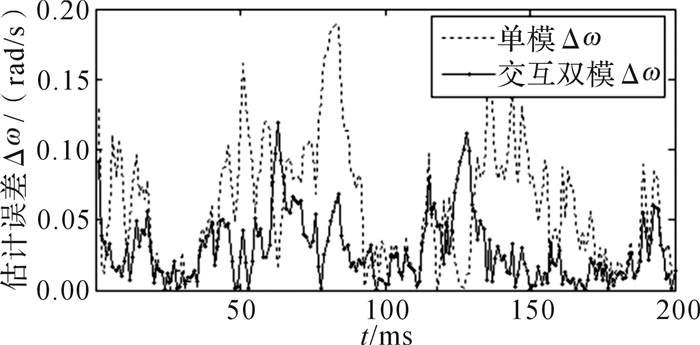
| 图 9 2种无迹卡尔曼滤波条件下的电角速度估计误差比较 Fig.9 Comparison of electrical angular velocity estimation error under the condition of two kinds of UKF |
|
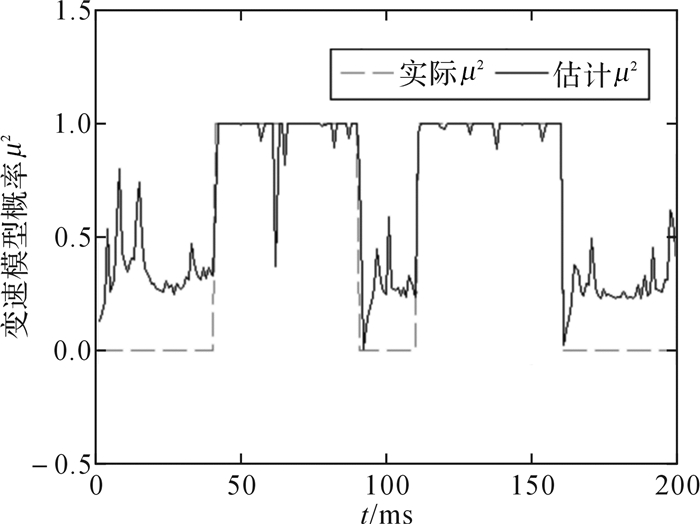
| 图 10 变速模型估计概率比较曲线 Fig.10 Comparison of estimation probability of variable speed model |
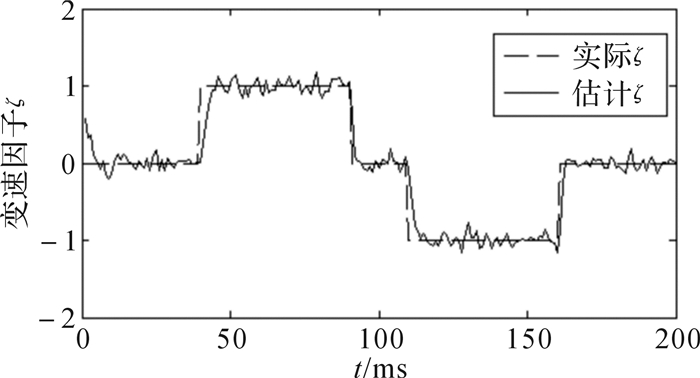
从图 8和图 9可以看出,在低速区和中、高速区,采用交互双模自适应无迹卡尔曼滤波算法时ω的精度明显提高,其估计曲线几乎与实际曲线重合。从图 10和图 11可以得知所采用的算法能够有效辨识出变速模型M2和变速因子ζ,表明交互双模自适应无迹卡尔曼滤波算法能够良好地跟踪永磁转子变速运动状态。
|
| 图 11 变速模型变速因子比较 Fig.11 Comparison of variable speed factor of variable speed model |
本文针对常规精度交流测速电机测速实时性和低速性能差的问题,以一类爪极永磁式交流测速电机为例,讨论了采用交互双模自适应降阶无迹卡尔曼滤波算法实时估计测速电机永磁转子转速的方法。仿真结果表明,在测速电机结构不对称条件下,该方法测速范围宽、精度高、实时性和变速动态响应良好。该方法可以推广到采用光电(磁)编码器为测速原件的系统,具有一定的工程应用指导意义。
| [1] |
鲁进军, 梅志千, 刘向红, 等.
电动机的高精度宽范围转速测量方法[J]. 中国电机工程学报, 2011, 31(24): 118–123.
LU Jin-jun, MEI Zhi-qian, LIU Xiang-hong, et al. Investigation of precision wide-range velocity measurement method for motor[J]. Proceedings of the CSEE, 2011, 31(24): 118–123. |
| [2] | YANG Y P, TING Y Y. Improved angular displacement estimation based on Hall-Effect sensors for driving a brushless permanent magnet motor[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 504–511. DOI:10.1109/TIE.2013.2247013 |
| [3] | HAGIWARA N, SUZUKI Y, MURASE H. A method of improving the resolution and accuracy of rotary encoders using a code compensation technique[J]. IEEE Transactions on Instrumentation and Measurement, 1992, 41(1): 98–101. DOI:10.1109/19.126640 |
| [4] |
王爽, 李铁才, 王治国.
基于CORDIC算法的高分辨率磁编码器设计[J]. 微电机, 2009, 42(8): 1–5.
WANG Shuang, LI Tie-cai, WANG Zhi-guo. Design of high resolution magnetic encoder based on CORDIC algorithm[J]. Micro Motors, 2009, 42(8): 1–5. DOI:10.3969/j.issn.1001-6848.2009.08.001 |
| [5] | HARNEFORS L, NEE H P. A general algorithm for speed and position estimation of AC motors[J]. IEEE Transactions on Industrial Electronics, 2000, 47(1): 77–83. DOI:10.1109/41.824128 |
| [6] |
吴忠, 吕绪明.
基于磁编码器的伺服电机速度及位置观测器设计[J]. 中国电机工程学报, 2011, 31(9): 82–87.
WU Zhong, LÜ Xu-ming. Design of angular velocity and position observer for servo motors with magnetic encoders[J]. Proceedings of the CSEE, 2011, 31(9): 82–87. |
| [7] |
汪兆栋, 文小琴, 游林儒, 等.
基于普通精度增量式编码器的永磁伺服电机低速检测与控制优化方法研究[J]. 电工技术学报, 2016, 31(21): 212–220.
WANG Zhao-dong, WEN Xiao-qin, YOU Lin-ru, et al. Research on detection and control optimized approach for permanent magnet servo motors at low speed with ordinary-resolution incremental encoder[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 212–220. DOI:10.3969/j.issn.1000-6753.2016.21.025 |
| [8] | YANG S H, LORENZ R D. Surface permanent-magnet machine self-sensing at zero and low speeds using improved observer for position, velocity and disturbance torque estimation[J]. IEEE Transactions on Industry Applications, 2012, 48(1): 151–160. DOI:10.1109/TIA.2011.2175472 |
| [9] |
王高林, 杨荣峰, 李刚, 等.
基于高频信号注入的IPMSM无位置传感器控制策略[J]. 电工技术学报, 2012, 27(11): 62–68.
WANG Gao-lin, YANG Rong-feng, LI Gang, et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 62–68. |
| [10] | HEJNYR W, LORENZ R D. Evaluating the practical low speed limits for back-EMF tracking based sensorless speed control using drive stiffness as a key metric[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1337–1343. DOI:10.1109/TIA.2011.2126013 |
| [11] |
李凤祥, 徐浩, 袁野, 等.
无刷直流电机无位置传感器转子位置辨识策略[J]. 电工技术学报, 2014, 29(12): 107–112.
LI Feng-xiang, XU Hao, YUAN Ye, et al. Rotor position identification strategy of brushless DC motors[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 107–112. DOI:10.3969/j.issn.1000-6753.2014.12.015 |
| [12] | QIAO Z W, SHI T N, WANG Y D, et al. New sliding-mode observer for position sensorless control of permanent magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 710–719. DOI:10.1109/TIE.2012.2206359 |
| [13] |
朱瑛, 程明, 花为, 等.
基于滑模变结构模型参考自适应的电气无级变速器无传感器控制[J]. 电工技术学报, 2015, 30(2): 64–72.
ZHU Ying, CHENG Ming, HUA Wei, et al. Sensorless control for electrical variable transmission based on sliding mode model reference adaptive system[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 64–72. DOI:10.3969/j.issn.1000-6753.2015.02.009 |
| [14] |
陆婋泉, 林鹤云, 冯奕, 等.
永磁同步电机无传感器控制的软开关滑模观测器[J]. 电工技术学报, 2015, 30(2): 106–113.
LU Xiao-quan, LIN He-yun, FENG Yi, et al. Soft switching sliding mode observer for PMSM sensorless control[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 106–113. DOI:10.3969/j.issn.1000-6753.2015.02.014 |
| [15] |
陈天翔, 张辑, 彭彦卿.
基于转矩滑模观测器的抗负载扰动控制方法[J]. 电力系统保护与控制, 2013, 41(8): 114–118.
CHEN Tian-xiang, ZHANG Ji, PENG Yan-qing. Anti-load disturbance control method based on torque sliding mode observer[J]. Transactions of China Electrotechnical Society, 2013, 41(8): 114–118. |
| [16] |
何栋炜, 彭侠夫, 蒋学程, 等.
永磁同步电机的改进扩展卡尔曼滤波测速算法[J]. 西安交通大学学报, 2011, 45(10): 59–64.
HE Dong-wei, PENG Xia-fu, JIANG Xue-cheng, et al. Improved extended Kalman filter velocity estimation for permanent magnet synchronous motor[J]. Journal of Xi'an Jiaotong University, 2011, 45(10): 59–64. |
| [17] |
赵治国, 朱强, 周良杰, 等.
分布式驱动HEV自适应无迹卡尔曼车速估计[J]. 中国科学:技术科学, 2016, 46(5): 481–492.
ZHAO Zhi-guo, ZHU Qiang, ZHOU Liang-jie, et al. Vehicle speed estimation in driving case based on distributed self-adaptive unscented Kalman filter for 4WD hybrid electric car[J]. Scientia Sinica Technologica, 2016, 46(5): 481–492. |
| [18] |
许波, 朱熀秋, 姬伟, 等.
改进型平方根无迹卡尔曼滤波及其在无轴承永磁同步电机无速度传感器运行中的应用[J]. 控制理论与应用, 2012, 29(1): 53–58.
XU Bo, ZHU Huang-qiu, JI Wei, et al. Modified square-root unscented Kalman filter and its application to speed sensorless control of bearingless permanent magnet synchronous motor[J]. Control Theory & Applications, 2012, 29(1): 53–58. |



