2. 四川华都核设备制造有限公司, 四川 都江堰 611800
2. Sichuan Huadu Nuclear Equipment Manufacturing Co., Ltd., Dujiangyan 611800, China
故障模式分级分析作为系统可靠性分析的重要内容,在可靠性设计改进、故障监测以及故障维修中显得尤其重要。传统故障模式分级分析常采用风险优先数(risk priority number, RPN)分析方法和危害性矩阵分析方法。传统RPN法虽然操作简单,但评价时对评价指标赋予相同权重,未考虑风险参数之间的相对关系并且主观性较强,由此导致分析结果往往与实际情况差距较大。为解决这些问题,陈政平等[1]在RPN分析中采用定量化的参数,提出了一种基于费用损失和工艺故障模式发生概率的定性与定量相结合的分析方法。王志琼等[2]将数据包络法和RPN法相结合,形成了一种新的故障模式风险排序方法。Shi等[3]引入模糊集理论和模糊层次分析法来分析故障模式。王浩伦等[4]引入三角模糊软集法来表示专家评价信息,通过“AND”运算对专家评价信息进行融合,最后得到故障模式风险评估三角模糊软集与风险因子融合指标权重。耿秀丽等[5]考虑了专家风险评估过程中元素隶属度有多个可选值的情况,引入犹豫模糊语义术语集和基于语义计算的方法来表征专家评估信息,提出了基于犹豫模糊集的故障模式风险等级评估方法。Zhou等[6]考虑了各风险因子的相对权重,提出了基于灰色理论和模糊集理论组合方法的RPN评价分析方法。Kutlu等[7]提出了一种基于TOPSIS(technique for order preference by similarity to an ideal solution,逼近理想解排序)法与模糊层次分析法的组合方法来对风险因子进行评断,进而进行RPN分析。Certa等[8]利用D-S证据理论作为数学框架来处理专家评估信息,较好地解决了由于认知不确定性而导致的风险参数输入评估问题。Bozdag等[9]采用基于区间二型模糊集的FMEA(failure mode and effect analysis,失效模式和效果分析)方法对故障模式风险等级进行评估。危害性矩阵分析方法在应用过程中需要大量统计数据来支撑,同时,绘图分析误差较大、效率较低,因此其实用性较差,文献鲜有报道。王锦妮等[10]对危害性矩阵分析方法进行了改进,将每个等级的严酷度划分为5个层次,并用显性直观的数值进行度量,作了一些有益的尝试,但是该方法在实际运用时依然存在较多问题。
据以往经验,对数控机床进行质量特性分析之前需要对复杂的整机进行分解。传统数控机床分解方法均是以设备的硬件结构为依据,将整机按“部件—组件—零件”的思路进行分解[11-12],这样的分解方法思路简单、清晰,但却存在两大问题:其一,对各组部件的相互作用关系没有加以考虑,没有体现分解后的零件功能,更无法全面分析多功能多质量特性之间的耦合;其二,忽略了设备的运动功能,使得分析的结果偏离实际。为解决这些问题,张根保、冉琰等[13-14]尝试从数控机床功能分解的角度进行可靠性分析,并提出了元动作的概念。引入元动作单元作为数控机床故障分析的研究主体可以将故障分析的粒度进行细化,使得数学建模更加容易,故障检测、定位及分级决策更简便,同时更具客观性。
本文在元动作单元概念的基础上,结合灰色聚类理论和粗糙集理论,提出一种基于元动作单元的数控机床故障分级决策方法。首先,介绍了基于系统功能的结构化分解基本流程,给出了元动作单元概念模型;然后,分析了元动作单元的故障模式类型与等级;接着,通过灰色定权聚类理论对元动作单元故障模式等级进行决策分析,再通过粗糙集理论对决策规则进行简化;最后,以某数控机床齿条移动元动作单元为分析主体进行了实例分析。
1 元动作单元的概念 1.1 FMA结构化分解数控机床是机电液一体化的复杂系统,为便于进行质量特性分析,首先要将数控机床分解为简单的基本单元以达到容易建模的目的,然后对基本单元进行质量特性分析,最后对整机的质量特性进行综合分析。按“部件—组件—零件”的分解方法虽然简单易行,但是在实际应用过程中却存在许多难以解决的困难,比如零件数目繁多导致的建模困难、零件故障数据缺乏导致的定量分析困难等。
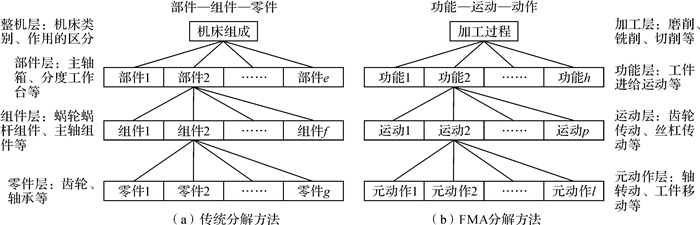
基于系统功能的结构化分解是将复杂的系统按照“功能(function)-运动(motion)-动作(action)”的路线自上而下逐层分解为最基本的动作,即FMA分解,将这种容易控制且易于分析的动作称为元动作。传统分解方法与FMA分解方法的基本流程如图 1所示。
|
| 图 1 传统分解方法与FMA分解方法的基本流程 Fig.1 Basic process of traditional decomposition method and FMA decomposition method |
由图 1可知,FMA分解的中心思想是将机床制造加工这种复杂的综合运动(即功能)进行逐层分解,直至分解为一系列最基本的且不可再分解的动作单元,这类似于整机拆分成零件的过程,只不过前者是以机床的功能为研究对象,后者则是以机床的结构为研究对象。因此,整机的功能运动是否正常实际上取决于各个元动作是否会发生故障。
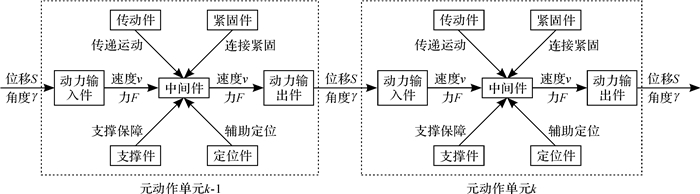
1.2 元动作单元概念模型根据对元动作分解过程的分析可以给出元动作单元的定义:元动作单元是指能够实现任意基本动作的一组零部件的整体。标准元动作单元的组成应包括动力输入件、中间件和动力输出件三类要素,其概念模型如图 2所示。
|
| 图 2 元动作单元概念模型 Fig.2 The concept model of meta-action unit |
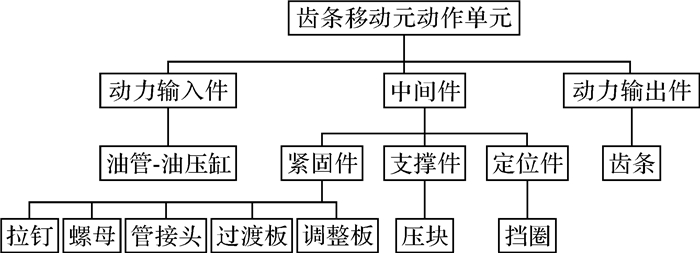
由图 2可知,元动作单元的动力输入件接收前一级元动作单元输出的位移和角度,经过中间件的传递,最后通过动力输出件将位移和角度输送到下一级元动作单元。其中,动力输入件和动力输出件是不可或缺的构成要素,而中间件是由传动件、紧固件、支撑件以及定位件组成的,对于不同的元动作单元,其中间件可能只包括其中的几类。值得注意的是,判断一个零件属于何种要素,要根据该零件在其所属的元动作单元的实际工作中主要扮演的角色(作用或功能)来确定,单独列举某个零件或某类零件是无法断定其所属类别的。
根据最基本的元动作——移动和转动,可将元动作单元分为移动元动作单元和转动元动作单元,而数控机床则可视为由一系列元动作单元组成的复杂机电产品。
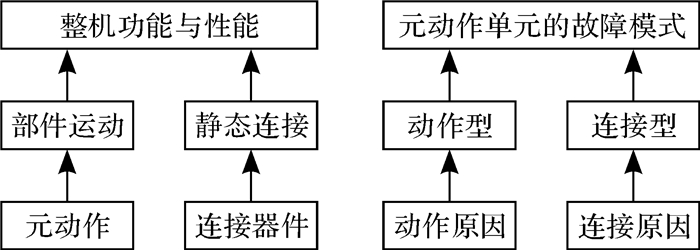
2 元动作单元的故障分析 2.1 故障模式类型分析数控机床之所以会出现问题,是因为元动作单元本身或关联元动作单元之间的连接发生了故障,对数控机床的功能或性能产生了影响,这些故障的表现形式称为故障模式。考虑到元动作单元自身的特点,可将元动作单元故障模式分为动作型和连接型两大类,如图 3所示。图中所提到的“动作”指的就是“元动作”,它造成部件的运动故障,最终导致机床的性能受到影响甚至某些功能无法正确完成。图中的“连接”有2类:一类指的是元动作单元本身的结构连接、运动连接;另一类是指关联元动作单元之间的连接,包括管道连接和线缆连接。结合企业历史数据和文献[15]的相关内容,笔者归纳总结了元动作单元故障模式,具体如表 1所示。
|
| 图 3 元动作单元的故障模式划分 Fig.3 Fault mode division of meta-action unit |
| 类型 | 子类型 | 故障模式 | 故障实例 |
| 动作型 | 动作表现类 | 动作不灵活 | 滚珠丝杠转动不灵活、操作杆移动滞缓等 |
| 误动作 | 牙嵌式安全离合器误动作、磁性联轴器误动作等 | ||
| 移动/转动不到位 | 导向管移动不到位、抓手移动不到位等 | ||
| 移动/转动超程 | 导向管移动过位、抓手移动过位等 | ||
| 动作不平稳 | 导向管移动不平稳、操作杆移动不平稳等 | ||
| 动作过程有异响、噪声 | 齿轮传动有异响、丝杠螺母移动异响等 | ||
| 制动失灵 | 砂轮主轴停止困难、修整轮停止时长时间空转等 | ||
| 动作完全失效、不动作 | 液压缸活塞不移动、刀库无换刀等 | ||
| 动作协调类 | 关联元动作不同步 | 驱动电机与抓手移动不同步等 | |
| 关联元动作发生干涉 | 齿轮啮合因几何尺寸问题卡死、碰撞等 | ||
| 关联元动作不协调 | 导向管移动未到位时抓手移动等 | ||
| 动作精度类 | 回零精度超差 | 刀库回零精度超差等 | |
| 定向精度超差 | 导向管定位精度超差、抓手移动定位精度超差等 | ||
| 移动/转动精度不高 | 开槽管旋转精度超差、齿条移动精度不高等 | ||
| 连接型 | 连接故障类 | 连接单元损坏 | 丝杆断裂、齿轮断齿、密封件损坏等 |
| 连接单元装配、结合不到位 | 螺母与丝杠装配间隙过大、防松螺母未拧紧、牙嵌式安全离合器装配不当等 | ||
| 泄漏(包括液、气、油) | 磁性联轴器漏油、蜗轮蜗杆单元漏油等 | ||
| 堵塞(包括液、气、油) | 油压缸堵塞等 |
元动作单元作为数控机床的基本组成单元,其故障模式多种多样,而且不同的故障模式对整机功能的影响也有所不同,将故障影响、经济损失、检测难度和维修难度作为分级标准,本文将元动作单元的故障模式分成3个等级:关键故障、主要故障和次要故障。
关键故障:故障一旦发生将导致元动作单元失效,以致系统功能受到较大影响,经济损失巨大,处理不当甚至会威胁到相关人员的生命安全。
主要故障:故障难以检测,会导致元动作单元损坏,系统功能受到影响,将造成较大经济损失。
次要故障:故障对系统的功能实现影响较小,易修理且所需费用不高。
快速、准确地对故障等级进行判断有助于设计人员有针对性地进行故障维修重点分析以及设计改进,也有助于维修保障人员选择适当的维修方式,避免出现花大代价处理次要问题,而严重问题却未被重视的情况。如何科学合理地制定决策规则从而判断故障所属等级是研究的难题,而本文提出的结合了灰色粗糙集组合理论的决策方法可以较好地予以解决。
2.3 基于灰色定权聚类的故障模式分级决策灰色定权聚类分析方法是一种多元统计方法,主要应用于系统模型不明确的关联分析以及模型建立,信息不完整情况下的预测、决策等问题[16]。
1) 故障信息矩阵的建立。
假设某数控机床的其中一个元动作单元出现了n类故障模式,将这些故障模式作为决策对象i,针对这些故障模式的评价指标共有m个,称这些评价指标为决策指标属性j,存在s个决策灰类,则决策对象i关于决策指标j的量化评价值xij(i=1, 2, …, n;j=1, 2, …, m)所组成的信息矩阵为:
| $ \mathit{\boldsymbol{X}} = \left( {{x_{ij}}} \right) = \left( {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1m}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}}\\ {{x_{31}}}&{{x_{32}}}& \cdots &{{x_{3m}}}\\ \vdots&\vdots &{}& \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nm}}} \end{array}} \right) $ | (1) |
2) 白化权函数fjk(xij)和决策权ηj的确定。
将fjk(xij)(j=1, 2, …, m; k=1, 2, …, s)称为决策指标j关于k灰类的白化权函数,决策指标j的决策权用ηj(j=1, 2, …, m)表示,且有:
| $ \sum\limits_{j = 1}^m {{\eta _j}} = 1 $ | (2) |
对于灰色定权聚类分析方法而言,白化权函数fjk(xij)的表达式通常由相关行业的专家给定,决策权ηj的值可通过专家法进行确定,也可通过下述方法确定:
①由决策对象i关于决策指标j的量化评价值xij(i=1, 2, …, n; j=1, 2, …, m)可得到决策矩阵X=(xij)n×m。
② 利用白化权函数fjk(xij)以及决策矩阵X求得规范化决策矩阵R=(rijk)n×m(k=1, 2, …, s),其中rijk的表达式如下:
| $ r_{ij}^k = f_j^k\left( {{x_{ij}}} \right) $ |
③ 由专家根据已知信息提供一个目标权重wjk(j=1, 2, …, m; k=1, 2, …, s)。
④ 由单目标(
若问题为效益型时,用
| $ \mathit{\boldsymbol{w}}_i^k = \left( {w_{i1}^k,w_{i2}^k, \cdots ,w_{im}^k} \right) $ |
⑤ 由n个权重向量wik组成矩阵W=(wijk)n×m;计算矩阵(WRT)(WRT)T的最大特征值λmaxk及对应的特征向量w=(w1k, w2k, …, wmk)T。
⑥ 对w作归一化处理即可得到决策权重向量η=(η1k, η2k, …, ηmk)T。
上述方法推证过程见文献[17],本文不再赘述。
3) 故障模式所属灰类的确定。
根据上述步骤得出的白化权函数、决策权以及决策对象i关于决策指标j的量化评价值,算出灰色定权聚类系数σik(i=1, 2, …, n; k=1, 2, …, s):
| $ \sigma _i^k = \sum\limits_{j = 1}^m {f_j^k\left( {{x_{ij}}} \right){\eta _j}} $ | (3) |
根据所得出的灰色定权聚类系数判定故障模式i所属的灰类k,判断式为:
| $ \sigma _i^{{k^ * }} = \mathop {\max }\limits_{1 \le k \le s} \left\{ {\sigma _i^k} \right\} $ | (4) |
灰色系统本身缺乏较强的并行计算能力与数据推理能力,一旦系统轻微改变,后续过程都需要重新计算[18]。因聚类结果缺乏柔性,所以需要对系统信息的处理过程进行优化,本文引入了粗糙集理论来解决该问题。
粗糙集理论作为一种新型的信息处理数学工具,主要应用于已知信息不精确、不完备、不统一等场合。科学合理地将灰色系统理论和粗糙集理论进行结合,能更好地解决信息不确定、不完全处理领域的问题。粗糙集理论的重点内容是知识约简,即利用已知的决策对象、决策指标、灰色聚类结果形成一个原始决策表,考虑到元动作单元故障模式的已知数据存在不完全性并且聚类结果存在灰性(即信息不精确)的特点,若直接对所建立的原始决策表进行知识约简,那么很可能会导致极小决策算法与问题的实际意义相悖。为了优化决策算法,使决策规则更具柔性,笔者先对原始决策表进行离散化处理,然后对它进行知识约简。
1) 建立原始决策表。
根据决策对象、决策指标、聚类结果建立决策表,令决策表DT=(U, P∪D),子集D={d}为决策属性集,子集P={aj|j=1, 2, …, m}为条件属性集,U={i|i=1, 2, …,n}为论域,aij表示决策对象i在条件属性aj上的值。
2) 决策表的离散化处理。
结合灰色聚类分析的特点,采用基于属性重要性即指标决策权值大小的离散化算法,其离散化过程如下[19]:
步骤1:初始化候选断点集,令CUT={Caj︱j=1, 2, …, m},其中Caj为条件属性aj的候选断点集。
步骤2:按属性重要性(即条件属性的决策权值)由小到大对属性aj(j=1, 2, …, m)进行排序,若出现重要性相同的情况,则依据各条件属性候选断点的个数从多到少进行排序。
步骤3:考察属性aj中的每一个候选断点Caj的存在性,即把原始决策表中与Caj相邻的2个属性值中的较小值改成较大值。如果此时的决策表不会产生冲突,那么把Caj从断点集中去除;否则,还原已修改的属性值。
步骤4:整理得到离散化后的决策表。
3) 利用可辨识矩阵法得到决策表的极小决策算法。
通过离散化后的决策表计算可辨识矩阵CD,用cuv表示其第u行第v列的元素,可辨识矩阵的元素可通过下列公式得到:
| $ {c_{uv}} = \left\{ \begin{array}{l} \left[ {{a_j}\left| {{a_j} \in P \wedge {a_{uj}} \ne {a_{vj}}} \right.} \right],d\left( u \right) \ne d\left( v \right)\\ \emptyset ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d\left( u \right) = d\left( v \right) \end{array} \right. $ | (5) |
式中:u, v=1, 2, …, n; d(u)表示决策表DT的决策属性子集D中第u个故障模式对应的值。
称布尔函数Δ为可辨识函数,其计算公式为:
| $ \Delta = \prod\limits_{\left( {x,y} \right) \in U \times U} {\sum {{c_{uv}}} } $ | (6) |
式中:当cuv=
4) 通过可辨识函数与离散化的决策表写出极小决策算法。
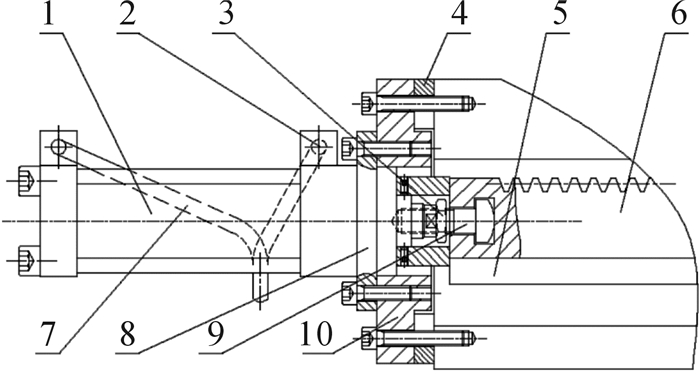
3 实例分析以某数控机床的齿条移动元动作单元为例,该元动作单元的结构如图 4所示,组成要素如图 5所示。
|
| 1—油压缸;2—管接头;3—螺母;4—调整板;5—压块;6—齿条;7—油管;8—挡圈;9—拉钉;10—过渡板 图 4 数控机床齿条移动元动作单元结构示意图 Fig.4 Structure diagram of the rack movement meta-action unit in the CNC machine tool |
|
| 图 5 数控机床齿条移动元动作单元组成要素 Fig.5 Constituent elements of the rack movement meta-action unit in the CNC machine tool |
将齿条移动元动作单元出现的6种故障模式,即齿条移动过位、漏油、齿条移动发出异响、齿面疲劳磨损、齿条断齿和齿条移动不平稳,进行故障分级决策分析。这6种故障模式按发生频度、危害程度、检测难度和维修难度这4个决策指标进行评价,邀请该领域专家按4个决策指标对这6种故障模式进行评分(分值越高表示程度越高),得到的量化评价值如表 2所示。
| 故障模式 | 发生频度 | 危害程度 | 检测难度 | 维修难度 |
| 齿条移动过位 | 60 | 93 | 84 | 53 |
| 漏油 | 88 | 62 | 60 | 45 |
| 齿条移动发出异响 | 55 | 75 | 74 | 61 |
| 齿面疲劳磨损 | 77 | 86 | 60 | 55 |
| 齿条断齿 | 86 | 93 | 51 | 69 |
| 齿条移动不平稳 | 67 | 70 | 72 | 49 |
由公式(1)得到量化评价值xij(i=1, 2, …, 6;j=1, 2, …, 4)组成的信息矩阵为:
| $ \mathit{\boldsymbol{X}} = \left( {{x_{64}}} \right) = \left( {\begin{array}{*{20}{c}} {60}&{93}&{84}&{53}\\ {88}&{62}&{60}&{45}\\ {55}&{75}&{74}&{61}\\ {77}&{86}&{60}&{55}\\ {86}&{93}&{51}&{69}\\ {67}&{70}&{72}&{49} \end{array}} \right) $ |
将关键故障、主要故障、次要故障这3个灰类作为聚类决策,提供决策规则。经相关专家给定,得到这4个决策指标关于3个灰类的白化权函数为:
| $ f_j^1\left( {{x_{ij}}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;{x_{ij}} < 70\\ \frac{{{x_{ij}} - 70}}{{20}},70 \le {x_{ij}} \le 90\\ 1,\;\;\;\;\;\;\;\;\;\;\;{x_{ij}} > 90 \end{array} \right. $ |
| $ f_j^2\left( {{x_{ij}}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;{x_{ij}} < 55\\ \frac{{{x_{ij}} - 55}}{{15}},55 \le {x_{ij}} \le 70\\ \frac{{85 - {x_{ij}}}}{{15}},70 \le {x_{ij}} \le 85\\ 0,\;\;\;\;\;\;\;\;\;\;{x_{ij}} > 85 \end{array} \right. $ |
| $ f_j^{\rm{3}}\left( {{x_{ij}}} \right) = \left\{ \begin{array}{l} {\rm{1}},\;\;\;\;\;\;\;\;\;\;{\rm{0}} \le {x_{ij}} < {\rm{4}}0\\ \frac{{65 - {x_{ij}}}}{{25}},40 \le {x_{ij}} \le 65\\ 0,\;\;\;\;\;\;\;\;\;\;{x_{ij}} > 65 \end{array} \right. $ |
通过专家法确定发生频度、危害程度、检测难度和维修难度这4个决策指标对应的决策权,分别为:η1=0.18,η2=0.28,η3=0.28,η4=0.26。
将信息矩阵、白化权函数和决策权代入公式(3)中计算可得到灰色定权聚类系数矩阵σ为:
| $ \begin{array}{l} \mathit{\boldsymbol{\sigma }} = {\left( {\sigma _i^k} \right)_{6 \times 3}} = \left[ {\begin{array}{*{20}{c}} {\sigma _1^1}&{\sigma _1^2}&{\sigma _1^3}\\ {\sigma _2^1}&{\sigma _2^2}&{\sigma _2^3}\\ {\sigma _3^1}&{\sigma _3^2}&{\sigma _3^3}\\ {\sigma _4^1}&{\sigma _4^2}&{\sigma _4^3}\\ {\sigma _5^1}&{\sigma _5^2}&{\sigma _5^3}\\ {\sigma _6^1}&{\sigma _6^2}&{\sigma _6^3} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {0.476\;0}&{0.078\;7}&{0.160\;8}\\ {0.162\;0}&{0.224\;0}&{0.297\;6}\\ {0.126\;0}&{0.496\;0}&{0.113\;6}\\ {0.287\;0}&{0.189\;3}&{0.160\;0}\\ {0.424\;0}&{0.242\;7}&{0.156\;8}\\ {0.028\;0}&{0.666\;7}&{0.166\;4} \end{array}} \right] \end{array} $ |
根据公式(4)可得:
| $ \mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{1}}^k} \right) = \sigma _{\rm{1}}^{\rm{1}} = {\rm{0}}{\rm{.476}}\;{\rm{0}},\mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{2}}^k} \right) = \sigma _{\rm{2}}^{\rm{3}} = 0.297\;6 $ |
| $ \mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{3}}^k} \right) = \sigma _{\rm{3}}^{\rm{2}} = {\rm{0}}{\rm{.496}}\;{\rm{0}},\mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{4}}^k} \right) = \sigma _{\rm{4}}^{\rm{1}} = 0.287\;0 $ |
| $ \mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{5}}^k} \right) = \sigma _{\rm{5}}^{\rm{1}} = {\rm{0}}{\rm{.424}}\;{\rm{0}},\mathop {\max }\limits_{1 \le k \le {\rm{3}}} \left( {\sigma _{\rm{6}}^k} \right) = \sigma _{\rm{6}}^{\rm{2}} = 0.666\;7 $ |
从上述结果可知:编号为1, 4, 5的故障模式,即齿条移动过位、齿面疲劳磨损、齿条断齿,属于关键故障灰类;编号为3, 6的故障模式,即齿条移动发出异响、齿条移动不平稳,属于主要故障灰类;编号为2的故障模式,即漏油,属于次要故障灰类。
若令a1、a2、a3、a4分别代表发生频度、危害程度、检测难度和维修难度这4个决策指标;d=1, 2, 3分别代表关键故障、主要故障和次要故障,则可通过灰色聚类结果得到齿条移动元动作单元故障模式分级的原始决策表。
| U | a1 | a2 | a3 | a4 | d |
| 1 | 60 | 93 | 84 | 53 | 1 |
| 2 | 88 | 62 | 60 | 45 | 3 |
| 3 | 55 | 75 | 74 | 61 | 2 |
| 4 | 77 | 86 | 60 | 55 | 1 |
| 5 | 86 | 93 | 51 | 69 | 1 |
| 6 | 67 | 70 | 72 | 49 | 2 |
根据原始决策表可得各指标的候选断点集为:
| $ {C_{{a_1}}} = \left\{ {58,64,72,82,87} \right\},{C_{{a_2}}} = \left\{ {66,73,81,90} \right\} $ |
| $ {C_{{a_3}}} = \left\{ {56,66,73,79} \right\},{C_{{a_4}}} = \left\{ {47,51,54,58,65} \right\} $ |
由于4个指标的决策权η1<η4<η2=η3,且Ca2与Ca3的断点个数相同,所以原始决策表存在2条离散化路径:a1→a4→a3→a2(路径1)和a1→a4→a2→a3(路径2),最终得到的2个离散化后的决策表如表 4和表 5所示。
| U | a1 | a2 | a3 | a4 | d |
| 1 | 88 | 93 | 84 | 69 | 1 |
| 2 | 88 | 62 | 84 | 69 | 3 |
| 3 | 88 | 75 | 84 | 69 | 2 |
| 4 | 88 | 93 | 84 | 69 | 1 |
| 5 | 88 | 93 | 84 | 69 | 1 |
| 6 | 88 | 75 | 84 | 69 | 2 |
| U | a1 | a2 | a3 | a4 | d |
| 1 | 88 | 93 | 84 | 69 | 1 |
| 2 | 88 | 75 | 60 | 69 | 3 |
| 3 | 88 | 75 | 84 | 69 | 2 |
| 4 | 88 | 93 | 60 | 69 | 1 |
| 5 | 88 | 93 | 60 | 69 | 1 |
| 6 | 88 | 75 | 84 | 69 | 2 |
用可辨识矩阵法对表 4进行知识约简,根据公式(5)和公式(6)可先后得出表 4的可辨识矩阵和可辨识函数分别为:
| $ {\mathit{\boldsymbol{C}}_{{\rm{D1}}}} = \left[ {\begin{array}{*{20}{c}} 0&{{a_2}}&{{a_2}}&0&0&{{a_2}}\\ {}&0&{{a_2}}&{{a_2}}&{{a_2}}&{{a_2}}\\ {}&{}&0&{{a_2}}&{{a_2}}&0\\ {}&{}&{}&0&0&{{a_2}}\\ {}&{}&{}&{}&0&{{a_2}}\\ {}&{}&{}&{}&{}&0 \end{array}} \right] $ |
| $ {\Delta _1} = {a_2} $ |
从而可得表 4的极小决策算法为:
| $ \left\{ \begin{array}{l} {a_{{2_{93}}}} \to d = 1\\ {a_{{2_{75}}}} \to d = 2\\ {a_{{2_{62}}}} \to d = 3 \end{array} \right. $ |
综合考虑原始决策表的离散化过程与最终得到的极小决策算法,得到的按路径1离散化后故障分级的决策规则用自然语言可解释为:当评价指标a2的量化值处于86~93之间时,决策对象应划分为关键故障灰类;当评价指标a2的量化值处于70~85之间时,决策对象应划分为主要故障灰类;当评价指标a2的量化值不高于69时,决策对象应划分为次要故障灰类。
同理可得表 5的可辨识矩阵、可辨识函数与极小决策算法分别为:
| $ {\mathit{\boldsymbol{C}}_{{\rm{D2}}}} = \left[ {\begin{array}{*{20}{c}} 0&{{a_2}{a_3}}&{{a_2}}&0&0&{{a_2}}\\ {}&0&{{a_3}}&{{a_2}}&{{a_2}}&{{a_3}}\\ {}&{}&0&{{a_2}{a_3}}&{{a_2}{a_3}}&0\\ {}&{}&{}&0&0&{{a_2}{a_3}}\\ {}&{}&{}&{}&0&{{a_2}{a_3}}\\ {}&{}&{}&{}&{}&0 \end{array}} \right] $ |
| $ {\Delta _2} = {a_2} \wedge {a_3} $ |
| $ \left\{ \begin{array}{l} {a_{{2_{93}}}} \to d = 1\\ {a_{{2_{75}}}}{a_{{3_{84}}}} \to d = 2\\ {a_{{2_{75}}}}{a_{{3_{60}}}} \to d = 3 \end{array} \right. $ |
综合考虑原始决策表的离散化过程与最终得到的极小决策算法,得到的按路径2离散化后故障分级的决策规则用自然语言可解释为:当评价指标a2的量化值处于86~93之间时,决策对象应划分为关键故障灰类;当评价指标a2的量化值处于70~85之间,且评价指标a3的量化值不低于72时,决策对象应划分为主要故障灰类;当评价指标a2的量化值低于86,且评价指标a3的量化值低于72时,决策对象应划分为次要故障灰类。
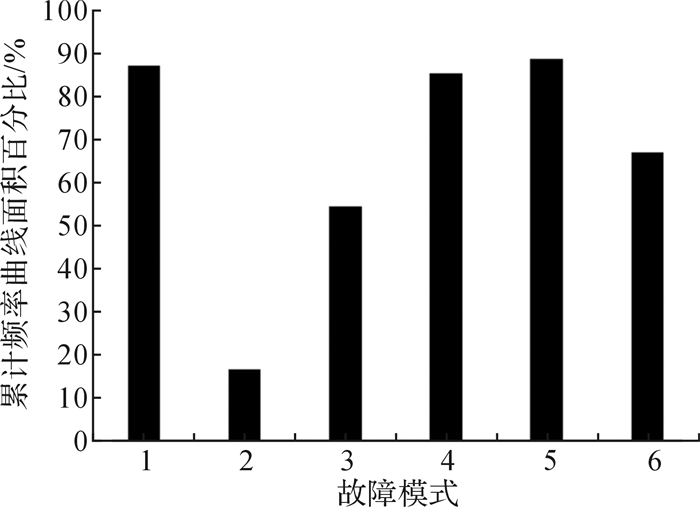
为验证案例分析的准确性,引用文献[15]的方法对此案例进行分析,得到故障模式重要度统计图, 如图 6所示。由图 6可得到6种故障模式重要度优先级排序为:齿条断齿、齿条移动过位、齿面疲劳磨损、齿条移动不平稳、齿条移动发出异响、漏油,其结果与本文所用方法得到的结论基本一致,而且本文所用方法避免了计算机仿真所带来的误差,能够通过较少的量化评价指标快速地对故障模式等级进行决策,所得结论更加明确且具有针对性,相较于实际工程应用中许多企业采用RPN法或危害性矩阵图法确定其数控机床故障等级而言,本文方法更加客观、准确且效率较高,便于企业设计人员进行重点分析、设计改进以及维修过程控制。
|
| 图 6 数控机床齿条移动元动作单元故障模式重要度统计图 Fig.6 Statistical diagram of the importance of rack movement meta-action unit failure mode in the CNC machine tool |
为快速、准确地判断数控机床的故障等级,本文提出了一种基于元动作单元并结合了灰色聚类理论与粗糙集理论的故障分级决策方法。首先,利用元动作的思想将复杂的数控机床进行功能分解以细化故障分析的粒度; 其次,给出了元动作单元的概念模型以及故障模式类型; 然后,通过灰色定权聚类分析法对故障模式的量化评价值进行分析,利用得出的聚类结果建立了数控机床故障模式分级的原始决策表,再通过粗糙集理论对原始决策表进行知识约简,最终得到离散化后的决策表以及极小决策算法,从而达到快速、准确判断数控机床故障等级的目的。通过实例分析验证了该方法的合理性与有效性。该方法提供了一种将元动作单元作为研究主体应用于数控机床故障分级分析中的新思路,同时在工程应用中为相关企业提供了一个确定数控机床故障等级的重要参考,具有较强的工程实践价值。
| [1] |
陈政平, 付桂翠, 赵幼虎.
改进的风险优先数(RPN)分析方法[J]. 北京航空航天大学学报, 2011, 37(11): 1395–1399.
CHEN Zheng-ping, FU Gui-cui, ZHAO You-hu. Improved analysis method of risk priority number[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(11): 1395–1399. |
| [2] |
王志琼, 申桂香, 张英芝, 等.
基于数据包络的松拉刀机构故障模式风险分析[J]. 华南理工大学学报(自然科学版), 2015, 43(7): 142–146.
WANG Zhi-qiong, SHEN Gui-xiang, ZHANG Ying-zhi, et al. Risk analysis of failure mode of clamping and releasing tool based on data envelopment analysis[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(7): 142–146. DOI:10.3969/j.issn.1000-565X.2015.07.020 |
| [3] | SHI Jun-li, WANG Ya-jun, JIN Hai-hua, et al. A modified method for risk evaluation in failure mode and effects analysis[J]. Journal of Applied Science and Engineering, 2016, 19: 177–186. |
| [4] |
王浩伦, 徐翔斌, 甘卫华.
基于三角模糊软集的FMEA风险评估方法[J]. 计算机集成制造系统, 2015, 21(11): 3054–3062.
WANG Hao-lun, XU Xiang-bin, GAN Wei-hua. Risk evaluation method in FMEA based on triangular fuzzy soft set[J]. Computer Integrated Manufacturing Systems, 2015, 21(11): 3054–3062. |
| [5] |
耿秀丽, 张永政.
基于犹豫模糊集的改进FMEA风险评估方法[J]. 计算机集成制造系统, 2017, 23(2): 340–348.
GENG Xiu-li, ZHANG Yong-zheng. Improved FMEA approach for risk evaluation based on hesitant fuzzy set[J]. Computer Integrated Manufacturing Systems, 2017, 23(2): 340–348. |
| [6] | ZHOU Q, THAI V V. Fuzzy andgrey theories in failure mode and effect analysis for tanker equipment failure prediction[J]. Safety Science, 2016, 83: 74–79. DOI:10.1016/j.ssci.2015.11.013 |
| [7] | KUTLU A C, EKMEKÇIO LU M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J]. Expert Systems with Applications, 2012, 39(1): 61–67. DOI:10.1016/j.eswa.2011.06.044 |
| [8] | CERTA A, HOPPS F, INGHILLERI R, et al. A Dempster-Shafer theory-based approach to the Failure Mode, Effects and Criticality Analysis (FMECA) under epistemic uncertainty:application to the propulsion system of a fishing vessel[J]. Reliability Engineering and System Safety, 2017, 159: 69–79. DOI:10.1016/j.ress.2016.10.018 |
| [9] | BOZDAG E, ASAN U, SOYER A, et al. Risk prioritization in failure mode and effects analysis using interval type-2 fuzzy stes[J]. Expert Systems with Applications, 2015, 42(8): 4000–4015. DOI:10.1016/j.eswa.2015.01.015 |
| [10] |
王锦妮, 火建卫.
定量危害性矩阵分析方法研究[J]. 航空工程进展, 2016, 7(1): 70–77.
WANG Jin-ni, HUO Jian-wei. Research on quantitative criticality matrix analysis method[J]. Advances in Aeronautical Science and Engineering, 2016, 7(1): 70–77. |
| [11] |
王波, 唐晓青, 耿如军.
机械产品装配关系建模[J]. 北京航空航天大学学报, 2010, 36(1): 71–76.
WANG Bo, TANG Xiao-qing, GENG Ru-jun. Modeling for assembly structure in mechanical product[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1): 71–76. |
| [12] |
陈循, 陶俊勇, 张春华.
可靠性强化试验与加速寿命试验综述[J]. 国防科技大学学报, 2002, 24(4): 29–32.
CHEN Xun, TAO Jun-yong, ZHANG Chun-hua. Reliability enhancement testing and accelerated life testing:an introductory review[J]. Journal of National University of Defense Technology, 2002, 24(4): 29–32. DOI:10.3969/j.issn.1001-2486.2002.04.008 |
| [13] |
张根保, 孙恒, 范秀君.
数控机床基于FMA的功能分解与可靠性分析[J]. 机械科学与技术, 2012, 31(4): 528–533.
ZHANG Gen-bao, SUN Heng, FAN Xiu-jun. Function decomposition and reliability analysis of CNC machine using function-motion-action[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(4): 528–533. |
| [14] | RAN Yan, ZHANG Gen-bao, ZHANG Lian. Quality characteristic association analysis of computer numerical control machine tool based on meta-action assembly unit[J]. Advances in Mechanical Engineering, 2016, 8(1): 1–10. |
| [15] |
周庆法.基于元动作单元的核换料机可靠性分析与控制技术研究[D].重庆: 重庆大学机械工程学院, 2017: 27-28.
ZHOU Qing-fa. Research on reliability analysis and control technology of nuclear refueling machine based on meta-action unit[D]. Chongqing: Chongqing University, College of Mechanical Engineering, 2017: 27-28. http://cdmd.cnki.com.cn/Article/CDMD-10611-1017838344.htm |
| [16] |
邓聚龙.
灰色系统基本方法[M]. 武汉: 华中科技大学出版社, 2005: 2-4.
DENG Ju-long. The primary methods of grey system theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2005: 2-4. |
| [17] |
徐泽水.
部分权重信息下多目标决策方法研究[J]. 系统工程理论与实践, 2002, 22(1): 43–47.
XU Ze-shui. On method for multi-objective decision-making with partial weight information[J]. Systems Engineering Theory and Practice, 2002, 22(1): 43–47. DOI:10.3321/j.issn:1000-6788.2002.01.007 |
| [18] |
吕宏辉, 钟珞, 夏红霞.
灰色系统与神经网络融合技术探索[J]. 微机发展, 2000(3): 3–5.
LÜ Hong-hui, ZHONG Luo, XIA Hong-xia. Exploring in fusion technology of grey system and neural networks[J]. Microcomputer Development, 2000(3): 3–5. |
| [19] |
王国胤.
Rough集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001: 112-114.
WANG Guo-yin. Rough set theory and knowledge acquisition[M]. Xi'an: Xi'an Jiaotong University Press, 2001: 112-114. |



