传统耗能器通过自身材料的塑性屈服、黏滞流动或摩擦等形式耗能,震后结构产生的塑性形变导致结构的修复成本高于重建成本或结构无法修复到正常使用状态。Sabelli等[1]对安装了普通耗能器的框架结构进行分析,结果表明普通耗能器在震后产生的最大残余变形达0.7%。Kiggins等[2]也作了类似分析, 得到了相似的结果。Kawashima等[3]对1995年日本神户地震后建筑物受损情况进行调查统计后发现,当柱结构顶端残余变形角超过1°时,其修复成本高于重建成本。Mccormick等[4]通过研究发现,当层间位移角超过1/200时结构的修复成本将超过重建成本,同时还研究了建筑物的残余变形对人生理和心理的影响,结果表明当残余变形达到1%时人会感到头晕及恶心。因此,残余变形是决定震后结构重建与否的一个重要因素。针对普通耗能器的不足,Christopoulos等[5-6]提出了自复位系统, 随后又对摩擦型自复位耗能器作了系统分析,结果表明该类耗能器既能通过自身耗能避免结构主体遭到破坏,又能通过复位力减小结构残余变形。池沛等[7]摒弃复杂的内、中、外筒嵌套模式,将复位系统与耗能系统分离,不但简化了耗能器的结构,而且降低了耗能器刚度。张爱林等[8]采用零预应力钢索作为复位系统,震后通过人工调节摩擦板对拉螺栓的预紧力使支撑继续复位,该构造避免了复杂的预应力施加过程并有效减小了耗能器残余变形。王涛等[9]采用零预应力的弹簧作为复位构件,也达到了较好的复位效果。周中哲等[10-12]采用类似于并联弹簧的双重复位系统作为耗能器的复位装置,发现该耗能器在增大支撑轴向变形的同时不削弱支撑复位性能。
根据以上学者对耗能支撑所作的有效改进,本文设计了一种零初始索力自复位耗能器(zero initial cable tension self-resetting energy dissipation device,ZTSEDD),该耗能器由传动装置(transmission device, TD)、碟形弹簧复位装置(disc spring reset device, DSRD)和双剪型摩擦耗能装置(double shear friction energy dissipation device, DSFEDD)组成,其中,TD通过钢索将结构位移传递给ZTSEDD,DSRD通过零预应力碟形弹簧提供恢复力,DSFEDD采用双剪型长孔螺栓板摩擦耗能。本文将对复位装置、耗能装置的结构以及耗能器的工作原理进行分析,基于ABAQUS建立其有限元模型,并对其工作性能进行研究。
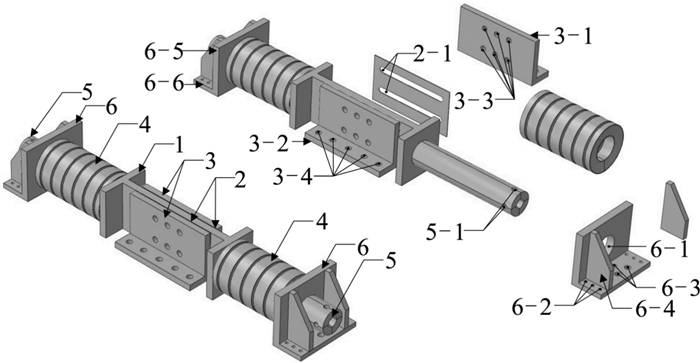
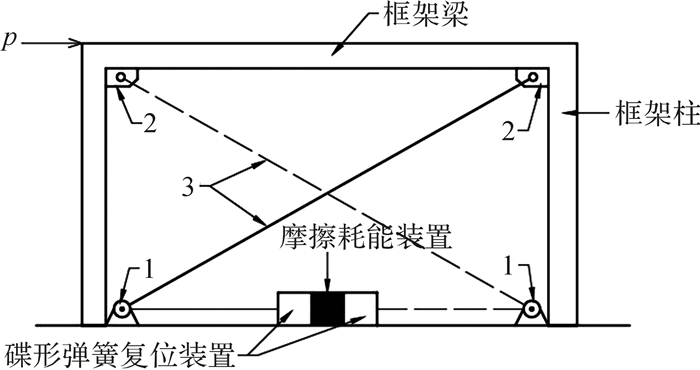
1 ZTSEDD的构造及其工作原理 1.1 构造形式本文所设计的耗能器的组装图及其耗能装置与复位装置的结构如图 1和图 2所示,图 1中p为加载在框架梁左端的外力,2套复位装置和传动装置对称安装在耗能装置两侧。耗能装置由摩擦外板、带有导滑槽的H型滑动主板叠合而成,中间嵌入黄铜板以保证滑动摩擦力能均匀稳定地传递。摩擦外板短肢通过锚栓固定在楼板上,摩擦外板长肢与H型滑动主板通过对拉预紧螺栓紧固。复位装置主要构件包括碟形弹簧、圆形内套筒及限位板。圆形内套筒一端焊接于H型滑动主板上,另一端穿过与楼板锚固的限位板。圆形内套筒上套有数组碟形弹簧,末端预留索孔。传动装置主要构件包括定滑轮、连接角板和高强度钢绞线,组装时高强度钢绞线一端锚固于与梁柱焊接的角板,另一端穿过锚固在地面上的定滑轮与复位装置圆形内套筒连接,通过调节钢绞线的长度,无需改变耗能装置和复位装置的构件尺寸,便可将ZTSEDD安装于不同尺寸的结构。
|
| 1—定滑轮; 2—连接角板; 3—高强度钢绞线 图 1 零初始索力自复位耗能器组装图 Fig.1 Assembly drawing of ZTSEDD |
|
| 1—H型滑动主板;2—黄铜板;3—摩擦外板;4—复合组合碟形弹簧;5—圆形内套筒;6—限位板;2-1—黄铜板长条孔;3-1—摩擦外板长肢;3-2—摩擦外板短肢;3-3—摩擦外板螺栓孔;3-4—摩擦外板锚栓孔;5-1—圆形内套筒索孔;6-1—限位板圆孔;6-2, 6-3—限位板锚栓;6-4—限位板肋板;6-5—限位板长肢;6-6—限位板短肢 图 2 碟形弹簧复位装置和双剪型摩擦耗能装置的结构示意图 Fig.2 Structure diagram of DSRD and DSFEDD |
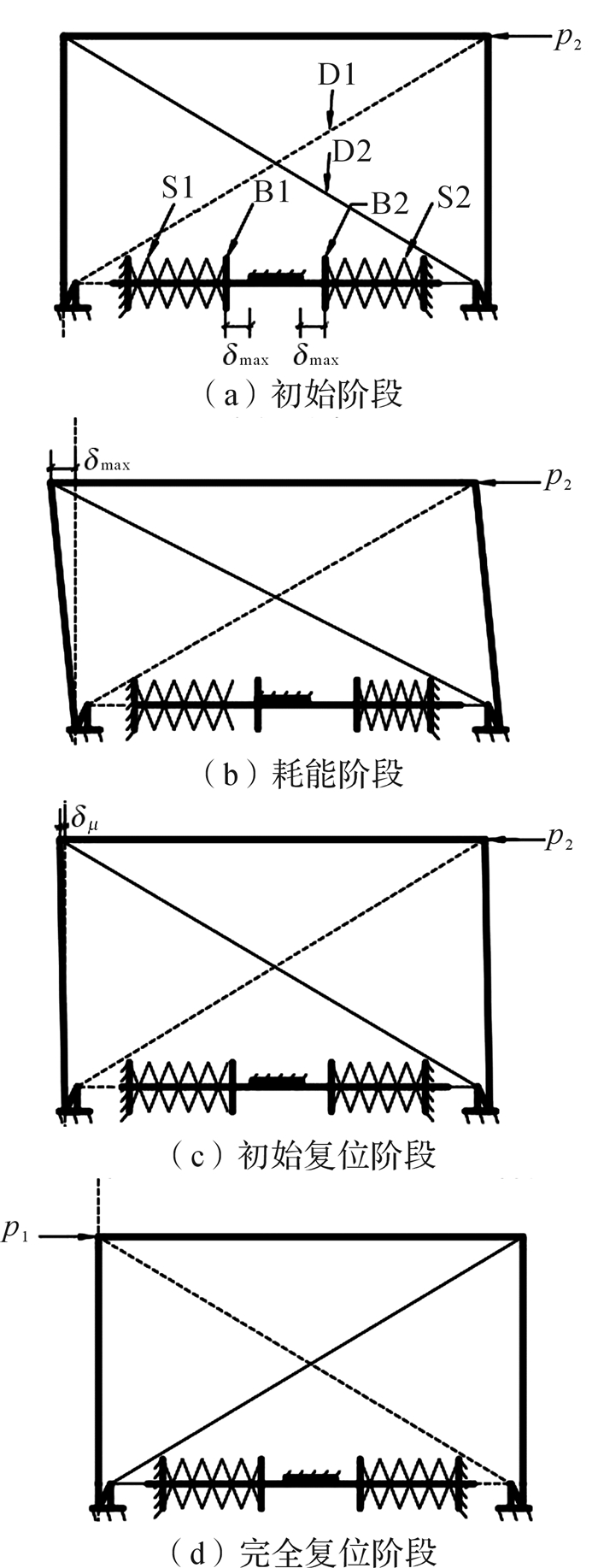
本文设计的耗能器独自承担相反方向的框架层间位移。不同阶段下其工作过程简图如图 3所示,其中:S1和S2表示复合组合碟形弹簧,B1和B2表示H型滑动主板的端板,C表示摩擦外板,D1和D2表示拉索,实线表示受力的钢索,虚线表示松弛的钢索。位于S1左端的构件为限位板1,位于S2右端的构件为限位板2,位于限位板1和限位板2之间的长轴为圆形内套筒和H型滑动主板的腹板,与H型滑动主板接触的为摩擦外板。为保证该耗能器在结构塑性变形状态下能正常工作,摩擦外板与H型滑动主板的腹板两端间的预留距离应大于δmax,δmax为结构在罕遇地震作用下按弹塑性理论计算的层间位移。
|
| 图 3 零初始索力自复位耗能器工作过程示意图 Fig.3 Working process diagram of ZTSEDD |
本文设计的耗能器的工作过程具体可分为以下几个阶段:
1) 耗能器框架整体向左侧发生层间位移,拉索2拉动自复位耗能器开始工作,即拉索2拉动滑动主板相对于摩擦外板滑动,产生摩擦耗能;同时端板2挤压碟形弹簧2,使得碟形弹簧2产生形变,如图 3(b)所示。
2) 当耗能器框架向左的层间位移达到最大值时,拉索2对滑动主板的拉力也达到最大值,则此时框架向相反方向移动,此过程中钢索2对滑动主板的拉力快速减小,当钢索2对滑动主板的拉力小于碟形弹簧2对滑动主板的弹力和滑动摩擦力之和时,滑动主板往反向运动,即滑动主板向初始位置的方向移动,此过程中碟形弹簧2对滑动主板的弹力大于滑动摩擦力,且碟形弹簧2对滑动主板的弹力逐渐减小,如图 3(c)所示。
3) 当耗能器框架经过初始位置后继续往反向运动时,位于另一侧的拉索1开始受力,碟形弹簧1开始工作,工作过程相同,如图 3(d)所示,如此循环工作。
4) 当耗能器框架停止移动后,碟形弹簧对滑动主板的弹力减小到等于滑动摩擦力时,滑动主板停止复位,此时滑动主板距初值位置的距离为滑动摩擦力作用下碟形弹簧的形变量。该耗能器向左运动与向右运动的过程相似。
5) 震后该耗能器停止工作,通过调节螺栓使H型滑动主板继续复位到初始位置。
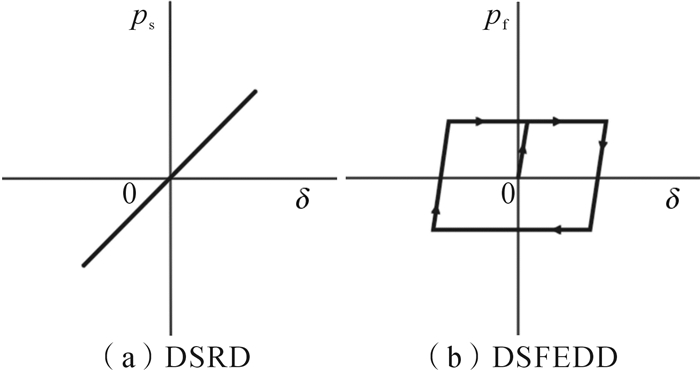
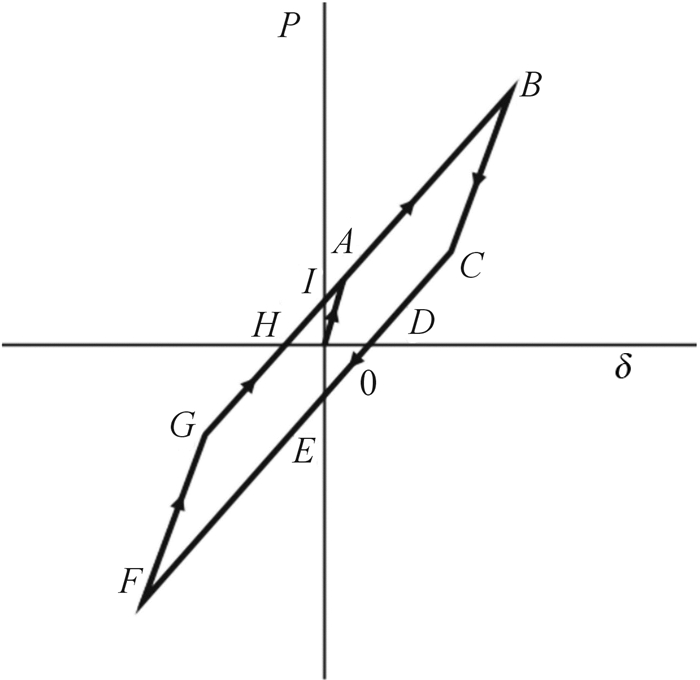
2 ZTSEDD的力学模型由ZTSEDD的工作原理可知,该耗能器恢复力由两部分组成:碟形弹簧的弹力ps(如图 4(a)所示)和摩擦耗能装置的滑动摩擦力pf(如图 4(b)所示)。设定2组耗能装置和复位装置构造参数均相同,该耗能器的力学模型如图 5所示, 其中P为耗能装置的恢复力。
|
| 图 4 碟形弹簧复位装置和双剪型摩擦耗能装置的力学模型 Fig.4 Mechanical models of DSRD and DSFEDD |
|
| 图 5 零初始索力自复位耗能器的力学模型 Fig.5 Mechanical model of ZTSEDD |
以耗能器的初始位置为运动原点、向右运动为正方向建立耗能器的复位力方程。图 3(a)所示状态为耗能器工作的初始阶段,耗能装置相当于框架的刚性支撑,耗能器的初始刚度为H型滑动主板的刚度K0,在此阶段(0 < δ≤δ0)耗能器的恢复力pa为:
| $ {p_{\rm{a}}} = \delta \cdot{K_0} $ | (1) |
| $ {\delta _0} = \frac{{{f_{\max }}}}{{{K_0}}} $ | (2) |
式中:fmax为耗能装置的滑动摩擦力。
当荷载p2≥fmax时(图 3(b)),圆形内套筒拉动H型滑动主板开始运动,耗能器的刚度由碟形弹簧决定,在此阶段(δ0 < δ≤δmax)耗能器的恢复力pb1为[13]:
| $ {p_{{\rm{b1}}}} = \left( {\delta - {\delta _0}} \right)\cdot{K_{\rm{s}}} + {f_{\max }} + \delta \cdot{K_0} $ | (3) |
| $ \begin{array}{*{20}{c}} {{K_{\rm{s}}} = \frac{{4E}}{{1 - {\mu ^2}}}\cdot\frac{{{t^2}}}{{{D^2}{K_1}}}\cdot K_4^2\cdot}\\ {\left\{ {K_4^2\left[ {{{\left( {\frac{{{h_0}}}{t}} \right)}^2} - 3\frac{{{h_0}}}{t}\cdot\frac{f}{t} + \frac{3}{2}{{\left( {\frac{f}{t}} \right)}^2}} \right] + 1} \right\}} \end{array} $ | (4) |
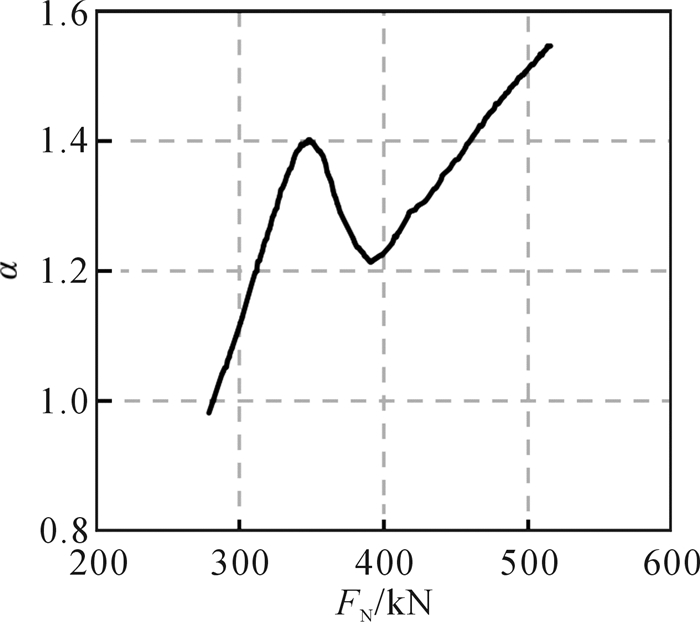
| $ {f_{\max }} = \alpha {\mu _{\rm{f}}}{F_{\rm{N}}} $ | (5) |
式中:μf和FN分别为耗能装置摩擦板的摩擦因数和对拉螺栓的总预紧力;Ks、E、μ、t和D分别为碟形弹簧的线刚度、弹性模量、泊松比、厚度和外径; K1、K4为计算系数; h0为碟形弹簧高度与其厚度之差;f为单片碟簧变形量;α为摩擦因子修正因数[14],取值参照图 6。
|
| 图 6 预紧力与摩擦因子修正因数的关系 Fig.6 Relationship between prestressing force and friction factor correction factor |
在耗能器到达最大层间位移的位置后开始反向运动时,该过程中H型滑动主板有短暂静止,耗能器刚度主要由H型滑动主板决定,此阶段(δmax-2δ0 < δ≤δmax)耗能器的恢复力pb2为:
| $ {p_{{\rm{b2}}}} = ({\delta _{\max }} - {\delta _0})\cdot{K_{\rm{s}}} + {f_{\max }} + (\delta - {\delta _{\max }}){K_0} $ | (6) |
当耗能器开始向初始位置方向移动时,此阶段弹簧2压着端板2向左运动直到耗能器停止移动,如图 3(c)所示,在此阶段(δμ < δ≤δmax-2δ0)耗能器的恢复力pc为:
| $ {p_{\rm{c}}} = {K_{\rm{s}}}\cdot{\delta _{\max }} - {f_{\max }} + (\delta + 2{\delta _0} - {\delta _{\max }})\cdot{K_{\rm{s}}} $ | (7) |
| $ {\delta _\mu } = \frac{{{f_{\max }}}}{{{K_{\rm{s}}}}} $ | (8) |
式中:δμ为在滑动摩擦力作用下碟形弹簧的形变量。
当作用在框架上的外力p1≥p2时,框架带动耗能器继续向左运动,再次回到耗能器的初始状态,如图 3(d)所示,在此阶段(0≤δ < δμ)耗能器的恢复力pd为:
| $ {p_{\rm{d}}} = {K_{\rm{s}}}\cdot({\delta _\mu } + 2{\delta _0}) - {f_{\max }} + \left( {\delta - {\delta _\mu }} \right)\cdot{K_{\rm{s}}} $ | (9) |
以上运动过程为耗能器在位移为正时的工作过程,位移为负的工作过程与此类似。
3 ZTSEDD设计流程ZTSEDD的设计流程如下:
1) 根据GB 50011—2010《建筑抗震设计规范》[15],分别计算耗能器原框架结构在多遇和罕遇地震作用下的层间位移。根据层间位移和上述工作原理可知,耗能器在框架产生塑性变形时若仍能正常工作,需满足以下层间位移要求:①组合叠合碟形弹簧压趴高度大于δmax; ②圆形内套筒的长度大于碟形弹簧的长度和δmax之和; ③滑动主板腹板长度大于4δmax和摩擦外板螺栓纵轴总距,且位于腹板中央的导滑槽和黄铜摩擦板导滑槽长度大于摩擦外板螺栓纵轴总距和2δmax之和。
2) 设定耗能器抗侧刚度最小值与框架抗侧刚度比值, 初步获得耗能器滑动摩擦力的估算值。
3) 为满足碟形弹簧高度构造要求,根据GB/T 1972—2005《碟形弹簧》[13],初步选取碟形弹簧型号、数量。
4) 由于圆形内套筒穿过碟形弹簧的内孔,且长度要满足碟形弹簧的运动范围,该套筒的长度与外径依据复合叠合碟形弹簧的长度以及内径确定。同时其厚度的选取需满足在(δmax·Ks+fmax)拉力作用下的强度与稳定性要求。
5) 据GB 50017—2010《钢结构规范》[16],计算耗能器在滑动摩擦力作用下所需对拉螺栓的型号与数量,确定螺栓排布以及纵轴螺栓总距。
6) 由于滑动端板要压缩碟形弹簧,因此端板的切面尺寸需大于碟形弹簧的切面尺寸,同时其厚度的选取需满足在(δmax·Ks+fmax)压力作用下的强度与稳定性要求。同时为了使构件尺寸协调一致,滑动主板的腹板以及摩擦外板的高度需与端板高度一致。此外滑动主板的腹板厚度和2倍摩擦外板的厚度的选取需满足在2fmax作用下的强度与稳定性要求。
7) 钢索的拉力主要作用在复位装置和摩擦装置上,因此钢索直径应在满足复位装置和摩擦装置在最大合力(δmax·Ks+fmax)作用下不发生塑性形变的要求下进行选择。其余构件应满足连接强度要求。
本文所设计耗能器的框架为钢框架,层高为3 m。在罕遇地震作用下结构的弹塑性层间位移角取1/50[15],在频遇地震作用下结构的弹性层间位移角取1/250[15]。该耗能器各构件的尺寸见表 1[14]。
| 构件名称 | 长度×宽度×厚度/mm×mm×mm |
| H型滑动主板的腹板 | 500×200×30 |
| H型滑动主板的端板 | 260×230×30 |
| 黄铜板 | 350×200×2 |
| 摩擦外板-长肢 | 350×200×25 |
| 摩擦外板-短肢 | 350×100×25 |
| 限位板-长肢 | 260×230×30 |
| 限位板-短肢 | 260×100×30 |
| 单片碟形弹簧 | ø200×ø102×11.25 |
| 圆形内套筒 | ø100×ø40×500 |
本文所设计耗能器的恢复力主要由复位装置和耗能装置提供。为保证有限元模型计算结果的精确性,首先分别对复位装置和耗能装置进行建模,再对耗能器整体建模分析。所建立的耗能器有限元模型中钢材[17]、黄铜、弹簧钢及螺栓的参数如表 2所示。
| 构件参数 | 数值 |
| 钢材抗拉强度设计值/MPa | 295 |
| 钢材弹性模量/MPa | 206 000 |
| 黄铜板弹性模量/MPa | 97 000 |
| 弹簧钢抗拉强度设计值/MPa | 1 235 |
| 碟形弹簧弹性模量/MPa | 206 000 |
| 螺栓抗拉强度设计值/MPa | 500 |
| 螺栓弹性模量/MPa | 206 000 |
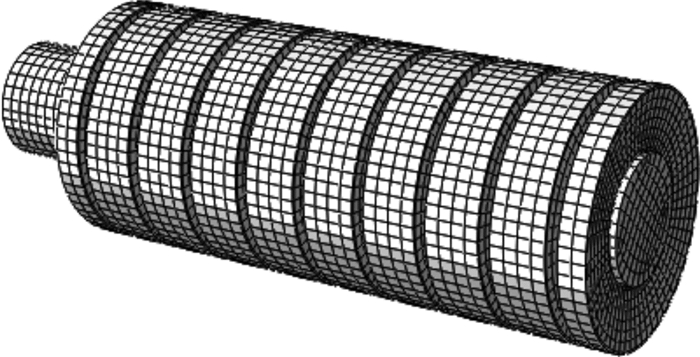
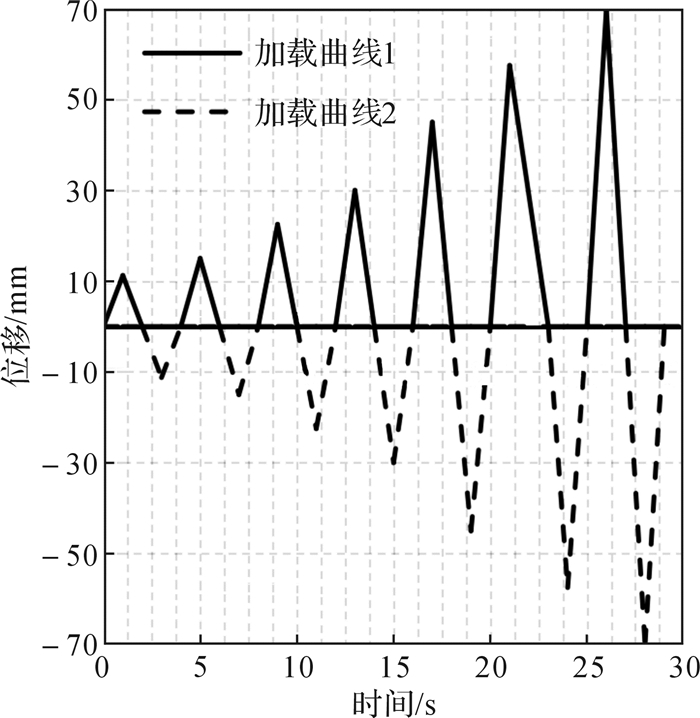
采用三维实体单元(C3D8I)对碟形弹簧复位装置进行建模,网格划分尽量精细以确保计算结果的精确性,其有限元模型如图 7所示。在该模型中,充分考虑碟形弹簧组合叠合之间的接触关系,法向采用硬接触,切向采用摩擦接触,摩擦系数的取值参照文献[13]。碟形弹簧与圆形内套筒之间采用硬接触。设置的边界条件与实际相近,将组合叠合碟形弹簧的最左端面设定为固端,将其最右端面的耦合点作为位移幅值加载端,圆形内套筒两端固定。位移幅值加载参考ANSI/AISC341[18],如图 8所示。
|
| 图 7 碟形弹簧复位装置有限元模型 Fig.7 Finite element model of DSRD |
|
| 图 8 碟形弹簧复位装置的位移幅值加载曲线 Fig.8 Displacement amplitude loading curve of DSRD |
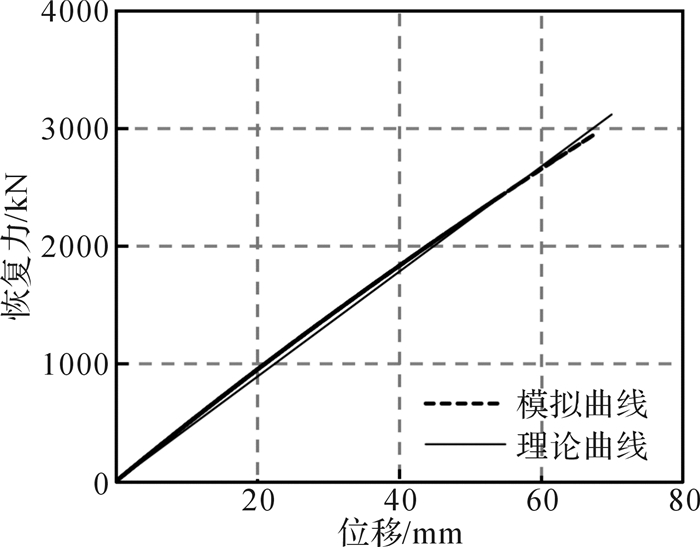
图 9为复位装置的模拟滞回曲线与理论滞回曲线的对比。可以看出:模拟滞回曲线与理论滞回曲线基本吻合,在位移幅值加载过程中复位装置恢复力曲线平滑、稳定,具有典型的胡克定律特性。
|
| 图 9 碟形弹簧复位装置数值模拟与理论分析滞回曲线 Fig.9 Numerical simulation and theoretical analysis hysteretic curves of DSRD |
耗能装置接触面的接触关系具有很强的非线性,故采用实体C3D8I单元进行建模, 如图 10所示。各摩擦板之间的接触关系如下:黄铜板与H型滑动主板、螺栓杆与外围摩擦板的螺栓孔之间采用绑定连接,黄铜板与外围摩擦板、螺栓帽与外围摩擦板采用摩擦接触,摩擦因数均参考文献[14]。外围摩擦板底端的位移、转角全部约束,在螺杆中间截面上加载螺栓预紧力,在与H型端板耦合的点上加载位移幅值,位移加载幅值参照图 8。金属材料定义为理想的弹塑性应力应变关系,遵循Von Misses屈服准则;摩擦行为采用经典库伦摩擦模型。耗能装置有限元模拟、试验分析及理论分析时的工况参数见表 3[14],其中Ti为每个螺栓的扭矩值。

|
| 图 10 双剪型摩擦耗能装置有限元模型 Fig.10 Finite element model of DSFEDD |
| 工况 | Ti/N·m | FN/kN | μf |
| 1 | 250 | 286.35 | 0.257 8 |
| 2 | 300 | 343.62 | 0.257 8 |
| 3 | 350 | 400.89 | 0.257 8 |
| 4 | 450 | 515.43 | 0.257 8 |
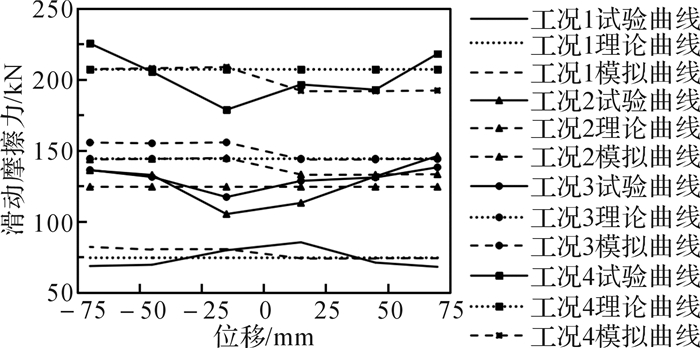
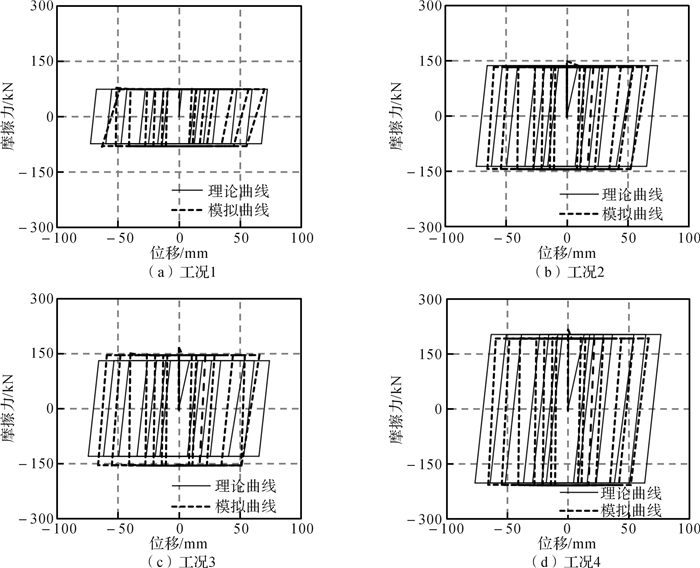
耗能装置在4种工况下的滑动摩擦力如图 11所示,工况1, 2和4下数值模拟数据和试验数据与理论数据波动一致。由文献[14]实验可知,钢-铜界面摩擦因子主要受铜摩擦板厚度与钢-铜界面咬合机制的影响。在初期,铜摩擦板厚度起主要作用,随着内外板的相互运动铜摩擦板会逐渐磨薄,摩擦因子逐渐减小;在后期,钢-铜截面咬合机制起主要作用,摩擦因子增大。因摩擦耗能装置有限元模型在模拟材质咬合机制性能方面稍强于模拟摩擦损耗,工况3下数值模拟数据和理论数据比试验数据略大,但由表 4可以看出,4种工况下滑动摩擦力的模拟值、理论值与试验值之间的误差的最大值仅为14.72%。位移幅值加载过程中H型滑动主板与摩擦外板之间的接触,不但存在滑动摩擦力,而且存在摩擦外板传递给H型滑动主板的法向压力。H型滑动主板在法向压力作用下,不断压缩并逐渐稳定,因此4种工况下耗能装置滑动摩擦力的数值模拟值为非恒定值。4种工况下摩擦耗能装置滞回曲线如图 12所示:数值模拟曲线与理论分析曲线基本吻合;滞回曲线呈规则矩形,具有典型的库伦定律特征。随着摩擦外板螺栓处预紧力的增加,耗能装置滑动摩擦力增大,因此,可通过调节螺栓预紧力控制耗能装置的滑动摩擦力大小。
|
| 图 11 不同工况下双剪型摩擦耗能装置滑动摩擦力比较 Fig.11 Comparision of sliding friction force of DSFEDD under different working conditions |
| 工况 | 滑动摩擦力 试验值/kN | 滑动摩擦力 模拟值/kN | 滑动摩擦力 理论值/kN | 模拟值与试验值的 误差/% | 理论值与试验值的 误差/% |
| 1 | 73.73 | 74.45 | 77.49 | 0.98 | 5.09 |
| 2 | 127.49 | 124.42 | 138.60 | 2.41 | 8.71 |
| 3 | 130.43 | 144.20 | 149.62 | 10.56 | 14.72 |
| 4 | 202.78 | 207.10 | 199.99 | 2.13 | 1.38 |
| 注:1)滑动摩擦力试验值、滑动摩擦力模拟值和滑动摩擦力理论值均为均值。 | |||||
|
| 图 12 不同工况下双剪型摩擦耗能装置滞回曲线对比 Fig.12 Comparison of hysteretic curves of DSFEDD under different working conditions |
所设计的ZTSEDD的有限元模型如图 13所示,2个圆形内套筒的一端与H型滑动主板的2个端板采用绑定接触,另一端穿过限位板的圆孔,限位板底部固定。在圆形内套筒外表面和限位板圆孔之间、碟形弹簧与限位板对立面之间设置硬接触。由于传动装置刚度大,工作过程中其形变对耗能器位移精度影响较小,将传动装置简化为RP-1和RP-2两个加载点,如图 13(b)所示。位移幅值加载曲线如图 8,加载曲线1和加载曲线2分别加载在RP-1和RP-2上。该耗能器有限元模型的其他参数见表 3。

|
| 图 13 零初始索力自复位耗能器有限元模型 Fig.13 Finite element model of ZTSEDD |
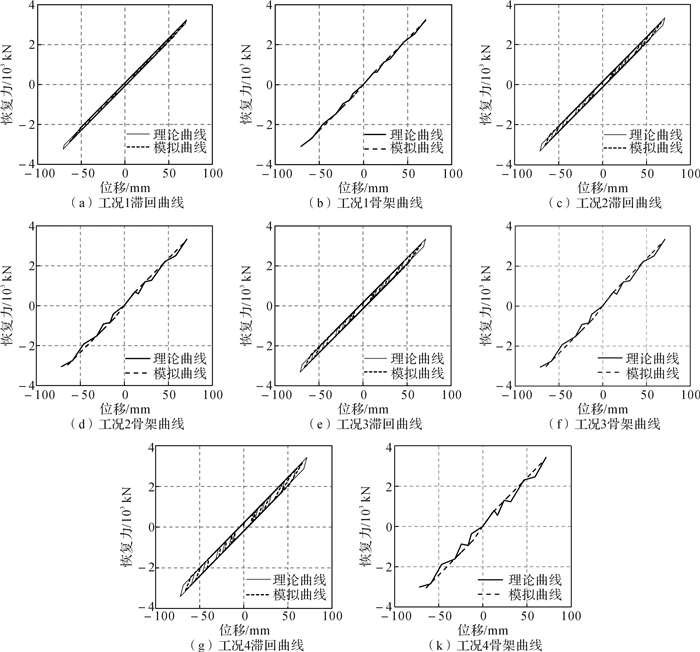
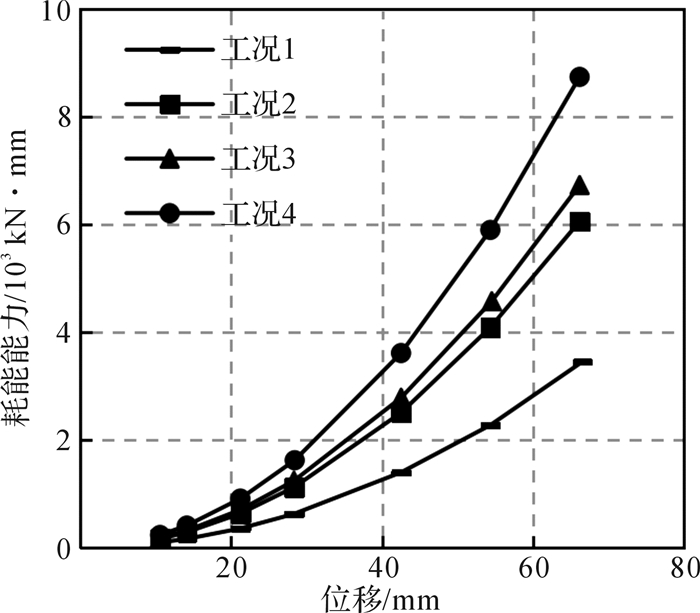
图 14为ZTSEDD的模拟滞回曲线、骨架曲线与其理论曲线的对比。可以看出:理论分析得出的滞回曲线、骨架曲线与有限元分析得出的曲线基本吻合,且随着螺栓预紧力的增加,滞回环的面积不断增大,可知随着螺栓预紧力的增加,耗能器的耗能能力不断增强。图 15为4种工况下耗能器耗能能力与位移的关系。可以看出耗能器耗能能力与位移成正相关关系。
|
| 图 14 不同工况下零初始索力自复位耗能器滞回曲线、骨架曲线的对比 Fig.14 Comparisons of hysteretic curves and skeleton curves of ZTSEDD under different working conditions |
|
| 图 15 不同工况下零初始索力自复位耗能器的耗能能力-位移关系 Fig.15 Energy dissipation-displacement relation of ZTSEDD under different working condition |
表 5为不同工况下该耗能器的位移数据。从表中可知,在4种工况下不同位移幅值加载过程中,当恢复力为0时,该耗能器距初始位置的距离几乎稳定不变且距离均小于框架的弹性层间位移, 表明ZTSEDD的复位性能较好。且该耗能器距初始位置的距离随预应力的增加而增长,调节预应力可以有效调节ZTSEDD复位距离。
| 工况 | FN/kN | +Dy1)/mm | +D02)/mm | -Dy/mm | -D0/mm |
| 11.25 | 1.821 7 | 11.25 | 1.667 7 | ||
| 15 | 1.820 9 | 15 | 1.666 7 | ||
| 22.5 | 1.820 4 | 22.5 | 1.666 7 | ||
| 1 | 286.35 | 30 | 1.820 1 | 30 | 1.666 7 |
| 45 | 1.819 9 | 45 | 1.666 7 | ||
| 57.5 | 1.819 5 | 57.5 | 1.666 7 | ||
| 70 | 1.819 5 | 70 | 1.666 7 | ||
| 11.25 | 3.272 9 | 11.25 | 1.667 7 | ||
| 15 | 3.271 4 | 15 | 1.666 9 | ||
| 22.5 | 3.270 8 | 22.5 | 1.666 7 | ||
| 2 | 343.62 | 30 | 3.270 5 | 30 | 1.666 7 |
| 45 | 3.270 2 | 45 | 1.666 7 | ||
| 57.5 | 3.271 0 | 57.5 | 1.666 7 | ||
| 70 | 3.269 8 | 70 | 1.666 7 | ||
| 11.25 | 3.635 3 | 11.25 | 3.330 6 | ||
| 15 | 3.633 6 | 15 | 3.329 0 | ||
| 22.5 | 3.633 1 | 22.5 | 3.328 7 | ||
| 3 | 400.89 | 30 | 3.632 8 | 30 | 3.328 7 |
| 45 | 3.632 5 | 45 | 3.328 7 | ||
| 57.5 | 3.633 5 | 57.5 | 3.328 4 | ||
| 70 | 3.632 9 | 70 | 3.328 4 | ||
| 11.25 | 4.721 9 | 11.25 | 4.326 5 | ||
| 15 | 4.719 2 | 15 | 4.324 5 | ||
| 22.5 | 4.719 6 | 22.5 | 4.324 1 | ||
| 4 | 515.43 | 30 | 4.718 6 | 30 | 4.324 1 |
| 45 | 4.718 4 | 45 | 4.324 2 | ||
| 57.5 | 4.719 8 | 57.5 | 4.323 7 | ||
| 70 | 4.718 2 | 70 | 4.323 7 | ||
| 注:1)Dy为位移加载幅值,向右为正,反之向左; 2)D0为恢复力为零时ZTSEDD距初始位置的位移,向右为正,反之向左。 | |||||
为了优化自复位耗能器结构及其复位性能,本文设计了零初始索力自复位耗能器,并对其工作性能进行了理论分析和数值模拟,得出以下结论:
1) 复位装置滞回曲线平滑,具有典型的胡克定律特性,能够在不同位移幅值状态下为耗能器提供稳定的恢复力。
2) 耗能装置滞回曲线呈矩形,具有典型的库伦摩擦定律特性,能为该耗能器提供稳定的滑动摩擦力。并由4种工况下螺栓预紧力与滑动摩擦力关系可知,调节耗能装置对螺栓的预紧力可以有效调节滑动摩擦力的大小。因此,根据结构特性需求调节对拉螺栓预紧力可满足不同结构耗能需求。
3) 耗能器滞回曲线呈平行四边形,曲线形状饱满,表明该耗能器耗能性能较好;在层间位移角达23/1000时,该耗能器仍能复位到结构弹性变形范围内,表明该耗能器复位性能较好。当耗能器停止复位后,可以松动预紧力螺栓使耗能器继续复位到初始位置。
4) 通过调节传动装置钢绞线长度,在不改变复位装置和耗能装置构造尺寸的基础上,使耗能器适用于不同开间、进深的框架结构, 便于它规格化生产。
5) 本文所设计的耗能器由传动装置、复位装置和耗能装置组成。它以钢材为原材料,结合了传统耗能支撑和自复位装置的优点,采用零预应力碟形弹簧作为复位装置,在拥有较强的耗能能力的同时也具备稳定的复位性能,避免了传统支撑的残余变形大、自复位装置预应力松弛和预应力施加过程复杂等缺点。各构件制作、安装、替换方便,便于工业化生产,可在实际工程中推广应用。
| [1] | SABELLI R, MAHIN S, CHANG C. Seismic demands on steel braced frame buildings with buckling-restrained braces[J]. Engineering Structures, 2003, 25(5): 655–666. DOI:10.1016/S0141-0296(02)00175-X |
| [2] | KIGGINS S, UANG C M. Reducing residual drift of buckling-restrained braced frames as a dual system[J]. Engineering Structures, 2006, 28(11): 1525–1532. DOI:10.1016/j.engstruct.2005.10.023 |
| [3] | KAWASHIMA K, MACRAE G A, HOSHIKUMA J I, et al. Residual displacement response spectrum[J]. Journal of Structural Engineering, 1998, 124(5): 523–530. DOI:10.1061/(ASCE)0733-9445(1998)124:5(523) |
| [4] | MCCORMICK J, ABURANO H, IKENAGA M, et al. Permissible residual deformation levels for building structures considering both safety and human elements[C]//Proceedings of the 14th World Conference on Earthquake Engineering. Beijing: Seismological Press, 2008: 12-17. |
| [5] | CHRISTOPOULOS C. Seismic response of self-centering hysteretic SDOF systems[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(5): 1131–1150. |
| [6] | CHRISTOPOULOS C, TREMBLAY R, KIM H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structures:development and validation[J]. Journal of Etructural Engineering, 2008, 134(1): 96–107. DOI:10.1061/(ASCE)0733-9445(2008)134:1(96) |
| [7] |
池沛, 董军, 彭洋, 等.
一种新型自复位耗能拉索支撑的理论研究与数值分析[J]. 振动与冲击, 2016, 35(21): 171–176, 219.
CHI Pei, DONG Jun, PENG Yang, et al. Theoretical analysis and numerical simulation for an innovative self-centering energy-dissipative tension-brace system[J]. Journal of Vibration and Shock, 2016, 35(21): 171–176, 219. |
| [8] |
张爱林, 叶全喜, 詹欣欣, 等.
装配式零初始索力摩擦耗能复位支撑受力机理分析[J]. 东南大学学报(自然科学版), 2017, 47(1): 142–149.
ZHANG Ai-lin, YE Quan-xi, ZHAN Xin-xin, et al. Force mechanism analysis of fabricated friction dissipation re-centering brace with zero initial cableforce[J]. Journal of Southeast University (Natural Science Edition), 2017, 47(1): 142–149. |
| [9] |
王涛, 黄俊奎, 孟丽岩, 等.
弹簧式自复位防屈曲支撑的抗震性能[J]. 黑龙江科技大学学报, 2015, 25(5): 557–564.
WANG Tao, HUANG Jun-kui, MENG Li-yan, et al. Study on seismic performance of self-centering buckling-restrained brace with springs[J]. Journal of Heilongjiang of Science & Technology, 2015, 25(5): 557–564. DOI:10.3969/j.issn.2095-7262.2015.05.019 |
| [10] |
周中哲, 陈映全.
钢造双核心自复位斜撑发展与耐震试验:应用复合纤维材料棒为预力构件[J]. 土木工程学报, 2012, 45(S2): 202–206.
ZHOU Zhong-zhe, CHEN Ying-quan. Development and seismic tests of steel dual-core self-centering braces:fiber-reinforced polymer composites as post-tensioning tendons[J]. China Civil Engineering Journal, 2012, 45(S2): 202–206. |
| [11] | CHOU C C, CHEN Y C, CHUNG P T, et al. Low-damage earthquake-resisting systems using sandwiched buckling-restrained braces and dual-core self-centering braces[J]. Applied Mechanics & Materials, 2013, 353. |
| [12] | OZBULUT O E, HURLEBAUS S. Application of an SMA-based hybrid control device to 20-story nonlinear benchmark building[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(13): 1831–1843. |
| [13] |
姜膺, 黄志福, 周冀平, 等.碟形弹簧: GB/T 1972-2005[S].北京: 中国标准出版社, 2005: 10-23.
JIANG Ying, HUANG Zhi-ping, ZHOU Ji-ping, et al. Disc springs: GB/T 1972-2005[S]. Beijing: China Standards Press, 2005: 10-23. |
| [14] |
郭子雄, 张鹏, 黄群贤, 等.
长孔螺栓板式摩擦耗能器滞回性能试验研究[J]. 福州大学学报(自然科学版), 2013, 41(4): 622–628.
GUO Zi-xiong, ZHANG Peng, HUANG Qun-xian, et al. Experimental research on behavior of slotted-bolted-plate friction damper device[J]. Journal of Fuzhou University (Natural Science Edition), 2013, 41(4): 622–628. |
| [15] |
黄世敏, 王亚勇, 戴国莹, 等.建筑抗震设计规范: GB 50011-2010[S].北京: 中国计划出版社, 2010: 43-47.
HUANG Shi-min, WANG Ya-yong, DAI Guo-ying, et al. Code for seismic design of building: GB 50011-2010[S]. Beijing: China Planning Press, 2010: 43-47. |
| [16] |
中华人民共和国住房和城乡建设部.钢结构设计规范: GB 50017-2010[S].北京: 中国计划出版社, 2010: 67-82.
Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of steel structures: GB 50017-2010[S]. Beijing: China Planning Press, 2010: 67-82. |
| [17] | ESMAEILY A, XIAO Y. Behavior of reinforced concrete columns under variable axial loads:analysis[J]. ACI Structual Journal, 2005, 102(5): 736–744. |
| [18] | AISC Committee on Specification. Seismic provisions for structural steel buildings: ANSI/AISC 341-10[S]. Chicao: American Institute of Steel Construction, 2010: 2-8. |



