酶联免疫分析仪作为医学检验常用的分析仪器,被广泛地用于流行病学、免疫学、内分泌学等领域,为医师在疾病的诊断、治疗、预防中提供重要的科学依据[1]。微量进样系统作为全自动酶联免疫分析仪处理系统的重要功能模块,在提高检测精度、加快反应速度、降低成本以及减少试剂用量等方面起着十分重要的作用,是全自动酶联免疫分析仪的关键部件之一[2]。国外对微量进样系统的研究起步较早,取得了领先的优势,如:法国的Pulssa科技公司生产的微量注射泵在有效行程下的理论进样精度突破了1 μL,可实现1 μL~1 mL的进样;Beckman公司的CX系列和Olympus公司的AU系列的全自动酶联免疫分析仪的注射泵在其控制系统的驱动下进样最小精度可达1 μL,以0.1 μL的进样分辨率步进[3-4]。而在国内,酶联免疫分析仪最小进样量还在5 μL左右,试剂消耗量较大,且控制精度不够高,稳定性和可靠性也较差[5-6]。相比于国产产品,国外酶联免疫分析仪的微量进样控制系统的自动化程度和进样精度高,稳定性强, 但价格非常高昂。
为提高国产全自动酶联免疫分析仪进样系统的精度与可靠性,满足小型化的发展要求,设计了高集成度的小型全自动微量进样臂,以STM32处理器为核心设计了自动进样运动控制系统,分析了进样臂的结构与控制系统方案,确立了提高进样效率、减少最小进样量的方法,并通过试验对进样臂位置精度进行校核,对进样系统的进样误差进行分析与补偿。
1 微量进样系统工作原理及进样臂结构设计 1.1 微量进样系统工作原理微量进样系统主要包括自动进样模块和移液模块,进样臂是自动进样模块的核心部分,它主要实现移液吸头的取、退以及试剂的精确吸取、排放等功能。移液模块配合进样模块进行试剂托盘的定位,完成试剂、吸头的供给,实现进样系统的自动化。微量进样系统工作流程图如图 1所示。

|
| 图 1 微量进样系统工作流程图 Fig.1 Working flow chart of micro-sampling system |
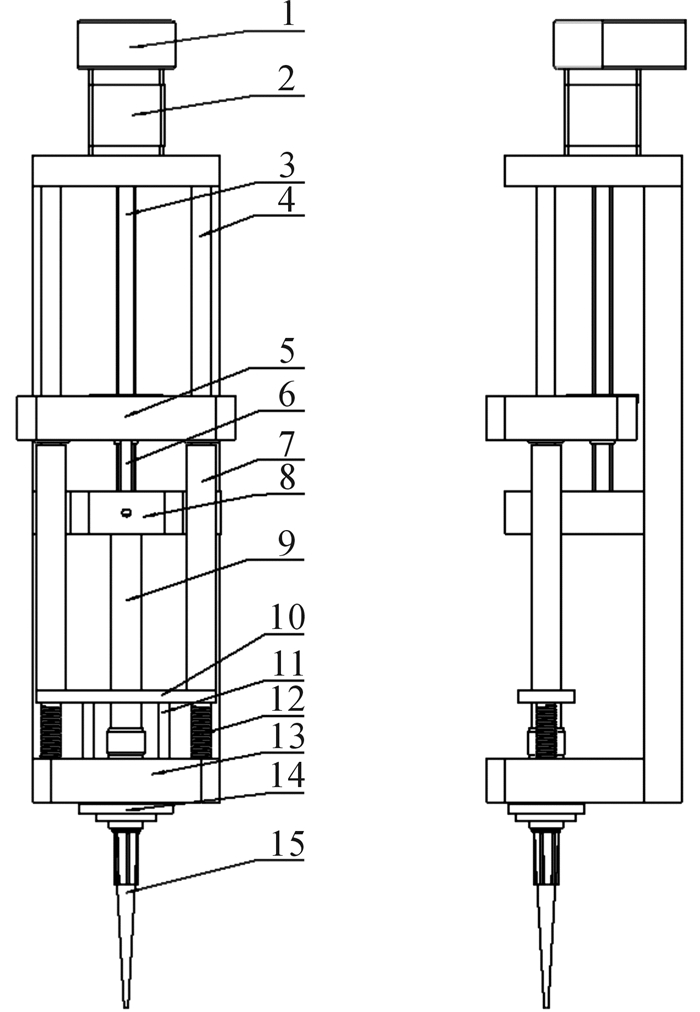
进样臂由取、退吸头模块,进样器及动力执行模块组成,如图 2所示。进样臂的丝杆步进电机旋转带动固定在螺母上的活塞杆上下平移,实现试剂的吸取、排放,此过程中竖直方向上的运动空间较大,采用丝杆与进样器活塞错位平行分布的方式,以节省工作空间。同时为提高步进电机的控制精度与可靠性,采用分体式旋转编码器反馈运动过程的位置信号。在定位板背面安装横向移动丝杆螺母运动副,使进样臂左右移动以实现多通道进样。进样器作为进样臂的核心元件,其密封性能直接影响取样精度,本方案采用上海高鸽工贸有限公司生产的250 μL进样器,这样既保证了进样臂的精度与可靠性,也降低了整个进样系统的成本。
|
| 1—分体式编码器;2—步进电机;3—滚珠丝杆;4—圆柱导轨;5—提拉固定板;6—柱塞杆;7—退吸头推杆;8—定位槽;9—进样器腔体;10—推板;11—连接杆;12—弹簧;13—定位板;14—退吸头盖;15—吸头 图 2 进样臂结构示意图 Fig.2 Structure diagram of injection arm |
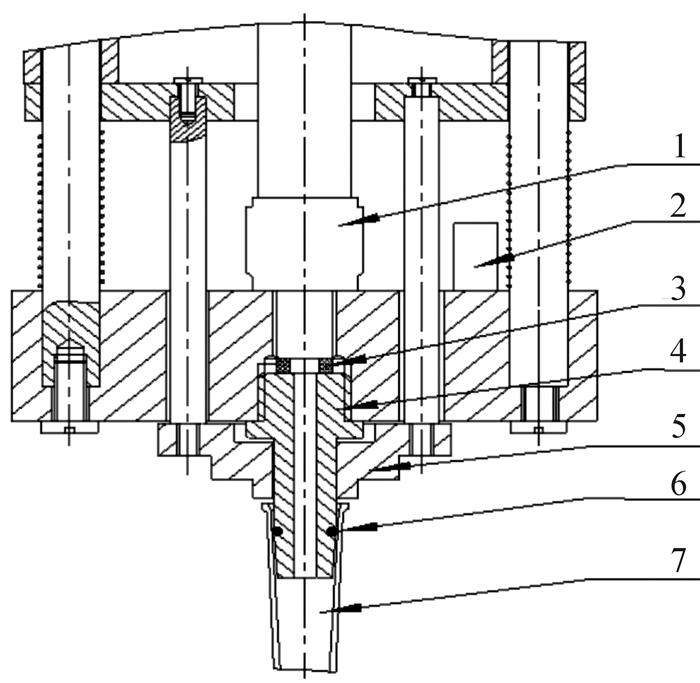
在检测过程中需进行多次液体混合反应,为了避免残留在进样器腔体内壁的余液造成交叉污染,进样的试剂往往只在移液吸头中,不进入进样器内腔,并在反应结束后更换移液吸头以保证重复检测的可靠性[7-8],为此在进样臂末端设计了取、退吸头的结构,吸头与安装柱之间通过O型密封圈密封。取、退吸头结构如图 3所示。
|
| 1—连接头; 2—限位传感器; 3—O型密封圈; 4—安装柱; 5—退吸头盖; 6—密封圈; 7—吸头 图 3 进样臂取、退吸头结构 Fig.3 Structureof taking and retracting pipette tips for injection arm |
吸头与安装柱通过静摩擦安装,退吸头盖在吸头被插上时触发限位传感器反馈电平变化信号,表明吸头已经取好;退吸头时,电机旋转控制提拉固定板下移从而下压推板使退吸头盖退去吸头,此时同样也会触发限位传感器反馈电平信号,该信号同时作为轴向运动的初始位置信号,以消除传动轴在周期循环工作中的累积定位误差。在推板与定位板之间装有压缩弹簧,使退吸头盖在没有外力时处于移动行程上端,避免重力因素对取吸头过程造成影响。通过合理的布局与功能规划,整个进样臂仅使用1个原动件便实现了移液和取、退吸头等多个功能。
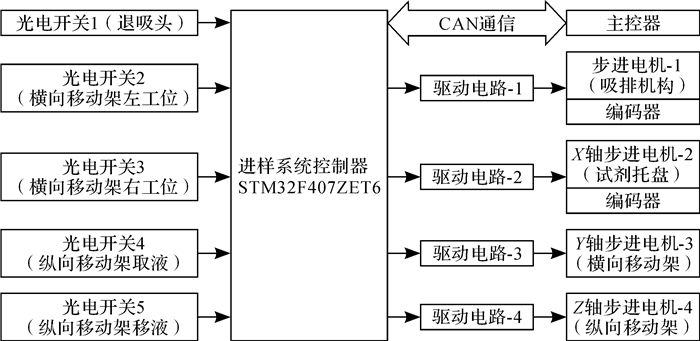
2 微量进样系统控制系统设计 2.1 控制系统方案设计本方案中采用基于CORTEX-M4内核的STM32F407ZET6芯片作为控制系统核心处理器,其主频高达168 MHz, 2个16位电机控制PWM(pulse width modulation,脉冲宽度调制)同步定时器、2个高级定时器与10个通用定时器,其中通用定时器及高级定时器均具有编码功能,完美地解决了步进电机的闭环控制的需求,同时处理器具有FPU(float point unit, 浮点运算单元),利于各算法的快速、精确实现,且它有丰富的通讯接口,方便和上位机或其他控制器建立通信。在本系统中运动控制系统单独使用一个控制器,与主控器建立CAN (controller area network, 控制器局域网络)通信进行信息交换,配置定时器输出不同频率的PWM以实现步进电机的控制,同时利用定时器的编码功能获取编码器输出的脉冲,从而得到执行机构的位置状态,实现执行机构位置的精确控制。在运动过程的关键位置节点使用光电传感器进行位置校核,以消除各轴运动的累积误差。微量进样系统运动控制系统框图如图 4所示。
|
| 图 4 微量进样系统运动控制系统框图 Fig.4 Block diagram of motion control system for micro-sampling system |
进样分辨率是进样系统的关键参数。本方案中进样系统通过丝杆螺母运动副进行进样,步进电机所接收到的脉冲数n与进样器进样量V的关系为:
| $ V = n\frac{T}{{360N}}{P_{\rm{h}}} \cdot \frac{S}{l} $ | (1) |
式中:T为步进电机步距角;Ph为丝杆导程;N为步进电机细分数;S为进样器总容量;l为进样器行程。
在进样系统中,传动机构采用的丝杆导程Ph=2 mm, 进样器总容量S=250 μL,行程l=50 mm,控制步进电机整步运行,以避免电机转子在非整步位置停止时产生振动和噪音。则进样系统的进样分辨率为:
微量进样机构的运动控制是酶联免疫分析系统实现自动化的关键。在微量进样过程中,进样臂需平滑而又快速地运动到相应位置,完成吸头的取、退以及试剂的吸、排操作;试剂托盘运动机构同样也需平滑而又快速地运动到正确位置,以确保进样臂动作的顺利完成。为提高全自动生化分析系统的工作效率,减少每个项目的测量时间,各运动副协调动作,减小轴与轴的交叉耦合干扰,是非常重要的。根据进样系统的工作特性,研究了微量进样系统的单轴运动控制算法以及多轴运动协调控制策略。
3.1 单轴运动控制算法步进电机的控制算法关系着系统的进样精度和取、退吸头时的冲击强度,对整个进样系统的稳定性来说是至关重要的。轴向运动过程中常会出现启动时负载力矩过大而引起失步,以及停止时电机输出转矩过大而产生过冲现象[9]。为避免电机在启动、停止时出现失步和过冲现象,对电机实行加减速控制,常用的加减速算法有梯形曲线、指数曲线和S型曲线[10]。
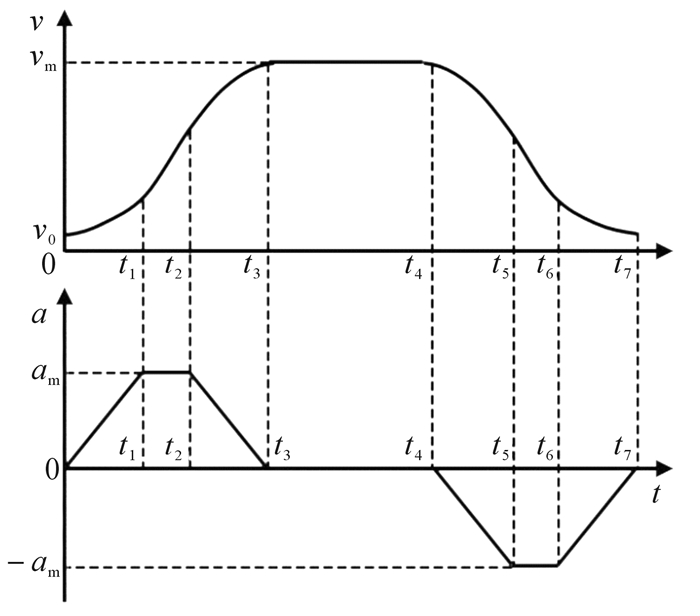
S型曲线常用来改善加速度的突变现象,可分为7个阶段:加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段,可通过调整不同阶段的参数得到不同的加减速特性,其加减速平稳,是一种综合性能突出的加减速模型[11]。其特性曲线如图 5所示。
|
| 图 5 S型曲线的速度和加速度曲线图 Fig.5 Velocity and acceleration curve of S-type curve |
为了确保步进电机稳定运行,单轴运动控制采用7个阶段的S型曲线控制算法,其运动方程如下:
| $ v\left( t \right) = \left\{ \begin{array}{l} {v_0} + \frac{1}{2}h{t^2}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {0, {t_1}} \right)\\ {v_1} + {a_{\rm{m}}}(t - {t_1}), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {{t_1}, {t_2}} \right), {v_1} = {v_0} + \frac{1}{2}ht_1^2\\ {v_2} + {a_{\rm{m}}}\left( {t - {t_2}} \right) - \frac{1}{2}h{\left( {t - {t_2}} \right)^2}, \;t \in \left[ {{t_2}, {t_3}} \right), {v_2} = {v_1} + {a_{\rm{m}}}({t_2} - {t_1})\\ {v_3}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {{t_3}, {t_4}} \right), {v_3} = {v_2} + {a_{\rm{m}}}\left( {{t_3} - {t_2}} \right) - \frac{1}{2}h{\left( {{t_3} - {t_2}} \right)^2}\\ {v_4} - \frac{1}{2}h{\left( {t - {t_4}} \right)^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {{t_4}, {t_5}} \right), {v_4} = {v_3}\\ {v_5} - {a_{\rm{m}}}(t - {t_4}), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {{t_5}, {t_6}} \right), {v_5} = {v_4} - \frac{1}{2}h{\left( {{t_5} - {t_4}} \right)^2}\\ {v_6} - {a_{\rm{m}}}\left( {t - {t_5}} \right) + \frac{1}{2}h{\left( {t - {t_5}} \right)^2}, \;\;\;\;t \in \left[ {{t_6}, {t_7}} \right), {v_6} = {v_5} - {a_{\rm{m}}}({t_6} - {t_5}) \end{array} \right. $ | (2) |
基于STM32的控制是通过改变PWM波的输出频率来实现步进电机的转速控制,对式(2)中的参数进行转换,时间t代表步进电机的步数,速度v代表脉冲频率,加速度a代表每步频率的增加量。在S型曲线加减速算法中参数较多, 算法不易直接实现,通常通过插补法来实现加速曲线,这样可缩短算法的代码执行周期,也容易通过改变参数的值实现它在不同场合的应用[11]。
利用STM32实现步进电机S型加减速的配置过程如下:
1) 根据选用电机频距特性曲线与各轴负载大小,计算得到步进电机运行的最大速度与最大加速度,确定步进电机在加速过程中所需要的步数,得到S型加减速曲线函数。
2) 利用插补法得到步进电机每一步运行的频率,并做成数组表,保存在STM32外部SRAM(static random-access memory,静态随机存取存储器)中。
3) 配置STM32高级定时器(TIM1或TIM8)输出PWM,对步进电机进行速度控制。在STM32控制器中,PWM输出频率由时钟预分频数和自动重装值TIMx->ARR决定,本方案采用设定好的预分频数,通过改变自动重装值来输出不同频率的PWM。
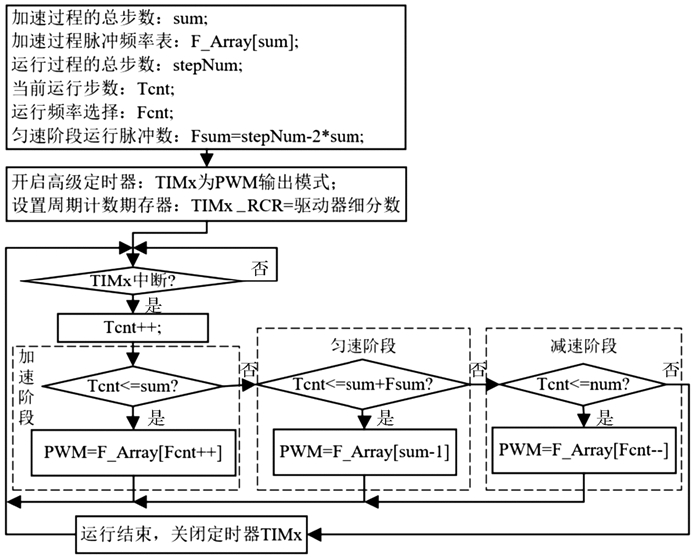
4) 设置PWM输出定时器为溢出中断, 以及高级定时器独有的周期计数定时器的TIMx_RCR=驱动器细分数。定时器每中断一次,则在中断服务函数中查询一次频率序列表,根据查询值改变定时器自动重载值,从而输出相应频率的PWM。这样可使步进电机在每一整步运行的频率一致,增强稳定性,并减少系统负荷。S型加、减速控制算法流程图如图 6所示。
|
| 图 6 S型加、减速控制算法流程图 Fig.6 Flow chart of S-type curve algorithm |
加速时间太长会影响系统执行效率,过短又达不到平滑的效果,为保证电机运行的稳定性和进样系统的高效性,设定加速过程时间tn∈(0.05, 0.2] s。为提高电机运行的稳定性,减小噪音,驱动电路采用32细分。经计算,进样臂步进电机最大运行速度vm=300 r/min,对应脉冲频率为32 kHz,启动速度v0=60 r/min,对应脉冲频率为6 400 Hz,最大每步加速频率fam=320 Hz,总加速运行步数为60步,其中加加速、减加速运行步数均为10步,电机每运行1个整步进行1次输出频率插补,以避免电机在非整步停止时产生振动和噪音。每步的实际输出脉冲频率设为Fn,则整个加速过程的实际时间应为:
| $ \begin{array}{l} t = 32\left( {\frac{1}{{{F_1}}} + \frac{1}{{{F_2}}} + \ldots + \frac{1}{{{F_{60}}}}} \right) = \\ \;\;\;\;\;{\rm{32}}\left( {\frac{{\rm{1}}}{{{\rm{6 400}}}}{\rm{ + }}\frac{{\rm{1}}}{{{\rm{6 502}}}}{\rm{ + }} \cdots {\rm{ + }}\frac{{\rm{1}}}{{{\rm{32 000}}}}} \right){\rm{ = 0}}{\rm{.072}}\;{\rm{9 s}} \end{array} $ | (3) |
完成整个S型加减速过程需要步距角T的个数m=120,进样丝杆的导程为2 mm,由式(1)计算可知,在该加减速模型下进样器的最小吸排体积
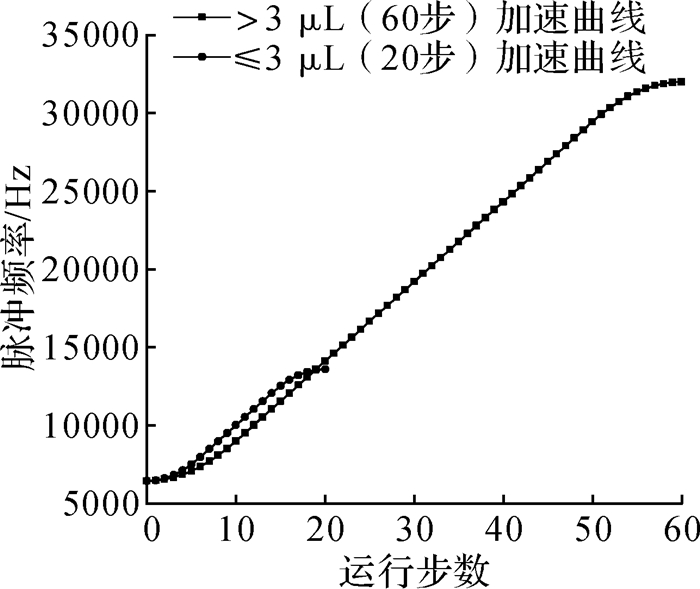
|
| 图 7 步进电机插补频率曲线 Fig.7 Stepping motor frequency interpolation curve |
为了提高工作效率,在进样过程中常需多轴同时运动,因此微量进样机构是一个复杂的多轴运动系统,其控制过程是一个高速度、高精度的定位过程。为实现多轴运动系统的精确控制,需分析其运动过程,研究其控制策略。
3.2.1 微量进样系统运动分析整个酶联免疫分析仪进样系统如图 8所示。根据各轴运动行程建立笛卡尔坐标系(XYZ轴坐标系),其中进样模块机械臂由Y向丝杆螺母副、a针Z向丝杆螺母副、b针Z向丝杆螺母副组成;移液模块由X向齿轮齿条副驱动。

|
| 图 8 微量进样系统机械结构 Fig.8 Mechanical structure of micro-sampling system |
将全自动酶联免疫分析仪进样系统任务分为两大块:1)水平运动:X,Y,Z向协调运动将试剂托盘以及进样臂移动到工作位置。2)垂直运动:进样臂进行取、退吸头及吸、排试剂等操作。
1) 进样臂水平运动精度要求。
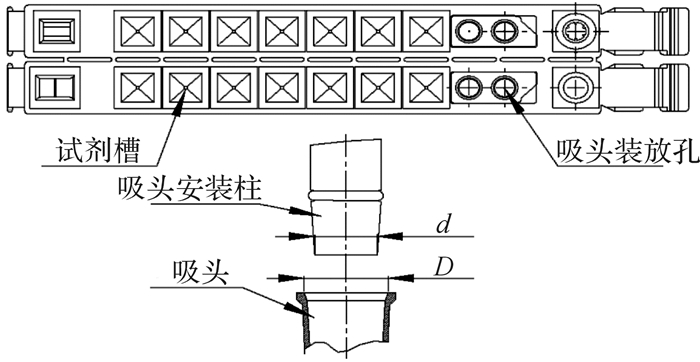
进样臂的水平运动高精度是确保进样臂能顺利取好一次性吸头,并将试剂放置在相应试剂槽中的前提。试剂条布局及吸头安装示意图如图 9所示。
|
| 图 9 试剂条布局及吸头安装示意图 Fig.9 Schematic diagram of reagent strip layout and suction head installation |
在本实验中采用的一次性吸头的口径D=5 mm,而进吸头安装柱的小端口径d=4.6 mm,为确保进样臂能顺利取到吸头,在XY平面内重复定位精度应小于(D-d)/2=0.2 mm。
2) 进样臂垂直运动精度要求。
Z向的定位精度关系着吸头尖端插入试剂的深度:当深度过浅时,吸液量不够;当深度过深时,会出现扎底、挂液等问题,从而导致交叉污染。为保证进样吸头吸取足够的试剂量,同时又避免出现扎底的现象,要求进样臂的垂直运动最大误差不超过1.0 mm。Z向的定位精度越高,便可在尽可能少的试剂里吸取足够的试剂量,减少试剂用量。
3.2.2 微量进样系统运动控制策略设计的酶联免疫分析仪进样系统共有4个轴向运动,分别为控制试剂托盘的X向运动、移液架的Z向运动、吸排机构的Y向运动以及吸排机构吸排液的Z向运动。其中试剂托盘、移液架、吸排机构的轴向运动为系统的进样操作提供精确的位置,为提高执行效率,需要同时执行各轴运动,而吸液、排液动作需要在位置确定后才执行。
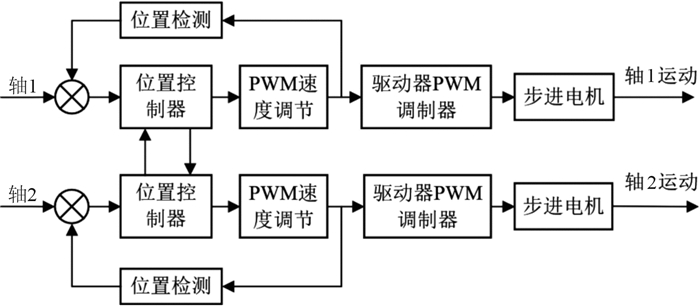
由于步进电机在低速运动过程中会产生振动和噪音,而进样过程中的关键是对位置的精确控制,对轮廓精度并没有严格的要求[13-14],所以在多轴运动控制过程中不改变单轴加减速运动特性,通过对各任务关键节点进行时序耦合,来避免各轴运动干涉。各轴之间的运动控制框图如图 10所示,控制器通过捕获输出脉冲,对进样系统各轴运动进行半闭环控制。
|
| 图 10 各轴之间的运动控制框图 Fig.10 Control block diagram of each axis movement |
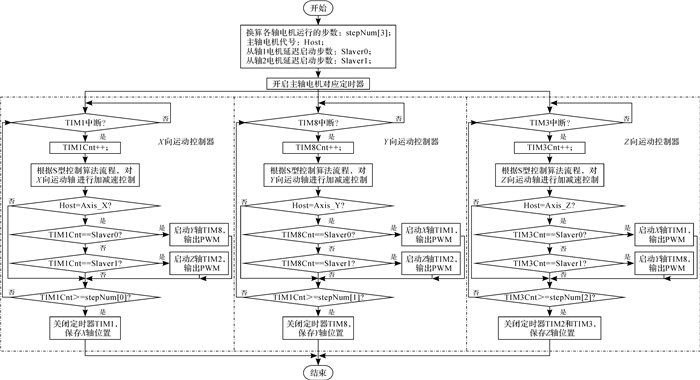
根据上述分析,为满足多轴协调控制,控制系统应具有同时控制3个步进电机的功能。为此将4个轴向运动分成3组,建立3组相互独立的控制方案, 这样STM32应同时输出3路频率可调的PWM。在单轴运动控制中,STM32的2个高级定时器(TIM1, TIM8)具有周期计数寄存器(TIMx_RCR),可以记录相应定时器输出PWM脉冲个数,并控制定时器进入中断的频率,利用两高级定时器分别控制2个轴向运动,第3路PWM波由2个通用定时器(TIM2与TIM3)来配合完成, TIM2设置成PWM比较输出模式,进行PWM输出,TIM3配置成外部计数模式,连接TIM2的PWM输出端进行脉冲捕获,并在计数溢出中断时更改TIM2重载初值重置PWM的输出频率,实现步进电机的加减速控制。通过上述配置,便可以实现多个电机的同步运行,将酶联免疫分析仪进样过程中各个动作分别写成任务函数进行封装。根据酶联免疫分析仪检测步骤调用相应的任务函数便可实现整个进样任务[15]。基于STM32的多轴协调运动控制算法的流程图如图 11所示。
|
| 图 11 基于STM32多轴协调运动控制算法流程图 Fig.11 Flow chart of multi-axis coordinated motion control algorithm based on STM32 |
多轴运动定位精度包括水平运动与垂直运动的定位精度。水平运动确保进样臂的吸头安装柱能对准吸头以及各试剂槽, 垂直运动完成取吸头以及控制吸头插入样本试剂的深度。下面分别进行校核。
1) 水平运动定位精度校核。
将进样吸头及各试剂槽的中心位置标注在十字网格纸片上,并将纸片固定在试剂托盘上,在吸头吸入染色剂后,编写进样系统任务函数,使吸头尖端按照移液工作流程移动到各任务点,网格纸片上便会留下标记,通过放大镜读取标记点与理论中心点的位置便可得到X,Y向的定位精度。选取网格中的10个取样点,循环遍历各个点,以理论中心为原点,统计取样点的轴向偏差,最终测试结果如表 1所示。
| mm | |||
| 测试轴 | 最大值 | 最小值 | 误差 |
| X轴 | 0.12 | 0.05 | 0.12 |
| Y轴 | 0.10 | 0.03 | |
由表 1可知,进样臂的水平运动定位精度最大值为0.12 mm,满足小于0.2 mm的要求。
2) 垂直运动定位精度校核。
在进样臂完成取吸头后,设置进样臂分别从10个不同的高度扎入样本液面,循环进行10次,统计吸头尖端距离液面的轴向距离,最终测试结果如表 2所示。
| mm | |||
| 测试轴 | 最大值 | 最小值 | 误差 |
| Z轴 | 0.45 | -0.20 | 0.65 |
由表 2可知,进样臂的垂直运动定位精度误差为0.65 mm,满足小于1.0 mm的要求。
4.2 进样测试与误差补偿上文已进行了进样系统的理论精度计算,而在实际进样过程中存在不定性因素影响着进样精度,如进样器的密封性、空气与液体体积的置换关系以及移液机构的传动精度等,为了检验进样系统的移液精度和控制精度,需进行试验验证。在试验过程中采用编码器对进样臂的吸液轴运动进行位置监测, 并将编码器计数值通过串口发送至上位机,以计算进样臂的传动误差与步进电机的控制误差。系统中所采用的编码器型号为HKT32-1000,其分辨率为1 000 P/R,则反馈脉冲数n与反馈进样量V的关系为:
| $ V = n\frac{{{P_{\rm{h}}}}}{{1000}} \cdot \frac{S}{l} $ | (4) |
在进样系统进样测试中,以100 μL为最大进样量进行滴定测试,使用称重法进行进样结果校验,参照国际标准ISO 8655-6[16],其允许误差如表 3所示。
| 标称容量/ μL | 检定点/ μL | 容量允许 误差/% | 重复性 误差/% |
| 100 | 10 | ±8.0 | ≤4.0 |
| 50 | ±3.0 | ≤1.5 | |
| 100 | ±2.0 | ≤1.0 |
其中规定的检定点为10,50,100 μL,以容量允许误差、重复性误差为检验项目,将测试数据与此进行对比。
测试的配置如下:
电机控制:驱动器配置32细分模式,使用7阶段S型曲线加减速控制算法。
检定点所需理论脉冲数:10 μL时,为6 400个;50 μL时,为32 000个;100 μL时,为64 000个。
测量介质:去离子水。
测量设备:0.01 mg的电子天平,型号为HZ-104/35SF。
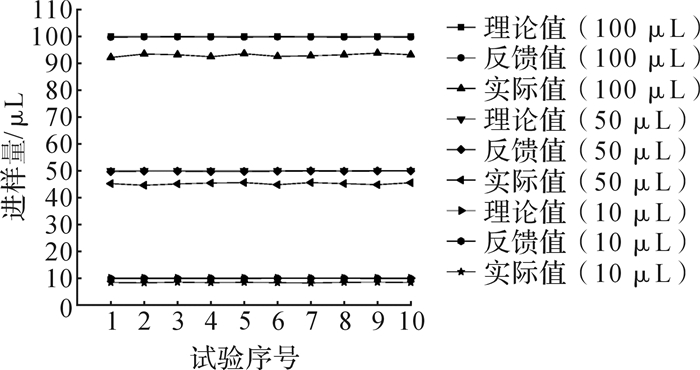
测量方式1:对给定进样量(10,50,100 μL)分别进行10次测量,统计每次测量结果。该测试用于检测进样系统的稳定性,试验数据如图 12所示。
|
| 图 12 采用测量方式1时的试验数据 Fig.12 Test data measured by method 1 |
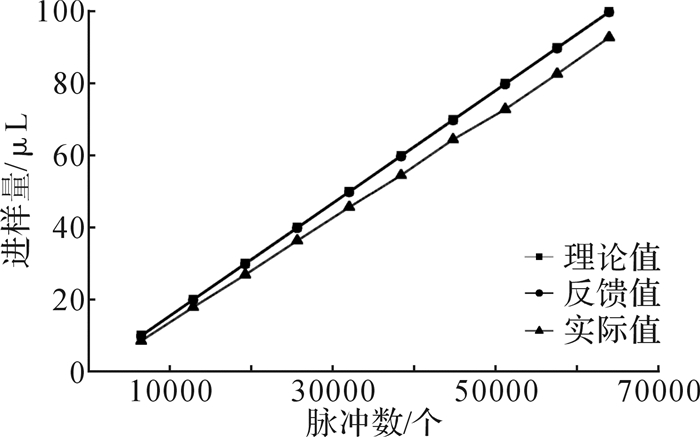
测量方式2:选取包括检定点在内的10个测量点进行测量,每个检测点进行10次测试,然后取平均值,试验数据如图 13所示。通过该试验可得到进样系统的吸液误差和执行机构传动误差之间的关系,以分析得到系统误差的来源。
|
| 图 13 采用测量方式2时的试验数据 Fig.13 Test data measured by method 2 |
通过测试可得出结论:1)系统具有较高的重复进样精度;2)编码器反馈值误差在其分辨率范围内,控制过程中并没有出现失步现象;3)进样器的空气置换误差及传动误差在总误差中占较大比重,并有一定误差积累现象。
经分析得到:进样系统存在系统误差和随机误差,且系统误差远大于随机误差;随机误差主要来源于结构件的制造精度误差和安装误差;系统误差主要取决于进样器自身的制造误差和压强变化对气液置换率影响,吸头内的空气具有拉伸性,在气液置换时一定体积的气体并不能置换得到同体积的液体[17-18]。因此,减小进样系统误差应从2个方面考虑:1)使用更高精度的结构件,以减小机械误差与传动误差;2)优化控制算法,采用算法补偿的方式对吸排环节进行误差补偿。
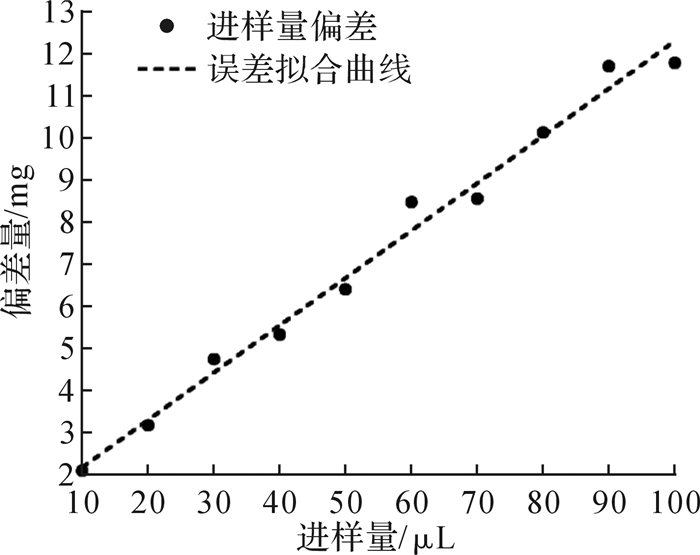
提高进样系统的机械结构件精度,将使得成本上升,所以本方案采用改进算法对进样误差进行线性补偿的方式减小系统误差。利用最小二乘法对试验数据中实际进液量与理论进样量的偏差进行线性拟合,如图 14所示。
|
| 图 14 进样误差数据拟合 Fig.14 Fitting liner of sample error data |
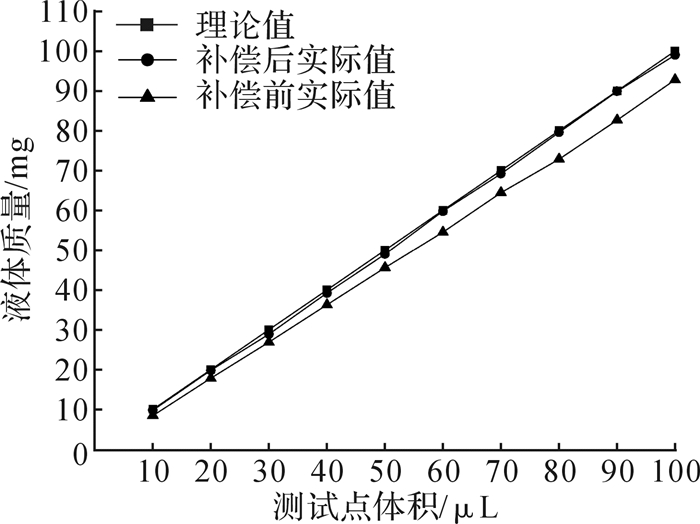
可得到拟合直线方程:y=0.1099x+1.0781。对拟合函数换算成试验的脉冲补偿函数:y=710.34x+690。将补偿函数融合到进样系统控制算法中,再次进行滴定试验,试验测试方法和步骤与测量方式2一致。测试结果与误差补偿前的对比如图 15所示。
|
| 图 15 误差补偿前后进样测试数据比较 Fig.15 Comparison of sample test data before and after error compensation |
测量结果的重复性误差R与进样精度E的计算公式分别为:
| $ R = \left( {s/{x_1}} \right) \times 100\% $ | (5) |
| $ E = \frac{{\bar x - {x_1}}}{{{x_1}}} \times 100\% $ | (6) |
式中:xl为目标进样量; s为标准差。
由式(5)、(6)可算得检定点(10,50,100 μL)在误差补偿前后的进样精度与重复性误差,如表 4所示。
| 检定量/μL | 进样精度/% | 重复性误差/% | |||
| 补偿前 | 补偿后 | 补偿前 | 补偿后 | ||
| 10 | ±7.2 | ±1.80 | ±2.4 | ±1.31 | |
| 50 | ±5.3 | ±1.28 | ±1.25 | ±0.56 | |
| 100 | ±3.2 | ±1.15 | ±1.0 | ±0.4 | |
测试结果表明最小二乘线性拟合校正方法有效降低了系统误差,系统在进样检试点(10,50,100 μL)的进样精度分别由±7.2%,±5.3%,±3.2%减小到±1.8%,±1.28%,±1.15%;重复性误差分别由±2.4%,±1.25%,±1.0%减小到±1.31%,±0.56%,±0.40%, 满足设计规范要求。
5 总结1) 针对酶联免疫分析仪小型化、高精度的需求,自主研发了小型微量自动进样系统。采用高精度标准进样器内嵌的方式,充分利用各传动机构的特点,通过合理布局与功能规划,设计了小型自动微量进样臂,提高了进样系统的可靠性与集成度,同时降低了仪器的生产成本。
2) 自动进样控制系统中通过插补法优化后的S型加减速控制算法,加快了程序执行效率,改善了步进电机的运动特性,避免了失步与过冲现象;根据进样量分段使用加减速插补曲线的方法,提高了进样系统使用范围与效率,实现进样系统最小进样量为1 μL,以0.05 μL的分辨率步进;利用基于STM32控制器的PWM模块能很好地实现步进电机的半闭环控制,实现多轴协调同步运动;模块化与任务封装的多轴控制策略,简化了多任务的执行过程,提高了微量进样系统的工作效率。
3) 通过滴定实验校核了进样臂位置精度与进样精度,实验证明,最小二乘线性拟合方法能有效地补偿进样误差,使得进样系统的精度与稳定性得到进一步提升,最终微量进样系统在检试点(10,50,100 μL)的进样精度分别达到了±1.8%,±1.28%,±1.5%,减少了检测试剂的用量,很好地满足了实用化的需求,对微量进样设备的研制具有一定指导意义。
| [1] | TAO L, LONG W, WANG Y Q. Design and implementation of the control system for an ARM9-based biochemical analyzer[J]. Advance Materials Research, 2011, 268/270: 454–457. DOI:10.4028/www.scientific.net/AMR.268-270 |
| [2] |
刘雄.800速全自动生化分析仪运动控制系统关键技术研究[D].绵阳: 西南科技大学计算机科学与技术学院, 2015: 1-3.
LIU Xiong. Research on key technologies about motion control system of 800-speed automatic biochemical analyzer[D]. Mianyang: Southwest University of Science and Technology, School of Computer Technology and Science, 2015: 1-3. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D652473 |
| [3] |
武通园.高速全自动化生化分析仪高精度加样技术研究[D].深圳: 深圳大学医学部, 2016: 1-4.
WU Tong-yuan. Research on high accuracy accumulation technology of high speed fully automatic biochemical analyzer[D]. Shenzhen: Shenzhen University, School of Health Science Center, 2016: 1-4. http://cdmd.cnki.com.cn/Article/CDMD-10590-1016763960.htm |
| [4] |
祝连庆, 张文昌, 董明利, 等.
一种提高全自动酶免分析仪微量移液精度的方法[J]. 仪器仪表学报, 2013, 34(5): 1008–1014.
ZHU Lian-qing, ZHANG Wen-chang, DONG Ming-li, et al. Method to improve the micropipette accuracy of full-automatic ELISA system[J]. Chinese Journal of Scientific Instrument, 2013, 34(5): 1008–1014. DOI:10.3969/j.issn.0254-3087.2013.05.008 |
| [5] | CHANG Zhu, SHANG Zhi-wu, LIU Zhen-wu, et al. A small automated enzyme immunoassay analyzer system design and implementation based on immunoenzymatic techniques[J]. Key Engineering Materials, 2016, 693: 1308–1313. DOI:10.4028/www.scientific.net/KEM.693 |
| [6] |
常海涛, 祝连庆, 娄小平, 等.
一种全自动酶免分析仪移液过程评估新方法[J]. 仪器仪表学报, 2014, 35(7): 1622–1629.
CHANG Hai-tao, ZHU Liang-qing, LOU Xiao-ping, et al. A fully automatic enzyme immunoassay analyzer shift liquid process to evaluate the new method instrument[J]. Chinese Journal of Instrumentation, 2014, 35(7): 1622–1629. |
| [7] |
刘镇武, 尚志武, 黄炎彬.
全自动生化进样系统的设计[J]. 工程设计学报, 2016, 23(6): 612–619.
LIU Zhen-wu, SHANG Zhi-wu, HUANG Yang-bin. Design of full automatic biochemical sampling system[J]. Chinese Journal of Engineering Design, 2016, 23(6): 612–619. |
| [8] |
林丽文, 吕慧.
关于全自动酶联免疫分析仪的携带污染分析[J]. 临床医学研究与实践, 2016, 1(13): 81.
LIN Li-wen, LÜ Hui. Analysis of carry contamination in enzyme immunoassay analyzer[J]. Clinical Research and Practice, 2016, 1(13): 81. |
| [9] |
杜新杰, 祝连庆, 娄小平, 等.
基于模糊PID的酶免分析仪加样臂运动控制[J]. 电子测量与仪器学报, 2014, 28(3): 327–333.
DU Xin-jie, ZHU Lian-qing, LUO Xiao-ping, et al. Fuzzy PID for adding sample arm movement control of ELISA processor[J]. Journal of Electronic Measurement and Instrument, 2014, 28(3): 327–333. |
| [10] |
黄兆斌, 黄云龙, 余世明.
几种步进电机加减速方法的对比研究及其应用[J]. 机电工程, 2011, 28(8): 951–953, 974.
HUANG Zhao-bin, HUANG Yun-long, YU Shi-ming. Several step stepper motor acceleration and deceleration method of comparative study and its application[J]. Mechanical and Electrical Engineering, 2011, 28(8): 951–953, 974. DOI:10.3969/j.issn.1001-4551.2011.08.013 |
| [11] |
杨超, 张冬泉.
基于S曲线的步进电机加减速的控制[J]. 机电工程, 2011, 28(7): 813–817.
YANG Chao, ZHANG Dong-quan. Control of acceleration and deceleration of stepping motor based on S curve[J]. Mechanical and Electrical Engineering, 2011, 28(7): 813–817. DOI:10.3969/j.issn.1001-4551.2011.07.011 |
| [12] |
刘慧英, 范宝山.
基于STM32的多步进电机控制系统研究[J]. 测控技术, 2010, 29(6): 54–57.
LIU Hui-ying, FAN Bao-shan. Study of control system of multiple step motors based on STM32[J]. Measurement & Control Technology, 2010, 29(6): 54–57. DOI:10.3969/j.issn.1000-8829.2010.06.015 |
| [13] |
张团善, 肖磊, 张娜.
基于STM32和FPGA的多轴运动控制器的设计[J]. 电子测量技术, 2011, 34(5): 61–63, 67.
ZHANG Tuan-shan, XIAO Lei, ZHANG Na. Design of multiaxial motion controller based on STM32 and FPGA[J]. Electronic Measurement Technology, 2011, 34(5): 61–63, 67. DOI:10.3969/j.issn.1002-7300.2011.05.017 |
| [14] |
程鑫.
多轴超精密同步运动控制系统中的数据交互机制[J]. 机械工程学报, 2014, 50(17): 149–156.
CHENG Xin. Data interchange mechanism in multi-axis ultra-precise synchronous motion control system[J]. Journal of Mechanical Engineering, 2014, 50(17): 149–156. |
| [15] |
龚燕妮.全自动生化分析仪多任务优化调度与检测方法研究[D].长沙: 湖南大学自动化学院, 2012: 31-35.
GONG Yan-ni. Research on multitask scheduling optimization and inspection of automatic biochemical analyzer[D]. Changsha: Hunan University, College of Electrical and Information Engineering, 2012: 31-35. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2172183 |
| [16] | ISO Technical Committees. Piston-operated volumetric apparatus Part6:Gravimetric methods for the determination of measurement error:ISO 8655-6:2002[J]. German:German Institute for Standardization, 2002: 12–13. |
| [17] |
刘志刚, 万良晨.
自动进样器的误差分析[J]. 广东技术师范学院学报(自然科学), 2014(3): 38–42.
LIU Zhi-gang, WAN Liang-chen. The error analysis of automatic sample injector[J]. Journal of Guangdong Polytechnic Normal University, 2014(3): 38–42. |
| [18] |
佟林, 王金涛, 刘子勇.
移液器使用及校准过程中影响因素分析[J]. 中国计量, 2012(5): 79–81.
TONG Lin, WANG Jin-tao, LIU Zi-yong, et al. Analysis on the influence factors of micro-volume pipette operation and calibration[J]. China Metrology, 2012(5): 79–81. DOI:10.3969/j.issn.1006-9364.2012.05.072 |


