2. 浙江大学 浙江省三维打印工艺与装备重点实验室, 浙江 杭州 310027;
3. 浙江永力达数控科技股份有限公司, 浙江 衢州 324000
2. Key Laboratory of 3D Printing Process and Equipment of Zhejiang Province, Zhejiang University, Hangzhou 310027, China;
3. Zhejiang Yonglida CNC Technology Co., Ltd., Quzhou 324000, China
热变形所带来的加工误差对数控机床的高速、高精化发展影响巨大。通过国内外学者开展的大量研究可知,数控机床内部热源和外部环境引致的热误差是其最大误差源,约占总制造误差的40%~70%[1-2]。主轴系统是数控机床的关键部件,其热态性能对于数控机床的切削速度和加工精度至关重要,是制约数控机床加工精度的最主要因素[3]。热设计是主轴系统热误差控制的重要手段,通过有效的热设计(如优化其冷却系统)可以在设计阶段获得较佳的主轴系统热态特性,达到减小热误差、提高加工精度、降低实验研究和样机制作成本的目的[4]。
目前,主轴系统的常用冷却方式是在其套筒内布置带有螺旋形流道的冷却套,来带走其内部产生的热量。Chien[5]、Sleiti[6]、陈文华[7]和王可[8]等人对螺旋形流道进行了流体传热特性和流动特性研究,研究表明螺旋形流道存在散热效率不高的缺点。因此,寻找一种更优的冷却结构成为国内外学者的研究热点。而在自然界中存在着诸如生物呼吸系统和循环系统等拥有较高能量和物质交换率的微管系统、拥有较高热能交换率和较低流动阻力的网络,可以为冷却结构的设计提供借鉴。Zhang等人[9]指出树状分形流道具有压降损失低、湿度分布均匀和散热效率高的特点。徐尚龙等人[10-11]建立了一种树形微通道冷却结构,将它用于芯片冷却,并将具有相同换热面积和边界条件的4种微通道散热结构(平行结构、网格结构、螺旋结构和分形结构)进行了对比分析,得出了分形结构的温度场分布均匀且温度最低。Xia等人[12-14]基于分形理论设计了一种具有树状分形流道的主轴温控结构,在考虑了流固耦合传热的基础上,通过仿真分析了该结构模型的流体动力学特性和热态特性,并与传统螺旋形流道结构的散热效果进行了对比,验证了树状分形流道结构的有效性。与此类似,动物的肝﹑肺﹑血管网络等传热或传质机构,也是一种自然优化的强化传质或换热的网络流道,在提高热交换效率的同时,还可以减少流体流动中的能量损失。昆虫翅膀的翅脉由它的气管演化而来,分布在翅膀表面,也是一种天然的具有良好输运特性的微管结构[15]。
本文以数值传热学相关理论为基础,通过研究鳞翅目昆虫翅脉,寻找昆虫翅脉特征的结构特征,借鉴昆虫翅脉结构对数控机床主轴系统的冷却结构进行热设计,构建出一种昆虫翅脉仿生流道冷却结构模型,并对昆虫翅脉仿生流道和螺旋形流道两种冷却结构进行流固耦合仿真对比分析,获得2种结构在相同条件下的温度场和流动状态结果,为改善主轴系统热态特性、减小主轴系统热误差提供参考。
1 基于昆虫翅脉仿生流道的主轴系统冷却结构模型图 1为一种鳞翅目昆虫的前翅翅脉结构示意图[15]。从图中可以看到其翅膀基本为三角形,主翅脉从三角形的最长边出发分叉延伸,这种分叉延伸方式的好处是可以通过较短的微通道来覆盖翅膀的大部分区域。

|
| 图 1 鳞翅目昆虫的前翅翅脉示意图 Fig.1 Schematic diagram of anterior wing vein of lepidoptera insect |
数控机床主轴系统的冷却套为一种圆环形结构,为了提高系统整体的散热效率,增强其温度场分布均匀性,笔者借鉴昆虫翅脉结构设计了一种拥有仿生流道的主轴系统,其结构如图 2所示。该结构依照鳞翅目昆虫前翅翅脉结构的特点,引入形态相似的分形流道散热结构,将冷却套中的分叉式流道结构依照昆虫翅脉型流道设置,在指定的区域内分布与翅脉相似的流道,并可以在需要加强散热的区域调整流道和增加分叉,以增强散热冷却效果。最终确定的流道结构如图 3,其结构参数如图 4所示。该冷却结构的特点是:流道由中部的直流道段和两侧的环形分形流道段组成;冷却液入口和冷却液出口分布在冷却套结构的上方和下方中部,两侧的环形分形流道结构对称分布,由若干多级直流道组成。冷却液从入口流入后由直流道段向左右方流动进入两侧分形流道,然后汇聚到下方的直流道段的出口流出。

|
| 1-前轴承;2-芯轴;3-冷却套;4-后轴承;5-主轴套;6-隔套 图 2 基于昆虫翅脉仿生流道的主轴系统结构示意图 Fig.2 Structure diagram of spindle system based on insect wing vein bionic channel |

|
| 图 3 昆虫翅脉仿生流道冷却结构示意图 Fig.3 Schematic diagram of insect wing vein bionic channel cooling structure |

|
| 图 4 昆虫翅脉仿生流道结构参数示意图 Fig.4 Structure parameter diagram of insect wing vein bionic channel |
仿生流道的结构参数需要满足如下关系:
| $ \left\{ \begin{array}{l} \frac{{{W_{h + 1}}}}{{{W_h}}} = n\\ \frac{{{L_{\rm{a}}}}}{{{L_{\rm{b}}}}} = m\\ {S_h} = 2{W_h} \times {L_{\rm{a}}} + 2{W_{h + 1}}\left( {{L_{\rm{b}}} + {L_{\rm{c}}}} \right)\\ {S_m} = 4\left( {{S_{h1}} + {S_{h2}} + {S_{h3}}} \right) + 2{S_{h4}}\\ \frac{{2{L_{\rm{b}}}\sin \theta }}{X} = z\\ D = \frac{{4A}}{P} \end{array} \right. $ | (1) |
式中:W代表流道宽度,L代表流道长度,h代表分级次数(最大值为4),下标a代表主支流道,b代表分叉处支流道,c表示分叉处直流道,n代表(h+1)与h级流道的宽度比,m代表主流道与分叉处流道的长度比,Sh为流道面积(Sh1、Sh2、Sh3和Sh4分别为第1级、第2级、第3级和第4级流道面积),Sm为分形流道总面积,X为流道的间距,θ为主流道与分叉处流道的夹角,z为分叉处流道长度、主流道与分叉处流道的夹角、流道的间距之间的关系系数,D为水力直径,A为截面积,P为截面周长。
2 冷却结构流固耦合传热数值模型根据流固耦合的传热数值计算理论,耦合传热可表示为[16]:
| $ {k_{\rm{s}}}\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) = {\rho _{\rm{s}}}{c_{\rm{p}}}\frac{{{\partial ^2}T}}{{\partial {t^2}}} $ | (2) |
式中:ks为固体传热系数,T为温度场,ρs为固体密度,cp为固体比热容,t为时间。
流动与传热过程遵循质量守恒、动量守恒和能量守恒三个物理基本定律,数值模型的控制方程如下:
1) 质量守恒方程。
根据单位时间内微元体中流体质量增量等于同一时间间隔内流入其中的净质量,可导出能量守恒方程如下[17]:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 $ | (3) |
式中:ρ为流体密度,u、v、w为流体速度矢量U在3个坐标轴上的分量。
| $ \frac{{\partial \rho }}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{U}}} \right) = 0 $ | (4) |
2) 动量守恒方程。
根据微元体中流体动量的增加率等于作用在微元体上各种力之和,并引入Newtown切应力公式及Stokes公式,则x、y、z方向上的动量守恒方程如下:
| $ \frac{{\partial u}}{{\partial t}} + {\rm{div}}\left( {u\mathit{\boldsymbol{U}}} \right) = \eta {\rm{div}}\left( {{\rm{grad}}\;u} \right) - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} $ | (5) |
| $ \frac{{\partial v}}{{\partial t}} + {\rm{div}}\left( {v\mathit{\boldsymbol{U}}} \right) = \eta {\rm{div}}\left( {{\rm{grad}}\;v} \right) - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} $ | (6) |
| $ \frac{{\partial w}}{{\partial t}} + {\rm{div}}\left( {w\mathit{\boldsymbol{U}}} \right) = \eta {\rm{div}}\left( {{\rm{grad}}\;w} \right) - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} $ | (7) |
式中:η为流体的动力黏度,p为管道水的压力。
3) 能量守恒方程。
根据微元体内热力学能的增加率等于进入微元体的净热流量与表面力、体积力对微元体做功之和,并引入导热Fourier定律,对于不可压缩流体,有:
| $ \begin{array}{*{20}{c}} {c{T_r}\left[ {\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{{\partial z}}} \right] = }\\ { - p\;{\rm{div}}\mathit{\boldsymbol{U}} + {\rm{div}}\left( {k\;{\rm{grad}}\;{T_r}} \right) + \mathit{\Phi } + {S_{\rm{h}}}} \end{array} $ | (8) |
式中:c为流体的质量热容;Tr为温度T在r(r=x, y, z)方向的分量;k为流体的导热率;Sh为流体的内热源;Φ为耗散函数(由于黏性作用使机械能转换为热能的部分),其计算公式为:
| $ \begin{array}{*{20}{c}} {\mathit{\Phi } = \eta \left[ {{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2}} \right] + {{\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}^2} + }\\ {{{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}^2} + k\;{\rm{div}}\mathit{\boldsymbol{U}}} \end{array} $ | (9) |
引入源项ST=Sh+Φ,则:
| $ \frac{{\partial T}}{{\partial t}} + {\rm{div}}\left( {\mathit{\boldsymbol{U}}T} \right) = {\rm{div}}\left( {\frac{k}{{\rho {c_p}}}{\rm{grad}}\;T} \right) + \frac{{{S_{\rm{T}}}}}{\rho } $ | (10) |
耗散率ε方程可表示为:
| $ \begin{array}{l} \rho \frac{{\partial \varepsilon }}{{\partial t}} + \rho {u_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\frac{{{c_1}\varepsilon }}{k}{\eta _{\rm{t}}}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - {c_2}\rho \frac{{{\varepsilon ^2}}}{k} \end{array} $ | (11) |
k方程(流体湍流脉动方程)为:
| $ \begin{array}{*{20}{c}} {\rho \frac{{\partial k}}{{\partial t}} + \rho {u_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + }\\ {{\eta _t}\frac{{\partial {u_j}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \varepsilon } \end{array} $ | (12) |
式中:ηt为湍流动力黏度系数; 下标i、j表示坐标方向。
3 螺旋形流道和仿生流道冷却结构有限元分析对流和热传导问题的解法可以通过质量守恒、动量守恒和能量守恒的控制方程获得。但是,上述三大控制方程的偏微分方程呈高度非线性,求解过程中伴随着大量计算,故在实际工程应用中通常采用数值分析方法,并借助计算流体动力学(computational fluid dynamics,CFD)工程软件来进行求解。本文所设计的昆虫翅脉仿生流道冷却结构仿真分析及其与螺旋形流道冷却结构的对比分析,都是采用Fluent商用CFD软件包来实现。冷却结构的有限元流固耦合步骤如图 5所示[18]。

|
| 图 5 有限元流固耦合分析步骤 Fig.5 Analysis steps of finite element fluid-structure interaction |
利用Fluent软件对仿生流道冷却结构模型进行网格划分,对于固体网格和流体网格均采用十节点的四面体单元(Solid187),在流体与固体壁面交界处增设边界层网格,之后对网格进行加密,尺寸大小设置为1 mm,划分网格后得到2 378 218个网格、588 866个节点。在进行流固耦合仿真过程中,热流密度和温度的连续性作为固体与流体能量方程耦合的边界条件。对流体采用标准K-epsilon模型,采用simple算法求解压力与速度耦合方程,离散方法采用Second Order Upwind格式,收敛残差为1×10-6。
3.1 基本假设和参数设置本文主要作原理性对比分析,为降低复杂度,在分析之前对模型作如下假设:
1) 流体的物理参数不随着温度的变化而改变。
2) 环境温度和环境空气物性恒定;空气流体不可压缩,固体域与流体域的初始温度为环境温度。
3) 流道壁面为非滑移壁面。
4) 忽略辐射散热和浮力的影响。
5) 只考虑内部轴承和主轴电机为主要热源,不考虑其他设备的散热对空气流场的影响。
为便于对比分析,对螺旋形流道和昆虫翅脉仿生流道两种冷却结构取相同的冷却液入口流速值、冷却液物性及加热面上的热流密度值,并假设热源在冷却系统结构上均匀分布。设定2种冷却流道基体材料为钢材,冷却液为水。冷却结构圆柱加热面上施加固定热流密度为25 000 W/mm2,入口处冷却液流速为1 m/s,冷却液初始温度为20 ℃。出口处将大气压边界条件作为参考压力。
3.2 流道流场分析流道中冷却液的流动状态是决定冷却结构冷却效果的关键因素,如图 6所示为2种流道结构流场稳态分析结果。从图 6(a)可知:在流动状态上,螺旋形流道中冷却液整体流动比较平缓,流速变化不大,流速方向沿着螺旋方向变化,冷却液最大流速约为1.882 m/s;从图 6(b)可知:昆虫翅脉仿生流道中冷却液流速变化比较均匀,在中间直线段变化比较大,这加快了冷却液向两端流动,且减小了冷却液流动的行程,增强了对流换热能力,当进入两侧流道分支后冷却液流动变得平缓,冷却液最大流速约为1.839 m/s。
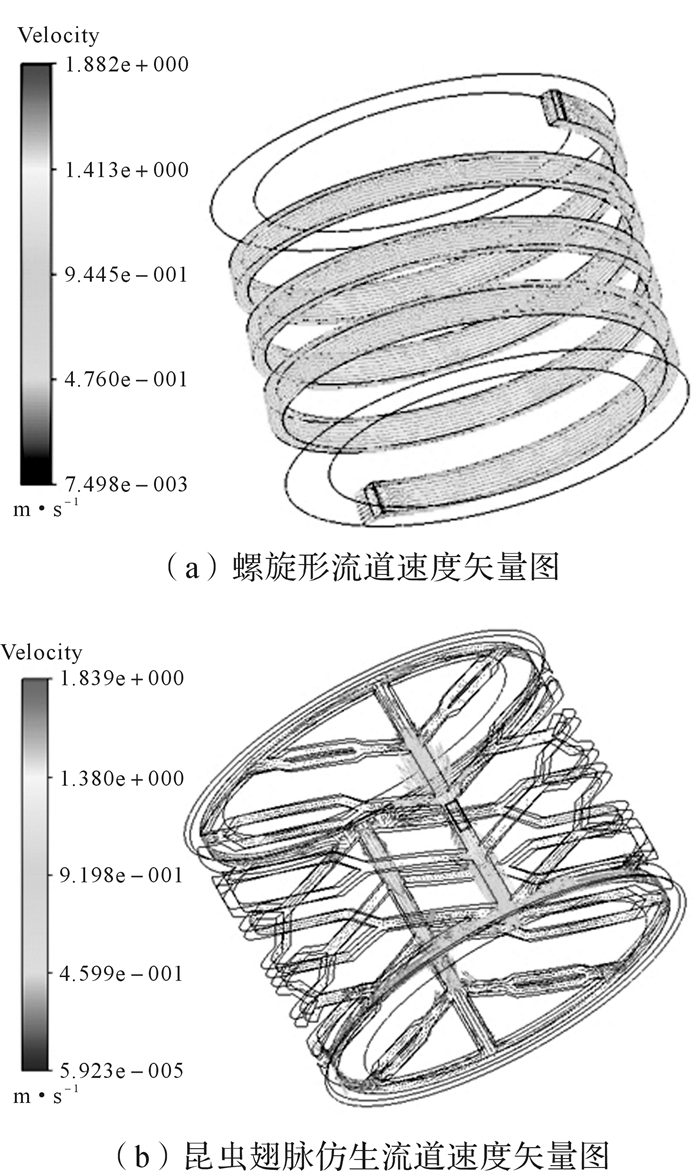
|
| 图 6 螺旋形流道和昆虫翅脉仿生流道流场分析结果 Fig.6 Flow field analysis results of spiral channel and insect wing vein bionic channel |
冷却结构的流道压降(流道入口压力与流道出口压力之差)也是表征流道流动特性的重要指标之一。压降对应于能耗,当流道压降较大时,则意味着能耗越多。如图 7所示为2种流道结构内部压力分析结果。当冷却液入口流速为1 m/s时,螺旋形流道的最大压力位于入口处,约为10 110 Pa,出口压力约为1 259 Pa,压降为8 851 Pa;昆虫翅脉仿生流道最大压力位于入口处,约为4 324 Pa,出口压力约为1 143 Pa, 压降为3 181 Pa。从出入口压力变化来看,昆虫翅脉仿生流道的压降要比螺旋形流道的小得多,这意味着前者的流动压力损失要比后者低,即昆虫翅脉仿生流道所消耗的能量比螺旋形流道要小。

|
| 图 7 螺旋形流道和昆虫翅脉仿生流道内部压力分析结果 Fig.7 Inner pressure analysis results of spiral channel and insect wing vein bionic channel |
图 8所示为螺旋形流道和昆虫翅脉仿生流道的压降随入口雷诺数的变化曲线。从图中可以看出压降随入口雷诺数的增大而增大,但是昆虫翅脉仿生流道压降增大的趋势要小于螺旋形流道的。
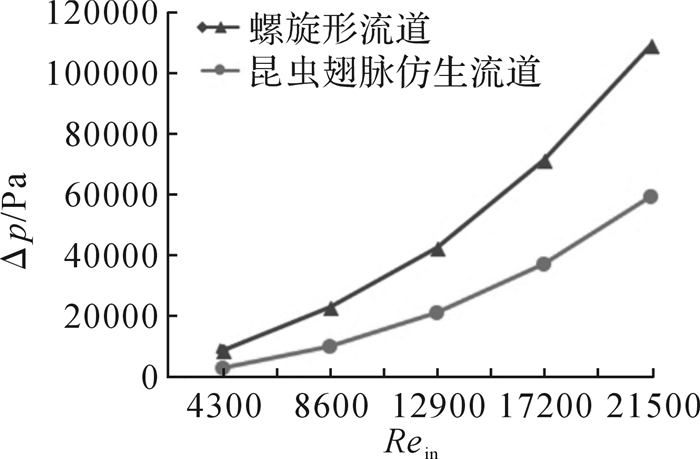
|
| 图 8 螺旋形流道和昆虫翅脉仿生流道的压降随入口雷诺数的变化曲线 Fig.8 Variation curve of pressure drop in spiral channel and insect wing vein bionic channel with inlet Reynolds number |
冷却结构与流道冷却液的热交换反映在加热面的温度场分布上。如图 9所示为螺旋形流道和昆虫翅脉仿生流道两种冷却结构加热面上的温度场分布云图。从图可知:螺旋形流道结构加热面的最高温度约为60.1 ℃,最低约为35.1 ℃;昆虫翅脉仿生流道结构加热面的最高温度约为49.4 ℃,最低温度约为33.5 ℃。相比较而言,后者的最高温度比前者降低了约17.8%,最低温度降低了约4.6%,显然后者的散热效果更为理想。同时,昆虫翅脉仿生流道结构加热面温差为15.9 ℃,与螺旋形流道的温差(25.0 ℃)相比减小了9.1 ℃,而且从图中也可以看出前者的温度场分布几乎对称,这也说明了前者的温度场分布更均匀。

|
| 图 9 螺旋形流道和昆虫翅脉仿生流道加热面温度场分析结果 Fig.9 Temperature field analysis results of heating surface of spiral channel and insect wing vein bionic channel |
图 10所示为螺旋形流道和昆虫翅脉仿生流道加热面最高与最低温度随入口冷却液流速的变化曲线。从图中可以看出:当冷却液入口流速较小时,2种流道结构加热面上的最低温度和最高温度相差较大;当冷却液入口流速增大时,加热面上的最低温度和最高温度差距逐渐减小。

|
| 图 10 螺旋形流道和昆虫翅脉仿生流道加热面最高与最低温度随入口冷却液流速的变化曲线 Fig.10 Variation curve of maximum and minimum temperature of heating surface in spiral channel and insect wing vein bionic channel with inlet coolant velocity |
将仿生学应用于数控机床主轴系统冷却系统结构设计,设计了一种新型基于鳞翅目昆虫翅脉仿生流道的冷却结构。在数值传热学相关理论的基础上建立了流固耦合传热数值模型,并通过Fluent有限元软件对基于传统螺旋形流道和昆虫翅脉仿生流道的2种冷却结构进行流固耦合仿真对比分析,发现虽然后者的冷却液流速与前者相比几乎相同,但是后者的流道压降比前者低了很多,能耗自然也要小得多。同时,昆虫翅脉仿生流道加热面的最大和最小温度都较低,散热效果更佳;其温差也较低,且温度场分布几乎对称,均温性能更佳。分析结果说明,新型昆虫翅脉仿生流道冷却结构与传统的螺旋形流道结构相比,在散热效果和流动特性方面都存在优势,可应用于解决数控机床主轴系统冷却结构的散热问题。
| [1] | MAYR J, JEDRZEJEWSKI J, UHLMANN E, et al. Thermal issues in machine tools[J]. CIRP Annals-Manufacturing Technology, 2012, 61(2): 771–791. DOI:10.1016/j.cirp.2012.05.008 |
| [2] |
邓小雷.
数控机床主轴系统热态特性分析技术[M]. 杭州: 浙江大学出版社, 2017: 1-64.
DENG Xiao-lei. Analysis techniques of thermal characteristics for CNC machine tool spindle system[M]. Hangzhou: Zhejiang University Press, 2017: 1-64. |
| [3] | ABELE E, ALTINTAS Y, BRECHER C. Machine tool spindle units[J]. CIRP Annals-Manufacturing Technology, 2010, 59(2): 781–802. DOI:10.1016/j.cirp.2010.05.002 |
| [4] |
邓小雷, 林欢, 王建臣, 等.
机床主轴热设计研究综述[J]. 光学精密工程, 2018, 26(6): 1415–1429.
DENG Xiao-lei, LIN Huan, WANG Jian-chen, et al. Review on thermal design of machine tool spindles[J]. Optics and Precision Engineering, 2018, 26(6): 1415–1429. |
| [5] | CHIENC H, JANG J Y. 3-D numerical and experimental analysis of a built-in motorized high-speed spindle with helical water cooling channel[J]. Applied Thermal Engineering, 2008, 28(17): 2327–2336. |
| [6] | SLEITIA K. Heat transfer and pressure drop through rectangular helical ducts[J]. Journal of Renewable & Sustainable Energy, 2011, 3(4): 681–197. |
| [7] |
陈文华, 贺青川, 何强, 等.
高速电主轴水冷系统三维仿真与试验分析[J]. 中国机械工程, 2010, 21(5): 550–555.
CHEN Wen-hua, HE Qing-chuan, HE Qiang, et al. Simulation and experimental analysis for high-speed spindle with water-cooling system[J]. Journal of Mechanical Engineering, 2010, 21(5): 550–555. |
| [8] |
王可, 刘继行, 孙兴伟.
螺旋水套与轴向水套水冷系统流固耦合对比分析[J]. 组合机床与自动化加工技术, 2014(11): 46–48.
WANG Ke, LIU Ji-xing, SUN Xing-wei. Comparative fluid-solid coupling analysis of spiral channel and axial channel water cooling system[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014(11): 46–48. |
| [9] | ZHANG C, CHEN Y, WU R, et al. Flow boiling in constructal tree-shaped minichannel network[J]. International Journal of Heat & Mass Transfer, 2011, 54(1): 202–209. |
| [10] |
徐尚龙, 郭宗坤, 秦杰, 等.
树形微通道热沉仿生建模及三维热流特性数值分析[J]. 中国机械工程, 2014, 25(9): 1185–1188.
XU Shang-long, GUO Zong-kun, QIN Jie, et al. Three dimensional numerical simulation of fluid flow and heat transfer in tree-shaped microchannels[J]. China Mechanical Engineering, 2014, 25(9): 1185–1188. DOI:10.3969/j.issn.1004-132X.2014.09.010 |
| [11] |
徐尚龙, 秦杰, 胡广新.
芯片冷却用微通道散热结构热流耦合场数值研究[J]. 中国机械工程, 2011, 22(23): 2863–2866.
XU Shang-long, QIN Jie, HU Guang-xin. Numerical study on heat-flow coupling field in microchannel heat sink structures for electronic chip cooling[J]. China Mechanical Engineering, 2011, 22(23): 2863–2866. |
| [12] | XIA C, FU J, LAI J, et al. Conjugate heat transfer in fractal tree-like channels network heat sink for high-speed motorized spindle cooling[J]. Applied Thermal Engineering, 2015, 90: 1032–1042. DOI:10.1016/j.applthermaleng.2015.07.024 |
| [13] |
夏晨晖.数控机床主轴温升特性快速辨识方法及新型温控结构的研究[D].杭州: 浙江大学机械工程学院, 2015: 99-127.
XIA Chen-hui. Research on fast identification method for machine tool spindle temperature rise characteristics and a novel cooling structure design[D]. Hangzhou: Zhejiang University, School of Mechanical Engineering, 2015: 99-127. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015630207.htm |
| [14] |
傅建中, 夏晨晖, 贺永, 等.一种基于分形流道的冷却套及电主轴: ZL201210334517.5[P].2015-07-29.
FU Jian-zhong, XIA Chen-hui, HE Yong, et al. An electric spindle and its cooling sleeve based on a fractal flow channel: ZL201210334517.5[P]. 2015-07-29. |
| [15] |
秦杰.仿生微流道散热器结构优化及流动散热特性研究[D].成都: 电子科技大学机械电子与工程学院, 2012: 1-33.
QIN Jie. Study on the structure optimization and flow heat dissipation characteristics of bionic microchannel[D]. Chengdu: University of Electronic Science and Technology, School of Mechanical and Electronic Engineering, 2012: 1-33. http://cdmd.cnki.com.cn/Article/CDMD-10614-1012471591.htm |
| [16] |
彭立印.柴油机缸内流体流动数值分析[D].成都: 西南交通大学机械工程学院, 2007: 6-14.
PENG Li-yin. Numerical analysis of airflow field in cylingder of disel engine[D]. Chengdu: Southwest Jiaotong University, School of Mechanical Engineering, 2007: 6-14. http://cdmd.cnki.com.cn/Article/CDMD-10613-2007117218.htm |
| [17] |
陶文铨.
数值传热学[M]. 西安: 西安交通大学出版社, 2001: 1-10.
TAO Wen-quan. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001: 1-10. |
| [18] |
王东.重型数控卧式镗车床关键部件热场流固耦合研究[D].哈尔滨: 哈尔滨理工大学机械动力工程学院, 2016: 29-42.
WANG Dong. Fluid-structure interaction research on thermal field of the key components of heavy-duty CNC horizontal boring lathe[D]. Harbin: Harbin University of Science and Technology, School of Mechanical and Power Engineering, 2016: 29-42. http://cdmd.cnki.com.cn/Article/CDMD-10214-1016056350.htm |


