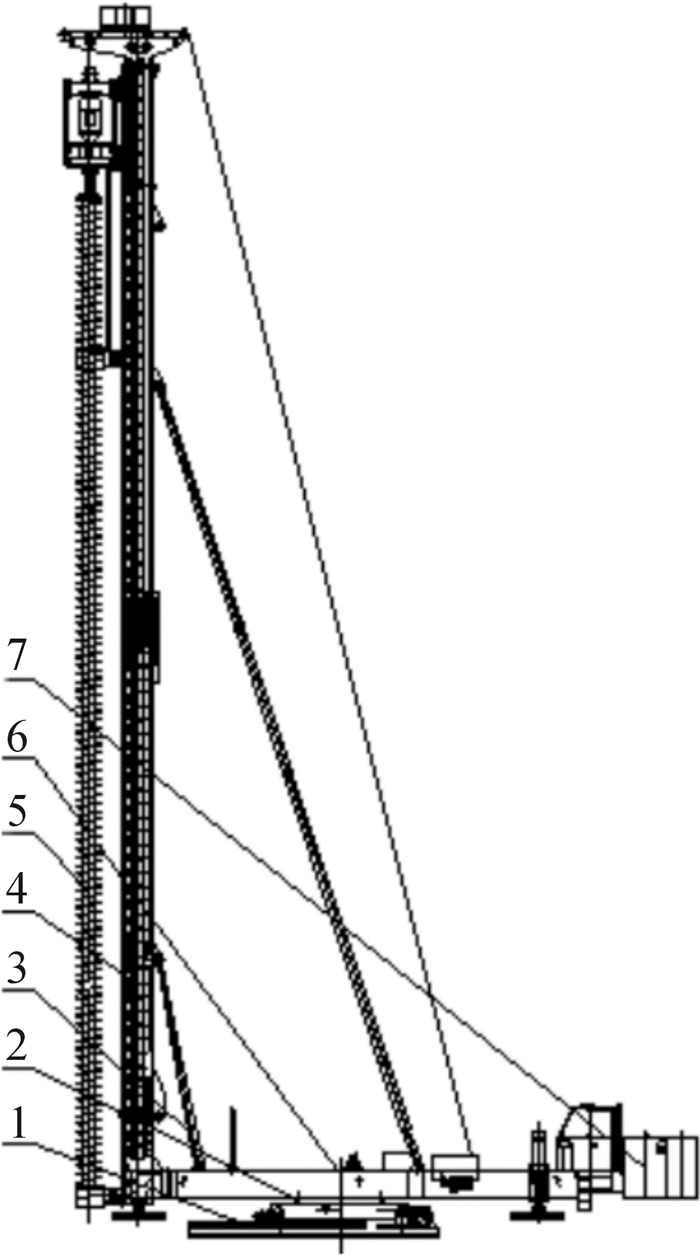
螺旋钻机是建筑工程中成孔作业常用的施工机械之一,它作业高效、噪音低且污染少,加之售价低廉,因此备受施工单位青睐,得到广泛应用与快速发展。螺旋钻机的结构如图 1所示,它主要由行走机构、回转机构、变幅机构、钻桅、钻进机构(动力头及钻杆)、机身及配重等组成。变幅机构作为螺旋钻机最重要的部件之一,主要对钻桅起支撑、变幅作用,保证钻进机构正常工作。此外,由于螺旋钻机钻桅工作时竖直起柱的特殊性,活动钻桅的变幅角度必须达到90°,而变幅机构则不需频繁变幅,这与其他工程机械的变幅是有明显区别的。
|
| 1—行走机构;2—回转机构;3—变幅机构;4—钻桅;5—钻进机构;6—机身;7—配重 图 1 螺旋钻机结构 Fig.1 Structure of auger driller |
针对不同工程机械,目前对其变幅机构的研究大多依托ADAMS、AMESim、Simulink和ANSYS软件,研究的方向主要集中在变幅机构运动学及其动力学分析[1-5]、变幅液压系统稳定性分析与优化[6-8]、变幅构件强度分析与结构优化[9-12]等方面,但对变幅机构铰点位置进行优化的研究比较少。事实上,变幅机构作为大部分具有回转、变幅功能的工程机械的必要机构,变幅机构性能的优良与否,跟铰点位置密切相关。由于铰点位置的设计需要综合考量的因素多,对设计者的经验要求非常高,传统设计中设计者不得不依赖大量的试算来确定一组相对合理的铰点位置。这种设计方法不仅存在工作量大、效率低的缺点,而且很有可能丢失铰点位置的最优解。
本文通过对螺旋钻机变幅机构的结构及工作原理进行分析,建立其力学模型,并用粒子群优化(particle swarm optimization, PSO)算法求解更为合理的螺旋钻机变幅机构铰点位置,为变幅机构铰点位置的优化布置提供思路。
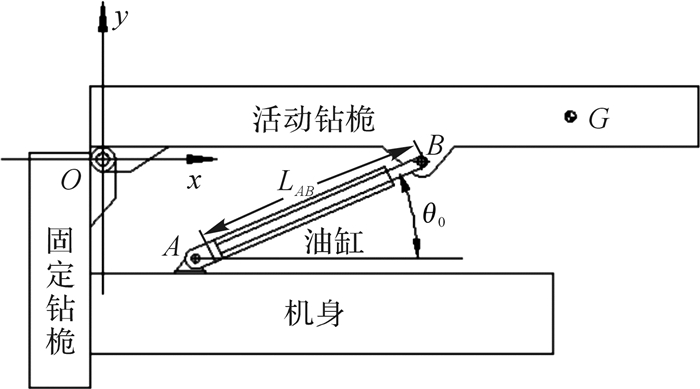
1 建立目标函数螺旋钻机变幅机构示意图如图 2所示,它主要由变幅油缸、固定钻桅、活动钻桅、机身四部分组成。压力油从油泵通过管路进入变幅油缸的进油口后,在压力油的驱动下,活动钻桅开始绕铰点O转动,从水平位置最终转到竖直位置,完成活动钻桅的起柱。由于钻桅整体的刚性较大,建模过程中视之为纯刚体。
|
| 图 2 螺旋钻机变幅机构示意图 Fig.2 Sketch graph of auger driller luffing mechanism |
为方便变幅机构静力学数学模型的建立和求解,将坐标系的原点设于固定铰点O,坐标轴方向如图 2所示,其中油缸初始长度为LAB, 变幅油缸的初始变幅角度为θ0。变幅油缸进油口的进油油量为Q,变幅油缸的缸径为D,伸出速度为v, 则有:
| $ v = \frac{{4Q}}{{{\rm{ \mathsf{ π} }}{D^2}}} $ | (1) |
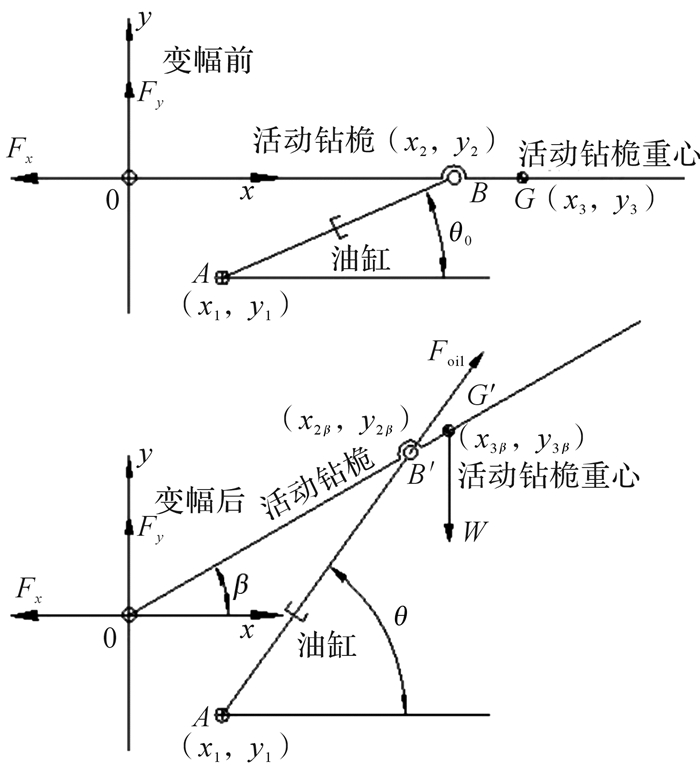
对变幅机构进行简化,如图 3所示。铰点A的坐标为(x1, y1),铰点B的初始坐标为(x2, y2),活动钻桅重心G的初始坐标为(x3, y3)。活动钻桅转动β后铰点B的坐标为(x2β, y2β),即为B′;重心G的坐标为(x3β, y3β),即为G′。
|
| 图 3 变幅机构活动钻桅受力图 Fig.3 Force diagram of the moving rig of luffing mechanism |
则直线AB的初始斜率为:
| $ k = \tan {\theta _0} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ | (2) |
油缸初始长度LAB为:
| $ {L_{AB}} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $ | (3) |
根据坐标变换可知:
| $ \left\{ \begin{array}{l} {x_{2\beta }} = {x_2}\cos \beta - {y_2}\sin \beta \\ {y_{2\beta }} = {x_2}\sin \beta + {y_2}\cos \beta \\ {x_{3\beta }} = {x_3}\cos \beta - {y_3}\sin \beta \\ {y_{3\beta }} = {x_3}\sin \beta + {y_3}\cos \beta \end{array} \right. $ | (4) |
即:
| $ \left[ {\begin{array}{*{20}{c}} {{x_{2\beta }}}\\ {{y_{2\beta }}}\\ {{x_{3\beta }}}\\ {{y_{3\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} \cos \beta \\ \sin \beta \\ 0\\ 0 \end{array}&\begin{array}{l} - \sin \beta \\ \cos \beta \\ 0\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ \cos \beta \\ \sin \beta \end{array}&\begin{array}{l} 0\\ 0\\ - \sin \beta \\ \cos \beta \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}}\\ {{x_3}}\\ {{y_3}} \end{array}} \right] $ | (5) |
其中:0°≤β≤90°。
根据式(5)可知,活动钻桅起柱完成(转动90°)后铰点B的坐标为(-y2, x2),即为B2,则起柱完成变幅油缸伸到最长时两铰点距离为:
| $ {L_{A{B_2}}} = \sqrt {{{\left( {{x_1} + {y_2}} \right)}^2} + {{\left( {{y_1} - {x_2}} \right)}^2}} $ | (6) |
则活动转桅的整个起柱时间为:
| $ {t_{\rm{s}}} = \frac{{{L_{A{B_2}}} - {L_{AB}}}}{v} = \frac{{{\rm{ \mathsf{ π} }}\left( {{L_{A{B_2}}} - {L_{AB}}} \right){D^2}}}{{4Q}} $ | (7) |
活动钻桅转动β时变幅油缸的倾角为θ,则:
| $ \theta = \arctan \frac{{{y_{2\beta }} - {y_1}}}{{{x_{2\beta }} - {x_1}}} $ | (8) |
铰点O到变幅油缸的距离为:
| $ d = \frac{{\left| {{x_1}{y_{2\beta }} - {x_{2\beta }}{y_1}} \right|}}{{\sqrt {{{\left( {{x_1} - {x_{2\beta }}} \right)}^2} + {{\left( {{y_1} - {y_{2\beta }}} \right)}^2}} }} $ | (9) |
在整个过程中活动钻桅的起柱非常缓慢,可以忽略活动钻桅的惯性力和各铰点处的摩擦力。根据图 3,按正交分解法建立活动钻桅的力学方程:
| $ \left\{ \begin{array}{l} W{x_{3\beta }} - {F_{{\rm{oil}}}}d = 0\\ {F_x} - {F_{{\rm{oil}}}}\cos \theta = 0\\ {F_y} + {F_{{\rm{oil}}}}\sin \theta - W = 0 \end{array} \right. $ | (10) |
式中:Fx、Fy为铰点为O的铰轴对活动钻桅x、y方向的约束力;Foil为油缸对活动钻桅的推力;W为活动钻桅的重量。
由于变幅油缸回油口接油箱,回油口压力可忽略不计,变幅油缸进油口油压可近似为变幅油缸油压,由式(10)可以得到:
| $ \left\{ \begin{array}{l} {p_{\rm{t}}} = \frac{{4W\left( {{x_3}\cos \beta - {y_3}\sin \beta } \right)}}{{{\rm{ \mathsf{ π} }}{D^2}d}}\\ {F_o} = \sqrt {F_x^2 + F_y^2} \end{array} \right. $ | (11) |
式中:pt为变幅油缸油压;Fo为Fx、Fy两者合力,即铰点O的受力。
在变幅机构中,变幅油缸最大油压是个很关键的参数,决定了液压系统零部件的选型,且变幅油缸推力、各铰点最大受力都和此参数相关,所以选择pt作为目标函数,即:
| $ {p_{\rm{t}}} = {F_1}\left( {{x_1},{y_1},{x_2},{y_2},\beta } \right) $ | (12) |
一方面,考虑到螺旋钻机在公路运输时的安全性,固定钻桅的高度不能超限,另一方面,由于螺旋钻机车身附件(如油箱、卷扬设备)安装的限制,固定钻桅的高度又不能过低,所以铰点A的约束条件如下:
| $ \left\{ \begin{array}{l} 800 \le {x_1} \le 1\;300\;{\rm{mm}}\\ - 1400 \le {y_1} \le - 1\;000\;{\rm{mm}} \end{array} \right. $ | (13) |
对于铰点B,从活动钻桅的结构上看,铰点B和O基本处于同一水平线上,限定约束条件为:
| $ - 40 \le {y_2} \le 40\;{\rm{mm}} $ | (14) |
变幅油缸的初始变幅角度θ0过小将导致变幅油缸长度过长,制造成本过高,油缸也有压杆失稳的可能,这明显不符合工程实际情况,结合文献[1]及相关设计经验,油缸初始变幅角限定条件为:20°≤θ0≤60°,根据式(2)有:
| $ {\rm{0}}{\rm{.364}} \le \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} \le \sqrt 3 $ | (15) |
由式(13)至(15)可以推得:
| $ 1\;354 \le {x_2} \le 5\;256\;{\rm{mm}} $ | (16) |
根据油缸的制造工艺要求,油缸初始长度LAB和伸长时的最大距离LAB2的比值应在0.65~0.9之间[13],即:
| $ {\rm{0}}{\rm{.65}} \le \frac{{{L_{AB}}}}{{{L_{A{B_2}}}}} \le 0.9 $ | (17) |
式(13)至(17)构成了优化的约束条件。
3 粒子群优化算法求解粒子群优化算法是一种能通过不断迭代搜寻找出最优解的智能优化算法,自1995年由Eberhart和Kennedy首次提出以来,已经广泛应用于函数优化[14]、神经网络训练[15]、路径规划[16]和模糊控制[17]等。从前文分析可知,变幅机构铰点优化属多变量多约束非线性的优化,很适合利用粒子群优化算法进行求解。粒子优化群算法的速度和位置迭代公式如下[18]:
| $ v_{id}^{k + 1} = \omega v_{id}^k + {c_1}{r_1}\left( {p_{id}^k - X_{id}^k} \right) + {c_2}{r_2}\left( {g_d^k - X_{id}^k} \right) $ | (18) |
| $ X_{id}^{k + 1} = X_{id}^k + v_{id}^{k + 1} $ | (19) |
式中:ω为惯性权重;k为迭代次数;c1、c2为学习因子;r1、r2为[0, 1]之间的随机数; vidk表示粒子群第i个粒子第k次迭代时d维分量的速度;Xidk表示粒子群第i个粒子第k次迭代时d维分量的位置;pidk示粒子群第i个粒子第k次迭代时搜索到的最优位置的d维分量;gdk为整个粒子群第k次迭代时搜索到的最优位置的d维分量。
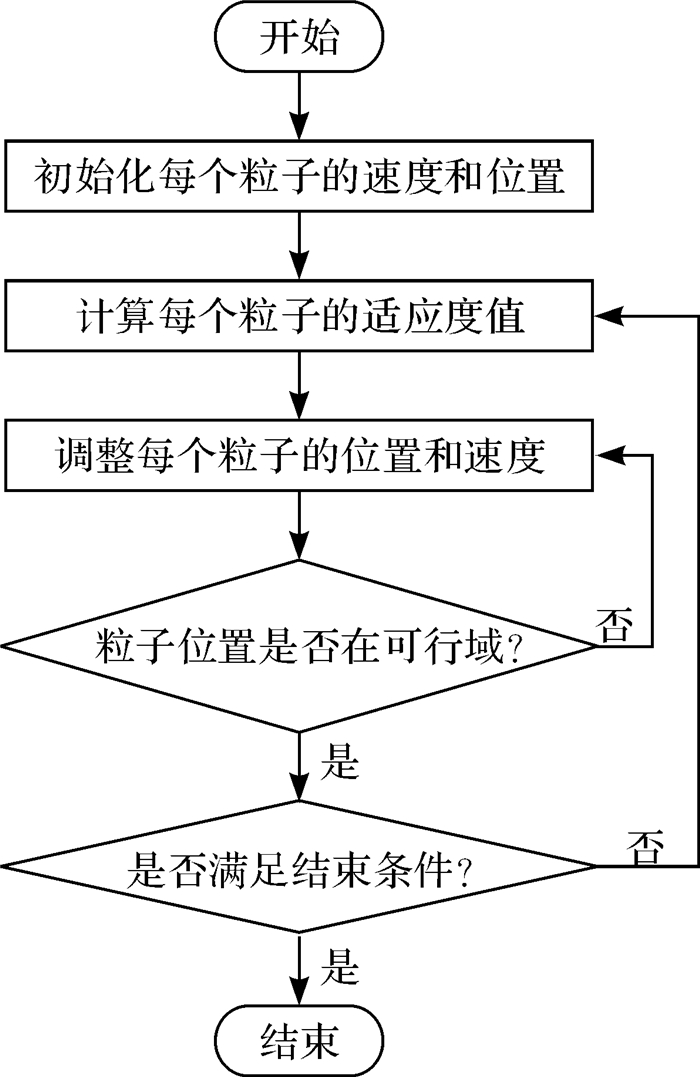
粒子群优化算法求解流程如图 4所示。
|
| 图 4 粒子群优化算法求解流程图 Fig.4 Solving flow chart of PSO algorithm |
通过前文分析可知,求最佳的铰点位置,实际上就是要求得最佳的A、B两铰点的初始坐标,即(x1, y1)、(x2, y2),使得变幅油缸最大油压最小。所以可以把(x1, y1, x2, y2)作为一个四维变量的粒子,每个粒子对应螺旋钻机变幅机构一组铰点位置。
基于粒子群优化算法的铰点优化步骤如下:
1) 设定粒子群优化算法的参数。
算法参数包括粒子的数量N、粒子的飞行速度v、程序的最大迭代次数kmax和精度阈值ε。粒子的数量N一般根据优化问题的难易程度和求解精度设置,本文选取粒子数N=15;取最大迭代次数kmax=100,精度阈值ε=0.005。粒子的速度既不能过大,也不能过小,这样粒子在搜索时不会错过全局最优解,按每维变化范围的15%选取粒子最大速度vmax,按每维变化范围的5%选取粒子最小速度vmin。
2) 设定粒子的初始位置和初始速度。
在粒子群可行区域内随机初始化粒子的位置,初始速度取粒子群最小速度vmin。初始位置即(x1, y1, x2, y2)的初始值。
3) 计算粒子的适应度值。
目标函数确定为变幅油缸的油压pt,优化的目的是使得变幅油缸的最大油压最小,所以适应度函数为:
| $ \min \left( {\max {p_{\rm{t}}}} \right) = {F_1}\left( {{x_1},{y_1},{x_2},{y_2},\beta } \right) $ | (20) |
4) 更新粒子位置和速度。
按式(18)和(19)更新位置和速度。若粒子的速度超差(即速度过大或过小),则按如下规则调整:若v>vmax,则取v=vmax;若v < vmin,则取v=vmin。
取惯性权重ωmax=1.2, ωmin=0.2,从而惯性权重ω=0.2+rand(),rand()表示[0, 1]的随机数;学习因子c1=c2=2。
5) 判断粒子位置是否满足边界约束条件。
按式(13)至(17)判断粒子位置是否满足边界约束条件,如不满足,说明粒子飞出可行域,则重新按式(18)和(19)更新,直到粒子位置落在可行域内。
6) 判断是否满足结束条件。
结合适应度函数,结束条件为:第k次迭代前后的变幅机构的最大油压的最小值变化率不超过设定阈值或迭代次数超限,即:
| $ \left| {\frac{{\min \left( {\max p_{\rm{t}}^k} \right) - \min \left( {\max p_{\rm{t}}^{k - 1}} \right)}}{{\min \left( {\max p_{\rm{t}}^{k - 1}} \right)}}} \right| \le \varepsilon \;或\;k > {k_{\max }} $ |
其他参数根据湖南长河机械有限公司生产的某型号28 m螺旋钻机的参数进行设置,如表 1所示。
| 参数 | 数值 | 单位 |
| 进油流量Q | 80 | L/min |
| 油缸缸径D | 220 | mm |
| G点坐标(x3, y3) | (14 940, 400) | mm |
| 活动钻桅重量W | 109 100 | N |
利用上述粒子群优化算法,使用MATLAB计算软件进行数据处理,得到铰点A和铰点B优化前后的2组坐标数据,具体数值见表 2。其中优化前方案是使用传统设计手法反复试算优选出来的。
| mm | ||||
| 优化前后 | x1 | y1 | x2 | y2 |
| 优化前 | 1 000 | -1 100 | 3 255 | -15 |
| 优化后 | 1 135 | -1 220 | 3 900 | -30 |
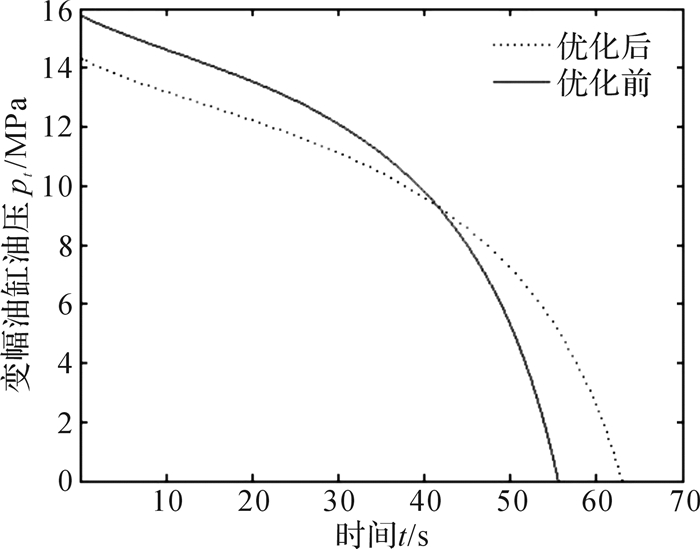
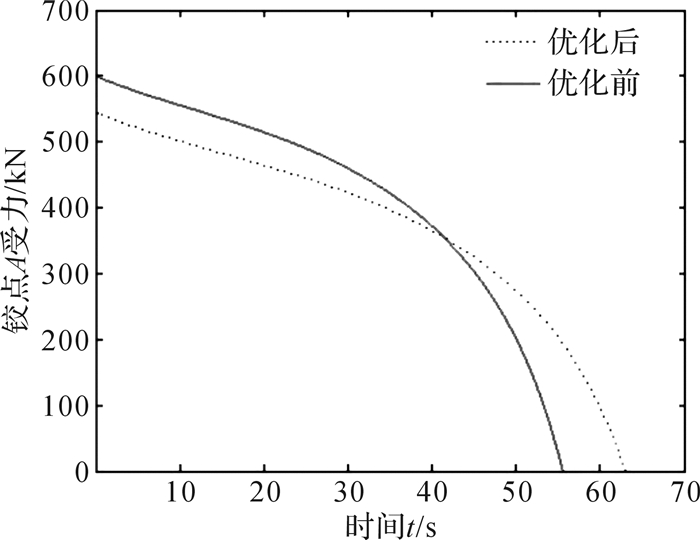
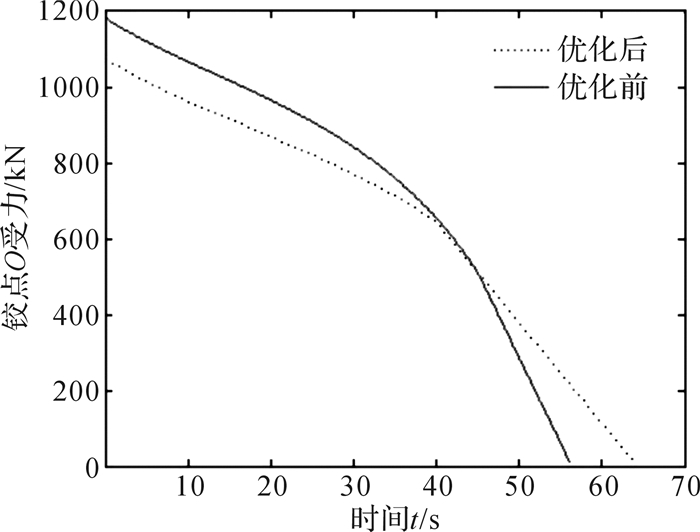
铰点位置优化前后变幅油缸油压及其各铰点受力曲线如图 5至图 7所示。
|
| 图 5 铰点位置优化前后变幅油缸油压对比 Fig.5 Comparison of the oil pressure of luffing cylinder before and after hinge point position optimization |
|
| 图 6 铰点位置优化前后铰点A受力对比 Fig.6 Comparison of the force of hinge point A before and after hinge point position optimization |
|
| 图 7 铰点位置优化前后铰点O受力对比 Fig.7 Comparison of the force of hinge point O before and after hinge point position optimization |
对比图 5至图 7,可以得到铰点位置优化前后变幅油缸最大油压pt max、铰点A最大受力Foil max、铰点O最大受力Fo max、起柱时间Ts, 如表 3所示。
| 优化前后 | pt max/MPa | Foil max/kN | Fo max/kN | Ts/s |
| 优化前 | 15.79 | 600.3 | 1181.9 | 56.1 |
| 优化后 | 14.34 | 545.0 | 1073.9 | 63.6 |
| 变化率/% | -9.2 | -9.2 | -9.1 | 7.5 |
从表 3可以看出,铰点位置优化后,变幅机构的起柱时间增加了7.5 s,这对螺旋钻机的施工几乎没有影响,而变幅油缸的最大油压和A、B、O铰点的最大受力减小明显。与此同时,从图 5可以看出,优化后变幅油缸整个起柱过程的油压变化变得平缓,这对提高液压系统性能、提高铰点处铰轴和铰座结构强度十分有利。
5 结论本文通过分析螺旋钻机变幅机构的特点,建立了其力学模型和铰点位置的粒子群优化算法模型,在满足粒子边界约束的前提下,通过粒子群不断迭代寻优,最终逼近最优位置,从而得到了更为合理的铰点位置组。通过分析优化前后的对比数据表明,利用粒子群优化算法取得的优化设计结果使得变幅机构的性能得到明显提升,说明粒子群优化算法在变幅机构铰点优化设计中是一种快捷、行之有效的方法。粒子群优化算法可以推广到所有具有类似结构的工程机械变幅机构的铰点优化中去。
此外值得一提的是,本文的优化是以适当牺牲系统的变幅时间为代价的,这对建筑工程机械螺旋钻机施工几乎没有影响,但对于某些对变幅时间有严格限制或者需要频繁变幅的机械,如云梯消防车等救援设备,则不能忽略该点,此时应将变幅时间设定为优化目标函数的约束条件。
| [1] |
许怡赦, 郭雄华.
安装角度对旋挖钻机变幅机构的力学影响[J]. 机械设计, 2012, 29(5): 27–30.
XU Yi-she, GUO Xiong-hua. Impact on mechanical behaviors of luffing mechanism of rotary drilling rig by installing angle[J]. Journal of Maching Design, 2012, 29(5): 27–30. |
| [2] |
康辉梅, 何清华, 朱建新.
旋挖钻机变幅机构的动力学建模与仿真[J]. 中南大学学报(自然科学版), 2010, 41(2): 532–538.
KANG Hui-mei, HE Qing-hua, ZHU Jian-xin. Dynamic modeling and simulation of mast link frame system of rotary drilling rig[J]. Journal of Central South of University (Science and Technology), 2010, 41(2): 532–538. |
| [3] |
姚婧辉.随车起重机变幅机构仿真研究[D].大连: 大连理工大学机械工程学院, 2009: 27-29.
YAO Jing-hui. The simulation of luffing mechanism of lorry loading crane[D]. Dalian: Dalian University of Technology, School of Mechanical Engineering, 2009: 27-29. http://cdmd.cnki.com.cn/Article/CDMD-10141-2010020785.htm |
| [4] |
钱森, 訾斌, 曹建斌, 等.
基于MATLAB/Simscape的汽车起重机变幅机构的优化与仿真[J]. 机械传动, 2012, 36(8): 40–43, 47.
QIAN Sen, ZI Bin, CAO Jian-bin, et al. Optimization and simulation of luffing mechanism of truck crane based on MATLAB/Simscape[J]. Journal of Mechanical Transmission, 2012, 36(8): 40–43, 47. |
| [5] |
魏乐.基于AMESim的50吨汽车起重机变幅系统仿真分析与实验研究[D].吉林: 吉林大学机械科学与工程学院, 2011: 29-30.
WEI Le. Boom system simulation analysis and experimental study of trucks crane based on AMESim[D]. Jilin: Jilin University, School of Mechanical Science and Engineering, 2011: 29-30. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011103069.htm |
| [6] |
胥军, 李刚炎, 杨飞, 等.
折叠式臂架系统变幅稳定性分析与优化[J]. 机械科学与技术, 2014, 33(1): 32–36.
XU Jun, LI Gang-yan, YANG Fei, et al. Luffing stability analysis and optimization of folding-boom arm system[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(1): 32–36. |
| [7] |
陈刚, 李平, 崔壮平, 等.
消防云梯车变幅液压驱动系统的建模仿真[J]. 中国工程机械学报, 2014, 12(1): 7–12.
CHEN Gang, LI Ping, CUI Zhuang-ping, et al. Modeling and simulation on hydraulic-driven luffing system for fire ladder trucks[J]. Chinese Journal of Construction Machinery, 2014, 12(1): 7–12. DOI:10.3969/j.issn.1672-5581.2014.01.002 |
| [8] |
吴晓强, 张春友.
消防云梯车变幅系统动态特性分析与改进设计[J]. 机械强度, 2016, 38(2): 221–224.
WU Xiao-qiang, ZHANG Chun-you. Dynamic characteristic analysis and design improvements of fire trucks luffing system[J]. Journal of Mechanical Strength, 2016, 38(2): 221–224. |
| [9] |
徐信芯, 夏北, 焦生杰, 等.
旋挖钻机大三角变幅机构受力性能有限元分析[J]. 现代制造工程, 2016(6): 17–22, 39.
XU Xin-xin, XIA Bei, JIAO Sheng-jie, et al. Finite element method analysis of performance for large triangular variable-range assembly for rotary drilling machines[J]. Modern Manufacturing Engineering, 2016(6): 17–22, 39. |
| [10] |
何晓艳, 秦四成.
旋挖钻机钻桅三角形连接架的有限元分析[J]. 工程机械, 2007, 38(10): 35–39, 143.
HE Xiao-yan, QIN Si-cheng. Finite element analysis of triangle connection of drill mast in rotary drilling rig[J]. Construction Machinery and Equipment, 2007, 38(10): 35–39, 143. DOI:10.3969/j.issn.1000-1212.2007.10.010 |
| [11] |
周曌.某型号旋挖钻机工作装置结构有限元分析[D].秦皇岛: 燕山大学机械工程学院, 2015: 37-40.
ZHOU Zhao. A certain type of rotary drilling rig working device finite element analysis of structure[D]. Qinhuangdao: Yanshan University, College of Mechanical Engineering, 2015: 37-40. http://cdmd.cnki.com.cn/Article/CDMD-10216-1015901483.htm |
| [12] |
李自贵, 马俊, 晋民杰, 等.
基于ADAMS的折臂式随车起重机工作机构优化设计[J]. 机械设计, 2015, 32(8): 36–40.
LI Zi-gui, MA Jun, JIN Min-jie, et al. Optimal design of working mechanism in the articulating boom crane based on ADAMS[J]. Journal of Machine Design, 2015, 32(8): 36–40. |
| [13] |
陆敏恂, 李万莉.
流体力学与液压传动[M]. 上海: 同济大学出版社, 2006: 93.
LU Min-xun, LI Wan-li. Fluid mechanics and hydraulic transmission[M]. Shanghai: Tongji University Press, 2006: 93. |
| [14] |
赵东波, 姚灵灵, 袁坤坤, 等.
基于粒子群算法多目标优化液压支架四连杆[J]. 工程设计学报, 2017, 24(4): 433–439.
ZHAO Dong-bo, YAO Ling-ling, YUAN Kun-kun, et al. Multi-objective optimization for four-bar mechanism of hydraulic support based on particle swarm optimization algorithm[J]. Chinese Journal of Engineering Design, 2017, 24(4): 433–439. DOI:10.3785/j.issn.1006-754X.2017.04.010 |
| [15] |
李松, 刘力军, 翟曼.
改进粒子群算法优化BP神经网络的短时交通流预测[J]. 系统工程理论与实践, 2012, 32(9): 2045–2049.
LI Song, LIU Li-jun, ZHAI Man. Prediction for short-tem traffic flow based on modified PSO optimized BP neural network[J]. System Engineering Theory and Practice, 2012, 32(9): 2045–2049. DOI:10.3969/j.issn.1000-6788.2012.09.024 |
| [16] |
孟庆宽, 仇瑞承, 张漫, 等.
基于改进粒子群优化模糊控制的农业车辆导航系统[J]. 农业机械学报, 2015, 46(3): 29–36, 58.
MENG Qing-kuan, QIU Rui-cheng, ZHANG Man, et al. Navigation system of agricultural vehicle based on fuzzy logic controller with improved particle swarm optimization algorithm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2015, 46(3): 29–36, 58. |
| [17] |
张万绪, 张向兰, 李莹.
基于改进粒子群算法的智能机器人路径规划[J]. 计算机应用, 2014, 34(2): 510–513.
ZHANG Wan-xu, ZHANG Xiang-lan, LI Ying. Path planning for intelligent robots based on improved particle swarm optimization algorithm[J]. Journal of Computer Applications, 2014, 34(2): 510–513. |
| [18] |
纪震, 廖惠莲, 吴青华.
粒子群算法及应用[M]. 北京: 科学出版社, 2009: 17.
JI Zhen, LIAO Hui-lian, WU Qing-hua. Particle swarm optimization algorithm and its application[M]. Beijing: Science Press, 2009: 17. |



