近几年来,高速公路、铁路的里程正以惊人的速度快速增长。凿岩设备的发展趋势是以自动化程度高的智能机器替代传统机械设备[1-2]。凿岩台车作为主流掘进开挖设备,其凿岩速度是整车性能的重要评价指标。现有设备大多不具备其最佳凿岩参数与岩石性质自动匹配的功能[3],使得凿岩过程中难以达到最佳凿岩速度。近些年来,国内外学者作了大量相关研究。北京科技大学毛信理等开展了推进力与回转速度自寻优控制的研究[4]。中南大学胡均平等[5]提出试行登山法的自寻最优控制,实现了多个凿岩参数的自适应。常欢欢和Liu等[6-7]研究了工作参数间的交互作用对钻进速度的影响规律,并得到最佳工作参数组合以及钻进速度与工作参数的回归关系。澳大利亚学者Cavanough等[8]确定了推进压力与回转压力、钻进速度之间的关系,通过控制推进压力来实现钻进系统的最优化控制,达到最大钻进速度。加拿大学者Sazidy等[9]研究了不同冲击力曲线对岩石破碎的影响,将比能耗和性能指数作为评价指标,得到最佳冲击力曲线。
在以往研究的基础上,对现有型号为GZT1的凿岩台车的电液控制系统进行优化设计[10-11]。本文研究以共轭斜量法作为寻优核心思想的控制方案,以实现最优凿岩参数的自动匹配,为进一步提高凿岩速度提供理论与实际指导依据。
1 凿岩参数间的相互作用关系在液压凿岩过程中,凿岩速度受多种因素的影响,主要因素有凿岩机输出的冲击能、活塞冲击频率、液压推进力、钎杆回转速度及岩石性质(岩石的强度、硬度、孔隙率等),除此之外,还包括钎头和钎杆的特性等[12]。在现场工作过程中,首先根据炮孔直径选择钎头,再由钻孔直径确定钎杆特性,两者一经确定即不再改变。
因此,凿岩过程中,在钎头和钎杆特性及冲击功率已定的情况下,影响凿岩速度v的因素主要有冲击能E、活塞冲击频率f、液压推进力FT及钎杆回转速度n,即:
| $ v = f\left( {E,f,{F_{\rm{T}}},n} \right) $ | (1) |
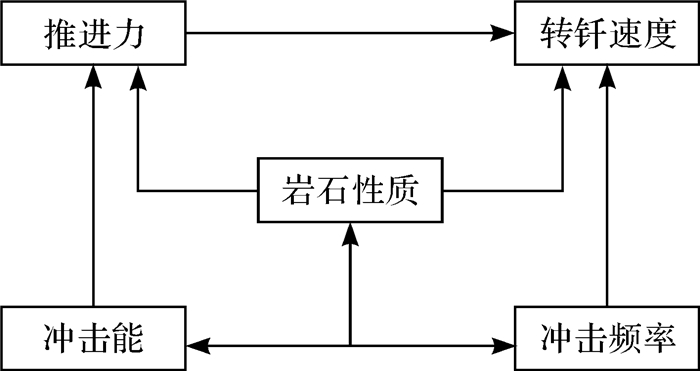
凿岩参数之间并不是相互独立的,各凿岩参数间的相互作用关系如图 1所示。为使凿岩速度达到最优,需使各个工作参数之间达到最优的匹配关系。
|
| 图 1 凿岩参数之间的相互作用关系 Fig.1 Interaction relationship between rock drilling parameters |
凿岩过程中,若对每个工作参数逐个进行寻优,则寻优时间较长,可能由于岩石性质的变化导致各参数最优值发生漂移。因此采用共轭斜量法[13]进行多变量分组动态寻优,使得凿岩参数快速达到最优值。
2.1 共轭斜量法基本原理对于函数F=f(X)=f(x1, x2, …, xn),选取基点Xk=(x1k, x2k, x3k, …, xnk),该点梯度的向量为:
| $ {\mathit{\boldsymbol{d}}_k} = \nabla f\left( {{X_k}} \right) = {\left( {\frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{1k}}}},\frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{2k}}}}, \cdots ,\frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{nk}}}}} \right)^{\rm{T}}} $ | (2) |
函数在基点Xk处沿dk方向上升最快, 选取下一个基点为Xk+1, 沿dk方向增加一个步距值αk,即:
| $ \begin{array}{l} {X_{k + 1}} = \left( {{x_{1k}} + {\alpha _{1k}} \cdot \frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{1k}}}},{x_{2k}} + {\alpha _{2k}} \cdot \frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{2k}}}}, \cdots ,} \right.\\ \;\;\;\;\;\;\;\;\left. {{x_{nk}} + {\alpha _{nk}} \cdot \frac{{\partial f\left( {{X_k}} \right)}}{{\partial {x_{nk}}}}} \right) \end{array} $ |
依照上述方法,不断迭代直至满足收敛条件。
将|dk|作为收敛的判断方法,即:
| $ \begin{array}{l} \left| {{\mathit{\boldsymbol{d}}_k}} \right| = \left| {\nabla f\left( {{X_k}} \right)} \right| = \\ \;\;\;\;\;\;\;\sqrt {\frac{{\partial f{{\left( {{X_k}} \right)}^2}}}{{\partial {x_{1k}}}} + \frac{{\partial f{{\left( {{X_k}} \right)}^2}}}{{\partial {x_{2k}}}} + \cdots + \frac{{\partial f{{\left( {{X_k}} \right)}^2}}}{{\partial {x_{nk}}}}} \end{array} $ | (3) |
若函数F=f(X)=f(x1, x2, …, xn)存在唯一极值点,则:离极值点越近,|dk|的值越小;离极值点越远,|dk|越大。因此可将|dk|作为是否达到极值点的依据,并将式(4)作为判断函数是否收敛的标准:
| $ \left| {{\mathit{\boldsymbol{d}}_k}} \right| < \xi $ | (4) |
式中:ξ为收敛的精度。
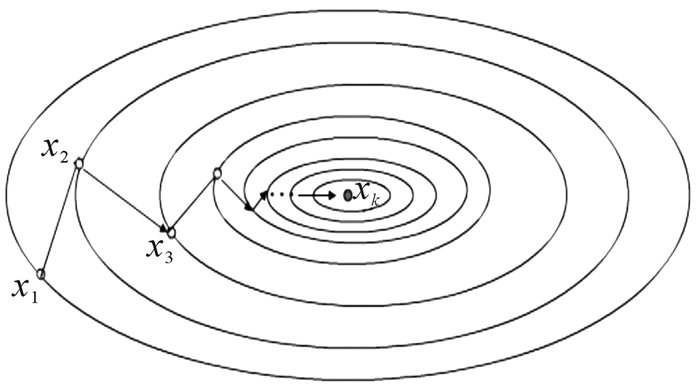
共轭斜量法的搜索路径如图 2所示。在离极值点远的地方选取较大的搜索步长,使之可以迅速收敛;在离极值点近的地方选取较小的搜索步长,以保证搜索精度;当达到设定的精度时,搜索结束,此时可认为搜索值即为极值点。
|
| 图 2 共轭斜量法的搜索路径 Fig.2 The search path of conjugate gradient method |
在寻优过程中,可通过对寻优次序的合理规划来减少寻优时间,防止陷入局部最优。本文将冲击能与冲击频率、推进力与转钎速度分为2组先后进行自寻优。
2.2.1 冲击能与冲击频率自寻优为保证冲击功近似恒定,冲击能与冲击频率沿相反方向进行寻优,因此只需要求冲击能E的变化方向,冲击频率f沿相反方向变化即可。
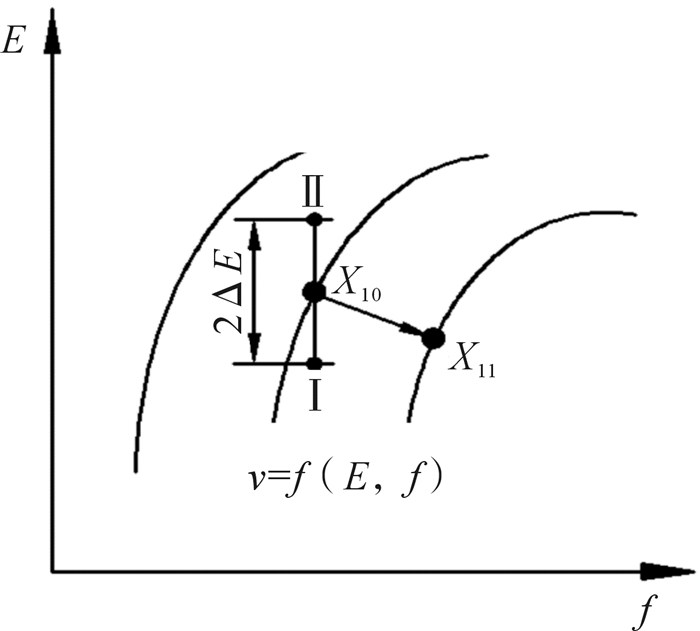
如图 3所示,在基点X10=(f0, E0, FT0, n0)处布置2个试验点,其中Ⅰ,Ⅱ点处的冲击能与冲击频率可分别表示为:
| $ \left\{ \begin{array}{l} {{E'}_0} = {E_0} - \Delta E,f' = {f_0}\\ {{E''}_0} = {E_0} + \Delta E,f'' = {f_0} \end{array} \right. $ | (5) |
|
| 图 3 冲击能与冲击频率自寻优时试验点布置示意图 Fig.3 Schematic diagram of test point layout for self-optimization of impact energy and impact frequency |
偏导数反映函数沿正方向的变化率,冲击能的偏导数可近似表示为:
| $ \frac{{\partial v}}{{\partial E}} = \frac{{\Delta v}}{{\Delta E}} = \frac{{{v_2} - {v_1}}}{{{{E''}_0} - {{E'}_0}}} = \frac{{{v_2} - {v_1}}}{{2\Delta {E}}} $ | (6) |
下一个基点X11=(f1, E1, FT0, n0)的变化方向为:
| $ {\mathit{\boldsymbol{d}}_{10}} = \frac{{\partial v}}{{\partial E}}\mathit{\boldsymbol{i}} - \frac{{\partial v}}{{\partial E}}\mathit{\boldsymbol{j}} $ | (7) |
基点X11处的冲击能E1与冲击频率f1可表示为:
| $ {E_1} = {E_0} + {\alpha _{11}} \cdot \frac{{\partial v}}{{\partial E}},{f_1} = {f_0} - {\alpha _{12}} \cdot \frac{{\partial v}}{{\partial E}} $ | (8) |
式中:α11,α12分别为冲击能与冲击频率的调整步长。
冲击能与冲击频率达到最优值的判断依据为:
| $ \left| {{\mathit{\boldsymbol{d}}_{1k}}} \right| = \left| {\frac{{\partial v}}{{\partial E}}} \right| < {\xi _1} $ | (9) |
式中:ξ1为冲击能与冲击频率的寻优精度。
当满足式(9)的判断依据时,冲击能与冲击频率的寻优结束,开始推进力与转钎速度的寻优;否则, 以下一基点值为中心,重复进行试验,直至满足判断依据为止。
2.2.2 推进力与转钎速度自寻优凿岩过程中,钎杆所受的回转扭矩M可表示为:
| $ M = {M_1} + {M_2} + {M_3} = {\mu _1}{F_{\rm{d}}}{A_1} + {\mu _2}{F_{\rm{T}}}{A_2} + {M_3} $ | (10) |
式中:M1为钎具外缘与岩壁产生的摩擦力矩;M2为钎具顶端与破碎面产生的摩擦力矩;M3为剪切岩石所受的扭转力矩;μ1、μ2分别为钎具外缘与岩壁间、钎具顶端与破碎面间的摩擦系数;A1、A2分别为钎具外缘与岩壁、钎杆顶端与破碎面的接触面积;Fd为钎具外缘与岩壁间的压紧力。
剪切岩石所受的扭转力矩为:
| $ {M_3} = {K_1} \cdot N \cdot \bar S \cdot \tau $ | (11) |
式中:K1为岩石凿痕对岩石强度的影响系数;N为钎齿的颗数;S为单颗球齿的剪切面积;τ为岩石的抗剪切强度。
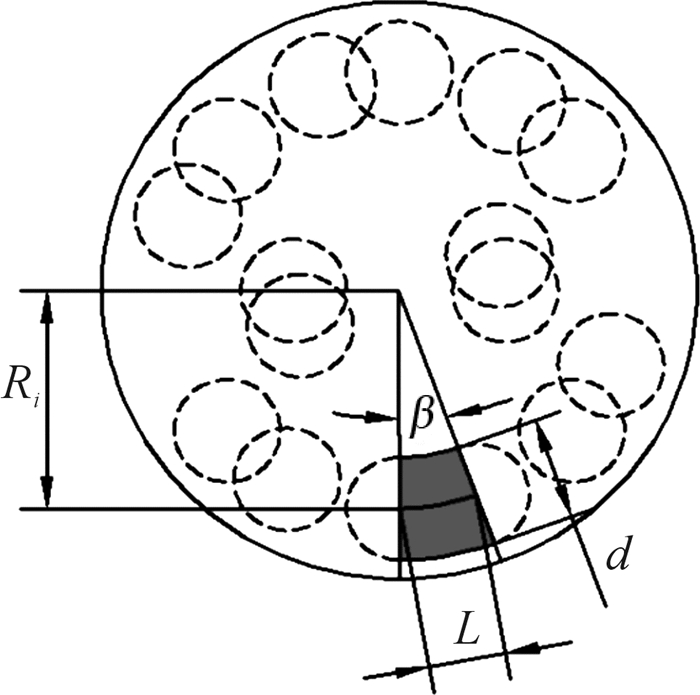
单颗球齿的剪切面积由图 4所示的阴影面积近似表示,即:
| $ \bar S = d \cdot L = d \cdot \beta \cdot {R_i} $ | (12) |
|
| 图 4 单颗球齿剪切面积示意图 Fig.4 The diagram of shear area of a single button |
式中:d为对应侵深的剪切宽度,可近似为钎齿的直径;L为剪切的长度;β为单次冲击周期内钎杆的转角;Ri为第i颗钎齿中心到钎头中心的距离。
联立式(10)至式(12),可以得出:
| $ \beta = \frac{{M - {u_1} \cdot {F_{\rm{d}}} \cdot {A_1} - {u_2} \cdot {F_{\rm{T}}} \cdot {A_2}}}{{{K_1} \cdot d \cdot {R_i} \cdot N \cdot \tau }} $ | (13) |
从而可求得系统所需要的转钎速度为:
| $ n = \beta \cdot f = \frac{{M - {u_1} \cdot {F_{\rm{d}}} \cdot {A_1} - {u_2} \cdot {F_{\rm{T}}} \cdot {A_2}}}{{{K_1} \cdot d \cdot N \cdot {R_i} \cdot \tau }} \cdot f $ | (14) |
由式(14)可知在凿岩钻孔过程中,转钎速度随推进力的增大而减小,生产实践表明,增大或减小推进力,回转压力会相应地上升或下降以匹配最优的转钎速度,从而保证在单个冲击周期内相邻的齿坑被连接起来,使得齿间间隙上的岩石能够被有效击碎,提高钻进速度。因此,可将转钎速度与推进力归为一组进行寻优。
2) 推进力与转钎速度自寻优过程。
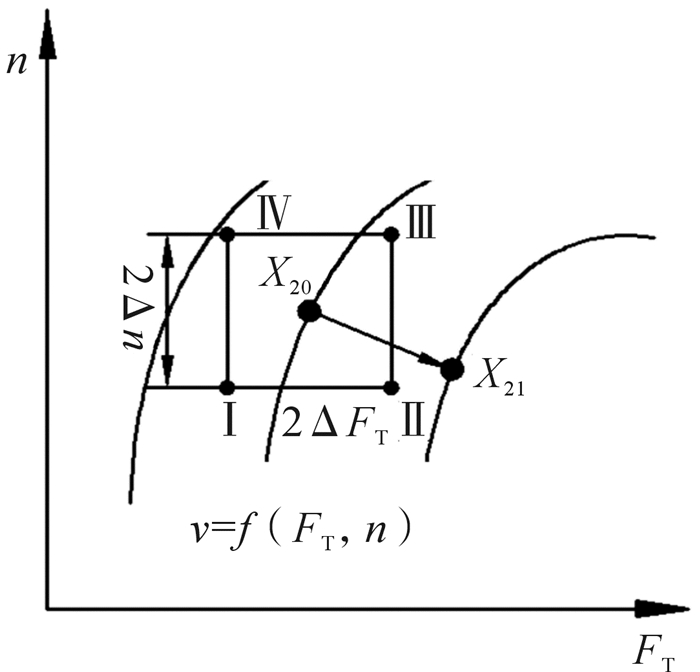
如图 5所示在基点X20=(EM, fM, FT0, n0)布置4个试验点,其中EM,fM分别为冲击能与冲击频率在寻优结束时的值,则Ⅰ,Ⅱ,Ⅲ,Ⅳ各点处推进力与转钎速度的取值分别为:
| $ \left\{ \begin{array}{l} {{F'}_{{\rm{T0}}}} = {F_{{\rm{T0}}}} - \Delta F,n' = {n_0} - \Delta n\\ {{F''}_{{\rm{T0}}}} = {F_{{\rm{T0}}}} + \Delta F,n'' = {n_0} - \Delta n\\ {{F'''}_{{\rm{T0}}}} = {F_{{\rm{T0}}}} + \Delta F,n''' = {n_0} + \Delta n\\ {{F''''}_{{\rm{T0}}}} = {F_{{\rm{T0}}}} - \Delta F,n'''' = {n_0} + \Delta n \end{array} \right. $ | (15) |
|
| 图 5 推进力和转钎速度自寻优时试验点布置示意图 Fig.5 Schematic diagram of test point layout for self-optimization of propulsion force and rotational speed |
若测得4个点的速度分别为v1、v2、v3和v4,则可求得推进力与转钎速度的偏导数分别为:
| $ \left\{ \begin{array}{l} \frac{{\partial v}}{{\partial {F_{\rm{T}}}}} \approx \frac{{\Delta v}}{{\Delta {F_{\rm{T}}}}} = \frac{1}{2}\left( {\frac{{{v_2} - {v_1}}}{{{{F''}_{{\rm{T0}}}} - {{F'}_{{\rm{T0}}}}}} + \frac{{{v_3} - {v_4}}}{{{{F'''}_{{\rm{T0}}}} - {{F''''}_{{\rm{T0}}}}}}} \right)\\ \frac{{\partial v}}{{\partial n}} \approx \frac{{\Delta v}}{{\Delta n}} = \frac{1}{2}\left( {\frac{{{v_3} - {v_2}}}{{n''' - n''}} + \frac{{{v_4} - {v_1}}}{{n'''' - n'}}} \right) \end{array} \right. $ | (16) |
则下一个基点X21=(EM, fM, FT1, n1)的变化方向为:
| $ {\mathit{\boldsymbol{d}}_{20}} = \frac{{\partial v}}{{\partial {F_{\rm{T}}}}}\mathit{\boldsymbol{i}} + \frac{{\partial v}}{{\partial n}}\mathit{\boldsymbol{j}} $ | (17) |
推进力FT1与转钎速度n1可表示为:
| $ {F_{{\rm{T1}}}} = {F_{{\rm{T0}}}} + {\alpha _{21}} \cdot \frac{{\Delta v}}{{\Delta {F_{\rm{T}}}}},{n_1} = {n_0} + {\alpha _{22}} \cdot \frac{{\partial v}}{{\partial n}} $ | (18) |
式中:α21, α22分别为推进力及转钎速度的调整步长。
寻优收敛的判断依据为:
| $ \left| {{\mathit{\boldsymbol{d}}_{2k}}} \right| = \sqrt {{{\left( {\frac{{\partial v}}{{\partial {F_{\rm{T}}}}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial n}}} \right)}^2}} < {\xi _2} $ | (19) |
式中:ξ2为推进力与转钎速度的寻优精度。
当满足式(19)的判断依据时,推进力与转钎速度值寻优结束; 否则, 以下一个基点值为中心,在其四周重复进行试验,直至满足判断依据为止。
3 凿岩参数的自寻优仿真分析基于上述分析,为提高仿真速度,在共轭斜量法的基础上,采用模糊变步长[16-18]和固定步长两种方式,通过MATLAB软件对凿岩参数的寻优效果进行仿真分析。
3.1 冲击能与冲击频率自寻优仿真分析在仿真时,通过调节冲击流量实现冲击能的无级调节,由控制器设定冲击频率[19],仿真的边界条件和寻优步长设置分别如表 1和表 2所示。
| 参数 | 调节范围 |
| 冲击流量QE/(L/min) | 40~60 |
| 冲击频率f/Hz | 30~60 |
| 冲击流量试探步长ΔQE/(L/min) | 1.2 |
| 寻优精度ξ1 | 0.3 |
| |d1k|模糊输入区间 | 0~5 |
| 步长设置 | 冲击流量步长/(L/min) | 冲击频率步长/Hz |
| 固定步长 | 1.5 | 2 |
| 模糊变步长 | 0~1.5 | 0~2 |
由于仿真无法获得准确的凿岩速度,在实际凿岩过程中,通过实际的隧道凿岩工况,拟合出凿岩速度与冲击能、冲击频率的关系为:
| $ v = - 0.4 \times {\left( {{Q_E} - 50} \right)^2} - 0.32 \times {\left( {f - 45} \right)^2} + 250 $ | (20) |
函数在边界条件内存在极大值点(50 L/min,45 Hz,250 cm/min),满足二元函数寻优要求。由表 3仿真结果可知凿岩速度的变化范围为138~250 cm/min,而在实际凿岩过程中,凿岩速度的变化区间也大致在该范围内,因此该方法可较好地模拟实际凿岩过程中的冲击能和冲击频率自寻优过程。
| 步长设置 | 起始坐标 | 终止坐标 | 迭代步数 |
| 固定步长 | (40 L/min,60 Hz,138 cm/min) | (49.92 L/min,45.27 Hz,249.93 cm/min) | 12 |
| 模糊变步长 | (40 L/min,60 Hz,138 cm/min) | (49.83 L/min,45.25 Hz,249.98 cm/min) | 8 |
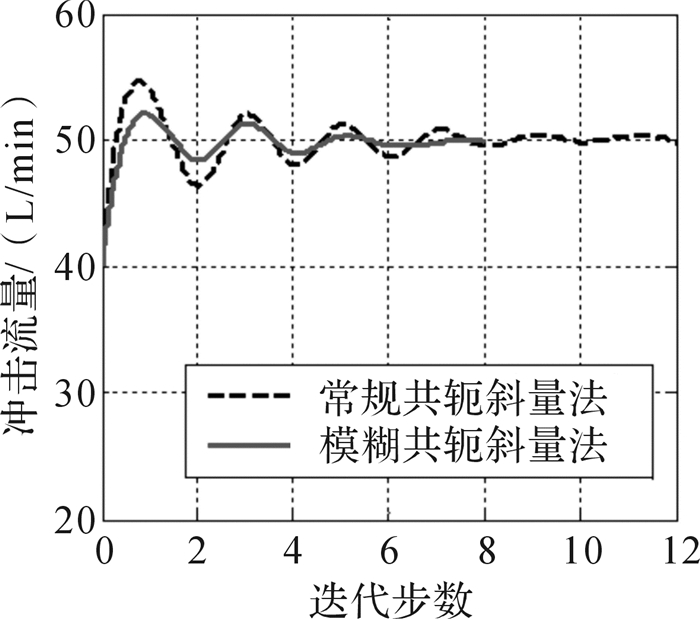
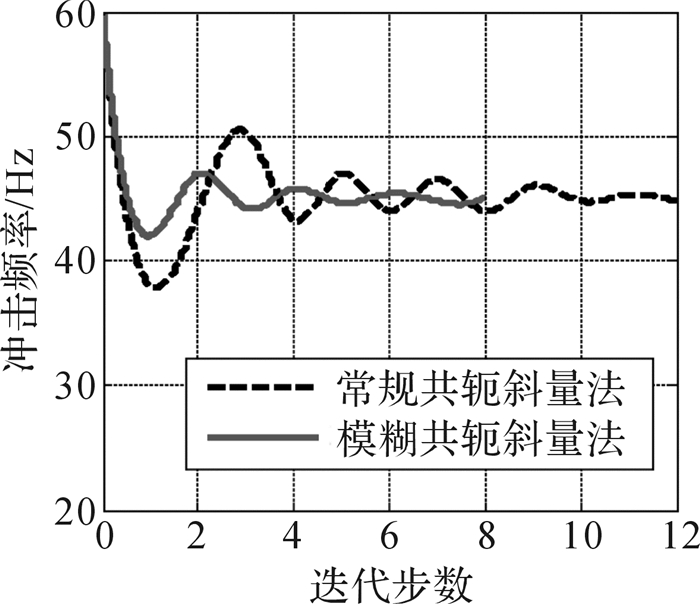
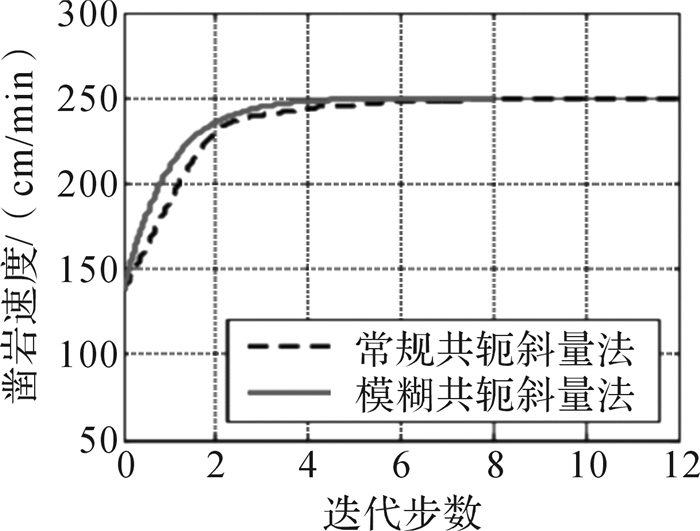
由表 3可知,采用固定步长时,迭代至第12步时满足寻优精度要求,而采用模糊变步长时仅迭代8步便满足寻优精度要求,这表明采用模糊变步长的方式可加快寻优速度。图 6和图 7分别为采用固定步长和模糊变步长方式时冲击流量和冲击频率的仿真曲线,由图可知,采用这2方式均能较快地使冲击流量和冲击频率收敛于最优值附近,且冲击流量与冲击频率始终沿相反方向变化,保证凿岩机近似恒功率输出。图 8为采用2种步长方式仿真时凿岩速度变化曲线,该图表明采用这2种方式均可使凿岩速度逐渐趋于最优值,验证了共轭斜量法能够实现冲击流量和冲击频率的同时寻优控制。同时,通过对比2种方法可知:采用模糊变步长的方式可明显减小工作参数的超调量,降低搜索过程中的不稳定性,提高控制品质。
|
| 图 6 冲击流量仿真曲线 Fig.6 The simulation curve of impact flow |
|
| 图 7 冲击频率仿真曲线 Fig.7 The simulation curve of impact frequency |
|
| 图 8 冲击能与冲击频率自寻优仿真时凿岩速度变化曲线 Fig.8 The variation curve of rock drilling speed when self-optimization simulation of impact energy and impact frequency |
通过控制推进油缸减压阀的先导压力实现推进力的无级调节,通过控制电比例换向阀的先导压力实现转钎速度的无级调节,仿真的边界条件和寻优步长设置分别如表 4和表 5所示。
| 参数 | 调节范围 |
| 减压阀先导压力/MPa | 2.0~5.5 |
| 换向阀先导压力/MPa | 2.0~5.5 |
| 减压阀先导压力试探步长ΔFT/MPa | 0.2 |
| 换向阀先导压力试探步长Δn/MPa | 0.2 |
| 寻优精度ξ2 | 0.3 |
| |d2k|模糊输入区间 | 0~5 |
| 步长设置 | 减压阀先导压力 步长/MPa | 换向阀先导压力 步长/MPa |
| 固定步长 | 0.3 | 0.3 |
| 模糊变步长 | 0.05~0.3 | 0.05~0.3 |
根据实际凿岩工况,拟合出凿岩速度与推进力、转钎速度的关系为:
| $ v = - 0.12 \times {\left( {{p_{\rm{F}}} - 37.5} \right)^2} - 0.08 \times {\left( {{p_{\rm{n}}} - 37.5} \right)^2} + 250 $ | (21) |
式中:pF为推进减压阀的先导压力;pn转钎换向阀的先导压力。
该函数在边界条件内存在极大值点(37.5 MPa,37.5 MPa,250 cm/min),由表 6仿真结果可知凿岩速度的变化范围为200~250 cm/min,与真实的凿岩工况较为接近。
| 步长设置 | 起始坐标 | 终止坐标 | 迭代步数 |
| 固定步长 | (2.20 MPa,2.20 MPa,201.95 cm/min) | (3.74 MPa,3.73 MPa,249.94 cm/min) | 15 |
| 模糊变步长 | (2.20 MPa,2.20 MPa,201.95 cm/min) | (3.75 MPa,3.74 MPa,249.97 cm/min) | 9 |
由表 6可以看出,采用固定步长时,迭代至第15步时满足寻优精度要求,而采用模糊变步长时仅迭代9步便满足寻优精度要求,这表明采用模糊变步长的方式可加快寻优速度。
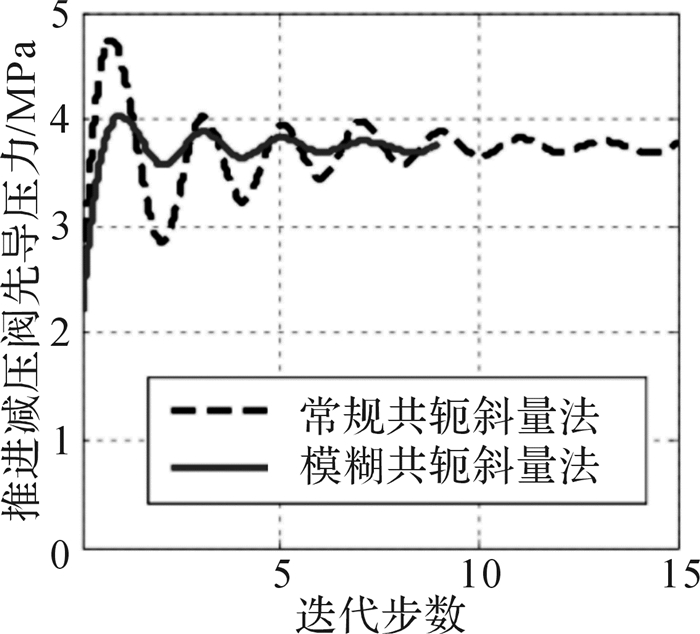
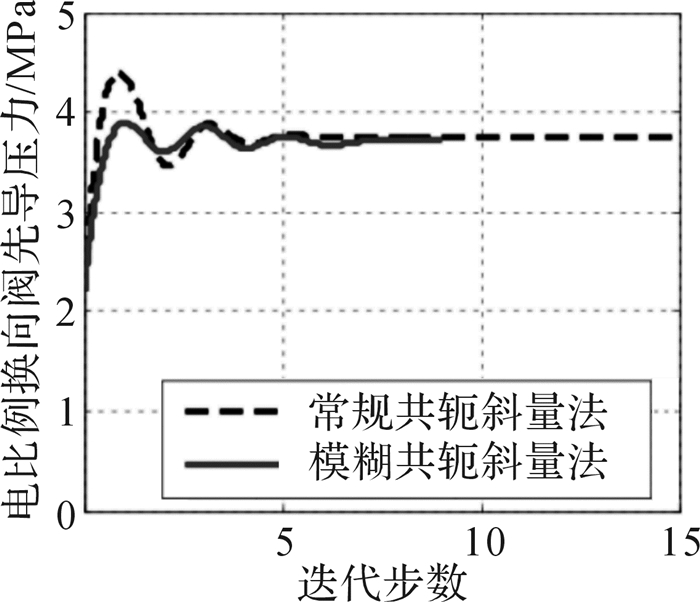
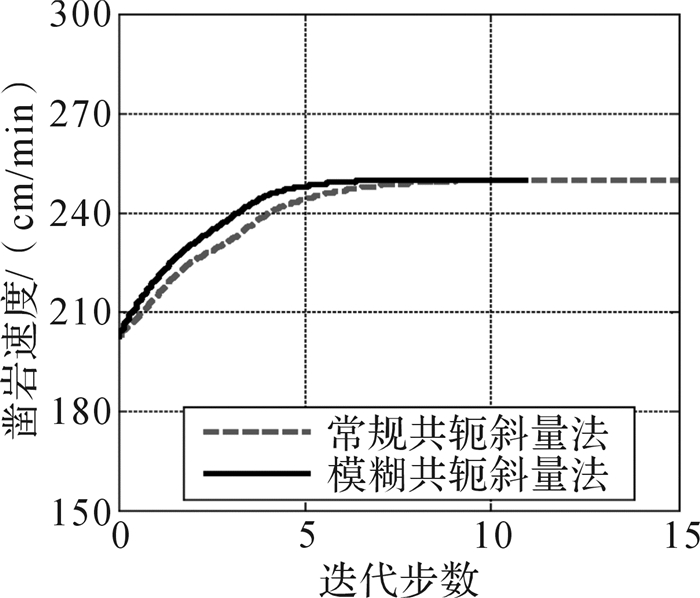
图 9和图 10分别为采用固定步长和模糊变步长方式时推进油缸减压阀先导压力和电比例换向阀先导压力的仿真曲线,由图可知,采用这2种方式均能较快地使减压阀先导压力和换向阀先导压力收敛于最优值附近,且减压阀先导压力和换向阀先导压力始终沿同一方向变化,即两者呈正相关,验证了推进力与转纤速度的相互作用对凿岩速度产生影响。图 11为采用2种步长方式仿真时凿岩速度变化曲线,该图表明采用2种方式均可使凿岩速度逐渐趋于最优值,验证了共轭斜量法能够实现推进力与转钎速度的同时寻优控制。同时,通过对比2种方法可知:采用模糊变步长的方式进行搜索寻优时,曲线变化更加平稳,超调量明显降低,寻优速度明显加快。
|
| 图 9 推进油缸减压阀先导压力仿真曲线 Fig.9 The forerunner pressure simulation curve of propelling cylinder pressure relief valve |
|
| 图 10 电比例换向阀先导压力仿真曲线 Fig.10 The forerunner pressure simulation curve of electric proportional change-over valve |
|
| 图 11 推进力与转钎速度自寻优仿真时凿岩速度变化曲线 Fig.11 The variation curve of rock drilling speed of self-optimization simulation of propulsion force and rotational speed |
通过对推进力与转钎速度进行自寻优试验来验证本文寻优方案的可行性。取钎具直径为48 mm,钻孔深度为3.5 m。设定凿岩机冲击流量为60 L/min,冲击频率在50~60 Hz之间,冲击能在300~360 J之间,其他参数设定如表 7。
| 参数 | 调节范围 |
| 推进力 | 8.5~22 kN |
| 转钎速度 | 190~340 r/min |
| 寻优精度ξ | 0.3 |
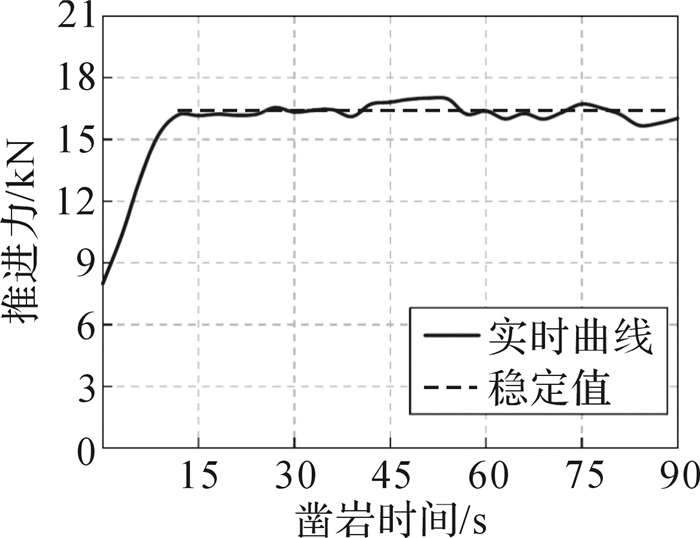
根据现场实际工况,将推进力初始值设定为8.5 kN,转钎速度初始值设为200 r/min。测得的相关凿岩参数经滤波后的变化趋势如图 12至图 14所示,前30秒试验数据如表 8所示。
|
| 图 12 推进力-时间的变化曲线 Fig.12 The variation curve of propulsive force-time |
|
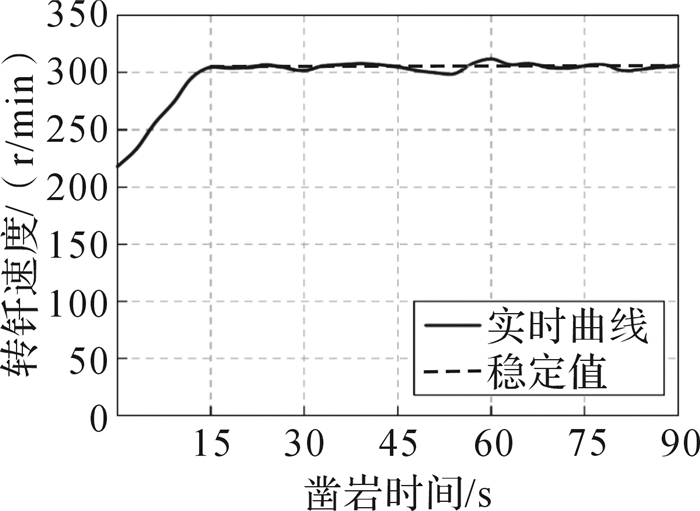
| 图 13 转钎速度-时间的变化曲线 Fig.13 The variation curve of rotational speed-time |
|
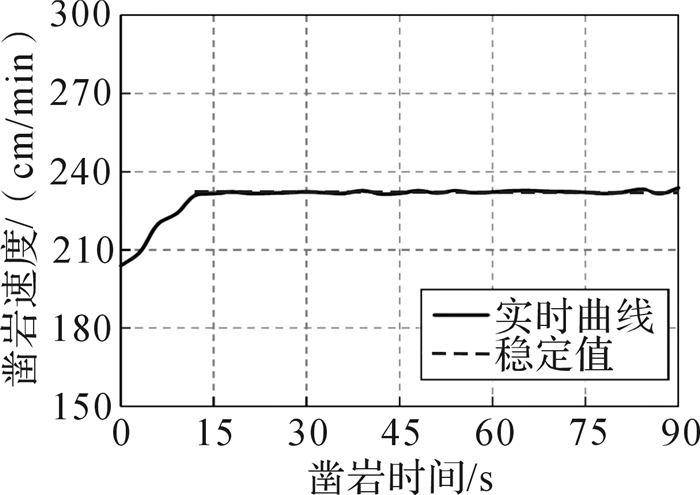
| 图 14 凿岩速度-时间的变化曲线 Fig.14 The variation curve of rock drilling speed-time |
| 时刻 | 推进力 FT/kN | 转钎速度 n/(r·min-1) | 凿岩速度 v/(cm·min-1) |
| 第0秒 | 8.55 | 200.13 | 204 |
| 第3秒 | 10.38 | 233.57 | 209 |
| 第6秒 | 13.33 | 256.41 | 220 |
| 第9秒 | 15.36 | 274.89 | 224 |
| 第12秒 | 16.23 | 296.95 | 231 |
| 第15秒 | 16.12 | 305.57 | 231 |
| 第18秒 | 16.24 | 304.63 | 232 |
| 第21秒 | 16.15 | 305.54 | 231 |
| 第24秒 | 16.28 | 307.18 | 231 |
| 第27秒 | 16.69 | 304.30 | 232 |
| 第30秒 | 16.53 | 303.33 | 235 |
由图 12和图 13可知,在试验过程中,随时间的增加,推进力和转钎速度均实时调整至最优的匹配参数,且两者沿同一方向变化,与前文所述的理论和仿真结果一致:大约在第13秒时推进力稳定于16.5 kN左右;大约在第15秒时转钎速度稳定于305 r/min。
分析图 14可知,现场实际初始工作速度为2.04 m/min, 经过寻优动态调整后,其工作速度稳定在2.31 m/min左右,则提高率η为:
| $ \eta = \frac{{\Delta v}}{{{v_0}}} \times 100\% = \frac{{2.31 - 2.04}}{{2.04}} \times 100\% = 13.2\% $ | (22) |
由上述结果可知,凿岩参数自寻优控制策略能够实现凿岩参数的自寻优控制,并且寻优速度快,工作参数的动态调整相对平稳,超调量小,表明了该寻优方案的优越性。
5 结语本文以共轭斜量法为主导思想,提出了凿岩参数自寻优控制策略,并采用两两分组寻优的方式进行仿真研究,证明该控制策略具有良好的寻优效果和收敛性。对推进力和转钎速度自寻优的试验研究证明:该自寻优控制策略能够实现凿岩参数的实时寻优控制,使相关凿岩参数收敛于最优值附近,并且寻优的速度较快,凿岩参数的动态变化较为平稳。将自寻优后的凿岩速度与现场凿岩速度初始值进行对比可知,该控制方式可提高凿岩速度,提高率达13.2%。本研究为实现智能台车自寻优控制提供了一种新的思路和方法,研究结果具有较大的工程实践意义。
| [1] |
刘忠, 张凯, 陈佳.
液压凿岩机的发展研究现状分析[J]. 建筑机械, 2013(15): 67–70, 10.
LIU Zhong, ZHANG Kai, CHEN Jia. The development research analysis of hydraulic rock drill[J]. Construction Machinery, 2013(15): 67–70, 10. |
| [2] | WALKER S. Hydraulic drills hammer through with new designs, tougher materials[J]. Engineering and Mining Journal, 2015, 216(4): 38–45. |
| [3] |
王恒升, 何清华, 邓春萍.
凿岩台车自动化控制系统的发展、现状及展望[J]. 测控技术, 2007, 26(3): 1–4.
WANG Heng-sheng, HE Qing-hua, DENG Chun-ping. The development and prospect of automatic control system of drill rig[J]. Measurement & Control Technology, 2007, 26(3): 1–4. DOI:10.3969/j.issn.1000-8829.2007.03.001 |
| [4] |
毛信理, 高澜庆, 陈纯.
微机控制液压凿岩机自寻最优工作参数的研究[J]. 矿山机械, 1989(3): 16–21.
MAO Xin-li, GAO Lan-qing, CHEN Chun. Research on self optimizing working parameters of hydraulic rock drill with microcomputer controll[J]. Mining & Processing Equipment, 1989(3): 16–21. |
| [5] |
胡均平, 杨襄璧, 吴万荣.
凿岩过程全参数自适应最优控制理论及实现方法[J]. 中南工业大学学报, 1998, 29(1): 72–75.
HU Jun-ping, YANG Xiang-bi, WU Wan-rong. The theory and method of all parameter's adaptive optimum control in rock-drilling process[J]. Journal of Central South University of Technology, 1998, 29(1): 72–75. |
| [6] |
常欢欢.凿岩台车钻进系统破岩性能研究[D].徐州: 中国矿业大学机电工程学院, 2016: 21-30.
CHANG Huan-huan. Research on rock breaking performance of drilling system for drilling jumbo[D]. Xuzhou: China University of Mining and Technology, School of Mechatronic Engineering, 2016: 21-30. http://cdmd.cnki.com.cn/Article/CDMD-10290-1016909865.htm |
| [7] | LIU Song-yong, CHANG Huan-huan, LI Hong-heng, et al. Numerical and experimental investigation of the impact fragmentation of bluestone using multi-type bits[J]. International Journal of Rock Mechanic and Mining Sciences, 2017, 91(11): 102–109. |
| [8] | CAVANOUGH Gary L, KOCHANEK Mark, CUNNINGHAM Jock B, et al. A self-optimizing control system for hard rock percussive drilling[J]. IEEE/ASME Transactions on Mechatronics, 2008, 13(2): 153–157. DOI:10.1109/TMECH.2008.918477 |
| [9] | SAZIDY M S, RIDEOUT D G, BUTT S D, et al. Modeling percussive drilling performance using simulated visco-elasto-plastic rock medium[C]//44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, Jun. 27-30, 2010. |
| [10] |
王东升, 林宏武, 赵宏强, 等.
凿岩回转推进全液压自适应控制系统[J]. 液压与气动, 2015(8): 51–54.
WANG Dong-sheng, LIN Hong-wu, ZHAO Hong-qiang, et al. Total hydraulic auto adjusting system for rock drilling's rotation and feed[J]. Chinese Hydraulics & Pneumatics, 2015(8): 51–54. DOI:10.11832/j.issn.1000-4858.2015.08.011 |
| [11] |
徐智.适应复杂工况的液压钻机推进回转控制系统研究[D].长沙: 中南大学机电工程学院, 2014: 11-15.
XU Zhi. Research on the feeding and rotating control system of hydraulic drilling rig to adopt complex conditions[D]. Changsha: Central South University, College of Mechanical and Electrical Engineering, 2014: 11-15. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014408847.htm |
| [12] |
高澜庆, 刘庭楷, 王保申, 等.
液压凿岩机主要工作参数对凿岩速度影响的试验研究[J]. 凿岩机械气动工具, 1996(4): 52–54.
GAO Lan-qing, LIU Ting-kai, WANG Bao-shen, et al. Experimental research on influence of the main working parameters of the hydraulic rock drill on the rate of drilling[J]. Rock Drilling Machinery & Pneumatic Tools, 1996(4): 52–54. |
| [13] |
李世顺, 黄正达.
下降的非线性共轭梯度法及其全局收敛性[J]. 浙江大学学报(理学版), 2009, 36(4): 389–395, 407.
LI Shi-shun, HUANG Zheng-da. Convergence of the descent nonlinear conjugate gradient methods[J]. Journal of Zhejiang University (Science Edition), 2009, 36(4): 389–395, 407. DOI:10.3785/j.issn.1008-9497.2009.04.007 |
| [14] |
朱建新, 李泽杰, 王东升, 等.
切削钻机凿岩过程的推进力控制研究[J]. 机械设计与研究, 2014, 30(6): 102–105, 113.
ZHU Jian-xin, LI Ze-jie, WANG Dong-sheng, et al. Research on the propulsion control of rotary cutting drill rig in rock drilling process[J]. Machine Design and Research, 2014, 30(6): 102–105, 113. |
| [15] | LI Xi-bing, SUMMERS D A, RUPERT G. Experimental investigation on the breakage of hard rock by the PDC cutters with combined action modes[J]. Tunneling and Under ground Space Technology, 2001, 16(2): 107–114. DOI:10.1016/S0886-7798(01)00036-0 |
| [16] | FENG G. A survey on analysis and design of model-based fuzzy control systems[J]. IEEE Transactions on Fuzzy Systems, 2006, 14(5): 676–697. DOI:10.1109/TFUZZ.2006.883415 |
| [17] |
李明, 杨成梧.
基于模糊推理的变步长LMS自适应滤波算法[J]. 控制工程, 2006, 13(3): 237–239.
LI Ming, YANG Cheng-wu. Variable step size LMS adaptive filtering algorithm based on fuzzy inference[J]. Control Engineering of China, 2006, 13(3): 237–239. DOI:10.3969/j.issn.1671-7848.2006.03.014 |
| [18] | YANG G, LIANG C, WANG L, et al. Fuzzy control method of the intelligent hydraulic impactor[C]//Intelligent Control and Automation (WCICA), 20108th World Congress on. IEEE, 2010: 4654-4657. |
| [19] |
赵宏强, 何清华, 朱建新, 等.
独立无级调节控制的新型液压冲击器[J]. 工程机械, 1999, 30(8): 11–13, 51.
ZHAO Hong-qiang, HE Qing-hua, ZHU Jian-xin, et al. New hydraulic impactor with independent step-less adjustment control[J]. Construction Machinery and Equipment, 1999, 30(8): 11–13, 51. |


