2. 中国科学院 深圳先进技术研究院, 广东 深圳 518000
2. Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518000, China
随着我国制造业的持续快速发展及“中国制造2025”的提出,各自动化工厂面临着巨大的机遇和挑战。自动导引车(automatic guided vehicle, AGV)是实现工厂自动化的重要一环,对物流业和仓储业的发展起到很大的作用[1]。目前,全向AGV的导向轮多采用麦克纳姆轮或球形轮[2-3],但由于其自身的结构特点,会导致AGV振动、打滑、运动稳定性欠佳及控制精度不高[4]。为克服这些缺点,本文设计了一种全新的基于轮毂电机的全转向导向机构,它具有直行、横行、两轮转向、四轮转向和零半径转向等多种转向模式,能够在狭小的空间内灵活自由地移动,并可搭载不同类型的搬运机器人以满足工业生产中的不同需求。
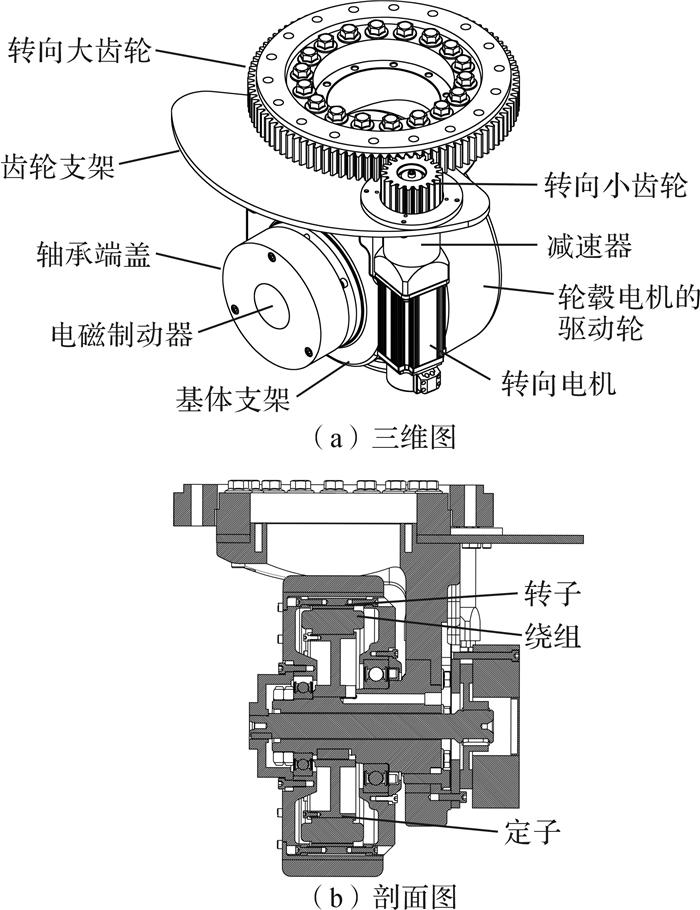
1 全转向导向机构的设计全向AGV是基于四轮独立转向和驱动的方式进行运动的,其导向机构主要由轮毂电机的驱动轮、转向电机、减速器、转向大小齿轮、电磁制动器及基体支架等组成,如图 1所示。全向AGV发生转向时,转向小齿轮绕着固定在车架上的转向大齿轮进行转动,可实现±90°的转向,这样就省去了传统转向拉杆机构,提高了转向平稳性;同时,该导向机构采取的是电磁制动,将刹车片集成到轮毂电机的制动轴上,提高了全向AGV的定位精度。轮毂电机和转向电机内分别装有速度编码器和转角编码器,可对速度和转角进行实时检测和反馈。
|
| 图 1 全转向导向机构结构简图 Fig.1 Structure diagram of full steering guidance mechanism |
由于设计的全转向导向机构主要作为搬运机器人的基础部件[5],为了不影响机器人的抓取效果及其路径规划的效果,该全转向导向机构的轮胎为刚性轮,且一直在中低速的工况下工作;此外,该导向机构紧固在车架上,并没有悬架结构和机械传动机构,可认为该导向机构不会产生侧偏运动和俯仰运动。假设该全向AGV运动时只有滚动且不会产生打滑的现象,由此可得出基于4WID-4WIS(四轮独立驱动四轮独立转向)的全向AGV的运动学模型。
2.1 四轮转向模式下的运动学模型当视觉导航系统给定的转向参考角为δ,驱动的参考速度为v时,可得出全向AGV的转向半径为:
| $ R = \frac{L}{{2\tan \delta }} $ | (1) |
式中:L为全向AGV的轴距。
由此可以分别得出左侧车轮和右侧车轮的转向半径Rl、Rr分别为:
| $ \left\{ \begin{array}{l} {R_{\rm{l}}} = \frac{L}{{2\tan \delta }} + \frac{B}{2}\\ {R_{\rm{r}}} = \frac{L}{{2\tan \delta }} - \frac{B}{2} \end{array} \right. $ | (2) |
式中:B为左轮和右轮之间的轮距。
根据式(1)和式(2)可以得出各个车轮的转角为:
| $ \left\{ \begin{array}{l} {\delta _{{\rm{lf}}}} = \arctan \left( {\frac{L}{{L/\tan \delta + B}}} \right)\\ {\delta _{{\rm{rf}}}} = \arctan \left( {\frac{L}{{L/\tan \delta - B}}} \right)\\ {\delta _{{\rm{lr}}}} = {\delta _{{\rm{lf}}}}\\ {\delta _{{\rm{rr}}}} = {\delta _{{\rm{rf}}}} \end{array} \right. $ | (3) |
基于给定车速,4个轮子的速度分别为:
| $ \left\{ \begin{array}{l} {v_{{\rm{lf}}}} = v{R_1}/\left( {R\cos {\delta _{{\rm{lf}}}}} \right)\\ {v_{{\rm{rf}}}} = v{R_{\rm{r}}}/\left( {R\cos {\delta _{{\rm{rf}}}}} \right)\\ {v_{{\rm{lr}}}} = v{R_1}/R\\ {v_{{\rm{rr}}}} = v{R_{\rm{r}}}/R \end{array} \right. $ | (4) |
式中:δlf为左前轮转角, δrf为右前轮转角, δlr为左后轮转角, δrr为右后轮转角;vlf为左前轮速度, vrf为右前轮的速度, vlr为左后轮的速度, vrr为右后轮的速度。
2.2 两前轮转向模式下的运动学模型当全向AGV发生两前轮转向时,其转向半径为:
| $ R = \frac{L}{{\tan \delta }} $ | (5) |
可得出左侧车轮和右侧车轮的转向半径Rl、Rr分别为:
| $ \left\{ \begin{array}{l} {R_{\rm{l}}} = \frac{L}{{\tan \delta }} + \frac{B}{2}\\ {R_{\rm{r}}} = \frac{L}{{\tan \delta }} - \frac{B}{2} \end{array} \right. $ | (6) |
由式(5)和(6)可推出4个轮子的转角分别为:
| $ \left\{ \begin{array}{l} {\delta _{{\rm{lf}}}} = \arctan \left( {\frac{L}{{L/\tan \delta + B/2}}} \right)\\ {\delta _{{\rm{rf}}}} = \arctan \left( {\frac{L}{{L/\tan \delta - B/2}}} \right)\\ {\delta _{{\rm{lr}}}} = {\delta _{{\rm{rr}}}} = 0 \end{array} \right. $ | (7) |
同理基于给定车速,4个轮子的速度可按式(4)计算。
2.3 零半径转向及横向行驶时的运动学模型当全向AGV发生原地转向时,即AGV绕着自身几何中心点进行转向,4个车轮的转角及速度关系为:
| $ \left\{ \begin{array}{l} {\delta _{{\rm{lf}}}} = {\delta _{{\rm{rr}}}} = - \arctan \left( {\frac{L}{B}} \right)\\ {\delta _{{\rm{rf}}}} = {\delta _{{\rm{lr}}}} = \arctan \left( {\frac{L}{B}} \right) \end{array} \right. $ | (8) |
| $ {v_{{\rm{lf}}}} = {v_{{\rm{rf}}}} = {v_{{\rm{lr}}}} = {v_{{\rm{rr}}}} $ | (9) |
当全向AGV横向行驶时,4个车轮转角为90°,4个车轮的速度均相等。
3 全向AGV运动控制策略设计的全向AGV是基于视觉导航系统进行上位控制的,根据运动指令和所建立的全向运动算法,可计算得到全向AGV每个轮子的转角和速度。为了快速精确地消除全向AGV的路径偏差,本文利用多步迭代最优控制和模糊控制对AGV路径偏差进行消除。
在全向AGV的路径偏差较小时采取最优控制。传统的最优控制采用LQR(linear quadratic regulator,线性二次型调节器)系统的最优控制器,只能对权矩阵Q、R进行试凑,具有复杂性和不确定性等缺陷[8-9],因此本文采用多步预测最优控制来消除较小的路径偏差。利用最优控制的约束条件,对转角和速度进行约束,根据每个轮子的转角和速度的关系,可以同时且快速精确地消除转角和速度偏差,使得实际路径达到期望目标。
在全向AGV路径偏差较大的情况下,由于其线性化模型难以建立,且迭代运算的过程比较复杂,因此采用模糊控制。模糊控制是利用规则库对系统进行控制,不需要建立精确的数学模型[6],本文采用的是二维模糊控制器,可保证整个控制系统的动态特性[7]。利用模糊控制对提高智能全向AGV的运动效率及稳定性有一定的优势。
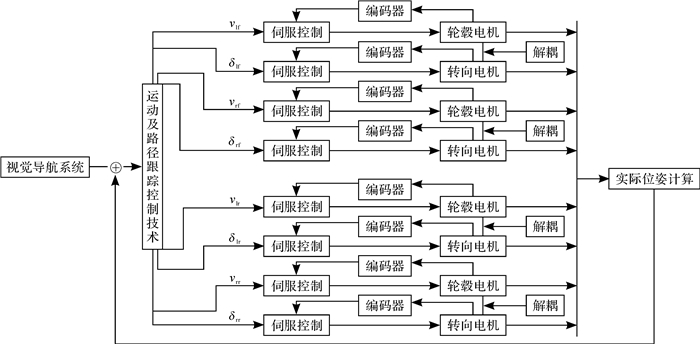
目前对于全向AGV底层电机控制的研究较少[10-12],且多集中在对底层电路的设计上。本文设计的全向AGV是利用转向电机和轮毂电机进行驱动的。根据上层的控制算法可知各车轮的转角和速度之间存在一定的关系,当路况比较复杂时,2个电机的控制精度会受到影响,进而使得2个电机之间产生控制耦合。为提高电机控制精度以及为路径跟踪控制提供充足的纠偏能力,对转向电机和轮毂电机进行底层的解耦控制[13-14]。本文利用参考模型的解耦思想[15-16],在2个电机之间设计了解耦控制器。全向AGV的运动控制策略如图 2所示。
|
| 图 2 全向AGV的运动控制策略图 Fig.2 Motion control strategy diagram of omnidirectional AGV |
对四轮独立控制的全向AGV的运动学误差进行分析,建立偏差较小时的全向AGV运动学模型。车体的位姿偏差可分解为车体的角度偏差eθ和车体的距离偏差ed:
| $ \left\{ \begin{array}{l} {e_\theta } = \omega + {{\dot \delta }_\theta } = 2v\tan \delta /L + {{\dot \delta }_\theta }\\ {e_d} = - v{e_\theta } - v\tan \delta + {{\dot \delta }_d} \end{array} \right. $ | (10) |
式中:ω为车体的角速度,ω=2vtan δ/L;
当全向AGV从某一状态k移动到下一个状态k+1时,其角度偏差和距离偏差可表示为:
| $ \left\{ \begin{array}{l} {e_{{\theta _{k + 1}}}} = {e_{{\theta _k}}} + 2{v_k}{T_{\rm{S}}}\tan \delta /L\\ {e_{{d_{k + 1}}}} = - {T_{\rm{S}}}{v_k}{e_{{\theta _k}}} - {T_{\rm{S}}}{v_k}\tan \delta + {e_{{d_k}}} \end{array} \right. $ | (11) |
式中:TS为运动控制的一个周期,vk为状态k下的驱动速度。
设控制量μk=tan δ,将误差偏差模型离散化后可得出:
| $ \left[ {\begin{array}{*{20}{c}} {{e_{{\theta _{k + 1}}}}}\\ {{e_{{d_{k + 1}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_{{\theta _k}}}}\\ { - {T_{\rm{S}}}{v_k}{e_{{\theta _k}}} + {e_{{d_k}}}} \end{array}} \right] + \left[ \begin{array}{l} 2{T_{\rm{S}}}{v_k}/L\\ - {T_{\rm{S}}}{v_k} \end{array} \right]{\mu _k} $ | (12) |
根据多步预测迭代最优控制思想,通过N步迭代可以将角度偏差和距离偏差同时减小为零,即:
| $ \left\{ \begin{array}{l} {e_{{\theta _N}}} = 0\\ {e_{{d_N}}} = 0 \end{array} \right. $ | (13) |
附加约束条件为转角约束和角速度约束:
| $ \left\{ \begin{array}{l} \left| {{\mu _k}} \right| \le {\mu _{\max }}\\ \left| {{\omega _k}} \right| = \left| {{\mu _{k + 1}} - {\mu _k}} \right|/{T_{\rm{S}}} \le {\omega _{\max }} \end{array} \right. $ | (14) |
利用多步迭代最优控制时,可实现最快的纠偏,只需表征控制能量[17]:
| $ J = \frac{1}{2}\sum\limits_{k = 0}^{N - 1} {\mu _k^2} $ | (15) |
将方程(12)引入Lagrange待定数列:
| $ {\mathit{\boldsymbol{\lambda }}_{k + 1}} = {\left[ {\begin{array}{*{20}{c}} {{\lambda _{1,k + 1}}}&{{\lambda _{2,k + 1}}} \end{array}} \right]^{\rm{T}}} $ | (16) |
则Hamilton函数为:
| $ \begin{array}{l} {H_k} = \frac{1}{2}\mu _k^2 + {\mathit{\boldsymbol{\lambda }}_{k + 1}}^{\rm{T}} \times \\ \;\;\;\;\;\;\;\;\left\{ {\left[ {\begin{array}{*{20}{c}} {{e_{{\theta _k}}}}\\ { - {T_{\rm{S}}}{v_k}{e_{{\theta _k}}} + {e_{{d_k}}}} \end{array}} \right] + \left[ \begin{array}{l} \frac{{2{T_{\rm{S}}}{v_k}}}{L}\\ - {T_{\rm{S}}}{v_k} \end{array} \right]{\mu _k}} \right\} \end{array} $ | (17) |
使目标函数式(15)取得极小值的最优控制序列vk满足:
| $ \left\{ \begin{array}{l} {\lambda _k} = \frac{{\partial {H_k}}}{{\partial {\mathit{\boldsymbol{X}}_k}}}\\ \frac{{\partial {H_k}}}{{\partial {\mu _k}}} = 0 \end{array} \right. $ | (18) |
式中:Xk=[eθk edk]T。
则由式(18)可推出:
| $ {\mu _k} = - \frac{{2C{T_{\rm{S}}}{v_k}}}{L} + {\lambda _{2k}} + \left( {k + 1} \right)C{T_{\rm{S}}}{v_k} $ | (19) |
式中:λ2k和C为待定参数。
将式(19)代入式(10),经迭代变换得到eθk、edk,即位姿偏差之间的关系,然后根据纠偏的目标:eθN=0,edN=0,求解出C和λ2k,再代入式(18),则可得到μk的控制量表达式为:
| $ {\mu _k} = - \frac{{2{L_{{e_{{\theta _0}}}}}}}{{{T_{\rm{S}}}{v_k}N}} + \gamma \left( {k - \frac{{N - 1}}{2}} \right) $ | (20) |
式中:
| $ \gamma = \frac{{\left[ {\frac{{24L{e_{{d_0}}}}}{{{{\left( {{T_{\rm{S}}}{v_k}} \right)}^2}}} + \left( {\frac{{24{L^2}}}{{{{\left( {{T_{\rm{S}}}{v_k}} \right)}^2}}} - \frac{{12LN}}{{{T_{\rm{S}}}{v_k}}} - \frac{{12L}}{{{T_{\rm{S}}}{v_k}}}} \right){e_{{\theta _0}}}} \right]}}{{\left( {7N - {N^3}} \right)}} $ |
在约束条件下,经过N步迭代的最优控制可以实现最快和精确的纠偏。
3.2 模糊控制器的设计根据上文的分析可知,AGV的路径偏差可分解为ed和eθ,其变化率分别为
| 输出控制量Uθ | |||||||
| Eθ | |||||||
| NB | NM | NS | O | PS | PM | PB | |
| NB | PB | PB | PB | PM | PS | O | O |
| NM | PB | PB | PM | PS | PS | O | O |
| NS | PM | PM | PM | PS | O | NS | NS |
| O | PM | PM | PS | O | NS | NM | NM |
| PS | PS | PS | O | NS | NM | NM | NM |
| PM | O | O | NS | NS | NM | NB | NB |
| PB | O | O | NS | NM | NB | NB | NB |
设转向电机的实际输出和理想输出分别为Y1、Y1m,轮毂电机的实际输出和理想输出分别为Y2、Y2m,G12是转向电机对轮毂电机的耦合作用,G21是轮毂电机对转向电机的耦合作用,G11、G22分别是两个电机的参考模型,Rn为第n条通道的主输入,由双输入和双输出的参考模型的解耦原理可得[15]:
| $ \begin{array}{l} \mathit{\boldsymbol{A}} \times \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{Y}}\\ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {{G_{11}}}&{{G_{12}}}\\ {{G_{21}}}&{{G_{22}}} \end{array}} \right)\\ \mathit{\boldsymbol{B}} = \left( {{B_1},{B_2}} \right)\\ {B_n} = \left( {{R_n} - {Y_n}} \right){C_n} + \left( {{Y_{n\;{\rm{m}}}} - {Y_n}} \right){C_{nn}}\\ \mathit{\boldsymbol{Y}} = \left( {{Y_1},{Y_2}} \right) \end{array} \right. \end{array} $ | (21) |
式中:n=1, 2。
令
| $ \begin{array}{*{20}{c}} {{Y_1} = \frac{{\left| \mathit{\boldsymbol{A}} \right|\left( {{R_1}{C_1} + {Y_{1{\rm{m}}}}{C_{11}}} \right)}}{{\left| \mathit{\boldsymbol{A}} \right|\left( {{C_1} + {C_{11}}} \right) + {A_{11}}}} - }\\ {\frac{{\sum\limits_{n = 1}^2 {{Y_n}{A_{1n}}} }}{{\left| \mathit{\boldsymbol{A}} \right|\left( {{C_1} + {C_{11}}} \right) + {A_{11}}}}} \end{array} $ | (22) |
式中:
| $ {Y_{1{\rm{m}}}} = \frac{{{R_1}{C_1}{G_{11}}}}{{1 + {C_1}{G_{11}}}},{R_1} = \frac{{{Y_{1{\rm{m}}}}\left( {1 + {C_1}{G_{11}}} \right)}}{{{C_1}{G_{11}}}} $ | (23) |
C11为设计的解耦控制器, C1表示主控制器参数。
将式(23)代入式(22)可得:
| $ \begin{array}{l} {Y_{1{\rm{m}}}} + {Y_{1{\rm{m}}}}\frac{{\left| \mathit{\boldsymbol{A}} \right| - {G_{11}}{A_{11}}}}{{\left| \mathit{\boldsymbol{A}} \right|{G_{11}}\left( {{C_1} + {C_{11}}} \right) + {G_{11}}{A_{11}}}} - \\ \;\;\;\;\;\;\;\;\frac{{{G_{11}}\left( {\sum\limits_{n = 1}^2 {{Y_n}{A_{1n}}} - {A_{11}}{Y_1}} \right)}}{{\left| \mathit{\boldsymbol{A}} \right|{G_{11}}\left( {{C_1} + {C_{11}}} \right) + {G_{11}}{A_{11}}}} = {Y_1} \end{array} $ | (24) |
同理可解得Y2。
在实际的控制系统中不考虑|A|=0的情况,当|A|≠0时,由式(24)可得出:只要满足其第2项和第3项的值趋于零,就能使实际输出趋于理想输出。合理地设计控制器就能实现系统的解耦控制,使得转向电机和轮毂电机具有良好的输入输出响应。
4 实验验证及结果分析为了验证本文所提出的运动控制策略的有效性及可靠性,开发了AGV样机进行实验, 该全向AGV的中心轴距为1 420 mm,左右车轮之间的轮距为1 026 mm,其运动控制方式为四轮独立转向和四轮独立驱动,车载视觉系统安装在车体的上方,主运动控制器采取自主研发的嵌入式系统。AGV样机如图 3所示。

|
| 图 3 基于4WID-4WIS的AGV样机 Fig.3 AGV prototype based on 4WID-4WIS |
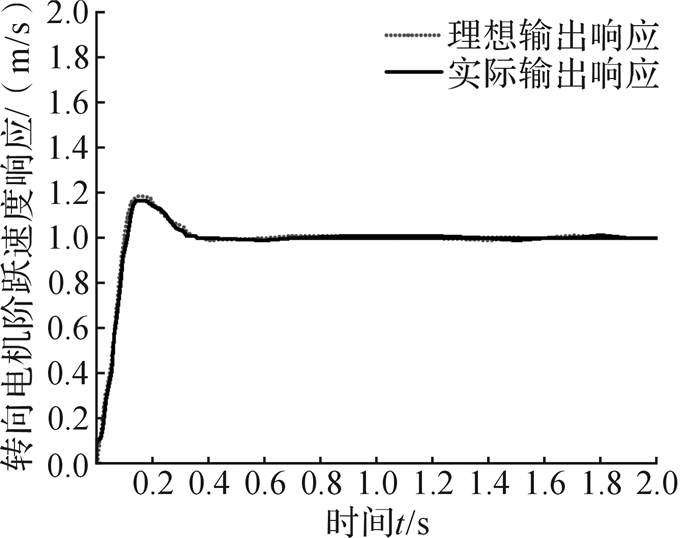
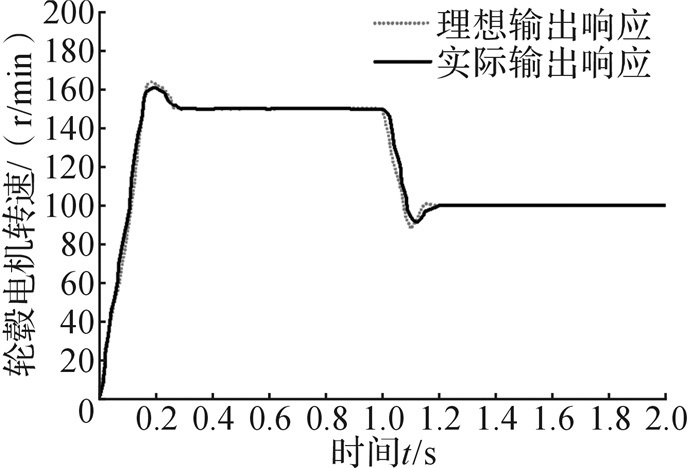
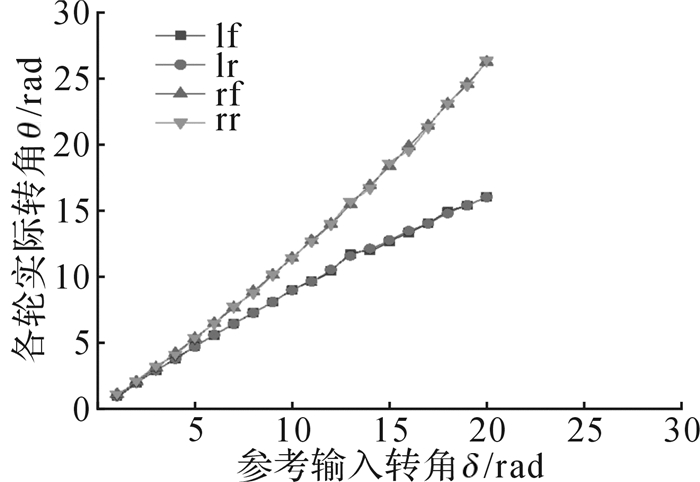
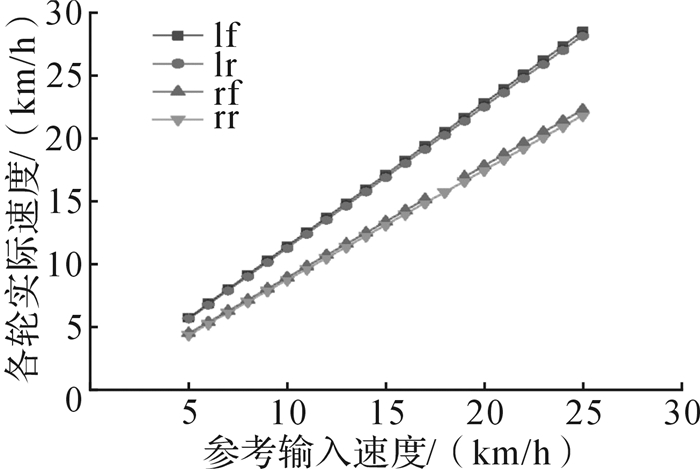
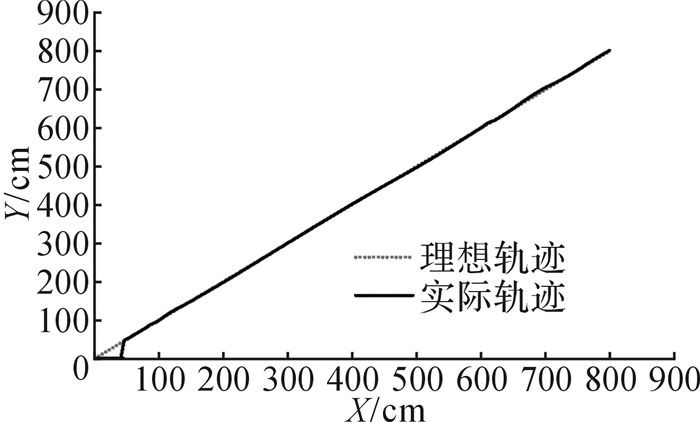
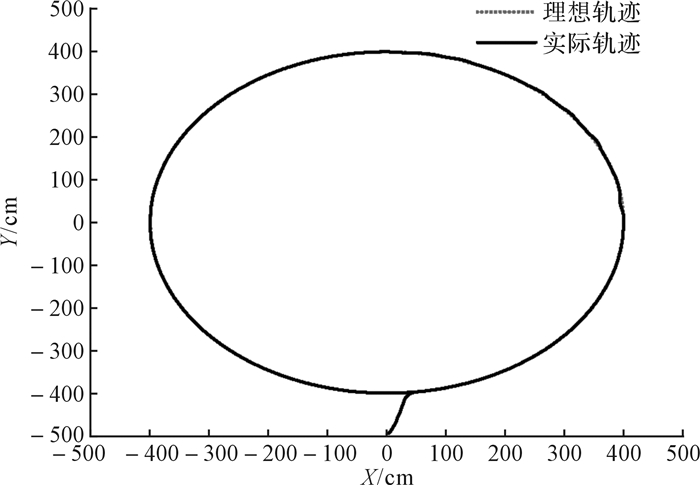
对解耦控制后的转向电机和轮毂电机进行实验,对转向电机进行阶跃速度响应实验,对轮毂电机进行加速、减速的变速实验,结果如图 4和图 5所示。在四轮转向模式下,利用工业PC(personal computer,个人计算机)连接运动控制器以输入不同的参考角度,通过转向传感器和速度传感器进行反馈,得出各轮转角的实验数据如图 6所示。在额定转角为0.174 rad时输入不同参考速度,得出各轮速度的实验数据如图 7所示。同时,对全向AGV进行直线跟踪实验,以1.8 km/h为输入速度,0 rad/s为转角输入速度,使得全向AGV位置的初始误差为:Xe=50 cm,Ye=60 cm,θe=0.785 rad,以(0,0) cm为起点时的跟踪结果如图 8所示;当跟踪轨迹为半径为4 m的圆时,以(0,0) cm为起点的跟踪效果如图 9所示。
|
| 图 4 转向电机阶跃响应结果 Fig.4 Step response result of steering motor |
|
| 图 5 轮毂电机加速减速实验结果 Fig.5 Acceleration and deceleration experiment result of in-wheel motor |
|
| 图 6 四轮转角输出实验 Fig.6 Four-wheel rotation angle output experiment |
|
| 图 7 额定转角为0.174 rad时全向AGV各车轮的速度 Fig.7 Wheel speed of omnidirectional AGV with nominal rotation angle of 0.174 rad |
|
| 图 8 全向AGV直线轨迹行走跟踪实验结果 Fig.8 Linear trajectory tracking experiment result for omnidirectional AGV |
|
| 图 9 全向AGV圆形轨迹行走跟踪实验结果 Fig.9 Circular trajectory tracking experiment result for omnidirectional AGV |
通过上述实验数据分析可得出,全向AGV的电机能够提供良好的输出响应,其转角和速度的误差也在理想的控制范围内,AGV在有路径偏差的情况下,具有良好的路径跟踪纠偏能力。
5 结论1) 设计了一种基于轮毂电机的全向AGV的导向机构,它能够使全向AGV在狭小的空间内灵活运动;基于4WID-4WIS控制方式建立了全向AGV的运动学模型并进行了运动学分析。
2) 针对该全向AGV设计了合理的偏差消除方案,在大偏差时采用模糊控制,在小偏差时采用多步预测最优控制;为了消除控制耦合的影响,在转向电机和轮毂电机间进行了解耦控制,使它们具有良好的输入输出响应,保证了控制精度。
3) 通过实验验证了该全向AGV具有良好的运行效果,满足工业使用要求,可为工业领域的应用提供一些借鉴和参考。
| [1] | WU Xing, LOU Pei-huang, YU Jun, et al. Intersection recognition and guide-path selection for a vision-based AGV in a bidirectional flow network[J]. International Journal of Advanced Robotic Systems, 2014, 11(3): 1–17. |
| [2] |
王曙光.
移动机器人原理与设计[M]. 北京: 人民邮电出版社, 2013: 32-38.
WANG Shu-guang. Principles and design of mobile robots[M]. Beijing: People's Posts and Telecommunications Press, 2013: 32-38. |
| [3] |
唐炜, 刘勇, 胡海秀, 等.
全向移动平台运动学分析及其自适应控制器设计[J]. 机械科学与技术, 2016, 36(6): 883–889.
TANG Wei, LIU Yong, HU Hai-xiu, et al. Kinematics analysis and self-adaptive controller design of omni-directional movement platform[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 36(6): 883–889. |
| [4] | GOSSELIN C, ANGELES J. Singularity analysis of closed-loop kinematic chains[J]. IEEE Transactions on Robotics and Automations, 1990, 6(3): 281–290. DOI:10.1109/70.56660 |
| [5] | LI Yuan-ping. Slip modelling estimation and control of omnidirectional wheel mobile robots with powered caster wheel[D]. Singapore: National University of Singapore, Department of Mechanical Engineering, 2009: 5-15. |
| [6] | CARIDA V F, MORANDIN Jr O, TUMA C C M. Approaches of fuzzy systems applied to an AGV dispatching system in a FMS[J]. The International Journal of Advanced Manufacturing Technology, 2015, 79(1/4): 615–625. |
| [7] |
汤兵勇, 路林吉, 王文杰.
模糊控制理论与应用技术[M]. 北京: 清华大学出版社, 2002: 152-194.
TANG Bing-yong, LU Lin-ji, WANG Wen-jie. Fuzzy control theory and application technology[M]. Beijing: Tsinghua University Press, 2002: 152-194. |
| [8] |
陈无畏, 孙海涛, 李碧春, 等.
基于标识线导航的自动导引车跟踪控制[J]. 中国机械工程, 2006, 42(8): 164–170.
CHEN Wu-wei, SUN Hai-tao, LI Bi-chun, et al. Tracking control of automatic guide vehicle based on marker line navigation[J]. China Mechanical Engineering, 2006, 42(8): 164–170. |
| [9] | JI Shou-wen, LI Ke-qiang, MIAO Li-xin, et al. Design of a new type of AGV based on computer vision[J]. Chinese Journal of Mechanical Engineering, 2004, 17(1): 97–101. DOI:10.3901/CJME.2004.01.097 |
| [10] |
武星, 楼佩煌, 唐敦兵.
自动导引车路径跟踪和伺服控制的混合运动控制[J]. 机械工程学报, 2011, 47(3): 43–48.
WU Xing, LOU Pei-huang, TANG Dun-bing. Integrated motion control of path tracking and servo control for an automated guided vehicle[J]. Journal of Mechanical Engineering, 2011, 47(3): 43–48. |
| [11] | WU Jin-bo, XU Guo-hua, YIN Zhou-ping. Robust adaptive control for a nonholonomic mobile robot with unknown parameters[J]. Journal of Control Theory and Applications, 2009, 7(2): 212–218. DOI:10.1007/s11768-009-7130-6 |
| [12] |
徐俊艳, 张培仁, 程剑锋.
基于Backstepping时变反馈和PID控制的移动机器人实时轨迹跟踪控制[J]. 电机与控制学报, 2004, 8(1): 35–38.
XU Jun-yan, ZHANG Pei-ren, CHENG Jian-feng. Real-time trajectory tracking control of mobile robot based on Backstepping time-varying state feedback and PID control method[J]. Electric Machines and Control, 2004, 8(1): 35–38. DOI:10.3969/j.issn.1007-449X.2004.01.010 |
| [13] |
刘晨辉.
多变量过程系统解耦理论[M]. 北京: 北京水利出版社, 1984: 213-241.
LIU Chen-hui. Process control of decoupling theory for multivariable system[M]. Beijing: Beijing Water Conservancy Press, 1984: 213-241. |
| [14] | MARINO R, CINILI F. Input-output decoupling control by measurement feedback in four-wheel-active-steering vehicles[C]//Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, Dec. 13-15, 2006. |
| [15] |
刘成, 赵福宇, 侯素霞, 等.
一种新的多变量参考模型解耦控制的方法[J]. 控制工程, 2009, 16(1): 12–15, 38.
LIU Cheng, ZHAO Fu-yu, HOU Su-xia, et al. A reference model decoupling method for multivariable systems[J]. Control Engineering, 2009, 16(1): 12–15, 38. DOI:10.3969/j.issn.1671-7848.2009.01.004 |
| [16] |
刘成, 赵福宇, 侯素霞, 等.
一种基于控制量一致的参考模型解耦方法[J]. 控制工程, 2009, 16(5): 571–574.
LIU Cheng, ZHAO Fu-yu, HOU Su-xia, et al. A reference model decoupling method based on consistency controller outputs[J]. Control Engineering, 2009, 16(5): 571–574. DOI:10.3969/j.issn.1671-7848.2009.05.016 |
| [17] |
钱晓明, 朱立群, 楼佩煌, 等.
基于位姿状态的全向运行型AGV路径跟踪优化控制方法[J]. 农业机械学报, 2018, 49(4): 20–26.
QIAN Xiao-ming, ZHU Li-qun, LOU Pei-huang, et al. Optimal path tracking control method of omni-directional mobile AGV based on pose state[J]. Transactions of the Chinese Society of Agricultural Machinery, 2018, 49(4): 20–26. |
| [18] |
杨天旭, 楼佩煌, 钱晓明.
融合多模糊控制器的全方位移动AGV的路径跟踪控制技术[J]. 机械设计与制造工程, 2016, 45(7): 57–61.
YANG Tian-xu, LOU Pei-huang, QIAN Xiao-ming. Fusion fuzzy controller of path tracking for the omni-directional mobile AGV[J]. Machine Design and Manufacturing Engineering, 2016, 45(7): 57–61. DOI:10.3969/j.issn.2095-509X.2016.07.013 |



