车载医疗救护隔振平台是一种将车辆作为载体、隔振平台置于车中并与车有效连接的医疗救护装备,用于运送危重伤员或病人等,保证伤员或病人免受车辆行驶过程中因振动而造成的二次伤害,这对于挽救生命至关重要。
隔振平台研究的不断深入为它在医疗救护中的应用奠定了基础,同时,有关隔振平台和车辆悬架的研究已得到同步发展。加拿大湖首大学(Lakehead University)的Zhou等[1]开发了具有被动和半主动两种模式的高静态低动态减振平台。澳大利亚阿德莱德大学(University of Adelaide)的Robertson等[2]提出了一种采用电磁铁元件的磁悬浮系统的隔振分析方法。英国布里斯托大学(University of Bristol)的Shaw等[3]采用双稳态复合板作为高静态低动态减振平台的变刚度元件,并通过理论分析和实验测试研究了减振效果。俄罗斯鲍曼州立技术大学(Bauman State Technical University)的Mikhailov等[4]开发了一种基于磁流变弹性体的减振平台,它能够有效消除频率在200 Hz以内、幅值不大于500 μm的振动。英国谢菲尔德大学(The University of Sheffield)的Khan等[5]提出了采用主动与半主动的混合控制方法。我国华中科技大学的Shan等[6]开发了一种小型气动减振器,通过建模分析了其隔振效果,并得到了实验验证。上海大学、上海应用数学和力学研究所的Lu等[7]通过理论分析和实验研究了两级非线性减振平台。东南大学的Xu等[8]全面考虑了高频和低频振动,将频率范围拓宽到0~500 Hz,采用MR(magnetorheological,磁流变液)和VE(viscoelastic,黏弹质)作为阻尼元件,建立了智能减振平台。哈尔滨工业大学深圳研究院的Li等[9]设计了一种基于位置/方向解耦的并联机构的五维减振器,并进行了动力学建模和模糊最优控制研究。
隔振平台的车载化正逐渐引起研究人员的兴趣。太原科技大学的高蓬、赵宇坤等[10-11]将仿生气动人工肌肉运用于急救车车载担架隔振平台,建立了缓冲减振系统数学模型,并以白噪声模拟路面输入进行了仿真。北京航天控制仪器研究所的贾楠等[12]研究了车载摄像稳定平台减振系统,建立了有限元模型并通过模态叠加法对系统进行了仿真。长春理工大学的姜昊等[13]设计了车载平台电子设备的抗振系统,通过减振器的布局方式研究,分析了不同布局方式下的振动耦合情况[13]。
车载医疗救护隔振平台的系统性研究还不多见。为了最大程度地获得减振效果,同时兼顾低成本,本文设计了一款新型车载医疗救护隔振平台,采用拉格朗日方法建立了平台数学模型,并进行了关键隔振参数的优化设计,进而建立了车载隔振平台全系统动力学模型,并进行了仿真分析。
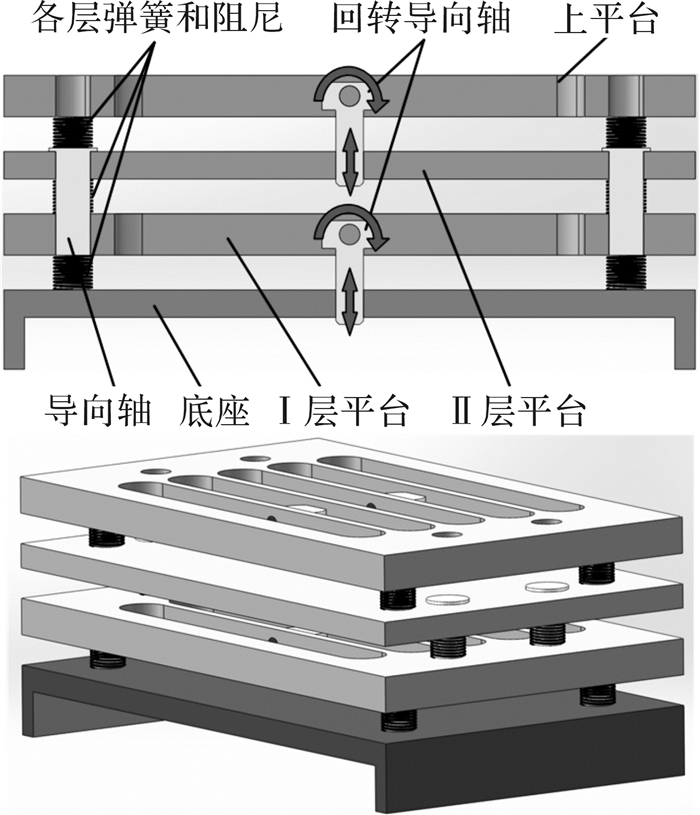
1 新型车载医疗救护隔振平台设计笔直设计了一款具有多层结构且各层之间具有相对移动和俯仰自由度的新型车载医疗救护多层隔振平台,它具有大长宽比、多层串联的结构特点。该平台由底座、Ⅰ层平台、Ⅱ层平台和上平台等主体结构组成,其截面剖视图和整体示意图如图 1所示。其中:底座与载体车辆的车体固结;Ⅰ层平台与底座之间通过回转导向轴、弹簧、阻尼相连,二者可以相对垂向移动和转动;Ⅱ层平台与Ⅰ层平台之间通过导向轴、弹簧、阻尼相连,二者之间仅能沿着导向轴垂向移动;上平台与Ⅱ层平台之间结构和底座与Ⅰ层平台之间结构相同,二者同样既可以相对移动又可以相对转动。
|
| 图 1 新型车载医疗救护隔振平台结构图 Fig.1 Structure graph of new vibration isolation platform for vehicle medical rescue |
为了获得隔振平台的最优减振效果,需要对其关键隔振参数进行优化设计。因此,首先对平台进行动力学建模,进而在典型激励作用下进行仿真优化。
2 新型车载隔振平台动力学建模及隔振参数优化由于车载隔振平台具有沿纵轴线(长度方向)的对称性,故可转化成平面机构进行分析,如图 2所示。平台底座与车辆悬架固结,车身的垂向位移zs和俯仰角位移θs作为平台系统的输入。在该激励下:Ⅰ层平台质心处向上垂向位移为z1,旋转角位移为θ1; Ⅱ层平台相对Ⅰ层平台的向外位移为z21; Ⅱ层平台质心处向上垂向位移为z2,满足z2-z1=z21cos θ1;上平台质心处向上垂向位移为z,旋转角位移为θ。

|
| 图 2 新型车载隔振平台动力学模型 Fig.2 Dynamics model of new vehicle vibration isolation platform for vehicle medical rescure |
根据图 2可知,平台系统具有5个自由度,因此可选取广义坐标。
| $ \mathit{\boldsymbol{q}} = \left[ {{q_1},{q_2}, \cdots ,{q_5}} \right] = \left[ {{z_1},{\theta _1},{z_2},z,\theta } \right] $ |
Ⅰ、Ⅱ层平台具有相同结构,分析过程中可视为它们具有相同质量和转动惯量。系统的动能E、势能U和耗散能D分别为:
| $ E = \frac{1}{2}m\left( {\dot z_1^2 + \dot z_2^2} \right) + \frac{1}{2}{m_0}{{\dot z}^2} + J\dot \theta _1^2 + \frac{1}{2}{J_0}{{\dot \theta }^2} $ | (1) |
| $ \begin{array}{l} U = \frac{1}{2}k{\left[ {{z_1} - {z_{\rm{s}}} + \frac{l}{2}\sin \left( {{\theta _1} - {\theta _{\rm{s}}}} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\frac{1}{2}k{\left[ {{z_1} - {z_{\rm{s}}} - \frac{l}{2}\sin \left( {{\theta _1} - {\theta _{\rm{s}}}} \right)} \right]^2} + k{z_{21}}^2 + \\ \;\;\;\;\;\;\;\frac{1}{2}k{\left[ {z - {z_{\rm{2}}} + \frac{l}{2}\sin \left( {\theta - {\theta _{\rm{1}}}} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\frac{1}{2}k{\left[ {z - {z_{\rm{2}}} - \frac{l}{2}\sin \left( {\theta - {\theta _{\rm{1}}}} \right)} \right]^2} \end{array} $ | (2) |
| $ \begin{array}{l} D = \frac{1}{2}c{\left[ {{{\dot z}_1} - {{\dot z}_{\rm{s}}} + \frac{l}{2}\left( {{{\dot \theta }_1} - {{\dot \theta }_{\rm{s}}}} \right)\cos \left( {{\theta _1} - {\theta _{\rm{s}}}} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\frac{1}{2}c{\left[ {{{\dot z}_1} - {{\dot z}_{\rm{s}}} - \frac{l}{2}\left( {{{\dot \theta }_1} - {{\dot \theta }_{\rm{s}}}} \right)\cos \left( {{\theta _1} - {\theta _{\rm{s}}}} \right)} \right]^2} + \\ \;\;\;\;\;\;\;c\dot z_{21}^2 + \frac{1}{2}c{\left[ {\dot z - {{\dot z}_2} + \frac{l}{2}\left( {\dot \theta - {{\dot \theta }_1}} \right)\cos \left( {\theta - {\theta _1}} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\frac{1}{2}c{\left[ {\dot z - {{\dot z}_2} - \frac{l}{2}\left( {\dot \theta - {{\dot \theta }_1}} \right)\cos \left( {\theta - {\theta _1}} \right)} \right]^2} \end{array} $ | (3) |
式中:m、J分别为Ⅰ、Ⅱ层平台质量和绕回转轴线的转动惯量;m0、J0分别为上层平台含负载的总质量和绕回转轴线的总转动惯量;c、k分别为各层平台之间隔振阻尼系数和弹簧刚度。
基于分析力学的拉格朗日法在机械系统动力学分析中具有突出优点[14-16]。根据该方法,图 2所示系统的拉格朗日方程可列写为:
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right) - \left( {\frac{{\partial L}}{{\partial {q_i}}}} \right) + \left( {\frac{{\partial D}}{{\partial {{\dot q}_i}}}} \right) = {Q_i}}&{\left( {i = 1,2, \cdots ,5} \right)} \end{array} $ | (4) |
式中:L为动能与势能之差,即L=E-U;Qi为对应于qi的非保守广义力,显然在本系统中,Qi=0。
考虑到发生振动时θs、θ1和θ均较小,可将公式(2)和(3)线性化, 并将公式(1)至(3)代入公式(4),可得如下微分方程组:
| $ \left\{ \begin{array}{l} m{{\ddot z}_1} + 2k\left( {2{z_1} - {z_2} - {z_{\rm{s}}}} \right) + 2c\left( {2{{\dot z}_1} - {{\dot z}_2} - {{\dot z}_{\rm{s}}}} \right) = 0\\ J{{\ddot \theta }_1} + \frac{{{l^2}}}{4}k\left( {2{\theta _1} - \theta - {\theta _{\rm{s}}}} \right) + \frac{{{l^2}}}{4}c\left( {2{{\dot \theta }_1} - \dot \theta - {{\dot \theta }_{\rm{s}}}} \right) = 0\\ m{{\ddot z}_2} + 2k\left( {2{z_2} - {z_1} - z} \right) + 2c\left( {2{{\dot z}_2} - {{\dot z}_1} - \dot z} \right) = 0\\ {m_0}\ddot z + 2k\left( {z - {z_2}} \right) + 2c\left( {\dot z - {{\dot z}_2}} \right) = 0\\ {J_0}\ddot \theta + \frac{{{l^2}}}{2}k\left( {\theta - {\theta _1}} \right) + \frac{{{l^2}}}{2}c\left( {\dot \theta - {{\dot \theta }_1}} \right) = 0 \end{array} \right. $ | (5) |
取状态变量:x1=z1,x2=θ1,x3=z2,x4=z,x5=θ,
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}}\\ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}} \end{array} \right. $ | (6) |
式中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{5 \times 5}}}&{{\mathit{\boldsymbol{I}}_5}}\\ {k{\mathit{\boldsymbol{A}}_0}}&{c{\mathit{\boldsymbol{A}}_0}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{4 \times 5}}}&{{\mathit{\boldsymbol{B}}_1}}&{{{\bf{0}}_{4 \times 3}}} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_1}}&{{\mathit{\boldsymbol{C}}_2}} \end{array}} \right] $ |
其中:
| $ {\mathit{\boldsymbol{A}}_0} = \left[ {\begin{array}{*{20}{c}} { - \frac{4}{m}}&0&{\frac{2}{m}}&0&0\\ 0&{ - \frac{{{l^2}}}{{2J}}}&0&0&{\frac{{{l^2}}}{{4J}}}\\ {\frac{2}{m}}&0&{ - \frac{4}{m}}&{\frac{2}{m}}&0\\ 0&0&{\frac{2}{{{m_0}}}}&{ - \frac{2}{{{m_0}}}}&0\\ 0&{\frac{{{l^2}}}{{2{J_0}}}}&0&0&{ - \frac{{{l^2}}}{{2{J_0}}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}}_1^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {\frac{{2k}}{m}}&{\frac{{2c}}{m}}&0&0\\ 0&0&{\frac{{{l^2}k}}{{4J}}}&{\frac{{{l^2}c}}{{4J}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{C}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{{2k}}{{{m_0}}}}&{ - \frac{{2k}}{{{m_0}}}}&0\\ 0&{\frac{{{l^2}k}}{{2{J_0}}}}&0&0&{ - \frac{{{l^2}k}}{{2{J_0}}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{C}}_2} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{{2c}}{{{m_0}}}}&{ - \frac{{2c}}{{{m_0}}}}&0\\ 0&{\frac{{{l^2}c}}{{2{J_0}}}}&0&0&{ - \frac{{{l^2}c}}{{2{J_0}}}} \end{array}} \right] $ |
I5表示5阶单位矩阵,0m×n表示m×n阶零矩阵。
隔振平台结构参数如表 1所示,为根据平台实际尺寸、材料等给定的固定值。
| 结构参数 | 数值 |
| 平台纵向长度l/m | 2.0 |
| Ⅰ、Ⅱ层平台质量m/kg | 158.0 |
| Ⅰ、Ⅱ层平台绕回转轴线的转动惯量J/(kg·m2) | 99.6 |
| 上层平台含负载的总质量m0/kg | 298.0 |
| 上层平台(含负载)绕回转轴线的总转动惯量J0/(kg·m2) | 156.0 |
本文的优化目标为最小化隔振平台上平台的垂向振动加速度和俯仰振动加速度,以实现减振的目的。状态方程(6)所确定的传递函数为:
| $ \mathit{\boldsymbol{G}}\left( s \right) = \mathit{\boldsymbol{C}}{\left( {s\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}} \right)^{ - 1}}\mathit{\boldsymbol{B}} $ | (7) |
根据A,B和C的表达式,G(s)的系数为k和c的函数,故对它们进行优化设计是首要的关键问题。
根据公式(6),应用MATLAB软件可在给定输入激励下优化平台隔振参数k和c。采用的优化方法为:同时对整个平台从底座处施加垂向和俯仰激励,考察其时域输出。垂向位移与转角位移输入采用相同激励信号,则二者微分后的速度信号也相同,分别如图 3、图 4所示。不同k、c组合下,激励所导致的上平台垂向和俯仰角加速度输出响应如图 5、图 6所示。

|
| 图 3 隔振平台底座处垂向位移和转角位移输入 Fig.3 Vertical displacement and angle displacement input at the base of vibration isolation platform |

|
| 图 4 隔振平台底座处垂向速度和转角速度输入 Fig.4 Vertical velocity and angular velocity input at the base of vibration isolation platform |

|
| 图 5 c值固定、不同k值下隔振平台上平台垂向加速度和俯仰角加速度输出 Fig.5 Vertical acceleration and pitch angular acceleration output of upper platform with fixed c value and different k values |

|
| 图 6 k值固定、不同c值下隔振平台上平台垂向加速度和俯仰角加速度输出 Fig.6 Vertical acceleration and pitch angular acceleration output of upper platform with fixed k value and different c values |
图 5为c值固定、不同k值下垂向加速度和俯仰角加速度曲线;图 6为k值固定、不同c值下垂向加速度和俯仰角加速度曲线。综合图 5、图 6可知,k值过大及c值过小会引起冲击,k值过小及c值过大会引起震荡失稳。由此可以确定k=10 000 N/m,c=10 000 Ns/m为最优数量级参数。
3 新型车载隔振平台全系统建模及仿真测试新型车载医疗救护隔振平台具有大长宽比的特点,长度方向通常沿车辆纵向。考虑到当前车辆悬架主要以被动悬架为主,故本文建立以车辆被动悬架为基体的隔振平台全系统动力学模型。
车载隔振平台全系统动力学模型如图 7所示。隔振平台参数上文已经确定。底座质量及其转动惯量也设置为与Ⅰ、Ⅱ层平台相同,即m、J,在对全系统进行仿真测试时必须予以考虑。给定平台纵向质心位置在车身质心位置后方0.4 m处,车辆被动悬架参数如表 2所示。

|
| 图 7 车载隔振平台全系统动力学模型 Fig.7 The whole system dynamic model of vehicle vibration isolation platform |
| 参数 | 数值 |
| 非簧载刚度kt1、kt2/(N/m) | 1 000 000 |
| 非簧载质量mt1、mt2/kg | 30.0 |
| 簧载刚度ks1、ks2/(N/m) | 1 000 000 |
| 簧载阻尼cs1、cs2/(Ns/m) | 298.0 |
| 簧载质量ms/kg | 500.0 |
| 簧载转动惯量Js/(kg·m2) | 910.0 |
| 质心距前轴距离ls1/m | 1.5 |
| 质心距后轴距离ls2/m | 1.3 |
ADAMS及MATLAB软件已广泛应用于机械系统的动力学分析和数据后处理[17-19]。根据图 7、表 1、表 2和优化确定的平台隔振参数,应用ADAMS软件建立动力学仿真模型。进而,针对2种典型路面激励,进行仿真测试,并与不放置隔振平台(即无平台)的车身直接输出进行比较。所选路面如图 8所示。

|
| 图 8 隔振平台仿真测试中的2种典型路面 Fig.8 Two typical pavements for the simulation test of vibration isolation platform |
1) 斜坡路面激励。
斜坡路面用于模拟车辆从水平路面经过斜坡行驶至更高层路面上。给定仿真条件如下:路面高度差为0.05 m,坡度为45°,车速为15 km/h。隔振平台上平台垂向加速度和俯仰角加速度响应曲线如图 9、图 10所示。

|
| 图 9 斜坡路面激励下隔振平台上平台垂向加速度曲线 Fig.9 Vertical acceleration curve of vibration isolation platform upper platform under slope road excitation |

|
| 图 10 斜坡路面激励下隔振平台上平台俯仰角加速度曲线 Fig.10 Pitch anglular acceleration curve of vibration isolation platform upper platform under slope road excitation |
2) 正弦起伏路面激励。
正弦起伏路面是一种极端恶劣的颠簸路面,常用于特种车辆的性能测试[20]。给定仿真条件如下:正弦起伏路幅值为0.05 m,凸起底部宽度(半波长)为0.3 m,车速为0.5 m/s。隔振平台上平台垂向加速度和俯仰角加速度响应曲线分别如图 11、图 12所示。

|
| 图 11 正弦起伏路面激励下隔振平台上平台垂向加速度曲线 Fig.11 Vertical acceleration curve of vibration isolation platform upper platform under sinusoidal road excitation |

|
| 图 12 正弦起伏路面激励下隔振平台上平台俯仰角加速度曲线 Fig.12 Pitch anglular acceleration curve of vibration isolation platform upper platform under sinusoidal road excitation |
从图 9至图 12可以看出,隔振平台可以有效衰减来自路面的振动激励,尤其是对于路况极端恶劣的起伏路面,隔振效果极为明显。
4 结论本文针对所设计的一款大长宽比、多层隔振车载医疗救护平台,采用基于分析力学的拉格朗日方法建立数学模型,通过仿真优化,得到了最优数量级的平台隔振参数。建立了基于被动悬架的车载隔振平台全系统动力学模型,并针对2种典型路面进行了仿真分析。结果表明,隔振平台能够有效衰减来自地面的振动激励,尤其对于恶劣的起伏路面,隔振效果更佳。这对伤病员的运送和救护具有特别重要的意义,尤其对于在事故多发的山区、工地等恶劣路况环境中的车载医疗救护。本文给出的平台隔振参数优化设计方法、车载隔振平台全系统建模及仿真方法较好地解决了车载隔振平台设计阶段的关键问题。
| [1] | ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254–1273. DOI:10.1016/j.jsv.2009.11.001 |
| [2] | ROBERTSON W S, KIDNER M R F, CAZZOLATO B S, et al. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation[J]. Journal of Sound and Vibration, 2009, 326(1/2): 88–103. |
| [3] | SHAW A D, NEILD S A, WAGG D J, et al. A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation[J]. Journal of Sound and Vibration, 2013, 332(24): 6265–6275. DOI:10.1016/j.jsv.2013.07.016 |
| [4] | MIKHAILOY V P, BAZINENKOV A M. A vibration control platform on the basis of magnetorheological elastomers[J]. Instruments and Experimental Techniques, 2016, 59(1): 131–135. DOI:10.1134/S0020441216010085 |
| [5] | KHAN Irfan Ullah, DAVID Wagg, NEIL D Sims. Improving the vibration suppression capabilities of a magneto-rheological damper using hybrid active and semi-active control[J]. Smart Materials and Structures, 2016, 25(8): 1–15. |
| [6] | SHAN Yu-hu, WU Wen-jiang, CHEN Xue-dong. Design of a miniaturized pneumatic vibration isolator with high-static-low-dynamic stiffness[J]. Journal of Vibration and Acoustics, 2015, 137(4): 1–8. |
| [7] | LU Ze-qi, YANG Tie-jun, BRENNAN Michael J, et al. Experimental investigation of a two-stage nonlinear vibration isolation system with high-static-low-dynamic stiffness[J]. Journal of Applied Mechanics, 2017, 84(2): 1–9. |
| [8] | XU Zhao-dong, ASCE A M, XU Fei-hong, et al. Intelligent vibration isolation and mitigation of a platform by using MR and VE devices[J]. Journal of Aerospace Engineering, 2016, 29(4): 1–10. |
| [9] | LI Bing, ZHAO Wei, WANG Shuai, et al. Dynamic modeling and control for a five-dimensional hybrid vibration isolator based on a position/orientation decoupled parallel mechanism[J]. Journal of Vibration and Control, 2016, 22(15): 3368–3383. DOI:10.1177/1077546314560388 |
| [10] |
高蓬, 孙大刚, 梁培根, 等.
急救车载担架人工肌肉隔振系统特性分析[J]. 噪声与振动控制, 2014, 34(3): 119–123.
GAO Peng, SUN Da-gang, LIANG Pei-gen, et al. Characteristics analysis of pneumatic artificial muscle isolation systems on ambulance vehicle-mounted stretchers[J]. Noise and Vibration Control, 2014, 34(3): 119–123. DOI:10.3969/j.issn.1006-1335.2014.03.025 |
| [11] |
赵宇坤, 孙大刚, 陈俊海, 等.
基于气动人工肌肉缓冲车载隔振平台特性研究[J]. 太原科技大学学报, 2017, 38(1): 48–54.
ZHAO Yu-kun, SUN Da-gang, CHEN Jun-hai, et al. Damping characteristics analysis of vehicular photoelectric platform with pneumatic artificial muscle[J]. Journal of Taiyuan University of Science and Technology, 2017, 38(1): 48–54. DOI:10.3969/j.issn.1673-2057.2017.01.010 |
| [12] |
贾楠, 牛静, 耿欣.
车载摄像稳定平台隔振系统优化研究[J]. 导航与控制, 2015, 14(4): 100–106.
JIA Nan, NIU Jing, GENG Xin. Research on optimization of carborne stabilized platform vibration isolation system[J]. Navigation and Control, 2015, 14(4): 100–106. DOI:10.3969/j.issn.1674-5558.2015.04.018 |
| [13] |
姜昊, 张立中, 李小明, 等.
某车载平台电子设备抗振系统设计[J]. 长春理工大学学报(自然科学版), 2016, 39(5): 13–19.
JIANG Hao, ZHANG Li-zhong, LI Xiao-ming, et al. Anti-vibration systems design of a vehicle platform electronic equipment[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2016, 39(5): 13–19. DOI:10.3969/j.issn.1672-9870.2016.05.004 |
| [14] |
潘坤, 丁洁玉, 董贺威, 等.
基于重心插值的多体系统动力学离散变分方法[J]. 青岛大学学报(自然科学版), 2017, 30(2): 77–82.
PAN Kun, DING Jie-yu, DONG He-wei, et al. Discrete variation method of multi-body system dynamics based on center of gravity interpolation[J]. Journal of Qingdao University (Natural Science Edition), 2017, 30(2): 77–82. |
| [15] | RIZVI S M H, ABID M, KHAN A Q, et al. H∞ control of 8 degrees of freedom vehicle active suspension system[J]. Journal of King Saud University-Engineering Sciences, 2016, 30(2): 1–9. |
| [16] |
王鑫, 袁晓光, 杨星.
基于拉格朗日方法的飞行器多体分离姿态动力学分析研究[J]. 西北工业大学学报, 2014, 32(1): 18–22.
WANG Xin, YUAN Xiao-guang, YANG Xing. Research on multi-body separation dynamics using Lagrange method[J]. Journal of Northwestern Polytechnical University, 2014, 32(1): 18–22. |
| [17] | TAHMASEBI M, ESMAILZADEH S M. Modeling and co-simulating of a large flexible satellites with three reaction wheels in ADAMS and MATLAB[J]. International Journal of Dynamics and Control, 2018, 6(1): 79–88. DOI:10.1007/s40435-016-0300-8 |
| [18] | MONTEIRO T P, CANALE A C. Development of a direct-dynamic model for a passenger vehicle on MATLAB Simulink[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 39(2): 1–16. |
| [19] | RANGASWAMY T, VIDHYASHANKAR S, MADHUSUDAN M, et al. Performance parameters analysis of an XD3P Peugeot engine using artificial neural networks (ANN) concept in MATLAB[J]. Journal of the Institution of Engineers (India):Series C, 2015, 96(2): 175–182. DOI:10.1007/s40032-014-0140-2 |
| [20] |
魏春雨, 周晓军, 魏燕定, 等.
基于Vortex的6自由度平台洗出运动仿真[J]. 浙江大学学报(工学版), 2012, 46(8): 1390–1396.
WEI Chun-yu, ZHOU Xiao-jun, WEI Yan-ding, et al. Washout motion simulation in 6-DOF parallel platform based on Vortex[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(8): 1390–1396. DOI:10.3785/j.issn.1008-973X.2012.08.006 |


