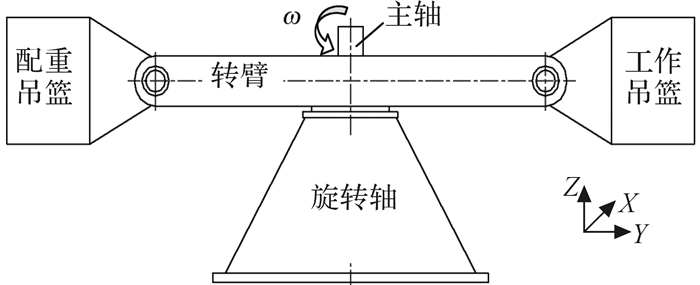
振动离心机可用于地震研究和飞行器离心振动复合环境试验研究,其结构如图 1所示。在试验中,将振动台安装在离心机吊篮内或直接安装在离心机转臂上,试验模型则安装在振动台上。离心机转臂绕主轴旋转形成离心过载环境,振动台的激振形成振动环境,从而为试验模型营造离心-振动复合环境。这种复合环境不仅可在岩土工程地震问题研究中模拟原型应力场的应力条件并精确再现原型在该条件下的真实动力响应[1-2],还可在航天航空研究领域模拟飞行器发射、飞行、再入过程必然经历的一种环境,以研究飞行器的环境适应能力。
|
| 图 1 振动离心机结构示意图 Fig.1 Structure diagram of centrifugal shaker |
用于研究岩土工程地震问题的土工振动离心机,其振动台安装在离心机吊篮内。在进行离心-振动试验时,因安装振动台的吊篮与离心机转臂间通过关节轴承联接,吊篮可相对于转臂在垂臂向(Z向)和切向(X向)上进行小角度转动,则垂臂向振动冲击和切向振动冲击可通过吊篮相对于转臂的摆振予以削弱[3],但顺臂向(Y向)的振动冲击必须通过顺臂隔振系统来隔离,否则该向的振动冲击将直接传递给离心机主轴,当振动冲击过大或发生共振时,将损毁离心机主机系统。用于研究飞行器环境适应性的振动离心机,其振动台直接安装在离心机转臂上,其振动方向通常也为顺臂向,所以也须安装顺臂隔振系统。
1 振动离心机顺臂隔振分析对于土工振动离心机,其顺臂隔振系统一般可安装在吊篮或转臂上。若将顺臂隔振系统安装在吊篮上,它须与振动台进行一体化设计以适应吊篮有限的安装空间,这不仅加大了振动台的设计难度,还会降低离心-振动复合试验的有效容量。若将顺臂隔振系统安装在转臂上,虽将导致离心机在运行过程中产生不平衡力,但这可避免前一种安装方式的缺陷,而且还可将转臂作为顺臂振动的反冲质量块而增大顺臂振动反冲质量比,这有助于提高振动台的运动精度[4]。因此,顺臂隔振系统优先选择安装在离心机转臂上。
当顺臂隔振系统安装在转臂上时,为了提高其隔振能力和抑制振动台与离心机转臂间的振动耦合,它应具有较小的动刚度和固有频率;为了提高其承载不平衡力的能力,它还应具有较大的轴向承载力;为了能在离心机转臂有限空间内安装使用,其结构尺寸应较小。
目前,采用弹簧、橡胶、软木及泡沫等材料设计隔振器来进行隔振的常规隔振技术已较成熟[5-10],但将它们用到振动离心机顺臂隔振的研究却鲜有报道。美国加州大学戴维斯分校的1080gt土工离心机虽可进行顺臂振动试验,但其顺臂隔振设计及使用情况并未公开报道。此外,也有通过板簧将离心机转臂吊装在固定于主轴的转臂支承上,则离心机顺臂振动冲击可通过板簧进行削弱或隔离。但该方案中若板簧设计不当,易引起转臂共振,而且,利用板簧承载大部分质量的转臂在进行高速旋转和顺臂振动时,其可靠性也很难得到保证。本文利用空气弹簧动刚度和固有频率小而轴向承载力大等特点[11],设计了一种安装于离心机转臂上的顺臂隔振系统[12],并对其隔振性能进行分析。
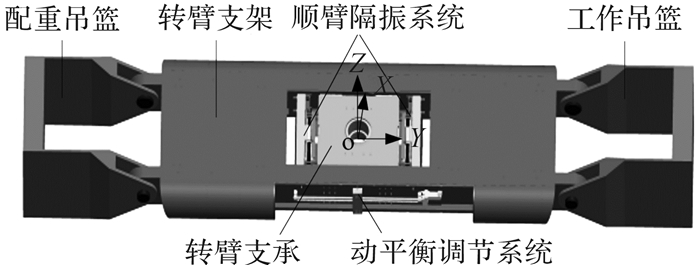
2 振动离心机顺臂隔振系统设计顺臂隔振系统成对使用,对称安装在转臂支承两侧的转臂支架上,如图 2所示。转臂支承固定在离心机主轴上,转臂支架通过直线导轨或滚柱链与转臂支承联接,这样转臂支架不仅可随主轴一起旋转,还可相对于转臂支承在顺臂向(Y向)移动[13]。
|
| 图 2 顺臂隔振系统安装布局示意图 Fig.2 Schematic diagram of installation layout of the vibration isolation system along the swing arm |
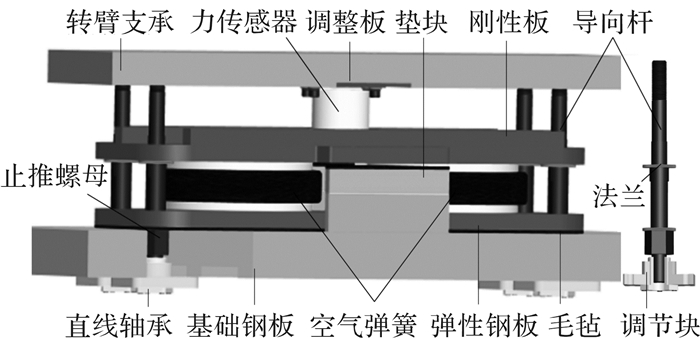
顺臂隔振系统的结构如图 3所示。基础钢板通过螺钉固定在转臂支架上,4根导向杆穿过刚性板和弹性钢板上带铜套的光孔,前端通过螺纹与转臂支承联接,后端穿过固定于基础钢板上的直线轴承,位于直线轴承外的调节块对4根导向杆进行平行调节。导向杆上设有法兰和止推螺母,可分别限制刚性板和弹性钢板远离转臂支承。导向杆不仅承载了刚性板和弹性钢板的重力,还要承载这2个板在顺臂方向上产生的离心力。力传感器安装在刚性板上的平面中心处以监测转臂的不平衡力。空气弹簧通过螺钉固定在刚性板和弹性钢板之间, 形成隔振主体。为提高隔振系统的不平衡力承载能力,隔振主体采用2个空气弹簧并联。
|
| 图 3 顺臂隔振系统的结构示意图 Fig.3 Structure diagram of vibration isolation system along the swing arm |
在安装顺臂隔振系统时,通过调整导向杆旋入转臂支承的深度,使得导向杆的法兰推动刚性板向转臂支承移动,直到力传感器刚好接触调整板(调整板为高碳合金钢,用螺钉联接于转臂支承),此时导向杆、刚性板和力传感器的位置保持相对固定。
离心机运行前,转臂处于平衡位置,将空气弹簧充气到设定气压。2套顺臂隔振系统的弹性钢板在空气弹簧轴向力作用下紧压在基础钢板上,调整导向杆上的止推螺母,使它与弹性钢板保持较小间隙δ1。此时,空气弹簧的轴向力将通过刚性板传递给力传感器,此力为顺臂隔振系统的预紧力。
离心机启动后,在不平衡力的作用下,转臂支架带动基础钢板沿顺臂方向移动,其中一边的空气弹簧被压缩,另一边的空气弹簧将伸长。转臂支架的移动将导致转臂质心偏离Z轴,从而产生附加不平衡力。随着离心加速度的增大,不平衡力随之增大,附加不平衡力也会增大,压缩端空气弹簧的压缩量和伸长端空气弹簧的伸长量都将增大。当空气弹簧伸长端的弹性钢板与止推螺母接触,该空气弹簧将不能再伸长,基础钢板将局部接触或脱开弹性钢板,而空气弹簧对基础钢板的轴向推力将减小甚至消失,被压缩的空气弹簧产生的轴向推力大部分或全部用于克服转臂产生的不平衡力。
为防止转臂产生的不平衡力过大而超过空气弹簧的承载能力,在设计振动离心机转臂时,一般采用全对称结构[13],并添加平衡调节系统[14],从而将转臂的不平衡力控制在较小范围。与此同时,顺臂隔振系统的基础钢板凸台上设有垫块,使它与刚性板间预留较小间距δ2(δ2>δ1)。若离心机在运行过程中出现异常情况,如试验模型变形导致转臂质心偏移而产生很大的不平衡力,空气弹簧压缩端的垫块将直接挤压刚性板,并将不平衡力通过垫块直接传递给力传感器,此时力传感器的读数超过设定安全值,离心机系统会立即报警停机[14]。
离心振动台对转臂的顺臂振动冲击被隔振系统削弱,从而降低了振动冲击对离心机主机系统的影响。为防止振动试验时基础钢板与弹性钢板发生直接碰撞,在基础钢板上粘贴毛毡;为方便拆装,垫块通过螺钉固定在基础钢板的凸台上;为防止空气弹簧压缩量过大而使垫块与刚性板直接碰撞,在垫块上粘贴毛毡。
在该隔振系统中,间隙δ1可通过止推螺母调节,间隙δ2可通过更换不同厚度的垫块进行调节。空气弹簧可根据离心-振动试验有效容量来选定。
3 顺臂隔振相关力学模型构建和系统隔振性能分析 3.1 空气弹簧动刚度模型对于单囊式橡胶空气弹簧,其载荷与气压的关系,以及气体状态方程分别为:
| $ P = \left( {p - {p_{\rm{a}}}} \right)A $ | (1) |
| $ p = {p_0}{\left( {\frac{{{V_0}}}{V}} \right)^n} $ | (2) |
式中:P为载荷; A为气囊有效承压面积; pa为标准大气压; p、V分别为任一位置处气囊内气体的绝对气压和容积;p0、V0分别为空气弹簧初始高度下气囊内气体的绝对气压和容积;n为多变指数。
空气弹簧的刚度为弱非线性,其任一位置的刚度K为:
| $ K = \frac{{{\rm{d}}P}}{{{\rm{d}}x}} $ | (3) |
式中:x为空气弹簧的轴向变形行程。
将式(1)和式(2)代入式(3), 可得空气弹簧任一位置的刚度表达式为:
| $ K = \frac{{{\rm{d}}P}}{{{\rm{d}}x}} = \left( {{p_0}\frac{{V_0^n}}{{{V^n}}} - {p_{\rm{a}}}s} \right)\frac{{{\rm{d}}A}}{{{\rm{d}}x}} - An{p_0}\frac{{V_0^n}}{{{V^{n + 1}}}}\frac{{{\rm{d}}V}}{{{\rm{d}}x}} $ | (4) |
在振动台顺臂振动过程中,作为反冲质量块的转臂质量远大于振动台可动部分质量,所以顺臂振动引起的在顺臂向的转臂位移非常小,即空气弹簧在隔振过程中轴向变形行程x很小,可近似为微振动过程。
对于微振动过程,有:
| $ K = \left( {{p_0} - {p_{\rm{a}}}} \right)\frac{{{\rm{d}}A}}{{{\rm{d}}x}} + n{p_0}\frac{{{A^2}}}{{{V_0}}} $ | (5) |
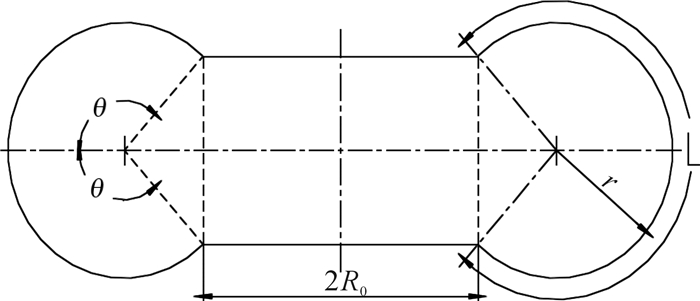
图 4为单囊式橡胶空气弹簧截面示意图。为减小顺臂隔振系统的空间尺寸,空气弹簧采用压合状态,即:90° < θ < 180°。根据图示结构关系可得出如下关系表达式[15]:
|
| 图 4 单囊式橡胶空气弹簧截面示意图 Fig.4 Schematic diagram of cross section of single bellows rubber air spring |
| $ A = {\rm{ \mathsf{ π} }}{\left( {{R_0} - r\cos \theta } \right)^2} $ | (6) |
| $ \begin{array}{*{20}{c}} {V = 2{\rm{ \mathsf{ π} }}\left[ {{R_0} + r\left( {\frac{4}{3} \cdot \frac{{{{\sin }^3}\theta }}{{2\theta - \sin 2\theta }} - \cos \theta } \right)} \right] \times }\\ {\frac{{{r^2}\left( {2\theta - \sin 2\theta } \right)}}{2} + {\rm{ \mathsf{ π} }}{R_0}^2\left( {H - x} \right)} \end{array} $ | (7) |
| $ H - x = 2r\sin \theta $ | (8) |
| $ L = 2\theta r = 2{\theta _0}{r_0} $ | (9) |
式中:R0为空气弹簧圆板半径,r为橡胶囊经线方向断面圆弧半径,θ为橡胶囊经线方向断面圆弧的半个圆心角,H为空气弹簧初始高度,L为橡胶囊经线方向断面圆弧长度,θ0、r0分别为空气弹簧初始高度下橡胶囊经线方向断面圆弧的半个圆心角和圆弧半径。
因x较小,为了简化计算,可用x的一次函数拟合r,即:
| $ r = {r_0} + Bx $ | (10) |
式中:B为常数,由空气弹簧结构确定。
因:x≪H,则:
| $ \begin{array}{l} K \approx {\rm{ \mathsf{ π} }}\left( {{p_0} - {p_{\rm{a}}}} \right) \times \\ \;\;\;\;\;\;\left[ {2B{r_0}\left( {1 - \frac{{2{R_0}}}{{\sqrt {4{r_0}^2 - {H^2}} }}} \right) + H\left( {\frac{1}{2} + \frac{{{R_0}}}{{\sqrt {4{r_0}^2 - {H^2}} }}} \right)} \right] + \\ \;\;\;\;\;\;\frac{{n{p_0}{{\rm{ \mathsf{ π} }}^2}}} \times {{{V_0}}}{\left[ {{R_0}^2 + {r_0}^2 - \frac{1}{4}{H^2} + {R_0}\sqrt {4{r_0}^2 - {H^2}} } \right]^2} \end{array} $ | (11) |
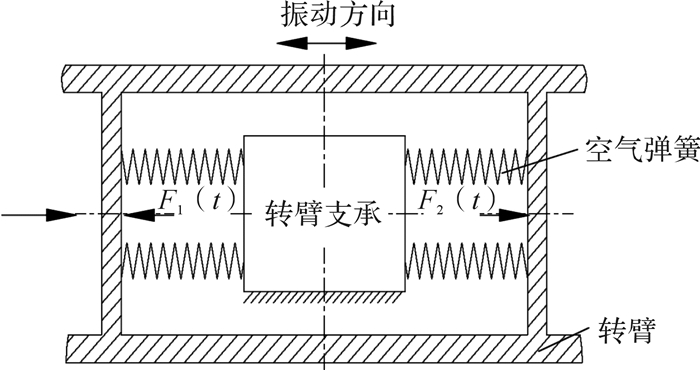
对所设隔振系统,转臂支承可视为刚性基础。离心振动台产生的顺臂振动冲击经隔振系统隔振后通过转臂传递给转臂支承。现对转臂进行受力分析,如图 5所示。
|
| 图 5 转臂受力分析 Fig.5 Stress analysis of swing arm |
当转臂受到不平衡力时,转臂将相对于转臂支承沿顺臂向移动,从而使隔振系统的工作状态发生改变:1)当不平衡力较小时,转臂只需在顺臂向产生较小位移即可使转臂支承两端空气弹簧产生的轴向压力差承载不平衡力,此时,空气弹簧伸长端的δ1虽会减小,但仍大于零;2)当不平衡力增大时,转臂在顺臂向的位移随之增大,以致空气弹簧伸长端隔振系统δ1减小为零,此时,空气弹簧压缩端的部分或全部轴向力用于承载不平衡力;3)当不平衡力继续增大时,空气弹簧压缩端的轴向力将全部用于承载不平衡力,甚至导致该端的δ2减小为零,此时不平衡力已超过离心机安全运行设定值,系统将立即报警停机。由此可见,第2种情况是隔振系统正常工作时最严酷的工况,本文仅对该工况进行分析。
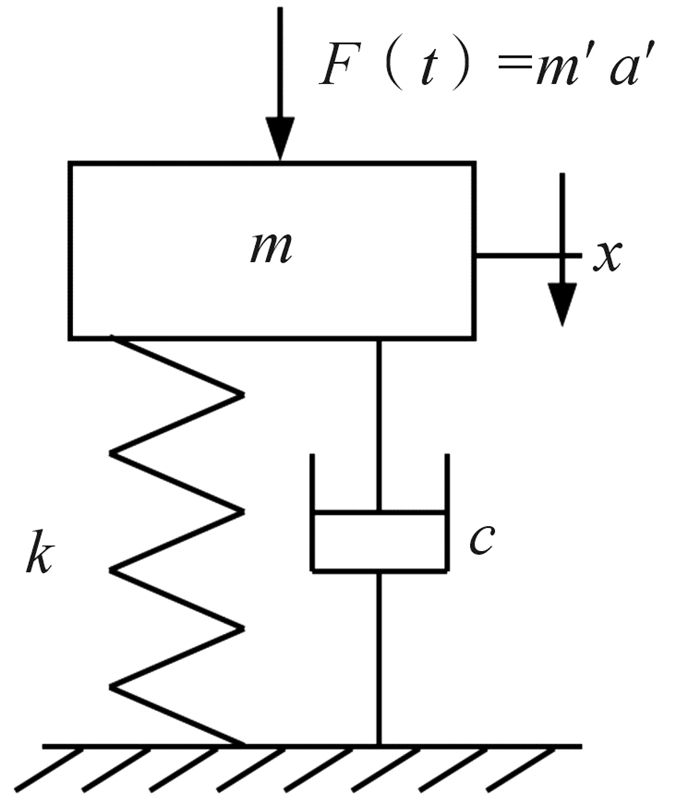
不考虑离心振动台可动部分与转臂间的弹性和阻尼,针对上述第2种情况,隔振系统可简化为图 6所示的单自由度隔振系统。
|
| 图 6 单自由度隔振系统 Fig.6 Single freedom degree vibration isolation system |
单自由度隔振系统的运动微分方程为:
| $ \left\{ \begin{array}{l} m\ddot x + c\dot x + kx = F\left( t \right)\\ F\left( t \right) = m'a' \end{array} \right. $ | (12) |
式中:m′、m分别为振动台可动部分质量和转臂质量,k为隔振系统的动刚度,c为系统的阻尼系数,a′为振动台可动部分的振动加速度。
设振动台的振幅为X′, 则该振动台的振动曲线为:y=-X′cos ωt,则式(12)可写成:
| $ m\ddot x + c\dot x + kx = {F_0}\cos \omega t $ | (13) |
其中:F0=m′X′ω2。
3.3 隔振性能分析在离心振动试验过程中,振动台产生的振动冲击经隔振后传递给转臂支承的最大位移和力是影响离心机安全运行的重要因素,因此在分析隔振系统的隔振性能时,需通过运动微分方程通解求出最大位移和力进行判定。
由于该隔振系统的阻尼由空气弹簧的阻尼和导轨滑动摩擦产生,阻尼较小。对于小阻尼系统,式(13)的通解x(t)为齐次解和特解之和:
| $ x\left( t \right) = {X_0}{{\rm{e}}^{ - \zeta {\omega _{\rm{n}}}t}}\cos \left( {{\omega _{\rm{d}}}t - {\varphi _0}} \right) + X\cos \left( {\omega t - \varphi } \right) $ | (14) |
式中:
对于初始条件:t=0,x=x0=0,
| $ \left\{ \begin{array}{l} {X_0} = - \frac{{\cos \varphi }}{{\cos {\varphi _0}}}X\\ \left| {{X_0}} \right| = \frac{X}{{\sqrt {1 - {\zeta ^2}} }}\\ \tan {\varphi _0} = \frac{{\zeta {\omega _{\rm{n}}} + \omega \tan \varphi }}{{{\omega _{\rm{d}}}}} \end{array} \right. $ | (15) |
根据(14)式可知x(t)的最大幅值Xt max可近似为:
| $ {X_{{\rm{t}}\max }} = \left| {{X_0}} \right| + X = \left( {\frac{1}{{\sqrt {1 - {\zeta ^2}} }} + 1} \right)X $ | (16) |
在离心振动试验过程中,在系统阻尼力作用下,传递到转臂支承的力为:
| $ {F_{\rm{t}}}\left( t \right) = kx + c\dot x $ | (17) |
将式(14)代入式(17)并整理得:
| $ \begin{array}{l} {F_{\rm{t}}}\left( t \right) = - {X_0}{{\rm{e}}^{ - \zeta {\omega _{\rm{n}}}t}}\sqrt {{{\left( {k - c\zeta {\omega _{\rm{n}}}} \right)}^2} + {{\left( {c{\omega _{\rm{d}}}} \right)}^2}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\sin \left( {{\omega _{\rm{d}}}t - {\varphi _0} - \alpha } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;X\sqrt {{k^2} + {{\left( {c\omega } \right)}^2}} \sin \left( {{\omega _{\rm{d}}} - {\varphi _0} - \beta } \right) \end{array} $ | (18) |
式中:
由式(18)可知Ft(t)的最大幅值Ft max可近似为:
| $ {F_{{\rm{t}}\max }} = {X_0}\sqrt {{{\left( {k - c\zeta {\omega _{\rm{n}}}} \right)}^2} + {{\left( {c{\omega _{\rm{d}}}} \right)}^2}} + X\sqrt {{k^2} + {{\left( {c\omega } \right)}^2}} $ | (19) |
因力传递率可表征隔振系统的隔振能力[16-17], 设Tηmax为隔振系统的最大力传递率,
| $ {T_{\eta \max }} = \frac{{{F_{{\rm{t}}\max }}}}{{{F_0}}} = \frac{{1 + \sqrt {\left( {1 - {\zeta ^2}} \right)\left[ {1 + {{\left( {2\zeta \eta } \right)}^2}} \right]} }}{{\sqrt {\left( {1 - {\zeta ^2}} \right)\left[ {{{\left( {1 - {\eta ^2}} \right)}^2} + {{\left( {2\zeta \eta } \right)}^2}} \right]} }} $ | (20) |
由式(20)可知:若ζ=0,要使Tηmax < 1,则η>
对于所设隔振系统,其阻尼比ζ和频率比η主要与阻尼c、隔振系统动刚度k和转臂质量m有关,而隔振系统要同时满足不平衡力承载和安装尺寸要求,其动刚度k很难有较大改变。为此,要减小ζ和增大η,有效途径是增大转臂的质量(即振动反冲质量)和减小转臂与转臂支承间的摩擦阻尼。
4 实例分析设振动台的最大振幅为10 mm,振动加速度幅值为20g(g为重力加速度),则振动台的振动曲线为y=-0.01cos 140t,振动加速度a′=20gcos 140t,其余参数设定如表 1所示。
| 参数 | 量值 |
| m′ | 800 kg |
| m | 30 000 kg |
| R0 | 143.5 mm |
| H | 59 mm |
| r | 36 mm |
| c | 2×104 N·s/m |
| p0 | 0.7 MPa |
| pa | 0.101 3 MPa |
| n | 1.33 |
| δ1 | 1 mm |
| δ2 | 5 mm |
根据表 1设定参数和前文推导公式,可求出隔振系统各性能参数,如表 2所示。
| 参数 | 量值 |
| B | 0.24 |
| K | 1.593×106 N/m |
| Xt max | 5.364×10-4 m |
| Ft max | 1.992×103 N |
| Tηmax | 0.013 |
| ω | 140 rad/s |
| ωn | 10.305 rad/s |
| ωd | 10.294 rad/s |
| η | 13.585 |
| ζ | 0.032 |
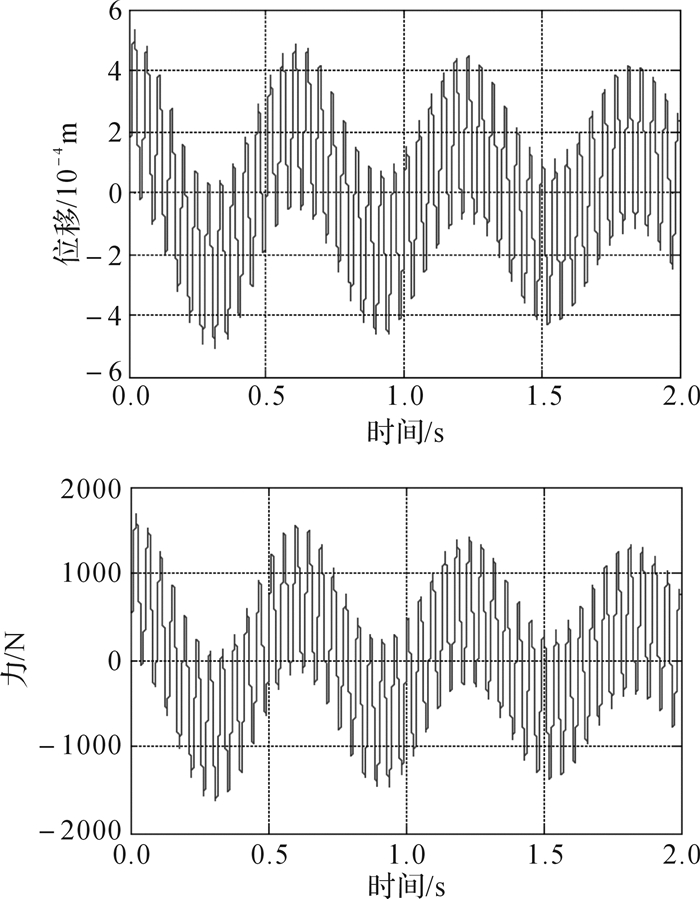
利用x(t)和Ft(t)的最大近似幅值近似关系式计算了上述性能参数理论值,为证明其有效性,现通过MATLAB进行仿真分析,并绘制隔振后隔振系统的位移及力曲线,如图 7所示。由图 7可看出,隔振后系统的最大位移和最大力的仿真值与理论计算值基本一致,且均不大于理论计算值。
|
| 图 7 隔振后转臂位移的和传递给转臂支承的力仿真曲线 Fig.7 Simulation curve of the displacement of swing arm and the force passed to the swing arm support after vibration isolation |
由于Tηmax远小于1,说明所设隔振系统对于给定输入波具有很好的隔振效果。
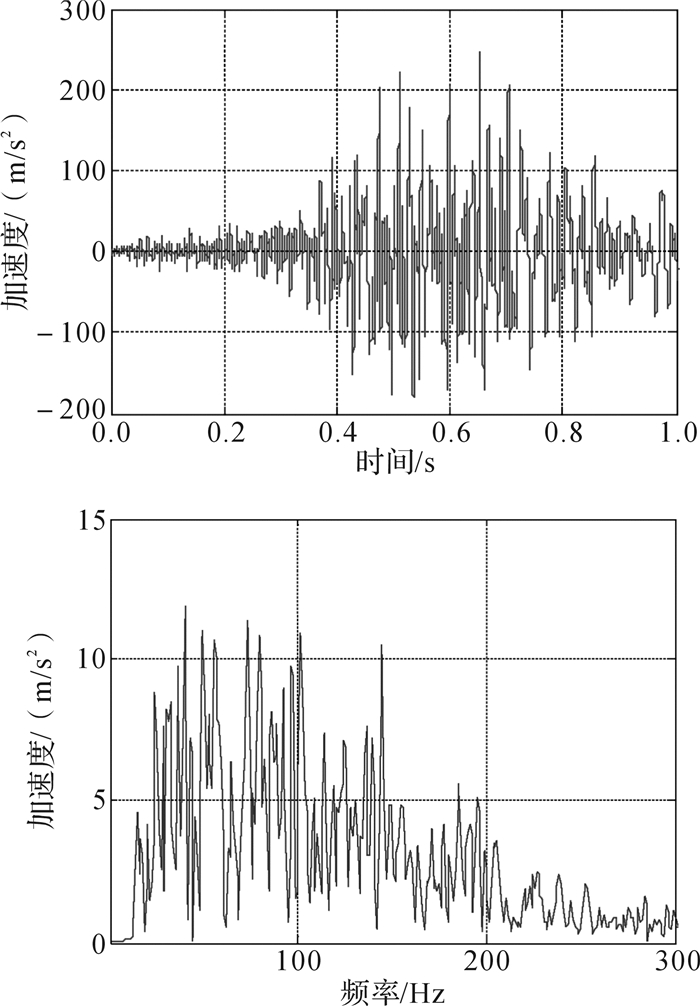
若输入波为地震波,还需考虑对其低频部分的隔振效果,但过低频率的地震波除外,这是因为过低频率的地震波能量较小,已无研究价值。原始地震波的频率较低,在模拟地震时,需根据缩尺比[18]将地震波加速度和频率放大,放大倍数为离心振动试验时的离心加速度相对于重力加速度的倍数。现以唐山地震波为例,设在50g离心场下对该地震波进行模拟,其加速度和频率需放大50倍,如图 8所示。从图 8可看出,放大50倍的唐山地震波的低频约为12 Hz,这时所设隔振系统将有较好的隔振效果。
|
| 图 8 放大50倍的唐山地震波及其频谱 Fig.8 Seismic wave of Tangshan and its frequency spectrum after amplified by 50 times |
地震模拟输入波的低频值取决于试验过程中的离心加速度,要使该隔振系统具有较好的隔振效果,地震模拟实验离心加速度不能太小,但过高的离心加速度将使离心振动台难以正常工作,为此可将离心加速度限定在50g~100g范围内,这可确保输入波的最低频率在10 Hz以上,此时该隔振系统的最大力传递率低于0.057。
另外,由表 2可知,空气弹簧轴向变形行程x非常小,这说明前文对此所作相关假设成立。当x非常小时,隔振系统可承载的最大不平衡力P0可近似为2个并联空气弹簧在初始状态的承载力,即P0=2×(p0-pa)A=1.013×105 N,这表明该隔振系统具有较大的不平衡力承载能力。
5 结论顺臂隔振是振动离心机在顺臂振动工况下稳定运行的关键。本文采用空气弹簧设计了一种安装于离心机转臂上的顺臂隔振系统,并对该系统进行分析,得出如下结论:以空气弹簧为主体的顺臂隔振系统不仅可有效隔离振动离心机的顺臂振动冲击,还可承载较大不平衡力;要使隔振系统具有隔振效果,其阻尼比至少大于
另外,本文在建立空气弹簧动刚度模型时,主要针对历时较短的离心振动工况,若离心振动试验历时较长,空气弹簧内气体不能再假定为绝热过程,需考虑温度对气体状态方程的影响。
| [1] | MADABHUSHI S P G. Modelling of earthquake damage using geotechnical centrifuges[J]. Current Science, 2004, 87(10): 1405–1416. |
| [2] | PARK H J, KIM D S, YUN W C. Evaluation of the seismic response of stone pagodas using centrifuge model tests[J]. Bulletin of Earthquake Engineering, 2014, 12(6): 2583–2606. DOI:10.1007/s10518-014-9598-9 |
| [3] |
冉光斌, 林明, 刘小刚, 等.
土工二维振动离心机主机结构的设计[J]. 机械设计与研究, 2015, 31(2): 132–135.
RAN Guang-bin, LIN Ming, LIU Xiao-gang, et al. Research and design to mainframe system of two-dimensional geotechnical centrifugal shaker[J]. Machine Design and Research, 2015, 31(2): 132–135. |
| [4] |
王永志, 袁晓铭, 孙锐.
大型振动离心机设备设计关键技术研究[J]. 世界地震工程, 2011, 27(2): 113–123.
WANG Yong-zhi, YUAN Xiao-ming, SUN Rui. Critical techniques of design for large scale centrifugal shakers[J]. World Earthquake Engineering, 2011, 27(2): 113–123. |
| [5] | 中国机械工程学会、中国机械设计大典编委会. 中国机械设计大典(第2卷):机械设计基础[M]. 南昌: 江西科学技术出版社, 2002: 1247-1317. |
| [6] | ARAKI Y, ASAI T, MASUI T. Vertical vibration isolator having piecewise-constant restoring force[J]. Earthquake Engineering & Structural Dynamics, 2009, 38(3): 1505–1523. |
| [7] | CARRELLA A, BRENNAN M J, KOVACIC I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322(4/5): 707–717. |
| [8] |
马丰伟, 孙玲玲, 宋孔杰, 等.
基于功率流的隔振控制研究[J]. 噪声与振动控制, 2006, 26(4): 14–16.
MA Feng-wei, SUN Ling-ling, SONG Kong-jie, et al. Study on control of vibration isolation with power flow[J]. Noise and Vibration Control, 2006, 26(4): 14–16. DOI:10.3969/j.issn.1006-1355.2006.04.004 |
| [9] |
张春良, 郑文, 梅德庆, 等.
复杂激励环境下精密隔振系统的振动传递率研究[J]. 中国机械工程, 2010, 21(1): 1–5.
ZHANG Chun-liang, ZHENG Wen, MEI De-qing, et al. Research on vibration transmissibility of vibration isolation system with complex vibration environment[J]. China Mechanical Engineering, 2010, 21(1): 1–5. |
| [10] |
钟民军, 胡世峰, 史铁林, 等.
基于状态空间理论单自由度隔振系统性能的研究[J]. 中国机械工程, 2009, 20(9): 1037–1040.
ZHONG Min-jun, HU Shi-feng, SHI Tie-lin, et al. Study on the performance of SDF vibration isolation system based on state-space theory[J]. China Mechanical Engineering, 2009, 20(9): 1037–1040. DOI:10.3321/j.issn:1004-132X.2009.09.008 |
| [11] |
张小龙, 东亚斌.
Duffing型隔振的力传递率及跳跃现象的理论分析[J]. 振动与冲击, 2012, 31(16): 38–42.
ZHANG Xiao-long, DONG Ya-bin. Theoretical analysis on force transmissibility and jump phenomena of Duffing spring type vibration isolator[J]. Journal of Vibration and Shock, 2012, 31(16): 38–42. DOI:10.3969/j.issn.1000-3835.2012.16.008 |
| [12] |
冉光斌, 胡绍全, 刘小刚, 等. 振动离心机隔振系统: CN 201210114859. 6[P]. 2012-09-05.
RAN Guang-bin, HU Shao-quan, LIU Xiao-gang, et al. Vibration isolation system for centrifugal shaker: CN201210114859. 6[P]. 2012-09-05. |
| [13] |
冉光斌, 余绍蓉, 刘小刚, 等.
土工二维振动离心机转臂的设计研究[J]. 工程设计学报, 2013, 20(1): 70–74.
RAN Guang-bin, YU Shao-rong, LIU Xiao-gang, et al. Research and design of swing arm system of two-dimensional geotechnical centrifugal shaker[J]. Chinese Journal of Engineering Design, 2013, 20(1): 70–74. DOI:10.3785/j.issn.1006-754X.2013.01.015 |
| [14] |
冉光斌, 冯英伟, 刘小刚, 等.
土工振动离心机动平衡调节系统的设计研究[J]. 机械设计与研究, 2012, 28(5): 123–126.
RAN Guang-bin, FENG Ying-wei, LIU Xiao-gang, et al. Design to dynamic balance system of geotechnical centrifugal shaker[J]. Machine Design and Research, 2012, 28(5): 123–126. DOI:10.3969/j.issn.1006-2343.2012.05.034 |
| [15] |
罗贤光.
曲囊式橡胶空气弹簧的一些力学问题[J]. 橡胶工业, 1997, 44(4): 228–232.
LUO Xian-guang. Mechanical problems of bellow-type rubber spring[J]. China Rubber Industry, 1997, 44(4): 228–232. |
| [16] | SUN H L, CHEN H B, ZHANG K, et al. Research on performance indices of vibration isolation system[J]. Applied Acoustics, 2008, 69(9): 789–795. DOI:10.1016/j.apacoust.2007.04.005 |
| [17] |
孙伟星, 徐时吟, 黄修长.
基于振动响应的隔振系统力传递率间接估算方法[J]. 噪声与振动控制, 2015, 35(4): 38–42.
SUN Wei-xing, XU Shi-yin, HUANG Xiu-chang. Indirect estimation of force transmissibility in a vibration isolation system based on vibration responses[J]. Noise and Vibration Control, 2015, 35(4): 38–42. |
| [18] |
包承纲, 饶锡保.
土工离心模型的试验原理[J]. 长江科学院院报, 1998, 15(2): 2–7.
BAO Cheng-gang, RAO Xi-bao. Principle of the geotechnical centrifuge model test[J]. Journal of Yangtze River Scientific Research Institute, 1998, 15(2): 2–7. |


