声隐身作为隐身技术的一个重要方面, 在高尖端军事研究领域备受重视,装备的低噪性有助于增强其自身隐蔽性以及反侦察性,例如:为完成某些特殊任务,潜艇在敌方探测设备下犹如“透明”对于侦查情报任务的成功是至关重要的;一直以来,飞行器的降噪问题在飞行器研制过程中扮演着举足轻重的角色。作为降低和控制噪声的一种有效、简单的结构,声衬在航空发动机、内燃机及各类机械设备中已经得到了广泛应用[1-2]。传统声衬的本质是一系列排列整齐的亥姆霍兹共振器, 它的工作频率是由其结构所决定的,且消声选择性强及消声频带过窄,因此这类声衬只对特定的某一较窄频带范围内的噪声敏感,超出该范围后其消声效果迅速减弱,缺乏灵活性。研究表明:通过改变穿孔板的厚度能够有效地调节声衬的消声量并提高抗冲击性;蜂窝腔体的长度决定降噪的频率范围,通过调整腔体高度可控制最大消声频率,已有的可调频式声衬大都采用机械结构进行调频,但在实际应用过程中存在结构复杂、响应速度慢、体积大及不利于安装等缺点,导致其使用受到了很大的限制。例如:空中客车法国分公司研发了一种用于进气道噪声抑制的声衬,在加载驱动电压后,电磁致动器工作,使腔体体积发生变化,从而拓宽了声衬的使用频率[3-9],但是这种声衬的安装较为复杂,不利于实际应用;韩彦南[10]提出了一种双级腔体结构,该结构将共振腔体分为2段,第1段腔体用于增大腔体体积的相对变化率,第2段腔体用于粘接压电片,该结构实现了在未施加电压条件下理论与仿真的误差为0.7%,但他所采用的直径为50 mm的压电片在施加200 V电压时出现了明显的左偏现象,不符合压电片逆压电效应这一原理;基于涡流消声方法,牛凯强[2]设计了压电致动声衬,该声衬具有比传统声衬更强的消声性能,但没有实现声衬消声频带的偏移。
声衬的特殊使用环境,要求声衬必须具有结构简单、占用体积小、响应速度快等优点。因此本文提出一种采用多级柔性壁代替传统声衬单一刚性壁的方法,通过逆压电效应,在柔性壁两端施加电压,通过压电变形改变声衬内部腔体体积,以拓宽其消声频带并实现消声频带的偏移。
1 声衬消声性能评价指标常见的声学性能评价指标有传递损失、插入损失和声压级等。传递损失(transmission loss,TL)与声源和消声管道终端的声学特性无关,只与自身结构有关[11]。故在初步评估系统的消声性能时,传递损失是最简单的一个评价指标。当消声管道进出口满足平面波条件时,传递损失可表示为:
| $ {T_{\rm{L}}} = {L_{{\rm{wi}}}} - {L_{{\rm{wt}}}} = 10\lg \frac{{{w_{\rm{i}}}}}{{{w_{\rm{t}}}}} = 20\lg \frac{{{p_{\rm{i}}}}}{{{p_{\rm{t}}}}} $ | (1) |
式中:Lwi为入射声压级, Lwt为透射声压级, wi为入射声功率, wt为透射声功率, pi和pt分别为入射声压和透射声压。
插入损失(insertion loss, IL)是指一个系统于插入消声元件前后在出口处的声压级差值。与传递损失不同,插入损失与声源和出声口的声学特征有关,故常用来描述整个系统的消声效果[12]。声压级差值(即减噪量)是指系统中任意两点声压级的差值,用LD表示,其定义为在声衬的进口端与出口端测得的平均声压级的差值[7],计算公式为:
| $ {L_{\rm{D}}} = {L_{{p_{\rm{j}}}}} - {L_{{p_{\rm{c}}}}} = 20\lg \frac{{{p_{\rm{j}}}}}{{{p_{\rm{c}}}}} $ | (2) |
式中:Lpj为声衬进口端的平均声压级, dB;Lpc为声衬出口端的平均声压级, dB; pj为进口端声压,Pa;pc为出口端声压,Pa。
若直接用声压级来评价声衬的消声性能,需要在良好的环境下进行实验,否则会造成较大的误差,因此在实验室用声压级来评价声衬的消声效果时,其误差在接受范围内,但在较为嘈杂的环境中,这种评价方法并不适用,并且这种方法未考虑声源的声学特性,而消声管道终端的声学特性会影响到测量值,故该方法在实际工作中不常采用[13-19]。
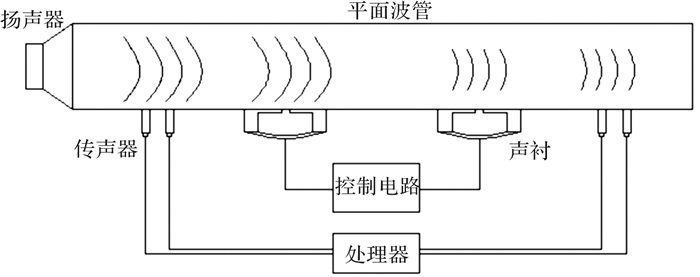
本文采用传递损失作为多级柔性壁声衬的声学性能评价指标。如图 1所示为传递损失测试示意图,消声管道一端为扬声器,另一端为吸声末端,管道中间附有多级声衬。
|
| 图 1 多级柔性壁声衬传递损失测试示意图 Fig.1 Diagram of transmission loss test for multistage flexible wall acoustic liner |
将压电片作为柔性壁代替传统声衬的刚性壁,其消声特性必然会发生改变,通过有限元法分析柔性壁的相关特性。图 2为用ANSYS软件分析得到的柔性壁一到四阶振动模态的有限元仿真结果。

|
| 图 2 柔性壁振动模态的有限元仿真结果 Fig.2 Finite element simulation results of flexible wall vibration mode |
从图 2可以看出,一阶振动模态下柔性壁的变形凸起端部呈轴对称均匀分布,且柔性壁中心点变形最大;二阶振型为一凸一凹的对称曲面;三阶振型为一凸一凹曲面;四阶振型为两凸两凹曲面。二到四阶振动模态下,柔性壁除中心点外其他位置处位移量分布不均且变形量不相同。从图 2可知在柔性壁振动模态有限元仿真中,只有一阶振型适合多级柔性壁声衬消声性能实验。
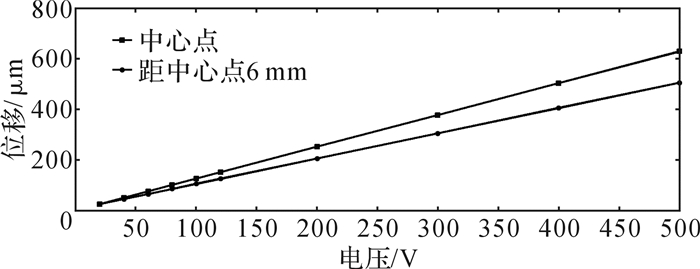
2.2 柔性壁静态仿真分析柔性壁静态分析是指在直流电压的作用下分析电压与柔性壁变形位移之间的关系,以直观反映柔性壁在直流电压下的变形情况。静态仿真时柔性壁参数如表 1所示。通过静态仿真得到的柔性壁在不同电压下中心点和距中心点6 mm处的变形情况如图 3和图 4所示。
|
| 图 3 正向电压下柔性壁变形情况静态仿真结果 Fig.3 Static simulation results of flexible wall deformation under positive voltage |

|
| 图 4 反向电压下柔性壁变形情况静态仿真结果 Fig.4 Static simulation results of flexible wall deformation under reverse voltage |
| 名称 | 材料 | 直径/mm | 厚度/mm |
| 压电陶瓷 | 钛酸钡 | 23 | 0.12 |
| 金属基板 | 黄铜 | 35 | 0.10 |
从静态仿真结果来看,柔性壁具有较好的形变性能,且柔性壁中心点的变形位移和电压成线性关系,且变形位移随电压的增大而增大。
3 多级柔性壁声衬的结构设计 3.1 结构设计的原理和方法多级柔性壁声衬是基于压电技术以声衬为基本单元的消声结构。声衬是由一系列亥姆霍兹共振器组成的,而亥姆霍兹共振器的封闭空腔体积﹑颈部高度以及颈部截面积都是不可改变的,故其消声频率唯一,并且由于其结构形式一定且不可调节,只能在较窄的特定频带内实现振动噪声控制,即在共振频率临界值较小邻域内具有消声效果,其他频率处的消声效果均十分不理想,即消声量基本为零。因此可通过设计多个不同尺寸结构的亥姆霍兹共振器,构成具有较大消声频带的多级声衬结构。该声衬与传统声衬相比,不仅具有较宽的消声频带,还能结合压电片的逆压电效应使得其消声频带发生偏移。亥姆霍兹共振器的结构尺寸参数与其共振频率f之间的关系为:
| $ f = \frac{c}{{2{\rm{ \mathsf{ π} }}}}\sqrt {\frac{{{S_{\rm{c}}}}}{{{{l'}_{\rm{c}}}V}}} $ | (3) |
式中:c为声速,Sc为颈部截面积,l′c为颈部声学高度,V为腔体体积。
多级柔性壁声衬设计方法:根据直径为35 mm的压电片在500 V电压下的形变体积量达到119.81 mm3,将它等效成相同半径的圆柱体,则施加电压之后的声衬等效腔体高度值近似为0.2 mm,以声衬腔体高度作为唯一的变量,以0.2 mm为梯度, 将腔体高度从3 mm依次递减至1 mm,形成11个不同高度的腔体,这样构成腔体高度依次递减,其余参数(颈部高度、颈部半径)相同的多级声衬结构。该声衬在有效拓宽消声频带的同时,其腔体底面积保持不变,腔体体积在施加电压之后发生变化,从而消声频带发生偏移。当外来声波频率与多级柔性壁声衬固有频率相同时,将会产生共振现象,这时振动速度达到最大,颈部空气柱往复运动的机械能转化为内能消耗量达到最大,消声效果达到最佳。
图 5所示为多级柔性壁声衬简化模型,图中lc为颈部高度,lv为空腔高度,位置1, 2分别代表传声管道上、下游,位置3, 4分别为颈部入、出口端面与传声管道和空腔的连接处,位置5为柔性壁面。

|
| 图 5 多级柔性壁声衬简化模型 Fig.5 Simplified model of multistage flexible wall acoustic liner |
已知侧支管道的声阻抗表达式如式(4)所示,为获得多级柔性壁声衬传递矩阵的解析表达式,需求出颈部与传声管道连接处的声阻抗Z3。
| $ \left[ {\begin{array}{*{20}{c}} {{p_1}}\\ {{\rho _0}{S_1}{u_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ {\left( {{S_{\rm{c}}}/c} \right)\left( {1/{Z_3}} \right)}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{p_2}}\\ {{\rho _0}{S_1}{u_2}} \end{array}} \right] $ | (4) |
式中:p1为传声管道上游声压,p2为传声管道下游声压,ρ0为空气密度,S1为传声管道截面积,u1、u2为传声管道上、下游处质点运动速度。
假设声音的传播方式为轴向平面波传播,则有:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{p_3}}\\ {{\rho _0}{S_{\rm{c}}}{u_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \left( {k{{l'}_{\rm{c}}}} \right)}&{{\rm{j}}\left( {c/{S_{\rm{c}}}} \right)\sin \left( {k{{l'}_{\rm{c}}}} \right)}\\ {{\rm{j}}\left( {{S_{\rm{c}}}/c} \right)\sin \left( {k{{l'}_{\rm{c}}}} \right)}&{\cos \left( {k{{l'}_{\rm{c}}}} \right)} \end{array}} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\cos \left( {k{l_{\rm{v}}}} \right)}&{{\rm{j}}\left( {c/{S_{\rm{c}}}} \right)\sin \left( {k{l_{\rm{v}}}} \right)}\\ {{\rm{j}}\left( {{S_{\rm{v}}}/c} \right)\sin \left( {k{l_{\rm{v}}}} \right)}&{\cos \left( {k{l_{\rm{v}}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{p_5}}\\ {\rho {S_{\rm{v}}}{u_5}} \end{array}} \right] \end{array} $ | (5) |
式中:l′c=lc+δ1+δ2,δ1和δ2分别为颈部与传声管道和共振腔连接处的端部修正;p3和p5分别为位置3与位置5处的声压;u3和u5分别为位置3与位置5处质点运动速度;k为波数;Sv为腔体截面积。
结合柔性壁面边界条件u5=0,得到:
| $ \frac{1}{{{Z_3}}} = {\rm{j}}\frac{{\tan \left( {k{{l'}_{\rm{c}}}} \right) + \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}}{{1 - \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{{l'}_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}} $ | (6) |
将式(6)代入式(4),得到:
| $ \left[ {\begin{array}{*{20}{c}} {{p_1}}\\ {{\rho _0}{S_1}{u_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ {{\rm{j}}\frac{{{S_{\rm{c}}}}}{c}\frac{{\tan \left( {k{{l'}_{\rm{c}}}} \right) + \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}}{{1 - \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{{l'}_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{p_2}}\\ {{\rho _0}{S_1}{u_2}} \end{array}} \right] $ | (7) |
声衬进、出口处的温度相同,且进、出口的横截面积也完全相同,则声衬的传递损失计算公式可表示为:
| $ {T_{\rm{L}}} = 20\lg \left\{ {\frac{1}{2}\left| {A + B\left( {\frac{{{S_1}}}{{{c_1}}}} \right) + c\left( {\frac{{{c_1}}}{{{S_1}}}} \right) + D} \right|} \right\} $ | (8) |
式中:c1为传声管道中的声速, A、B、C和D为4级参数。
联立式(7)和式(8),得到多级柔性壁声衬的传递损失表达式为:
| $ {T_{\rm{L}}} = 10\lg \left\{ {1 + {{\left[ {\frac{{{S_{\rm{c}}}}}{{2{S_1}}}\frac{{\tan \left( {k{{l'}_{\rm{c}}}} \right) + \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}}{{1 - \left( {{S_{\rm{v}}}/{S_{\rm{c}}}} \right)\tan \left( {k{{l'}_{\rm{c}}}} \right)\tan \left( {k{l_{\rm{v}}}} \right)}}} \right]}^2}} \right\} $ | (9) |
具体端部修正可以用式(10)计算得出:
| $ {\delta _1} + {\delta _2} = 0.85\left( {1 - 1.25\frac{r}{R}} \right) + 0.85r $ | (10) |
式中:r为颈部半径,R为腔体半径。
3.2 声衬模型建立与实物加工根据声衬结构设计基础及实际消声管道尺寸,为保证实验精度及使共振频率具有更大的变化范围,最终确定多级柔性壁声衬的具体参数:颈部半径为0.6 mm,颈部高度为2 mm,腔体直径为30 mm,腔体外围直径为35 mm,相邻颈部中心距为40 mm,声衬总长为465 mm,声衬截面尺寸为90 mm×90 mm。图 6是新型多级柔性壁声衬结构示意图;图 7是多级柔性壁声衬实物图,其材质为铝合金。

|
| 图 6 多级柔性壁声衬结构示意图 Fig.6 Structure diagram of multistage flexible wall acoustic liner |

|
| 图 7 多级柔性壁声衬实物图 Fig.7 Physical map of multistage flexible wall acoustic liner |
搭建柔性壁性能测试平台, 测试其静、动态特性并分析相关影响因素。实验设备主要有防震实验台、柔性壁、驱动电源以及激光测微仪,具体测试现场图如图 8所示。

|
| 图 8 柔性壁性能测试现场图 Fig.8 Flexible wall performance test site map |
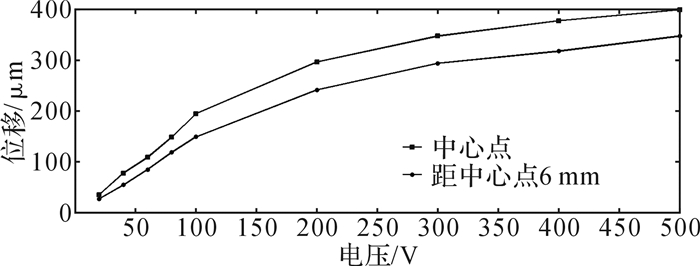
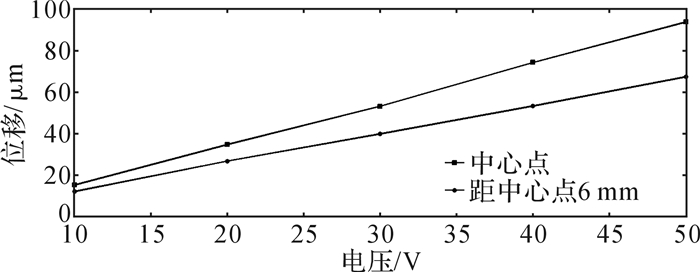
实验测试方法为:使用非接触式测量,用驱动电源对柔性壁施加电信号,激光测微仪对正柔性壁上的测试点,通过激光测微仪记录并显示数据。可对柔性壁施加正、反向电压:压电陶瓷接正极、金属基板接负极为正向电压,金属基板接正极、压电陶瓷接负极为反向电压,并设定正向电压不超过500 V,反向电压不超过50 V。选取柔性壁中心点和距中心点6 mm处呈十字型对称分布的4个点为测试点,测试得到柔性壁的变形特性曲线,实验结果如图 9和图 10所示。
|
| 图 9 正向电压下柔性壁变形情况实验结果 Fig.9 Experimental results of flexible wall deformation under positive voltage |
|
| 图 10 反向电压下柔性壁变形情况实验结果 Fig.10 Experimental results of flexible wall deformation under reverse voltage |
从实验结果来看:当对柔性壁施加电压时,其变形位移随着电压的增大而增大;当对柔性壁施加正向电压时,会出现不规则变化,即呈现非线性分布。对比仿真和实验结果,两者误差不大,验证了仿真结果的正确性。
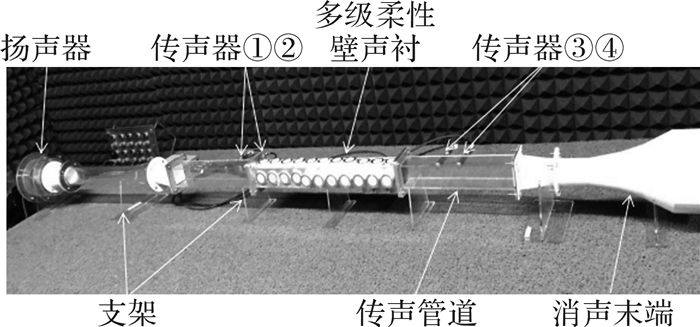
4.2 声衬消声性能测试搭建声衬消声性能测试平台,如图 11所示,测试仪器主要有计算机、功率放大器、扬声器、传声器、传声管道、多级柔性壁声衬、采集卡和消声末端等。通过LabVIEW数据采集程序采集数据后,将数据导入MATLAB软件进行处理得出多级柔性壁声衬的传递损失曲线。
|
| 图 11 多级柔性壁声衬消声性能测试平台 Fig.11 Slience performance test platform for multistage flexible wall acoustic liner |
多级柔性壁声衬消声性能测试的起始频率为1 074 Hz,截止频率为1 583 Hz,测试步长为2 Hz;测试电压范围为-100~200 V,取值间隔为25 V。具体测试结果如图 12所示。

|
| 图 12 多级柔性壁声衬消声性能测试结果 Fig.12 Slience performance test results of multistage flexible wall acoustic liner |
由实验结果可以看出,随着电压的变化,声衬的消声频带发生了明显偏移。在不施加电压时,该多级柔性壁声衬的传递损失曲线在1 386 Hz处达到峰值;当施加100,200 V正向电压时,传递损失峰值频率偏移至1 370,1 364 Hz处。将柔性壁电极反接,在施加-25,-50,-75,-100 V反向电压时,声衬传递损失曲线分别在1 408,1 410,1 416,1 420 Hz处达到峰值。根据上述分析可知,在施加-100~200 V电压时,共振频率偏移了56 Hz,这表明所设计的新型多级柔性壁声衬可以实现消声频带的偏移。
5 结论通过对柔性壁的仿真及实验研究,验证了其良好的形变性能;针对单个腔体声衬消声频带过窄的缺陷,对声衬腔体结构进行了优化,提出采用多级腔体的方法,在保证消声效果的同时,有效拓宽了消声频带。
对所设计的多级柔性壁声衬进行了加工,并对样品进行消声性能测试,结果表明在未施加电压时,多级柔性壁声衬的传递损失曲线在1 386 Hz达到峰值,当分别施加-100, 100及200V电压时,传递损失曲线的峰值频率分别为1 420, 1 370及1 364 Hz。通过调节电压幅值,多级柔性壁声衬的消声频带实现了56 Hz的偏移。
声衬结构与压电片的结合使用为进一步拓宽声衬消声频带范围提供了技术手段,同时为基于声衬结构的噪声控制提供新思路与新方法。
| [1] |
敖庆波, 汤慧萍, 朱纪磊, 等.
航空发动机高温声衬材料的研究现状[J]. 材料导报, 2009, 23(14): 507–509.
AO Qing-bo, TANG Hui-ping, ZHU Ji-lei, et al. Research status of high temperature acoustic liner materials for aeroengine[J]. Materials & Information Review, 2009, 23(14): 507–509. |
| [2] |
牛凯强. 压电致动声衬及其消声性能研究[D]. 太原: 中北大学机械工程学院, 2016: 25.
NIU Kai-qiang. Powder-actuated acoustic liner and its anechoic performance[D]. Taiyuan: North University of China, School of Mechanical Engineering, 2016: 25. |
| [3] |
刘文文. 赫姆霍兹消声器的消声性能研究[D]. 哈尔滨: 哈尔滨工业大学汽车工程学院, 2010: 45-47.
LIU Wen-wen. Study on the muffler performance of the Helmholtz muffler[D]. Harbin: Harbin Institute of Technology, School of Automobile Engineering, 2010: 45-47. |
| [4] |
张立. 基于压电技术的飞机壁板结构振动与噪声控制[D]. 西安: 西北工业大学宇航学院, 2014: 20.
ZHANG Li. Study on vibration control for aircraft structure based on piezoelectric technique[D]. Xi'an: Northwestern Polytechnical University, School of Aeronautics, 2014: 20. |
| [5] |
张京明, 刘文文, 崔双双.
赫姆霍兹消声器共振腔结构形状对消声性能的影响[J]. 四川兵工学报, 2010, 9(2): 79–82.
ZHANG Jing-ming, LIU Wen-wen, CUI Shuang-shuang. Influence of the shape of the resonant cavity of Helmholtz muffler on the noise cancellation performance[J]. Journal of Sichuan Armed Forces, 2010, 9(2): 79–82. |
| [6] |
徐航手, 康钟绪, 季振林.
排气消声器传递损失的实验测量与分析[J]. 噪声与振动控制, 2009, 7(4): 128–131.
XU Hang-shou, KANG Zhong-xu, JI Zhen-lin. Experimental measurement and analysis of transmission loss of exhaust silencers[J]. Noise and Vibration Control, 2009, 7(4): 128–131. DOI:10.3969/j.issn.1006-1355.2009.04.035 |
| [7] |
沈丹东, 马炳和, 邓进军, 等.
压电式微型合成射流器结构参数优化设计[J]. 航空学报, 2011, 15(9): 1755–1760.
SHEN Dan-dong, MA Bing-he, DENG Jin-jun, et al. Optimization design of structural parameters of piezoelectric micro synthetic jet[J]. Acta Aeronautica et Astronautica Sinica, 2011, 15(9): 1755–1760. |
| [8] |
黄志平, 朱敬燕, 杨春.
船舶舱室噪声控制设计措施[J]. 中国水运, 2016, 21(9): 10–11, 14.
HUANG Zhi-ping, ZHU Jing-yan, YANG Chun. Design measures for noise control of ship cabins[J]. China Water Transport, 2016, 21(9): 10–11, 14. |
| [9] |
黄全振.
压电智能结构振动控制系统研究[M]. 北京: 知识产权出版社, 2017: 164.
HUHAG Quan-zhen. Research on vibration control system of piezoelectric smart structure[M]. Beijing: Intellectual Property Publishing House, 2017: 164. |
| [10] |
韩彦南. 可调频声衬及其控制技术研究[D]. 太原: 中北大学机械工程学院, 2017: 65-66.
HAN Yan-nan. The research of tunable piezoelectric acoustic liner and its control[D]. Taiyuan: North University of China, School of Mechanical Engineering, 2017: 65-66. |
| [11] |
余飞. 乘用车消声器设计及试验评价[D]. 武汉: 武汉理工大学汽车工程学院, 2011: 12-16.
YU Fei. Passenger car muffler design and test evaluation[D]. Wuhan: Wuhan University of Technology, School of Automobile Engineering, 2011: 12-16. |
| [12] |
张铁锋. 基于PVDF的智能微夹钳的研究[D]. 武汉: 华中科技大学机械科学与工程学院, 2008: 33-34.
ZHANG Tie-feng. Research on smart micro-clamp based on PVDF[D]. Wuhan: Huazhong University of Science and Technology, School of Mechanical Science and Engineering, 2008: 33-34. |
| [13] |
毕嵘. 复合式消声器声学特性的分析方法和实验研究[D]. 合肥: 合肥工业大学机械工程学院, 2012: 66-68.
BI Rong. Analytical method and experimental study of acoustic characteristics of composite muffler[D]. Hefei: Hefei University of Technology, School of Mechanical Engineering, 2012: 66-68. |
| [14] |
季振林.
消声器声学理论与设计[M]. 北京: 科学出版社, 2015: 27-32.
JI Zhen-lin. Acoustic theory and design of mufflers[M]. Beijing: Science Press, 2015: 27-32. |
| [15] |
阚君武, 唐可洪, 王淑云, 等.
压电悬臂梁发电装置的建模与仿真分析[J]. 光学精密工程, 2008, 18(1): 71–75.
KAN Jun-wu, TANG Ke-hong, WANG Shu-yun, et al. Modeling and simulation analysis of piezoelectric cantilever beam generator[J]. Optics and Precision Engineering, 2008, 18(1): 71–75. DOI:10.3321/j.issn:1004-924X.2008.01.013 |
| [16] |
邓进军, 苑伟政, 罗剑.
MEMS技术在流动分离主动控制中的应用[J]. 西北工业大学学报, 2010, 28(3): 381–387.
DENG Jin-jun, YUAN Wei-zheng, LUO Jian. Two MEMS actuators for application-oriented active control of flow separation[J]. Journal of Northwestern Polytechnical University, 2010, 28(3): 381–387. DOI:10.3969/j.issn.1000-2758.2010.03.014 |
| [17] |
赵斌兴. 基于压电检测的光声技术研究[D]. 成都: 电子科技大学光电信息学院, 2015: 45.
ZHAO Bin-xing. Photoacoustic technology based on piezoelectric detection[D]. Chengdu: University of Electronic Science and Technology of China, School of Optoelectronic Information, 2015: 45. |
| [18] |
张颖异, 李运刚, 田颖.
先进发动机高温材料的研究进展[J]. 飞航导弹, 2011(12): 73–77.
ZHANG Ying-yi, LI Yun-gang, TIAN Ying. Research progress on advanced engine high temperature materials[J]. Aerospace Missile, 2011(12): 73–77. |
| [19] |
吕海峰, 潘宏侠, 黄晋英.
一种调频式共振消声器的设计[J]. 振动、测试与诊断, 2012, 10(6): 1021–1025, 1041.
LÜ Hai-feng, PAN Hong-xia, HUANG Jin-ying. Design of a frequency-modulated resonance muffler[J]. Vibration, Test and Diagnosis, 2012, 10(6): 1021–1025, 1041. DOI:10.3969/j.issn.1004-6801.2012.06.028 |



