2. 北京航空航天大学 自动化科学与电气工程学院, 北京 100191
2. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China
在汽车电动座椅组装完成后,需要调整其位姿以满足相应的企业标准。目前,只能通过人工并借助激光测距仪来进行座椅位姿的调整,调整时直接以激光测距仪所测数值为参考,先拨动调整座椅位姿开关依次使各固定的激光测距仪所测的值达到经验值,然后再依次拨动各开关使激光测距仪的测量值达到参考值,但由于存在耦合现象(即一个开关的拨动会影响多个激光测距仪的测量值),会使得调节过程中已调到参考值的激光测距仪的数值发生改变,甚至超出其公差要求,因此需反复拨动各开关以完成位姿的调整,导致调整过程耗时长,生产效率低下。
现有的多自由度机构位姿的求解多是通过视觉测量、激光跟踪等空间测量技术,测量机构特征点在参考坐标系和机构连体坐标系中的坐标值,将机构位姿求解问题转变为2个坐标系之间的点匹配问题。丁雅斌等[1]提出一种基于单目摄像机拍摄立体靶标序列图像信息的末端执行器六维位姿误差辨识方法,通过构造具有平行四边形几何约束的4个空间特征点,并以平行四边形的2个消隐点为约束,建立空间刚体位姿与其二维图像映射关系模型,实现末端位姿的精确定位。李海涛等[2]提出一种数控机床几何精度的位姿测量原理和几何误差分离原理,通过一台固定于机床上的数控精密转台和一台激光跟踪仪获得了机床运动轴的位姿信息。采用机器视觉的方法来进行机构的位姿检测可以获得很高的检测精度,但需处理大量的图像信息[3],效率低,不能满足实时检测的要求。在多自由度机构上张贴红色标签等醒目特征虽然能提高检测速度[4],但对标签的张贴位置又有很高的精度要求,这样反而会增加检测、调整的难度。
本文通过激光测距仪测量汽车电动座椅表面部分点的坐标信息[5-7],根据座垫表面的拟合曲线和座椅的几何结构,建立参考坐标系并分析座椅外部轮廓上点的坐标与各驱动关节的转角和位移之间的数学关系[8],据此计算出座椅的实时位姿并给出座椅位姿调整方案,实现座椅位姿准确、高效的调整,并通过仿真和实验来验证所提方法的可行性。
1 汽车电动座椅结构及其出厂位姿标准 1.1 汽车电动座椅结构组成汽车电动座椅主要由四大机构组成:调整座椅前后位置的滑轨机构、调整座椅整体高度的四杆机构、调整座椅前端高度的摆动导杆机构和调整靠背倾角的调角器机构。各机构的驱动机构均具有自锁功能。
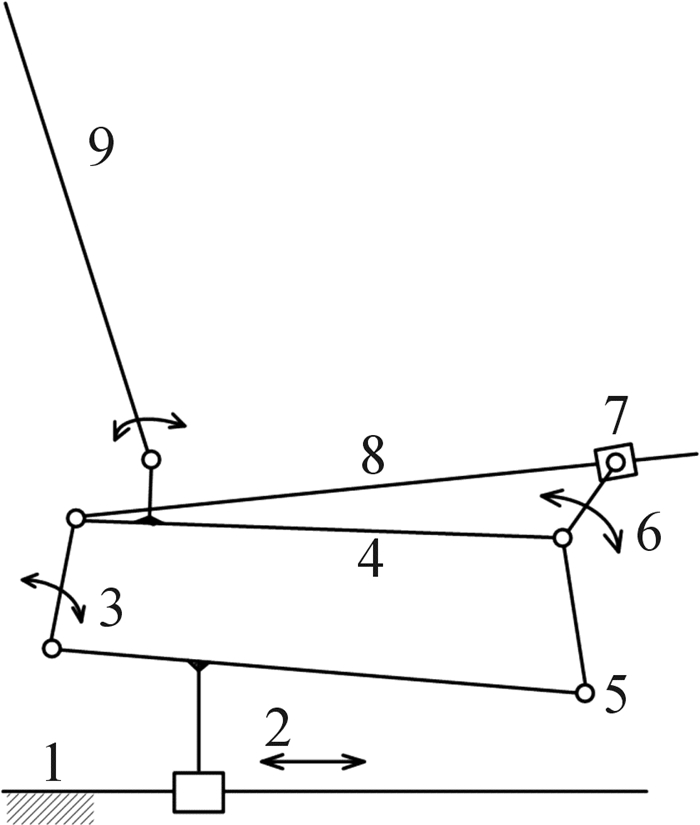
图 1为汽车电动座椅结构组成示意图。图中:座椅机架1和基座滑块2组成滑轨机构,用于调整座椅前后位置;2,3,4和5组成四杆机构,用于调整座椅高度,其中连杆3为驱动杆;摆动导杆机构用于调整座椅前端高度,它以曲柄摇杆机构的连杆4为机架,座垫驱动杆6为主动杆,通过驱动滑块7在一定范围内移动,使得摇杆8升降;靠背9与连杆4通过转动副相连,其倾角可在一定范围内调整。
|
| 1—机架;2—基座滑块;3—基座驱动杆;4—基座连杆;5—基座连架杆;6—座垫驱动杆;7—座垫滑块;8—座垫摇杆;9—靠背 图 1 汽车电动座椅结构组成示意图 Fig.1 The schematic diagram of automobile electric seat structure composition |
各个汽车厂商的汽车电动座椅出厂位姿标准不尽相同,本文以某汽车厂的汽车电动座椅出厂位姿标准作为所提座椅位姿调整方法的评价标准,具体如表 1所示。与表 1所定位姿等价的基于各驱动关节的转角或位移的座椅出厂位姿标准如表 2所示,其中:H1为座椅出厂时的位移,H2与H3分别为座椅出厂时座垫前后与机架之间的高度,α、β、θ分别为座椅出厂时各个驱动关节的转角。
| 参数 | H1/mm | H3-H2/mm | θ/(°) |
| 标准值及公差 | 0-5+0 | 40-5+5 | 8-4+4 |
| 参数 | H1/mm | α/(°) | β/(°) | θ/(°) |
| 标准值及公差 | 0-5+0 | 65-5+5 | 50-7+7 | 8-4+4 |
座椅位姿由各驱动关节的转角或位移决定,求出当前位姿下各驱动关节的转角或位移,对照座椅出厂位姿标准所确定的各驱动关节的转角或位移目标值进行座椅位姿的调整。
针对座椅传动机构的转角和位移不能直接测量以及调整过程中位姿的耦合问题,采用控制变量法调整座椅位姿,每次只调整一个驱动关节,因为同一时刻调整的关节变量少,所以可以通过激光测距仪所测得的位置坐标值结合座椅几何结构和座垫表面的拟合曲线计算出该关节的转角或位移,进而将该关节调整至标准位置。座椅为多自由度串联机构,而串联机构的耦合只存在于前端连杆的转动或移动对后端连杆位姿的影响[5],所以在进行座椅位姿调整时,从前端到末端依次调整各驱动关节的转角或位移则可以消除机构耦合对座椅调整的不利影响。
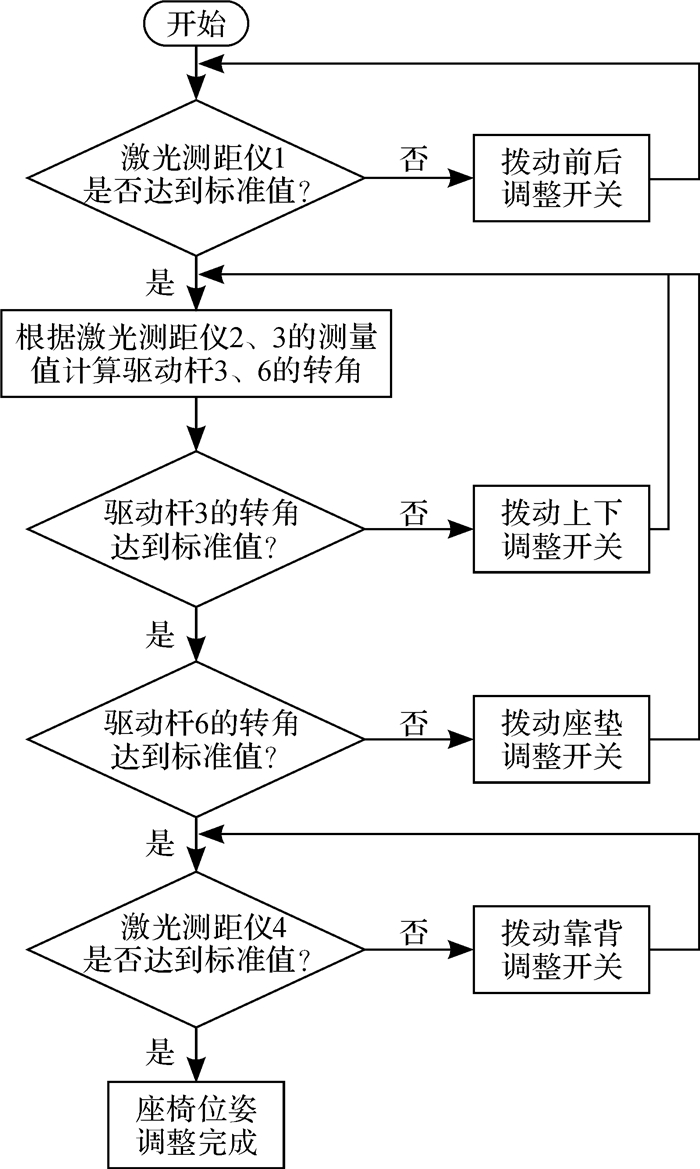
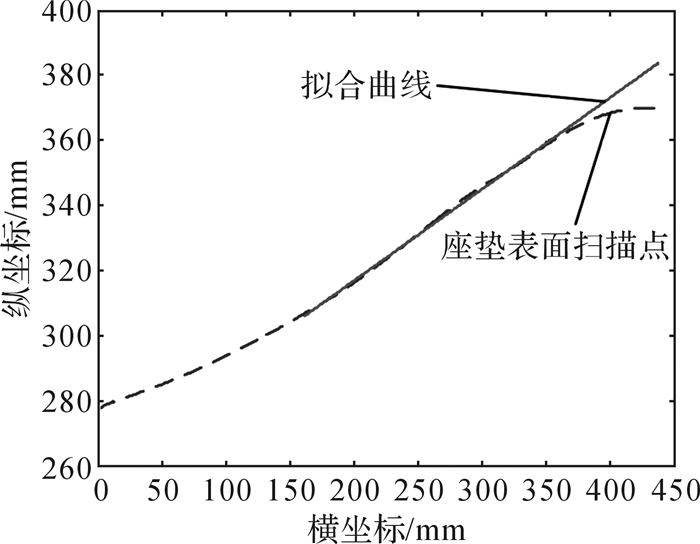
2.2 座椅几何结构分析与模型的建立 2.2.1 座垫表面的拟合曲线电动座椅的运动是在对称平面内的平面运动。座垫曲面与对称平面的交线为曲线,通过Leica AT901-MR型激光跟踪仪测量对称平面内座垫表面的曲线。对用激光测距仪采集到的坐标值作曲线拟合,得到的座垫表面的拟合曲线,如图 2所示。座垫表面拟合曲线和实测曲线之间的误差如图 3。在实际座椅位姿调整过程中,激光测距仪所测得的座椅的位移变化范围在[150, 450] mm(之前已完成滑轨的调整,因此激光测距仪所测范围较小),所以只对该范围内的点作曲线拟合。拟合结果表明:座垫表面拟合曲线与实测曲线的误差在-1~1 mm内,远小于标准所允许的公差。

|
| 图 2 汽车电动座椅座垫表面的拟合曲线 Fig.2 Fitting curve of cushion surface of automobile electric seat |
|
| 图 3 汽车电动座椅座垫表面的拟合曲线与实测曲线的误差 Fig.3 Error of fitting curve and measured curve of cushion surface of automobile electric seat |
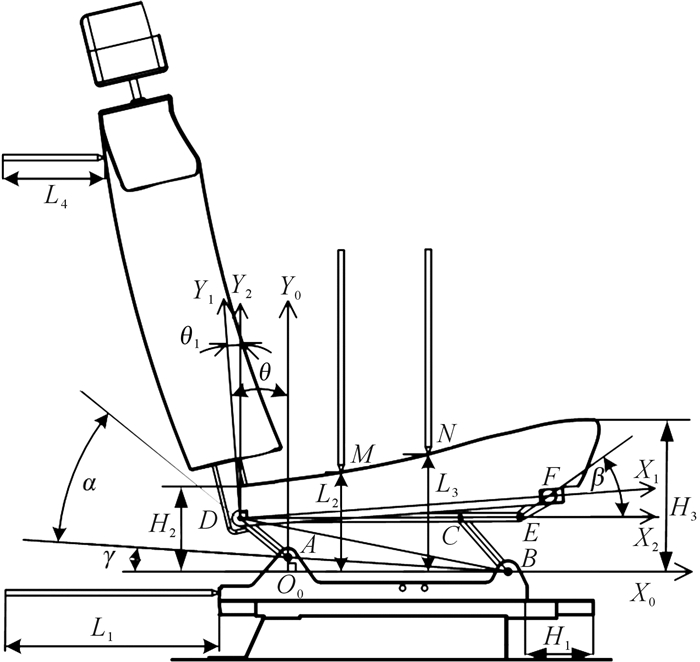
图 4为电动座椅的几何结构示意图,图中的2个横杆和2个竖杆分别表示相应激光测距仪发射的激光。为求解各结构之前的几何关系,如图 4建立3个坐标系:X0O0Y0、X1O1Y1及X2O2Y2。其中:坐标系X0O0Y0与连杆2固连,X0轴沿水平方向且过基座滑块2的铰链中心B,Y0轴过基座滑块2的铰链中心A;坐标系X1O1Y1与座垫摇杆8固连,X1轴与座垫摇杆8的铰链中心D、F的连线重合,O1与D点重合;坐标系X2O2Y2与连杆4固连,X2轴与座垫摇杆的铰链中心D、E的连线重合,O2与D点重合。图中:θ为Y1轴和Y2轴的夹角;α为EF和DE延伸线的夹角,β为AD和BA延伸线的夹角,α、β为需要求解的座垫上两驱动关节的转角;γ为A、B连线相对于水平线的倾角,为常值;M、N两点为激光测距仪投射到座垫表面上的点,L2和L3为激光测距仪所测点在坐标系X0O0Y0中的纵坐标。图 4中各点之间连线AB、AD、BD、CD、BC、OA、DE和EF的长度已知。
|
| 图 4 座椅的几何结构图 Fig.4 The geometric structure of the seat |
座垫表面的拟合曲线的方程可表示为:
| $ y={{k}_{1}}\cdot x+{{b}_{1}} $ | (1) |
式中:k1为拟合曲线在坐标系X1O1Y1中的斜率, k1=0.2815,b1=260.552 9。
1) 座垫与水平面之间的夹角θ。
座垫表面的拟合直线相对于X1轴的倾角为:
| $ \varepsilon =\text{arctan}\ {{k}_{1}} $ | (2) |
座垫表面的拟合直线相对于X0轴的倾角为:
| $ {{\theta }_{0}}=\text{arctan}(\frac{{{Y}_{N0}}-{{Y}_{M0}}}{{{X}_{N0}}-{{X}_{M0}}}) $ | (3) |
可求得:
| $ \theta ={{\theta }_{0}}-\varepsilon =\text{arctan}(\frac{{{Y}_{N0}}-{{Y}_{M0}}}{{{X}_{N0}}-{{X}_{M0}}})-\text{arctan}{{k}_{1}} $ | (4) |
式中:(XM0, YM0)为点M在坐标系X0O0Y0中的坐标; (XN0, YN0)为点N在坐标系X0O0Y0中的坐标。
2) 座垫上前驱动关节的转角α。
坐标系X0O0Y0与坐标系X1O1Y1之间的映射关系为:
| $ \left\{ \begin{array}{l} {x_0} = {x_1}\cdot{\rm{cos}}\theta-{y_1}\cdot{\rm{sin}}\theta + a\\ {y_0} = {y_1}\cdot{\rm{cos}}\theta-{x_1}\cdot{\rm{sin}}\theta + b\\ a =-{L_{AD}}\cdot{\rm{cos}}\left( {\alpha + \gamma } \right)\\ b = - {L_{AD}}\cdot \sin\left( {\alpha + \gamma } \right)\\ {y_1} = {k_1}\cdot{x_1} + {b_1} \end{array} \right. $ | (5) |
式中:(a, b)为O1在坐标系X0O0Y0中的坐标;LAD为连线AD的长度。
将(XM0, YM0)、γ及LAD代入式(5),得:
| $ \begin{array}{l} \alpha =- \gamma- {\rm{arcsin}}(\frac{{{\rm{sin}}{k_1} + \theta \cdot{\rm{cos}}{k_1}}}{\zeta }) + \\ {\rm{arcsin}}\left[{\frac{{\mu \cdot\left( {{Y_{M0}}-{L_{OA}}} \right)-{X_{M0}}\cdot\left( {\nu-{b_1}} \right)}}{{{L_{AD}}\cdot\zeta }}} \right] \end{array} $ | (6) |
其中:
| $ \begin{array}{l} \zeta = \sqrt {{\mu ^2} + {\nu ^2}} \\ \mu = {\rm{cos}}{k_1}-\theta \cdot{\rm{sin}}{k_1}\\ \nu = {\rm{sin}}{k_1}-\theta \cdot{\rm{cos}}{k_1} \end{array} $ |
式中:μ、ν、ζ为中间变量。
3) 座垫上后驱动关节的转角β。
依据正弦定理求β。
| $ \left\{ \begin{array}{l} \theta = {\theta _1} + {\theta _2}\\ {\theta _2} = \angle ADB + \angle BDC-\alpha-\gamma \\ \beta = {\rm{arcsin}}(\frac{{{L_{DF}}\cdot{\rm{sin}}{\theta _2}}}{{{L_{EF}}}})\\ {L_{BD}} = \sqrt {{L_{AB}}^2 + {L_{AD}}^2 + 2\cdot{L_{AD}}\cdot{L_{AB}}\cdot{\rm{cos}}\alpha } \\ \angle ADB = {\rm{arccos}}(\frac{{{L_{AD}}^2 + {L_{BD}}^2-{L_{AB}}^2}}{{2\cdot{L_{BD}}\cdot{L_{AD}}}})\\ \angle BDC = {\rm{arccos}}(\frac{{{L_{CD}}^2 + {L_{BD}}^2 - {L_{BC}}^2}}{{2\cdot{L_{BD}}\cdot{L_{CD}}}})\\ {L_{DF}} = {L_{DE}}\cdot{\rm{cos}}{\theta _1} + \sqrt {{{({L_{DE}}\cdot{\rm{cos}}{\theta _1})}^2} + {L_{EF}}^2 - {L_{DE}}^2} \end{array} \right. $ | (7) |
由式(7)解得:
| $ \begin{array}{l} \beta = {\rm{arcsin}}\left[{\frac{1}{{{L_{EF}}}}\cdot({L_{DE}}\cdot{\rm{cos}}{\theta _1} + } \right.\\ {\left. {\sqrt {{{({L_{DE}}\cdot{\rm{cos}}{\theta _1})}^2} + {L_{EF}}^2-{L_{DE}}^2} } \right]^2} \end{array} $ | (8) |
1) 激光测距仪布置。
由图 1可知,座椅是一个平面机构,因而激光测距仪均布置在座椅的对称平面内。为实现在每个驱动关节调整时都有一个激光测距仪反馈信号,在各个驱动关节均布置一个激光测距仪。激光测距仪的布置如图 5所示,激光测距仪1用于测滑轨的位置,2和3用于测座垫表面的位置,激光测距仪4用于测靠背的位置,且激光测距仪2、3和4均位于对称平面内。
|
| 图 5 激光测距仪的布置 Fig.5 The layout of laser rangefinder |
2) 调整流程。
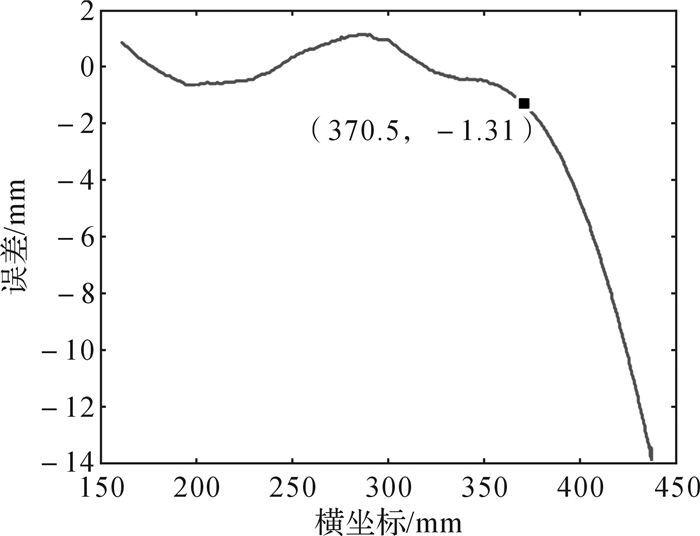
汽车电动座椅位姿调整流程如图 6所示。
|
| 图 6 汽车电动座椅位姿调整流程 Fig.6 Position and orientation adjustment flow for automobile electric seat |
本文通过ADAMS和MATLAB/Simulink建立座椅的虚拟样机仿真系统,进行联合仿真验证[6-8]。
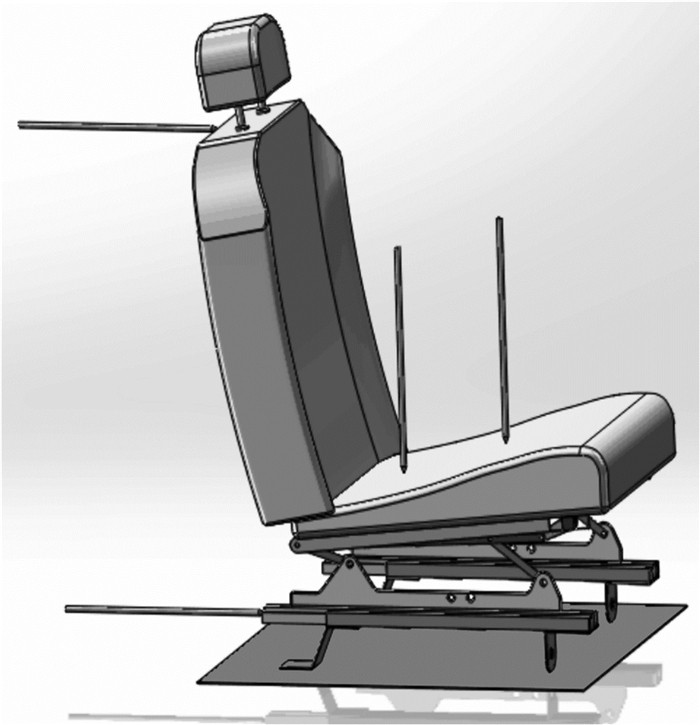
利用SolidWorks建立汽车电动座椅三维模型[9],如图 7所示。将该模型导入ADAMS中,设置基本参数,添加必要的运动副;之后再添加4根推杆在各自运动方向的位移值L1、L2、L3及L4,这4个变量作为ADAMS模块输出至MATLAB/Simulink的输出变量[10]。在水平导轨上添加牵引力,在曲柄摇杆机构的曲柄上添加旋转扭矩T1,在基座驱动杆上添加旋转扭矩T2,在靠背的旋转副上添加扭矩T3, 这4个变量作为由MATLAB/Simulink输入至ADAMS的输入变量[11]。
|
| 图 7 汽车电动座椅三维模型 Fig.7 3D model of the automobile eletctric seat |
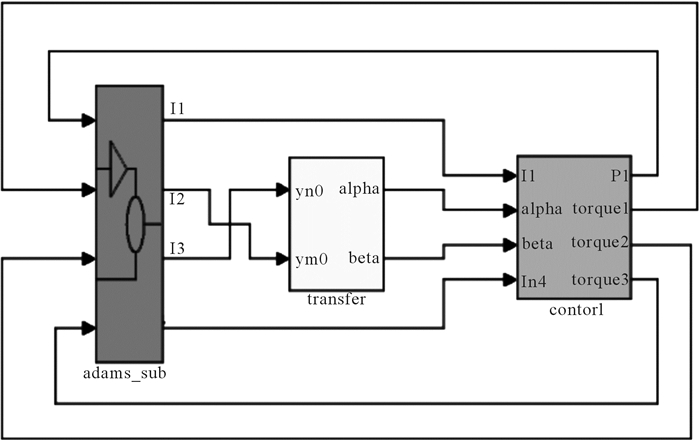
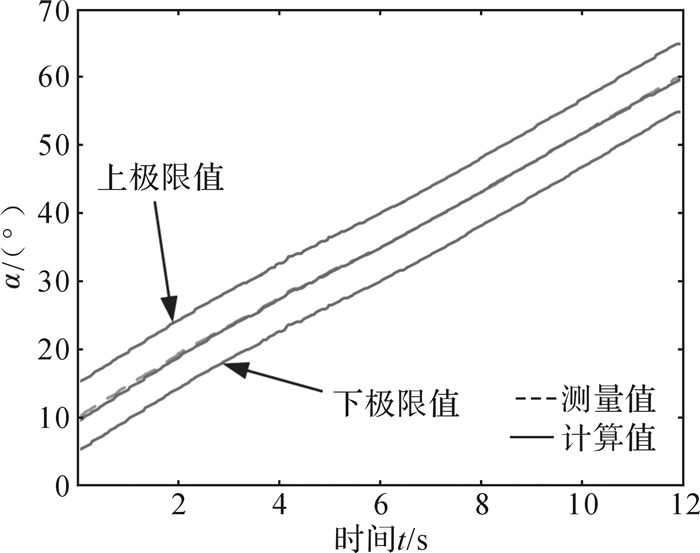
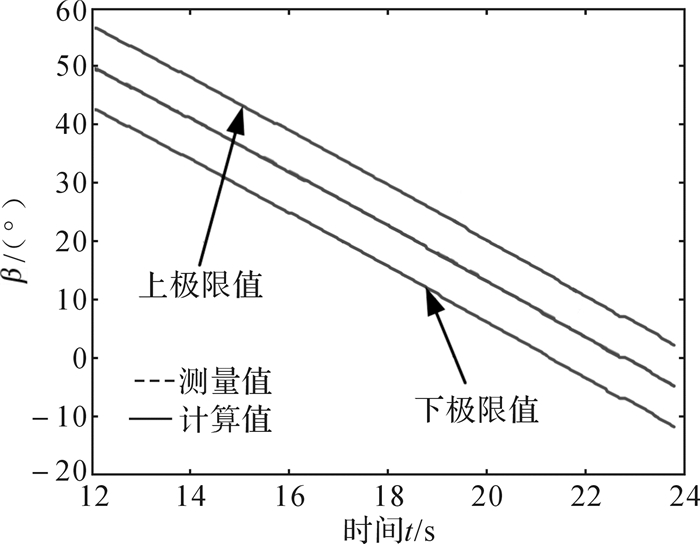
根据上述座椅位姿的调节方法、座椅各机构转角的求解公式(4)、(6)、(8)以及座垫表面的拟合曲线方程(1),在MATLAB/Simulink中建立系统的控制模型[9, 12],如图 8,控制模型可以接收到ADAMS采集到的L1、L2、L3和L4并输出座椅位姿的数据。座垫上的2个驱动关节的转角α和β的测量值和仿真计算值分别如图 9和图 10所示(因为滑轨的位移可以直接测量,靠背的调整基于座垫调整,所以座椅位姿调整的精度取决于座垫上2个驱动关节转角的精度)。
|
| 图 8 汽车电动座椅虚拟样机仿真系统控制模型 Fig.8 Control model of virtual prototype simulation system for automobile electric seat |
|
| 图 9 转角α的测量值与仿真计算值比较 Fig.9 Comparison between measured value and simulated value of the angle α |
|
| 图 10 转角β的测量值与仿真计算值比较 Fig.10 Comparison between measured value and simulated value of the angle β |
由图 9和图 10可知,在调整的角度范围内,测量值与计算值之差满足座椅出厂位姿标准所允许的公差要求。
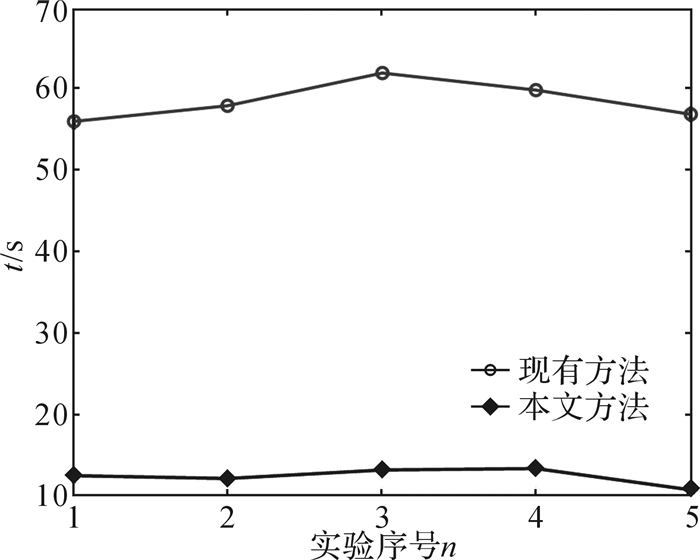
3.2 实验验证汽车电动座椅位姿调整装置[13-15]如图 11所示,根据本文提出的调整方法进行座椅位姿的调整。在各转动关节上加装磁编码器AS5040(分辨率为10位),用于测量各关节的实际转角。在实验过程中,将座椅调整至任意一初始位姿,在控制系统中输入目标位姿,进行自动位姿调整,调整完成后磁编码器所测转角和位移与目标转角和位移的关系如表 3,其中αT、βT表示测量值,αC、βC表示计算值。由于标准所允许的公差较大,所以所测数据仅保留小数点后一位。比较本文所提出的调整方案与现有调整方案完成相同的调整过程所用的时间,如图 12所示。

|
| 图 11 汽车电动座椅位姿调整装置 Fig.11 Position and orientation adjustment device for the automobile electric seat |
|
| 图 12 不同方法下座椅位姿调整时间对比 Fig.12 Comparison of seat position and orientation adjustment time obtained by different methods |
| 实验序号 | L1/mm | L2/mm | L3/mm | L4/mm | αT/(°) | αC/(°) | |Δα|/(°) | βT/(°) | βC/(°) | |Δβ|/(°) |
| 1 | 122.3 | 91.4 | 152.6 | 127.4 | 50.0 | 50.6 | 0.6 | 44.1 | 43.2 | 0.9 |
| 2 | 78.0 | 90.6 | 125.8 | 155.7 | 50.0 | 50.4 | 0.4 | 42.1 | 41.2 | 0.9 |
| 3 | 125.5 | 78.3 | 118.0 | 223.7 | 36.4 | 35.7 | 0.7 | 25.2 | 24.2 | 1.0 |
| 4 | 88.5 | 109.7 | 138.5 | 112.9 | 82.7 | 82.1 | 0.6 | 30.1 | 29.2 | 0.9 |
| 5 | 151.5 | 106.5 | 127.0 | 156.1 | 48.5 | 48.0 | 0.5 | 40.1 | 38.9 | 1.2 |
按本文所提方法进行座椅出厂位姿调整,是通过目标值与计算值的比较来进行座椅各角度或位移的调节,直至计算值与目标值相等。由实验数据可知,测量值与计算值之差符合企业标准所允许的公差要求,即各关节的转角满足出厂标准;同时采用本文方法进行座椅位姿调整可明显提高座椅出厂位姿调整的效率。实验中出现的误差主要来自两方面:1)对座垫表面进行曲线拟合时产生的误差;2)不同于生产线上的机械定位,实验环境下座椅初始位置的摆放和激光测距仪固定的位置是通过人工定位的,在座椅摆放时易受人的主观因素的影响,进而造成不确定误差。但是,上述因素造成的α、β的绝对误差的期望值为0.56°和0.98°,绝对误差的方差分别为0.013°和0.017°,远小于出厂标准要求的5°和7°,不会影响座椅出厂检验的合格性。
4 结论1) 本文提出了基于控制变量法的座椅位姿调整方法,通过4步调整即可完成座椅的位姿调整,并通过仿真和实验进行了验证。
2) 实验结果表明,虽然调整过程中存在误差,但能满足工程精度要求。
3) 相较于现行的调整方法,本文提出的调整方法简单可行,可显著提高座椅调整的工作效率。
4) 本文所进行的分析、仿真及实验是针对某一型号的座椅进行的,对于有不同传动机构、自由度的座椅,需重新进行座垫表面曲线拟合以及座椅几何结构分析。同时,因为电动座椅的前后移动、升降、靠背倾角、座椅长度扶手位置等调节结构是依次串联设计的,所以根据本文所提的方法从起始端向末端依次调整,可避免输出耦合,通过对座椅几何结构的分析改变相应的传感器的布置位置和数量逐一完成相应关节转角或位移的求解,就可以按本文提出的调整方法完成座椅位姿调整。
| [1] |
丁雅斌, 梅江平, 张文昌, 等.
基于单目视觉的并联机器人末端位姿检测[J]. 机械工程学报, 2014, 50(21): 174–179.
DING Ya-bin, MEI Jiang-ping, ZHANG Wen-chang, et al. Position and orientation measurement of parallel robot based on monocular vision[J]. Journal of Mechanical Engineering, 2014, 50(21): 174–179. |
| [2] |
李海涛, 郭俊杰, 邓玉芬, 等.
数控机床几何精度的位姿测量原理[J]. 西安交通大学学报, 2016, 50(11): 62–68.
LI Hai-tao, GUO Jun-jie, DENG Yu-fen, et al. Pose measuring principle of geometric accuracy of numerical control machine tools[J]. Journal of Xi'an Jiaotong University, 2016, 50(11): 62–68. DOI:10.7652/xjtuxb201611010 |
| [3] | ANDREFF N, MARTINET P. Unifying kinematic modeling, identification and control of a Gough-Stewart, parallel robot into a vision-based framework[J]. IEEE Transactions on Robotics, 2006, 22(6): 1077–1086. DOI:10.1109/TRO.2006.882931 |
| [4] |
孙美霞, 任立红, 韩华, 等.
基于立体视觉的串联机器人跟踪检测系统[J]. 计算机工程, 2012, 38(13): 240–243.
SUN Mei-xia, REN Li-hong, HAN Hua, et al. Series robot tracking detection system based on stereo vision[J]. Computer Engineering, 2012, 38(13): 240–243. DOI:10.3778/j.issn.1002-8331.2012.13.051 |
| [5] |
张建亮, 周建忠, 罗敬文, 等.
汽车座椅调角器激光焊接工艺研究[J]. 应用激光, 2015, 35(2): 216–220.
ZHANG Jian-liang, ZHOU Jian-zhong, LUO Jing-wen, et al. Study on laser welding technology of automobile seat recliner[J]. Applied Laser, 2015, 35(2): 216–220. |
| [6] |
张振久, 胡泓.
基于激光跟踪仪的转台系统几何误差检测[J]. 中国激光, 2012, 39(11): 180–186.
ZHANG Zhen-jiu, HU Hong. Measurement of geometric error of rotary stage system based on laser tracker[J]. Chinese Journal of Lasers, 2012, 39(11): 180–186. |
| [7] |
杨凡.
激光跟踪仪测距精度评定方法研究[J]. 测绘通报, 2013(S1): 273–275.
YANG Fan. Laser tracker ranging accuracy evaluation method research[J]. Bulletin of Surveying and Mapping, 2013(S1): 273–275. |
| [8] |
熊有伦, 丁汉, 刘恩沧.
机器人学[M]. 北京: 机械工业出版社, 1993: 65-70.
XIONG You-lun, DING Han, LIU En-cang. Robotics[M]. Beijing: Mechanical Industry Press, 1993: 65-70. |
| [9] |
郑黎明, 黄剑波.
基于ADAMS和Simulink的太阳跟踪器联合仿真[J]. 光学精密工程, 2014, 22(5): 1212–1219.
ZHENG Li-ming, HUANG Jian-bo. Co-simulation of solar tracker based on ADAMS and Simulink[J]. Optics and Precision Engineering, 2014, 22(5): 1212–1219. |
| [10] | ZHU X, LIU Z, YANG J. Research on co-simulation method in ADAMS and MATLAB for missile seeker's stabilization platform design[C]//Proceedings of 13th International Conference on Systems Simulation, Singapore, Nov. 6-8, 2013. |
| [11] | WANG Y, LI K, ZHOU H, et al. Dynamic analysis and co-simulation ADAMS-Simulink for a space manipulator joint[C]//International Conference on Fluid Power and Mechatronics, Harbin, Aug. 5-7, 2015. |
| [12] |
郭卫东, 李守忠, 马璐.
ADAMS 2013应用实例精解教程[M]. 北京: 机械工业出版社, 2015: 234-264.
GUO Wei-dong, LI Shou-zhong, MA Lu. ADAMS 2013 application examples of fine tutorial[M]. Beijing: Mechanical Industry Press, 2015: 234-264. |
| [13] |
赵波, 李博.
汽车座椅高度调整机构开发与应用[J]. 机械设计与制造, 2012(4): 83–85.
ZHAO Bo, LI Bo. Development and application of height adjusting mechanism of automobile seat[J]. Machinery Design & Manufacture, 2012(4): 83–85. DOI:10.3969/j.issn.1001-3997.2012.04.031 |
| [14] |
杜宝江, 唐红朋, 程建建, 等.
可变环境下汽车座椅可控重复测试系统的设计与研究[J]. 现代制造工程, 2014(9): 55–58.
DU Bao-jiang, TANG Hong-peng, CHENG Jian-jian, et al. Design and research on the retest system for car seats in variable environment[J]. Modern Manufacturing Engineering, 2014(9): 55–58. DOI:10.3969/j.issn.1671-3133.2014.09.012 |
| [15] |
吴彦强, 张若青, 刘冰.
汽车座椅检测装置的研制[J]. 测控技术, 2013, 32(3): 120–123.
WU Yan-qiang, ZHANG Ruo-qing, LIU Bing. Development of the car seat detection device[J]. Measurement & Control Technology, 2013, 32(3): 120–123. DOI:10.3969/j.issn.1000-8829.2013.03.029 |


