2. 四川宝石机械专用车有限公司, 四川 广汉 618300;
3. 长江大学 资源与环境学院, 湖北 武汉 430100
2. Sichuan Baoshi Special Vehicle Machinery Co., Ltd., Guanghan 618300, China;
3. College of Resources and Environment, Yangtze University, Wuhan 430100, China
钻井作业中会产生大量的钻井液、岩屑以及落地油(钻井及完井作业过程中因管外漏、钻杆等粘附而带出的原油)等废弃物,这些废弃物的直接排放会对地下水以及周边生态环境造成严重污染[1-3]。振动筛是对井口返回钻井液进行最基本处理的常规固相控制设备,是一种过滤性的机械分离设备。振动筛作为井口返回钻井液处理工序的第1道设备,其筛分效率非常重要。钻井液回收、岩屑干燥以及HSE(health safety environment,健康、安全、环境)管理体系要求是提高振动筛筛分效率需要关注的3个因素。提高振动筛筛分效率的关键是提高振动筛振动强度,但是振动筛强度的提高会造成钻井液飞溅,同时,岩屑等固相颗粒对筛网的冲击也会随之增大,使得筛网寿命缩短。因此国内外技术人员开始致力于研究新型钻井液振动筛[4-6]。
在钻井液固液分离作业中使用固相控制设备可以追溯到20世纪早期,利用重力从钻井液中分离出页岩和颗粒物的技术已经成功用于全球钻探工艺[7-12]。近年来的研究指出,振动筛固液分离作业中最关键的技术是使用气流。Mud-Cube公司的固相控制系统采用真空传送带技术(vacuum conveyer belt technology)取代了自20世纪30年代以来一直沿用的机械振动法来分离钻井液中的固相颗粒,这一方法具有更高的过滤效率。MI-SWACO公司的产品理念是为所有钻井环境设计高性能振动筛,为所有陆上和海上的钻探工作提供先进的振动筛方案。他们提出了负压振动筛的概念,他们关注的是:真空系统在振动筛内提供气流从而产生压差,这不仅可以加快岩屑上流体的去除,而且能够减少有害气体的排放[13-14]。然而,其方案存在的问题是:负压虽然使钻井液获得了除振动惯性力和重力外的透筛能力,但可能会造成糊筛;为了改进固相颗粒输送振动筛的结构,增加了成本。
综上所述,本文基于理论力学和固相颗粒在振动筛上的运移规律[15-17],主要研究单颗粒在负压振动筛上的运移规律,并建立单颗粒的动力学方程。同时讨论各种参数对固相颗粒运移速度的影响,以及固相运移状态一致的情况下振动筛参数的变化,为负压振动筛的结构设计和参数选择提供理论依据。
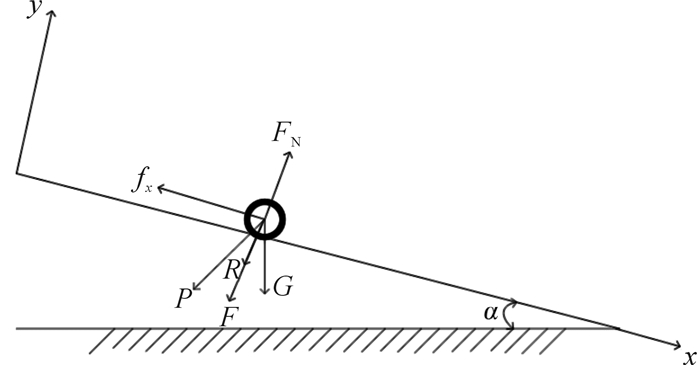
1 固相颗粒的动力学分析 1.1 力学模型钻井液中的固相颗粒在筛面上的状态一般分为淹没和非淹没状态,本文主要研究非淹没状态下单颗粒在筛面上的运移规律。实践证明,非淹没状态下固相颗粒在筛面上的运动形式有:正向滑行、反向滑行、抛掷运动以及相对静止。区别于传统的钻井液振动筛,现有的力学模型不适合用于负压振动筛筛面上固相颗粒的运移分析。本文以直线负压振动筛为例,提出了新的力学模型,如图 1所示。
|
| 图 1 直线负压振动筛上固相颗粒受力示意图 Fig.1 Force analysis of solid particle on linear negative vacuum pressure vibrating screen |
根据图 1,可以得到固相颗粒分别在x和y方向上的受力情况为:
| $ \left\{ \begin{array}{l} {F_x} = G\sin \alpha - {f_x} - {P_x}\\ {F_y} = {F_{\rm{N}}} - G\cos \alpha - F - {P_y} - R \end{array} \right. $ | (1) |
式中:G为固相颗粒重力;α为筛面倾角(直线振动筛中α=0°);fx=μFN,表示固相颗粒在x方向上所受摩擦力,μ是摩擦系数, FN为固相颗粒对筛面的正压力;R为钻井液对颗粒的黏结力;Px,Py为固相颗粒在x,y方向上的惯性力。
| $ \left\{ \begin{array}{l} {P_x} = m\left( {{a_x} + \Delta \ddot x} \right)\\ {P_y} = m\left( {{a_y} + \Delta \ddot y} \right) \end{array} \right. $ | (2) |
式中:m为固相颗粒的质量;ax,ay为筛面在x,y方向上的加速度;
| $ F = \frac{3}{4}m\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}{\left( {v - {v_{{\rm{s}}y}}} \right)^2} $ | (3) |
式中:CD为气体阻力系数;ds为颗粒直径;ρ为空气密度;ρs为颗粒密度;v为气流速度,
假设筛面的运动是稳定的,每个点的运动轨迹与质心相同。因此,负压振动筛的运动轨迹方程为:
| $ \left\{ \begin{array}{l} x = \lambda \cos \delta \sin \omega t\\ y = \lambda \sin \delta \sin \omega t \end{array} \right. $ | (4) |
由式(4)可求得负压振动筛在x,y方向上的速度以及加速度:
| $ \left\{ \begin{array}{l} {v_x} = \lambda \omega \cos \delta \cos \omega t\\ {v_y} = \lambda \omega \sin \delta \cos \omega t \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {a_x} = - \lambda {\omega ^2}\cos \delta \sin \omega t\\ {a_y} = - \lambda {\omega ^2}\sin \delta \sin \omega t \end{array} \right. $ | (6) |
式中:λ为振动筛振幅;δ为振动方向角;ω为振动筛角速度。
1.2 抛掷运动抛掷运动是反映振动筛工作性能的一项重要特性,其中,抛掷指数是重要参数。当固相颗粒通过抛掷运动离开筛面时,颗粒和筛面的加速度必须相同,即相对加速度
| $ G\cos \alpha + \frac{3}{4}m\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}{\left( {v - {v_{{\rm{s}}y}}} \right)^2} + R = m\lambda {\omega ^2}\sin \delta \sin {\varphi _0} $ | (7) |
式中φ0为抛始角。
当FN=0 N时,非淹没状态下的固相颗粒有离开筛网的趋势。由于固相颗粒表面有钻井液,颗粒不会立即起跳。只有固相颗粒与筛面钻井液完全脱离接触后,颗粒所受的黏结力R才能消失。非淹没状态下颗粒将要起跳时,其运动受静切力
| $ R = \frac{{{\rm{ \mathsf{ π} }}{d_{\rm{s}}}{\tau _0}}}{4} + {\sigma _{\rm{m}}}{\rm{ \mathsf{ π} }}{d_{\rm{s}}} $ | (8) |
式中:τ0为钻井液动切应力;σm为钻井液表面张力。实验证明:σm>σw,σw为水的表面张力,在温度为20~25 ℃时,σm大致范围为:
| $ 7.25 \times {10^{ - 2}}{\rm{N/m}} = {\sigma _{\rm{w}}} < {\sigma _{\rm{m}}} < 0.1{\rm{N/m}} $ |
方程(7)没有解析解,使用数值计算方法可以求得抛始角φ0, 从而得到抛掷指数D,如式(9)所示:
| $ D = \frac{1}{{\sin {\varphi _0}}} = \frac{{\lambda {\omega ^2}\sin \delta }}{{g\cos \alpha + \frac{3}{4}\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}{u^2} + \frac{3}{{2{d_{\rm{s}}}{\rho _{\rm{s}}}}}\left( {{\tau _0} + \frac{{2{\sigma _{\rm{m}}}}}{{{d_{\rm{s}}}}}} \right)}} $ | (9) |
式中u为颗粒和气流之间的相对速度。
抛掷指数D表示筛面上固相颗粒所受驱动力和阻力之比,当D>1时,固相颗粒才能离开筛面发生抛掷运动。
颗粒离开筛面后,主要受重力和吸力作用,假设固相颗粒和气流之间的相对速度为uy,根据式(1)、(2)、(3)以及(6)可以得到其相对加速度为:
| $ \Delta \ddot y = - g\cos \alpha - \frac{3}{4}\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}u_y^2 - {a_y} $ | (10) |
固相颗粒相对于筛面的速度Δẏ=uy-u0-vy。关于t求导,即可求得颗粒和筛面之间的相对加速度为:
| $ \Delta \ddot y = \frac{{{\rm{d}}{u_y}}}{{{\rm{d}}t}} - {a_y} $ | (11) |
将式(11)代入式(10),得到:
| $ \frac{{{\rm{d}}{u_y}}}{{{\rm{d}}t}} + \frac{3}{4}\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}u_y^2 + g\cos \alpha = 0 $ | (12) |
根据颗粒抛掷运动可以得到初始条件:uy|t=0=uy0=u0+vy0, 其中:
| $ {v_{y0}} = \lambda \omega \sin \delta \cos {\varphi _0},{u_0} = - v $ |
结合初始条件解微分方程(12),得到uy的表达式为:
| $ {u_y} = K\tan \left( {C - Bt} \right) $ | (13) |
式中:
当t=0 s时, 固相颗粒开始抛离筛面,随着时间增加,固相颗粒的速度越来越小,直到uy=0 m/s,固相颗粒到达最高点,整个过程花费的时间t=C/B。因此固相颗粒的抛掷高度为:
| $ \Delta y = \int_0^{C/B} {{u_y}{\rm{d}}t} = \frac{4}{3}\frac{{{d_{\rm{s}}}}}{{{C_{\rm{D}}}}}\frac{{{\rho _{\rm{s}}}}}{\rho }\ln \sqrt {1 + {{\left( {\frac{{{u_{y0}}}}{K}} \right)}^2}} $ | (14) |
当固相颗粒抛离筛面之后, 它在x方向上的摩擦力fx=0, 根据式(1)可以得到颗粒沿筛面x方向的运动方程为:
| $ m\left( {{a_x} + \Delta \ddot x} \right) = mg\sin \alpha $ | (15) |
由此可以得到颗粒沿筛面x方向的相对加速度为:
| $ \Delta \ddot x = g\sin \alpha + \lambda {\omega ^2}\cos \delta \sin \omega t $ | (16) |
对
| $ \begin{array}{l} \Delta x = g\sin \alpha \frac{{{{\left( {\varphi - {\varphi _0}} \right)}^2}}}{{2{\omega ^2}}} + \lambda \cos \delta \left( {\sin {\varphi _0} - \sin \varphi } \right) + \\ \;\;\;\;\;\;\;\lambda \cos \delta \cos{\varphi _0}\left( {\varphi - {\varphi _0}} \right) \end{array} $ | (17) |
由此可求得固相颗粒抛掷运动的平均速度为:
| $ \begin{array}{l} {v_x} = \frac{{\Delta x}}{{t - {t_0}}} = \frac{{\Delta x}}{{\left( {\varphi - {\varphi _0}} \right)/\omega }} = g\sin \alpha \frac{{\varphi - {\varphi _0}}}{{2{\omega ^2}}} + \\ \;\;\;\;\;\;\;\lambda \omega \cos \delta \left( {\frac{{\sin {\varphi _0} - \sin \varphi }}{{\varphi - {\varphi _0}}} + \cos {\varphi _0}} \right) \end{array} $ | (18) |
式中φ是抛止角,φ=φ0+ωt。
1.3 滑行运动当固相颗粒与筛面接触且相对静止时,颗粒和筛网有相同的运动轨迹。当颗粒开始滑行时,颗粒所受摩擦力与滑行方向相反。颗粒在筛面上的滑行有2种情况:正向滑行和反向滑行。如图 1所示,筛面对颗粒的极限摩擦力为:
| $ {F_{\rm{s}}} = \mp {f_{\rm{s}}}{F_{\rm{N}}} $ | (19) |
式中:Fs为极限摩擦力;fs为摩擦系数,fs=tan αs;αs为静摩擦角;“-”表示正向滑行, 即颗粒沿x轴正方向滑行;“+”表示反向滑行,颗粒沿x轴反方向滑行。
由于黏结力R远远小于重力、气流对颗粒的吸力以及振动筛惯性力,因此在考虑摩擦力的时候,黏结力可以忽略不计。
滑动开始的瞬间,颗粒沿筛面x方向的相对加速度
| $ \begin{array}{*{20}{c}} {G\sin \alpha + m\lambda {\omega ^2}\cos \delta \sin \omega t \mp }\\ {{f_{\rm{s}}}\left( { - m\lambda {\omega ^2}\sin \delta \sin \omega t + G\cos \alpha + F} \right) = 0} \end{array} $ | (20) |
当颗粒正向滑行时,颗粒正向滑行指数Dk为:
| $ {D_{\rm{k}}} = \frac{1}{{\sin \omega t}} = \frac{{\lambda {\omega ^2}\cos \left( {\delta - {\alpha _{\rm{s}}}} \right)}}{{g\sin \left( {{\alpha _{\rm{s}}} - \alpha } \right) + \frac{F}{m}\sin {\alpha _{\rm{s}}}}} $ | (21) |
相似地,颗粒反向滑行指数Dq为:
| $ {D_{\rm{q}}} = \left| {\frac{1}{{\sin \omega t}}} \right| = \frac{{\lambda {\omega ^2}\cos \left( {\delta + {\alpha _{\rm{s}}}} \right)}}{{g\sin \left( {{\alpha _{\rm{s}}} + \alpha } \right) + \frac{F}{m}\sin {\alpha _{\rm{s}}}}} $ | (22) |
由于反向滑行在大多数情况下是对固液分离不利或者毫无意义的,因此可以通过选定正向滑行指数和反向滑行指数进行控制,通常Dk=2~3, Dq=1。根据式(23)可以算得振动方向角:
| $ \left\{ \begin{array}{l} \frac{{{D_{\rm{k}}}}}{{{D_{\rm{q}}}}} = \frac{{\cos \left( {\delta - {\alpha _{\rm{s}}}} \right)}}{{\cos \left( {\delta + {\alpha _{\rm{s}}}} \right)}} = c\\ \delta = \arctan \left[ {\frac{{c - 1}}{{\left( {c + 1} \right)\tan {\alpha _{\rm{s}}}}}} \right] \end{array} \right. $ | (23) |
当颗粒在筛面滑行时, vsx>vx。结合式(21)和(23)即可得到振幅λ的表达式:
| $ \lambda = \frac{{{D_{\rm{k}}}\left[ {g + \frac{3}{4}\frac{{{C_{\rm{D}}}}}{{{d_{\rm{s}}}}}\frac{\rho }{{{\rho _{\rm{s}}}}}{{\left( {v - {v_{{\rm{s}}x}}} \right)}^2}} \right]\sin {\alpha _{\rm{s}}}}}{{{\omega ^2}\cos \left( {\delta - {\alpha _{\rm{s}}}} \right)}} $ | (24) |
单颗粒的运移规律如上所述,通过这些运动理论可以获得固相颗粒在负压振动筛上的理论平均运移速度,并与传统振动筛上的固相颗粒运移速度进行比较,进一步说明负压振动筛的优越性以及它在防止钻井液污染中所具有的优势。
以直线负压振动筛为例,筛面倾角α=0°, 筛网目数为200目,筛网面积A=1 085 mm×510 mm。固相颗粒密度ρs=2.6×103 kg/m3,筛面和固相颗粒之间的静摩擦系数为1.5[23]。根据筛网尺寸,固相颗粒直径范围为0.074~5 mm。此外,筛面上为大气压,筛面下为负压,其相对压力为-0.02 MPa,在该压强下空气的密度为2.34 kg/m3,空气阻力系数CD=0.44。真空泵选择ZJP系列。
2.1 振动方向角δ的影响计算时取ω=50π rad/s (f=25 Hz),λ=3 mm, D=3.3,固相颗粒直径ds=1 mm。真空泵型号选择ZJP-150,即真空泵抽速为150 L/s。
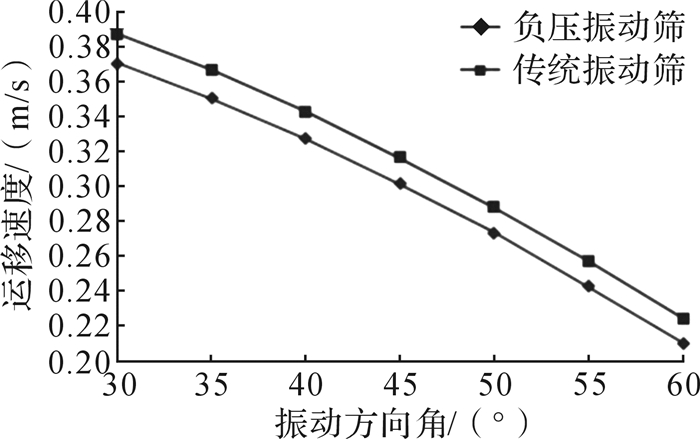
固相颗粒在筛网上运移的理论平均速度由公式(18)计算,在相同条件下改变振动方向角得到一系列固相颗粒运移速度,如图 2所示。从图 2可以看出:振动方向角δ的变化对固相颗粒运移速度的影响是明显的, 随着δ增大,运移速度降低;传统振动筛上固相颗粒的平均运移速度比负压振动筛上固相颗粒的平均运移速度快。
|
| 图 2 振动方向角对固相颗粒运移速度的影响 Fig.2 The influence of vibration direction angel on solid particle conveyance speed |
计算时取λ=3 mm, D=3.3, δ=45°,颗粒直径ds=1 mm。真空泵型号选择ZJP-150,即真空泵抽速为150 L/s。
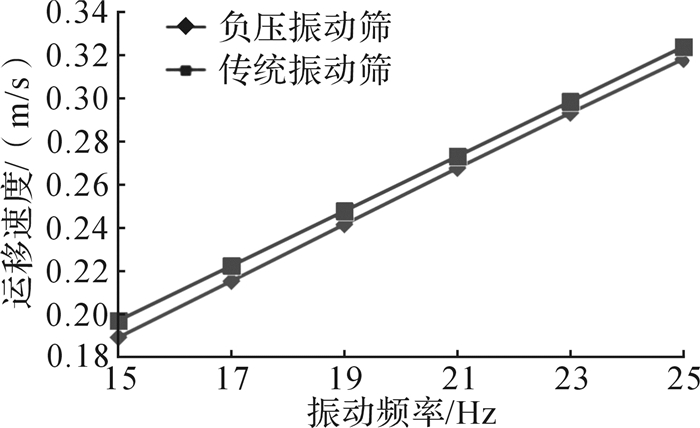
根据公式(18),改变振动频率,固相颗粒的运移速度也随之变化,如图 3所示。从图 3可知,固相颗粒的运移速度随着振动频率的增加而增加,并且负压振动筛和传统振动筛上的固相颗粒速度有明显区别。
|
| 图 3 振动频率对固相颗粒运移速度的影响 Fig.3 The influence of vibration frequency on solid particle conveyance speed |
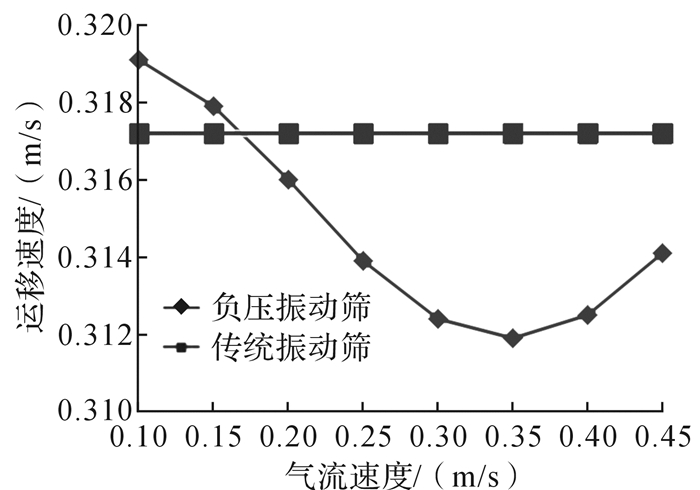
计算时取ω=50π rad/s (f=25 Hz), λ=3 mm, D=3.3和δ=45°,颗粒直径ds=1 mm。气流速度变化时固相颗粒运移速度的变化如图 4所示。从图中可以发现:空气流速主要对负压振动筛上颗粒运移产生影响,在负压振动筛上固相颗粒的运移速度随气流速度的增加先减小然后增大,且气流速度越接近vy0,固相颗粒运移速度越小。可以通过该曲线选择最佳真空泵。
|
| 图 4 气流速度对固相颗粒运移速度的影响 Fig.4 The influence of velocity of gas flow on solid particle conveyance speed |
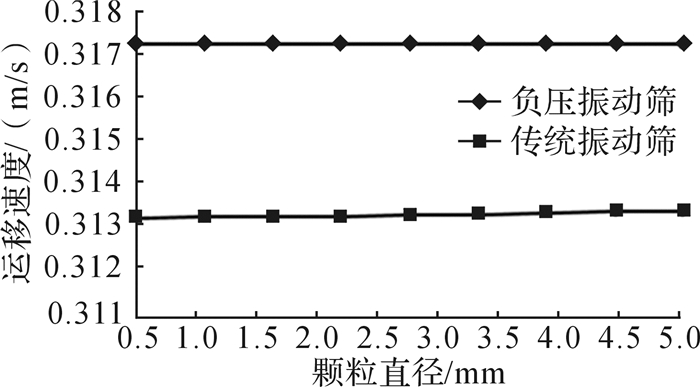
计算时取ω=50π rad/s (f=25 Hz), λ=3 mm, D=3.3和δ=45°,真空泵选择ZJP-150。改变固相颗粒直径,可以得到一系列固相颗粒运移速度,如图 5所示。显而易见,固相颗粒直径对颗粒的运移速度影响不大,但是在相同工作条件下,负压振动筛和传统振动筛上固相颗粒的运移速度是有明显差别的。
|
| 图 5 颗粒直径对固相颗粒运移速度的影响 Fig.5 The influence of particle diameter on solid particle conveyance speed |
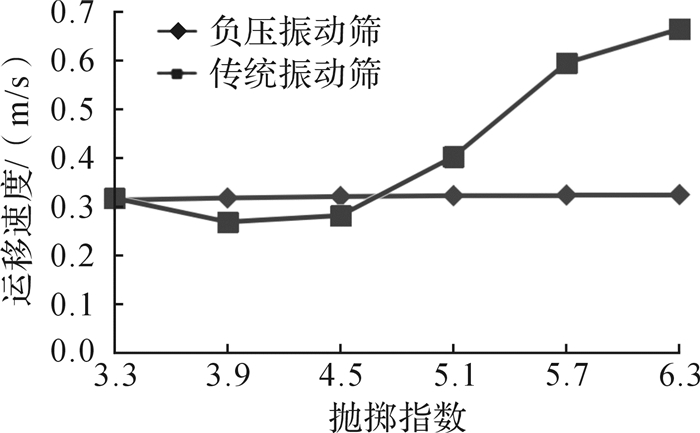
计算时取ω=50π rad/s (f=25 Hz), λ=3 mm和δ=45°, 颗粒直径ds=1 mm,真空泵选择ZJP-150。改变抛掷指数D,固相颗粒的运移速度也发生变化,如图 6所示。从图中可以发现,负压振动筛上抛掷指数对固相颗粒的运移速度影响不大,其运移速度几乎都在0.3 m/s左右。而传统振动筛上固相颗粒的运移速度随着抛掷指数的增大呈波浪式变化。另外过大的抛掷指数需要很大的激振力,这对振动筛的强度要求也会提高,因此,应合理选择抛掷指数。
|
| 图 6 抛掷指数对固相颗粒运移速度的影响 Fig.6 The influence of throwing index on solid particle conveyance speed |
负压系统使筛网上固相颗粒的运移速度变慢,为了确定负压系统的应用是否会对振动筛结构参数产生影响,从而增加成本, 现对固相颗粒正向滑行时的负压振动筛和传统振动筛的结构参数进行比较。
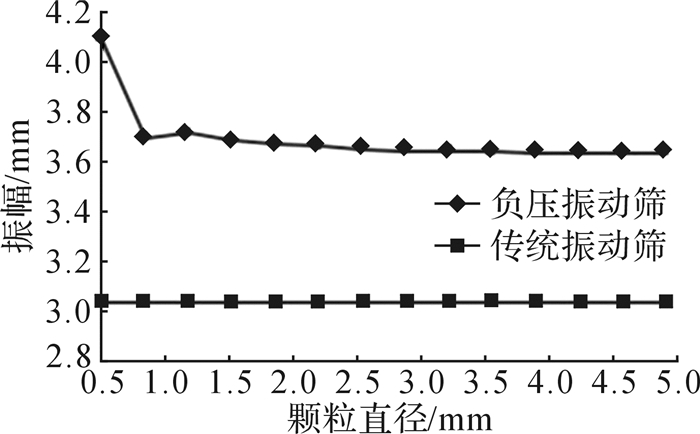
计算时取ω=50π rad/s, δ=45°,真空泵选择ZJP-150。当固相颗粒开始在振动筛筛面上滑行时,根据公式(23)和(24)计算出负压振动筛的振动方向角δ和振幅λ。取正向滑行指数与反向滑行指数的比值c=2,3, 振动方向角变化情况如表 1所示。在相同工作条件下,固相颗粒正向滑行时负压振动筛和传统振动筛的振动方向角没有区别。同样地,计算出相同工作条件下不同粒径的固相颗粒正向滑行时负压振动筛和传统振动筛的振幅变化情况, 结果如图 7所示。由图可知,在一定粒径范围内,不同粒径固相颗粒正向滑行时振动筛的振幅不发生变化,但对于负压振动筛,在相同工作条件下,其振幅要稍大于传统振动筛的振幅。这是由于吸附力的存在,使得固相颗粒在负压振动筛上正向滑行时需要更大的惯性力。综上,负压系统的应用不会明显改变振动筛的结构参数,说明该方案可行。
| 振动筛 | δ | |
| c=2 | c=3 | |
| 传统振动筛 | 15° | 18° |
| 负压振动筛 | 15° | 18° |
|
| 图 7 颗粒直径对振动筛振幅的影响 Fig.7 The influence of particle diameter on amplitude of vibrating screen |
基于气固两相流理论,获得了在非淹没状态下固相颗粒在负压振动筛上的运移规律。提出了负压振动筛上固相颗粒运移的力学模型,对不同参数下颗粒的运移速度进行了分析。这些结论可以为负压振动筛的应用和发展提供理论依据。
振动方向角δ、振动频率f以及气流速度v对固相颗粒的运移速度会产生影响,而颗粒直径ds对运移速度几乎不会产生影响。通常情况下负压振动筛上固相颗粒的运移速度小于传统振动筛上固相颗粒的运移速度,这种现象更有利于固液分离,以回收更多的钻井液干燥岩屑。因此,负压振动筛比传统振动筛更具有优越性。
通过负压振动筛和传统振动筛振幅和振动方向角之间的比较,可以发现负压系统的应用对振动筛结构参数的影响较小,说明这个方案可行,而且负压振动筛可以在原有传统振动筛的结构基础上直接进行改进,可有效地节约成本。因此,负压振动筛可替代传统振动筛应用在固相控制系统中。
| [1] |
王明才.
试析钻井生产中的环境污染与治理[J]. 中国化工贸易, 2012, 4(2): 153, 155.
WANG Ming-cai. Environmental pollution and treatment in experimental drilling production[J]. China Chemical Trade, 2012, 4(2): 153, 155. |
| [2] |
谢水祥, 邓皓, 王蓉沙, 等.
钻井环境污染过程控制技术综述[J]. 油气田环境保护, 2008, 18(2): 38–40.
XIE Shui-xiang, DENG Hao, WANG Rong-sha, et al. Summarization of process control technology for drilling environmental pollution[J]. Environmental Protection of Oil & Gas Fields, 2008, 18(2): 38–40. DOI:10.3969/j.issn.1005-3158.2008.02.013 |
| [3] |
袁姗姗.
钻井生产过程中的环境污染及治理[J]. 油气田环境保护, 2009, 19(1): 47–50.
YUAN Shan-shan. Environmental pollution and control in drilling process[J]. Environmental Protection of Oil & Gas Fields, 2009, 19(1): 47–50. DOI:10.3969/j.issn.1005-3158.2009.01.017 |
| [4] |
史万明, 李志伟, 万国华, 等. 一种真空负压固液分离振动筛: CN105032756A[P]. 2015-11-11.
SHI Wang-ming, LI Zhi-wei, WANG Guo-hua, et al. A vacuum negative pressure solid-liquid separation shaker: CN105032756A[P]. 2015-11-11. |
| [5] |
侯勇俊, 王钰文, 方潘, 等. 脉冲负压振动设备: CN206071498U[P]. 2017-04-05.
HOU Yong-jun, WANG Yu-wen, FANG Pan, et al. Pulse negative pressure vibration equipment: CN206071498U[P]. 2017-04-05. |
| [6] |
丹尼尔·盖·波默洛. 用于干燥钻探切削物的真空系统和方法的优化: CN105498339A[P]. 2016-04-20.
DANIEL GAY Pomero. Optimization of vacuum systems and methods for drying drilling cutters: CN105498339A[P]. 2016-04-20. |
| [7] | HOBEROCK L L. A study of vibratory screening of drilling fluids[J]. Journal of Petroleum Technology, 1980, 32(11): 1889–1902. DOI:10.2118/8226-PA |
| [8] | HOBEROCK L L, STANBERY S R. Pressure dynamics in wells during gas kicks:Part 1-component models and results[J]. Journal of Petroleum Technology, 1981, 33(8): 1357–1366. DOI:10.2118/9256-PA |
| [9] |
侯勇俊, 曹丽娟.
波浪形筛网固相运移规律研究[J]. 石油矿场机械, 2010, 39(1): 1–4.
HOU Yong-jun, CAO Li-juan. Solids migration model of undulating molded vibratory screen shale shaker[J]. Oil Field Equipment, 2010, 39(1): 1–4. DOI:10.3969/j.issn.1001-3482.2010.01.001 |
| [10] | KROKEN A, SOUZA E, MARTINS A L, et al. Evaluating an alternate cutting separation technology: is the mudCube a fit for Brazilian Offshore drilling[C]//Offshore Technology Conference, Rio de Janeiro, Oct. 29-31, 2013. |
| [11] | ZHAN Fu-li, XIN Tong, HUI Huang-xia, et al. A study of particles looseness in screening process of a linear vibrating screen[J]. Journal of Vibroengineering, 2016, 18(2): 671–681. |
| [12] | ROTICH N, TUUNILA R, ELKAMEL A, et al. Dynamic population balance and flow models for granular solids in a linear vibrating screen[J]. Aiche Journal, 2016, 62(11): 3889–3898. DOI:10.1002/aic.v62.11 |
| [13] | MELHUS T, MOWREY C, VASSHUS J K, et al. Intelligent, automated shale conveyance: rotary screen vacuum assisted gas and solids separation system for drilling fluids[C]//2010 AADE Fluids Conference and Exhibition, Houston, Apr. 6-7, 2010. |
| [14] | MISWACO. Oilfield screens: setting the bar in solids control[EB/OL]. [2017-09-06]. https://www.slb.com/~/media/Files/miswaco/catalogs/oilfield_screens_catalog.pdf2014. |
| [15] | LAL M, HOBEROCK L L. Solids-conveyance dynamics and shaker performance[J]. SPE Drilling Engineering, 1988, 3(4): 385–394. DOI:10.2118/14389-PA |
| [16] |
朱维兵, 张明洪.
钻井液振动筛固相运移动力学分析[J]. 石油机械, 2000, 28(7): 37–39.
ZHU Wei-bing, ZHANG Ming-hong. Dynamic analysis of solids conveyance of shale shaker[J]. China Petroleum Machinery, 2000, 28(7): 37–39. DOI:10.3969/j.issn.1001-4578.2000.07.015 |
| [17] |
侯勇俊, 田道云, 张明洪.
筒式网振动筛固相运移动力学研究[J]. 石油学报, 2004, 25(6): 109–112.
HOU Yong-jun, TIAN Dao-yun, ZHANG Ming-hong. Solid conveyance dynamics of shale shaker with roller screen[J]. Acta Petrolei Sinica, 2004, 25(6): 109–112. DOI:10.3321/j.issn:0253-2697.2004.06.023 |
| [18] | ZHU Wei-bing, DENG Cheng-zhong, WANG He-shun. Kinematic law of solids on a drilling fluid vibrating screen[J]. Petroleum Science & Technology, 2013, 31(16): 1608–1616. |
| [19] | SAVAGE S B, PFEFFER R, ZHAO Z M. Solids transport, separation and classification[J]. Powder Technology, 1996, 88(3): 323–333. DOI:10.1016/S0032-5910(96)03137-3 |
| [20] | WYPYCH P W, YI J. Minimum transport boundary for horizontal dense-phase pneumatic conveying of granular materials[J]. Powder Technology, 2003, 129(1/3): 111–121. |
| [21] | MARCUS R D, LEUNG L S, KLINZING G E, et al. Pneumatic conveying of solids:a theoretical and practical approach[J]. Drying Technology, 1993, 11(4): 859–860. DOI:10.1080/07373939308916871 |
| [22] | HILTON J E, CLEARY P W. The influence of particle shape on flow modes in pneumatic conveying[J]. Chemical Engineering Science, 2011, 66(3): 231–240. DOI:10.1016/j.ces.2010.09.034 |
| [23] |
张明洪, 邓嵘, 徐倩.
钻井振动筛的工作理论与测试技术[M]. 北京: 石油工业出版社, 2013: 85-100.
ZHANG Ming-hong, DENG Rong, XU Qian. Working theory and testing technology of drilling shaker[M]. Beijing: Petroleum Industry Press, 2013: 85-100. |


