优化设计,即遵循一定的优化思想,通过不断改进设计模型和设计参数,使设计效果最佳。结构优化一般划分为拓扑优化、形状优化和尺寸优化,用到的主要方法是数学归纳法和优化准则法[1]。实践证明,工程结构优化设计能缩短设计周期,提高设计水平,较原设计方案, 优化设计方案一般可以使工程造价降低5%~30%[2]。近年来,常使用响应面法(response surface method,RSM)来高效地解决优化问题, 如用RSM优化桥梁主桁架结构[3]、铝合金壁板和汽车配件参数[4]、立式加工中心[5]和涡轮增压器叶轮方案[6]。在包含有限元分析的优化设计中, 采用RSM可减少有限元迭代次数, 大大缩短计算时间,进而提高优化效率[7-8]。本文利用响应面法优化桁架结构的形状,并与文献[9]进行对比以验证响应面法的高效性。
1 响应面法简介响应面法(RSM)是利用函数关系拟合仿真模型, 采用筛选试验来确定优化方向。以RSM为指向,往满足约束条件和质量最轻方向寻找最优解,参考差动电路的负反馈调节机制,设定好收敛条件:约束值与其均值相对误差小于5%,就可以搜索到最佳设计。
1.1 一阶模型优化一阶模型中某些参数相互独立,且与所要优化的性能响应呈线性关系,其数学模型为:
| $ y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \ldots + {\beta _k}{x_k} + \varepsilon $ |
式中:βi(i=1,2, …, k)为待定系数,β0为约束均值, ε为y的误差。
一阶模型优化的实质是利用最小二乘法拟合回归方程,以单位步长等值线法线方向为搜索方向,当精度小于设置的收敛容差则搜索出最优解。但是实际中设计参数往往有交互作用,系统有二次弯曲效应,则必须用更高阶的多项式, 例如二阶模型[10]。
1.2 二阶模型优化RSM的原理是当某点周围一定数量点的实际函数值已知时,在充分靠近这个点的区域内,可用曲面代替实际函数进行计算。响应面函数表达式如下:
| $ y = {\beta _0} + \sum\limits_{i = 1}^n {{\beta _i}{X_i}} + \sum\limits_{i = 1}^n {{\beta _{ii}}X_i^2} + \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {{\beta _{ij}}{X_i}{Y_j} + \varepsilon } } $ |
式中:βi,βii,βij为待定系数,β0为约束均值,ε为y的误差。
用响应面方法求最优点时,通过多因素三水平矩阵:将连续函数化成离散型试验点,但是通过有限个试验点来取代连续函数,势必造成误差ε变大,为此采用Box和Behnken创立的中心复合BBD因子设计法(见图 1(a))和Cornell创立的中心复合CCD因子设计法(见图 1(b))来解决误差大的问题。
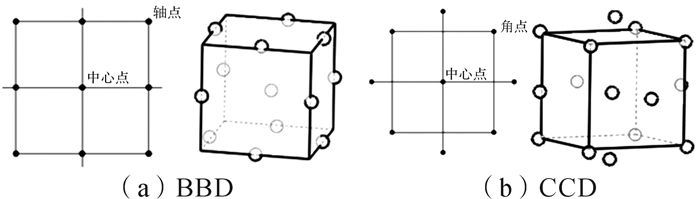
|
| 图 1 中心复合因子设计法示意图 Fig.1 Schematic diagram of central composite factor design method |
基于响应面法的优化是一种序贯方法,进行析因设计分析后再用响应面法找到最优解。其搜索过程为:从全局出发,先利用线性一阶模型以一定的步长找到大概范围,此时精度往往不高,通过析因分析,如果设计变量交互作用的所有P值都小于或接近显著水平(a=0.05)[11],则利用二阶模型进行,即在大概范围内找到应力约束均值β0与许应力σS的相对误差Δ1 < 5%的最佳领域。最佳领域是由中心点和中心点上下范围构成的,从而将问题转化为通过负反馈调节机制来确定中心点和搜索的水平范围。寻找最佳领域内最优解的过程是:先得到约束与目标函数的回归方程,再利用遗传算法、Minitab优化器、Design-expert优化器得到回归方程的解,其解即为最优解,最后回代验证[12]。由于迭代结束的判定条件是优化的应力约束S与许应力σS的相对误差Δ2 < 5%,最优解有小幅波动,取效果相对较好的结果。图 2所示为基于响应面法的优化流程。
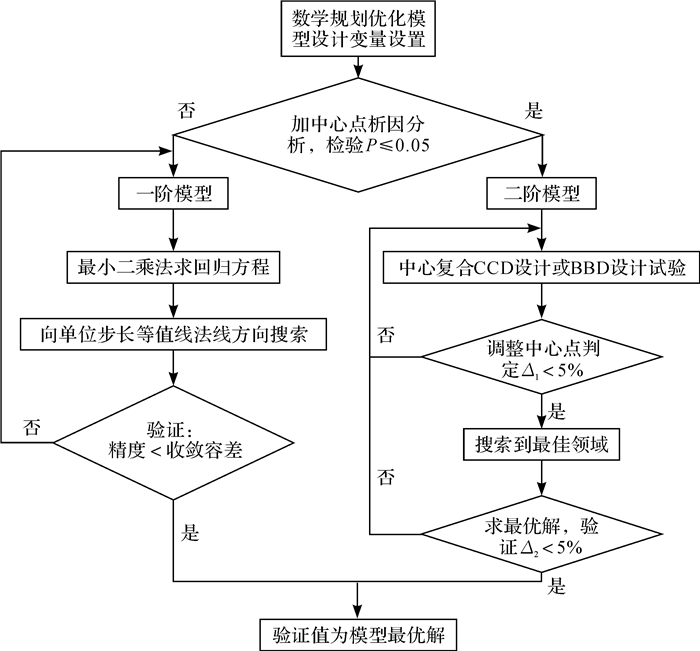
|
| 图 2 基于响应面法的优化流程 Fig.2 Optimization process based on response surface method |
如图 3所示为工程应用的10杆桁架结构,其杨氏模量为9 800 MPa, 载荷为9.8 MN, 各部件的截面面积Ai=10 cm2,各杆长度均为360 cm。图中p表示向下的拉力。目标函数为结构总体积最小,约束条件为杆的许应力σS=196 MPa。
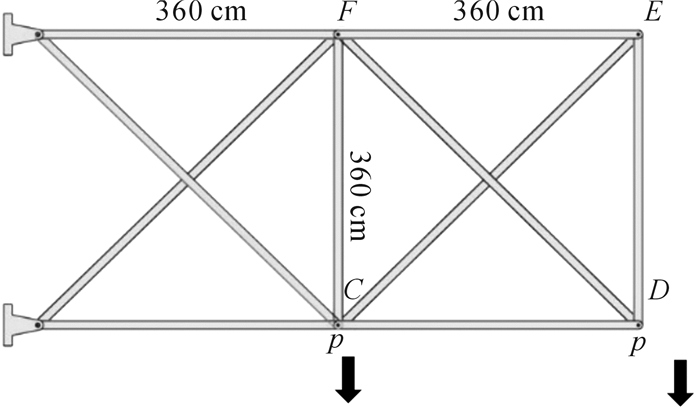
|
| 图 3 10杆桁架结构 Fig.3 Truss structure with ten bars |
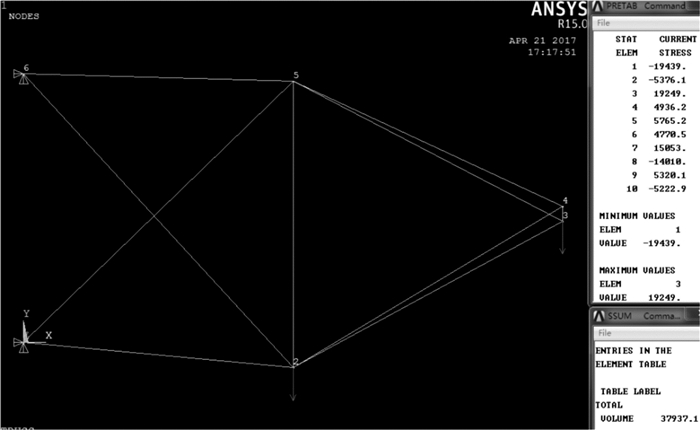
编写并运行APDL(ANSYS parametric design language,参数化设计语言)程序, 建立10杆桁架的有限元模型,其初始形状的ANSYS应力分析如图 4所示。
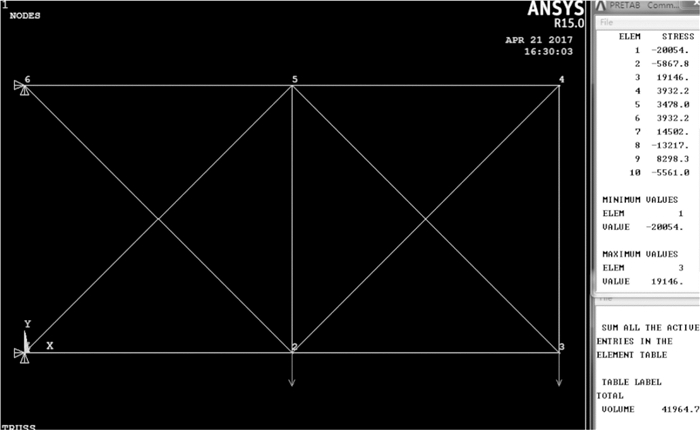
|
| 图 4 10杆桁架初始形状的ANSYS应力分析图 Fig.4 ANSYS stress analysis of the initial shape of truss with ten bars |
节点C,D,E,F纵坐标值分别为yC,yD,yE,yF,单位为cm; V为桁架总体积,单位为dm3; S为所有桁架杆的最大应力,单位为MPa。10杆桁架初始形状下的应力与体积分别为:V=419.647 dm3, S=200.54 MPa。
可见其应力S比许应力σS=196 MPa大,且体积过大,故有优化余地。
3.2 线性分析首先确定全局搜索范围,根据实际经验和文献[9]可知,节点C,D,E和F越集中于中间越好,且节点C和F对称,D和E对称,yC,yF变化幅度小于yD,yE,因此设计参数定为:yC∈[-90, 90] cm,yD∈[-180, 180] cm,yE∈[180, 540] cm,yF∈[270, 450] cm。各节点的原点为:yC=0 cm,yD=0 cm,yE=360 cm,yF=360 cm。
分析形变参数yC, yD, yE, yF对目标体积V是否有影响且影响是否为线性。通过析因设计分析能够求出误差估计量及检测二次弯曲性,从而判断分析设计因子对响应的影响是采用一阶模型还是二阶模型。
首先,对以初始形状为中心点的水平设置进行析因分析,如表 1,其中-1,0,1为编码值,方便水平设置,yC,yD,yE, yF的跨度值分别为180,360,360,180 cm。
| 编码 | yC/cm | yD/cm | yE/cm | yF/cm |
| 1 | 90 | 180 | 540 | 450 |
| 0 | 0 | 0 | 360 | 360 |
| -1 | -90 | -180 | 180 | 270 |
用Minitab软件建立全因子设计表,按照全因子分析表,相应改变APDL程序中yC,yD,yE,yF值, 在ANSYS中运行,得到21组实验数据,将这些数据对应输入全因子分析表中,对V进行方差分析[10],如表 2。
| 模型 | 自由度 | 调整后的偏差平方和 | 调整后的平均偏差平方和 | F值 | P值 |
| 线性 | 4 | 429775098 | 107443774 | 8.60×1011 | 0 |
| yC | 1 | 70694884 | 70694884 | 5.66×1011 | 0 |
| yD | 1 | 144192664 | 144192664 | 1.15×1012 | 0 |
| yE | 1 | 144192664 | 144192664 | 1.15×1012 | 0 |
| yF | 1 | 70694884 | 70694884 | 5.66×1011 | 0 |
| 双因子交互作用 | 6 | 5973838 | 995640 | 7.97×109 | 0 |
| yC*yD | 1 | 2491268 | 2491268 | 1.99×1010 | 0 |
| yC*yE | 1 | 495651 | 495651 | 3.97×109 | 0 |
| yC*yF | 1 | 0 | 0 | 5 | 0.076 |
| yD*yE | 1 | 0 | 0 | 5 | 0.076 |
| yD*yF | 1 | 495651 | 495651 | 3.97×109 | 0 |
| yE*yF | 1 | 2491268 | 2491268 | 1.99×1010 | 0 |
| 三因子交互作用 | 4 | 0 | 0 | 5 | 0.054 |
| yC*yD*yE | 1 | 0 | 0 | 5 | 0.076 |
| yC*yD*yF | 1 | 0 | 0 | 5 | 0.076 |
| yC*yE*yF | 1 | 0 | 0 | 5 | 0.076 |
| yD*yE*yF | 1 | 0 | 0 | 5 | 0.076 |
| 弯曲效应 | 1 | 11604167 | 11604167 | 9.28×1010 | 0 |
| 失拟 | 1 | 0 | 0 | ||
| 纯误差 | 4 | 0 | 0 | ||
| 合计 | 20 | 447353103 |
由表 2可知,线性P值小于0.05,可以得出yC,yD,yE,yF对V有显著影响;交互作用的P值接近0.05,说明yC,yD,yE,yF对V有交互响应,说明该模型为二阶模型。
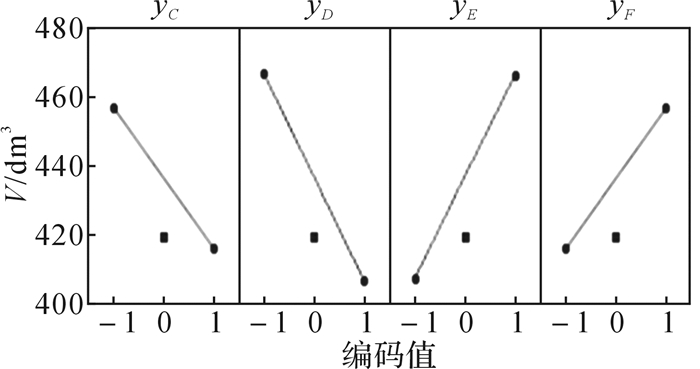
3.3 试验调整上述以初始形状为中心点的21次试验中存在S < 196 MPa的实验,说明表 2的水平设置范围偏大,包含了最佳领域,更包含了最优解。而体积V太大,有优化空间,可调整中心点值, 让中心点逼近最佳领域。图 5为析因分析的V主效应图,横坐标表示编码值,纵坐标表示体积值。
|
| 图 5 析因分析的V主效应图 Fig.5 V main effect diagram of factorial analysis |
从图 5可看出yC,yD,yE,yF对体积V的影响是显著的,为了使V变小,应减小yC,yD,yE,yF对V的影响,则初始形状中心值必须调整,即:yC,yD大幅度提高,且由于yD斜率更大,其提高幅度更大;同样,yE,yF大幅度提高,yE提高幅度更大。以相同的范围设置水平, 并通过主效应的反馈来调整中心点。根据响应面法的反馈来相应改变中心点和搜索水平范围,如表 3为改变后的中心点和搜索水平范围。
| 编码 | yC/cm | yD/cm | yE/cm | yF/cm |
| 2 | 120 | 330 | 390 | 430 |
| 1 | 75 | 240 | 300 | 385 |
| 0 | 30 | 150 | 210 | 340 |
| -1 | -15 | 60 | 120 | 295 |
| -2 | -60 | -30 | 30 | 250 |
同上述用Minitab软件建立7个中心点单区组响应面全因子设计表,按照全因子分析表,相应改变APDL程序中yC, yD, yE, yF值,在ANSYS中运行,得到31组实验数据。
此时考虑约束S的影响(S≤σS), 对S进行方差分析,得到S关于yC,yD,yE,yF的回归方程:
| $ \begin{array}{l} S = (21\;059 + 1\;232.3{y_C} + 109.0{y_D} - \\ \quad 133.0{y_E} - 619.8{y_F} + 165.9y_C^2 - 44.0y_D^2 + \\ \quad 289.4y_E^2 + 220.3y_F^2 + 74{y_C} \times {y_D} + \\ \quad 65{y_C} \times {y_E} - 137{y_C} \times {y_F} + 14{y_D} \times \\ \quad {y_E} + 65{y_D} \times {y_F} + 48{y_E} \times {y_F}) \times {10^{ - 2}} \end{array} $ |
从回归方程中看出平均值β0=210.59 MPa,比约束值(196 MPa)大,说明该中心点并没有落在最佳领域内,但是31次实验中有部分试验的S < 196 MPa,说明最佳领域在上述水平范围内。
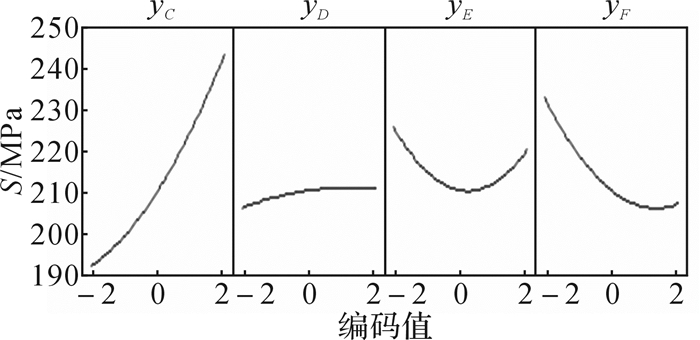
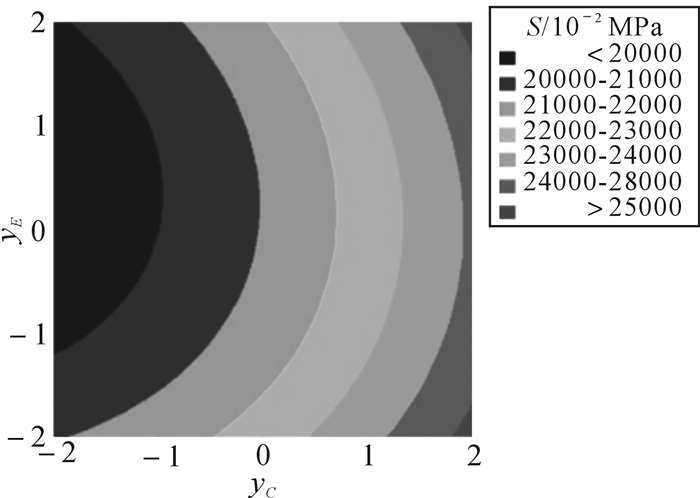
图 6为中心复合设计的S主效应图,横坐标表示编码值,纵坐标表所有杆中最大应力值。从图可以看出,yD,yE,yF在中心点附近已使得S达到最小,但yC值还需要调小,调小yC值就能使中心点落在最佳领域内,其余中心点值不变。图 7为中心复合设计的yC与yE对S的效应等值线图,该图进一步说明只需要调小yC值即可使中心点落在最佳领域。
|
| 图 6 中心复合设计的S主效应图 Fig.6 S main effect diagram of center composite design |
|
| 图 7 中心复合设计的yC与yE对S的效应等值线图 Fig.7 Contour map of effect of yC and yE on S in central composite design |
重新设置水平搜索,设置水平范围不变,如表 4。
| 编码 | yC/cm | yD/cm | yE/cm | yF/cm |
| 2 | 30 | 330 | 390 | 430 |
| 1 | -15 | 240 | 300 | 385 |
| 0 | -60 | 150 | 210 | 340 |
| -1 | -105 | 60 | 120 | 295 |
| -2 | -150 | -30 | 30 | 250 |
同上述步骤得到中心复合计算结果,利用中心复合结果求回归方程,得到:
| $ \begin{array}{l} S = (19\;537.0 + 163.0{y_C} - 111.9{y_D} - 71.8{y_E} - \\ \quad 691.2{y_F} + 296.2y_C^2 + 15.3y_D^2 + 26.4y_E^2 + \\ \quad 292.1y_F^2 + 106.6{y_C} \times {y_D} + 86.8{y_C} \times \\ \quad {y_E} + 195.3{y_C} \times {y_F} + 20.6{y_D} \times {y_E} + \\ \quad 39.6{y_D} \times {y_F} + 21.6{y_E} \times {y_F}) \times {10^{ - 2}} \end{array} $ |
| $ \begin{array}{l} V = (38\;904.6 - 1\;356.2{y_C} - 185.6{y_D} + \\ \quad 520.5{y_E} + 996.6{y_F} + 47.1y_C^2 + 430.8y_D^2 + \\ \quad 430.4y_E^2 + 61.1y_F^2 - 52.0{y_C} \times {y_D} - \\ \quad 180.0{y_C} \times {y_E} - 20.9{y_C} \times {y_F} - 579.1{y_D} \times \\ \quad {y_E} + 43.5{y_D} \times {y_F} - 113.1{y_E} \times {y_F}) \times {10^{ - 2}} \end{array} $ |
从二阶模型回归方程中得S的均值为195.37 MPa,与约束值(196 MPa)的相对误差为3.214%, 因此可以判断该中心点落在最佳领域,通过表 1、表 3及表 4的水平设置进行3次迭代就可以找出最佳领域,最佳领域即为表 4的中心点和各中心点的上下范围,由S,V二阶回归方程可求解最佳领域的最优解[13-15]。
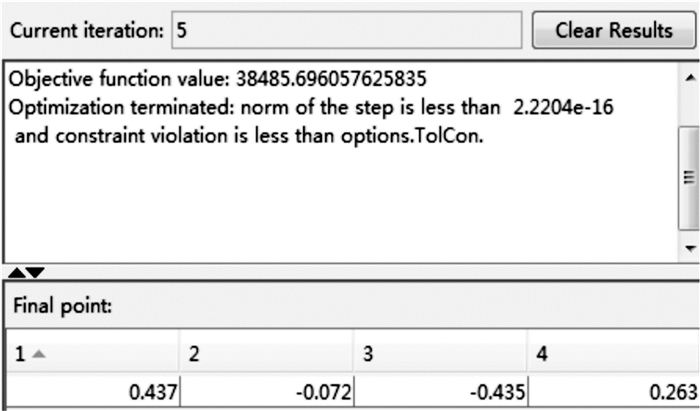
3.5 最佳领域内寻最优解 3.5.1 MATLAB遗传算法求解最优解在MATLAB中按回归方程设置好目标函数和约束条件,迭代5次后得到yC,yD,yE,yF。
如图 8(图中目标函数值单位为10-2 dm3)所示,在最大应力S=196 MPa下优化的体积V=384.86 dm3,yC,yD,yE,yF的值分别为-40.335,143.52,170.85,351.835 cm,代入APDL程序,运行ANSYS进行验证。可得最大拉应力为192.64 MPa,最大压应力为192.57 MPa,则最大应力S=192.64 MPa,体积V=382.408 dm3。
|
| 图 8 MATLAB中最优解的运算结果 Fig.8 Operation result of the optimal solution in MATLAB |
如图 9所示,Minitab优化的最优解yC,yD,yE,yF的编码值分别为0.585 9,0.141 4,-0.303 0,0.222 2,对应自然值分别为-33.634 5,162.726,182.73,349.999 cm,得到应力S=196.2 MPa,体积V=382.70 dm3。将yC,yD,yE,yF自然值代入APDL程序,运行ANSYS进行验证。可得最大压应力为194.39 MPa, 最大拉应力为192.49 MPa, 则最大应力S=194.39 MPa,体积V=379.37dm3。
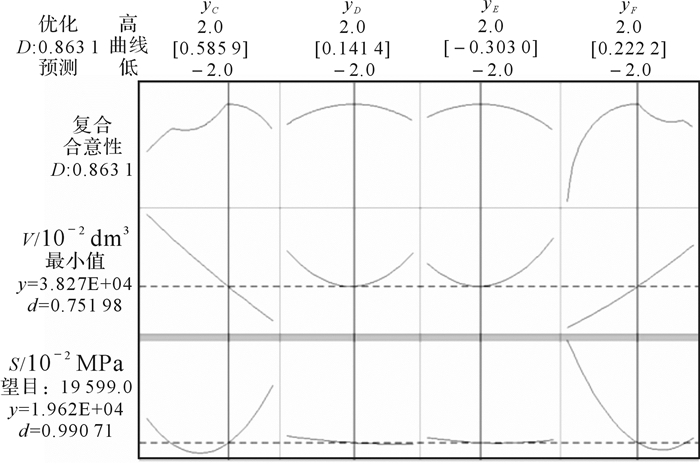
|
| 图 9 Minitab优化解图 Fig.9 Minitab optimal solution |
如图 10(图中V的单位为10-2 dm3, S的单位为10-2 MPa)所示,Design-expert优化的最优解yC,yD,yE,yF编码值为0.56,0.19,-0.27,0.24,对应的自然值分别为-34.35,168,188.4,350.8 cm,得到应力S=196 MPa,体积V=383.234 dm3。将yC,yD,yE,yF自然值代入APDL程序,运行ANSYS进行验证。得到最大压应力为192.14 MPa, 最大拉应力为194.4 MPa,则最大应力S=194.4 MPa, 体积V=379.891 dm3。最优解S,V值与验证值接近且S满足约束条件。

|
| 图 10 Design-expert优化参数设置示意图 Fig.10 Parameter setting diagram for Design-expert optimization |
图 11所示为Design-expert优化所得的最佳领域和最优解,图中凸起部分为最佳领域,0.863为Design-expert优化的最优解。
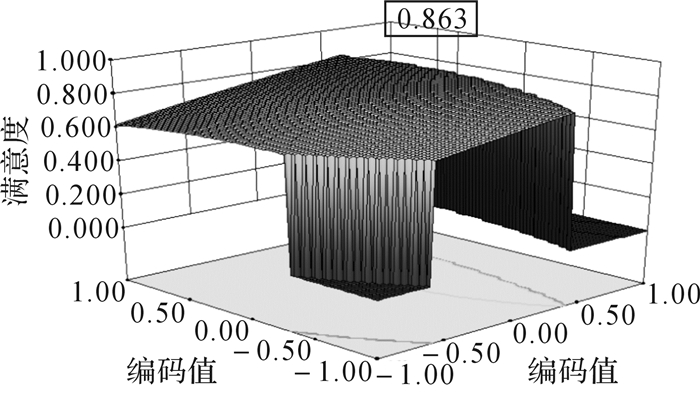
|
| 图 11 Design-expert优化的最佳领域和最优解 Fig.11 The best areas and optimal solution of Design-expert optimization |
将以上3种方法所得的形状优化值yC,yD,yE,yF设计参数回代APDL程序验证的值接近,虽然存在误差但是在可接受范围内,最后均取ANSYS回代验证值。初始形状、本文3种优化解和文献[9]形状优化后的应力和体积对比如表 5所示。
| 最优解 | 初始形状 | MATLAB遗传算法优化 | Minitab响应面优化 | Design-expert响应面优化 | 文献[9]方法 |
| yC/cm | 0 | -40.335 | -33.6345 | -34.35 | 19.58 |
| yD/cm | 0 | 143.52 | 162.726 | 168 | 158.78 |
| yE/cm | 360 | 170.85 | 182.73 | 188.4 | 333.87 |
| yF/cm | 360 | 351.835 | 349.999 | 350.8 | 352.62 |
| ANSYS验证值V/dm3 | 419.647 | 382.408 | 379.371 5 | 379.891 | 386.35 |
| ANSYS验证值S/MPa | 200.54 | 192.64 | 194.39 | 194.4 | 208.31 |
从表 5可知由Minitab响应面优化法求解的体积最小,效果最好,在最大应力S=194.39 MPa下的体积为379.37 dm3,比初始形状下的体积(419.647 dm3)减小9.6%,比文献[9]中的体积384.2 dm3减少6.97 dm3;优化应力约束与许应力σS相对误差在5%内,体现了响应面法的优越性。最终优化形状的效果图如图 12所示。
|
| 图 12 10杆桁架最终优化形状的效果图 Fig.12 Impression drawing of the final optimization shape of truss with ten bars |
1) 对比结构的初始形状,在满足约束的前提下利用响应面法优化后结构体积减小了很多,能满足轻量化设计要求。响应面优化法比其他方法如文献[9]的实验设计法的优化效果好,且只需迭代3次,体现了其优越性。
2) 利用响应面法优化工程实际结构问题时,要求试验者有工程基础知识和经验。通过响应面法的反馈调整,在确定的全局内,人为设置中心点和搜索水平范围,从而提高寻优效率。
3) 通过本文可看出响应面法在工程应用中寻找在约束条件下的最佳配比设计有着高效性,通过离散试验拟合连续函数可快速找到最优解。
| [1] |
王栋.
结构优化设计:探索与进展[M]. 北京: 国防工业出版社, 2013: 1-214.
WANG Dong. Structural optimization:exploration and development[M]. Beijing: National Defense Industry Press, 2013: 1-214. |
| [2] |
蔡新, 郭兴文, 张旭明.
工程优化设计[M]. 北京: 中国水利水电出版社, 2003: 20-29.
CAI Xin, GUO Xing-wen, ZHANG Xu-ming. Engineering optimum design[M]. Beijing: China Water & Power Press, 2003: 20-29. |
| [3] |
杨书仪, 刘德顺, 文泽军.
基于响应面法的桥梁主桁架结构优化设计[J]. 机械设计, 2007, 24(6): 14–16.
YANG Shu-yi, LIU De-shun, WEN Ze-jun. Structural optimization design of bridge main truss based on method of respond surface[J]. Journal of Machine Design, 2007, 24(6): 14–16. DOI:10.3969/j.issn.1001-2354.2007.06.005 |
| [4] |
吕辉, 于德介, 谢展, 等.
基于响应面法的汽车盘式制动器稳定性优化设计[J]. 机械工程学报, 2013, 49(9): 45–49.
LÜ Hui, YU De-jie, XIE Zhan, et al. Optimization of vehicle disc brakes stability based on response surface method[J]. Journal of Mechanical Engineering, 2013, 49(9): 45–49. |
| [5] |
姜衡, 管贻生, 邱志成, 等.
基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 56–60.
JIANG Heng, GUAN Yi-sheng, QIU Zhi-cheng, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11): 56–60. |
| [6] | JANG Choon-man, CHOI Ka-ram. Optimal design of splitters attached to turbo blower impeller by RSM[J]. Journal of Thermal Science, 2012, 21(3): 215–222. DOI:10.1007/s11630-012-0538-1 |
| [7] |
王永菲, 王成国.
响应面法的理论与应用[J]. 中央民族大学学报(自然科学学报), 2005, 14(3): 236–240.
WANG Yong-fei, WANG Cheng-guo. The theory and application of the response surface method[J]. Journal of the Central University for Nationalities (Natural Science Edition), 2005, 14(3): 236–240. |
| [8] |
张建方. 关于试验设计的效率及有关问题[J]. 数理统计与管理, 2007, 26(5): 92-801.
ZHANG Jian-fang. On the efficiency of experiment design and its some related problem[J]. 2007, 26(5): 92-801. |
| [9] |
杨冬梅, 小木曾望, 室津义定.
基于实验设计法的工程结构优化设计[J]. 计算力学学报, 2001, 18(2): 173–178.
YANG Dong-mei, KOGISO Nozomu, MUROTSU Yoshisada. Structural optimization based on the experimental design method[J]. Chinese Journal of Computational Mechanics, 2001, 18(2): 173–178. DOI:10.3969/j.issn.1007-4708.2001.02.009 |
| [10] |
MONTGOMERY Douglas C. 实验设计与分析[M]. 6版. 傅钰生, 张健, 王振羽, 等译. 北京: 人民邮电出版社, 2009: 8-371.
MONTGOMERY Douglas C. Experimental design and analysis[M]. 6th ed. Translated by FU Yu-sheng, ZHANG Jian, WANG Zhen-yu, et al. Beijing: People's Posts and Telecommunications Press, 2009: 8-371. |
| [11] |
盛骤, 谢式千, 潘承毅.
概率论与数理统计[M]. 北京: 高等教育出版社, 2013: 219-263.
SHENG Zhou, XIE Shi-qian, PAN Cheng-yi. Probability theory and mathematical statistics[M]. Beijing: Higher Education Press, 2013: 219-263. |
| [12] |
隋允康, 宇慧平.
响应面方法的改进及其对工程优化的应用[M]. 北京: 科学出版社, 2011: 1-265.
SUI Yun-kang, YU Hui-ping. The improvement of response surface method and its applications to engineering optimization[M]. Beijing: Science Press, 2011: 1-265. |
| [13] | KANGA Soo-Chang, KOH Hyun-Moo, CHOO Jinkyo F. An efficient response surface method using moving least squares approximation for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2010, 25(4): 365–371. DOI:10.1016/j.probengmech.2010.04.002 |
| [14] |
张振伟, 姚卫星, 周琳, 等.
桁架结构尺寸和形状协同优化方法研究[J]. 航空工程进展, 2012, 3(2): 138–143.
ZHANG Zhen-wei, YAO Wei-xing, ZHOU Lin, et al. Study on size and shape collaborative optimization method of truss structure[J]. Advances in Aeronautical Science and Engineering, 2012, 3(2): 138–143. DOI:10.3969/j.issn.1674-8190.2012.02.003 |
| [15] |
李响, 李为吉.
基于序列响应面方法的协同优化算法[J]. 西北工业大学学报, 2003, 21(1): 79–82.
LI Xiang, LI Wei-ji. On revised collaborative optimization using sequential response surface method[J]. Journal of Northwestern Polytechnical University, 2003, 21(1): 79–82. DOI:10.3969/j.issn.1000-2758.2003.01.020 |


