2. 常熟理工学院 汽车工程学院, 江苏 苏州 215500
2. School of Automotive Engineering, Changshu Institute of Technology, Suzhou 215500, China
在结构优化设计中,强度、刚度、稳定性是三个主要的研究问题。现有的结构拓扑优化方法多以考虑结构刚度为主,如体积约束下的最大刚度和刚度约束下的最小体积等[1]。而对于许多细长受压结构,如起重机臂架等,稳定性问题的重要性是高于刚度问题的。因此,在结构优化设计中顾及稳定性问题,具有现实意义与应用价值。Browne等[2]将0-1规划引入屈曲约束下以质量最小化为目标的拓扑优化问题中,推导了几何刚度矩阵的解析式,提出了一种基于一阶导数的求解算法。Zhou[3]研究了线性屈曲响应下壳结构的拓扑优化问题,指出失稳模态的识别是主要难点,并提出了屈曲约束下拓扑优化问题中的另外2个难点是:避免“奇异拓扑”现象与提高失稳特征值计算精度。隋允康等[4-5]基于ICM(independent continuous mapping,独立、连续、映射)方法研究了屈曲约束条件下连续体结构的拓扑优化问题,对以质量最小为目标函数,屈曲临界力为约束条件的优化模型进行了求解。Guo等[6]对应力与局部屈曲约束下的桁架结构拓扑优化问题进行了研究,使用二阶平滑扩展技术与ε松弛法克服了桁架结构拓扑优化中的奇异问题,而后采用尺寸优化算法求解桁架结构拓扑优化问题。Lund[7]使用DMO(discrete material optimization,离散材料优化)方法对层状复合材料板结构的失稳载荷因子最大化问题展开研究。程耿东等[8]研究了单工况作用下考虑局部稳定性约束的圆截面桁架结构的拓扑优化问题,以内力为设计变量将优化模型转化为线性约束数学规划,并以单纯形法为基础进行求解。高兴军[9]基于移动渐进线法研究了稳定性约束下连续体结构柔度最小化的拓扑优化问题,提出了两阶段改进优化算法。Neves等[10-11]针对小体积约束条件下细长结构中稳定性不足的问题,在拓扑优化中引入了临界载荷约束,将稳定性问题转化为线性特征值问题进行求解。综上所述,目前对考虑稳定性约束的拓扑优化方法的研究相对较少,且研究多集中于桁架结构的拓扑优化。
变密度法[12]是连续体结构拓扑优化的有效方法,本文将稳定性约束引入变密度法中,建立以结构柔度最小为目标,失稳载荷因子和体积为约束的拓扑优化数学模型。通过计算结构柔度、体积及失稳载荷因子对单元相对密度的灵敏度,基于拉格朗日乘子法和Kuhn-Tucker条件,推导出单元相对密度迭代更新的优化准则。同时,利用基于约束条件的泰勒展开式对优化准则中的拉格朗日乘子进行计算。为求解优化准则中的几何应变能,推导了平面四节点四边形单元几何刚度矩阵的显式表达式。最后,通过一个平面优化问题算例对本文方法进行验证,以期通过对比无失稳约束的变密度法优化结果来说明该方法的有效性。
1 优化问题数学模型基于经典变密度法,建立以单元相对密度为设计变量,结构最小柔度为目标函数,体积和失稳载荷因子为约束条件的优化问题数学模型,如式(1)所示:
| $ \left\{ \begin{array}{l} {\rm{find}}\;\;\;\rho = \left( {{\rho _1},{\rho _2}, \cdots ,{\rho _i}, \cdots ,{\rho _n}} \right)\\ \min \;\;\;C\left( \rho \right) = {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{KU}} = \sum\limits_{i = 1}^n {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\mathit{\boldsymbol{u}}_i^{\rm{T}}f\left( {{\rho _i},{\mathit{\boldsymbol{k}}_0}} \right){\mathit{\boldsymbol{u}}_i}} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}},i = 1,2, \cdots ,n\\ \;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{K}} + {\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}} \right){\varphi _1} = 0\\ \;\;\;\;\;\;\;\;V = \sum\limits_{i = 1}^n {{\rho _i}{v_i}} \le {V^ * }\\ \;\;\;\;\;\;\;\;{\lambda _1} \ge {\lambda ^ * }\\ \;\;\;\;\;\;\;\;0 < {\rho _{\min }} \le {\rho _i} \le 1 \end{array} \right. $ | (1) |
式中:ρ为单元相对密度矢量;C为结构柔度;n为结构中单元的数量;U为结构节点位移矢量;K为结构总刚度矩阵;ui为单元i节点位移矢量;ki为单元i的刚度矩阵;k0为刚度矩阵常量;F为结构载荷矢量;Kg为结构的几何刚度矩阵;λ1为第1阶失稳载荷因子;φ1为第1阶屈曲模态;V为结构体积;vi为单元i(即实体单元)的体积;V*为约束体积;λ*为失稳载荷因子下限;ρmin为单元相对密度下限。
2 基于SIMP法的材料插值模型使用变密度法进行连续体结构拓扑优化时,需要对中间密度值进行惩罚,从而使单元相对密度趋向0或1,避免灰度单元的出现。本文使用目前最流行的SIMP(solid isotropic microstructures with penalization,固体各向同性惩罚微结构)法[13]对单元相对密度进行插值,插值公式为:
| $ {E_{\left( {{\rho _i}} \right)}} = {\left( {{\rho _i}} \right)^p}{E_0} $ | (2) |
式中:E(ρi)为插值后的弹性模量;p为惩罚因子;E0为实体材料的弹性模量。
3 灵敏度计算对于式(1)中的结构柔度C(ρ)、体积V和第1阶失稳载荷因子λ1,在后续优化准则的推导中,需使用到它们对设计变量ρi的一阶偏导,即灵敏度。下面对C(ρ),V,λ1的灵敏度进行推导。
3.1 结构柔度灵敏度根据式(1)中结构柔度的表达式,可得柔度C的灵敏度表达式:
| $ \frac{{\partial C}}{{\partial {\rho _i}}} = \frac{{\partial \left( {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{KU}}} \right)}}{{\partial {\rho _i}}} = \frac{{\partial {\mathit{\boldsymbol{U}}^{\rm{T}}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{KU}} + {\mathit{\boldsymbol{U}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{U + }}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{K}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial {\rho _i}}} $ | (3) |
式中U=K-1F。
由材料插值模型及平面四边形单元的刚度矩阵,可得ki=(ρi)pk0,进而可求得刚度矩阵及其逆矩阵对设计变量的偏导:
| $ \left\{ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{k}}_i}}}{{\partial {\rho _i}}} = p \cdot {\left( {{\rho _i}} \right)^{p - 1}}{\mathit{\boldsymbol{k}}_0} = \frac{p}{{{\rho _i}}}{\left( {{\rho _i}} \right)^p}{\mathit{\boldsymbol{k}}_0} = \frac{p}{{{\rho _i}}}{\mathit{\boldsymbol{k}}_i}\\ \frac{{\partial \mathit{\boldsymbol{k}}_i^{ - 1}}}{{\partial {\rho _i}}} = \frac{{ - \frac{{\partial {\mathit{\boldsymbol{k}}_i}}}{{\partial {\rho _i}}}}}{{\mathit{\boldsymbol{k}}_i^2}} = - \frac{p}{{{\rho _i}}}\mathit{\boldsymbol{k}}_i^{ - 1} \end{array} \right. $ | (4) |
将U=K-1F及式(4)代入式(3), 可得:
| $ \begin{array}{l} \frac{{\partial C}}{{\partial {\rho _i}}} = \frac{{\partial {{\left( {{\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)}^{\rm{T}}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{KU}} + {\mathit{\boldsymbol{U}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{U}} + {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{K}}\frac{{\partial \left( {{\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)}}{{\partial {\rho _i}}} = \\ \;\;\;\;\;\;\;\;\; - \frac{p}{{{\rho _i}}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i} + \frac{p}{{{\rho _i}}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i} - \frac{p}{{{\rho _i}}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i} = \\ \;\;\;\;\;\;\;\;\; - \frac{p}{{{\rho _i}}}{c_i} \end{array} $ | (5) |
式中ci为单元i的柔度。
3.2 体积灵敏度体积灵敏度如式(6)所示:
| $ \frac{{\partial V}}{{\partial {\rho _i}}} = \frac{{\partial \left( {\sum\limits_{i = 1}^n {{\rho _i}{v_0}} } \right)}}{{\partial {\rho _i}}} = {v_0} $ | (6) |
由结构稳定性线性特征值理论,可得经典的稳定性分析特征方程[14]为:
| $ \left( {\mathit{\boldsymbol{K}} + {\lambda _k}{\mathit{\boldsymbol{K}}_{\rm{g}}}} \right){\varphi _k} = 0 $ | (7) |
式中:λk, φk为第k阶失稳载荷因子及对应的失稳屈曲模态。
| $ \varphi _k^{\rm{T}}\mathit{\boldsymbol{K}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k} = 0 $ | (8) |
式(8)对设计变量ρi求偏导,得:
| $ \begin{array}{l} \frac{{\partial \varphi _k^{\rm{T}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{K}}{\varphi _k} + \varphi _k^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}{\varphi _k} + \varphi _k^{\rm{T}}\mathit{\boldsymbol{K}}\frac{{\partial \varphi _k}}{{\partial {\rho _i}}} + \frac{{\partial {\lambda _k}}}{{\partial {\rho _i}}}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k} + \\ {\lambda _k}\frac{{\partial \varphi _k^{\rm{T}}}}{{\partial {\rho _i}}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{K}}_g}}}{{\partial {\rho _i}}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}\frac{{\partial {\varphi _k}}}{{\partial {\rho _i}}} = 0 \end{array} $ | (9) |
由于K, Kg为对称矩阵,则可得:
| $ \left\{ \begin{array}{l} \frac{{\partial \varphi _k^{\rm{T}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{K}}{\varphi _k} = \varphi _k^{\rm{T}}\mathit{\boldsymbol{K}}\frac{{\partial {\varphi _k}}}{{\partial {\rho _i}}}\\ \frac{{\partial \varphi _k^{\rm{T}}}}{{\partial {\rho _i}}}{\mathit{\boldsymbol{K}}_g}{\varphi _k} = {\lambda _k}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}\frac{{\partial {\varphi _k}}}{{\partial {\rho _i}}} \end{array} \right. $ | (10) |
根据式(10)、式(9)可简化为:
| $ \begin{array}{*{20}{c}} {2{{\left( {\frac{{\partial {\varphi _k}}}{{\partial {\rho _i}}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{K}}{\varphi _k} + {\lambda _k}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k}} \right) + \varphi _k^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}{\varphi _k} + }\\ {\frac{{\partial {\lambda _k}}}{{\partial {\rho _i}}}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{K}}_{\rm{g}}}}}{{\partial {\rho _i}}}{\varphi _k} = 0} \end{array} $ | (11) |
将式(7)代入式(11),得:
| $ \varphi _k^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}{\varphi _k} + \frac{{\partial {\lambda _k}}}{{\partial {\rho _i}}}\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{K}}_{\rm{g}}}}}{{\partial {\rho _i}}}{\varphi _k} = 0 $ | (12) |
式(12)经变换得到失稳载荷因子λk的灵敏度,如式(13)所示:
| $ \begin{array}{l} \frac{{\partial {\lambda _k}}}{{\partial {\rho _i}}} = - \frac{{\varphi _k^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}{\varphi _k} + {\lambda _k}\varphi _k^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{K}}_{\rm{g}}}}}{{\partial {\rho _i}}}{\varphi _k}}}{{\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k}}} = \\ \;\;\;\;\;\;\;\;\; - \frac{p}{\rho }\frac{{\psi _{ki}^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\psi _{ki}} + {\lambda _k}\psi _{ki}^{\rm{T}}{\mathit{\boldsymbol{k}}_{{\rm{g}}i}}{\psi _{ki}}}}{{\varphi _k^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _k}}} \end{array} $ | (13) |
式中:kgi为单元i的几何刚度矩阵,ψki为单元i的第k阶失稳模态。
4 考虑稳定性的变密度法优化准则利用上述优化问题数学模型及计算得到的灵敏度,采用拉格朗日乘子法推导优化准则。
首先构建数学模型的拉格朗日函数:
| $ \begin{array}{l} L = C + \beta _1^{\rm{T}}\left( {\mathit{\boldsymbol{KU}} - \mathit{\boldsymbol{F}}} \right) + \beta _2^{\rm{T}}\left( {\mathit{\boldsymbol{K}} + {\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}} \right){\varphi _1} + \\ \;\;\;\;\;\;{\mu _1}\left( {V - {V^ * } + x_1^2} \right) + {\mu _2}\left( {{\lambda ^ * } - {\lambda _1} + x_2^2} \right) + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^n {{\mu _{3i}}\left( {{\rho _{\min }} - {\rho _i} + x_{3i}^2} \right)} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^n {{\mu _{4i}}\left( {{\rho _i} - 1 + x_{4i}^2} \right)} \end{array} $ | (14) |
式中:β1,β2,μ1,μ2,μ3i,μ4i为拉格朗日乘子;x1,x2,x3i,x4i为松弛变量。
当目标函数C取得极值时,拉格朗日函数(14)需满足以下库恩-塔克(Kuhn-Tucker)条件:
| $ \left\{ \begin{array}{l} \frac{{\partial L}}{{\partial {\rho _i}}} = \frac{{\partial C}}{{\partial {\rho _i}}} + \beta _1^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{KU}}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{K}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {{\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \\ \;\;\;\;\;\;\;\;\;{\mu _1}\frac{{\partial V}}{{\partial {\rho _i}}} - {\mu _2}\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}} - {\mu _{3i}} + {\mu _{4i}} = 0\\ \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}}\\ \left( {\mathit{\boldsymbol{K}} + {\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}} \right){\varphi _1} = 0\\ {\mu _1}\left( {V - {V^ * }} \right) = 0,{\mu _1} \ge 0\\ {\mu _2}\left( {{\lambda ^ * } - {\lambda _1}} \right) = 0,{\mu _2} \ge 0\\ {\mu _{3i}}\left( {{\rho _{\min }} - {\rho _i}} \right) = 0,{\mu _{3i}} \ge 0\\ {\mu _{4i}}\left( {{\rho _i} - 1} \right) = 0,{\mu _{4i}} \ge 0 \end{array} \right. $ | (15) |
针对设计变量ρi的取值情况:当ρi=ρmin时,设计变量半径下限起约束作用,有μ3i>0, μ4i=0;当ρi=1时,设计变量半径上限起约束作用,有μ3i=0, μ4i>0;当ρmin < ρi < 1时,设计变量半径上下限均不起约束作用,有μ3i=0,μ4i=0。故式(15)可改写为:
| $ \left\{ \begin{array}{l} \frac{{\partial C}}{{\partial {\rho _i}}} + \beta _1^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{KU}}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{K}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {{\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \\ {\mu _1}\frac{{\partial V}}{{\partial {\rho _i}}} - {\mu _2}\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}} = {\mu _{3i}} - {\mu _{4i}}\left\{ \begin{array}{l} > 0,{\rho _i} = {\rho _{\min }}\\ < 0,{\rho _i} = 1\\ = 0,{\rho _{\min }} < {\rho _i} < 1 \end{array} \right.\\ \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}}\\ {\mu _1}\left( {V - {V^ * }} \right) = 0,{\mu _1} \ge 0\\ {\mu _2}\left( {{\lambda ^ * } - {\lambda _1}} \right) = 0,{\mu _2} \ge 0 \end{array} \right. $ | (16) |
考虑上式中μ3i-μ4i=0的情况,即:
| $ \begin{array}{l} \frac{{\partial C}}{{\partial {\rho _i}}} + \beta _1^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{KU}}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {\mathit{\boldsymbol{K}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\frac{{\partial \left( {{\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _1}} \right)}}{{\partial {\rho _i}}} + \\ \;\;\;\;\;\;\;\;\;{\mu _1}\frac{{\partial V}}{{\partial {\rho _i}}} - {\mu _2}\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}} = 0 \end{array} $ | (17) |
将式(17)展开并整理,得到:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{U}}^{\rm{T}}}}}{{\partial {\rho _i}}}\left( {2\mathit{\boldsymbol{KU}} + \mathit{\boldsymbol{K}}{\beta _1}} \right) + \left( {{\mathit{\boldsymbol{U}}^{\rm{T}}} + \beta _1^{\rm{T}}} \right)\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{U}} + \\ \beta _2^{\rm{T}}\left( {\mathit{\boldsymbol{K}} + {\lambda _1}{\mathit{\boldsymbol{K}}_{\rm{g}}}} \right)\frac{{\partial {\varphi _1}}}{{\partial {\rho _i}}} + \beta _2^{\rm{T}}\left( {\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}} + {\lambda _1}\frac{{\partial {\mathit{\boldsymbol{K}}_{\rm{g}}}}}{{\partial {\rho _i}}}} \right){\varphi _1} + \\ \beta _2^{\rm{T}}\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}}{\mathit{\boldsymbol{K}}_{\rm{g}}}{\varphi _1} + {\mu _1}{v_i} - {\mu _2}\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}} = 0 \end{array} $ | (18) |
其中,β1为结构平衡约束拉格朗日乘子,β2为屈曲特征方程拉格朗日乘子,因结构平衡和屈曲方程始终满足,故β1,β2可取任意值,取β1=-2U,β2=φ1。将式(5),(6)和(13)代入式(18)后化简得到:
| $ \begin{array}{l} - \frac{p}{{{\rho _i}}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i} + {\mu _1}{v_i} + \frac{p}{{{\rho _i}}}\left( {\psi _{1i}^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\psi _{1i}} + } \right.\\ \left. {{\lambda _1}\psi _{1i}^{\rm{T}}{\mathit{\boldsymbol{k}}_{{\rm{g}}i}}{\psi _{1i}}} \right)\left( {1 + \frac{{{\mu _2}}}{{{E_{\rm{g}}}}}} \right) = 0 \end{array} $ | (19) |
整理得到:
| $ {f_i} = \frac{{ - 2p{e_{{\rm{s}}i}} + p\left( {{e_{{\rm{b}}i}} + {\lambda _1}{e_{{\rm{g}}i}}} \right)\left( {1 + {\mu _2}/{E_{\rm{g}}}} \right)}}{{{\mu _1}{v_i}{\rho _i}}} = 1 $ | (20) |
式中:Eg=φ1TKgφ1,为结构的几何应变能; egi=ψ1iTkgiψ1i, 为单元i的几何应变能,ψ1i为单元i的第1阶失稳模态; esi=uiTkiui为单元i的静力学应变能; ebi=ψ1iTkiψ1i为在第1阶失稳模态下的应变能。fi即为基于拉格朗日函数和Kuhn-Tucker条件推导出的单元相对密度优化准则,则单元相对密度的迭代公式可表示为:
| $ \rho _i^{\left( {t + 1} \right)} = \left\{ \begin{array}{l} {\left( {f_i^{\left( t \right)}} \right)^\delta }\rho _i^{\left( t \right)},\;\;\;\;\;{\rho _{\min }} < {\left( {f_i^{\left( t \right)}} \right)^\delta }\rho _i^{\left( t \right)} < 1\\ {\rho _{\min }},\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {f_i^{\left( t \right)}} \right)^\delta }\rho _i^{\left( t \right)} \le {\rho _{\min }}\\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {f_i^{\left( t \right)}} \right)^\delta }\rho _i^{\left( t \right)} \ge 1 \end{array} \right. $ | (21) |
式中:ρi(t)表示单元i在第t次迭代对应的单元相对密度,δ为阻尼系数,引入δ可减缓优化进程,保证数值计算的稳定性。
要计算得到fi(t), 首先需要求得拉格朗日乘子μ1和μ2,μ1是拉格朗日函数中体积约束所引入的乘子,故μ1的取值需满足体积约束条件,而μ2则满足失稳载荷因子约束条件。假设设计变量由第t次迭代的ρi(t)更新到第t+1次迭代的ρi(t+1)时,结构体积由V(t)更新为V(t+1),结构失稳载荷因子由λ1(t)更新为λ1(t+1)。将V(t+1)在V(t)领域内泰勒展开,并保留到一阶项,则有:
| $ \begin{array}{l} {V^{\left( {t + 1} \right)}} = {V^{\left( t \right)}} + \sum\limits_{i = 1}^n {\frac{{\partial V}}{{\partial {\rho _i}}}\left| {_{{\rho _i} = \rho _i^{\left( t \right)}}} \right.\left( {\rho _i^{\left( {t + 1} \right)} - \rho _i^{\left( t \right)}} \right)} = {V^{\left( t \right)}} + \\ \sum\limits_{i = 1}^n {{v_i}\rho _i^{\left( t \right)}\left[ {\frac{{ - 2pe_{{\rm{s}}i}^{\left( t \right)} + p\left( {e_{{\rm{b}}i}^{\left( t \right)} + {\lambda _1}e_{{\rm{g}}i}^{\left( t \right)}} \right)\left( {1 + {\mu _2}/E_{\rm{g}}^{\left( t \right)}} \right)}}{{{\mu _1}{v_i}\rho _i^{\left( t \right)}}} - 1} \right]} \end{array} $ | (22) |
同理展开第1阶失稳载荷因子λ1(t+1), 可以得到:
| $ \begin{array}{*{20}{c}} {\lambda _1^{\left( {t + 1} \right)} = \lambda _1^{\left( t \right)} + \sum\limits_{i = 1}^n {\frac{{\partial {\lambda _1}}}{{\partial {\rho _i}}}\left| {_{{\rho _i} = \rho _i^{\left( t \right)}}} \right.\left( {\rho _i^{\left( {t + 1} \right)} - \rho _i^{\left( t \right)}} \right)} = }\\ {\lambda _1^{\left( t \right)} - \sum\limits_{i = 1}^n {p\frac{{{e_i} + {\lambda _1}{e_{{\rm{g}}i}}}}{{{E^{\left( t \right)}}}}} \times }\\ {\left[ {\frac{{ - 2pe_{{\rm{s}}i}^{\left( t \right)} + p\left( {e_{{\rm{b}}i}^{\left( t \right)} + {\lambda _1}e_{{\rm{g}}i}^{\left( t \right)}} \right)\left( {1 + {\mu _2}/E_{\rm{g}}^{\left( t \right)}} \right)}}{{{\mu _1}{v_i}\rho _i^{\left( t \right)}}} - 1} \right]} \end{array} $ | (23) |
在优化过程中,考虑到V(t+1)=V*,λ1(t+1)=λ1*,即可通过联立求解式(22)和式(23)得到拉格朗日乘子μ1,μ2。
5 几何刚度矩阵显式推导在式(19)中,还需使用egi=ψ1iTkgiψ1i计算单元i的几何应变能。因此,首先需要计算单元的几何刚度矩阵kg[15], 单元的刚度矩阵的计算公式为[16]:
| $ {\mathit{\boldsymbol{k}}_{\rm{g}}} = \int {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{SG}}{\rm{d}}V} $ | (24) |
式中:G是与单元形函数有关的微分矩阵,S是与单元应力有关的矩阵,V为单元体积。对于平面四边形单元,G和S的表达式如下[17]:
| $ \begin{array}{l} \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}&0\\ 0&{\frac{\partial }{{\partial x}}}\\ {\frac{\partial }{{\partial y}}}&0\\ 0&{\frac{\partial }{{\partial y}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{N_m}}&0&{{N_q}}&0&{{N_u}}&0&{{N_v}}&0\\ 0&{{N_m}}&0&{{N_q}}&0&{{N_u}}&0&{{N_v}} \end{array}} \right] = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} \begin{array}{l} {N_{m,x}}\\ 0\\ {N_{m,y}}\\ 0 \end{array}&\begin{array}{l} 0\\ {N_{m,x}}\\ 0\\ {N_{m,y}} \end{array}&\begin{array}{l} {N_{q,x}}\\ 0\\ {N_{q,y}}\\ 0 \end{array}&\begin{array}{l} 0\\ {N_{q,x}}\\ 0\\ {N_{q,y}} \end{array}&\begin{array}{l} {N_{u,x}}\\ 0\\ {N_{u,y}}\\ 0 \end{array}&\begin{array}{l} 0\\ {N_{u,x}}\\ 0\\ {N_{u,y}} \end{array}&\begin{array}{l} {N_{v,x}}\\ 0\\ {N_{v,y}}\\ 0 \end{array}&\begin{array}{l} 0\\ {N_{v,x}}\\ 0\\ {N_{v,y}} \end{array} \end{array}} \right] \end{array} $ | (25) |
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_{xx}}}&{{\mathit{\boldsymbol{s}}_{xy}}}\\ {{\mathit{\boldsymbol{s}}_{yx}}}&{{\mathit{\boldsymbol{s}}_{yy}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\sigma _x}}&0&{{\tau _{xy}}}&0\\ 0&{{\sigma _x}}&0&{{\tau _{xy}}}\\ {{\tau _{xy}}}&0&{{\sigma _y}}&0\\ 0&{{\tau _{xy}}}&0&{{\sigma _y}} \end{array}} \right] $ | (26) |
式中:Nm, Nq, Nu, Nv为四边形单元的形函数。
将G和S代入式(24),可得平面四边形单元的几何刚度矩阵的显式表示:
| $ {\mathit{\boldsymbol{k}}_{\rm{g}}} = \int {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{SG}}{\rm{d}}V} = \left[ {\begin{array}{*{20}{c}} {k_{\rm{g}}^{mm}}&0&{k_{\rm{g}}^{mq}}&0&{k_{\rm{g}}^{mu}}&0&{k_{\rm{g}}^{mv}}&0\\ 0&{k_{\rm{g}}^{mm}}&0&{k_{\rm{g}}^{mq}}&0&{k_{\rm{g}}^{mu}}&0&{k_{\rm{g}}^{mv}}\\ {k_{\rm{g}}^{qm}}&0&{k_{\rm{g}}^{qq}}&0&{k_{\rm{g}}^{qu}}&0&{k_{\rm{g}}^{qv}}&0\\ 0&{k_{\rm{g}}^{qm}}&0&{k_{\rm{g}}^{qq}}&0&{k_{\rm{g}}^{qu}}&0&{k_{\rm{g}}^{qv}}\\ {k_{\rm{g}}^{um}}&0&{k_{\rm{g}}^{uq}}&0&{k_{\rm{g}}^{uu}}&0&{k_{\rm{g}}^{uv}}&0\\ 0&{k_{\rm{g}}^{um}}&0&{k_{\rm{g}}^{uq}}&0&{k_{\rm{g}}^{uu}}&0&{k_{\rm{g}}^{uv}}\\ {k_{\rm{g}}^{vm}}&0&{k_{\rm{g}}^{vq}}&0&{k_{\rm{g}}^{vu}}&0&{k_{\rm{g}}^{vv}}&0\\ 0&{k_{\rm{g}}^{vm}}&0&{k_{\rm{g}}^{vq}}&0&{k_{\rm{g}}^{vu}}&0&{k_{\rm{g}}^{vv}} \end{array}} \right] $ | (27) |
式中:
| $ \begin{array}{l} k_{\rm{g}}^{rs} = \int {\int\limits_A {\left[ {{N_{r,x}},{N_{r,y}}} \right]\left[ {\begin{array}{*{20}{c}} {{\sigma _x}}&{{\tau _{xy}}}\\ {{\tau _{xy}}}&{{\sigma _y}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{N_{s,x}}}\\ {{N_{s,y}}} \end{array}} \right]{\rm{d}}x{\rm{d}}y} } = \\ \int {\int\limits_A {\left[ {{N_{s,x}}\left( {{N_{r,x}}{\sigma _x} + {N_{r,y}}{\tau _{xy}}} \right) + {N_{s,y}}\left( {{N_{r,x}}{\tau _{xy}} + {N_{r,y}}{\sigma _y}} \right)} \right]{\rm{d}}x{\rm{d}}y} } = \\ \int {\int\limits_A {{N_{s,x}}{N_{r,x}}{\sigma _x}{\rm{d}}x{\rm{d}}y} } + \int {\int\limits_A {\left( {{N_{s,x}}{N_{r,y}} + {N_{s,y}}{N_{r,x}}} \right){\tau _{xy}}{\rm{d}}x{\rm{d}}y} } + \\ \int {\int\limits_A {{N_{s,y}}{N_{r,y}}{\sigma _y}{\rm{d}}x{\rm{d}}y} } = k_{{\rm{g}}x}^{rs} + k_{{\rm{g}}xy}^{rs} + k_{{\rm{g}}y}^{rs} \end{array} $ | (28) |
| $ \left\{ \begin{array}{l} k_{{\rm{g}}x}^{rs} = \int {\int\limits_A {{N_{s,x}}{N_{r,x}}{\sigma _x}{\rm{d}}x{\rm{d}}y} } \\ k_{{\rm{g}}xy}^{rs} = \int {\int\limits_A {\left( {{N_{s,x}}{N_{r,y}} + {N_{s,y}}{N_{r,x}}} \right){\tau _{xy}}{\rm{d}}x{\rm{d}}y} } \\ k_{{\rm{g}}y}^{rs} = \int {\int\limits_A {{N_{s,y}}{N_{r,y}}{\sigma _y}{\rm{d}}x{\rm{d}}y} } \end{array} \right. $ | (29) |
式中:r=m, q, u, v; s=m, q, u, v。
对于平面四边形单元,有:
| $ {N_r} = \frac{1}{4}\left( {1 + {\xi _r}\xi } \right)\left( {1 + {\eta _r}\eta } \right),r = m,q,u,v $ | (30) |
其中ξ,η为局部坐标,它们与整体坐标x,y的转换关系为:
| $ \xi = \frac{1}{a}\left( {x - {x_0}} \right),\eta = \frac{1}{b}\left( {y - {y_0}} \right) $ | (31) |
其中2a,2b为四边形单元的边长。
因此,可求得形函数对坐标x, y的微分为:
| $ \left\{ \begin{array}{l} {N_{r,x}} = \frac{1}{{4a}}{\xi _r}\left( {1 + {\eta _r}\eta } \right)\\ {N_{r,y}} = \frac{1}{{4b}}\left( {1 + {\xi _r}\xi } \right){\eta _r} \end{array} \right. $ | (32) |
将式(32)代入式(29),得:
| $ \left\{ \begin{array}{l} k_{gx}^{rs} = \frac{{{\sigma _x}b}}{{4a}}{\xi _r}{\xi _s}\left( {1 + \frac{{{\eta _r}{\eta _s}}}{3}} \right)\\ k_{gxy}^{rs} = \frac{{{\tau _{xy}}}}{4}\left( {{\xi _r}{\eta _s} + {\xi _s}{\eta _r}} \right)\\ k_{gy}^{rs} = \frac{{{\sigma _y}a}}{{4b}}{\eta _r}{\eta _s}\left( {1 + \frac{{{\xi _r}{\xi _s}}}{3}} \right) \end{array} \right. $ | (33) |
变密度拓扑优化方法由于引入了中间密度单元,会在优化的过程中出现低密度区域,导致虚假模态的出现,影响优化进程。本文采用文献[9]提出的虚假模态处理方法,以识别虚假模态。将低密度区域模态应变能贡献比值作为判断指标,设定一个密度阀值ρr,依据密度值将单元分为2个集合:Cl={i|ρi≤ρr}和Ch={i|ρi≥ρr}。然后计算两集合中单元的应变能之比,依据式(34)识别虚假模态。
| $ \frac{{E{c_{\rm{l}}}}}{{E{c_{\rm{h}}}}} \le {M_{\rm{r}}} $ | (34) |
式中:ECl为低密度单元的应变能,ECh为高密度单元的应变能; Mr为识别系数, 其取值在(0, 1)之间。
7 优化方法流程考虑结构稳定性的变密度拓扑优化方法的具体流程如图 1所示。首先建立优化问题的数学模型并初始化基本参数;然后进行静力学分析,并提取单元应力(用于构建应力矩阵S)及应变能(用于求解式(20)中的应变能esi);之后进行屈曲分析,获取结构的失稳模态(用于计算式(20)中结构及单元的几何应变能Eg, egi, ebi);基于以上静力学及屈曲分析得到的分析结果,利用式(24)计算得到几何刚度矩阵kg并使用Eg=φ1TKgφ1和egi=ψ1iTkgiψ1i两等式进一步计算得到结构和单元的几何应变能;进而得到单元柔度、体积和失稳载荷因子的灵敏度;然后使用式(23)、(24)计算拉格朗日乘子μ1,μ2,并代入式(20)得到优化迭代算子fi; 最后判断是否满足优化终止条件V≤V*和λ1≥λ*,满足则优化停止,否则利用式(20)更新单元相对密度并进入下一次优化迭代。
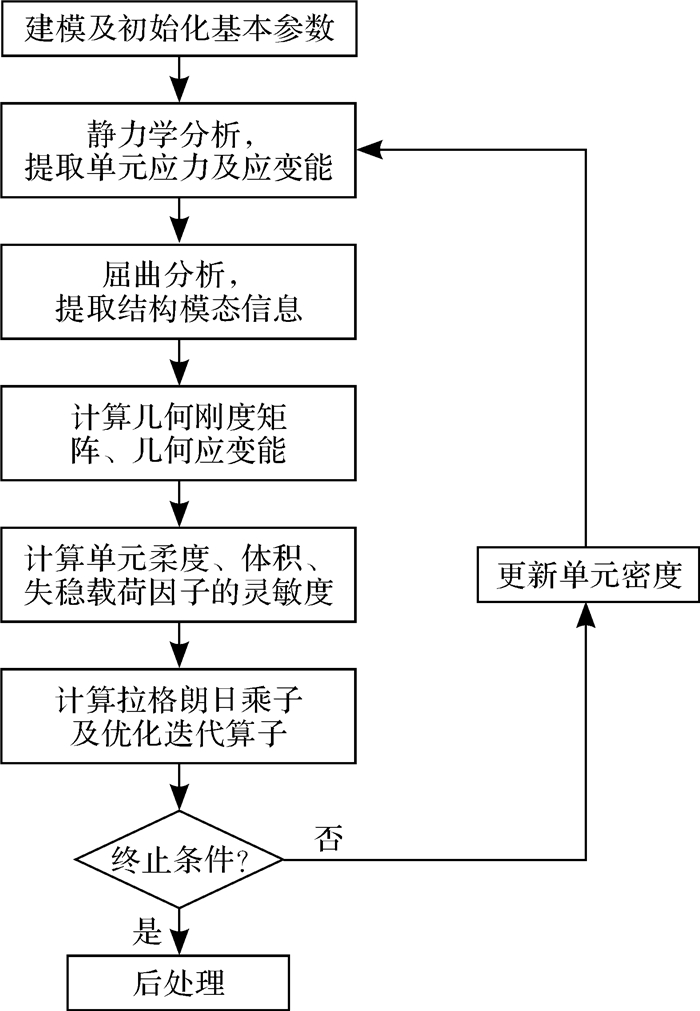
|
| 图 1 考虑结构稳定性的变密度拓扑优化方法流程图 Fig.1 The flow chart of variable density topology optimization method considering structural stability |
图 2所示为受压柱模型,设计域宽度W=1 m,高度H=2 m,结构的材料参数及优化设计参数如表 1所示。在设计域顶端中部施加均布载荷P=107 Pa。使用40×80个的四节点四边形平面应变单元对设计域进行网格离散。求解在体积和失稳载荷因子约束下以结构柔度最小为目标的拓扑优化问题。
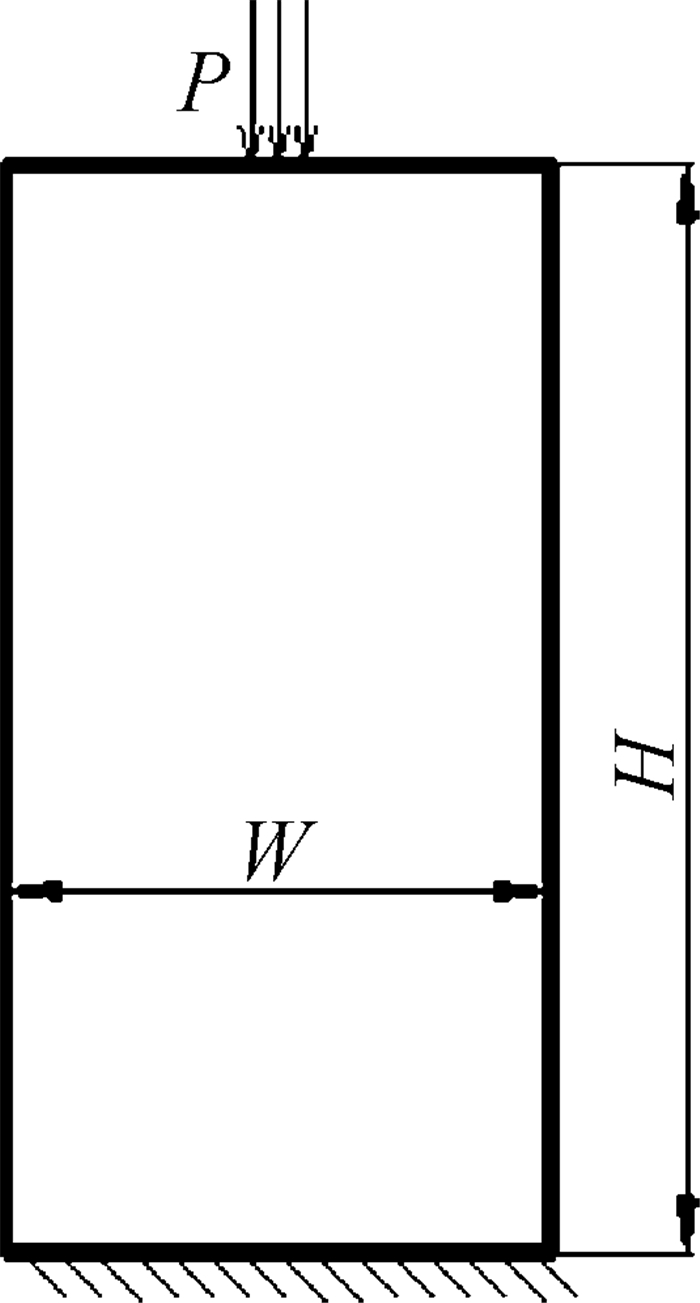
|
| 图 2 受压柱模型 Fig.2 Compression column model |
| 参数 | 数值 |
| 弹性模量E/GPa | 206 |
| 泊松比ν | 0.3 |
| 体积约束V* | 0.4V0 |
| 失稳载荷因子约束λ* | 0.6λ0 |
| 相对密度下限ρmin | 0.001 |
| 半径上限rmax/mm | 30 |
| 阻尼系数δ | 0.3 |
图 3为柔度C、体积V和失稳载荷因子λ1的优化过程曲线,在优化过程中,经历了18次优化迭代后,结构的柔度增大,体积和失稳载荷因子减小。如表 2所示,最终优化停止时,柔度为41 772 N·m,是初始柔度的2.17倍;失稳载荷因子为104.4,是初始失稳载荷因子的57%;体积为初始体积的58%。由此可见体积并未达到给定的0.4V0的约束条件,这是因为失稳载荷因子低于给定的0.6λ0时,优化过程停止。说明2个约束条件不一定能同时得到满足。
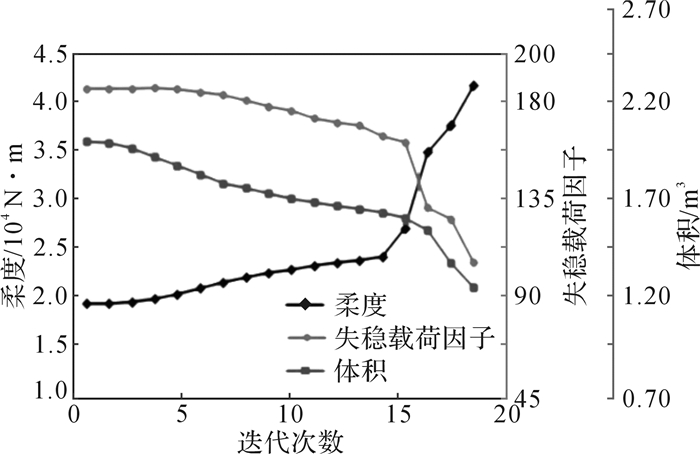
|
| 图 3 柔度、体积、失稳载荷因子的优化过程曲线 Fig.3 The optimization process curve of flexibility, volume and instability load factor |
| 参数 | 优化前 | 考虑稳定性的优化结果(比值) | 不考虑稳定性的优化结果(比值) |
| 柔度/N·m | 19 235 | 41 772(2.17) | 25 788(1.34) |
| 失稳载荷因子 | 184.2 | 104.4(0.57) | 44.9(0.24) |
| 体积/m3 | 2 | 1.16(0.58) | 1.16(0.58) |
图 4为优化过程中结构的拓扑变化过程、失稳模态云图以及相应的优化过程数据。由图可见结构下部两侧的材料被保留以保证稳定性和一定的刚度,同时在上部两侧及中间区域去除材料以减小体积。与图 3相对应来看,在第14次迭代之前,结构主要在顶部两侧及底部中央去除材料,优化进程较缓。在第14次迭代以后,结构内部开始出现孔洞,优化进程加快。最终,失稳载荷因子约束条件破坏,优化终止。
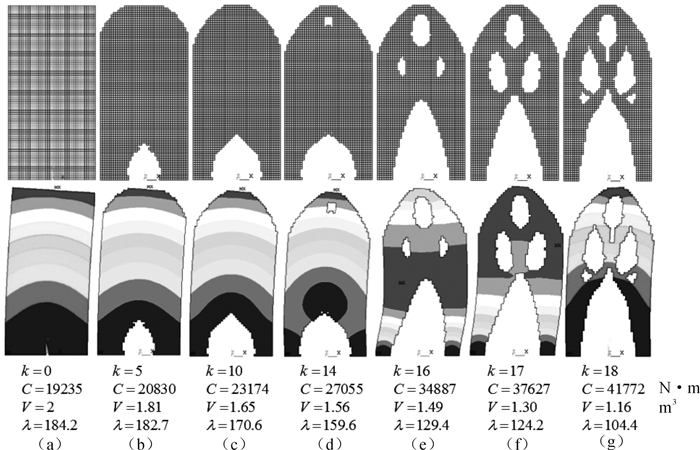
|
| 图 4 优化过程拓扑变化及相应的失稳模态 Fig.4 The topology changes and instability modes in the optimization process |
为实现对比说明,针对不考虑稳定性的拓扑优化问题,利用仅考虑体积约束下以结构柔度最小为目标的传统变密度法对上述模型进行拓扑优化。在上述考虑稳定性约束的优化问题中,优化后模型的体积收敛为初始模型体积的0.58,因此使用V*=0.58 V0作为体积约束条件进行优化。图 5为不考虑稳定性约束时的拓扑优化构型及失稳模态。可见,与考虑稳定性时的优化结果不同,材料主要分布在最短传力路径上,以实现柔度最小化的目标。具体优化结果见表 2, 表中比值是指优化后结果与优化前结果的比值。由表 2可见:在相同的体积下(0.58V0),不考虑稳定性约束时,得到的柔度为25 788 N·m,失稳载荷因子为44.9;而考虑稳定性时,得到的柔度为41 772 N·m,失稳载荷因子为104.4。因此,考虑稳定性的变密度拓扑优化方法能非常有效地提高结果的稳定性,但可能在结构刚度方面有一些妥协。
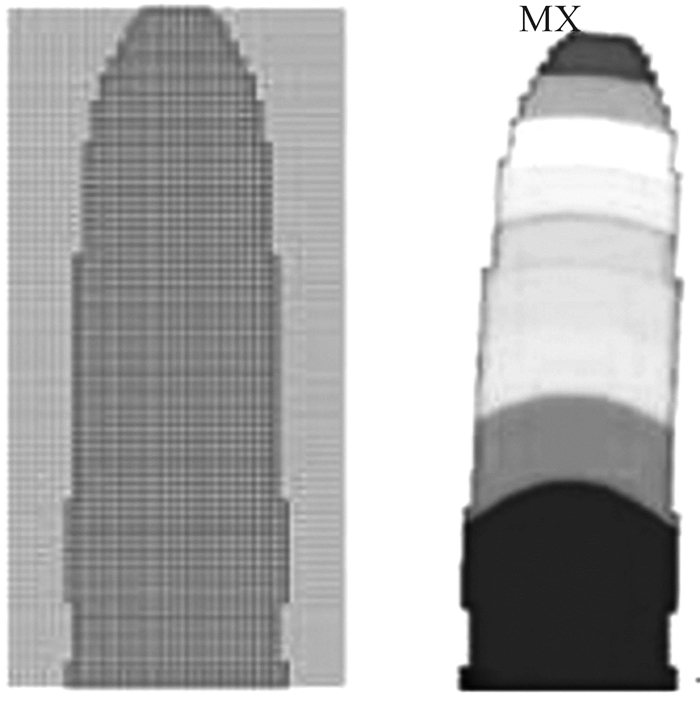
|
| 图 5 不考虑稳定性约束时的拓扑优化构型及失稳模态 Fig.5 The topology optimization configuration and instability modes without considering stability constraints |
对优化过程进一步研究后发现,当改变网格单元的大小后,优化过程会受到一定的影响。当减小网格单元的大小时,即使用42×84个四节点四边形平面应变单元对设计域进行网格离散时,保持其余条件不变,迭代16次后,失稳载荷因子为74.87,体积与原始体积比值为0.59,拓扑优化后得到的优化结构如图 6所示,与使用40×80个单元迭代16次得到的优化结构不同。通过分析发现,在优化过程中网格单元大小的改变会导致局部结构失稳现象的出现,从而影响最终的优化结果。
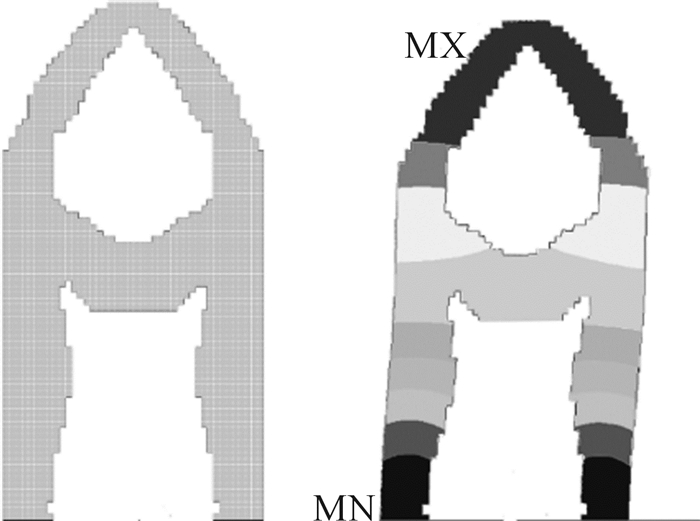
|
| 图 6 使用40×80个单元进行网格离散时的拓扑优化结果 Fig.6 The topology optimization result of grid discretization using 40×80 units |
通过引入失稳载荷因子约束,提出了一种考虑结构稳定性的变密度拓扑优化方法。其中,通过推导单元的几何刚度矩阵,计算几何应变能,从而得到失稳载荷因子的灵敏度是求解优化问题的关键。优化算例表明,该考虑稳定性约束的变密度拓扑优化方法能显著提高结构的稳定性,需要注意的是,虽然该方法提高了结构的稳定性,但在柔度方面会有一定妥协。即在相同的约束条件下,结构的刚度优化和稳定性优化将会在一定程度上相互约束。此外,使用体积和失稳载荷因子双约束条件时,2个约束条件不一定都能得到满足,并且边界条件的设定会对静力学分析及屈曲分析过程产生影响,进而影响最终的优化结果。在进行屈曲分析时,网格单元的大小会影响求解精度,也会影响优化过程。
| [1] |
焦洪宇, 周奇才, 李文军, 等.
基于变密度法的周期性拓扑优化[J]. 机械工程学报, 2013, 49(13): 132–138.
JIAO Hong-yu, ZHOU Qi-cai, LI Wen-jun, et al. Periodic topology optimization using variable density method[J]. Journal of Mechanical Engineering, 2013, 49(13): 132–138. |
| [2] | BROWNE P A, BUDD C, GOULD N, et al. A fast method for binary programming using first-order derivatives, with application to topology optimization with buckling constraints[J]. International Journal for Numerical Methods in Engineering, 2012, 92(12): 1026–1043. DOI:10.1002/nme.v92.12 |
| [3] | ZHOU M. Topology optimization for shell structures with linear buckling responses[C]//World Congress on Computational Mechanics in Conjunction with the Second Asian-Pacific Congress on Computational Mechanics, Beijing, Sept. 5-10, 2004. |
| [4] |
隋允康, 边炳传.
屈曲与应力约束下连续体结构的拓扑优化[J]. 工程力学, 2008, 25(8): 6–12.
SUI Yun-kang, BIAN Bing-chuan. Topology optimization of continuum structures under buckling and stress constraints[J]. Engineering Mechanics, 2008, 25(8): 6–12. |
| [5] |
隋允康, 边炳传, 叶红玲.
连续体结构屈曲约束的ICM方法拓扑优化[J]. 计算力学学报, 2008, 25(3): 345–351.
SUI Yun-kang, BIAN Bing-chuan, YE Hong-ling. Topological optimization of the continuum structure subjected to the buckling constraints with ICM method[J]. Chinese Journal of Computational Mechanics, 2008, 25(3): 345–351. |
| [6] | GUO X, CHENG G, YAMAZAKI K. A new approach for the solution of singular optima in truss topology optimization with stress and local buckling constraints[J]. Structure Multidiscipline Optimization, 2001, 22(5): 364–372. DOI:10.1007/s00158-001-0156-0 |
| [7] | LUND E. Buckling topology optimization of laminated multi-material composite shell structures[J]. Composite Structures, 2009, 91(2): 158–167. DOI:10.1016/j.compstruct.2009.04.046 |
| [8] |
程耿东, 郭旭.
考虑局部稳定性约束的桁架拓扑优化设计[J]. 大连理工大学学报, 1995, 35(6): 770–775.
CHENG Geng-dong, GUO Xu. Inverstigation of truss topology optimization under local buckling constraints[J]. Journal of Dalian University of Technology, 1995, 35(6): 770–775. |
| [9] |
高兴军. 稳定性约束下连续体结构两尺度拓扑优化[D]. 广州: 华南理工大学工木与交通学院, 2015: 46-47.
GAO Xing-jun. Two-scale topology optimization of continuum structures under buckling constraints[D]. Guangzhou: South China University of Technology, School of CML Engineering and Transportation, 2015: 46-47. |
| [10] | NEVES M M, RODRIGUES H, GUEDES J M. Generalized topology design of structures with a buckling load criterion[J]. Structural Optimization, 1995, 10(2): 71–78. DOI:10.1007/BF01743533 |
| [11] | NEVES M M, SIGMUND O, BENDSØE M P. Topology optimization of periodic microstructures with a penalization of highly localized buckling modes[J]. International Journal for Numerical Methods in Engineering, 2002, 54(6): 809–834. DOI:10.1002/nme.v54:6 |
| [12] | SIGMUND O, BENDSOE M P. Material interpolations schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635–654. |
| [13] | MARTINEZ J M. A note on the theoretical convergence properties of the SIMP method[J]. Structural & Multidisciplinary Optimization, 2005, 29(4): 319–323. |
| [14] |
王勖成.
有限单元法[M]. 北京: 清华大学出版社, 2003: 30-50.
WANG Xu-cheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 30-50. |
| [15] | CLOUGH R W. Dynamics of structures[M]. New York: McGraw-Hill, 1993: 366. |
| [16] | EDWARD L.Wilson. Three-dimensional static and dynamic analysis of structures[M]. Berkley: Computer & Structures, Inc., 1996: 9-11. |
| [17] | IVO Senjanovi, VLADIMIR N, CHO D S. A simplified geometric stiffness in stability analysis of thin-walled structures by the finite element method[J]. International Journal of Naval Architecture & Ocean Engineering, 2012, 4(3): 313–321. |



