2. 华中科技大学 机械科学与工程学院, 湖北 武汉 430074
2. School of Mechanical Science & Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
随着计算机仿真技术的发展,仿真模型越来越精确,同时所需要的仿真时间也成几何倍数增长。为了节约计算时间,提高设计效率,Kriging模型[1]、RBF(radial basis function,径向基函数)模型[2]和SVR(support vector regression,支持向量回归)模型[3]等近似模型已经被广泛用于工程设计优化中,如:王国春等[4]将Kriging模型应用于汽车前部结构的耐撞性优化,使B柱加速度最大值达到最小; 高伟钊等[5]基于Kriging模型进行泡沫填充锥形薄壁结构的耐撞性稳健性设计优化; 潘志雄[6]利用径向基函数建立了近似模型,并将它应用于传感器飞机的总体优化设计。
然而,上述学者均采用单一精度的仿真模型进行设计优化,这种方法存在的固有缺点是:若选择高精度的仿真模型,可能会增加不必要的计算代价;若选用低精度的仿真模型,则难以保证设计优化结果的可靠性。解决这一问题的方法是采用变复杂度近似模型[7]。廖代辉等[8]在高/低精度模型之间建立差值Kriging模型,结合多目标粒子群算法进行汽车安全性和轻量化优化。谢晖等[9]在低精度简化模型和高精度模型中建立差值补偿近似模型, 在此模型和简化模型基础上构造新的样本点数据, 并利用RBF近似模型建立新的近似模型,进行汽车碰撞多目标设计优化。但是以上研究的不足在于:1)这些近似模型无法预测自身的预测误差,必须通过交叉验证等计算量较大的方式求解预测误差;2)这些方法通过建立变复杂度近似模型来进行设计优化,并没有根据优化迭代过程中得到的信息自适应地更新变复杂度近似模型,以提高优化解附近的近似模型精度。
综上,本文提出一种基于序贯层次Kriging模型的结构设计优化方法,充分利用层次Kriging模型能预测自身预测误差的优点,结合遗传算法(genetic algorithms, GA),在优化过程中自适应更新变复杂度近似模型,以提高优化解附近的近似模型精度。并将该方法应用于微型飞行器机身结构的设计优化中,以验证该方法的有效性和优越性。
1 层次Kriging模型层次Kriging模型是由Kriging模型扩展而成的,在这个模型中,低精度分析模型的输出可用来帮助预测高精度分析模型的输出[10-11]。
为了构建高精度分析模型的近似模型,首先构建低精度分析模型的近似模型,并将它用于此后的协助预测。低精度分析模型的Kriging模型可以表示为[1]:
| $ {Y_{{\rm{lf}}}}\left( \mathit{\boldsymbol{x}} \right) = {\beta _{0, {\rm{lf}}}} + {Z_{{\rm{lf}}}}\left( \mathit{\boldsymbol{x}} \right) $ | (1) |
式中:β0, lf是一个未知的常数,Zlf(x)是一个平稳的高斯随机过程。
建立一个基于样本点数据集(Slf, ys, lf)的Kriging模型。在Kriging模型拟合后,低精度近似模型在任意未经试验点x的预测可以写成:
| $ \widehat {{y_{{\rm{lf}}}}}\left( \mathit{\boldsymbol{x}} \right) = {\beta _{0, {\rm{lf}}}} + \mathit{\boldsymbol{r}}_{{\rm{lf}}}^{\rm{T}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{R}}_{{\rm{lf}}}^{-1}\left( {{\mathit{\boldsymbol{y}}_{{\rm{s, lf}}}}-{\beta _{0, {\rm{lf}}}}\mathit{\boldsymbol{E}}} \right) $ | (2) |
式中:β0, lf=(ETRlf-1E)-1ETRlf-1(ys, lf);Rlf是nlf×nlf维矩阵,是表示观测点之间相关性的矩阵;nlf是低精度样本点数量;E是元素全为1的nlf维列向量;rlf是表示未经试验点和观测点之间的相关性的向量。
与传统的Kriging模型不同,层次Kriging模型表示为:
| $ Y\left( \mathit{\boldsymbol{x}} \right) = {\beta _0}\widehat {{y_{{\rm{lf}}}}}\left( \mathit{\boldsymbol{x}} \right) + Z\left( \mathit{\boldsymbol{x}} \right) $ | (3) |
低精度近似模型
| $ {\rm{Cov}}\left[{Z\left( \mathit{\boldsymbol{x}} \right), Z\left( {\mathit{\boldsymbol{x'}}} \right)} \right] = {\sigma ^2}R\left( {\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}}} \right) $ | (4) |
式中:σ2是Z(x)的过程方差;R(x, x′)是空间相关函数, 它只取决于x, x′两点之间的欧氏距离。
假设高精度函数可以用观测到的高精度数据ys的一个线性组合来近似,当x为未经试验点时,层次Kriging模型的预测为:
| $ \begin{array}{l} \hat y\left( \mathit{\boldsymbol{x}} \right) = {\beta _0}\widehat {{y_{{\rm{lf}}}}}\left( \mathit{\boldsymbol{x}} \right) + {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{-1}}\left( {{\mathit{\boldsymbol{y}}_{\rm{s}}}-{\beta _0}\mathit{\boldsymbol{F}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\mathit{\boldsymbol{V}}_{{\rm{HK}}}} \end{array} $ | (5) |
式中:β0=(FTR-1F)-1FTR-1ys,是一个比例系数, 它表明高/低精度函数相互关联的程度;F是元素全为1的nhf维列向量;nhf是高精度样本点数量;R表示高精度观测点之间相关性的矩阵;向量VHK只取决于观测数据, 并可以在层次Kriging模型的拟合阶段计算得到。一旦得到VHK, 在预测任意未经试验点x处的响应值
尽管层次Kriging模型能有效平衡建模效率与建模精度,但它仍然是由有限的样本点构建得到,其预测值与仿真模型响应值之间存在误差。若基于一次性建模得到的层次Kriging模型进行结构设计优化,难以保证求解结果的精度,尤其是优化解附近的精度,从而无法满足设计需要。
为了解决这一问题,本文提出一种基于序贯层次Kriging模型和GA[12]的结构设计优化方法,在优化过程中序贯更新层次Kriging模型,以提高最优解附近的精度,得到可靠的设计解。
层次Kriging模型与其他类型的变复杂度近似模型相比,其优点为能够提供预测点x处的均方误差,且误差为正态分布。根据6σ设计准则,在99.86%的置信概率下,层次Kriging模型在x处的预测区间为[13-14]:
| $ \left\{ \begin{array}{l} f\left( \mathit{\boldsymbol{x}} \right) = \hat f\left( \mathit{\boldsymbol{x}} \right) \pm 0.5{I_{\rm{p}}}\left( \mathit{\boldsymbol{x}} \right)\\ {I_{\rm{p}}}\left( \mathit{\boldsymbol{x}} \right) = 6\sigma \left( \mathit{\boldsymbol{x}} \right) \end{array} \right. $ |
式中:
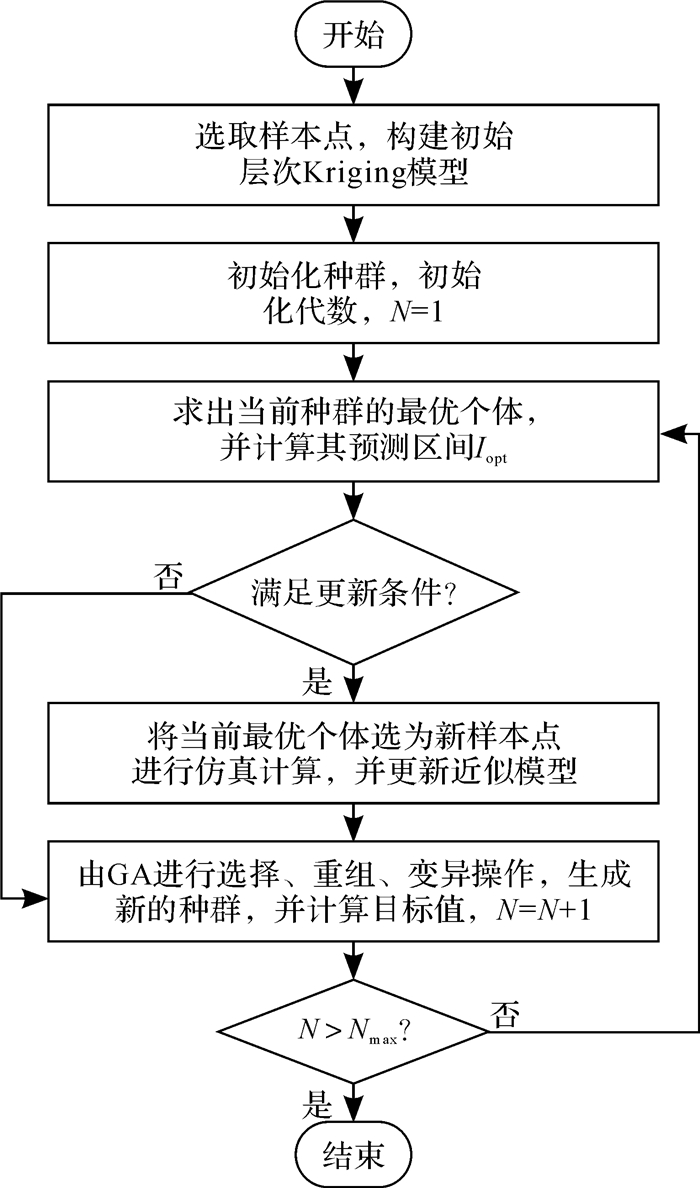
图 1为本文提出的基于序贯层次Kriging模型和GA的结构设计优化方法的流程。在图 1中,GA中的个体目标值都通过层次Kriging模型计算。
|
| 图 1 基于序贯层次Kriging模型和GA的结构设计优化流程 Fig.1 Flow chart of structure design optimization based on sequential hierarchical Kriging model and GA |
本文方法的核心部分为更新准则。当同时满足以下2个条件时,更新层次Kriging模型:
1) Iopt=0.5Ip(x*)<ε,其中x*为当前最优解,ε为设计人员根据问题需求设定的优化解允许误差。
2) 当前遗传代数为5的整数倍,且当前的总计算成本低于预设的最大成本。
设置条件1)的目的是提高优化解附近的层次Kriging模型的精度。之所以设定条件2),是因为可接受的最大计算成本有限,且遗传算法需要一定代数以收敛到最优解。
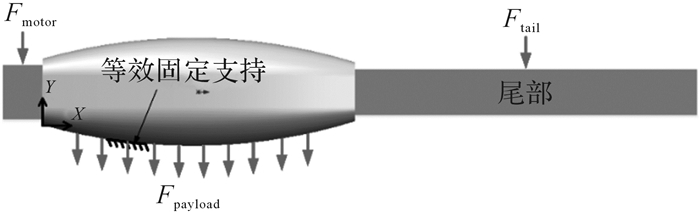
3 微型飞行器机身结构设计优化 3.1 问题描述与仿真模型为了证明所提出的方法在结构设计优化中的有效性和优越性,本文选用微型飞行器机身的优化作为验证案例[15]。微型飞行器机身的几何模型如图 2所示,机身选用轻型ABS(acrylonitrile butadiene styrene,丙烯腈-丁二烯-苯乙烯共聚物)材料,选择5个影响机身性能的参数作为机身优化的设计变量,设计变量的变化范围如表 1所示,机身所受载荷和材料属性如表 2所示。图 3给出了机身的受力及边界条件。机身总共受到3个力的作用:前部发动机的重力Fmotor、尾部的重力Ftail以及机身内表面的分布载荷Fpayload。机翼的质量很小,可忽略不计。

|
| 图 2 微型飞行器机身的几何模型 Fig.2 The geometric model of the micro-aerial vehicle fuselage |
| 设计变量 | 范围 |
| A1/mm | [46, 50] |
| A2/mm | [85, 95] |
| A3/mm | [40, 46] |
| D/mm | [40, 50] |
| L/mm | [250, 260] |
| 载荷 | 数值 | 材料属性 | 数值 |
| Fmotor/N | 5.9 | 杨氏模量/(N/mm2) | 1 960 |
| Ftail/N | 2.7 | 泊松比 | 0.3 |
| Fpayload/(N/mm2) | 0.1 |
|
| 图 3 微型飞行器机身的受力及边界条件 Fig.3 The force and boundary condition of micro-aerial vehicle fuselage |
微型飞行器机身在某一设计参数下的高/低精度仿真模型和最大变形分布如图 4所示,其中低精度仿真模型的含有1 380个单元,高精度仿真模型含有46 023个单元。采用Solidworks-ANSYS-MATLAB集成建模仿真,获取1个高精度仿真模型样本点大约需要1 min,而获得低精度仿真模型样本点大约需要8 s,即获取高/低精度样本点的计算时间比约为7.5。

|
| 图 4 微型飞行器机身高/低精度仿真模型网格划分及最大变形分布图 Fig.4 Grid division and maximum deformation distribution map of high/low-fidelity simulation model for the micro-aerial vehicle fuselage |
微型飞行器机身设计优化目标为最小化机身的最大变形,约束条件为机身的最大应力不超过36 MPa,该优化问题可以描述为:
| $ \begin{array}{l} \min {f_1} = u\left( {{A_1}, {A_2}, {A_3}, D, L} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sigma \le {\rm{36}}\;{\rm{MPa}}\\ \;\;\;\;\;\;{\rm{46}} \le {A_1} \le 50\;{\rm{m}}\;{\rm{m}}\\ \;\;\;\;\;\;{\rm{85}} \le {A_2} \le 95\;{\rm{m}}\;{\rm{m}}\\ \;\;\;\;\;\;40 \le {A_3} \le 46\;{\rm{m}}\;{\rm{m}}\\ \;\;\;\;\;\;40 \le D \le 50\;{\rm{m}}\;{\rm{m}}\\ \;\;\;\;\;\;250 \le L \le 260\;{\rm{m}}\;{\rm{m}} \end{array} $ |
采用最优拉丁超立方设计(optimal Latin-hypercube design,OLHD)[16-17]选取60个低精度样本点和20个高精度样本点, 建立初始的层次Kriging模型。为了说明序贯层次Kriging模型的优越性,在相同计算成本下(用OLHD选取28个高精度样本点)建立单精度Kriging模型。利用50个随机选取的样本点分别计算序贯层次Kriging模型和单精度Kriging模型的误差指标,即最大绝对误差(maximum absolute error,MAE)和均方根误差(root mean square error,RMSE)[18], 其计算公式如下:
| $ \begin{array}{l} {\rm{MAE}} = \max \left( {\left| {\hat y\left( {{\mathit{\boldsymbol{x}}_i}} \right)- y\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right|} \right), i = 1, 2, \cdots, n\\ \;\;\;\;\;\;\;\;{\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left[{\hat y\left( {{\mathit{\boldsymbol{x}}_i}} \right)-y\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right]}^2}} }}{n}} \end{array} $ |
式中:
序贯层次Kriging模型与单精度Kriging模型的误差指标如表 3所示。
| 模型 | MAE | RMSE |
| 序贯层次Kriging模型 | 0.017 9 | 0.008 0 |
| 单精度Kriging模型 | 0.030 4 | 0.010 3 |
从表 3可以看到,在相同计算成本下,序贯层次Kriging模型的最大误差和均方根误差均小于单精度Kriging模型,说明前者的精度更高。
采用本文方法对微型飞行器机身结构进行设计优化,其中的参数设置如表 4所示。当遗传算法的代数达到100时,算法终止。
| 参数 | 数值 |
| 最大遗传代数 | 100 |
| 种群数量 | 40 |
| 最大允许的样本点更新数量 | 10 |
| ε | 0.01 |
为了验证本文方法的有效性,首先采用高精度仿真模型和GA进行优化计算,所得到的优化结果如表 5所示,该优化结果为微型飞行器机身结构设计优化的真实解。
| 最优设计变量/mm | 最大变形/mm |
| [46.05, 85.93, 85.93, 40.00, 251.27] | 7.67 |
采用本文方法对微型飞行器机身结构进行设计优化,考虑到遗传算法具有随机性,进行3次计算,结果如表 6所示。为了进一步验证本文方法的合理性和正确性,将这些优化解进行高精度仿真,计算结果如表 7所示。
| 计算次数 | 样本点更新数量 | 最优设计变量/mm | 最大变形/mm |
| 第1次 | 6 | [47.00, 85.07, 44.48, 40.00, 252.53] | 7.69 |
| 第2次 | 7 | [46.12, 85.77, 43.71, 40.01, 250.31] | 7.67 |
| 第3次 | 5 | [46.06, 86.96, 45.97, 40.39, 250.99] | 7.69 |
| 优化解编号 | 最大变形/mm | |
| 序贯层次Kriging预测值 | 高精度仿真模型响应值 | |
| 1 | 7.69 | 7.69 |
| 2 | 7.67 | 7.68 |
| 3 | 7.69 | 7.70 |
可以看到,由本文方法所得的3个优化结果都与采用高精度仿真模型得到的优化解非常接近,均可以看作近似最优解。同时,优化解处序贯层次Kriging模型预测值与高精度仿真模型响应值几乎相同,说明本文提出的方法所求得的近似最优解非常可靠,能满足实际工程的需要。
4 结语为了提高基于仿真模型的设计优化的精度和效率,本文提出一种基于序贯层次Kriging模型的结构设计优化方法。在该方法中,采用GA进行优化求解,并在GA的迭代过程中序贯更新层次Kriging模型,以提高模型在设计点附近的预测精度。将该方法应用于微型飞行器机身结构的设计优化中,结果表明:1)与单精度Kriging模型相比,序贯层次Kriging模型能充分利用高/低精度样本点的信息,其预测精度更高;2)本文提出的方法仅需要较少计算量就能求解得到近似最优解,为解决类似的结构设计优化问题提供了参考。
| [1] |
韩忠华.
Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197–3225.
HAN Zhong-hua. Kriging surrogate model and its application to design optimization:a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197–3225. |
| [2] | SHI R, LIU L, LONG T, et al. Sequential radial basis function using support vector machine for expensive design optimization[J]. AIAA Journal, 2016, 55(1): 214–227. |
| [3] | DUTTA S, PAL S K, SEN R. On-machine tool prediction of flank wear from machined surface images using texture analyses and support vector regression[J]. Precision Engineering, 2016, 43: 34–42. DOI:10.1016/j.precisioneng.2015.06.007 |
| [4] |
王国春, 成艾国, 胡朝辉, 等.
基于Kriging模型的汽车前部结构的耐撞性优化[J]. 汽车工程, 2011, 33(3): 208–212.
WANG Guo-chun, CHENG Ai-guo, HU Chao-hui, et al. Crashworthiness optimization of vehicle front structure based on Kriging model[J]. Automotive Engineering, 2011, 33(3): 208–212. |
| [5] |
高伟钊, 莫旭辉, 付锐, 等.
基于Kriging的泡沫填充锥形薄壁结构耐撞性6σ稳健性优化设计[J]. 固体力学学报, 2012, 33(4): 370–378.
GAO Wei-zhao, MO Xu-hui, FU Rui, et al. Optimization of crashworthiness 6σ based on Kriging foam filled tapered thin-walled structure[J]. Chinese Journal of Solid Mechanics, 2012, 33(4): 370–378. DOI:10.3969/j.issn.0254-7805.2012.04.004 |
| [6] |
潘志雄.
基于径向基函数的优化代理模型应用研究[J]. 航空工程进展, 2010, 1(3): 242–245.
PAN Zhi-xiong. Application of optimal proxy model based on radial basis function[J]. Advances in Aeronautical Science and Engineering, 2010, 1(3): 242–245. DOI:10.3969/j.issn.1674-8190.2010.03.009 |
| [7] | ZHOU Q, SHAO X, JIANG P, et al. An adaptive global variable fidelity metamodeling strategy using a support vector regression based scaling function[J]. Simulation Modelling Practice and Theory, 2015, 59: 18–35. DOI:10.1016/j.simpat.2015.08.002 |
| [8] |
廖代辉, 成艾国, 钟志华.
基于变复杂度近似模型的汽车安全性和轻量化优化[J]. 中国机械工程, 2013, 24(15): 2118–2121.
LIAO Dai-hui, CHENG Ai-guo, ZHONG Zhi-hua. Vehicle safety and lightweight optimization based on variable complexity approximation model[J]. China Mechanical Engineering, 2013, 24(15): 2118–2121. DOI:10.3969/j.issn.1004-132X.2013.15.025 |
| [9] |
谢晖, 陈龙, 李凡.
RBF近似模型在汽车碰撞变复杂度建模中的应用[J]. 机械科学与技术, 2016, 35(10): 1624–1628.
XIE Hui, CHEN Long, LI Fan. RBF approximation model in the automobile collision complexity modeling application[J]. Mechanical Science and Technology, 2016, 35(10): 1624–1628. |
| [10] | HU J X, ZHOU Q, JIANG P, et al. An adaptive sampling method for variable-fidelity surrogate models using improved hierarchical Kriging[J]. Engineering Optimization, 2018, 50(1): 145–163. DOI:10.1080/0305215X.2017.1296435 |
| [11] | HAN Z H, GÖRTZ S. Hierarchical Kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(9): 1885–1896. DOI:10.2514/1.J051354 |
| [12] | HOMAIFAR A, QI C X, LAI S H. Constrained optimization via genetic algorithms[J]. Simulation, 1994, 62(4): 242–253. DOI:10.1177/003754979406200405 |
| [13] | SHU L, JIANG P, ZHOU Q, et al. An on-line variable fidelity metamodel assisted multi-objective genetic algorithm for engineering design optimization[J]. Applied Soft Computing, 2018, 66: 438–448. DOI:10.1016/j.asoc.2018.02.033 |
| [14] | KOCH P N, YANG R J, GU L. Design for six sigma through robust optimization[J]. Structural and Multidisciplinary Optimization, 2004, 26(3/4): 235–248. |
| [15] | NGUYEN J, PARK S, ROSEN D. Heuristic optimization method for cellular structure design of light weight components[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(6): 1071–1078. DOI:10.1007/s12541-013-0144-5 |
| [16] | PARK J S. Optimal Latin-hypercube designs for computer experiments[J]. Journal of Statistical Planning and Inference, 1994, 39(1): 95–111. DOI:10.1016/0378-3758(94)90115-5 |
| [17] |
陈代君, 熊世峰.
嵌套拉丁超立方设计的优化[J]. 系统科学与数学, 2017, 37(1): 53–65.
CHEN Dai-jun, XIONG Shi-feng. Optimization of nested Latin hypercube design[J]. Journal of Systems Science and Mathematical Sciences, 2017, 37(1): 53–65. |
| [18] | WILLMOTT C J, MATSUURA K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance[J]. Climate research, 2005, 30(1): 79–82. |


