随着微电子机械系统(micro electro mechanical systems,MEMS)领域加工技术的发展,芯片集成度不断提高,对微尺寸高效散热结构的需求不断提升。微槽道热沉最早于1981年由Tuckerman等[1]提出,可用于对微尺寸、高功率电子元件进行有效的冷却。微槽道的流动传热与常规尺度下的有所不同。Shah和London[2]对不同截面形状下微槽道层流流动阻力进行了大量研究,总结出了一系列插值关联式。夏国栋等[3]对硅基梯形槽道的流动传热进行了实验研究,得出了硅基梯形槽的Nusselt实验关联式,并与他人的研究结果进行了比较。Wu等[4]对底角为54.7°、长短边比不同的光滑梯形硅基微槽道的流动摩擦系数进行了研究。Qu等[5]对硅基微槽道流动压降进行了研究,结果表明微槽道压力梯度与摩擦系数均比基于常规层流理论的预测值高,认为这可能是受到了微槽道表面粗糙度的影响,并提出粗糙度-黏度模型进行验证。
研究表明,微槽道的截面形状和尺寸显著影响其散热性能。Salimpour等[6]对微槽道截面形状进行了优化,结果表明正方形截面的散热效率最高。Wang等[7]采用逆问题方法对单层矩形通道进行了优化设计,得到了截面纵横比、通道宽度和间距的参考值。Jeevan等[8]通过一维和二维FEM(finite element method,有限元方法)对堆叠通道的热阻模型进行了研究,并利用遗传算法对其尺寸进行了优化。Liu等[9]提出了一种改进的热边界条件来正确表征热通量分布, 并对压力水头下的矩形截面微槽道热沉进行了优化设计。邵宝东等[10]建立了单层微槽热沉的热阻网络模型,通过序列二次规划(sequential quadratic programming,SQP)法对热沉进行了热阻和压降的多目标优化设计。
尽管目前已对微槽热沉结构优化进行了很多研究,但是由于耦合传热过程的复杂性,许多研究中的优化方案存在截面形状选择较单一,热阻网络模型精度较低,采用速度入口进行优化导致大流阻模型虚假占优等问题。本文以微槽热阻和压降最小化为目标,以微泵输出功率作为入口边界条件,采用多目标序列二次规划法对单层四边形等截面硅基微槽道热沉的槽道截面形状、占空比、槽道高度进行优化设计,并通过数值模拟进行验证。
1 物理模型和计算区域本文采用ANSYS Workbench进行建模和网格划分,采用CFD-Fluent流体分析软件进行模拟计算。为确保N-S方程的有效性,需要对流场克努森数Kn进行计算,计算方法如下:
| $ Kn=\frac{\lambda }{l} $ |
式中:l为流场特征长度; λ为流体分子平均自由程,
50 ℃时工质流体的克努森数为2.128×10-7,满足连续介质假设的要求(Kn < 0.01),说明N-S方程适用于本文研究。
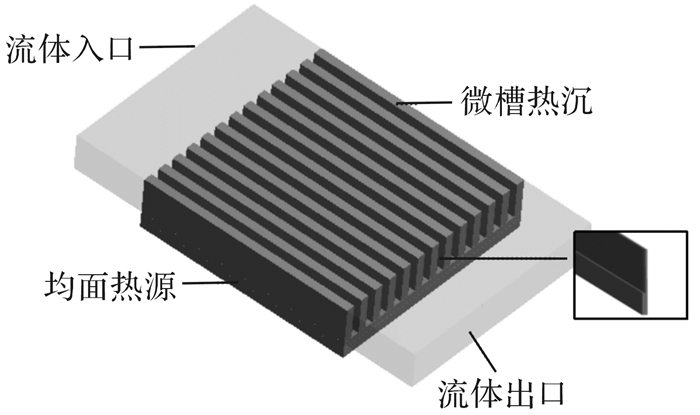
图 1为硅基微槽热沉的基本结构,由于结构具有对称性,故取半槽道作为计算区域。槽道高度为H,鳍底宽为Sb,槽底宽为Wb,槽顶宽为Wt。流场顶部由Pyrex玻璃盖板密封。热沉材料为硅,流体介质为无离子水。硅基厚度为750 μm,底面为边长L=0.006 m的正方形,底部为均布热源,热流密度q=3×106 W/m2,发热功率Ph=q×L2=108 W。入口泵功Pf=0.03 W,流体温度为27 ℃。选取合适的优化结果,以进出口压降、参考线温度曲线和整体热阻为研究对象,分析不同热沉结构的散热性能。
|
| 图 1 硅基微槽热沉基本结构 Fig.1 Basic structure of silicon substrate microchannel heat sink |
对于热沉总体结构离散为2L/(Sb+Wb)个半槽道结构,即热沉总热阻Rtotal相当于2L/(Sb+Wb)个半槽道热阻并联,包括单基底传导热阻Rbase、基底对流热阻Rbase, conv和鳍片总热阻Rfin, total,记为:
| $ \left\{ \begin{align} &{{R}_{\text{total}}}={{R}_{\text{base}}}+\frac{{{S}_{\text{d}}}+{{W}_{\text{d}}}}{2L}{{\left( {{R}_{\text{fin, total}}}^{-1}+{{R}_{\text{base, conv}}}^{-1} \right)}^{-1}} \\ &{{R}_{\text{base}}}={{H}_{\text{b}}}/\left( {{k}_{\text{s}}}{{L}^{2}} \right) \\ &{{R}_{\text{base, conv}}}=1/\left( {{h}_{\text{conv}}}{{W}_{\text{d}}}L \right) \\ \end{align} \right. $ |
式中:Rfin, total由热阻网络模型迭代确定; Rbase只与基底厚度有关,且在基底高度Hb=0 mm时有最小值,为非设计区域,本文取Hb=0.25 mm;hconv为耦合面对流换热系数,hconv=3.5×104 W/m2·K;ks为硅基传热系,ks=149 W/m·K。
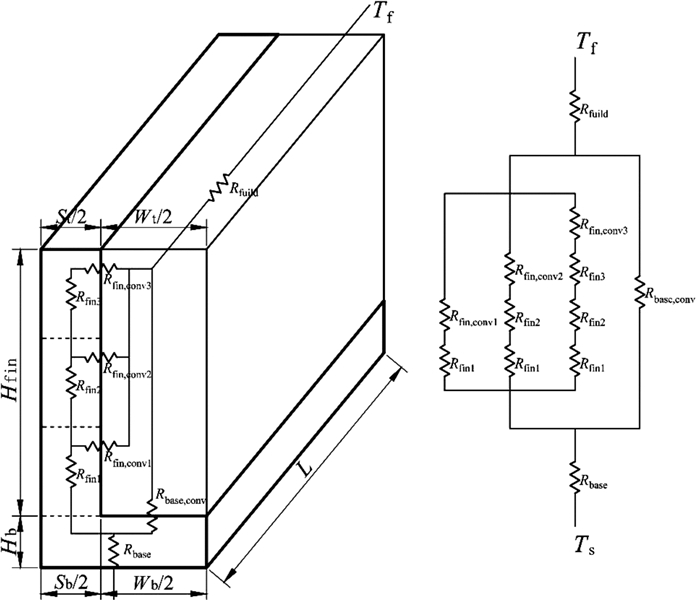
2.1.2 微槽鳍片热阻网络模型的离散化处理本节采用离散化思想,将半槽道划分为n个控制体积,n=3时半槽道热阻网络模型如图 2所示。第i段控制体积处的传导热阻Rfin, i和对流热阻Rfin, conv, i为:
|
| 图 2 半槽道热阻网络模型示意图 Fig.2 Diagram of half-channel thermal resistance network model |
| $ \begin{align} &{{R}_{\text{fin}, i}}=\sum\limits_{m=1}^{i}{\frac{{{H}_{\text{fin}}}}{{{k}_{\text{s}}}L{{S}_{\text{d}i}}n}}=\frac{{{H}_{\text{fin}}}m}{{{k}_{\text{s}}}L{{S}_{\text{d}i}}n} \\ &\ \ \ \ \ \ \ {{R}_{\text{fin, conv}, i}}=\frac{n}{{{h}_{\text{conv}}}L{{H}_{i}}} \\ \end{align} $ |
式中:Sdi是微元等效厚度,Hi为微元与工质接触宽度,计算方法如下:
| $ \begin{align} &{{S}_{\text{d}i}}=\frac{1}{2}\left( {{S}_{\text{b}}}+\frac{\left( 2i-1 \right)}{2}\cdot \frac{{{W}_{\text{b}}}-{{W}_{\text{t}}}}{n} \right) \\ &\ \ \ \ \ {{H}_{i}}=\frac{1}{n}\sqrt{{{\left( \frac{{{W}_{\text{t}}}-{{W}_{\text{d}}}}{2} \right)}^{2}}+H_{\text{fin}}^{2}} \\ \end{align} $ |
鳍片总热阻为:
| $ {R_{{\rm{fin, total}}}} = \mathop {\lim }\limits_{n \to ▌} {\left[{\sum\limits_{i = 1}^n {{{\left( {{R_{{\rm{fin}}, i}} + {R_{{\rm{fin, conv}}, i}}} \right)}^{-1}}} } \right]^{ -1}} $ |
分别取n=1 000个和n=10 000个,H=500 μm, Sb=50 μm, Wb=50 μm, Wt=50 μm进行循环求解,所得总热阻Rtotal分别为0.146 056 K/W和0.146 018 K/W,两者相差为0.26‰,可认为n=1 000个时结果已满足稳定性条件。无离散热阻网络计算方法所得结果为0.226 786 K/W,较离散化热阻模型高55.27%。
2.1.3 对流换热系数计算根据夏国栋等[3]的实验结果,在较低雷诺数下,梯形微槽道单相流体传热的努塞尔数Nu可用如下关联式计算:
| $ Nu = 4.73 + \frac{{0.086{{\left( {{Re} Pr {D_{\rm{h}}}/L} \right)}^{1.33}}}}{{1 + 0.1Pr {{\left( {{Re} {D_{\rm{h}}}/L} \right)}^{0.83}}}} $ |
式中:Pr是工质流体近壁面普朗特数,为便于计算,本文根据经验对无离子水工质普朗特数Prw作常物性假设,取工质温度为50 ℃,即Prw=3.54;Dh是微槽道特征长度,本文取为微槽道水力直径; 对流场雷诺数Re的计算如下:
| $ Re = \frac{{u{D_{\rm{h}}}}}{\nu } $ |
其中ν为工质运动黏度,本文取入口工质动力黏度,作常物性假设:ν=ν20 ℃=1.007×10-6 m2/s。
Nu与对流换热系数hconv的关系为:
| $ {h_{{\rm{conv}}}} = \frac{{Nu \cdot {k_{\rm{f}}}}}{{{D_{\rm{h}}}}} $ |
式中:kf是工质流体的导热率,u为工质流体流速。
2.2 模型压降目标函数由于微小空间内部三维效应、惯性力效应和表面粗糙度的影响,微槽道流动阻力特性与常规尺寸下流道的阻力特性存在一定差异。虽然已有大量的微槽流动阻力研究成果[2-5],但都是针对特定结构及模型的实验关联式,适用区间较小,优化过程中容易造成计算失真,缺乏优化所需的普适性。本文采用层流流动阻力的经典预测公式[11]作为阻力控制条件:
| $ fRe = 64 $ |
槽道内沿程压降满足如下方程:
| $ \Delta P = \frac{{f\rho {u^2}L}}{{2{D_{\rm{h}}}}} $ |
多目标优化的思想是对控制模型的各个分目标函数提供一种评价方法,将多目标优化问题转化为评价方法下的单目标优化问题。在确定若干分目标函数Fj(x)时,通过MATLAB计算得到满足自变量容差的非劣解空间,随后通过搜索寻找符合评价标准的非劣解并返回相应的xj作为优化结果。
本文提出功效系数化的加权目标到达法作为评价方法。功效系数用以描述相应非劣解在解空间中的一维坐标。当不同分目标函数的解空间数量级差异较大时,无量纲化的功效系数可以合理地表达不同优化目标的重要度。解向量x对应分目标函数Fj(x)的功效系数计算方法如下:
| $ {p_j}\left( \mathit{\boldsymbol{x}} \right) = \frac{{{F_{j\min }}\left( \mathit{\boldsymbol{x}} \right)-F\left( \mathit{\boldsymbol{x}} \right)}}{{{F_{j\min }}\left( \mathit{\boldsymbol{x}} \right)-{F_{j\max }}\left( \mathit{\boldsymbol{x}} \right)}} $ |
同理可得目标功效系数p(g),本文优化目标为热阻和压降, 故j=2,构造评价函数通式如下:
| $ \begin{array}{l} G\left( \mathit{\boldsymbol{x}} \right) = \left\{ {{w_1}{{\left[{{p_1}\left( \mathit{\boldsymbol{x}} \right)-{p_1}\left( \mathit{\boldsymbol{g}} \right)} \right]}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{w_2}{\left[{{p_2}\left( \mathit{\boldsymbol{x}} \right)-{p^2}\left( \mathit{\boldsymbol{g}} \right)} \right]^2} + \cdots + \\ {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;{w_j}{{\left[{{p_j}\left( \mathit{\boldsymbol{x}} \right)-{p_j}\left( \mathit{\boldsymbol{g}} \right)} \right]}^2}} \right\}^{\frac{1}{2}}}, \sum\limits_{k = 1}^j {{w_k}} = 1 \end{array} $ |
该函数代表解向量x对应的目标函数值点与目标点g在解空间中无量纲坐标系下的加权距离,分别选取热阻和压降的理想结果(g1=[0, 0])和约束内分目标边界结果(g2=[Rmin, ΔPmin])作为期望目标,命名为理想点法和边界点法,并将2种情形下的优化结果进行比对。
3.2 最优解搜索方法多目标优化方法是求解关于目标向量x的评价方法G(x)在一定约束条件下的最优问题。先从符合约束的解空间中选取j个分目标函数Fj(x)的非劣解组成非劣解向量空间,再通过评价函数G(x)从非劣解向量空间中筛选最优解。其标准形式为:
| $ \mathop {\min }\limits_{x \in {R^n}} F\left( \mathit{\boldsymbol{x}} \right) = \mathop {\min }\limits_{x \in {R^n}} \left[{{f_1}\left( \mathit{\boldsymbol{x}} \right), {f_2}\left( \mathit{\boldsymbol{x}} \right), \cdots, {f_m}\left( \mathit{\boldsymbol{x}} \right)} \right] $ |
且满足约束:
| $ \left\{ \begin{array}{l} {A_j}\left( \mathit{\boldsymbol{x}} \right) \le 0\\ {\rm{Ae}}{q_j}\left( \mathit{\boldsymbol{x}} \right) = 0, j = 1, 2, \cdots, {m_e}\\ {\rm{nonlcon}}\left( \mathit{\boldsymbol{x}} \right) \le 0\\ {\rm{nonleq}}\left( \mathit{\boldsymbol{x}} \right) = 0, j = {m_{e + 1}}, {m_{e + 2}}, \cdots, m\\ {\mathit{\boldsymbol{x}}_1} \le \mathit{\boldsymbol{x}} \le {\mathit{\boldsymbol{x}}_{\rm{u}}} \end{array} \right. $ |
本文采用序列二次规划法对G(x)求优,其基本思想是在迭代点处构造二次规划子问题,近似原来的约束优化问题,通过对子问题的求解获得约束优化问题的改进迭代点。不断重复这一过程直至求出满足要求的迭代点。
MATLAB序列二次规划算法Fmincon函数可搜索给定初值附近区域的局部最优解。本文通过MultiStart函数在设计区间内随机生成多个迭代点,搜索设计区间内不同区域的局部最优解,并返回其中的最优解向量作为全局最优解。设置起始点数K=5 000,自变量终止容差为10-9,最大迭代次数和评价次数均为104。
3.3 优化约束条件为满足加工要求,需要对微槽道结构参数加以限制,避免非劣解空间中出现不符合实际要求的极端情况。优化对象为梯形微槽道的几何尺寸,分别为槽道高度H、鳍底宽Sb、槽底宽Wb和槽顶宽Wt。结构设计范围为:
1) 槽顶、槽底、鳍底的宽度下限为50 μm,上限为1 000 μm;槽道高度上限为500 μm。
2) 槽道占空比在40%~80%范围内。
3) 取半槽道上下底宽度Wl=(Wb+Wt)/2,槽道纵横比α1=H/Wl < 10。
4) 当雷诺数过大时,微槽道内流动将发生转捩,不再符合层流状态下的流动特性。目前对于微槽道流动转捩临界雷诺数的研究较多,一般认为较常规尺度下转捩的临界雷诺数Re=2 300,微槽道流动的转捩临界值受微尺度效应影响将会变小,具体变化与试验试件表面粗糙度相关。本文采用Wang和Peng[12]的微槽道实验得出的转捩临界值作为雷诺数约束,即应满足100≤Re≤1 000。
5) 以往的微槽热沉研究往往以入口工质流速作为不同模型的边界条件[13-18]。从能量角度分析,当工质流入模型的速度相同时,流入高流阻模型的工质压力势能大,总体能量占优,而向热沉供水的泵功应恒定不变,存在矛盾。故本文对不同结构模型采用功率平衡条件,基于零静压出口,根据入口泵功Pf添加如下约束:
| $ {P_{\rm{f}}} = \Delta P{\rm{d}}V = \Delta PHL{v_{{\rm{in}}}} $ |
式中:V为工质体积;由于本文芯片为正方形,故流体入口宽度为热沉长度L;vin为入流速度。
将入口速度与沿程阻力损失作为未知量加入目标向量,利用2.2节中的方程进行求解。
综上所述,对于目标向量x=[H, Sb, Wb, Wt, vin, ΔP]取标准量纲为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_1} = \left[{0.00005, 0.00005, 0.00005, 0.00005} \right]\\ {\mathit{\boldsymbol{x}}_{\rm{u}}} = \left[{0.0005, 0.001, 0.001, 0.001} \right]\\ {W_{\rm{l}}} = \left( {{W_{\rm{t}}} + {W_{\rm{b}}}} \right)/2\\ {\alpha _1} = H/{W_{\rm{l}}}, {\alpha _2} = {W_{\rm{l}}}/H\\ {\alpha _1} \le 10, {\alpha _2} \le 10\\ \beta = {W_{\rm{b}}}/\left( {{S_{\rm{b}}} + {W_{\rm{b}}}} \right)\\ 40\% \le \beta \le 80\% \\ 100 \le Re \le 1000\\ {P_{\rm{f}}} = \Delta PHL{v_{{\rm{in}}}} \end{array} \right. $ |
取热阻权重为w,采用边界点法和理想点法时部分权系数下梯形微槽热沉几何尺寸的优化结果分别如表 1和表 2所示。
| 权重w | H/μm | Sb/μm | Wb/μm | Wt/μm |
| 0.3 | 500.00 | 50.74 | 76.23 | 126.93 |
| 0.4 | 500.00 | 50.00 | 70.96 | 120.96 |
| 0.5 | 500.00 | 50.00 | 64.50 | 114.50 |
| 0.6 | 500.00 | 50.00 | 58.77 | 108.77 |
| 0.7 | 500.00 | 50.00 | 53.41 | 103.41 |
| 权重w | H/μm | Sb/μm | Wb/μm | Wt/μm |
| 0.3 | 500.00 | 50.00 | 65.31 | 115.31 |
| 0.4 | 500.00 | 50.00 | 54.08 | 104.08 |
| 0.5 | 500.00 | 50.00 | 50.00 | 100.00 |
| 0.6 | 500.00 | 50.00 | 50.00 | 99.15 |
| 0.7 | 500.00 | 50.00 | 50.00 | 88.66 |
通过表 1和表 2可看出槽道截面积随热阻权重增加而减小。优化目标点为边界点时,鳍片截面形状始终为三角形,鳍底宽为约束下限,槽道高度为约束上限。这说明微槽道热阻主要为对流换热热阻而非传热热阻。目标点为理想点时,槽底宽达到约束下限,鳍片截面形状随热阻权重增加有向矩形转化的趋势,这说明相比于边界点,理想点作为目标点进行优化时, 优化结果更偏向于减小热阻。
3.5 截面形状讨论由3.4节的结果可知优化结果与槽道限高及最小尺寸约束相关。本节讨论w=0.5且无最小尺寸约束时调整槽道高度上限对优化结果的影响。表 3和表 4分别为w=0.5时采用边界点法和理想点法所获得的梯形微槽热沉几何尺寸的优化结果。
| 权重w | H/μm | Sb/μm | Wb/μm | Wt/μm |
| 0.5 | 700.00 | 43.31 | 64.97 | 108.28 |
| 0.5 | 600.00 | 43.42 | 65.13 | 108.54 |
| 0.5 | 500.00 | 43.45 | 65.18 | 108.63 |
| 0.5 | 400.00 | 42.64 | 65.95 | 107.80 |
| 0.5 | 300.00 | 35.68 | 73.18 | 101.00 |
| 0.5 | 200.00 | 22.37 | 89.45 | 89.47 |
| 权重w | H/μm | Sb/μm | Wb/μm | Wt/μm |
| 0.5 | 700.00 | 35.00 | 52.50 | 87.50 |
| 0.5 | 600.00 | 31.91 | 47.86 | 79.77 |
| 0.5 | 500.00 | 32.78 | 49.18 | 81.96 |
| 0.5 | 400.00 | 33.50 | 50.25 | 83.74 |
| 0.5 | 300.00 | 32.89 | 54.16 | 85.11 |
| 0.5 | 200.00 | 22.01 | 70.39 | 77.59 |
由计算结果可以看出,当槽道限高大于300 μm时,Sb+Wb≈Wt,此时鳍片截面形状为三角形,槽道截面为梯形。随着限高减小时,Sb+Wb>Wt,鳍片开始产生明显的顶距。当限高达到200 μm时,2种评价方法下槽道截面形状已明显向矩形转化。这是由于限高较高时鳍片与流场接触面积大,传热能力的设计空间相对过剩。鳍顶热阻需要计算鳍底传热热阻,换热效率低,因而可以降低鳍片上部的传热效率以减少流动阻力。当限高较低时,换热面积有限,为保证换热效率,必须充分发挥鳍片换热能力,尽可能减小传热热阻,故流道截面形状向矩形转化。
4 数值仿真及讨论 4.1 网格无关性验证对H=500 μm,Sb=50 μm,Wb=64.50 μm,Wt=114.50 μm的槽道模型采用4种网格划分参数方案进行网格划分, 在10.37 kPa压力工况下进行模拟,4种网格划分参数方案如表 5所示。
| 划分方案 | 节点数/个 | 单元数/个 | 热源面均温/K |
| 1 | 382 291 | 323 400 | 336.966 |
| 2 | 632 918 | 543 750 | 330.942 |
| 3 | 915 120 | 784 460 | 336.939 |
| 4 | 1 496 196 | 1 312 800 | 336.929 |
从表 5可知方案3满足计算精度且节省计算资源,满足网格无关性,故采取该方案进行数值模拟。
4.2 计算方法为保证流入不同模型的工质满足功率约束,取由MATLAB算得的不同模型工质流速为入口条件,在给定的入流泵功下,硅基微槽内工质流动状态为低雷诺数下的层流,故选取lamniar层流模型。计算类型为稳态计算,压力速度耦合方式为SIMPLEC,梯度离散采用单元最小二乘法,压力离散采用二阶方法,对流项离散采用二阶迎风方法。分别对w=0.5时目标点为边界点和理想点的优化结果进行模拟计算,并和Sb相同的矩形截面槽道模型(对照模型)的模拟结果进行对比验证。不同槽底宽和槽顶宽时梯形截面槽道模型(优化模型)的网格划分情况如表 6所示。
| Wb/μm | Wt/μm | 单元数/个 | 纵横比 | 倾斜度 |
| 64.50 | 114.50 | 784 460 | 2.839 1 | 0.121 43 |
| 64.50 | 64.50 | 757 222 | 2.815 6 | 0.120 91 |
| 50.00 | 100.00 | 704 080 | 2.986 8 | 0.133 19 |
| 50.00 | 50.00 | 699 242 | 2.921 5 | 0.141 27 |
热沉性能评价以热阻、芯片最高温度、局部温升梯度以及压降四个参数作为评价标准。
热阻反映了介质间传热能力的大小,是评价热沉降温性能的重要指标。热沉总热阻由热沉传热热阻、耦合面对流热阻和工质热阻三部分组成,计算方法如下:
| $ {R_{{\rm{total}}}} = \frac{{{T_{\rm{s}}}-{T_{\rm{f}}}}}{{q{L^2}}} $ |
式中:Ts为热源均温,Tf为入口流体温度。
优化程序仅计算热沉及界面热阻,热沉热阻Rtatal通过3.2节的方程进行计算,此时Ts为耦合面温度。热阻计算结果及误差分析见表 7,热阻计算结果与模拟结果最大误差为17.65%,两者吻合较好,说明离散化热阻网络模型具有较高的预测精度。造成误差的原因主要是流场流动特性求解精度不够高,且热阻网络模型为单向耦合,对流场作常物性假设,未充分考虑工质热阻及物性变化。当微槽道内工质流量较小时,流场变化较为剧烈,对传热效率影响较大,应考虑流场与热沉的双向耦合效应。
| 热阻 | 边界点法优化模型 | 理想点法优化模型 | 边界点法对照模型 | 理想点法对照模型 |
| 计算值/(K/W) | 0.358 7 | 0.331 9 | 0.325 6 | 0.297 4 |
| 模拟值/(K/W) | 0.311 4 | 0.303 7 | 0.277 0 | 0.272 8 |
| 相对误差/% | 15.2 | 9.29 | 17.65 | 8.65 |
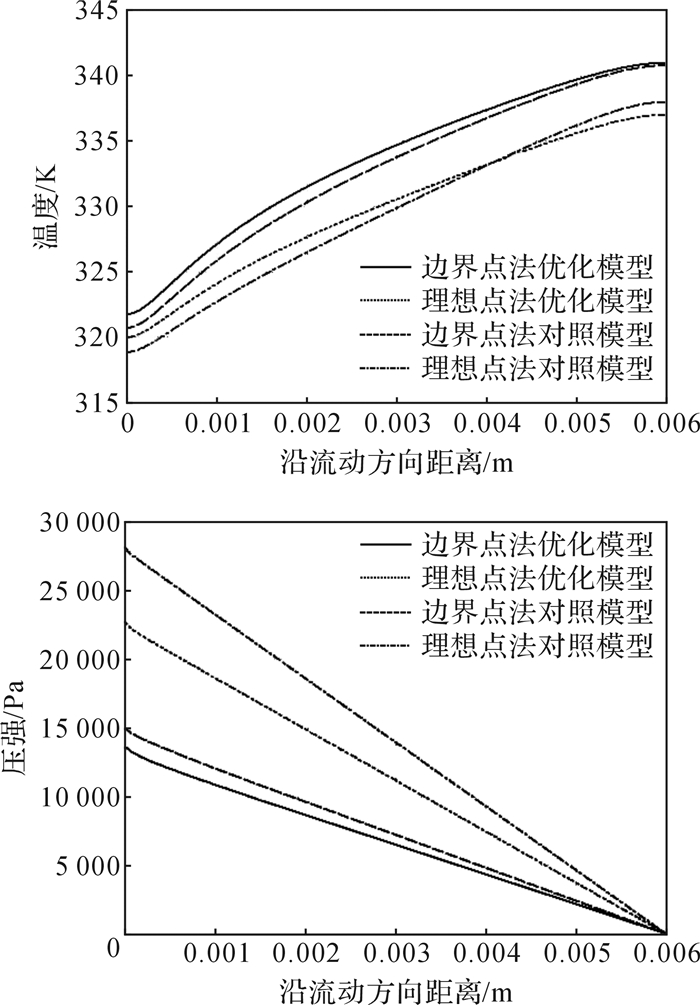
取芯片表面沿介质流动方向中线为芯片温度参考线,流场中心处流线为流场压降参考线,得到w=0.5时采用边界点法和理想点法所得的温度、压降变化结果,如图 3所示。可以看出,优化模型与对照模型的温升梯度无显著差别,整体相差约4 K左右。由表 8可知,原始的矩形截面槽道模型经过优化后压降减小率可达到热阻增加比率的3~4倍。
|
| 图 3 不同热沉模型的温度和压降随流动方向距离变化曲线 Fig.3 Variation curves of temperature and pressure drop of heat sink changing with flow direction distance under different heat sink model |
| 模型 | 边界点法 | 理想点法 | |||
| 热阻/(K/W) | 压降/Pa | 热阻/(K/W) | 压降/Pa | ||
| 对照模型 | 0.277 0 | 22 931.4 | 0.272 8 | 28 322.5 | |
| 优化模型 | 0.311 4 | 13 864.1 | 0.303 7 | 15 183.4 | |
| 变动幅度 | +12.42% | -39.54% | +11.33% | -46.39% | |
综合考虑热阻、芯片最高温度、局部温升梯度以及工质压降,可认为w=0.5(均衡权重)时, 优化模型的综合性能更优。
5 结论本文提出了适用于微槽热沉的离散化热阻网络模型,以恒定泵功作为入口条件,目标功效系数到达法为评价函数,通过MATLAB全局优化方法对热阻和压降模型求解,由有限元分析软件对结果进行验证,得出如下结论:
1) 通过有限元方法对优化后的硅基微槽热沉结构进行了仿真模拟,结果表明,本文方法可以根据设计需求调整评价函数,对热阻和压降进行协同优化,满足提升热沉综合性能的设计要求。为恒定泵功下层流微槽热沉的设计优化提供了一种可行的方法,对于微尺度无相变热沉的设计具有重要意义。
2) 微槽道高度较高,换热面积相对充足时,鳍片截面形状倾向于三角形。槽道高度较低时,截面形状倾向于矩形。
3) 离散热阻网络模型具有更高预测精度,且对计算资源占用较小。在微槽道水力直径较小时,热阻传热效率受工质物性变化影响较大。故应构建流场-热沉的双向耦合热阻模型,对水力直径小于100 μm的微槽热沉的优化设计作进一步研究。
| [1] | TUCKERMAN D B, PEASE R F W. High-performance heat sinking for VLSI[J]. IEEE Electron Device Letters, 1981, 2(5): 126–129. DOI:10.1109/EDL.1981.25367 |
| [2] | SHAH R K, LONDON A L. Laminar flow forced convection in ducts:a source book for compact heat exchanger analytical data[M]. Salt Lake City: Academic Press, 1978: 431-455. |
| [3] |
夏国栋, 柴磊, 齐景智.
梯形硅基微通道热沉流体流动与传热特性研究[J]. 北京工业大学学报, 2011, 37(7): 1079–1084.
XIA Guo-dong, CHAI Lei, QI Jing-zhi. Study on flow and heat transfer characteristics of trapezoidal silicon-based microchannel heat sink fluid[J]. Journal of Beijing University of Technology, 2011, 37(7): 1079–1084. |
| [4] | WU H Y, CHENG P. Friction factors in smooth trapezoidal silicon microchannels with different aspect ratios[J]. International Journal of Heat & Mass Transfer, 2003, 46(14): 2519–2525. |
| [5] | QU W, MALA G M, LI D. Pressure-driven water flows in trapezoidal silicon microchannels[J]. International Journal of Heat & Mass Transfer, 2000, 43(3): 353–364. |
| [6] | SALIMPOUR M R, SHARIFHASAN M, SHIRANI E. Constructal optimization of the geometry of an array of micro-channels[J]. International Communications in Heat & Mass Transfer, 2011, 38(1): 93–99. |
| [7] | WANG Z H, WANG X D, YAN W M, et al. Multi-parameters optimization for microchannel heat sink using inverse problem method[J]. International Journal of Heat & Mass Transfer, 2011, 54(13): 2811–2819. |
| [8] | JEEVAN K, QUADIR G A, SEETHARAMU K N, et al. Optimization of thermal resistance of stacked micro-channel using genetic algorithms[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2005, 15(1): 27–42. |
| [9] | LIU D, GARINELLA S V. Analysis and optimization of the thermal performance of microchannel heat sinks[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2003, 15(1): 7–26. |
| [10] |
邵宝东, 孙兆伟, 王丽凤.
热阻网络模型在微槽冷却热沉优化设计中的应用[J]. 吉林大学学报(工学版), 2007, 37(6): 1263–1267.
SHAO Bao-dong, SUN Zhao-wei, WANG Li-feng. Application of thermal resistance net model in optimization design of microchannel cooling heat sink[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(6): 1263–1267. |
| [11] | GUO Z Y. Characteristics of microscale fluid flow and heat transfer[C]//MEMS Proceedings of the International Conference on Heat Transfer and Transport Phenomena in Microscale, Buff, Oct. 15-20, 2000. |
| [12] | WANG B X, PENG X F. Experimental investigation on liquid forced-convection heat transfer through microchannels[J]. International Journal of Heat & Mass Transfer, 1994, 37(S1): 73–82. |
| [13] |
邵宝东, 孙兆伟, 王丽凤.
微槽冷却热沉结构尺寸的优化设计[J]. 吉林大学学报(工学版), 2007, 37(2): 313–318.
SHAO Bao-dong, SUN Zhao-wei, WANG Li-feng. Optimization design of microchannel cooling heat sink[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(2): 313–318. |
| [14] |
魏琪. 基于熵产最小的微槽冷却热沉优化设计[C]//中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集. [2017-11-10]. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6765198.
WEI Qi. Entropy production-based optimum design of microchannel heat sink[C]//Proceedings of Annual Conference of Chinese Institute of Research for Mathematics, Mechanics, Physics and High New Technology. [2017-11-10]. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6765198. |
| [15] | CHAI Lei, XIA Guo-dong, HUA Sheng-wang. Numerical study of laminar flow and heat transfer in microchannel heat sink with offset ribs on sidewalls[J]. Applied Thermal Engineering, 2016, 92: 32–41. DOI:10.1016/j.applthermaleng.2015.09.071 |
| [16] |
蔡奇彧, 徐尚龙, 吴益昊. 三维硅基微通道散热器优化设计与数值分析[C]//电子机械与微波结构工艺学术会议论文集. [2017-11-10]. http://xueshu.baidu.com/s?wd=paperuri:(bbd6e2b4630624c6bd83d0107489d6ff)&filter=sc_long_sign&sc_ks_para=q%3D三维硅基微通道散热器优化设计与数值分析&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_us=4679032634342608770.
CAI Qi-yu, XU Shang-long, WU Yi-hao. Optimum design and numerical analysis of three-dimensional silicon-based microchannel radiator[C]//Proceedings of the Progress of Electromechanical and Microwave Structures. [2017-11-10]. http://xueshu.baidu.com/s?wd=paperuri:(bbd6e2b4630624c6bd83d0107489d6ff)&filter=sc_long_sign&sc_ks_para=q%3D三维硅基微通道散热器优化设计与数值分析&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_us=4679032634342608770. |
| [17] | HUANG Shan-bo, ZHAO Jin, GONG Liang, et al. Thermal performance and structure optimization for slotted microchannel heat sink[J]. Applied Thermal Engineering, 2017, 115: 1266–1276. DOI:10.1016/j.applthermaleng.2016.09.131 |
| [18] | XU Jin-liang, SONG Yan-xi, ZHANG Wei, et al. Numerical simulations of interrupted and conventional microchannel heat sinks[J]. International Journal of Heat and Mass Transfer, 2008, 51(25/26): 5905–5917. |



