2. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China
故障树分析(failure tree analysis,FTA)是研究数控机床可靠性的一种重要方法,它能够有效识别系统所面临的风险,为提高系统可靠性提供重要的技术支撑。故障树分析用顶事件的状态来评定系统是否失效,其有效概率是度量系统可靠性的依据。传统故障树分析将故障树基本事件的发生概率视为一个确定值,则通过基本事件确定的顶事件的发生概率是一个唯一值,因此只有在保证基本事件信息充分、明确的情况下,可靠性分析结果才是准确可信的[1]。但在数控机床的故障树分析中,其基本事件的可靠性信息往往是模糊不确定的,如零部件失效不仅与客观的不确定因素有关,而且与人为失误、设计经验不足等模糊不确定的主观因素相关,因此用确定值来描述数控机床故障树分析中基本事件的发生概率是不完全正确的。对于这种存在主观影响因素、数据资料不完整等现象的不确定性事件,适合用模糊集理论来处理[2-3]。
将模糊集理论引入机械系统的可靠性研究中,其优点在于能够使用模糊集理论中模糊数的隶属度函数来描述机械系统可靠性影响因素中常见的不确定性情况,从而使得整个可靠性分析的结果更为严谨可靠。模糊集理论中的三角模糊数能够很好地处理数据资料不足或精度不高等模糊问题[4],已成功应用于航空导弹系统可靠性分析[5]和高速冲床可靠性分配研究[6]。但是将三角模糊数运用到数控机床的可靠性分析中仍存在问题,即:三角模糊数的隶属度函数曲线为三角形,只能用1个点来表示最概然值,而数控机床可靠性分析中受模糊因素影响而无法准确赋值的参数,其概然值往往没有明显的峰值,而呈扁平分布。因此用三角模糊数来处理这些参数会出现较大的模拟误差,影响系统可靠性分析结果。而梯形模糊数能够很好地解决上述问题,在兼具三角模糊数优点的同时,其隶属度函数曲线为梯形,对于峰值相对较宽的参数分布有着很好的拟合效果[7]。故本文将梯形模糊数运用到数控机床的可靠性分析中,以数控磨床砂轮架系统中主轴振动异响为例进行模糊故障树分析,通过专家打分的方式来获取基本事件发生概率的原始数据,以梯形模糊数的形式表示,然后采取一种基于梯形模糊数质心距离的相似度度量方法对专家打分结果进行加权处理,以集成后的最终结果作为各基本事件的发生概率。根据模糊算子和模糊数的运算法则来计算系统的模糊故障率,确定系统的可靠度。最后,类比工程中“临界重要度”的概念首次提出了“模糊临界重要度”,并确定了其计算方法,以它为指标对基本事件的重要度进行全面的评价。
1 砂轮架系统故障树建立数控磨床是数控机床的精加工设备,其功能是利用磨具对工件的表面进行磨削加工。本文以北京第二机床厂生产的MKS1632数控磨床为研究对象,该型号数控磨床由床身、砂轮架、修整装置、工作台、工件装夹系统、测量系统、防护装置、液压系统、润滑系统、冷却系统及电气系统等11个单元模块组成。其中砂轮架系统是数控磨床的一个重要组成部分,它直接与加工工件相接触,承受较高的载荷,同时由于结构相对复杂,系统故障率较高。因此对砂轮架系统进行全面细致的故障树分析,对提高数控磨床的可靠性有着重要的意义。目前国内对砂轮架系统的研究侧重在模态分析和结构优化方面[8-10], 对砂轮架系统的故障模式研究较少。笔者借与北京第二机床厂合作的机会,对该厂MKS1632数控磨床砂轮架系统的故障模式和原因进行了较为细致的研究。
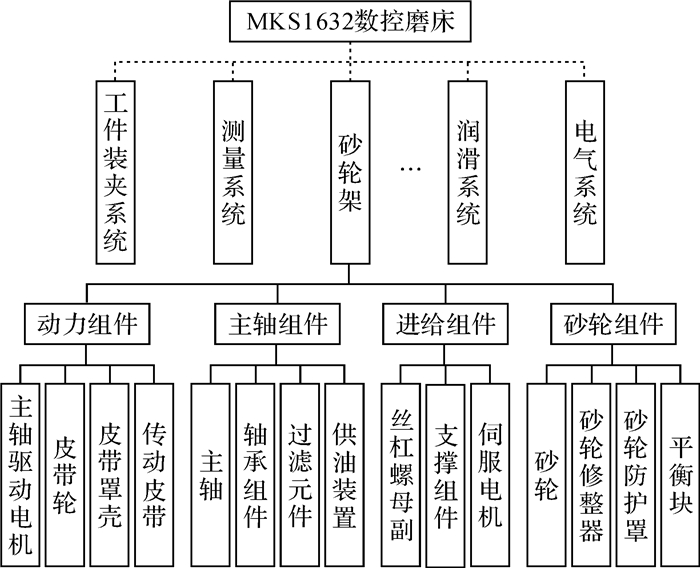
砂轮架系统的主要功能是驱动砂轮以可接受的精度完成规定的运动轨迹。该系统由动力组件、主轴组件、进给组件和砂轮组件构成。MKS1632数控磨床砂轮架系统的组成如图 1所示。
|
| 图 1 MKS1632数控磨床砂轮架系统的组成 Fig.1 Composition of grinding wheel rack system of MKS1632 CNC grinder |
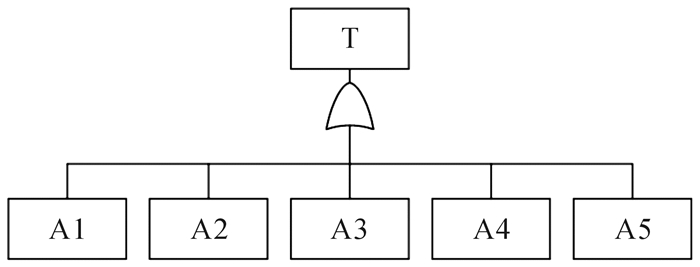
砂轮架系统故障树分析是将砂轮架系统失效作为顶事件,将导致砂轮架系统失效的各种故障模式作为次顶事件,再将故障模式逐层往下分解直至确定所有可能导致顶事件发生的基本事件,并确定各级事件间的逻辑关系,并用相应逻辑门进行连接。现假设砂轮架系统故障树分析中各基本事件之间相互独立,通过对砂轮架系统的结构、各部件的功能进行分析,并结合北京第二机床厂提供的大量原始故障数据,建立砂轮架系统故障树,如图 2所示。
|
| 图 2 砂轮架系统故障树 Fig.2 Fault tree of grinding wheel rack system |
图 2中:T表示砂轮架系统失效,A1表示主轴振动异响,A2表示电机故障,A3表示主轴不转,A4表示顶尖动作不到位,A5表示主轴润滑油压力不足。
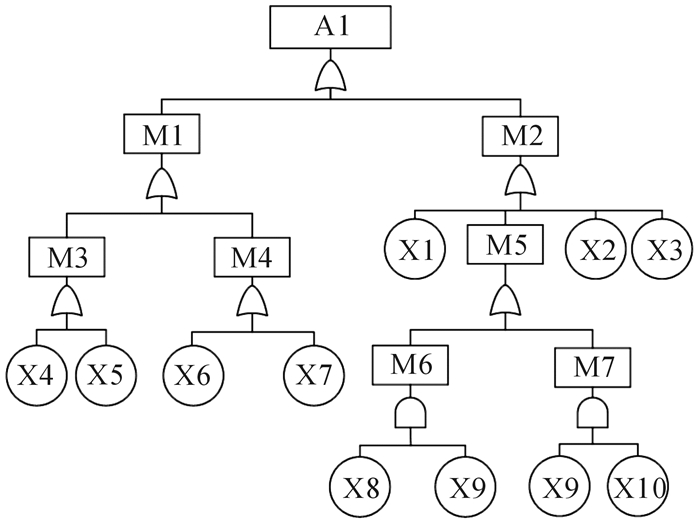
图 3为砂轮架系统主轴振动异响故障树。图 3中:M1表示轴承失效,M2表示主轴润滑不良, M3表示轴承质量不合格,M4表示轴承润滑不良,M5表示润滑油滞留,M6表示过滤网受损,M7表示管路堵塞, X1表示液压泵故障,X2表示油箱油位过低,X3表示蓄能器故障,X4表示装配时轴承损坏,X5表示外检失误,X6表示润滑脂注入量不合理,X7表示润滑脂含有杂质,X8表示过滤网质量不合格,X9表示润滑油不干净,X10表示过滤网过滤精度不匹配。
|
| 图 3 砂轮架系统主轴振动异响故障树 Fig.3 Fault tree of grinding wheel rack system about spindle vibration sound |
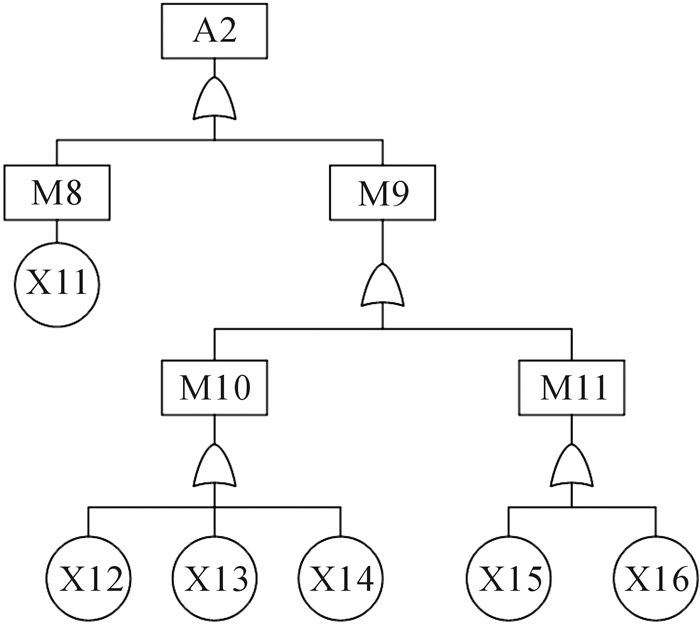
图 4为砂轮架系统电机故障故障树。图 4中:M8表示电机质量不合格,M9表示电机装配不良,M10表示电机轴与主轴不平行,M11表示电机皮带轮端面与主轴带轮端面不共面,X11表示外检失误,X12表示电机座螺母装配不良,X13表示电机座与电机配合平面度超差,X14表示主轴箱电机座配合平面度超差,X15表示主轴箱电机座配合平面位置尺寸超差,X16表示主轴轴承、端盖及带轮等轴向间隙不合理。
|
| 图 4 砂轮架系统电机故障故障树 Fig.4 Fault tree of grinding wheel rack system about the motor failure |
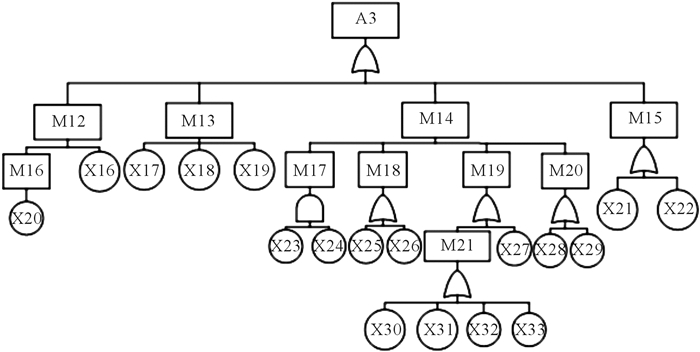
图 5为砂轮架系统主轴不转故障树。图 5中:M12表示传动皮带松动,M13表示油液过脏,M14表示液压油供油不足,M15表示轴承损坏,M16表示皮带制造精度不一,M17表示阀、管道堵塞,M18表示过滤网堵塞,M19表示油液泄漏,M20表示泵故障,M21表示液压缸、阀、管接头或压力表等接头处密封元件损坏,X16表示皮带未及时更换,X17表示液压油长期未更换,X18表示油品保存不妥、含杂质,X19表示油路、管壁不干净,X20表示外购件检查不严,X21表示润滑不到位,X22表示轴承装配不良,X23表示液压油流速过低,X24表示液压油含杂质过多,X25表示滤芯质量不合格,X26表示过滤网长期未更换,X27表示油管损坏、老化,X28表示电机转向错误,X29表示泵疲劳损坏,X30表示液压油中所含固体颗粒磨损阀芯和密封圈,X31表示液压油温度过高加速密封元件老化,X32表示液压油生化腐蚀金属管壁,X33表示液压系统压力过大损坏密封件。
|
| 图 5 砂轮架系统主轴不转故障树 Fig.5 Fault tree of grinding wheel rack system about spindle not-rotating |
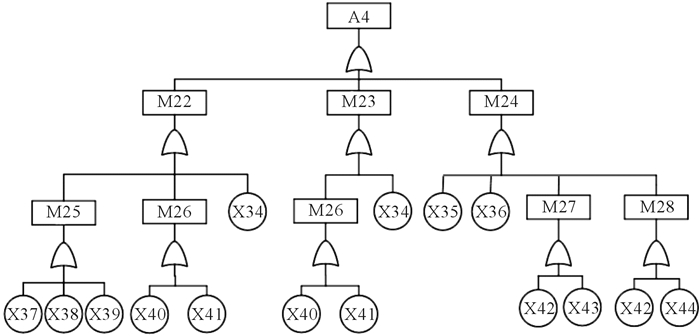
图 6为砂轮架系统顶尖动作不到位故障树。图 6中:M22表示顶尖前进无动作,M23表示顶尖不回退,M24表示顶尖顶紧超时,M25表示无信号发送,M26表示电磁阀故障,M27表示液压油压力不足,M28表示液压缸润滑不良,X34表示套筒挤死,X35表示液压缸支架松动,X36表示信号开关位置不正确,X37表示信号开关支架松动,X38表示信号开关损坏,X39表示信号线损坏,X40表示电磁阀阀芯卡住,X41表示电磁阀损坏,X42表示油缸润滑不良,X43表示油管破损漏油,X44表示套筒润滑不良。
|
| 图 6 砂轮架系统顶尖动作不到位故障树 Fig.6 Fault tree of grinding wheel rack system about top movements failure |
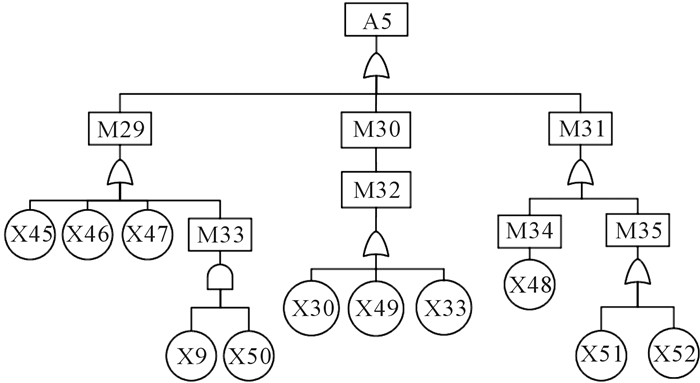
图 7为砂轮架系统主轴润滑油压力不足故障树。图 7中:M29表示润滑油供油不足,M30表示主轴润滑油泄漏,M31表示管路故障,M32表示控制阀、管接头、压力继电器或压力表接头等处密封元件损坏,M33表示滤芯堵塞,M34表示管道堵塞,M35表示管道破裂,X45表示电机损坏,X46表示联轴器损坏,X47表示润滑油泵磨损严重,X48表示液压油中有杂质,X49表示润滑油中混入空气与水污染物腐蚀金属物质,X50表示长期不更换滤芯,X51表示管道质量差,X52表示冲击力作用。
|
| 图 7 砂轮架系统主轴润滑油压力不足故障树 Fig.7 Fault tree of grinding wheel rack system about insufficient lubricating oil pressure of spindle |
由于篇幅的限制,下文将以砂轮架主轴振动异响这一故障模式为例,将模糊集理论运用到故障树的定量分析中,其他几种故障模式均可采用此方法进行分析。
2.1 梯形模糊数模糊集理论主要用于处理不精确的或模糊的问题[11],其基本思想是把经典集合中的绝对隶属关系灵活化,或称模糊化[12]。该理论通过特征函数表示元素集合的隶属程度,这种隶属关系不再是绝对地用二值集合(0,1)来表示,而是可以在区间[0, 1]中取值,所取值的大小对应隶属程度的高低。
设U是一个由对象组成的论域,A为定义在论域U上的一个模糊集,有:
| $ \mu _A^ \sim \left( x \right):U \to \left( {0,1} \right),x \in U $ |
其中
梯形模糊数的定义为:设q为实数域R上的一个模糊数,定义一个隶属函数
| $ \mu _q^ \sim \left( x \right) = \left\{ \begin{array}{l} \frac{{x - a}}{{b - a}},\;\;\;\;a \le x < b\\ 1,\;\;\;\;\;\;\;\;b \le x \le c\\ \frac{{d - x}}{{d - c}},\;\;\;\;c < x \le d\\ 0,\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (1) |
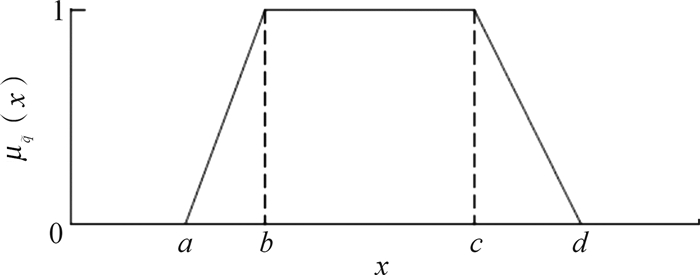
式中q为梯形模糊数,记作q=(a, b, c, d),其中-∞<a≤b≤c≤d<∞,b≤x≤c称为相对最概然区间。当a=b=c=d时,q失去模糊性,为一确定值;当b=c时,q退化为一个三角模糊数,由此可认为三角模糊数是梯形模糊数的一种特殊情况,采用梯形模糊数比三角模糊数更具普遍性;当a>0时,q为正梯形模糊数。本文采用正梯形模糊数进行故障树分析,其隶属函数如图 8所示。
|
| 图 8 正梯形模糊数隶属函数 Fig.8 Membership function of positive trapezoidal fuzzy number |
设2个梯形模糊数q1=(a1, b1, c1, d1)和q2=(a2, b2, c2, d2),根据经典扩张原则可知梯形模糊数q1和q2满足如下代数运算法则[13]:
1) 加法。
| $ {q_1} \oplus {q_2} = \left( {{a_1} + {a_2},{b_1} + {b_2},{c_1} + {c_2},{d_1} + {d_2}} \right) $ |
2) 减法。
| $ {q_1}\Theta {q_2} = \left( {{a_1} - {a_2},{b_1} - {b_2},{c_1} - {c_2},{d_1} - {d_2}} \right) $ |
3) 乘法。
| $ {q_1} \otimes {q_2} = \left( {{a_1}{a_2},{b_1}{b_2},{c_1}{c_2},{d_1}{d_2}} \right) $ |
传统故障树分析中使用的“与”门和“或”门算子为[14]:
| $ {q_{{\rm{AND}}}} = \prod\limits_{i = 1}^n {{q_i}} $ |
| $ {q_{{\rm{OR}}}} = 1 - \prod\limits_{i = 1}^n {\left( {1 - {q_i}} \right)} $ |
式中qi表示基本事件i发生的概率,为确定值。在本文的模糊故障树分析中,第i个基本事件发生的概率qi为梯形模糊数,不再是确定值。
根据模糊数学多元扩张原理,故障树分析中的模糊算子为[15-16]:
| $ \begin{array}{l} {q_{{\rm{AND}}}} = \left( {{a_{{\rm{AND}}}},{b_{{\rm{AND}}}},{c_{{\rm{AND}}}},{d_{{\rm{AND}}}}} \right) = \prod\limits_{i = 1}^n {{q_i}} = \\ \;\;\;\;\;\;\;\;\;\;\left( {\prod\limits_{i = 1}^n {{a_i}} ,\prod\limits_{i = 1}^n {{b_i}} ,\prod\limits_{i = 1}^n {{c_i}} ,\prod\limits_{i = 1}^n {{d_i}} } \right) \end{array} $ | (2) |
| $ \begin{array}{l} {q_{{\rm{OR}}}} = \left( {{a_{{\rm{OR}}}},{b_{{\rm{OR}}}},{c_{{\rm{OR}}}},{d_{{\rm{OR}}}}} \right) = 1\Theta \prod\limits_{i = 1}^n {\left( {1\Theta {q_i}} \right)} = \\ \;\;\;\;\;\;\;\;\left[ {1 - \prod\limits_{i = 1}^n {\left( {1 - {a_i}} \right)} ,1 - \prod\limits_{i = 1}^n {\left( {1 - {b_i}} \right)} ,} \right.\\ \;\;\;\;\;\;\;\;\left. {1 - \prod\limits_{i = 1}^n {\left( {1 - {c_i}} \right)} ,1 - \prod\limits_{i = 1}^n {\left( {1 - {d_i}} \right)} } \right] \end{array} $ | (3) |
现以砂轮架系统主轴振动异响为例进行模糊故障树分析,根据建立的故障树可得最小割集为:X1,X2,X3,X4,X5,X6,X7,X8X9,X9X10。
上述故障树中各项基本事件发生概率的原始数据采取专家评分的方式进行确定,由北京第二机床厂的6位专家根据机床的故障数据以及各自的相关经验分别对上述10个基本事件的发生概率进行评估,并以梯形模糊数的形式进行打分。由于各个专家有各自的经验和特长,而经验相对丰富的专家做出的评价往往更为准确,因此其评分在最终结果中所占比例应该相对高一些,故本文采取一种基于梯形模糊数质心距离的相似度度量方法来集成这6位专家的判断。
确定各个基本事件发生概率的梯形模糊数按如下步骤进行:
1) 由6位专家以梯形模糊数的形式分别给出该基本事件的发生概率qi=(ai, bi, ci, di)(i=1, 2, …,6);
2) 分别计算这6位专家的单个判断qi的质心,记为C(qi)=(xi, yi)(i=1, 2, …,6),计算公式如下:
| $ {{\bar x}_i} = \frac{{\int_{{a_i}}^{{b_i}} {\frac{{x\left( {x - {a_i}} \right)}}{{{b_i} - {a_i}}}{\rm{d}}x} + \int_{{b_i}}^{{c_i}} {x{\rm{d}}x} + \int_{{c_i}}^{{d_i}} {\frac{{x\left( {{d_i} - x} \right)}}{{{d_i} - {c_i}}}{\rm{d}}x} }}{{\int_{{a_i}}^{{b_i}} {\frac{{x - {a_i}}}{{{b_i} - {a_i}}}{\rm{d}}x} + \left( {{c_i} - {b_i}} \right)\int_{{c_i}}^{{d_i}} {\frac{{{d_i} - x}}{{{d_i} - {c_i}}}{\rm{d}}x} }} $ |
| $ {{\bar y}_i} = \frac{{\int_{{a_i}}^{{b_i}} {{{\left( {\frac{{y - {a_i}}}{{{b_i} - {a_i}}}} \right)}^2}{\rm{d}}y} + \left( {{c_i} - {b_i}} \right) + \int_{{c_i}}^{{d_i}} {{{\left( {\frac{{{d_i} - y}}{{{d_i} - {c_i}}}} \right)}^2}{\rm{d}}y} }}{{2\left[ {\int_{{a_i}}^{{b_i}} {\frac{{y - {a_i}}}{{{b_i} - {a_i}}}{\rm{d}}y} + \left( {{c_i} - {b_i}} \right) + \int_{{c_i}}^{{d_i}} {\frac{{{d_i} - y}}{{{d_i} - {c_i}}}{\rm{d}}y} } \right]}} $ |
3) 计算每两个判断qi,qj之间的距离,记为d(qi, qj)(i, j=1, 2, …, 6),计算公式如下:
| $ d\left( {{q_i},{q_j}} \right) = \sqrt {{{\left( {{{\bar x}_i} - {{\bar x}_j}} \right)}^2} + {{\left( {{{\bar y}_i} - {{\bar y}_j}} \right)}^2}} $ |
4) 令Q=max d(qi,qj),计算每两个判断qi,qj之间的相似度,记为S(qi,qj), 计算公式如下:
| $ S\left( {{q_i},{q_j}} \right) = 1 - \frac{{d\left( {{q_i},{q_j}} \right)}}{Q} $ |
从式中可以看出,当2个判断之间的质心距离最大时,它们的相似度为0;当2个判断之间的质心重合的时候,d(qi,qj)=0,它们的相似度达到最大值, 为1。
5) 计算每个判断qi的平均一致程度,记为A(qi),其中i=1, 2, …, 6, 计算公式如下:
| $ A\left( {{q_i}} \right) = \frac{1}{5}\sum\limits_{j = 1,j \ne i}^6 {S\left( {{q_i},{q_j}} \right)} $ |
6) 计算每个判断qi的相对一致程度系数,记为wi,计算公式如下:
| $ {w_i} = \frac{{A\left( {{q_i}} \right)}}{{\sum\limits_{j = 1}^6 {A\left( {{q_j}} \right)} }} $ | (4) |
由公式(4)可知:0<wi<1,且
7) 根据上面所求的相对一致程度系数计算6位专家的集成判断q:
| $ \begin{array}{l} q = \sum\limits_{i = 1}^6 {{w_i}} \cdot {q_i} = \\ \;\;\;\;\;\left( {\sum\limits_{i = 1}^6 {{w_i}} \cdot {a_i},\sum\limits_{i = 1}^6 {{w_i}} \cdot {b_i},\sum\limits_{i = 1}^6 {{w_i}} \cdot {c_i},\sum\limits_{i = 1}^6 {{w_i}} \cdot {d_i}} \right) \end{array} $ | (5) |
通过将6位专家各自打分确定的每项基本事件发生概率的原始数据按上述方法进行加权平均, 获得数控磨床砂轮架系统主轴振动异响故障树中基本事件的发生概率,见表 1。
| 代号 | 基本事件 | 发生概率 |
| X1 | 液压泵故障 | (0.005 92, 0.006 95, 0.007 41, 0.009 51) |
| X2 | 油箱油位过低 | (0.022 31, 0.024 11, 0.024 97, 0.025 86) |
| X3 | 蓄能器故障 | (0.004 32, 0.004 76, 0.005 21, 0.007 31) |
| X4 | 装配时轴承损坏 | (0.013 54, 0.0147 9, 0.017 21, 0.025 46) |
| X5 | 外检失误 | (0.020 10, 0.023 57, 0.026 41, 0.031 45) |
| X6 | 润滑脂注入量不合理 | (0.012 48, 0.014 71, 0.016 35, 0.017 53) |
| X7 | 润滑脂含有杂质 | (0.006 53, 0.007 11, 0.008 06, 0.008 74) |
| X8 | 过滤网质量不合格 | (0.008 36, 0.009 21, 0.009 60, 0.010 25) |
| X9 | 润滑油不干净 | (0.042 51, 0.047 36, 0.052 88, 0.066 46) |
| X10 | 过滤网过滤精度不匹配 | (0.002 96, 0.003 21, 0.003 70, 0.004 39) |
基本事件发生概率的模糊性决定了顶事件发生概率的模糊性[17], 因此顶事件的发生概率也用梯形模糊的形式表示。根据图 3确定的故障树最小割集以及前文介绍的梯形模糊数的模糊算子和代数运算法则,可以计算出顶事件(砂轮架主轴振动异响)发生概率的梯形模糊数为:
| $ {q_{{{\rm{A}}_1}}} = \left( {0.08273,0.09285,0.10179,0.12039} \right) $ |
计算结果表明砂轮架系统主轴振动异响发生的概率为8.273%~12.039%,其最概然区间为[0.092 85,0.101 79],即顶事件发生概率位于该区间的可能性最大,这一结果与北京第二机床厂的实际情况相吻合。
2.4 模糊临界重要度分析由工程实践经验可知,故障树分析中基本事件的重要性是不同的。对各基本事件的重要度进行准确全面的评价有助于企业确定系统的薄弱环节,并进行针对性的改进,从而降低提高系统可靠性所需成本。在现有模糊故障树研究中,均采用模糊重要度作为评价基本事件重要性的指标,与传统故障树分析中的概率重要度类似,它反映的是基本事件的灵敏度,即基本事件发生概率的变化率对顶事件发生概率的影响程度,但不能反映基本事件自身发生概率的大小。然而在数控机床可靠性研究中,某些基本事件的灵敏度虽然不高,但它有着较高的发生概率,这类基本事件同样需要引起企业重视。为了克服这一缺陷,本文首次提出“模糊临界重要度”的概念,并确定其计算方法。它类似于传统故障树分析中的临界重要度,从基本事件的灵敏度和发生概率大小的双重角度综合评价基本事件的重要性,是一种更为全面的评价标准。下文将介绍模糊临界重要度的计算方法,并对砂轮架系统主轴振动异响故障树分析中各基本事件的模糊临界重要度进行求解。
在传统故障树分析中,临界重要度的计算公式为:
| $ \begin{array}{l} {I_{\rm{G}}}\left( i \right) = \frac{{\partial R\left( {{q_1},{q_2}, \cdots ,{q_n}} \right)}}{{R\left( {{q_1},{q_2}, \cdots ,{q_n}} \right)}}/\frac{{\partial {q_i}}}{{{q_i}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{q_i}}}{{R\left( {{q_1},{q_2}, \cdots ,{q_n}} \right)}}\\ \;\;\;\;\;\;\;\;\;\;\;\left[ {R\left( {{q_1}, \cdots ,{q_{i - 1}},1,{q_{i + 1}}, \cdots ,{q_n}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {R\left( {{q_1}, \cdots ,{q_{i - 1}},0,{q_{i + 1}}, \cdots ,{q_n}} \right)} \right] \end{array} $ |
式中:IG(i)表示基本事件i的临界重要度;qi表示基本事件i的发生概率;R(q1, q2, …, qn)是顶事件的发生概率,它是关于q1, q2, …, qn的n元函数。
在临界重要度的计算公式中,基本事件的发生概率是一个确定值,而在模糊故障树分析中,基本事件的发生概率用模糊数来表示。因此笔者可以假设基本事件仍为发生和不发生两种,只是无法获取基本事件发生概率的确定值而用模糊数描述[15],这样可以根据临界重要度的概念,定义一个用于评价模糊故障树分析中基本事件重要性的指标——模糊临界重要度。
令系统的结构函数φ(X)=φ(x1, x2, …, xn);基本事件i的发生概率的梯形模糊数为qxi,其隶属函数为μqxi;顶事件的模糊概率qA≡q(qx1, qx2, …, qxn), 其隶属函数为μqA, 则根据扩张原理有[12]:
| $ {\mu _{{q_A}}}\left( y \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \mathop {\sup \min }\limits_{X \in {H^{ - 1}}\left( y \right)} \left[ {{\mu _{{q_{{x_i}}}}}, \cdots ,{\mu _{{q_{{x_n}}}}}} \right],\\ 0, \end{array}&\begin{array}{l} {H^{ - 1}}\left( y \right) \ne 0\\ 其他 \end{array} \end{array}} \right. $ |
记:q(qxi, …, qxi-1, 1, qxi+1, …, qxn)≡qAi1,q(qxi, …, qxi-1, 0, qxi+1, …, qxn)≡qAi0,分别为基本事件i在xi=1和xi=0时顶事件的失效模糊概率,则定义基本事件i的模糊临界重要度FG(i)为:
| $ {F_{\rm{G}}}\left( i \right) \equiv \frac{{\int_0^1 {x{\mu _{{q_{{x_i}}}}}{\rm{d}}x} \cdot \int_0^1 {{\mu _{{q_A}}}{\rm{d}}x} }}{{\int_0^1 {x{\mu _{{q_A}}}{\rm{d}}x} \cdot \int_0^1 {{\mu _{{q_{{x_i}}}}}{\rm{d}}x} }}\left( {\frac{{\int_0^1 {x{\mu _{{q_{{A_{i1}}}}}}{\rm{d}}x} }}{{\int_0^1 {{\mu _{{q_{{A_{i1}}}}}}{\rm{d}}x} }} - \frac{{\int_0^1 {x{\mu _{{q_{{A_{i0}}}}}}{\rm{d}}x} }}{{\int_0^1 {{\mu _{{q_{{A_{i0}}}}}}{\rm{d}}x} }}} \right) $ | (6) |
式中:
由计算公式(6)可知模糊临界重要度包含了基本事件的发生概率和灵敏度两项指标,是一种较为准确全面的评价标准。
按照公式(6)可计算出数控磨床砂轮架系统主轴振动异响故障树中各基本事件的模糊临界重要度, 如表 2所示。
| 代号 | 基本事件 | 模糊临界重要度 |
| X1 | 液压泵故障 | 0.066 18 |
| X2 | 油箱油位过低 | 0.228 36 |
| X3 | 蓄能器故障 | 0.048 71 |
| X4 | 装配时损坏轴承 | 0.161 07 |
| X5 | 外检失误 | 0.234 97 |
| X6 | 润滑脂注入量不合理 | 0.140 76 |
| X7 | 润滑脂含有杂质 | 0.071 17 |
| X8 | 过滤网质量不合格 | 0.004 40 |
| X9 | 润滑油不干净 | 0.006 09 |
| X10 | 过滤网过滤精度不匹配 | 0.001 67 |
由表 2中各基本事件的模糊临界重要度可知,外检失误、油箱油位过低、装配时轴承损坏、润滑脂注入量不合理这4项基本事件的重要度相对较高,是导致砂轮架系统主轴振动异响的主要原因。这与北京第二机床厂的故障统计结果相吻合,同时该结果作为一种定量依据,为企业提高产品的可靠性起到一定的作用。
3 结论本文通过统计整理数控磨床砂轮架系统的大量原始故障数据,并结合对砂轮架系统结构和功能的分析建立了较为完整的砂轮架系统故障树,对数控磨床砂轮架系统的可靠性研究有一定的参考意义。为了解决数控磨床砂轮架系统的故障树分析中基本事件难于准确赋值的情况,本文将模糊集理论应用到传统故障树定量分析中,采用梯形模糊数的形式来表示事件的发生概率。同时在确定各基本事件重要度的过程中,克服了模糊重要度无法反映基本事件自身发生概率大小的缺陷,首次提出了模糊临界重要度的概念,并确定其计算公式,从发生概率的大小和灵敏度两方面来综合评价数控磨床砂轮架系统故障树分析中各基本事件的重要度,从而帮助企业确定了系统的薄弱环节,为提高系统的可靠性提供了一种定量依据。该方法在可靠性工程上具有广阔的应用前景。
| [1] |
李兵, 朱梅林, 陈晓伟, 等.
模糊故障树分析法在内燃机可靠性中的应用研究[J]. 内燃机学报, 1999, 17(1): 66–69.
LI Bing, ZHU Mei-lin, CHEN Xiao-wei, et al. A study on fuzzy fault tree analysis method in application to internal combustion engines reliability[J]. Transactions of CSICE, 1999, 17(1): 66–69. |
| [2] | LIANG G S, WANG M J J. Fuzzy fault-tree analysis using failure possibility[J]. Microelectronics Reliability, 1993, 33(4): 583–597. DOI:10.1016/0026-2714(93)90326-T |
| [3] | ADAM S, MARKOWSKI M, SAM M. Fuzzy logic for process safety analysis[J]. Journal of Loss Prevention in the Process Industries, 2009, 22(6): 695–702. DOI:10.1016/j.jlp.2008.11.011 |
| [4] |
李飞, 黄瑾辉, 曾光明, 等.
基于梯形模糊数的沉积物重金属污染风险评价模型与实例研究[J]. 环境科学, 2012, 33(7): 2352–2358.
LI Fei, HUANG Jin-hui, ZENG Guang-ming, et al. Assessment model for heavy metal pollution in sediment based on trapezoidal fuzzy numbers and case study[J]. Environmental Science, 2012, 33(7): 2352–2358. |
| [5] |
于卫东, 韩卫国, 位秀雷.
基于模糊故障树的舰空导弹系统可靠性分析[J]. 兵器装备工程学报, 2017, 38(8): 54–57.
YU Wei-dong, HAN Wei-guo, WEI Xiu-lei. Reliability analysis of ship-to-air missile weapon system based on fuzzy fault tree[J]. Journal of Ordnance Equipment Engineering, 2017, 38(8): 54–57. DOI:10.11809/scbgxb2017.08.013 |
| [6] |
李太福, 王栓虎, 解德乾, 等.
基于模糊理论的高速冲床可靠性分配[J]. 锻压技术, 2011, 36(5): 71–75.
LI Tai-fu, WANG Shuan-hu, XIE De-qian, et al. Reliability allocation for high-speed punch based on fuzzy theory[J]. Forging and Stamping Technology, 2011, 36(5): 71–75. DOI:10.3969/j.issn.1000-3940.2011.05.018 |
| [7] |
李如忠, 童芳, 周爱佳, 等.
基于梯形模糊数的地表灰尘重金属污染健康风险评价模型[J]. 环境科学学报, 2011, 31(8): 1790–1798.
LI Ru-zhong, TONG Fang, ZHOU Ai-jia, et al. Fuzzy assessment model for the health risk of heavy metals in urban dusts based on trapezoidal fuzzy numbers[J]. Acta Scientiae Circumstantiae, 2011, 31(8): 1790–1798. |
| [8] |
徐宏海, 李晓阳.
带超长滚珠丝杠的立式玻璃磨边机砂轮架模态分析[J]. 振动与冲击, 2013, 32(18): 189–194.
XU Hong-hai, LI Xiao-yang. Modal analysis of a grinding wheel carriage for a vertical glass-edge grinding machine with a long ball screw[J]. Journal of Vibration and Shock, 2013, 32(18): 189–194. DOI:10.3969/j.issn.1000-3835.2013.18.036 |
| [9] |
柳懿麟. 高速高精凸轮轴磨床砂轮架结构设计与优化[D]. 武汉: 华中科技大学机械科学与工程学院, 2014: 50-56.
LIU Yi-lin. Structure design and optimization of grinding carriage for high-speed and high-precision grinder[D]. Wuhan: Huazhong University of Science and Technology, School of Mechanical Science & Engineering, 2014: 50-56. http://cdmd.cnki.com.cn/Article/CDMD-10487-1015010230.htm |
| [10] |
王成禹, 王玉琢, 邹世文, 等.
高精度随动数控凸轮轴磨床砂轮架模态分析[J]. 机床与液压, 2016, 44(17): 147–151.
WANG Cheng-yu, WANG Yu-zhuo, ZOU Shi-wen, et al. Modal analysis of high precision servo CNC camshaft grinding machine's grinding carriage[J]. Machine Tool & Hydraulics, 2016, 44(17): 147–151. DOI:10.3969/j.issn.1001-3881.2016.17.033 |
| [11] |
何新贵.
模糊知识处理的理论与技术[M]. 北京: 国防工业出版社, 1994: 21-24.
HE Xin-gui. Fuzzy theories and fuzzy techniques in knowledge processing[M]. Beijing: National Defend Industry Press, 1994: 21-24. |
| [12] |
王永传, 郁文贤, 庄钊文.
基于故障率为模糊数的故障树分析方法研究[J]. 系统工程理论与实践, 2000, 20(12): 102–107.
WANG Yong-chuan, YU Wen-xian, ZHUANG Zhao-wen. A study of fault tree analysis based on failure rate as fuzzy number[J]. System Engineering-Theory and Practice, 2000, 20(12): 102–107. DOI:10.3321/j.issn:1000-6788.2000.12.017 |
| [13] |
武庄, 石柱, 何新贵.
基于模糊集合论的故障树分析方法及其应用[J]. 系统工程与电子技术, 2000, 22(9): 72–75.
WU Zhuang, SHI Zhu, HE Xin-gui. A fault tree analysis method based on fuzzy set theory and its application[J]. Systems Engineering and Electronics, 2000, 22(9): 72–75. DOI:10.3321/j.issn:1001-506X.2000.09.023 |
| [14] |
刘惟信.
机械可靠性设计[M]. 北京: 清华大学出版社, 1996: 39-43.
LIU Wei-xin. Mechanical reliability design[M]. Beijing: Tsinghua University Press, 1996: 39-43. |
| [15] | SINGER D. A fuzzy set approach to fault tree and reliability analysis[J]. Fuzzy Sets and Systems, 1990, 34(2): 145–155. DOI:10.1016/0165-0114(90)90154-X |
| [16] | MENTES A, HELVACIOGLU I. An application of fuzzy fault tree analysis for spread mooring systems[J]. Ocean Engineering, 2011, 38(2/3): 285–294. |
| [17] |
俞树荣, 杨慧来.
基于梯形模糊数的长输管道故障树分析[J]. 兰州理工大学学报, 2009, 35(5): 62–65.
YU Shu-rong, YANG Hui-lai. Fault tree analysis of oil and gas pipe-lines with trapezoidal fuzzy number[J]. Journal of Lanzhou University of Technology, 2009, 35(5): 62–65. DOI:10.3969/j.issn.1673-5196.2009.05.014 |
| [18] |
王永传, 郁文贤, 庄钊文.
一种故障树模糊重要度分析的新方法[J]. 国防科技大学学报, 1999, 21(3): 66–69.
WANG Yong-chuan, YU Wen-xian, ZHUANG Zhao-wen. A new method of the importance analysis of FTA[J]. Journal of National University of Defense Technology, 1999, 21(3): 66–69. |



