2. 中车戚墅堰机车车辆工艺研究所有限公司 技术研发中心, 江苏 常州 213011;
3. 盐城工学院 汽车工程学院, 江苏 盐城 224051
2. Technology Center, CRRC Qishuyan Institute Co., Ltd., Changzhou 213011, China;
3. School of Automotive Engineering, Yancheng Institute of Technology, Yancheng 224051, China
盘式制动器是利用制动盘与制动块之间的摩擦作用来实现设备减速或停止运行的一种机械装置,由于具有散热快、质量轻、调整方便等优点,该装置在交通工具和工业装备中得到广泛应用。但是当制动器工作时,有时会产生振动噪声,影响周围环境,从而降低产品的市场竞争力。研究表明,制动盘与制动块之间的法向接触刚度对制动器动力学特性及振动噪声有重要影响[1-3],因此需要准确辨识两者之间的法向接触刚度(为方便叙述,下文简称接触刚度)。
尽管从理论上可以依据Hertz弹性接触模型[4]和G-W统计学接触模型计算制动盘与制动块之间的接触刚度[5-6],但是准确获取时变的制动盘与制动块的特征参数较为困难。目前多位学者开展了制动盘与制动块之间的接触刚度辨识的实验研究,Triches等将制动块置于刚性体表面,然后在制动块上方再放置一重物,通过锤击试验测得系统固有频率,然后根据动力学关系计算出制动块的接触刚度[7-8]。Sherif等认为制动盘与制动块摩擦系统中制动盘与制动块之间的接触刚度是系统的主要刚度,并根据摩擦尖叫频率对接触刚度进行了参数辨识[9]。Giannini等基于盘-梁试验装置,发现制动块的约束作用使制动盘受力不对称而产生模态裂分,并利用裂分的频率差值辨识了制动盘与制动块之间的接触刚度[10]。Oura等通过试验发现制动盘与制动块之间的动态接触刚度大于静态接触刚度,且其数值大小与加载频率无关,但随压力增大而增大[11]。Goto等根据受压力作用的制动器模态频率测试结果,对制动盘与制动块之间的接触刚度进行了辨识,认为接触刚度具有依赖制动压力和模态频率的特性,并进行了制动器有限元复特征值分析和制动尖叫台架试验的对照研究,但作者并未给出制动盘与制动块之间的接触刚度的实际辨识结果,也未作深入探讨[12]。需要指出的是,由于简化的装置结构和工况与实际制动器存在较大区别,测得的结果不能代表实际制动盘与制动块之间的接触刚度。另外,由于制动器振动噪声影响因素有很多,当前基于结构模态耦合理论形成的有限元复特征值分析方法,仍存在过预测或欠预测问题[13-14]。为了提高分析精度,建立准确的制动器零件间的接触关系,是当前制动器振动噪声研究的一个重要方向[15]。
本文针对一款乘用车浮钳盘式制动器,利用制动器台架试验测得约束状态下制动盘的模态频率特征,结合有限元模态分析,对制动盘与制动块之间的接触刚度进行辨识;并分析了制动压力、制动盘振动模态对接触刚度的影响。
1 浮钳盘式制动器的工作原理浮钳盘式制动器的基本结构与工作原理如图 1所示,当它开始工作时,位于钳体中的活塞在制动液的作用下,推动右侧制动块与制动盘接触,同时钳体向右移动,并带动左侧制动块与制动盘接触。随着制动管路压力增大,作用于两侧制动块上的压力随之增大,从而对旋转的制动盘产生摩擦作用,使之减速或停止。
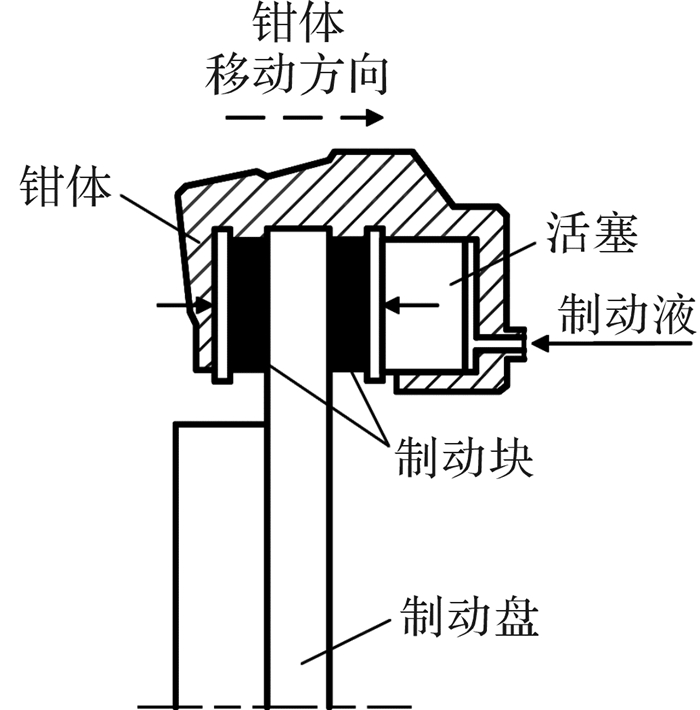
|
| 图 1 浮钳盘式制动器的基本结构与工作原理示意图 Fig.1 Schematic diagram of the basic structure and working principle of floating caliper disc brake |
本文采用制动器模态试验和有限元分析相结合的方法[16-17],以准确分析制动盘与制动块的模态特性和辨识两者之间的接触刚度,具体分析过程如图 2所示。
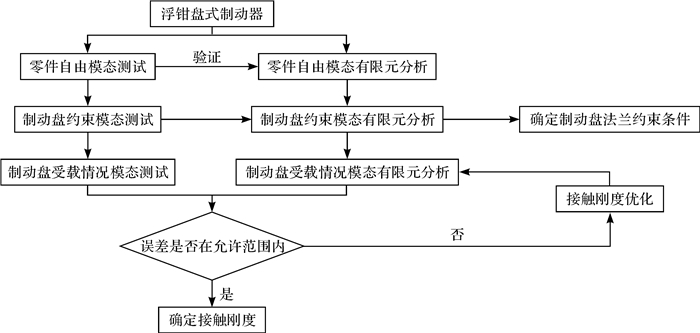
|
| 图 2 制动盘与制动块之间的接触刚度的辨识流程 Fig.2 Identification process of contact stiffness between brake disc and brake pad |
针对如图 3所示的浮钳盘式制动器,将它拆解后,分别将制动盘和制动块放置在海绵上,利用锤击方法,测得其自由模态频率,然后利用ABAQUS软件建立两者的有限元模型,采用表 1所示的制动盘与制动块材料特性参数,进行自由模态特性有限元分析,获得制动盘和制动块的各阶模态频率,与实测结果相比,误差在5%范围内。

|
| 图 3 浮钳盘式制动器实物图 Fig.3 Physical map of the floating caliper disc brake |
| 零件 | 材料 | 弹性模量/ GPa |
泊松比 | 密度/ (kg/m3) |
| 制动盘 | HT150 | 135 | 0.25 | 7 250 |
| 背板 | 45号钢 | 206 | 0.26 | 7 800 |
| 摩擦材料 | 半金属 | 10 | 0.35 | 2 600 |
对于安装在轮毂法兰上的制动盘,在进行有限元建模时,对5个安装孔进行x,y,z三个方向平移自由度的约束,受法兰约束的制动盘及自由状态的制动块在1~10 kHz内的模态特性测试结果与有限元分析结果分别如图 4、图 5和表 2所示,其中(m, 0)代表制动盘的第m阶面外振动模态。从表 2可知,有限元分析结果与测试结果的误差亦在5%以内,表明了有限元建模的正确性和有效性。
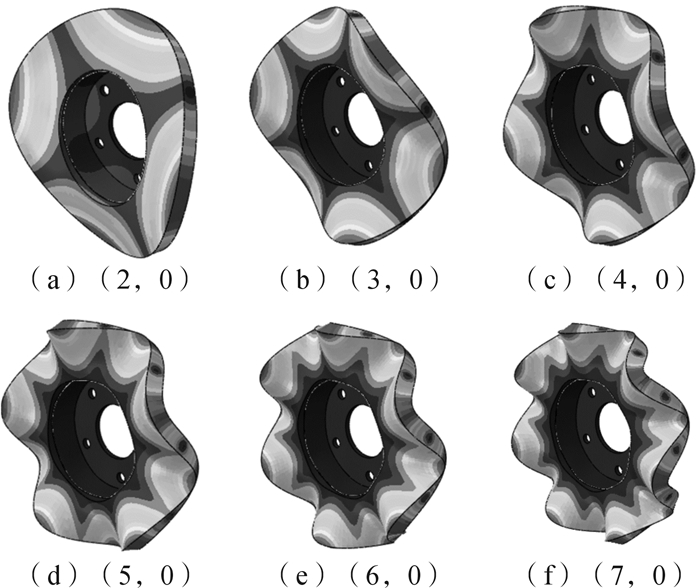
|
| 图 4 受法兰约束的制动盘面外模态振型 Fig.4 Out-of-plane modal shapes of the brake disc under flange constraint condition |
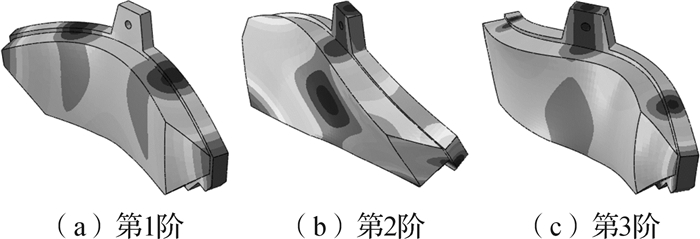
|
| 图 5 自由状态下的制动块模态振型 Fig.5 Modal shapes of the brake pad in free state |
| 零件 | 模态阶次 | 模态频率/Hz | 误差/% | |
| 测试结果 | 有限元分析结果 | |||
| 制动盘 | (2, 0) | 1 227 | 1 264 | 3.02 |
| (3, 0) | 2 217 | 2 199 | -0.81 | |
| (4, 0) | 3 544 | 3 522 | -0.62 | |
| (5, 0) | 5 223 | 5 192 | -0.59 | |
| (6, 0) | 7 190 | 7 149 | -0.57 | |
| (7, 0) | 9 393 | 9 339 | -0.57 | |
| 制动块 | 1 | 2 903 | 2 898 | -0.17 |
| 2 | 4 662 | 4 583 | -1.69 | |
| 3 | 6 374 | 6 675 | 4.72 | |
为了辨识制动盘与制动块之间的接触刚度,本文建立了两者装配体的简化有限元模型,如图 6所示。考虑到钳体在轴向上具有较高的刚度,会限制制动块的移动,因此对制动块背板受载位置施加了相应的弹性约束。在设置制动盘与制动块界面接触特性时,在切向上采用基于罚函数法的面-面接触关系,仅需确定接触面的摩擦系数;ABAQUS软件允许法向接触刚度采用缺省设置,自动根据硬点接触的罚函数法进行计算。其中罚函数法是利用主从结合面节点位移变形,结合材料弹性模量确定各节点之间的接触刚度,并引入可在0.01~10范围内选择的罚因子,以避免过大的接触刚度导致病态矩阵的出现和计算不收敛,但这会与实际接触刚度存在一定偏差。本文通过在制动盘与制动块之间的“法向特性”栏中输入经过优化的接触刚度数值,进行后续的有限元分析。
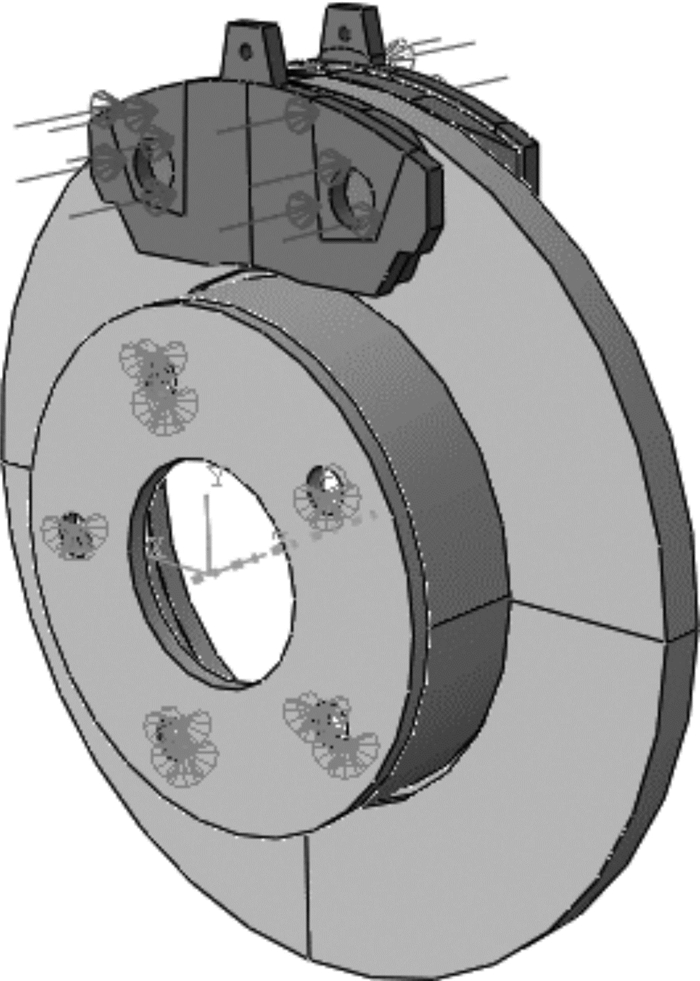
|
| 图 6 制动盘与制动块装配体的有限元模型 Fig.6 Finite element model of the assembly of brake disc and brake pads |
针对安装于台架轮毂法兰上的盘式制动器(图 3),在其制动盘表面布置加速度传感器,在每次施加一定制动压力并保持稳定后,应用锤击法对制动盘进行模态实验,部分压力下制动盘模态频率响应测试结果如图 7所示。结果表明,当制动压力增加到3 MPa时,制动盘的第5阶面外模态频率为5 532 Hz,根据本文方法,结合有限元模态分析,可以辨识出此时制动盘与制动块之间的单位面积接触刚度为4.73×1010 N/m3。
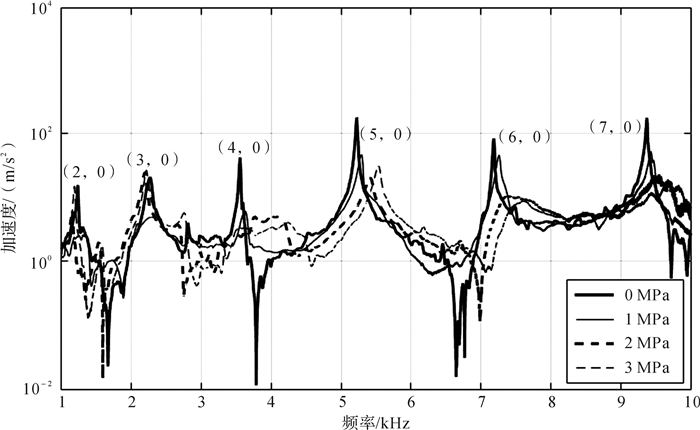
|
| 图 7 不同制动压力下制动盘的面外模态频率响应特性 Fig.7 Out-of-plane modal frequency response characteristics of the brake disc under different brake pressures |
摩擦对偶件之间的接触刚度与材料特性、结构尺寸、表面粗糙度等因素密切相关[5, 18]。本文研究发现制动盘与制动块之间的接触刚度还与制动压力及制动盘振动模态有关。
3.1 制动压力的影响根据在不同制动压力下测得的制动盘第5阶面外模态频率变化情况,可以辨识得到制动盘与制动块之间的单位面积接触刚度和制动压力的关系,如图 8所示。可以看出,当制动压力低于3 MPa时,接触刚度随压力较快地增大;当制动压力大于3 MPa时,随着压力的增加,接触刚度增大速度趋于平缓。这是由于制动块摩擦材料具有一定的孔隙度,当压力较小时,孔隙尺寸较大,其减小程度受压力变化的影响明显;当压力增大后,摩擦材料逐渐被压实,孔隙尺寸减小,接触刚度随压力变化不再明显。
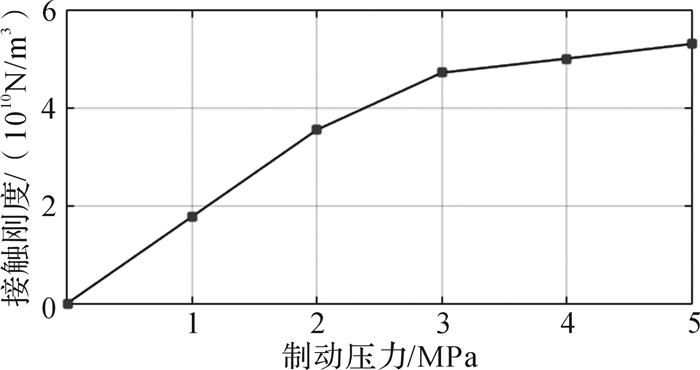
|
| 图 8 制动盘与制动块之间的接触刚度随制动压力的变化曲线 Fig.8 Change curve of contact stiffness between brake disc and brake pad with brake pressure |
考虑到制动压力增大后,制动器系统的阻尼逐渐增强,制动盘的部分模态不容易被激发。对比图 7中不同压力下制动盘面外模态频率响应曲线,发现当制动压力为1 MPa时,能够激发出制动盘的第4,5,6,7阶振动模态,辨识得到制动盘与制动块之间的单位面积接触刚度和制动盘模态阶次的关系,如图 9所示。

|
| 图 9 制动盘与制动块之间的接触刚度和制动盘模态阶次的关系 Fig.9 Relationship between contact stiffness between brake disc and brake pad and mode order of brake disc |
结果表明,当制动盘处于第4,5,6阶振动模态时,制动盘与制动块之间的接触刚度随着模态阶次的升高而增大;相对于第6阶振动模态,制动盘处于第7阶振动模态时的制动盘与制动块之间的接触刚度略有减小。这是由于当制动盘处于低阶模态时,根据振型分析,制动盘面仅有少部分区域同时与制动块充分接触;随着模态阶次的升高,制动盘面与制动块有更多区域充分接触。随着接触面积的增大,接触刚度不断增大。但是,当制动盘处于更高模态时,由于制动盘与制动块的接触位置关系,接触面积不再明显增大或会略有减小,使得接触刚度也基本保持稳定或略有减小。
4 结论本文采用模态试验与有限元分析相结合的方法,根据不同压力条件下浮钳盘式制动器模态频率的变化,辨识得到制动盘与制动块之间的法向接触刚度,发现它与制动压力大小和制动盘振动模态之间存在密切关系:
1) 随着制动压力的增大,由于制动块摩擦材料的孔隙度减小,制动盘与制动块之间的接触刚度增大,会提高制动盘的面外模态频率。
2) 随着制动盘模态阶次的提高,由于制动盘与制动块在谐振状态接触面积的变化,接触刚度会先增大然后基本保持不变,使得制动盘的面外模态频率随之变化。
本文提出的制动盘与制动块之间的动态法向接触刚度辨识方法及其压力和模态依赖特性,可用于建立准确的制动器盘块间的接触关系,以开展制动器振动噪声仿真研究。
基于模态频率特征的制动盘与制动块之间的接触刚度的辨识方法也存在一定局限性。当制动盘受到一定压力时,由于系统阻尼作用,可能导致部分模态不能被有效激发,会影响在该工况下的制动盘与制动块之间的接触刚度的辨识。
| [1] | HOFFMANN N, FISCHER M, ALLGAIER R, et al. A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations[J]. Mechanical Research Communications, 2002, 29(4): 197–205. DOI:10.1016/S0093-6413(02)00254-9 |
| [2] | ABDO J A. Investigation of contact stiffness and its relation to friction-induced noise and vibration[J]. International Journal of Modelling and Simulation, 2006, 26(4): 295–302. DOI:10.1080/02286203.2006.11442380 |
| [3] | KANG J. Effect of contact stiffness on brake squeal analysis using analytical FE squeal model[J]. Transactions of the Korean Society for Noise and Vibration Engineering, 2014, 24(10): 744–755. |
| [4] | HERTZ H. On the contact of elastic solids[J]. Journal für die Reine und Angewandte Mathematik, 1882, 92: 156–171. |
| [5] | GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences, 1966, 295: 300–319. DOI:10.1098/rspa.1966.0242 |
| [6] | GREENWOOD J A, WILLIAMSON J B P. Developments in the theory of surface roughness[C]//Proceedings of 4th Leeds-Lyon Symposium on Tribology: Surface Roughness Effects in Lubrication, London, Mechanical Engineering Publications, 1977: 167-177. |
| [7] | TRICHES Júnior M, GERGES S N Y, JORDAN R. Analysis of brake squeal noise using finite element method:a parametric study[J]. Applied Acoustics, 2008, 69(2): 147–162. DOI:10.1016/j.apacoust.2007.10.003 |
| [8] | TRICHES Júnior M, GERGES S N Y, CORDIOLI J. Analysis of brake squeal noise using FEM part Ⅰ: determination of contact stiffness between rotor and pads[J]. SAE Technical Paper, 2004-01-3330. https://www.sae.org/publications/technical-papers/content/2004-01-3330/ |
| [9] | SHERIF H, BLOUET J, CRETEGNY J, et al. Experimental investigation of self-excited squeal[J]. SAE Technical Paper, 892451, 1989. https://www.sae.org/publications/technical-papers/content/892451/ |
| [10] | GIANNINI O, SESTIERI A. Predictive model of squeal noise occurring on a laboratory brake[J]. Journal of Sound and Vibration, 2006, 296(3): 583–601. DOI:10.1016/j.jsv.2006.02.022 |
| [11] | OURA Y, KURITA Y, NISHIZAWA Y, et al. Comparison of pad stiffness under static pressure and vibration with small amplitude[J]. SAE Technical Paper, 2012-01-1818. https://www.sae.org/publications/technical-papers/content/2012-01-1818/ |
| [12] | GOTO Y, AMAGO T, CHIKU K, et al. Experimental identification method for interface contact stiffness of FE model for brake squeal[C]//Proceedings of the IMechE Conference on Braking 2004: Vehicle Braking and Chassis Control, Leeds, Wiley, 2004: 143-155. |
| [13] | WILL J. CAE-based robustness evaluation of brake systems[J]. SAE Technical Paper, 2015-01-2656. https://www.sae.org/publications/technical-papers/content/2015-01-2656/ |
| [14] | ZHANG Z, OBERST S, LAI J C S. On the potential of uncertainty analysis for prediction of brake squeal propensity[J]. Journal of Sound and Vibration, 2016, 377(1): 123–132. |
| [15] | BALLINGER R. A discussion of complex eigenvalue analytical methods as they relate to the prediction of brake noise[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2016, 9(1): 183–198. DOI:10.4271/2016-01-1299 |
| [16] |
张学玲, 唐毅, 徐燕申.
用实验模态与有限元方法识别结合面接触刚度的方法[J]. 组合机床与自动化加工技术, 2005(11): 56–60.
ZHANG Xue-ling, TANG Yi, XU Yan-shen. A contact stiffness identification method of combined interface by FEM along with modal experiment[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2005(11): 56–60. DOI:10.3969/j.issn.1001-2265.2005.11.021 |
| [17] | ZHENG Y, HOU Z, RONG Y. The study of fixture stiffness-part Ⅱ:contact stiffness identification between fixture components[J]. International Journal of Advanced Manufacturing Technology, 2008, 38(1/2): 19–31. |
| [18] | PHARR G M, OLIVER W C, BROTZEN F R. On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation[J]. Journal of Material Research, 1992, 7(3): 613–617. DOI:10.1557/JMR.1992.0613 |


