流式细胞术(flow cytometry, FCM)是20世纪60年代末开始发展起来的技术,它是集激光技术、微弱荧光检测技术、高速数字信号处理技术、计算机数值分析技术、流体动力学以及荧光化学技术、单克隆抗体技术于一体的新型高科技细胞分析技术[1-2],已被广泛应用于免疫学、细胞学、海洋湖泊微生物学、食品微生物学以及临床医学等方面[2-7],被誉为细胞生物实验室的CT(computed tomography,电子计算机断层扫描)[2]。
流式细胞仪液流聚焦系统通过流动动力学聚焦、惯性力聚焦以及超声聚焦等原理实现样品流聚焦[8-11],使其分析速度高达每秒上万个细胞,以此获取每个细胞的生理特征信息和生化免疫特征信息。但细胞在聚焦样品流中呈Poisson分布,而流动室激发的激光光斑能量强度呈高斯分布,因此样品聚焦流直径和样品聚焦流在流动室中的位置均会影响细胞特征信号的分辨率(coefficient of variation,CV)[1-2, 12]。马玉婷、于虎等[13-14]通过Fluent对流式细胞仪流动室作液流聚焦仿真分析,得出样品流速大小、鞘液流速大小以及进样针在流动室中的相对位置均对样品聚焦流直径和聚焦位置产生较大影响。因此,在流式细胞仪液流聚焦系统设计中,为实现细胞特征信号探测CV值低于2%,需要测量样品流速、鞘液流速、样品聚焦流直径以及样品聚焦流在流动室流道中的相对位置。
目前,市场上流式细胞仪的样品上样方式主要有注射泵上样、空气正压上样以及蠕动泵负压上样等,本文采用的是蠕动泵负压上样方式。根据蠕动泵运动特点[15-16]可知,除了在泵滚轮处出现流速波动外,滚轮与滚轮之间的流速近似为匀速,故可采用平均流量称重法测量样品流速。基于光学显微镜平台,采用显微成像法测量样品聚焦流直径及样品聚焦流在流动室中的位置。
1 样品流速测量方法 1.1 平均流量称重法蠕动泵组件存在加工和装配误差,以及蠕动泵泵管和电子器件存在差异性等问题,导致每个蠕动泵的控制电压与样品流速之间的线性关系均不同。因此,在实际应用中,需要明确每个蠕动泵的控制电压与样品流速之间的关系,以便更精确地控制样品流速。通常,流式细胞仪低速上样时,样品流速低至10 μL/min;高速上样时,样品流速高至100 μL/min。市场上可测量该低流速的传感器很少,如Sensirion公司的微流量传感器,不仅价格昂贵,还需额外配置计算机等设备。蠕动泵负压上样时,在蠕动泵滚轮与滚轮之间的样品流是匀速流动的。根据该特点,可采用平均流量称重法来测量样品流速。
所谓平均流量称重法,即:在给定的控制电压Vi和时间间隔ti下,用吸水纸吸收输出的样品(实际测试中采用纯净水),再用精度优于1 mg的精密天平测量吸水纸所吸收的样品质量mi,最后将该质量mi换算为样品流速。样品流速Qi的计算公式可表达为:
| $ {{Q}_{i}}=\left( {{m}_{2i}}-{{m}_{1i}} \right)/\rho {{t}_{i}} $ | (1) |
式中:Qi为在控制电压Vi下的样品流速,μL/min;m2i为吸水纸在蠕动泵抽样ti后的质量,g;m1i为吸水纸在蠕动泵初始抽样时的质量,g;ρ为样品密度,g/μL;ti为蠕动泵抽样时间,min。
1.2 样品流速补偿为提高流式细胞仪样品低速运行时的流速测量精度,需延长抽样时间,因长时间抽样测量,需要考虑样品在空气中的蒸发速度Q0,其测量方法是:在吸水纸上滴少许样品,用精密天平测量时间间隔t0前后吸水纸的质量,再等效为蒸发速度,其计算公式可表达为:
| $ {{Q}_{0}}=\left( {{m}_{10}}-{{m}_{20}} \right)/\rho {{t}_{0}} $ | (2) |
式中:Q0为样品在空气中的蒸发速度,μL/min;m10为吸水纸初始质量,g;m20为吸水纸在时间间隔t0后的质量,g;t0为测量时间间隔,min。
样品流速补偿公式为:
| $ {{{{Q}'}}_{i}}={{Q}_{0}}+{{Q}_{i}} $ | (3) |
式中:Q′i为流速补偿后的样品流速,μL/min。
1.3 样品流速控制函数根据蠕动泵的结构特点,其控制电压与样品流速呈线性关系,可表示为:
| $ Q\left( V \right)=a+b\cdot V $ | (4) |
现采用最小二乘法来拟合该线性函数,使得其偏差平方和最小,即:
写成矩阵形式为:
| $ \left[ \begin{matrix} m&\sum\limits_{i=1}^{m}{{{V}_{i}}} \\ \sum\limits_{i=1}^{m}{{{V}_{i}}}&\sum\limits_{i=1}^{m}{V_{i}^{2}} \\ \end{matrix} \right]\left[ \begin{matrix} a \\ b \\ \end{matrix} \right]=\left[ \begin{align} &\sum\limits_{i=1}^{m}{{{{{Q}'}}_{i}}} \\ &\sum\limits_{i=1}^{m}{{{V}_{i}}\cdot {{{{Q}'}}_{i}}} \\ \end{align} \right] $ | (5) |
通过该矩阵方程,可计算出蠕动泵控制电压与输出流速的线性表达式。利用该表达式,可控制样品流速。
2 样品流速测量实验 2.1 样品蒸发速度测量在室温为22 ℃,湿度为40%的条件下,采用去离子纯净水进行蒸发速度测量,根据公式(2)可计算去离子纯净水在空气中的蒸发速度为1.0 μL/min,如表 1所示。
| 实验组 | m10/g | t0/min | m20/g | Q0/(μL/min) |
| 1 | 2.152 | 30 | 2.123 | 1.0 |
| 2 | 1.221 | 30 | 1.190 | 1.0 |
采用2款蠕动泵(A泵和B泵)进行样品流速测量,控制电压从0.1 V到1 V递增,考虑样品在空气中蒸发的速度,根据公式(1)和公式(3)可计算样品流速,同时与Sensirion公司微流量传感器测量的对应控制电压下的流速Qa作比对,如表 2所示。
| 泵组 | 实验组 | Vi/V | m1i/g | m2i/g | ti/min | Q′i/ (μL/min) |
Qa/ (μL/min) |
| A泵 | 1 | 0.1 | 1.004 | 1.320 | 30 | 11.5 | 9.2 |
| 2 | 0.3 | 1.323 | 2.323 | 30 | 34.3 | 37.2 | |
| 3 | 0.5 | 1.947 | 3.106 | 20 | 59.0 | 56.1 | |
| 4 | 0.7 | 1.323 | 2.159 | 10 | 84.6 | - | |
| 5 | 1.0 | 1.918 | 3.115 | 10 | 120.7 | - | |
| B泵 | 6 | 0.1 | 0.594 | 0.811 | 30 | 8.2 | 7.1 |
| 7 | 0.3 | 0.936 | 1.790 | 30 | 29.5 | 32.4 | |
| 8 | 0.5 | 1.965 | 2.943 | 20 | 49.9 | 52.6 | |
| 9 | 0.7 | 2.040 | 2.722 | 10 | 69.2 | - | |
| 10 | 1.0 | 2.052 | 3.096 | 10 | 105.4 | - |
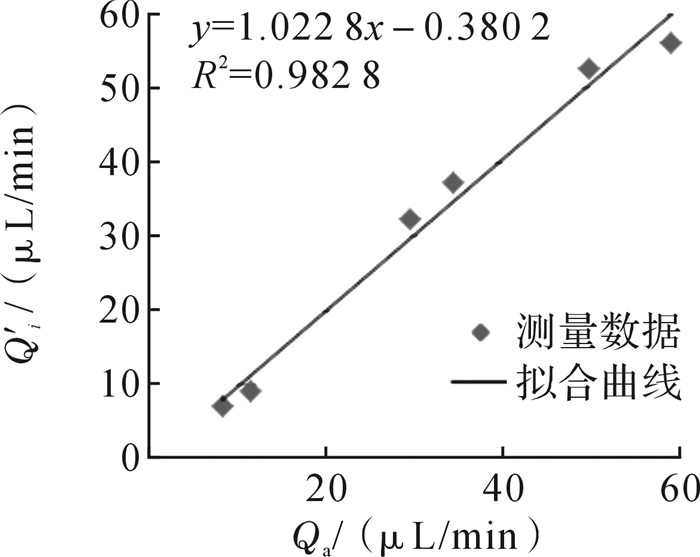
根据实验结果,对用微流量传感器和平均流量称重法测得的样品流速作线性相关拟合,如图 1所示。2种方法测得结果的线性相关系数为0.982 8,说明平均流量称重法可替代微流量传感器来测量样品流速。
|
| 图 1 微流量传感器和平均流量称重法测量的样品流速的线性相关曲线 Fig.1 The linear correlation curve of the sample flow rate measured by micro-flow sensor and average flow weighing method |
根据公式(5)可计算出A泵和B泵的样品流速与控制电压的关系函数分别为:
| $ {{{{Q}'}}_{\text{A}}}=122.27\cdot {{V}_{\text{A}}}-1.483, R_{\text{A}}^{2}=0.999\ 7 $ | (6) |
| $ {{{{Q}'}}_{\text{B}}}=106.59\cdot {{V}_{\text{B}}}-2.987, R_{\text{B}}^{2}=0.998\ 5 $ | (7) |
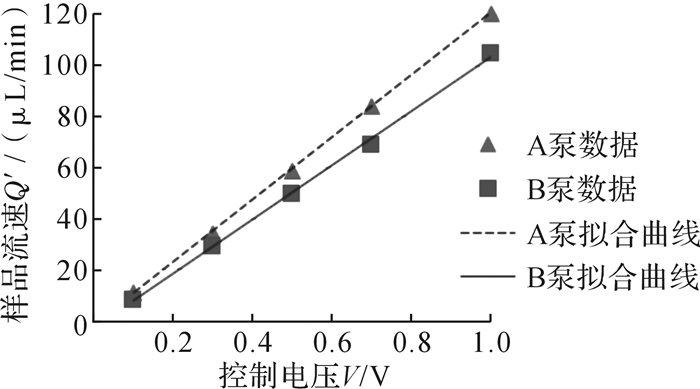
A泵和B泵的样品流速与控制电压的拟合曲线如图 2所示。根据计算结果,A泵和B泵的样品流速与控制电压的线性相关系数分别为0.999 7和0.998 5,说明拟合曲线与实验数据吻合程度非常高,可利用该线性函数来控制样品流速。通过样品流速与控制电压的拟合曲线,还可以对流式细胞仪做绝对计数,只需对上样计时和在对应的控制电压下对流式细胞仪细胞计数即可。
|
| 图 2 样品流速与蠕动泵控制电压的关系曲线 Fig.2 The correlation curve of sample flow rate and peristaltic pump's control voltage |
流动室中样品流在鞘液作用下聚焦形成样品聚焦流。为了观测样品聚焦流的位置和直径,现采用显微成像法。其中光学显微镜采用Mitutoyo MF-A2010D,其精密平移台精度为1 μm,并采用50倍显微物镜。为了便于显微镜观测,样品采用18%浓度的水溶性亮蓝,鞘液采用去离子纯净水。搭建的测量平台如图 3所示。根据观测到的样品聚焦流偏离流动室流道中心线的位置,可为液流器件组装精度的测量提供指导依据。

|
| 图 3 样品聚焦流直径与位置测量平台 Fig.3 The platform for measuring the diameter and position of sample focusing core flow |
流动室流道的长、宽均为230 μm,利用显微镜上的十字刻度尺,并通过调节X-Y平移台和旋转台,将流动室的流道中心线调到与该十字刻度尺的中心线重合位置,如图 4所示。在目镜中观测样品聚焦流左侧与右侧的位置,记为x1,x2。则该聚焦流的直径d及偏离流动室流道中心线的距离Δ为:
| $ d={{x}_{2}}-{{x}_{1}} $ | (8) |
| $ \mathit{\Delta }=\left| \frac{{{x}_{1}}+{{x}_{2}}}{2} \right| $ | (9) |

|
| 图 4 利用显微成像法观测到的样品聚焦流在十字刻度尺中的位置 Fig.4 The position of sample focusing core flow in the cross scale observed by microscopic imaging method |
为了分析鞘液流速Qsh和样品流速Q′对样品聚焦流直径d的影响,在不同鞘液流速和样品流速下,利用显微成像法对样品聚焦流的直径和位置进行测量。在鞘液流速为8.4×103 μL/min,不同样品流速下测得的数据以及根据公式(8)和(9)计算的样品聚焦流直径d和偏心距离Δ如表 3所示。
| 实验组 | Q′/(μL/min) | x1/mm | x2/mm | d/μm | Δ/μm |
| 1 | 66.6 | -0.014 3 | 0.017 1 | 31.4 | 1.40 |
| 2 | 47.4 | -0.010 8 | 0.014 5 | 25.3 | 1.85 |
| 3 | 36.7 | -0.007 9 | 0.013 5 | 21.4 | 2.80 |
| 4 | 23.0 | -0.005 5 | 0.011 5 | 17.0 | 3.00 |
| 5 | 14.0 | -0.002 3 | 0.009 9 | 12.2 | 3.80 |
| 6 | 10.7 | -0.001 7 | 0.009 4 | 11.1 | 3.85 |
| 7 | 6.2 | 0.000 3 | 0.008 8 | 8.5 | 4.55 |
| 8 | 3.4 | 0.001 5 | 0.007 3 | 5.8 | 4.40 |
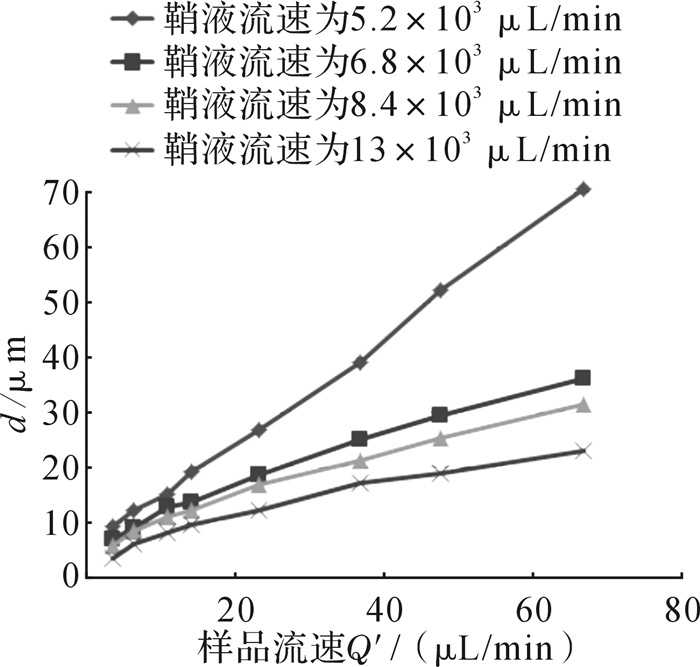
在不同鞘液流速下,样品聚焦流直径随样品流速的变化规律如图 5所示。从该图中可以看出在鞘液流速恒定时,样品聚焦流直径随样品流速的增大而增大;在样品流速恒定时,样品聚焦流直径随鞘液流速的增大而减小。实验测试结论与文献[7]的仿真结论一致。
|
| 图 5 不同鞘液流速下样品聚焦流直径与样品流速之间的关系 Fig.5 The relationship between the diameter of the sample focusing core flow and the sample flow rate under different sheath fluid flow rate |
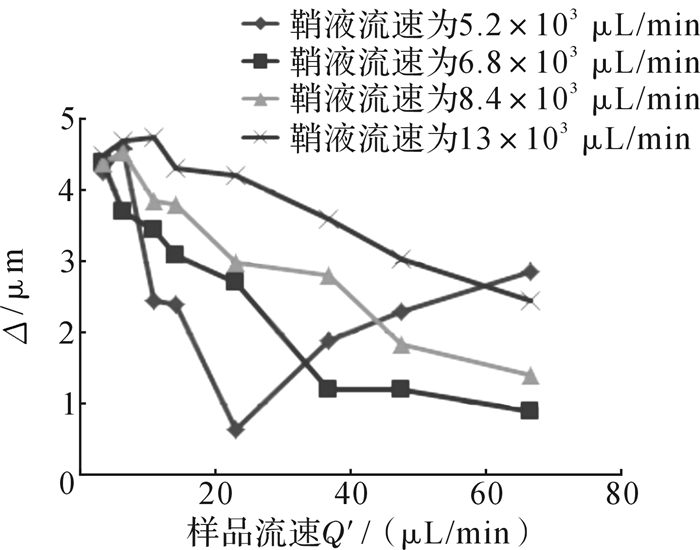
在不同鞘液流速下,样品聚焦流偏离流动室流道中心线的距离Δ随样品流速的变化规律如图 6所示。从该图中可以发现,当液流器件组装存在偏心时,在鞘液流速大于6.8×103 μL/min下,偏心距离随样品流速的增大而减小;在鞘液流速较小时,如为5.2×103 μL/min下,偏心距离先随着样品流速增大而减小,后随着样品流速增大而增大; 在样品流速为23 μL/min时,偏心距离最小;在样品流速恒定时,偏心距离随鞘液流速增大而增大。
|
| 图 6 不同鞘液流速下样品聚焦流偏离流动室流道中心线的距离与样品流速之间的关系 Fig.6 The relationship between the distance of sample focusing core flow deviating from the flow channel centerline and the sample flow rate under different sheath fluid flow rate |
1) 流式细胞仪采用蠕动泵负压抽取样品时,根据蠕动泵运行特点,可利用本文提出的平均流量称重法替代微流量传感器来测量每分钟微升量级的样品流速。
2) 蠕动泵的控制电压与样品流速呈线性关系,利用最小二乘法拟合该线性关系,本文分析的2款蠕动泵的样品流速与控制电压的线性相关系数分别为0.999 7和0.998 5,吻合度非常好,表明可利用该线性关系对A泵和B泵的样品流速作精确控制。
3) 采用显微成像法分析了鞘液流速和样品流速对样品聚焦流的直径及偏离流动室流道中心线的距离的影响,为流式细胞仪的样品流速和鞘液流速的调控提供了指导方法;同时,通过观测样品聚焦流偏离流动室流道中心的距离,可为提高液流器件组装精度提供指导依据。
| [1] |
梁智辉, 朱慧芬, 陈九武.
流式细胞术基础原理与实用技术[M]. 武汉: 华中科技大学出版社, 2008: 1-5.
LIANG Zhi-hui, ZHU Hui-fen, CHEN Jiu-wu. Fundamental principles and practical techniques of flow cytometry[M]. Wuhan: Huazhong University of Science Technology Press, 2008: 1-5. |
| [2] | HOWARD M Shapiro. Practical flow cytometry[M]. New Jersey: Wiley-Liss, 2003: 1-2. |
| [3] | BENDALL S C, SIMONDS E F, QIU P, et al. Single-cell mass cytometry of differential immune and drug responses across a human hematopoietic continuum[J]. Science, 2011, 332(6030): 687–696. DOI:10.1126/science.1198704 |
| [4] | BJORNSON Z B, NOLAN G P, FANTL W J. Single-cell mass cytometry for analysis of immune system functional states[J]. Current Opinion in Immunology, 2013, 25(4): 484–494. DOI:10.1016/j.coi.2013.07.004 |
| [5] | RUBEN Props, KERCKHOF Frederiek-Maarten, PETER Rubbens, et al. Absolute quantification of microbial taxon abundances[J]. The ISME Journal, 2017, 11(2): 584–587. DOI:10.1038/ismej.2016.117 |
| [6] | WENG X, NEETHIRAJAN S. Ensuring food safety:quality monitoring using microfluidics[J]. Trends in Food Science & Technology, 2017, 65: 10–22. |
| [7] | NEVEL S V, KOETZSCH S, PROCTOR C R, et al. Flow cytometric bacterial cell counts challenge conventional heterotrophic plate counts for routine microbiological drinking water monitoring[J]. Water Research, 2017, 113: 191–206. DOI:10.1016/j.watres.2017.01.065 |
| [8] | MENAKE E Piyasena, STEVEN W Graves. The intersection of flow cytometry with microfluidics and microfabrication[J]. Lab Chip, 2014, 14(6): 1044–1059. DOI:10.1039/C3LC51152A |
| [9] | NORASYIKIN Selamat, EHSAN A A. Particles trajectories simulation of hydrodynamic focusing in circular and rectangular polymer microflow cytometer[J]. International Journal of Applied Engineering Research, 2017, 12(7): 1311–1315. |
| [10] | SHIVHARE P K, BHADRA A, SAJEESH P, et al. Hydrodynamic focusing and interdistance control of particle-laden flow for microflow cytometry[J]. Microfluidics & Nanofluidics, 2016, 20(6): 1–14. |
| [11] | OLSON R J, SHALAPYONOK A, KALB D J, et al. Imaging FlowCytobot modified for high throughput by in-line acoustic focusing of sample particles[J]. Limnology & Oceanography Methods, 2017, 15(10): 867–874. |
| [12] | AHMAD Ahsan Nawaz, ZHANG Xiang-jun, MAO Xiao-le, et al. Sub-micrometer-precision, three-dimensional(3D) hydrodynamic focusing via "microfluidic drifting"[J]. Lab on a Chip, 2014, 14(2): 415–423. DOI:10.1039/C3LC50810B |
| [13] |
马玉婷, 严心涛, 陈忠祥, 等.
流式细胞仪液流聚焦系统仿真分析与设计[J]. 分析仪器, 2014(1): 17–22.
MA Yu-ting, YAN Xin-tao, CHEN Zhong-xiang, et al. Simulated analysis and design of flow cytometer focusing system[J]. Analytical Instrumentation, 2014(1): 17–22. DOI:10.3969/j.issn.1001-232x.2014.01.004 |
| [14] |
于虎, 祝连庆, 郭阳宽, 等.
流式细胞仪流动室流场特性仿真[J]. 计算机仿真, 2015, 32(8): 230–234.
YU Hu, ZHU Lian-qing, GUO Yang-kuan, et al. Simulation of fluid field characteristic of flow cytometry flow chamber[J]. Computer Simulation, 2015, 32(8): 230–234. DOI:10.3969/j.issn.1006-9348.2015.08.050 |
| [15] | OLA Jakobsson, CARL Grenvall, MARIA Nordin, et al. Acoustic actuated fluorescence activated sorting of microparticles[J]. Lab on a Chip, 2014, 14(11): 1943–1950. DOI:10.1039/C3LC51408K |
| [16] | MATHIAS Busek, MARTIN Nötzel, CHRISTOPH Polk, et al. Peristaltic pneumatic pump-characterisation via μPIV, non-invasive pressure measurement and simulation[J]. Journal of Sensors and Sensor Systems, 2013, 2(2): 165–169. |


