2. 天津大学 机械工程学院, 天津 300072
2. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China
为应对日益严苛的燃油经济性法规,各大汽车主机厂纷纷推出搭载三缸增压汽油发动机的车型。三缸增压发动机固有的不平衡性及增压强化后不断增大的热负荷使整机可靠性面临严峻考验[1]。排气歧管作为连接增压器与缸盖的重要部件,直接承受来自增压器和缸盖的振动载荷及高温热负荷作用,工作环境极其恶劣,开裂失效故障日益增多,其安全性与可靠性受到越来越多人的关注。
鉴于排气歧管金属温度能够在极短时间内达到700 ℃以上,散热主要通过与缸盖的热传导和与周围环境的对流、辐射换热等方式,加上频繁的启停工况引起温度大范围地变化,容易导致排气歧管局部区域形成较大温度梯度,产生较大热应力[2-4],多数学者的研究主要集中于热疲劳失效,认为由热负荷引起的大的热应力是导致排气歧管产生疲劳破坏的主要因素[5-6]。针对排气歧管高温低周疲劳的相关研究表明:Kandil-Brown-Miller疲劳模型计算结果与实验数据偏差最小,较适合用于预测排气歧管高温低周疲劳寿命[7]。另外,当考虑材料热物性、非线性损伤演化规律以及加载次序等因素的影响时,基于Lemaitre低周疲劳扩展模型的排气歧管高温低周疲劳寿命分析结果显示风险区域主要位于排气总管出口及各排气支管与法兰面接合处[8]。从结构改进的角度来看,对于排气总管风险区域,采取周向加筋措施能够大幅降低排气总管热应力[9];而对于各排气支管,通过改变排气歧管弯曲半径、法兰结构和开应力释放槽等能有效缓解排气管热应力,改善失效状况[10]。
标定工况(即最大输出功率点,本文为发动机在5 500 r/min下的全负荷状态)下整机平均振动加速度能够达到20g,运转过程中的瞬时振动加速度甚至超过100g,而材料受高温蠕变等影响,其抗拉强度及疲劳极限都会下降,排气歧管与法兰面之间焊接处的失效主要由振动引起[11]。对于增压发动机,增压器工作时引起的振动载荷谱是造成排气歧管振动疲劳失效的主要原因之一[12]。除增压器外,其他与排气歧管相连的附件所引起的振动载荷对排气歧管疲劳寿命也有较大影响,尤其是加速度载荷作用下产生的动应力不能忽略[13]。
单独从热负荷或振动载荷的角度进行疲劳寿命分析可以深入揭示单一因素的作用机理,但高强化增压发动机排气歧管的疲劳损伤实际是热负荷与振动载荷耦合作用的结果。在满足工程应用要求的前提下,为综合考虑热应力和振动载荷动应力的影响以及高温状态下可能出现的塑性变形,本文引入Neuber准则,以某三缸增压发动机为研究对象,就振动载荷耦合热负荷对排气歧管低周疲劳寿命的影响展开研究。
1 基本理论及方法 1.1 Neuber准则1961年,Neuber提出应力集中部位的应力集中系数Kσ与应变集中系数Kε之积等于理论应力集中系数Kt的平方[14]:
| $ {K_\sigma } = \frac{\sigma }{S} $ | (1) |
| $ {K_\varepsilon } = \frac{\varepsilon }{e} $ | (2) |
| $ {K_{\rm{t}}} = \sqrt {{K_\sigma }{K_\varepsilon }} $ | (3) |
式中:S, e为名义应力与名义应变,σ, ε为应力集中处实际应力与实际应变。
联立式(1)至式(3)得Neuber双曲线:
| $ \sigma \varepsilon = {\left( {{K_{\rm{t}}}S} \right)^2}/E $ | (4) |
式中E为弹性模量。
已知材料的循环应力—应变曲线方程为:
| $ \varepsilon = \frac{\sigma }{E} + {\left( {\frac{\sigma }{{K'}}} \right)^{1/n'}} $ | (5) |
式中:K′为循环强度系数,n′为循环应变硬化指数。
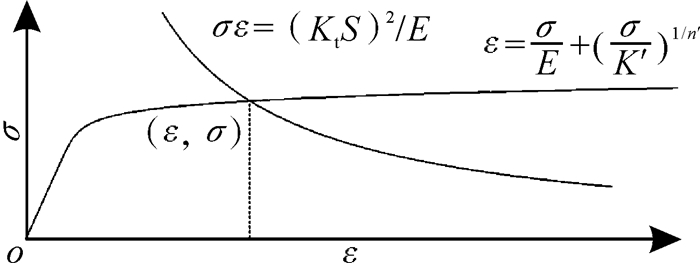
当名义应力一定且理论应力集中系数已知时,Neuber双曲线与材料的循环应力—应变曲线交点(如图 1)即为实际应力σ与实际应变ε。交点方程如下:
| $ \frac{{{{\left( {{K_{\rm{t}}}S} \right)}^2}}}{E} = \frac{{{\sigma ^2}}}{E} + \sigma {\left( {\frac{\sigma }{{K'}}} \right)^{1/n'}} $ | (6) |
|
| 图 1 Neuber双曲线与材料的循环应力—应变曲线的交点 Fig.1 Intersection of the Neuber hyperbola and the cyclic stress—strain curve of material |
对于理想弹性材料,KtS为应力集中处的应力值[15],假设应力集中处应力、应变分别为σe, εe,则公式(6)变为如下形式:
| $ \frac{{{{\left( {{\sigma _{\rm{e}}}} \right)}^2}}}{E} = \frac{{{\sigma ^2}}}{E} + \sigma {\left( {\frac{\sigma }{{K'}}} \right)^{1/n'}} $ | (7) |
根据式(7)即可根据理想弹性变形下名义应力值得到实际应力σ和实际应变ε。
在循环加载情况下,将式(4)和式(5)中应力、应变的具体数值改为应力、应变变化范围,并用缺口疲劳系数Kf代替理论应力集中系数Kt,得:
| $ \Delta \sigma \Delta \varepsilon = {\left( {{K_{\rm{f}}}\Delta S} \right)^2}/E $ | (8) |
| $ \frac{{\Delta \varepsilon }}{2} = \frac{{\Delta \sigma }}{{2E}} + {\left( {\frac{{\Delta \sigma }}{{2K'}}} \right)^{1/n'}} $ | (9) |
联立式(8)与式(9)可得局部应力和局部应变范围交点方程:
| $ \frac{{{{\left( {{K_{\rm{f}}}\Delta S} \right)}^2}}}{{2E}} = \frac{{\Delta {\sigma ^2}}}{{2E}} + \Delta \sigma {\left( {\frac{{\Delta \sigma }}{{2K'}}} \right)^{1/n'}} $ | (10) |
在理想弹性状态下,当名义应力由S1(A点)变为S2(B点)时,式(10)中KfΔS=S2-S1,根据式(9)和式(10)即可得到A,B间应力幅Δσ和应变幅Δε。
假设A点实际应力、应变为σA,εA,则B点实际应力σB、应变εB为:
| $ \left\{ \begin{array}{l} {\sigma _B} = {\sigma _A} + \Delta \sigma \\ {\varepsilon _B} = {\varepsilon _A} + \Delta \varepsilon \end{array} \right. $ | (11) |
依次反复求解,即可得出循环加载情况下应力集中处的实际应力—应变响应。
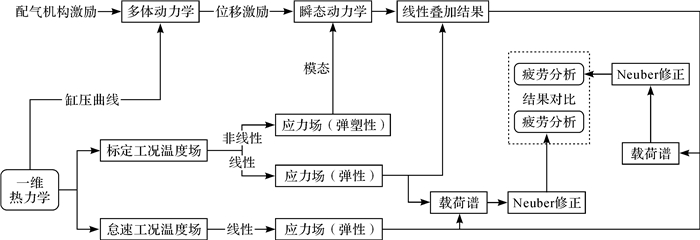
1.2 排气歧管疲劳寿命分析方法简述排气歧管疲劳寿命分析涉及一维热力学、热固耦合、多体动力学、瞬态动力学及疲劳损伤计算,需综合考虑各线性与非线性因素,整个分析过程如图 2所示。由于分析流程中间环节较多,为得到高可信度的结果,需保证分析过程边界条件的准确性。
|
| 图 2 排气歧管疲劳寿命分析流程图 Fig.2 Flow chart of exhaust manifold fatigue life analysis |
研究所用发动机的进气形式为涡轮增压,其他基本参数如表 1所示。基于发动机几何参数及试验数据,利用boost软件搭建发动机整机的一维热力学模型。发动机台架试验装置如图 3所示,利用空气流量计和热电偶分别测得标定工况下进气管总流量和距3个排气管进口30 mm处的气体温度,并利用boost软件输出对应位置进气管流量和排气管气体温度稳态值,结果如表 2所示。通过比较可以看出试验值与仿真值误差在5%以内,表明利用boost软件仿真得到的标定工况下温度场分析边界精度满足要求。
| 参数 | 数值 |
| 缸径/mm | 75 |
| 活塞行程/mm | 75 |
| 气缸数(直列)/个 | 3 |
| 压缩比 | 9.8 |
| 排量/L | 0.998 |
| 额定功率/kW | 75(5 500 r/min) |
| 最大扭矩/N·m | 150(1 700~4 500 r/min) |

|
| 图 3 发动机台架试验装置 Fig.3 Engine bench test device |
| 对比项 | 试验值 | 仿真值 | 误差 |
| 进气管质量流量/kg·h-1 | 313.40 | 298.51 | -4.75% |
| 排气管1气体温度/℃ | 808.70 | 801.00 | -0.95% |
| 排气管2气体温度/℃ | 808.84 | 821.00 | 1.50% |
| 排气管3气体温度/℃ | 849.46 | 889.70 | 4.74% |
为更准确地模拟发动机实际工作状态,采用流固耦合方法对排气歧管内外流场同时进行计算。内流场主要计算高温废气与内壁面对流换热,外流场用于模拟外壁面与环境的换热过程。
在进行排气歧管流固耦合分析时,对于内流场的边界设置,在3个排气支管进口分别施加由boost软件仿真得到的瞬态质量流量及温度,出口施加瞬态压力及温度;而对于外流场,边界条件参数主要采用经验数据,其中外流场入口气体质量流量设为150 kg·h-1,入口温度设为26.85 ℃,出口静压为100 kPa,出口温度为36.85 ℃,其余外壁面的边界温度设为26.85 ℃。在进行材料属性设置时,排气歧管材料设为高Ni奥氏体球墨铸铁,流体域内的气体属性为理想气体。在设置求解器时,因为排气歧管内气体运动存在强烈的湍流特征,所以采用标准的k-ε模型进行气流运动的模拟。同时,仿真过程主要是对排气歧管的瞬态特征进行模拟,所以采用隐式非定常求解器进行求解计算。虽然排气歧管内气流运动与热交换具有瞬态性,但是在稳定工况下,可以认为排气系统的热量交换具有稳态特征,即排气歧管内外表面具有稳定的温度与换热系数。因此可以将一个工作循环内排气歧管的瞬态近壁面温度和换热系数进行时平均处理,将它作为整个内外壁面近壁面的稳定温度与换热系数边界。另外,考虑到瞬态计算达到收敛需要经过1~2个循环的过渡阶段,因此仿真时长设为发动机3个工作过程循环,并将第3个循环的计算结果进行时平均处理后作为内外壁面温度与换热系数边界。
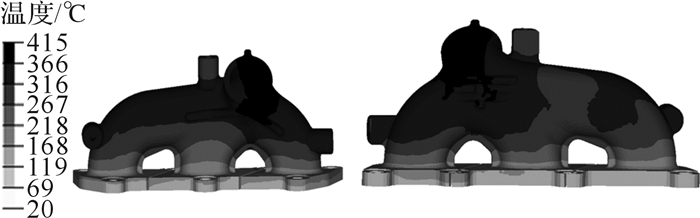
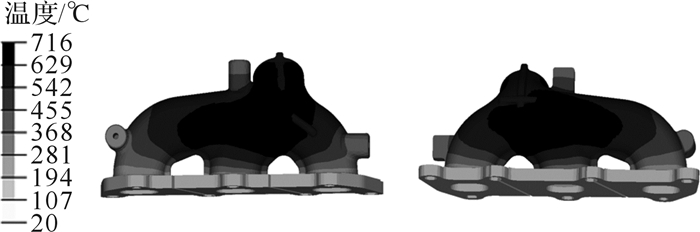
在Abaqus软件中对整个排气系统的温度场进行计算。除内外流场近壁面温度和换热系数外,催化器、油管、水管等附件的载荷边界主要基于boost,flowmaster及经验值来施加固定温度和换热系数/辐射率。图 4和图 5分别为计算得到的怠速(本文为发动机在750 r/min下的零负荷状态)和标定工况下排气系统的温度场。
|
| 图 4 怠速工况下排气系统温度场 Fig.4 Temperature field of exhaust system under idle condition |
|
| 图 5 标定工况下排气系统温度场 Fig.5 Temperature field of exhaust system under rated condition |
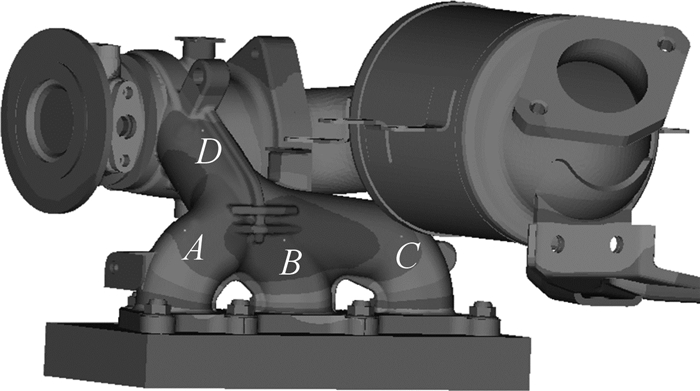
由于在计算温度场时在边界条件设置上作了一定的简化处理,为验证温度场计算结果的准确性,在各排气支管及涡壳上选择4个测点,温度测点分布如图 6所示,利用红外线测温仪进行温度测量。基于以往的测试经验,采用红外线测温仪测得的温度会比利用热电偶测得的低25 ℃左右,这需要对红外线测温仪的测试结果进行修正处理。标定工况下修正后的测试值与计算值如表 3所示,通过对比可以看出,测试结果与计算结果较吻合,说明温度场计算结果能够较准确地反映排气系统实际温度场的分布情况。
|
| 图 6 排气支管和涡壳表面温度测试点 Fig.6 Temperature test point on the exhaust branch pipe and scroll surface |
| 测试点 | 实测值/℃ | 仿真值/℃ | 误差/% |
| A | 564 | 584.4 | 3.62 |
| B | 660 | 692.1 | 4.86 |
| C | 587 | 580.6 | -1.09 |
| D | 589 | 605.6 | 2.82 |
依据经验,怠速工况下振动加速度值不及标定工况下的1/10,因此,可以忽略怠速工况下振动载荷的影响。为获取标定工况下排气系统振动载荷边界条件,需对由发动机和变速箱所组成的整体系统进行多体动力学分析。将图 7所示的发动机网格模型分为平衡轴、曲轴、连杆、进气系统、排气系统及悬置等模块,保留前60阶模态分别进行模态缩减,利用缩减文件在Excite-PU中建立柔性多体动力学模型,模型中各连接单元刚度阻尼值由AVL推荐公式计算得到。在进行载荷设置时,除标定工况下的燃气压力外,还需要施加气门弹簧力、气门落座力以及凸轮轴承力等配气机构运动激励。考虑到多体动力学计算的收敛问题,以及瞬态动力学计算初始使用的零位移条件,需要经过几个工作循环的过渡计算,因此,多体动力学分析时选择进行10个工作循环计算,并将得到的排气系统与机体缸盖的9个螺栓连接点的第4至第10个循环的X,Y,Z方向(规定沿气缸轴线方向为Z方向,发动机前端到飞轮端的方向为X方向)瞬时位移结果作为瞬态动力学分析激励载荷。

|
| 图 7 发动机网格模型 Fig.7 Engine grid model |
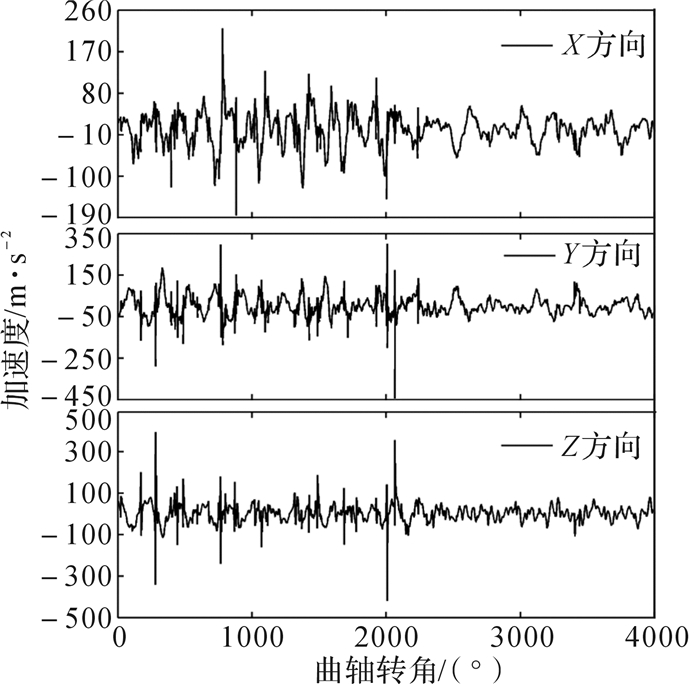
提取排气管1与缸盖螺栓连接处某点在X,Y,Z方向上的振动加速度结果,如图 8所示。分别对3个方向瞬态加速度的绝对值求平均值,得到3个方向加速度平均值分别为2.548g, 3.260g, 2.953g。从图 8可以看出:3个方向上的振动加速度瞬态值随曲轴转角呈周期性变化,每个周期内均会出现一个峰值,这符合此点所处位置以及三缸发动机发火规律,且所得加速度结果在正常范围内,表明瞬时位移结果可以用于后续动应力计算。
|
| 图 8 排气支管1与缸盖螺栓连接处某点的振动加速度 Fig.8 Vibration acceleration of a certain point at the connection of exhaust branch pipe 1 and cylinder head bolt |
模态法相对于直接积分法而言具有巨大的优势,求解容易收敛,比较适合于工程应用,因此本文排气系统动应力的计算采用模态法。鉴于上文已用Neuber准则修正弹性结果,所以疲劳分析中在计算怠速及标定工况下排气系统应力时不考虑塑性变形。鉴于固体各阶固有频率受温度和预应力影响较大,相比冷态条件,热态条件下排气歧管的固有频率呈现下降趋势,并且扭转刚度受温度升高的影响比弯曲刚度大[16-19],为得到准确的模态和动应力结果,约束模态分析模型,采用考虑弹塑性变形的标定工况应力场。
在进行常规热应力计算时,除温度外,还需要考虑螺栓预紧力的影响,预紧力依据高强度螺栓计算标准进行计算[20],并选择计算结果最大值作为预紧力加载值。对于排气系统隔热罩与涡轮增压器和排气歧管之间的螺栓连接,预紧力统一施加为10 kN,催化器与支架、排气管法兰面与简化缸盖之间螺栓连接预紧力为34.85 kN,图 9和图 10分别为怠速及标定工况下排气系统应力场。

|
| 图 9 怠速工况下排气系统应力场 Fig.9 Stress field of exhaust system under idle condition |

|
| 图 10 标定工况下排气系统应力场 Fig.10 Stress field of exhaust system under rated condition |
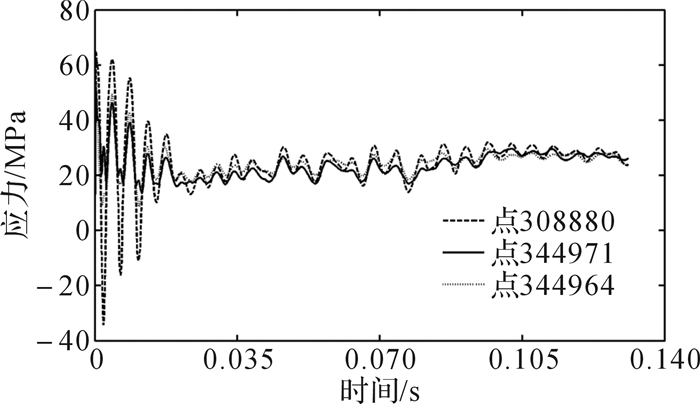
在进行动应力计算时,提取标定工况下排气系统应力场前45阶模态,在排气系统与机体缸盖的9个螺栓连接处分别施加位移激励并进行模态瞬态动力学计算,初始条件选择零位移条件。提取排气歧管上网格节点编号为344964,308880和344971的3个点的动应力结果,绘制应力—时间历程曲线,如图 11所示,从图中可以看出经过0.030 s后系统达到正常状态,低周疲劳分析时主要使用0.030 s以后的动应力结果。
|
| 图 11 排气歧管上某三点应力—时间历程曲线 Fig.11 Stress—time history curve of three points on the exhaust manifold |
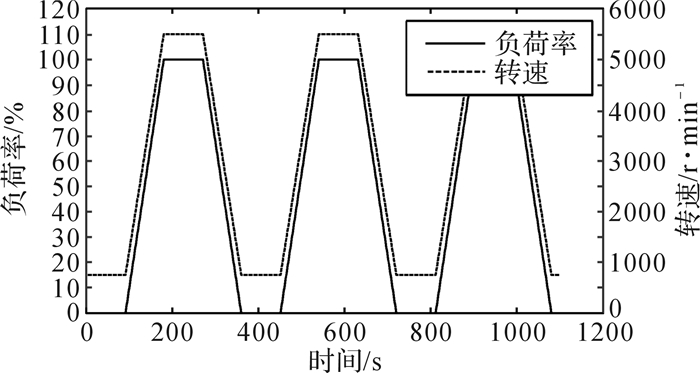
疲劳寿命评估主要参照发动机低周疲劳试验标准进行,如图 12所示。整个发动机疲劳试验过程可以分解为以下4个阶段的交替循环:怠速工况、怠速工况上升至标定工况、标定工况、标定工况下降至怠速工况,每个阶段的持续时间为90 s。依据本发动机排气歧管800 h低周疲劳寿命设计标准,为满足设计要求,发动机排气歧管怠速-标定工况交替循环次数需大于8 000次。
|
| 图 12 发动机低周疲劳试验过程 Fig.12 Engine low cycle fatigue test process |
按照常规的疲劳计算方法,在怠速和标定工况下分别加载两工况弹性应力场,对于两者之间的过渡阶段,按照两工况起点与终点数值作线性化处理;当考虑振动载荷时,对于标定工况,选取相应时长的动应力结果与标定工况下的弹性应力场结果进行线性叠加,过渡阶段处理方式参照常规低周疲劳分析。使用fe-safe进行疲劳分析时,对2种情况下得到的载荷谱运用Neuber准则分别作塑性修正。由于排气歧管部分区域已经发生塑性变形,疲劳算法选择主应变法,并使用Morrow方法进行平均应力修正。
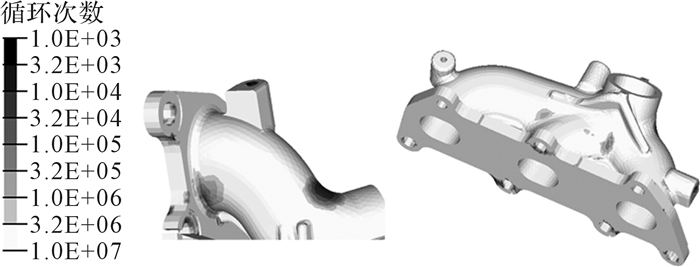
3.2 疲劳寿命结果对比图 13和图 14分别为不考虑和考虑振动载荷影响时排气歧管的低周疲劳寿命。
|
| 图 13 不考虑振动载荷时排气歧管的低周疲劳寿命 Fig.13 Low cycle fatigue life of exhaust manifold without considering vibration load |

|
| 图 14 考虑振动载荷时排气歧管的低周疲劳寿命 Fig.14 Low cycle fatigue life of exhaust manifold with considering vibration load |
从图 13可以看出疲劳寿命较低区域位于排气管3与排气出口交汇处,最低循环次数出现在点344971处,为10 850次,满足该发动机800 h低周疲劳寿命设计要求。通过与应力场、温度场的对比分析,可以发现疲劳寿命较低点主要位于温度较高、承受拉应力的区域。虽然标定工况下各排气管间交汇处温度能够达到600 ℃以上,且应力水平为180~270 MPa,但由于此区域承受的是压应力,铸铁抗压能力远强于抗拉,疲劳寿命远高于标准要求,最低循环次数为170 300次;排气管1,3与法兰面相接处受压应力作用,虽然应力值较高,但法兰面靠近缸盖水套,冷却好,温度较低,同时因怠速工况下此区域也承受压应力,总体循环应力幅较低,基本不存在疲劳破坏风险;而排气管3背面与法兰面相接处受拉应力作用,尽管怠速工况下此处也承受拉应力,但标定工况下该处应力接近材料屈服极限,因此疲劳寿命较低,最低循环次数为25 010次。
当考虑振动载荷影响时,从图 14可以看出,危险区域基本相同,疲劳寿命最低区域依然是排气管3与排气出口交汇处,最低循环次数下降至8 112次,位于点344964处,且整个区域有向排气管背面加筋处移动的趋势,同时危险区域明显扩大;对于各排气管间交汇处,疲劳寿命变化不大,但受影响区域明显扩大;对于排气管背面与法兰面相接区域,受影响区域扩大的同时循环次数也大幅下降,最低循环次数为10 600次,位于点308880处。结合0.06 s时排气系统的应力场(如图 15)及图 11的应力—时间历程曲线可以发现,排气管3靠近正面加筋处主要处于压应力区域,压应力为15~32 MPa,这对原本所受拉应力有减弱作用;而靠近背面加筋处主要受拉应力作用,应力水平为20~40 MPa,这会加剧原本所受拉应力负荷,从而出现危险点向此区域移动扩大的趋势;排气管3背面与法兰面相接区域振动载荷的应力场也表现为拉应力,应力为20~35 MPa,这会使原本接近或发生屈服区域应变大幅增加,因此此区域循环次数大幅下降,同时危险区域扩大;对于排气管间交汇处,因振动载荷引起的应力较低且处于拉压交替变化,应力在-20~10 MPa之间变化,对原本受压应力作用的该区域疲劳寿命影响较小。虽然靠近排气管正面加筋处振动载荷引起压应力较大,达到75 MPa,但此处在怠速和标定工况下都受压应力作用,且应力水平较低,所以疲劳破坏风险较低。

|
| 图 15 0.06 s时排气系统应力场 Fig.15 Stress field of exhaust system at 0.06 s |
根据上述结果可知,在加载振动载荷以后,排气支管3背面与法兰面相接区域最低循环次数由25 010次下降为10 600次,疲劳寿命下降高达57%以上。而对于整个排气歧管,循环次数由10 850次下降为8 112次,疲劳寿命下降幅度达到了25.2%。
3.3 发动机疲劳试验为评估排气歧管可靠性,参照发动机低周疲劳试验标准进行台架试验,试验结果如图 16所示。经过800 h耐久试验,未发现排气歧管出现损坏情况,证明排气歧管设计能够满足要求。同时,仿真分析结果也高于800 h标准要求,具有一定的参考意义。

|
| 图 16 发动机排气歧管疲劳试验结果 Fig.16 Engine exhaust manifold fatigue test result |
1) 通过引入Neuber弹塑性修正公式,对常规高温低周疲劳弹性状态载荷谱以及叠加振动动应力载荷谱进行弹塑性变形修正,以考虑高温状态下可能产生的塑性变形影响。
2) 常规高温低周疲劳破坏风险点主要位于各排气管交汇处等高温拉应力区域,同时排气管与法兰面结合区域也存在一定的疲劳损坏风险。
3) 相比常规高温低周疲劳结果,加载振动载荷会使部分区域疲劳寿命下降57%以上,排气歧管整体疲劳寿命下降幅度接近25.2%。结果表明在评估排气歧管低周疲劳寿命时,有必要考虑整机振动载荷的影响。
| [1] |
朱廉洁, 刘晓伟, 孙跃辉, 等.
三缸发动机整车怠速振动性能研究[J]. 噪声与振动控制, 2015, 35(6): 119–122.
ZHU Lian-jie, LIU Xiao-wei, SUN Yue-hui, et al. Study on idle vibration performance of an automobile with a three-cylinder engine[J]. Noise and Vibration Control, 2015, 35(6): 119–122. |
| [2] | DESAI D. Prediction of vibration and thermal behaviour of an automotive exhaust manifold:a comparative study[J]. WIT Transactions on Engineering Sciences:Materials Characterisation Ⅶ, 2015, 90: 331–341. |
| [3] | EROGLU S, DUMAN I, GUZEL A H, et al. Durability analysis of heavy duty engine exhaust manifold using CFD-FE coupling[C]//SAE 2016 World Congress and Exhibition, Detroit, Apr. 12-14, 2016. |
| [4] |
骆旭薇, 石勇, 李斌, 等.
应用FEA-CFD耦合方法对某增压柴油机排气歧管的开裂失效分析及设计改进[J]. 内燃机工程, 2015, 36(6): 144–150.
LUO Xu-wei, SHI Yong, LI Bin, et al. An FEA-CFD coupled analysis on the crack failure of the exhaust manifold of a turbo-charged diesel engine and design optimization[J]. Chinese Internal Combustion Engine Engineering, 2015, 36(6): 144–150. |
| [5] | LI Da-lei, YIN Yue-feng, CHEN Guang-fei, et al. Thermal fatigue analysis of the engine exhaust manifold[J]. Advanced Materials Research, 2012, 482/484: 214–219. DOI:10.4028/www.scientific.net/AMR.482-484 |
| [6] |
曹元福, 杨振宇, 柯妍, 等.
排气歧管热负荷仿真与试验研究[J]. 汽车工程, 2012, 34(5): 418–422.
CAO Yuan-fu, YANG Zhen-yu, KE Yan, et al. Simulation and experimental study on the thermal loads of exhaust manifold[J]. Automotive Engineering, 2012, 34(5): 418–422. |
| [7] | SESANA R, DELPRETE C, VERCELLI A. Multiaxial damage assessment and life estimation:application to an automotive exhaust manifold[J]. Procedia Engineering, 2010, 2(1): 725–734. DOI:10.1016/j.proeng.2010.03.078 |
| [8] | MASHAYEKHI M, TAGHIPOUR A, ASKARI A, et al. Continuum damage mechanics application in low-cycle thermal fatigue[J]. International Journal of Damage Mechanics, 2013, 22(2): 285–300. DOI:10.1177/1056789512448076 |
| [9] | PARTOAA A A, ABDOLZADEH M, REZAEIZADEH M. Effect of fin attachment on thermal stress reduction of exhaust manifold of an off road diesel engine[J]. Journal of Central South University, 2017, 24(3): 546–559. DOI:10.1007/s11771-017-3457-1 |
| [10] |
李哲琨. 排气歧管的热应力缓解技术研究[D]. 北京: 北京理工大学机械与车辆学院, 2015: 41-67.
LI Zhe-kun. Study on thermal stress alleviating technology of diesel exhaust manifold[D]. Beijing: Beijing Institute of Technology, School of Mechanical Engineering, 2015: 41-67. |
| [11] | CHOI B. A study on vibration fatigue of the engine exhaust manifold[J]. Journal of the Korean Society of Mechanical Technology, 2013, 15(5): 661–666. DOI:10.17958/ksmt |
| [12] |
马学军. 柴油机排气歧管的振动疲劳分析[D]. 太原: 中北大学机械工程学院, 2016: 43-56.
MA Xue-jun. Vibration fatigue analysis of diesel engine exhaust manifold[D]. Taiyuan: North University of China, School of Mechanical Engineering, 2016: 43-56. |
| [13] | SISSA S, GIACOPINI M, ROSI R. Low-cycle thermal fatigue and high-cycle vibration fatigue life estimation of a diesel engine exhaust manifold[J]. Procedia Engineering, 2014, 74: 105–112. DOI:10.1016/j.proeng.2014.06.233 |
| [14] | CONLE A, NOWACK H. Verification of a neuber-based notch analysis by the companion-specimen method[J]. Experimental Mechanics, 1977, 17(2): 57–63. DOI:10.1007/BF02326427 |
| [15] | KILAMBI S, TIPTON S M. Numerical evaluation of the original "Neuber's rule" for pure out-of-plane shear loading[J]. Journal of Strain Analysis for Engineering Design, 2013, 48(8): 522–535. DOI:10.1177/0309324713496407 |
| [16] | RAJADURAI S, PRASAD M G, KAVIN R, et al. Modal analysis for exhaust manifold in hot condition, is there a need?[J]. SAE Technical Papers, 2014-28-0036. |
| [17] |
史晓鸣, 杨炳渊.
瞬态加热环境下变厚度板温度场及热模态分析[J]. 计算机辅助工程, 2006, 15(S1): 15–18.
SHI Xiao-ming, YANG Bing-yuan. Temperature field and mode analysis of flat plate with thermal environment of transient heating[J]. Computer Aided Engineering, 2006, 15(S1): 15–18. |
| [18] |
吕红明.
边界条件对短梁结构有限元分析影响的研究[J]. 工程设计学报, 2013, 20(4): 321–325.
LÜ Hong-ming. Study on the influence of boundary conditions on the finite element analysis of short beam[J]. Chinese Journal of Engineering Design, 2013, 20(4): 321–325. |
| [19] |
苏荣华, 王碧珺, 丁文文, 等.
旋转轮盘应力刚化效应对模态特性影响分析[J]. 工程设计学报, 2009, 16(4): 292–296.
SU Rong-hua, WANG Bi-jun, DING Wen-wen, et al. Influence analysis of stress stiffening effect of rotating wheel-disc on its modal characteristics[J]. Chinese Journal of Engineering Design, 2009, 16(4): 292–296. |
| [20] | Verein Deutscher Ingenieure. Systematic calculation of high duty bolted joints joints with one cylindrical bolt: VDI 2230-2003E[S]. Düsseldorf: Verein Deutscher Ingenieure, 2003: 1-171. |



