2. 云南省复杂有色金属资源清洁利用国家重点实验室(培育基地), 云南 昆明 650093
2. State Key Laboratory Breeding Base of Complex Nonferrous Metal Resources Cleaning Utilization in Yunnan Province, Kunming 650093, China
微流控是一种以在微米尺度空间对流体进行操控为主要特征,以微尺度下流体输运为平台,以低雷诺数层流、非牛顿流体、界面效应和多物理场耦合效应理论为基础的科学技术,目前已广泛应用于医学、生物工程和航天航空等领域[1]。20世纪70年代,Little[2]在制作芯片上的冷却器时,采用Sandhlasting方法制作出具有垂直边壁面的流道,但粗糙的流道底部严重影响了微流道的通流特性,这促使人们着眼于研究流道内壁粗糙度的影响。Chaudhury, Daniel和Lorenceau等学者[3-5]相继发现,具有亲/疏水梯度和锥形结构特征的一维微通道结构因存在表面能梯度和拉普拉斯压力,能够促使液体实现单方向搬运。进一步研究表明,许多自然生物进化出这种结构来实现集水、集雾,Parker,Zheng和Ju等学者[6-8]分析了单向自搬运现象并提出了相应理论观点。但是上述研究并没有针对流体运输表面结构特征对其单向自搬运效率的影响给出规律性的结论和机理分析。陈华伟等[9]发现了猪笼草口缘区表面液体单方向搬运的新现象,通过显微镜观察其表面结构、材质与连续搬运原位,揭示了结构特征、材质对液体单方向搬运的影响规律,同时建立了连续搬运机制模型。可见,定量研究二维表面上的快速定向液体搬运是微流控领域的重要研究课题[10]。
本文以微米级单向微流道模型为研究对象,充分考虑实际工作过程中流道内壁粗糙度和结构特征对微流道流场的影响,并将微流道等效为连续的二维锥形结构,利用仿真软件分析了粗糙度等效齿高、齿数和齿倾角以及流动方向对流体单方向连续搬运效率的影响,最后通过实验验证了数值计算结果的准确性。
1 微流道内流场的数学建模对于特征尺度在微纳米级的微通道,其内表面亲/疏水梯度和加工过程中不可避免形成的粗糙度[11-14],会增大流道内壁的表面能梯度,从而在泰勒毛细升力和表面张力梯度的作用下增大了流动方向的梯度拉普拉斯力,形成短距离的流动自搬运效果,宏观表现为微流道出口平均速度vout大于入口速度vin。这种运动规律与宏观流动的沿程损失结论相悖,而与材料表面/界面力学中的分子力黏附、吸合现象相似,因而本文从微流道内壁移动接触线问题入手,通过分析微流道内受限流体的界面滑移、界面扩散及其动力学规律,研究微流道内液固之间的相互作用,探索法向/横向毛细力与微纳系统黏附失效之间的关系,最终定量地给出微流道内流场在流固耦合作用下的流动规律和流体分子动力学规律。
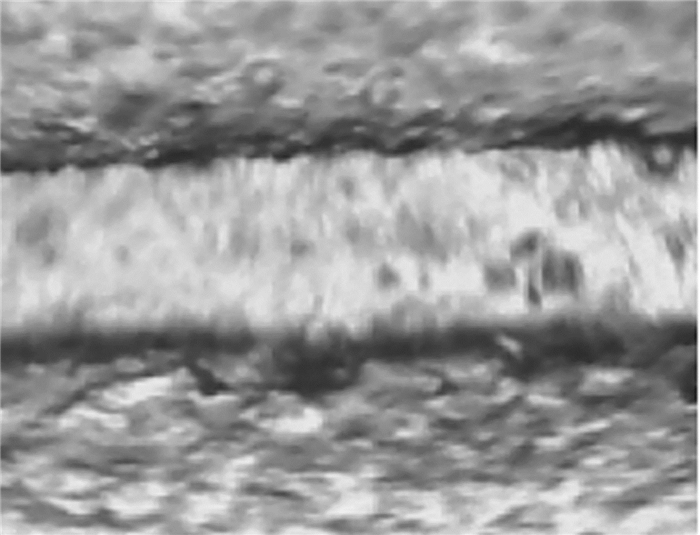
本文主要研究微流控芯片中微米级流道内流体的流动特性。如图 1所示,将微流控芯片放入夹具中,用螺钉固定住夹具,保证在实验过程中输液管道不会轻易从微流控芯片上脱落。光敏树脂通过3D打印形成通径为60 μm的直线型微流道,当深蓝色液态染色剂流经该微流道时,通过湛京ES-44-SM光学显微镜可以清楚地观察到:微流道内壁并不是光滑的,而是存在微米级凹凸不平的结构,如图 2所示。

|
| 图 1 微流控芯片实物图 Fig.1 Physical graph of microfluidic chip |
|
| 图 2 微流控芯片内部流道结构示意图 Fig.2 Structure scheme of microfluidic chip internal channel |
根据Casimir效应可知,当2个介电物体间的距离d满足100 nm < d < 7 μm时,Casimir效应起主导作用[15],此时在微流道内壁齿隙间的空腔内形成一个能量梯度,由这个能量梯度产生的Casimir力使流道内部近壁层产生一个水平方向的推动力,加快了流体在流道内的流动速度。由于微流道特征尺寸为几十微米,齿隙高度为几微米至十几微米,因此近壁面Casimir力的作用范围为整个流域高度方向的10%左右,可以明显观测出流道出口较入口的速度增量,即单向自搬运现象。而对于特征尺度在毫米级及以上的宏观流动而言,其流道内流动特征则依赖该处雷诺数的大小,此时壁面粗糙度的作用微乎其微。
本文将微流道内壁粗糙度影响等效为连续锯齿的作用效果,分析不同近壁面粗糙度对流体自搬运特性产生的影响。
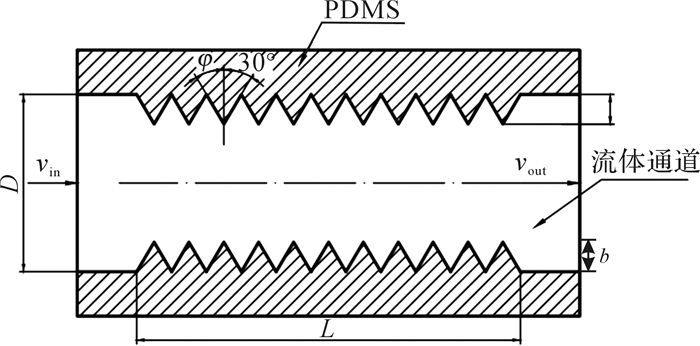
图 3所示为微流道横截面结构剖面示意图。通过分析来流作用于微流道内壁时齿倾角φ、齿高b和齿数n对流道内流线分布、局部涡流和自搬运效率K的影响规律,来研究微流道内壁粗糙度对微流道内流体单向流动自搬运效果的影响规律。定义自搬运效率K=vout/vin,通过分析K值的大小和变化规律,可以整体衡量微流道内流体单相自搬运效果的强弱程度。
|
| 图 3 微流道横截面结构剖面示意图 Fig.3 Structural profile scheme of microchannel cross section |
本文选用的是微流道内马赫数极低的牛顿流体,其本构关系[16]为:
| $ {\sigma _{{x_y}}} = - p{\delta _{{x_y}}} + \lambda {\delta _{{x_y}}}\blacksquare \cdot \mathit{\boldsymbol{V}} + 2\mu {\mathit{\boldsymbol{e}}_{{x_y}}} $ | (1) |
式中:λ=-2μ/3, μ为流体黏性系数;σxy为应力张量, exy为单位向量, δxy为单位张量, 其中x,y分别表示通道的长度与高度方向;p为压力。
由于
| $ {\sigma _{{x_y}}} = - p{\delta _{{x_y}}} + 2\mu {\mathit{\boldsymbol{e}}_{{x_y}}} $ | (2) |
图 3所示的微流道中流体的连续性方程及沿着y方向和x方向的动量方程分别为:
| $ \frac{{\partial \omega }}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0 $ | (3) |
| $ v\frac{{\partial v}}{{\partial y}} + \omega \frac{{\partial v}}{{\partial x}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {x^2}}} $ | (4) |
| $ v\frac{{\partial \omega }}{{\partial y}} + \omega \frac{{\partial \omega }}{{\partial x}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{{{\partial ^2}\omega }}{{\partial {y^2}}} + \frac{{{\partial ^2}\omega }}{{\partial {x^2}}} - {k^2}\omega $ | (5) |
式中:ρ为流体密度;k为曲率;v为流体质点速度沿y方向的分量;ω为流体质点速度沿x方向的分量。
入口的边界条件为vin=v0;出口的边界条件为vout=v1, p1=0。作为迟滞的van der Waals力,微流道粗糙内壁处的Casimir力满足Derjaguin法近似条件,其一般形式[17-18]为:
| $ {F_{{\rm{Casimir}}}} = {\eta _{\rm{m}}}{\eta _{\rm{T}}}{\eta _{\rm{g}}}\left( {1 + {\Delta _{{\rm{corr}}}}} \right){F_0} $ | (6) |
式中:ηm是和介质材料相关的修正因子,ηm<1;ηT是和温度相关的修正因子,ηT>1;ηg是和流道几何形状相关的修正因子;Δcorr是不同修正因子间的相关系数;F0为距离为d时2个理想平板间单位面积的Casimir力,在绝对零度下,它可以表示为:
| $ {F_0} = - \frac{{{{\rm{ \mathsf{ π} }}^2}hc}}{{240{d^4}}} $ | (7) |
式中:h为Planck常数除以2π,h=1.055×10-34 Js;c为光速;d为固面间距。
对于流动区域而言,一个系统的平衡状态由其Helmholtz自由能的极小值决定。
| $ F = U - TS $ | (8) |
式中:U是系统自由能,即系统中各原子自漩相互作用的能量总和;TS是不能自由做功部分的束缚能,T为热力学温度,S为系统熵值。
对于等温条件下的流动介质,其内能U变化不大,要使Helmholtz自由能达到最小,则需使系统的熵值S取极大值。
2 粗糙度等效参数对流体自搬运的影响分别取流通道内壁粗糙度的等效齿数n为3,5,7,11,齿高h取0, 6, 8, 10 μm,齿倾角φ取30°, 45°, 60°, 75°,进行数值仿真模拟。流道的材质为PDMS(polydimethylsiloxane,聚二甲基硅氧烷),流体为去离子水。在分析过程中,定义流体为非定常二维不可压缩流,其他参数均为软件默认值。微流道的入口边界为速度入口,出口边界为标况大气压。采用COMSOL Multiphysiscs 5.0进行网格划分和数值计算,其中流道内部的网格划分为极细等级,通道外部的PDMS材料网格划分为常规等级。
2.1 齿数的影响1) 流场特征。
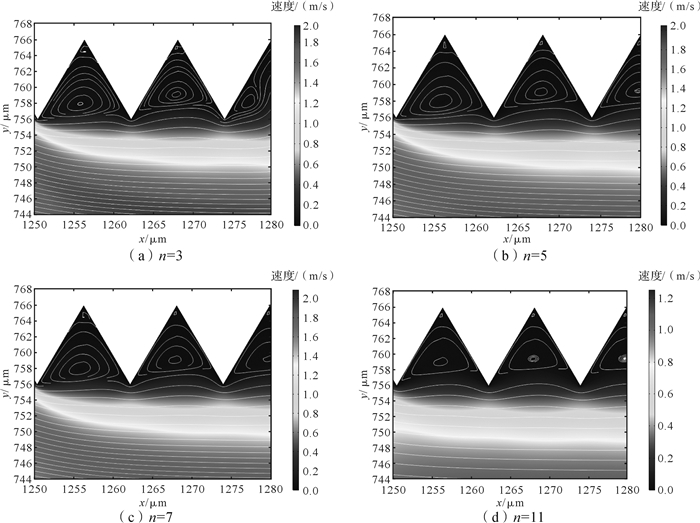
如图 4所示,随着齿数n从3增加到11,两齿之间形成比较明显的逆时针主漩涡,且涡漩的涡量逐渐减小。在齿根部分形成旋转方向与主漩涡相反的伴生涡,伴生涡的大小和强度基本保持不变,其强度很小,这主要是因为主漩涡在转动过程中,流体分子与齿底发生了摩擦。值得注意的是:在相同齿数下,沿流动方向的齿间隙内的涡强逐渐增加,而且其内部伴生涡的涡强逐渐减小。
|
| 图 4 齿数对微流道内流体连续自搬运的影响 Fig.4 Influence of tooth number on continuous directional liquid transport of fluid in microchannel |
2) 搬运效率。
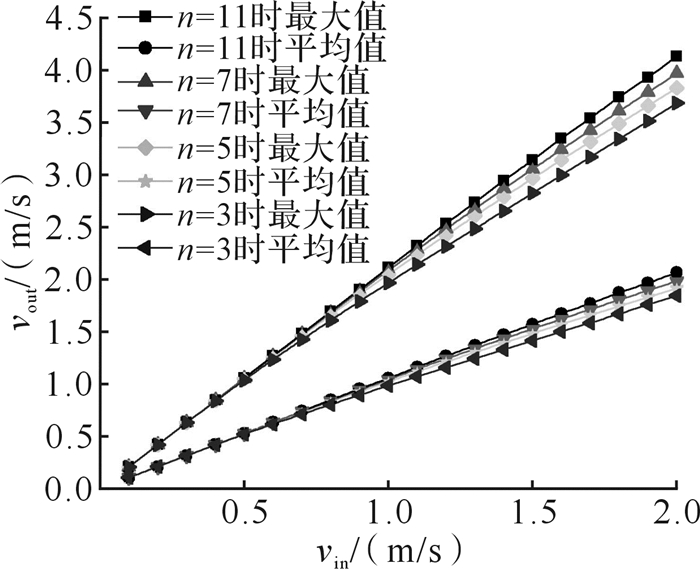
由图 5可知,在相同齿数下,随着入口速度从0.1 m/s增加到2 m/s时,出口速度的最大值和平均值均增加,且前者的增幅较大。在相同入口速度下,随着齿数从3增加到11,出口速度的最大值和平均值均增加,最大值增幅约为平均值增幅的2倍。这主要是因为当流体在内壁粗糙的微流道内流动时,近壁面齿间隙间形成流动漩涡,漩涡的特征尺寸略小于齿间隙高度,因而在排空吸引力的作用下加剧了流动方向的流体运动速度。齿数为3和5时出口速度最大值和平均值的曲线斜率相差较大,齿数为7和11时出口速度最大值和平均值的曲线斜率相差较小。由此可以推测:当齿数继续增加时,相邻齿数的出口速度的最大值和平均值的差别会越来越小。
|
| 图 5 不同齿数下微流道出口速度的最大值与平均值 Fig.5 Maximum value and average value of the outlet velocity of microchannel under different number of tooth |
为进一步表征通过微流道中流体分子在流动过程中受到的固体表面作用和Casimir力的强度,定义此时微流道内流体连续自搬运效率为:
| $ K = \frac{{{v_{{\rm{out}} - {\rm{mean}}}}}}{{{v_{{\rm{in}}}}}} $ | (9) |
式中:vout-mean表示微流道出口速度的平均值;vin表示微流道入口速度。
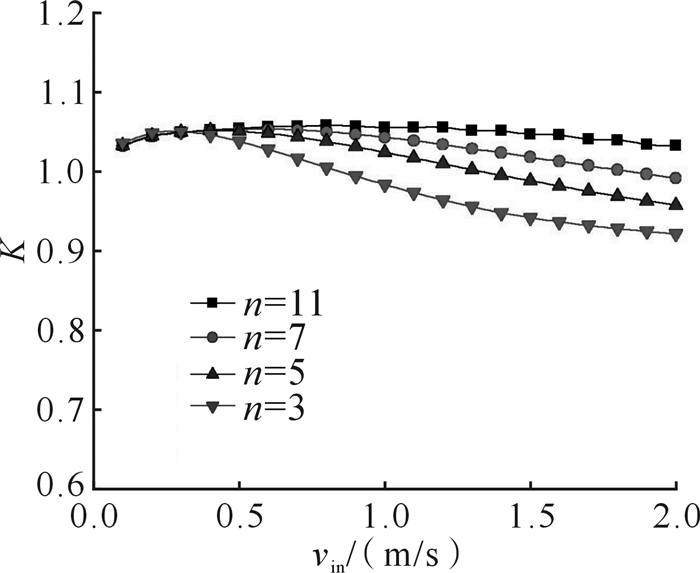
由图 6可知:在相同齿数下,入口速度从0.1 m/s增加到0.3 m/s时,连续自搬运效率K相同且呈现增加趋势;入口速度从0.3 m/s增加到2 m/s时,连续自搬运效率K均呈现减小的趋势。这主要是因为随着入口速度的增大,流体分子间的自由能增强而熵力相对减弱,交叠排空区减小,因而受壁面作用的排空吸引力作用减弱。在相同速度下,齿数从3增加到11时,连续自搬运效率K增加,这主要是因为齿间隙作用的增强增大了流体分子的无序度,系统的熵值在齿隙不断作用下逐渐恢复到最大值,流体分子之间的排布更为拥挤复杂,相同受限空间内产生了更大的交叠排空区,产生了较大的吸引力。齿数为11时的连续自搬运效率K相对齿数为3,5和7时的连续自搬运效率K下降得较慢,由此可以预测:当齿数继续增加,连续自搬运效率K下降得会越来越慢。
|
| 图 6 不同齿数下流体连续自搬运效率 Fig.6 Continuous directional transport efficiency of fluid under different number of tooth |
1) 流场特征。
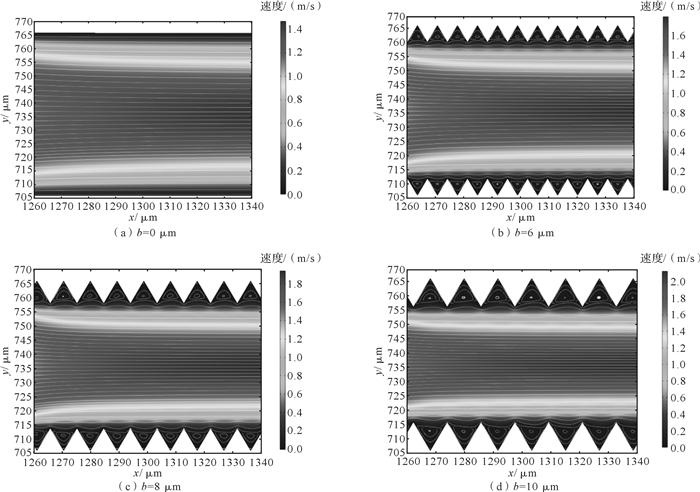
随着齿高b从0 μm增加到10 μm,两齿之间形成比较明显的逆时针主漩涡,涡漩的涡量逐渐增加,并且在齿根部分会形成旋转方向与主漩涡相反的伴生涡。伴生涡的大小和强度随齿高的增加而增加,但强度较主漩涡相差非常大。齿间漩涡的形成主要是因为流体进入流道时受到法向毛细-桥力,原本驻留在齿间隙底部的气体未能及时排出而在液体与固体表面之间形成了纳米气桥。
如图 7所示,随着液体主漩涡的形成和发展,和气桥接触的流体分子在毛细力作用下产生黏附失效;同时浸润部分由于横向毛细力作用,分子之间互相靠近以降低其势能,形成了由漂浮力和摩擦力共同引起的反向伴生涡。值得注意的是:在相同齿高下,沿着流动方向,齿间隙内的涡强逐渐增大,而内部的伴生涡的涡强逐渐减小。
|
| 图 7 齿高对微流道内流体连续自搬运的影响 Fig.7 Influence of tooth height on continuous directional liquid transport of fluid in microchannel |
2) 搬运效率。
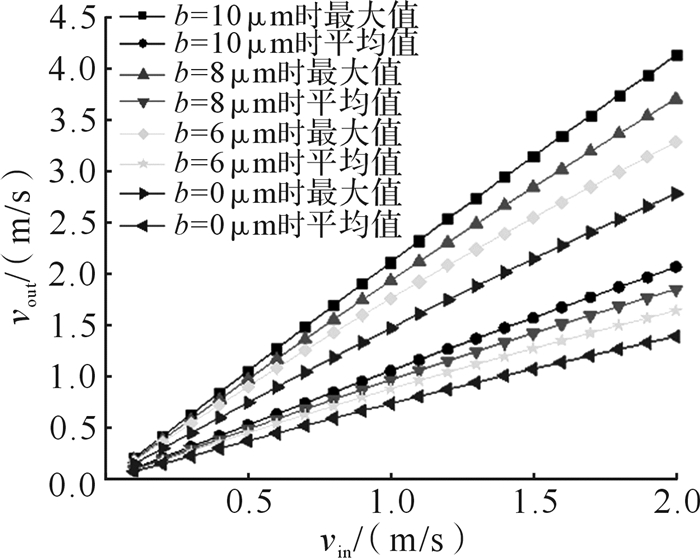
由图 8可知, 在相同齿高下,随着入口速度从0.1 m/s增加到2 m/s,出口速度的最大值和平均值均增加,最大值增加的幅度比平均值增加的幅度大。在相同速度下,随着齿高从0 μm增加到10 μm,出口速度的最大值和平均值均增加,最大值增加的幅度约为平均值增幅的2倍。可见齿高造成的近壁面吸附影响大于入口动能的影响, 并且入口速度越大,这种吸附力的作用强度越大。齿高为6,8和10 μm时出口速度最大值和平均值曲线的斜率相较齿高为0 μm时的更相近。由此可以推断:当齿高继续增加时,相邻齿高的出口速度最大值和平均值曲线的倾斜会比齿高为6,8,10 μm时的更加接近。
|
| 图 8 不同齿高下微流道出口速度的最大值与平均值 Fig.8 Maximum value and average value of the outlet velocity of microchannel under different height of tooth |
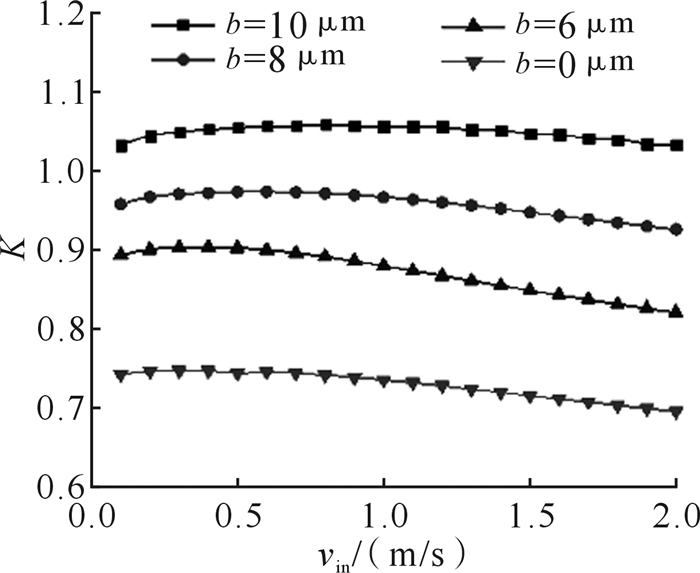
由图 9可知, 在相同齿高下,入口速度从0.1 m/s增至2 m/s时,流体连续自搬运效率K均呈现先增加再减小的趋势。这也是因为系统自由能增大降低了熵力作用,从而减弱了排空吸引力作用强度。在相同速度下,随着齿高从0 μm增至10 μm,流体连续自搬运效率K增大,这印证了近壁面粗糙度增大了流场运动无序度,进而提高系统Helmholtz自由能。由此可以预见:在粗糙度范围内,当齿高继续增加,相邻齿间的连续自搬运效率K会相差越来越小。
|
| 图 9 不同齿高下流体连续自搬运效率 Fig.9 Continuous directional transport efficiency of fluid under different height of tooth |
1) 流场特征。
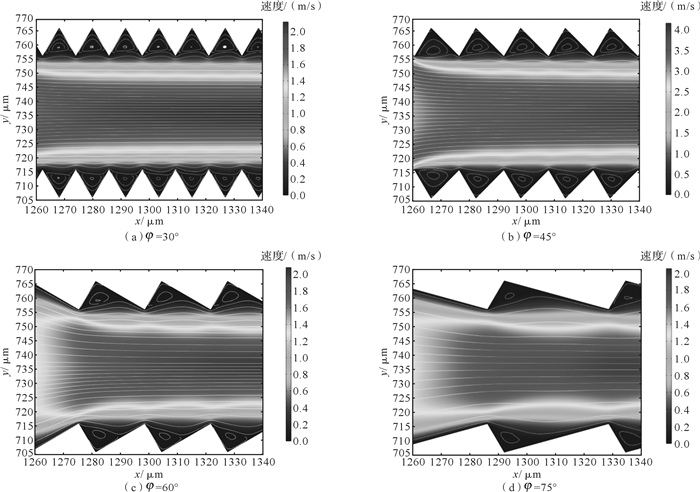
如图 10所示,随着齿倾角φ从30°增加到75°,两齿之间形成比较明显的逆时针主漩涡,其涡量逐渐减小,并且在齿根部分会形成旋转方向与主漩涡相反的伴生涡,且伴生涡的涡强逐渐减小。这主要是因为主漩涡在转动过程中,流体分子和齿底发生了摩擦。当齿倾角大于45°时,伴生涡逐渐退化;在齿倾角为60°时,伴生涡已经完全退化。值得注意的是,在相同齿倾角下,沿流动方向的齿间隙内的涡强逐渐增大,但内部伴生涡的涡强逐渐减小。
|
| 图 10 齿倾角对微流道内流体连续自搬运的影响 Fig.10 Influence of tooth dip angle on continuous directional liquid transport of fluid in microchannel |
2) 搬运效率。
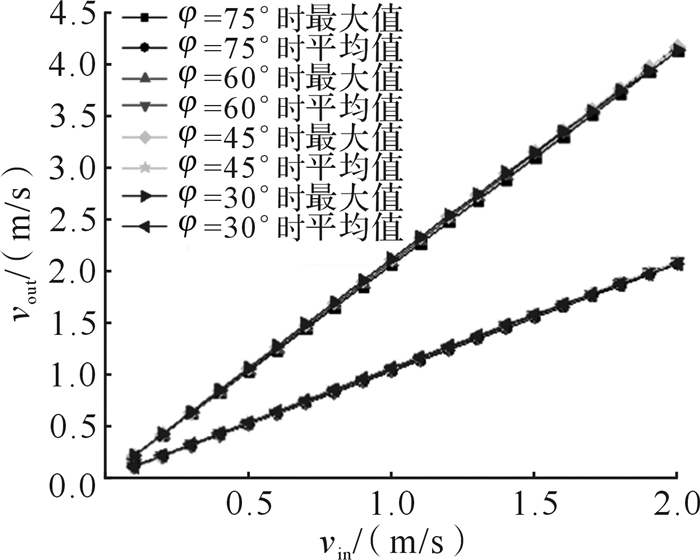
由图 11可知,相同齿倾角下,随着入口速度从0.1 m/s增至2 m/s,出口速度最大值与平均值均增加,最大值增幅比平均值增幅大。在相同速度下,随着齿倾角从30°增至75°,出口速度最大值和平均值基本保持一致,且最大值增幅近似是平均值增幅的2倍。可以推测:当齿倾角进一步增大时,出口速度最大值和平均值与齿倾角为30°,45°,60°,75°时的变化规律保持一致。
|
| 图 11 不同齿倾角下微流道出口速度的最大值与平均值 Fig.11 Maximum value and average value of the outlet velocity of microchannel under different dip angle of tooth |
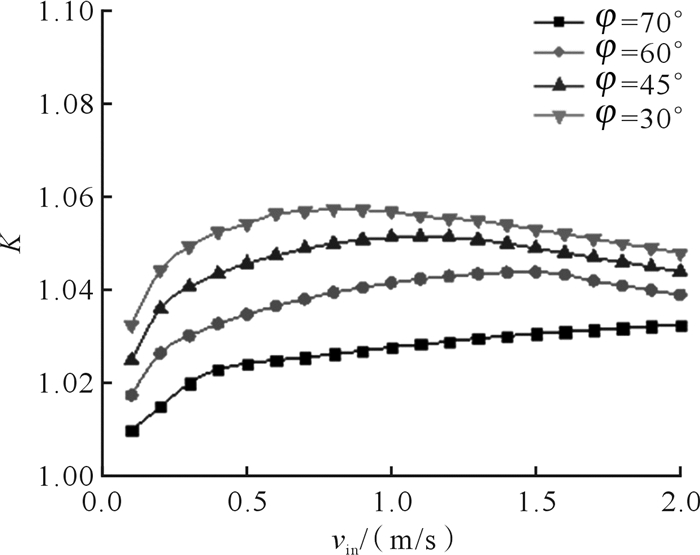
由图 12可知,在相同齿倾角下,入口速度从0.1 m/s增加到2 m/s时,流体连续自搬运效率K均呈现先增加再减小的趋势。只有当齿倾角为75°时,流体连续自搬运效率K一直增加。在相同速度下,随着齿倾角从30°增至75°,流体连续自搬运效率K逐渐减小。这主要是由于迎风角的增大减小了齿间隙漩涡流动的强度,使微流道内的整体脉动强度增大,脉动频率降低。齿倾角为75°时的流体连续自搬运效率K相对齿倾角为60°,45°和30°时的流体连续自搬运效率K较稳定。由此可以预测:随着齿倾角继续增加,流道内流体连续自搬运效率K会越来越稳定;而随着齿倾角逐渐减小,流道内的连续自搬运效率K会逐渐增大。
|
| 图 12 不同齿倾角下的流体连续自搬运效率 Fig.12 Continuous directional transport efficiency of fluid under different dip angle of tooth |
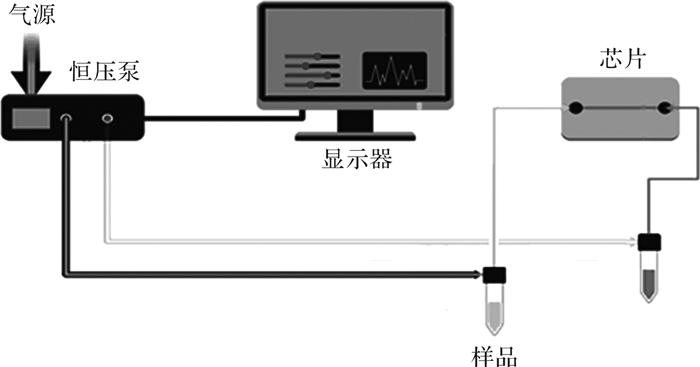
本文按照图 13所示的实验原理图搭建了如图 14所示的实验装置, 其中:恒压泵为汶颢WH-HYB000201流体控制恒压泵,对微流道的观测借助湛京ES-44-SM光学显微镜,控制和显示功能由华硕K53SJ笔记本电脑及其配套软件实现。恒压泵与显示器通过数据线连接,通过显示器可将显微镜观测到的微流控芯片内部流动状态显示出来,恒压泵与样品容器通过气体管道和输液管道连接,2个样品容器之间通过微流控芯片连接。恒压泵将气源以一定的压力通过供气管道泵入样品容器,供气管道口在样品液面以上,气体进入样品容器之后,样品在气压作用下通过输液管道进入芯片,流体通过微流控芯片内部通道从输液管道另一端口流出并进入样品容器。
|
| 图 13 微流道内流体连续自搬运的实验原理图 Fig.13 Experimental schematic for continuous directional liquid transport of fluid in microchannel |

|
| 图 14 微流道内流体连续自搬运的实验装置 Fig.14 Experiment device for continuous directional liquid transport of fluid in microchannel |
本文采用3D打印方法制成的微流控芯片如图 15所示,并设计制造专用微芯片夹具将它与其它测量控制装置相互连接,如图 1所示。通入流体后,在250倍的放大倍数下观察微流控芯片内部通道,如图 16所示, 通过对比染色剂通入前后的微流道内的情况,确定此时微流道内壁加工表面具有的较小间距和微小峰谷的最大不平度为10 μm量级。

|
| 图 15 微流控芯片实物图 Fig.15 Physical graph of microfluidic chip |

|
| 图 16 微流控芯片内部通道实物图 Fig.16 Physical graph of microfluidic chip internal channel |
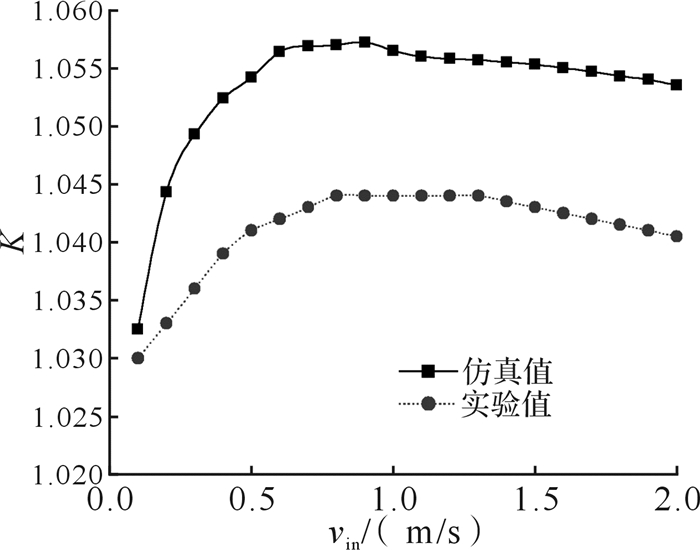
如图 17所示,当齿高为10 μm时,入口速度从0 m/s增加到2 m/s,流体连续自搬运效率K的实验值与仿真值的变化趋势一致,但实验数据较仿真结果小,两者之间最大偏差在10%以内,符合误差要求。出现该情况的原因是实际管道内壁粗糙度不唯一以及测量过程中存在细微误差。
|
| 图 17 b=10 μm时流体连续自搬运效率的实验值与仿真值 Fig.17 Experimental value and simulation value of continuous directional transport efficiency of fluid with b=10 μm |
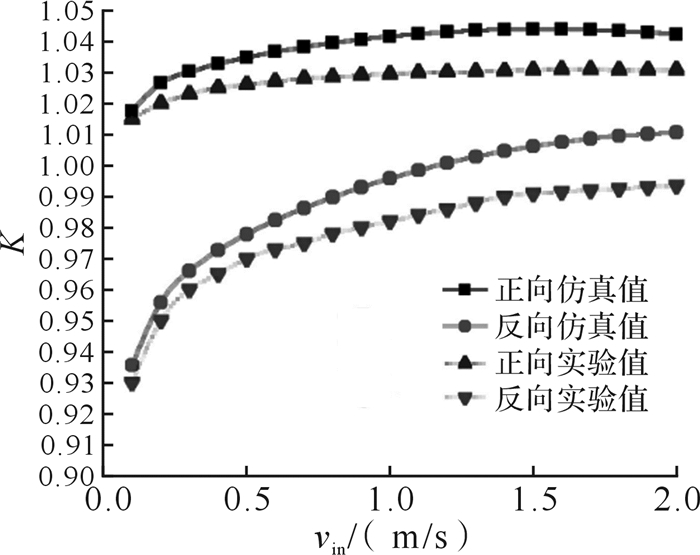
如图 18所示,当假设粗糙度等效齿角均匀且都等于60°时,对不同的微流控芯片改变进口方向进行实验,可知:随着入口速度的加大,正向和反向的实验数据和仿真结果均呈逐渐增加的趋势,且入口速度较小时流体连续自搬运效率K增大较快。随着入口速度增大到1.0 m/s以上时,流体连续自搬运效率逐渐稳定。对比实验数据和仿真结果可知,两者偏差在入口速度较大时较明显,这主要是由压力损失以及测量误差造成的。
|
| 图 18 不同流动方向下流体连续自搬运效率的实验值和仿真值 Fig.18 Experimental value and simulation value of continuous directional transport efficiency of fluid under different flow direction |
通过以上2组实验数据与仿真数据的比较可以发现,实验所得数据和仿真结果所得结论一致,且两者误差小于5%,表明本文所得结论真实可靠。
4 结论本文基于微流体动力学理论,研究了微流道内壁表面粗糙度对流道内流体流动特性和连续自搬运现象的影响,分析了微流道内壁粗糙度的等效齿数、齿高和倾斜角对流场特征和搬运效率的影响规律,并搭建实验台完成了实验验证,对微电子机械系统的小型化和集成化设计具有一定的参考意义。
1) 微流道内壁表面粗糙度严重影响流道内流体输运时的流动特性,界面效应和表面能共同作用造成出口速度增加的连续自搬运现象。在此基础上,进一步给出了基于Casimir效应和表面能特征的微纳尺度液体流动的控制方程。
2) 借助多物理场仿真软件COMSOL分析了不同粗糙元齿数、齿高、齿倾角和流动方向对微流道内流体流动规律以及能量变化的影响。明确了齿间流动漩涡的变化规律和伴生涡的特征;并通过定义流体连续自搬运效率K,定量描述微流道出口速度较入口速度的增加程度,明确表征了微流道内流体连续自搬运效率的大小。
3) 通过实验,对比分析了不同流动方向对同一微流道内流体连续自搬运效率的影响。实验数据和仿真结果趋势一致且误差合理,验证了本文理论分析的正确性和物理模型的合理性,表明本文粗糙度齿型结构参数对流体微流动特性影响研究所得结论是有效、可靠的。
| [1] |
包福兵. 微纳尺度气体流动和传热的Burnett方程研究[D]. 杭州: 浙江大学航空航天学院, 2008: 1-125.
BAO Fu-bing. Burnett simulation of micro-and Nanoscale gas flow and heat transfer[D]. Hangzhou: Zhejiang University, School of Aeronautics and Astronautics, 2008: 1-125. |
| [2] | LITTLE W A. Microminiature refrigeration:small is better[J]. Physica B+C, 1992, 109/110: 2001–2009. |
| [3] | CHAUDHURY M K, WHITESIDES G M. How to make water run uphill[J]. Science, 1992, 256: 1539–1541. DOI:10.1126/science.256.5063.1539 |
| [4] | DANIEL S, CHAUDHURY M K, CHEN J C. Fast drop movements resulting from the phase change on a gradient surface[J]. Science, 2001, 291: 633–636. DOI:10.1126/science.291.5504.633 |
| [5] | LORENCEAU É, QUÉRÉ D. Drops on a conical wire[J]. Journal of Fluid Mechanics, 2004, 510: 29–45. DOI:10.1017/S0022112004009152 |
| [6] | PARKER A R, LAWRENCE C R. Water capture by a desert beetle[J]. Nature, 2001, 414: 33–34. DOI:10.1038/35102108 |
| [7] | ZHENG Y, BAI H, HUANG Z, et al. Directional water collection on wetted spider silk[J]. Nature, 2010, 463: 640–643. DOI:10.1038/nature08729 |
| [8] | JU J, BAI H, ZHENG Y, et al. A multi-structural and multi-functional integrated fog collection system in cactus[J]. Nature Communications, 2012, 3(4): 1247. |
| [9] |
陈华伟, 张鹏飞, 张力文, 等.
猪笼草口缘区表面液体单方向连续搬运机制[J]. 中国科学基金, 2016(3): 217–219.
CHEN Hua-wei, ZHANG Peng-fei, ZHANG Li-wen, et al. Continuous directional water transport on the peristome surface of Nepenthes alata[J]. Bulletin of National Natural Science Foundation of China, 2016(3): 217–219. |
| [10] | CHEN H, ZHANG P, ZHANG L, et al. Continuous directional water transport on the peristome surface of Nepenthes alata[J]. Nature, 2016, 532: 85–89. DOI:10.1038/nature17189 |
| [11] | ALAM T, LEE P S, YAP C R. Effects of surface roughness on flow boiling in silicon microgap heat sinks[J]. International Journal of Heat and Mass Transfer, 2013, 64(7): 28–41. |
| [12] | NATRAJAN V K, CHRISTENSEN K T. The impact of surface roughness on flow through a rectangular microchannel from the laminar to turbulent regimes[J]. Microfluidics and Nanofluidics, 2010, 9(1): 95–121. DOI:10.1007/s10404-009-0526-2 |
| [13] | CROCE G, D'AGARO P, NONINO C. Three-dimensional roughness effect on microchannel heat transfer and pressure drop[J]. International Journal of Heat and Mass Transfer, 2007, 50(25/26): 5249–5259. |
| [14] |
谭德坤. 微流道内表面效应对流体流动及传热特性的影响[D]. 南昌: 南昌大学机电工程学院, 2014: 1-102.
TAN De-kun. Surface effects on fluid flow and heat transfer characteristics in microchannels[D]. Nanchang: Nanchang University, School of Mechatronics Engineer-ing, 2014: 1-102. |
| [15] |
赵亚溥.
表面与界面物理力学[M]. 北京: 科学出版社, 2012: 1-588.
ZHAO Ya-pu. Surface and interface mechanics[M]. Beijing: Science Press, 2012: 1-588. |
| [16] |
林建忠, 包福兵, 张凯, 等.
微纳流动理论及应用[M]. 北京: 科学出版社, 2010: 1-268.
LIN Jian-zhong, BAO Fu-bing, ZHANG Kai, et al. Theory and application of micro-nano flow[M]. Beijing: Science Press, 2010: 1-268. |
| [17] | BORDAG M, MOHIDEEN U, MOSTEPANENKO V M. New developments in the Casimir effect[J]. Physics Reports, 2001, 353(1/3): 1–12. |
| [18] | BUKS E, ROUKES M L. Stiction, adhesion energy, and the Casimir effect in micromechanical systems[J]. Physical Review B, 2001, 63(3): 003402. |



