无人潜航器(unmanned underwater vehicle,UUV)是指通过遥控或自动控制在水下航行的作战工具[1-2],具有智能性高、隐身性能好、机动能力强等优点。无人潜航器外形及结构特征与鱼雷较为相似,在完成任务后进行回收或状态异常时,需要采用排载方式或上浮装置产生正浮力,以便回收[3-4]。使用浮囊产生正浮力是一种重要的回收方法,它具有浮囊占用体积小、产生正浮力大、可重复利用等优点[5],但也存在系统复杂、潜航器运动与浮囊充气相互影响等缺点,对浮囊的设计和使用提出了较高的要求。吕汝信[6]系统地研究了浮囊式上浮装置的工作过程,在潜航器运动分析、浮囊充气过程控制及导流罩设计等方面进行了大量的试验研究并积累了丰富的设计经验。近几年,程文鑫、叶慧娟等[7-8]针对气囊的充气过程建立了精确的数学模型,对气囊的充气过程进行了较深入的分析;王栋等[9]通过建立CAE仿真模型分析了浮囊式操雷在海面上的漂浮过程,为充气式浮囊的设计提供了重要参考。但是在上述研究中,并未有人将潜航器运动与浮囊充气过程结合起来并对相关影响因素进行详细分析。
本文在已有研究的基础上,将潜航器运动过程与浮囊充气过程相结合,通过建立潜航器停车后的运动模型,并使用DOE(design of experiment, 试验设计)方法来分析浮囊的延迟充气时间和充气过程时间(即设计因子)对潜航器运行的最大深度和浮囊最大阻力(即设计目标)的影响,通过分析设计因子交互效应、主效应曲线、相关性图及Pareto图,明确了设计因子与设计目标的关系,以期为后续潜航器及浮囊式上浮装置的理论研究和工程设计提供参考。
1 无人潜航器停车后的运动模型 1.1 无人潜航器受力分析无人潜航器在完成任务后,调整航行的深度、速度和姿态角,发动机停车,开始执行上浮程序。以停车为起始时间,分段分析潜航器的运动过程:
1) 停车至螺旋桨停止惯性旋转。停车后,螺旋桨由于惯性不会立刻停止旋转,继续为潜航器提供动力T,但随着转速逐渐减小,最终经过t1时间后完全停止,潜航器失去动力。
2) 螺旋桨停止惯性旋转至浮囊开始充气。螺旋桨停止旋转后,潜航器仍具有一定速度,螺旋桨转为被动态,使得阻力R增大,潜航器在阻力R和负浮力(mg-Fl)作用下继续运动,经过t2时间后浮囊开始充气展开。
3) 浮囊开始充气至充气结束。在浮囊充气过程中,其体积逐渐增大,潜航器受到浮囊阻力Rf和浮力Ff的作用,其运动状态改变明显,最终经过t3时间后浮囊充气至最大体积,充气结束。
4) 浮囊充气结束至潜航器到达最大深度。浮囊充气结束后,潜航器在浮囊阻力和浮力的作用下减速,到达最大深度后开始上浮。
图 1所示为潜航器在上浮过程中的受力情况。

|
| 图 1 上浮运动过程中无人潜航器的受力示意图 Fig.1 The force diagram of UUV in the floating movement process |
分别在x, y方向建立潜航器的动力学方程:
| $ \left\{ \begin{array}{l} (T - R - {R_{\rm{f}}}){\rm{cos}}\theta = M{a_x}\\ (T - R - {R_{\rm{f}}}){\rm{sin}}\theta + {F_{\rm{f}}} - (mg - {F_{\rm{l}}}) = M{a_y} \end{array} \right. $ | (1) |
式中:(mg-Fl)为潜航器的负浮力,在运动过程中保持不变;T,R,Rf, Ff分别为潜航器受到的推力、阻力, 浮囊阻力、浮力,其计算公式分别为:
| $ \left\{ \begin{array}{l} T = K\rho {n^2}{D^4}\\ R = \frac{1}{2}\rho {C_{\rm{x}}}{v^2}{S_{\rm{x}}}\\ {R_{\rm{f}}} = \frac{1}{2}\rho {C_{\rm{x}}}f{v^2}{S_{\rm{f}}}\\ {F_{\rm{f}}} = \rho Vg \end{array} \right. $ | (2) |
式中:K为推力系数;ρ为水的密度;n和D分别为螺旋桨的转速和直径;v为潜航器的速度;Cx, Cxf分别为潜航器和浮囊的阻力系数;Sx,Sf分别为潜航器和浮囊的浸湿面积;V为浮囊的体积。
图 2所示为在不同阶段中潜航器所受各力的变化趋势。经过t1时间螺旋桨转为被动态后, 潜航器阻力系数Cx会迅速增大;在浮囊充气过程中,假设浮囊的体积随时间线性变化,其阻力Rf和浮力Ff亦随时间线性变化。

|
| 图 2 无人潜航器所受各力的变化趋势示意图 Fig.2 Schematic diagram of the force change trend of UUV |
无人潜航器停车时的状态参数为:深度为50 m、速度为50节(25.7 m/s)、俯仰角为-45°。初步设定时间分段参数为:t1=1 s, t2=3 s, t3=6 s,即潜航器停车后1 s失去动力,停车后3 s浮囊开始充气,充气过程时间为3 s。利用上述初始条件并结合文献[5]中各参数的取值进行运动分析与计算,可以得到无人潜航器停车后的运动速度、深度及浮囊阻力随时间的变化情况,如图 3、图 4所示。

|
| 图 3 无人潜航器运动速度和深度随时间变化曲线 Fig.3 The variation curve of velocity and depth of UUV with time |

|
| 图 4 浮囊阻力随时间的变化曲线 Fig.4 The variation curve of resistance force of floating bag with time |
由图 3和图 4可知:无人潜航器速度曲线在第1秒、第3秒出现明显波动,表明该时刻潜航器的受力发生较大变化;潜航器运行的最大深度为108 m;浮囊从第3秒开始受到阻力作用,阻力迅速上升,达到最大后开始缓慢下降。上述结果与文献[5]的结果较为吻合,表明了本文所建立的潜航器动力学模型的正确性。
2 无人潜航器运动过程的DOE分析 2.1 DOE方法DOE(design of experiments,试验设计)分析方法是基于数理统计学理论建立的,用来合理而有效地获得信息数据,它在工程和科研领域有着广泛的应用[10]。DOE分析过程包括试验计划、试验执行和结果分析三个步骤。本文中无人潜航器运动过程的DOE分析如下:
1) 试验计划:明确设计因子和设计目标。在确定潜航器停车状态时,以浮囊的延迟充气时间t2和浮囊的充气过程时间Δt=t3-t2为设计因子,以潜航器运行的最大深度Hmax和浮囊最大阻力Rmax为设计目标;为使计算更加精确,采用最优拉丁超立方设计方法建立设计因子矩阵。
2) 试验执行:编制计算机程序,严格按照设计因子矩阵运行。
3) 结果分析:绘制无人潜航器运行的最大深度和浮囊最大阻力的散点图,t2和Δt的交互效应曲线、主效应曲线、相关性图及Pareto图,对试验结果进行分析,得出相应的结论。
2.2 结果分析考虑到潜航器运行的最大深度是其工作的重要边界,浮囊最大阻力则关系到浮囊能否保持结构完整而不影响正常工作,因此以这2个参数作为重点分析对象。计算完成后,绘制潜航器运行的最大深度Hmax和浮囊最大阻力Rmax的散点图,如图 5所示。

|
| 图 5 无人潜航器运行的最大深度和浮囊最大阻力的散点图 Fig.5 Scatter diagram of the maximum operation depth of UUV and the maximum resistance force of floating bag |
从散点图可以看出,Hmax随t2和Δt的增大而减小,呈现出一定的线性特征,其中t2的影响相对较大;Rmax随t2和Δt的增大而迅速减小,呈现出明显的指数特征。
为进一步对Rmax进行分析,根据散点图特征取其对数lnRmax作为目标值,并绘制散点图,如图 6所示。可以看到,lnRmax随t2和Δt的增大而减小,表现出负相关关系。

|
| 图 6 浮囊最大阻力对数值的散点图 Fig.6 Scatter diagram of maximum resistance force logarithm of floating bag |
散点图能直观地表现出目标值随设计因子的变化趋势,但无法进行精确的定量分析。为此,对设计因子t2和Δt的交互效应、主效应曲线进行分析,并通过相关性图和Pareto图得出模型中设计因子与目标的相关性及设计因子对目标的贡献程度。在分析设计因子的主效应前应明确其交互效应,否则有可能导致主效应被歪曲或掩盖。
图 7为t2和Δt的交互效应曲线。图中,设计因子t2和Δt的高低水平为:低水平为0~4 s,高水平为6~10 s。可以看到,设计因子t2和Δt对Hmax和lnRmax的交互效应曲线均基本保持平行状态,表明两者的交互效应较弱,对主效应的影响较小。

|
| 图 7 t2和Δt的交互效应曲线 Fig.7 The interaction curves of the t2 and Δt |
设计因子的主效应曲线是基于不同水平下各目标响应的平均值来绘制的,反映了设计因子对目标的影响能力。若在不同水平下响应有较大差别,即曲线变化较大,说明设计因子对目标的影响显著。图 8为t2和Δt的主效应曲线。从图中看出:对于Hmax,设计因子t2的主效应曲线要比Δt的更陡峭,说明其影响相对更为显著;而对于lnRmax,在低水平时t2和Δt的主效应曲线较为接近,均产生了较大影响,在中高水平下呈现一定差别, t2的主效应曲线在中等水平时就出现反转,而Δt的主效应曲线在高水平时才开始呈现反转趋势。

|
| 图 8 t2和Δt的主效应曲线 Fig.8 The main effect curve of the t2 and Δt |
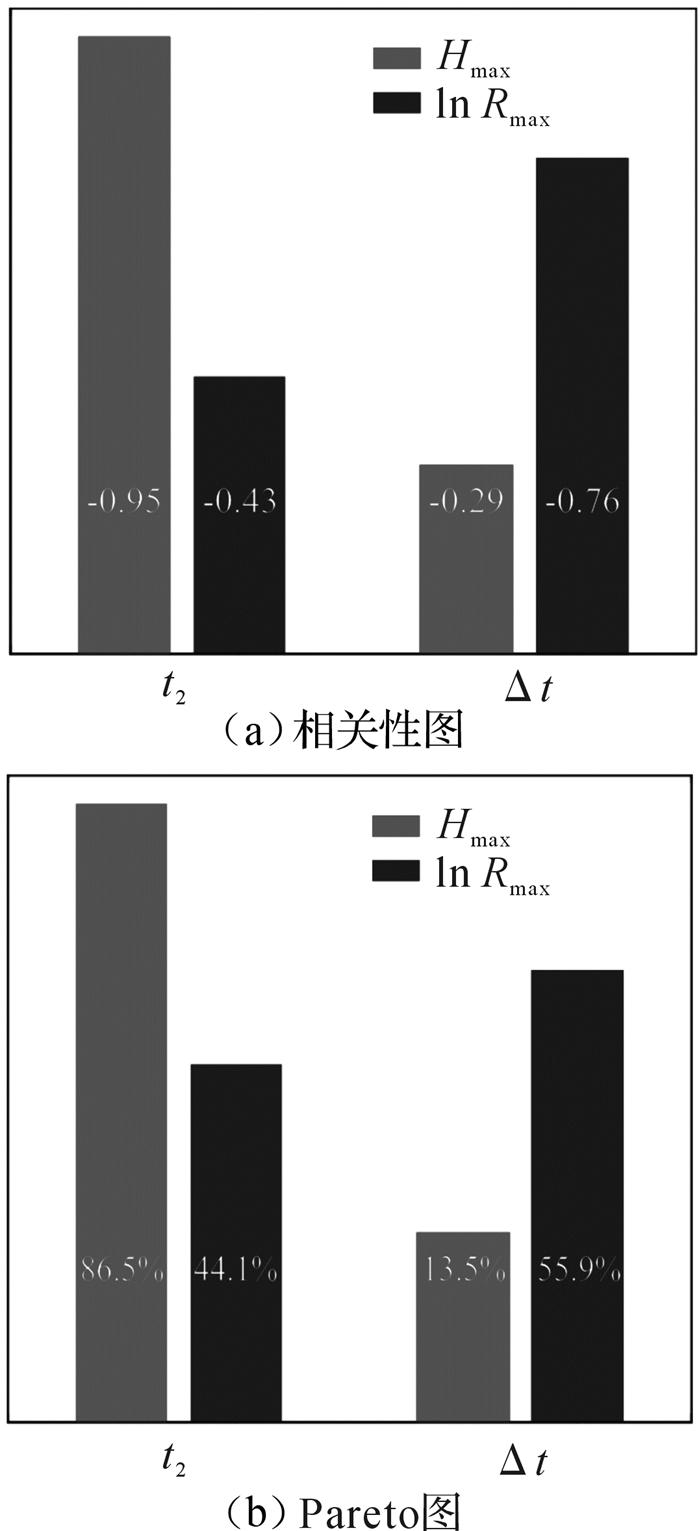
图 9分别为t2和Δt的相关性图和Pareto图。相关性表示的是设计因子与设计目标的线性相关关系,其绝对值越接近1,表明相关程度越强;Pareto图则反映了各设计因子对设计目标的贡献程度百分比。从图 9可以看到,t2与Hmax的相关性和t2对Hmax的贡献程度都非常高,均明显高于Δt,说明Hmax主要与t2相关,并由t2决定其值;对于lnRmax,Δt的相关性和贡献程度相对更高,且相关性明显高于t2,但贡献程度与t2无明显的差距,说明lnRmax由t2和Δt共同决定,Δt影响稍大。
|
| 图 9 t2和Δt的相关性图和Pareto图 Fig.9 The correlation and Pareto graphs of t2 and Δt |
1) 将无人潜航器的运动过程和浮囊充气过程相结合,建立了潜航器停车后运动模型,分析结果与文献[5]相吻合,表明该运动模型的正确性。
2) 对模型进行DOE分析,获得了无人潜航器运行的最大深度和浮囊最大阻力的散点图;对设计因子t2和Δt的交互效应及与主效应进行分析,得到了设计因子t2和Δt的相关性图和Pareto图。
3) 分析结果表明:Hmax主要与t2相关,并由t2决定其值;lnRmax由t2和Δt共同决定,且Δt的影响稍大。在工程设计中,可以先通过调整t2来明确Hmax的设计值,然后通过Δt确定lnRmax的设计值。
| [1] |
何希盈, 蔡祥, 韩晓晨.
无人潜航器水下战场信息感知[J]. 水雷战与舰船防护, 2015, 23(4): 45–47.
HE Xi-ying, CAI Xiang, HAN Xiao-chen. Underwater battlefield information awareness by UUV[J]. Mine Warfare & Ship Self-defence, 2015, 23(4): 45–47. |
| [2] |
何萍, 阳明.
国外海军无人潜航器发展应用与趋势[J]. 论证与研究, 2011, 12(6): 43–46.
HE Ping, YANG Ming. Development, application and prospects of naval UUVs in oversea countries[J]. Demonstration and Research, 2011, 12(6): 43–46. |
| [3] |
张宇文.
鱼雷总体设计原理与方法[M]. 西安: 西北工业大学出版社, 1998: 10-21.
ZHANG Yu-wen. The collectivity design principle and method of torpedo[M]. Xi'an: Northwestern Polytechnical University Press, 1998: 10-21. |
| [4] |
尹韶平, 杨芸.
鱼雷总体技术的发展与展望[J]. 鱼雷技术, 2005, 13(3): 1–5.
YIN Shao-ping, YANG Yun. A summary of development in torpedo overal design technologies[J]. Torpedo Technology, 2005, 13(3): 1–5. |
| [5] |
吕汝信.
鱼雷上浮装置研究[J]. 鱼雷技术, 2000, 8(2): 8–11.
LÜ Ru-xin. Study of floating device of the training topedo[J]. Torpedo Technology, 2000, 8(2): 8–11. |
| [6] |
吕汝信. 负浮力操雷上浮技术研究[D]. 西安: 西北工业大学航海学院, 2005: 31-39.
LÜ Ru-xin. Study of floating technology of negative buoyant training torpedo[D]. Xi'an: Northwest Polytechnical University, School of Marine Science and Technology, 2005: 31-39. |
| [7] |
程文鑫, 蔡卫军, 杨春武, 等.
鱼雷浮囊充气过程建模与仿真[J]. 鱼雷技术, 2014, 22(2): 87–90.
CHENG Wen-xin, CAI Wei-jun, YANG Chun-wu, et al. Modeling and simulation of inflation process for torpedo inflatable collar[J]. Torpedo Technology, 2014, 22(2): 87–90. |
| [8] |
叶慧娟, 王昕晔, 张宁.
环形气囊水下展开过程仿真分析[J]. 鱼雷技术, 2015, 23(3): 166–171.
YE Hui-juan, WANG Xin-ye, ZHANG Ning. Simulation on underwater inflation process of annular bladder[J]. Torpedo Technology, 2015, 23(3): 166–171. |
| [9] |
王栋, 金先龙, 曹源, 等.
波浪作用下浮囊式操雷海面漂浮数值模拟[J]. 系统仿真学报, 2013, 25(5): 894–898.
WANG Dong, JIN Xian-long, CAO Yuan, et al. Numerical simulation of floating airbag-type experimental torpedo under wave[J]. Journal of System Simulation, 2013, 25(5): 894–898. |
| [10] |
赖宇阳.
Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012: 51-68.
LAI Yu-yang. The theory and example analysis of Isight parameter optimization[M]. Beijing: Beihang University Press, 2012: 51-68. |



