由于工程车辆自重和载重量较大,当它发生翻车事故时,巨大的冲击载荷会严重破坏驾驶室的结构,入侵驾驶人员的生存空间[1]。翻车保护结构(roll-over protective structure, ROPS)能在翻车事故中为驾驶人员提供有效的保护。目前国际标准中仅给出了ROPS性能试验标准,尚无相关的设计标准。ROPS设计属于弹塑性大变形设计,其性能试验是破坏性试验。由于大变形理论的复杂性和破坏性试验的经济条件制约,目前国内外的ROPS设计仍依赖于传统经验[2-3]。
本文以载重量为220 t的重型矿用自卸车ROPS为研究对象,运用HyperWorks软件和LS-DYNA软件对ROPS进行多工况拓扑优化设计和有限元分析,以提高ROPS的整体刚度和侧向能量吸收效果[4]。基于Optistruct优化模块中的变密度法,以单元密度为设计变量,结构各部件位移及整体体积分数为约束条件,各工况加权应变能最小为优化目标,通过优化得到了ROPS的最优材料分布,综合考虑制造工艺后确定设计方案[5-7]。同时,通过动态加载分析来验证设计方案符合国际标准要求,并对优化后的ROPS性能与原性能进行对比分析,以期为工程车辆ROPS的设计提供重要参考。
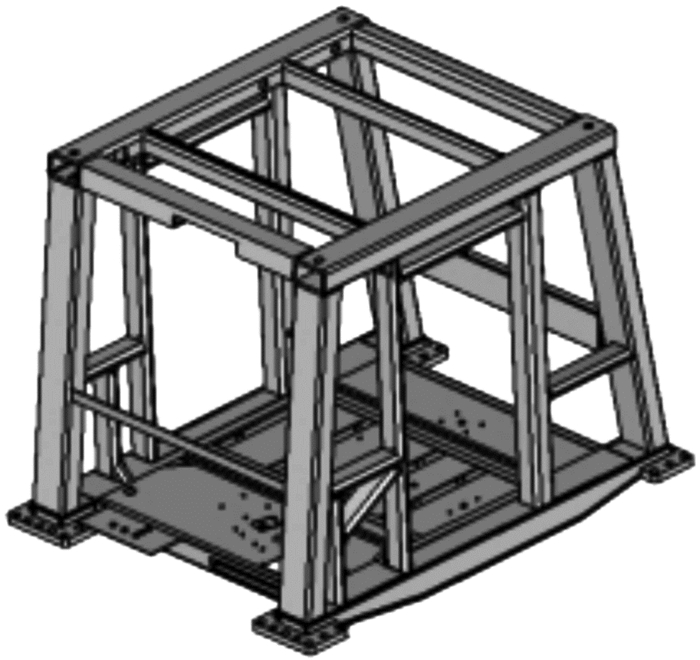
1 ROPS有限元分析与实验验证 1.1 ROPS有限元模型建立220 t重型矿用自卸车的ROPS(质量为2 279.3 kg)为四立柱框架式结构,主要由型钢和少量板材焊接而成,所用材料为Q345,其几何模型如图 1所示。
|
| 图 1 ROPS几何模型 Fig.1 ROPS geometric model |
利用HyperWorks软件中的前处理模块HyperMesh对ROPS的几何模型进行中面抽取和几何清理,选择合适的单元尺寸对ROPS进行网格划分。同时按国际标准设置载荷分配器(load distribution device, LDD)和挠曲极限量(deflection-limiting volume, DLV)。LDD是为避免ROPS因作用点载荷过大而发生局部穿入的装置[5]; DLV用以规定与司机生存空间有关的容许挠曲的极限容量。根据国际标准进行ROPS加载试验时,需要将ROPS安装在车架上,但根据作者对300 t矿用自卸车ROPS研究表明,车架刚度很大,但对ROPS加载实验的影响很小[6],所以将车架简化为4个刚性底座。最终得到ROPS有限元模型如图 2所示。该模型的节点为71 345个,单元为69 314个。

|
| 图 2 ROPS有限元模型 Fig.2 ROPS finite element model |
根据ISO3471—2008的要求,ROPS的加载实验有4项:最小侧向承载能力、最小能量吸收能力、最小垂向承载能力和最小纵向承载能力的实验[8]。自卸车质量为145 t,根据国际标准规定,ROPS性能要求如表 1所示。
| 参数 | 侧向承载能力/kN | 侧向能量吸收能力/kJ | 垂向承载能力/kN | 纵向承载能力/kN |
| 数值 | 870 | 172.55 | 2 843.4 | 696 |
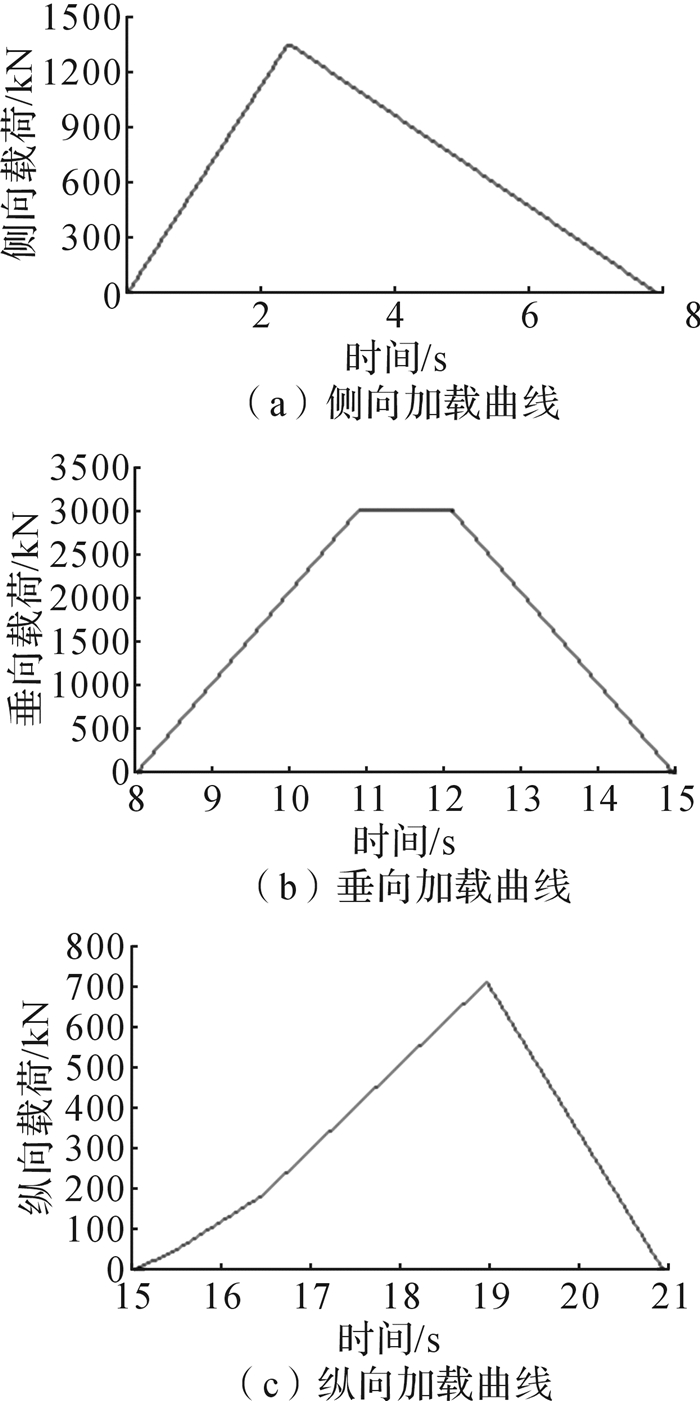
根据性能要求设计3个方向的加载曲线, 如图 3所示。侧向加载时,在达到侧向载荷要求后还需要继续加载至能量吸收满足要求。
|
| 图 3 ROPS动态仿真加载曲线 Fig.3 ROPS dynamic simulation loading curve |
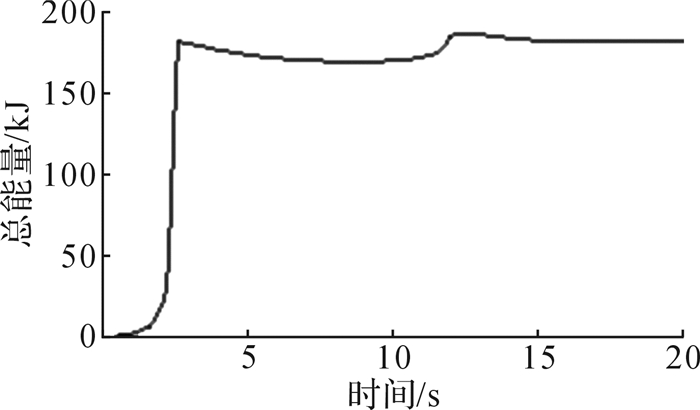
经过LS-DYNA计算求解,得到侧向加载工况下的总能量与时间的关系,如图 4所示。从图中可以发现,能量吸收达到175.1 kJ后满足侧向能量吸收要求。
|
| 图 4 侧向加载工况下ROPS的总能量—时间曲线 Fig.4 Total energy—time curve of ROPS under lateral loading condition |
加载过程中ROPS内侧与DLV距离最近时刻的位置如图 5所示[9]。在3个工况下, ROPS内侧均未入侵DLV,表明ROPS的承载能力符合国际标准要求。

|
| 图 5 ROPS内侧与DLV距离最近时刻的位置 Fig.5 The position at the moment of the inside of ROPS approaching DLV closest |
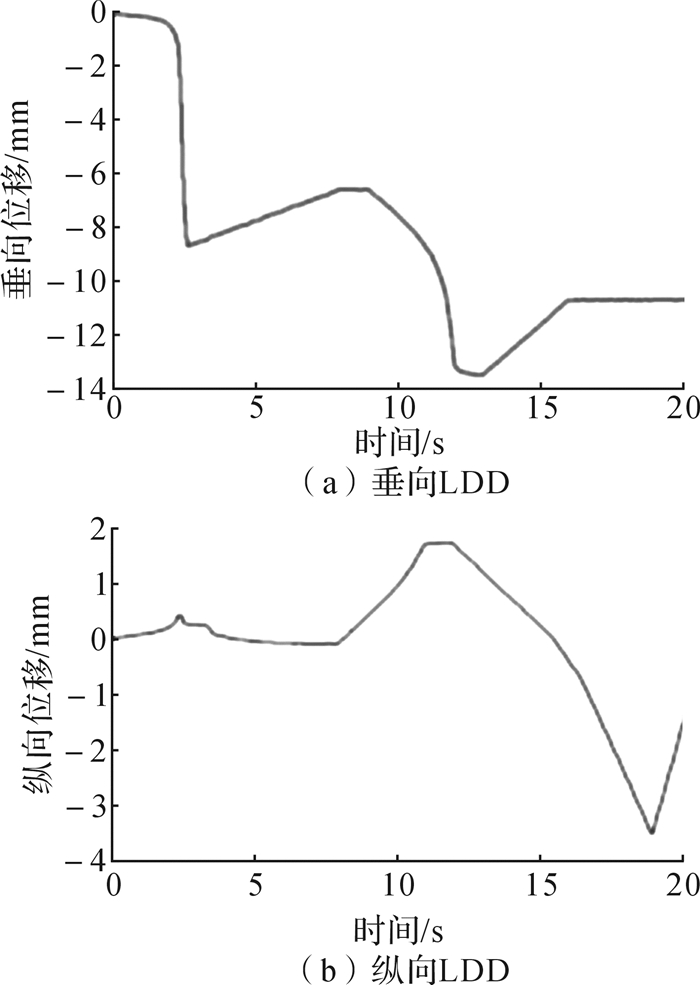
加载过程中,垂向LDD中心点的垂向位移—时间曲线和纵向LDD中心点的纵向位移—时间曲线如图 6所示。从图中可以发现,垂向LDD中心点的最大垂向位移为13.6 mm,纵向LDD中心点的最大纵向位移为3.5 mm。
|
| 图 6 LDD中心点位移—时间曲线 Fig.6 Displacement—time curve of LDD center point |
按照ISO 3471—2008要求对ROPS进行侧向加载实验。将ROPS固定在试验台上,利用侧向加载油缸对LDD施加侧向载荷,通过传感器输出数据,满足能量吸收要求后停止加载。实验前后ROPS的变形情况如图 7所示。

|
| 图 7 侧向加载实验前后ROPS的变形情况 Fig.7 Deformation of ROPS before and after lateral loading experiment |
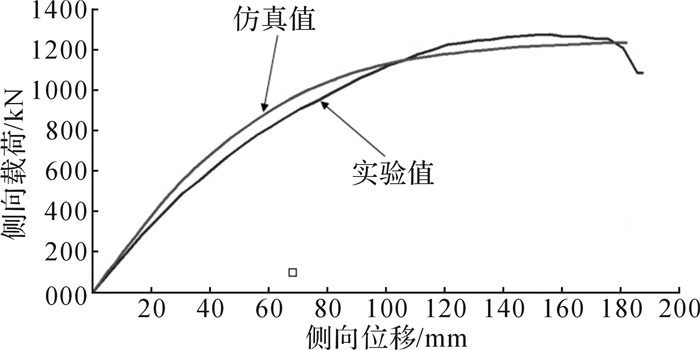
从图 7可以看出,侧向加载试验过程中ROPS任何构件均未入侵DLV。侧向加载过程中侧向位移与侧向载荷曲线的仿真结果与实验结果对比如图 8所示。为了提高计算速度,在有限元建模时省略了车架,并且采用了质量缩放,使得仿真结果与实验结果存在一定的误差,但是曲线变化趋势基本吻合,证明有限元仿真的结果是正确的。
|
| 图 8 侧向位移—侧向载荷曲线的仿真结果与实验结果对比 Fig.8 Comparison between simulated results and experimental results of lateral displacement—lateral load curve |
本文以载重量为220 t的电动轮矿用自卸车ROPS为对象,预留出前挡风玻璃、两侧车门以及驾驶员乘坐的空间,并设计了LDD和DLV,采用六面体单元来构建ROPS拓朴优化初始模型,得到58 691个单元、296 354个节点,如图 9所示。

|
| 图 9 ROPS拓扑优化初始模型 Fig.9 ROPS topology optimization initial model |
拓扑优化通过预先设定设计域和非设计域来控制优化区域[10],由于本文是采用结构拓扑优化方法得到整体ROPS的,故将LDD,DLV和车架底座设置为非设计区域,其余部分均为设计区域[11]。
2.2 载荷、约束条件和优化目标根据ROPS性能要求,在OptiStruct模块中分别设置侧向、垂向和纵向三个工况的载荷步[12]。把车架底座设置为刚体材料,并在底座节点施加全约束。
ROPS作为主要受力部件,需要满足多工况下的力学性能要求。为得到结构的最佳力学性能,本文以ROPS整体结构的多工况组合应变能最小化为优化目标。
为保证ROPS满足最小承载能力要求,在初始模型的侧面和顶面设置位移约束[13],使ROPS在加载过程中不会入侵DLV。为了保证结构轻量化,给设计区域施加最大体积分数约束,为20%[14]。在工程实际中,当某些零部件尺寸过小时,会给加工制造带来不便,且在优化过程中容易出现数值计算不稳定而导致的优化结果出现棋盘格的现象,因此需要加入最小成员尺寸约束,既可以避免零部件尺寸过小带来的不便又可以解决棋盘格问题[15]。此外还加入了对称性约束。
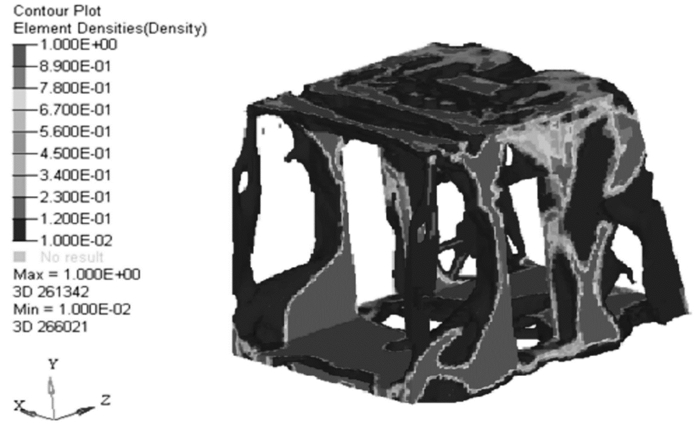
2.3 拓扑优化结果经过80步迭代得到符合约束条件且各工况组合应变能最小的ROPS,其拓扑优化密度云图如图 10所示。此时Current Value为0.08,因此只显示单元密度不小于0.08的单元[16]。
|
| 图 10 ROPS拓扑优化密度云图 Fig.10 ROPS topology optimization density nephogram |
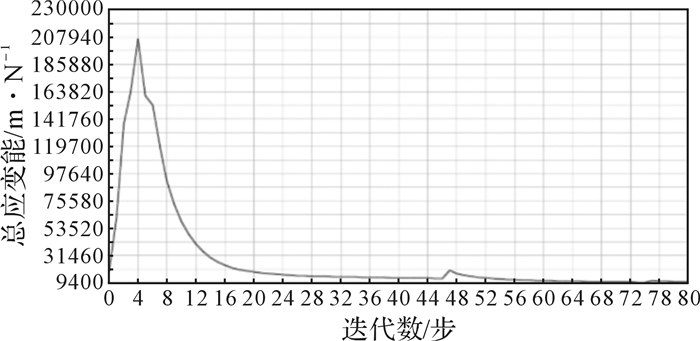
拓扑优化过程中目标函数的迭代曲线如图 11。目标函数的迭代曲线呈下降趋势,且最终趋于稳定,验证了ROPS拓扑优化模型的正确性[17]。
|
| 图 11 拓扑优化过程中目标函数迭代曲线 Fig.11 Iterative curve of objective function in the process of topology optimization |
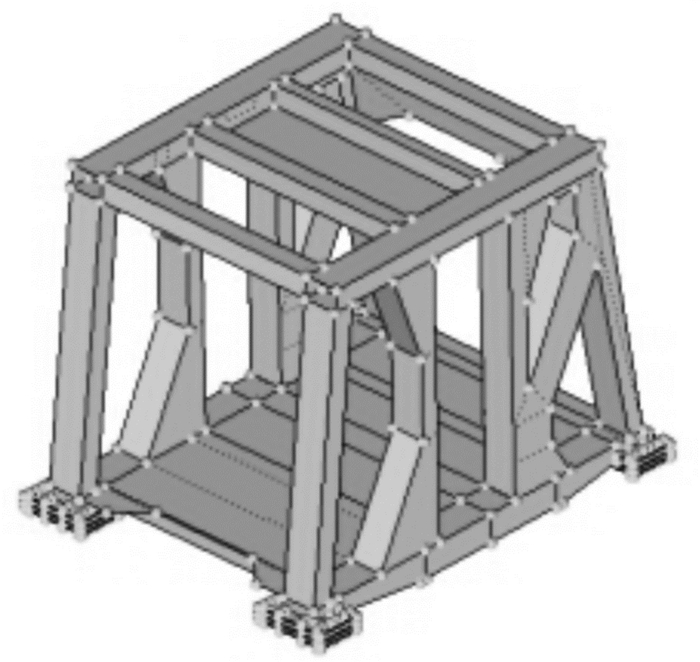
拓扑优化模型只是一个初步的拓扑形态,不能满足实际生产要求,还应结合工程实际对ROPS进行优化设计[18],优化后ROPS的质量为1 729.7 kg。优化设计后的ROPS模型如图 12所示。
|
| 图 12 拓扑优化设计后的ROPS模型 Fig.12 ROPS model after topology optimization design |
建立拓扑优化设计后ROPS的有限元模型,如图 13所示。根据国际标准规定进行3个方向的加载分析。侧向加载时由于要满足能量吸收要求,最大侧向载荷需调整至1 231 kN。

|
| 图 13 拓扑优化设计后的ROPS有限元模型 Fig.13 ROPS finite element model after topology optimization design |
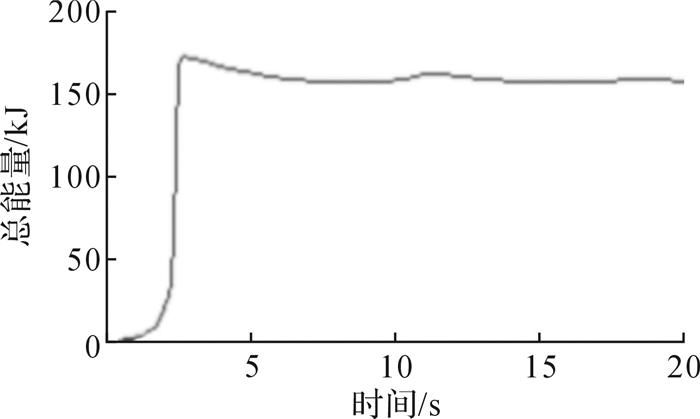
通过LS-DYNA求解运算,得到侧向加载工况下的总能量与时间的关系曲线如图 14所示。总能量达到175 kJ后满足国际标准规定的能量吸收要求。
|
| 图 14 侧向加载工况下优化后ROPS的总能量—时间曲线 Fig.14 Total energy—time curve of optimized ROPS under lateral loading condition |
在加载过程中,优化后的ROPS内侧与DLV距离最近时刻的位置如图 15所示,侧向加载过程中的最小距离为33.1 mm,垂向加载过程中的最小距离为65.8 mm。在加载过程中ROPS没有入侵DLV,符合国际标准的规定。

|
| 图 15 优化后ROPS与DLV距离最近时刻的位置 Fig.15 The position at the moment of the inside of optimized ROPS approaching DLV closest |
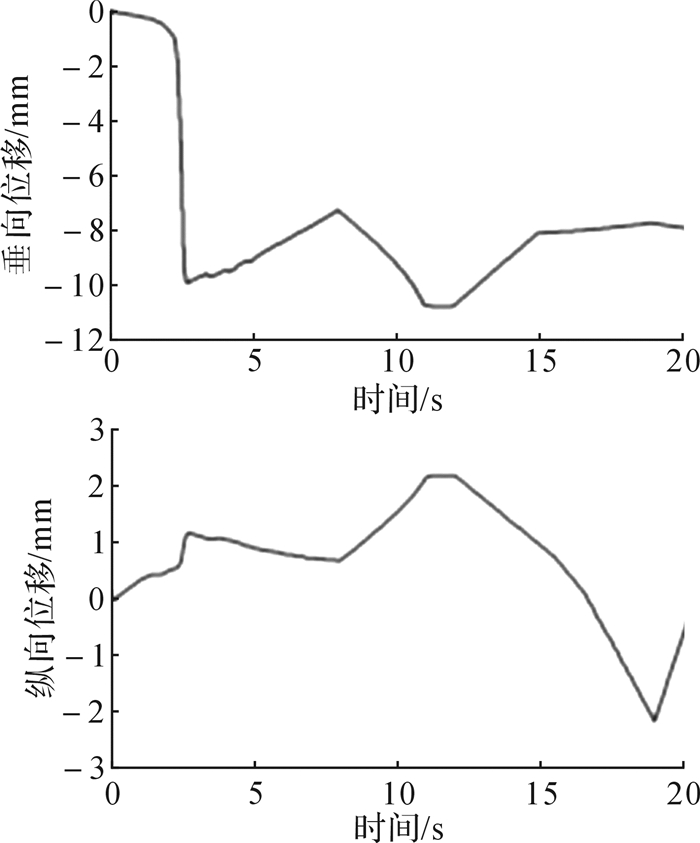
加载过程中,优化后ROPS垂向LDD中心点的垂向位移—时间曲线和纵向LDD中心点的纵向位移—时间曲线如图 16所示。垂向LDD中心点的最大垂向位移为10.7 mm,纵向LDD中心点的最大纵向位移为2.3 mm。
|
| 图 16 优化后ROPS的LDD中心点位移—时间曲线 Fig.16 Displacement—time curve of LDD center point for optimized ROPS |
1) 原ROPS质量为2 279.3 kg,拓扑优化设计后的ROPS质量为1 729.7 kg,减重24.1%,取得了较好的轻量化效果。
2) ROPS侧向吸能效果的评判指标是:达到能量吸收要求的最大侧向力与最小侧向承载能力之差的大小。原ROPS满足能量吸收需要的载荷为1 324.5 kN,拓扑优化设计后的ROPS所需载荷为1 231 kN,小于原ROPS,在满足侧向承载能力的前提下,提高了7.1%的能量吸收效果,有效减轻了侧向载荷对ROPS内部的冲击。
3) 加载过程中LDD中心点的最大位移可以衡量结构的垂向刚度和纵向刚度。拓扑优化设计的ROPS相较于原ROPS,在加载过程中,垂向位移减小21.3%,纵向位移减小34.4%,证明垂向刚度和纵向刚度均有明显提升。
4 结论本文以220吨重型矿用自卸车ROPS为研究对象,以多工况组合应变能最小为优化目标,对ROPS进行了多工况拓扑优化设计。通过与原ROPS的安全性能进行对比后发现,新的ROPS减重24.1%,侧向吸能效果提高7.1%,垂向LDD中心点垂向位移减小21.3%,纵向LDD中心点纵向位移减小34.4%,材料分布更加合理,安全性能更好。
| [1] |
唐华平, 来佳峰, 姜永正, 等.
大型自卸车翻车保护结构有限元分析[J]. 中南大学学报(自然科学版), 2013, 44(12): 4847–4854.
TANG Hua-ping, LAI Jia-feng, JIANG Yong-zheng, et al. Finite element analysis on roll-over protective structure of large dump truck[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 4847–4854. |
| [2] |
马守业.
矿山车辆驾驶室翻车保护结构安全要求与计算机仿真[J]. 煤矿安全, 2017, 48(2): 120–123.
MA Shou-ye. Safety requirements of roll-over-protective structure for mine vehicle cab and computer simulation[J]. Safety in Coal Mines, 2017, 48(2): 120–123. |
| [3] | AGIUS D, KOUROUSIS K, TAKLA M, et al. Enhanced nonlinear material modelling for the analysis and qualification of rollover protective structures[J]. Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering, 2016, 230(11): 1558–1568. DOI:10.1177/0954407015618851 |
| [4] | DUMITRACHE P, GOANTA A M. Validation by numerical simulation of the behaviour of protective structures of machinery cabins subjected to standardized shocks[J]. IOP Conference Series:Materials Science and Engineering, 2017, 227(1): 012041. |
| [5] |
彭骥, 谭峰, 卫亚斌, 等.
快堆装载机支臂结构的动静态性能拓扑优化设计方法[J]. 工程科学与技术, 2017, 49(S2): 251–256.
PENG Ji, TAN Feng, WEI Ya-bin, et al. Dynamic-static topology optimization design method of fast reactor loader arm[J]. Advanced Engineering Sciences, 2017, 49(S2): 251–256. |
| [6] |
许洪斌, 陈亚洁, 刘妤, 等.
微耕机操纵装置动态特性分析及结构拓扑优化[J]. 机械设计, 2017, 34(4): 80–85.
XU Hong-bin, CHEN Ya-jie, LIU Yu, et al. Dynamic characteristics analysis and topology optimization of tiller manipulator[J]. Journal of Machine Design, 2017, 34(4): 80–85. |
| [7] | MARIANO V, OSVALDO M, PASCUAL M. Topology design for multiple loading conditions of continuum structures using isolines and isosurfaces[J]. Finite Elements in Analysis & Design, 2010, 46(3): 229–237. |
| [8] |
方传青, 宋立霞.
某新型矿用自卸车ROPS和FOPS的有限元分析[J]. 矿山机械, 2017, 45(9): 18–23.
FANG Chuan-qing, SONG Li-xia. FEA on ROPS & FOPS of a new-type mining dump truck[J]. Mining & Processing Equipment, 2017, 45(9): 18–23. |
| [9] |
王子源, 李学飞, 马铸, 等.
大型装载机翻车保护结构的有限元分析及试验研究[J]. 矿山机械, 2011, 39(8): 39–43.
WANG Zi-yuan, LI Xue-fei, MA Zhu, et al. FEA and experimental study on ROPS for large loaders[J]. Mining & Processing Equipment, 2011, 39(8): 39–43. |
| [10] | LIU Bao-shou, HUANG Xiao-dong, SUN Guang-yong, et al. Topological design of structures under dynamic periodic loads[J]. Engineering Structures, 2017, 142: 128–136. DOI:10.1016/j.engstruct.2017.03.067 |
| [11] | NANTHAKUMAR S S, ZHUANG Xiao-ying, HAROLD S, et al. Topology optimization of flexoelectric structures[J]. Journal of the Mechanics and Physics of Solids, 2017, 105: 217–234. DOI:10.1016/j.jmps.2017.05.010 |
| [12] |
于凌涛, 杨景, 王岚, 等.
基于灵巧度的手术机械臂尺寸与拓扑结构优化[J]. 哈尔滨工程大学学报, 2017, 38(12): 1–7.
YU Ling-tao, YANG Jing, WANG Lan, et al. Dexterity-based optimization of dimension and structure for a surgical robot[J]. Journal of Harbin Engineering University, 2017, 38(12): 1–7. |
| [13] |
张庆, 张斌, 李洪彪, 等.
分动器箱体结构拓扑优化设计[J]. 机械传动, 2016, 40(6): 115–118.
ZHANG Qing, ZHANG Bin, LI Hong-biao, et al. Topology optimization design of transfer case housing[J]. Journal of Mechanical Transmission, 2016, 40(6): 115–118. |
| [14] | WANG Hao, YU Wei-dong, CHEN Gen-liang. An approach of topology optimization of multi-rigid-body mechanism[J]. Computer-Aided Design, 2016, 84: 39–55. |
| [15] | WEI Zhan-guo, CHENG Xu-feng, LIU Jin-hao. A finite element model of roll-over protective structures for wheel loader frame[J]. Applied Mechanics and Materials, 2012, 138/139: 737–742. |
| [16] | SEONGYEOL G, SEMYUNG W, JAEYUB H, et al. Topology optimization of thin plate structures with bending stress constraints[J]. Computers and Structures, 2016, 175(C): 134–143. |
| [17] | ZHAO Xuan, ZHANG Wen-ming, YANG Jue. Simulation of roll-over protective structure and falling object protective structure tests on heavy-duty mining dump truck[J]. Applied Mechanics and Materials, 2014, 529: 188–192. DOI:10.4028/www.scientific.net/AMM.529 |
| [18] | ZHANG En-guang, WANG Li, SHAN Wen-ju. Finite element analysis and topology optimization design for motional board of injection molding machine[J]. Applied Mechanics and Materials, 2014, 607: 573–576. DOI:10.4028/www.scientific.net/AMM.607 |



