自无砟轨道技术发展以来,多种无砟轨道施工机械已经研制成功并投入了实际应用[1-3]。我国自主研制的无轨伸缩式门式起重机(以下简称“门机”),主要用于吊装轨枕、轨排等构件。该门机可实现变高、变跨、倾斜起吊,是一种适用性强、效率高的无砟轨道吊装设备。图 1为其结构简图,主体结构由车架、起升机构、液压缸、横梁、行走轮组、转向架、垂直伸缩支腿和水平伸缩支腿等组成。其工作原理为:当门机移动至施工地点后,水平液压缸伸出打开水平支腿,行走轮组根据隧道地面弧度摆动至合适的角度后支撑在隧道上,垂直支腿通过液压缸伸出,门机便可开始工作。

|
| 图 1 无轨伸缩式门式起重机结构简图 Fig.1 The trackless telescopic gantry crane structure diagram |
目前,国内对无轨伸缩式门机结构设计大多采用以经典力学和数学为基础的经验设计法,为保证设备安全性,安全系数通常取值较大,导致结构设计存在较大的冗余,使整机偏重,因此对门机进行轻量化设计具有实际意义。
1 门机整机优化模型的建立以某公司研发的变跨度无轨伸缩式门机为例,其额定起升载荷Q=1.2×105 N,小车自重GXC=3×104 N。
根据设计要求,无轨伸缩式门机的计算工况有以下2种:
工况1:小车满载作用于车架上,按静轮压计算门机静刚度,不计结构自重及动载系数。此时小车轮压p1为:
| $ {p_1} = \frac{{{G_{{\text{XC}}}} + Q}}{4} = 37\;500\;{\text{N}} $ |
工况2:小车满载作用于车架上,计算结构强度,考虑结构自重pG,起升冲击系数φ1=1.1,根据起升状态级别及起升速度计算得到起升动载系数φ2=1.117,通过在运行方向设置加速度(取a=0.12 m/s2),由程序自动施加水平惯性力pH[4]。此时小车轮压p2为:
| $ {p_2} = \frac{{{\varphi _1}{G_{{\text{XC}}}} + {\varphi _2}Q}}{4} = 41\;760\;{\text{N}} $ |
由于门机支腿变跨机构的高度和宽度是根据使用工况要求事先确定的,不能作相应的调整,故选择水平支腿、垂直支腿、横梁、转向架等主要结构件的截面尺寸及各板厚作为设计变量,如表 1所示。
| mm | ||
| 设计变量 | 变量含义 | 取值范围 |
| L1 | 垂直支腿截面高度 | 240~260 |
| B1 | 垂直支腿截面宽度 | 320~390 |
| H1 | 水平支腿截面高度 | 320~390 |
| T1 | 支腿板厚 | 6~14 |
| T2 | 水平支腿上下滑板厚度 | 16~30 |
| T3 | 垂直支腿前后滑板厚度 | 12~18 |
| T4 | 垂直支腿左右滑板厚度 | 14~24 |
| T5 | 横梁板厚 | 5~10 |
| T6 | 水平支腿上下接触面板厚 | 6~14 |
| T7 | 水平支腿左右接触面板厚 | 6~14 |
| T8 | 车架上下支撑板厚 | 6~10 |
| T9 | 车架左右支撑板厚 | 6~14 |
| T10 | 车架加强筋板厚 | 6~14 |
| T11 | 转向架板厚 | 6~14 |
| T12 | 横梁法兰板厚 | 50~70 |
| T13 | 车架腹板厚 | 6~14 |
| T14 | 车架中心板厚 | 6~14 |
以无轨伸缩式门机的结构刚度及强度为约束条件,门机结构自重最轻为优化目标,建立的数学模型为:
| $ \begin{array}{l} {\rm{min}}\;f(x) = {\rm{T\_MASS}}\\ {\rm{s}}{\rm{.t}}\\ \;\;\;\;\;{\rm{DG}} - \left[ f \right] \le 0\\ \;\;\;\;\;{\rm{SG}} - [\sigma ] \le 0\\ \;\;\;\;\;{x_{\rm{l}}} \le {x_i} \le {x_{\rm{u}}} \end{array} $ |
式中:T_MASS为门机结构自重; DG为门机在工况1时的垂直静挠度; [f]为门机许用静位移,取[f]=B/800=3.775 mm,B为门机主梁跨度,B=3 020 mm; SG为门机在工况2时的等效应力;[σ]为材料许用应力,门机材料为Q345钢,取安全系数n=1.34,则[σ]=345/1.34=257 MPa[5]; xu, xl为设计变量上、下限,具体取值见表 1。
1.3 门机有限元模型利用ANSYS中的APDL语言定义无轨伸缩式门机各参数,采用Solid45单元模拟接触对滑块(板),Shell63模拟其余板结构,Beam188模拟伸缩液压缸,通过约束X, Y, Z三个方向的平动自由度来模拟液压缸铰接处的铰接,其有限元模型如图 2所示。整个系统离散成121 652个单元,其中68 882个为壳单元,52 768个为实体单元,2个为质量单元。所用材料Q345钢的弹性模量E=2.1×1011 N/m2,泊松比μ=0.3,材料密度ρ=7 850 kg/m3。

|
| 图 2 无轨伸缩式门式起重机有限元模型 Fig.2 The finite element model of trackless telescopic gantry crane |
该门机垂直支腿内外套之间、水平支腿与车架之间通过滑块(板)连接,这属于典型的非线性接触问题。由于非线性接触分析计算量大且存在计算不收敛的可能,工程上常采用节点耦合模型代替接触模型以提高计算效率[6-7]。为了保证计算精度,在ANSYS中分别建立门机接触模型和节点耦合模型,计算2种模型在上述2种工况下的相对误差。结果表明:在工况1下2种模型垂直方向挠度相对误差为5.4%,在工况2下2种模型最大等效应力相对误差为1.3%,结果差异不大,说明节点耦合模型能较好地模拟接触模型,因此采用节点耦合模型来代替接触模型进行优化计算。
2 门机轻量化设计Isight是集试验设计、近似建模、质量设计于一体的优化软件[8],被广泛应用于飞机、汽车等复杂产品的优化设计[9-10]。通过Isight软件集成和复杂的仿真流程,可以简化优化流程,从而提高计算效率。
图 3为无轨伸缩式门机轻量化设计流程图。通过在ANSYS中建立门机APDL参数化模型,并将模型集成至Isight软件中,通过最优拉丁超立方设计方法生成设计变量初始样本点,通过试验设计(design of experiment, DOE)灵敏度分析选出对结构强度、刚度与质量影响较大的设计变量,再构建响应面近似模型,当近似模型精度满足优化要求后,对近似模型进行优化计算。

|
| 图 3 无轨伸缩式门式起重机轻量化设计流程图 Fig.3 The flow chart of lightweight design for trackless telescopic gantry crane |
试验设计(DOE)是当今产品开发、优化设计中的重要统计方法之一,主要用于辨识关键参数、构建经验公式以及近似模型等。最优拉丁超立方设计方法比传统的试验设计方法具有更高的空间填充性与均匀性,只需较少的样本点就可达到较高的试验拟合精度,是一种效率高、均衡性好的设计方法。
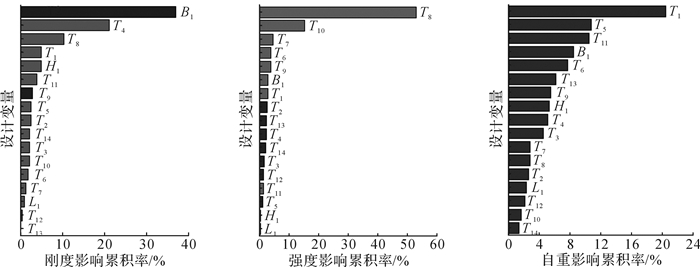
由于设计变量较多,为了减少次要变量个数从而提高计算效率,采用最优拉丁超立方设计方法产生样本数据点,通过Isight中DOE方法筛选出对结构响应灵敏度较高的设计变量。图 4所示为DOE计算结果。
|
| 图 4 设计变量对门机刚度、强度、自重影响的Pareto图 Fig.4 Pareto diagram of the influence of design variables on the gantry crane stiffness, strength, weight |
根据图 4计算结果可知,B1, T4, T8, T1, H1对结构刚度影响较大,T8, T10对强度影响较大,T1, T5, T11, B1, T6对质量影响较大。综合考虑,选取B1, H1, T1, T4, T5, T6, T8, T10, T11这9个参数作为响应面近似模型的设计变量。
2.2 响应面近似模型的构建响应面近似建模方法是通过数学模型构建多项式函数来拟合复杂的响应关系,不仅可以得到响应目标与设计变量之间的关系,还可以使设计变量以最优的组合来逼近目标函数[11],这给优化设计带来了极大的方便。
对于工程问题,一般选择二阶多项式拟合函数即可满足计算精度要求[12],其表达式为:
| $ y\left( x \right) = {\beta _0} + \sum\limits_{c = 1}^m {{\beta _c}{x_c}} + \sum\limits_{c = 1}^m {{\beta _{cc}}x_c^2} + \sum\limits_{c = 1}^m {\sum\limits_{d = c + 1}^m {{\beta _{cd}}{x_c}{x_d}} } $ | (1) |
式中:y(x)为拟合函数;xc(c=1, 2, …, m)为输入变量,m为输入变量个数;β0, βc, βcc, βcd为多项式待定系数。
式(1)可以通过多元线性回归处理,即:
| $ \begin{array}{*{20}{c}} {y\left( x \right) = {\beta _0} + {\beta _1}{x_1} + \cdots + {\beta _p}{x_p} + \varepsilon }\\ {p = 2m + \frac{{m\left( {m - 1} \right)}}{2}} \end{array} $ |
一般设ε~N(0, δ2),再利用t(t≥p+1)个样本点求出βc(c=0, 1, …,p),当设计矩阵的秩大于等于p+1时,XTX为非奇异矩阵。根据式(2)、式(3)求出β,从而得出拟合二阶多项式响应面的拟合函数。
| $ \beta = {({\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}})^{ - 1}}({\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}}) $ | (2) |
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&{{x_1},1}&{{x_1},2}& \cdots &{{x_1},p}\\ 1&{{x_2},1}&{{x_2},2}& \cdots &{{x_2},p}\\ \cdots & \cdots & \cdots &{}& \cdots \\ 1&{{x_t},1}&{{x_t},2}& \cdots &{{x_t},p} \end{array}} \right],\mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}}\\ \cdots \\ {{y_t}} \end{array}} \right] $ | (3) |
在构建近似模型时,将DOE方法筛选出的9个设计变量作为输入参数,以DG,SG和T_MASS为输出响应。一般在设计空间内样本点个数越多,计算结果越准确,为了保证近似模型可信度,选择试验样本点为250个,从中随机抽取10个样本点用作误差分析,由程序计算得出近似模型的R2误差、均方根误差、平均误差及最大误差,如表 2所示。对比发现,各项误差均在程序允许范围之内,说明近似模型具有较高的可信度,可以用来代替仿真程序进行优化计算。
| 输出项 | R2误差[0.9 1) | 均方根值(0 0.2] | 平均误差(0 0.2] | 最大误差(0 0.3] |
| DG | 0.969 29 | 0.051 95 | 0.036 46 | 0.124 37 |
| SG | 0.960 10 | 0.066 50 | 0.050 49 | 0.151 18 |
| T_MASS | 0.999 93 | 0.002 6 | 0.002 21 | 0.005 03 |
| 注:1)括号表示各误差的允许范围。 | ||||
优化设计是通过搜索、迭代来寻求最优解,传统梯度优化和直接搜索方法易陷入局部最优,而全局优化算法如多岛遗传算法、模拟退火法、粒子群算法比传统优化算法具有更优良的全局求解能力和计算效率[13-14]。本文选择多岛遗传算法对结构进行优化设计。
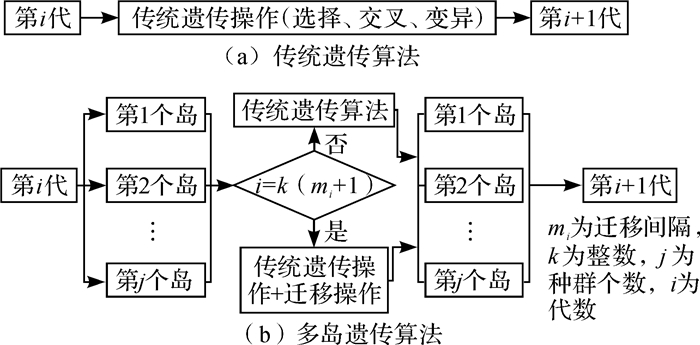
多岛遗传算法是对传统遗传算法的改进,图 5为2种算法相邻两代之间的进化流程图。与传统遗传算法不同的是,多岛遗传算法将设计种群分解为子种群,也称为“岛”,该算法对种群进行选择、交叉、变异等操作时均在每个岛上进行,同时,岛屿之间通过定期迁移来保持优化解的多样性,从而改进搜索质量而防止早熟现象的发生[15]。
|
| 图 5 传统遗传算法和多岛遗传算法相邻两代之间的进化流程 Fig.5 Evolutionary processes between two adjacent generations of traditional genetic algorithm and multi-island genetic algorithm |
多岛遗传算法能在设计空间中快速收敛至全局最优,具有较强的稳健性与普适性。文献[16]将该算法应用于架车机结构优化,轻量化效果明显;文献[17]将该算法应用于飞轮结构参数优化设计,改善了结构冗余现象;文献[18]将该算法应用于起重机小车架结构轻量化设计,避免了材料的浪费。目前,多岛遗传算法作为一种智能全局优化算法,广泛应用于求解各类复杂工程优化问题。
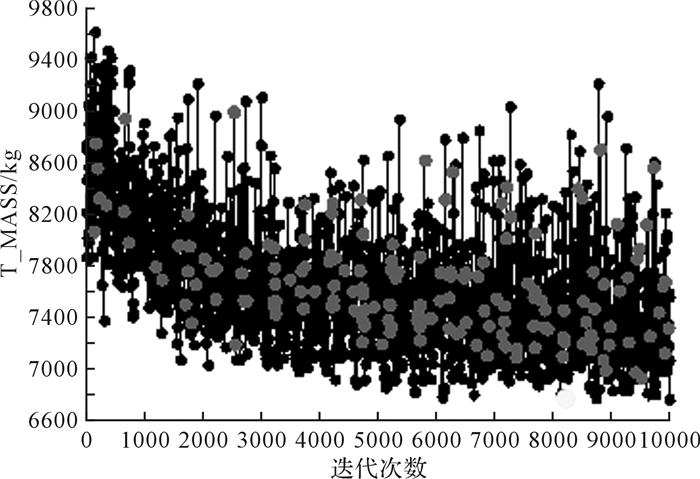
在设置算法参数时,选择子群规模为10,岛屿个数为10,优化过程总共进化代数为100。为了更快引入新结构,需要设置较高的交叉概率来保持搜索顺畅,故设定交叉概率为0.8。为了保持群体多样性,设定变异概率为0.08。门机目标函数的寻优历程如图 6所示。由图可知,模型在迭代至8 420次时得到满足约束条件的最优解。
|
| 图 6 门机目标函数寻优历程 Fig.6 Objective function optimization process of gantry crane |
由于钢材厚度及各截面尺寸参数为离散整数,经过对设计变量的离散化处理,其优化前后结果对比如表 3所示。
| 参数 | 初始值 | 优化圆整值 |
| B1/mm | 381 | 320 |
| H1/mm | 380 | 321 |
| T1/mm | 10 | 6 |
| T4/mm | 22 | 14 |
| T5/mm | 6 | 5 |
| T6/mm | 10 | 6 |
| T8/mm | 8 | 6 |
| T10/mm | 10 | 6 |
| T11/mm | 10 | 6 |
| DG/mm | -1.976 | -2.353 |
| SG/MPa | 88.7 | 146.6 |
| T_MASS/kg | 8 820 | 6 756 |
从表 3可知,对比于初始值,门机各设计参数均有所减小,而位移和等效应力值均增大,但都在允许范围内,表明门机轻量化效果明显。
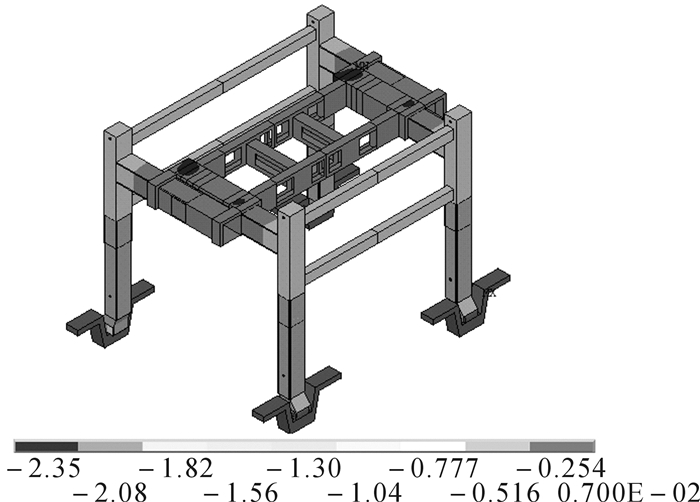
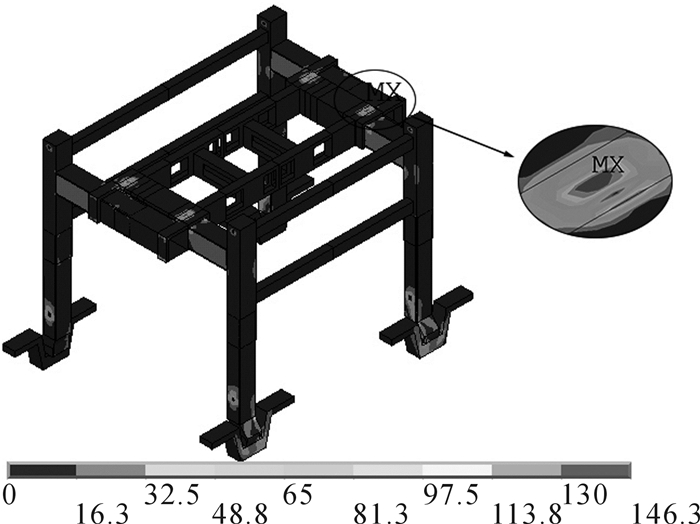
为验证近似模型的计算精度,将各设计参数优化值代入节点耦合模型,得到2种工况下的计算结果, 如图 7和图 8所示。无轨伸缩式门机在工况1下的垂直方向最大静位移为2.35 mm,在工况2下的最大等效应力为146.3 MPa,与近似模型优化结果(见表 3)相比,误差分别为0.13%,0.21%,误差较小,因此近似模型可以代替原模型。
|
| 图 7 优化后工况1下门机垂直方向位移等值线图 Fig.7 The vertical displacement contour diagram of gantry crane under condition 1 after optimization |
|
| 图 8 优化后工况2下门机等效应力图 Fig.8 The von mises stress diagram of gantry crane under condition 2 after optimization |
优化后,无轨伸缩式门机结构的刚度、强度均满足设计要求,各设计变量的值均有所减少,其总质量减轻2 064 kg,相较于原自重减少了23.4%,优化效果显著。
3 结论1) 以节点耦合模型代替接触模型进行优化计算可以避免计算效率低与不收敛等问题,通过调用Isight平台中最优拉丁超立方方法产生设计变量样本点,再由DOE模块调用有限元分析软件ANSYS完成灵敏度分析并构建近似模型,减少了计算量。
2) 利用多岛遗传算法对无轨伸缩式门机响应面近似模型进行优化,该方法能极大提高优化效率,同时使门机结构自重降低23.4%,对无轨伸缩式门机的设计具有重要指导作用。
| [1] |
卿三惠, 胡健, 陈叔.
京津城际高速铁路无砟轨道施工技术及装备创新[J]. 高速铁路技术, 2010, 1(1): 61–65.
QING San-hui, HU Jian, CHEN Shu. Construction technology and equipment innovation for ballastless track of Beijing-Tianjin intercity high speed railway[J]. High-Speed Railway Technology, 2010, 1(1): 61–65. |
| [2] |
陈叔, 史渡, 龚成光.
CRTS-Ⅱ型板式无碴轨道施工成套设备国产化研制[J]. 建设机械技术与管理, 2008, 21(6): 66–71.
CHEN Shu, SHI Du, GONG Cheng-guang. Development of homemade whole set equipment of CRTS-Ⅱ gravelless rail board construction[J]. Construction Machinery Technology and Management, 2008, 21(6): 66–71. |
| [3] |
赵国祝. 双块式无砟轨道快速施工综合技术及配套设备、工装技术[D]. 西安: 西安建筑科技大学土木工程学院, 2012: 15-21.
ZHAO Guo-zhu. The comprehensive technique and the matched equipment, the tooling technology which are used in the fast construction of the double-block ballastless track[D]. Xi'an: Xi'an University of Architecture and Technology, School of Civil Engineering, 2012: 15-21. |
| [4] |
全国起重机械标准化技术委员会. 起重机设计规范: GB/T3811-2008[S]. 北京: 中国标准出版社, 2008: 10-11.
National Standardization Technical Committee for Crane Machinery. Crane design code: GB/T3811-2008[S]. Beijing: China Standard Press, 2008: 10-11. |
| [5] |
王金诺, 于兰峰.
起重运输机械金属结构[M]. 北京: 中国铁道出版社, 2002: 43-47.
WANG Jin-nuo, YU Lan-feng. Hoisting and conveying machinery metal structure[M]. Beijing: China Railway Press, 2002: 43-47. |
| [6] |
邵明, 胡青春, 谢文牧.
基于ANSYS Workbench的折臂式随车起重机吊臂有限元分析[J]. 现代制造工程, 2014, 35(10): 86–89.
SHAO Ming, HU Qing-chun, XIE Wen-mu. The finite element analysis on boom of articulated crane boom based on ANSYS Workbench[J]. Modern Manufacturing Engineering, 2014, 35(10): 86–89. DOI:10.3969/j.issn.1671-3133.2014.10.018 |
| [7] |
纪爱敏, 彭铎, 刘木南.
三种工况下大型吊臂的有限元分析[J]. 工程机械, 2006, 37(2): 30–33.
JI Ai-min, PENG Duo, LIU Mu-nan. Finite element analysis of large boom under three working conditions[J]. Construction Machinery, 2006, 37(2): 30–33. |
| [8] |
赖宇阳.
Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012: 3-7.
LAI Yu-yang. Parameter optimization theory and examples of Isight[M]. Beijing: Beihang University Press, 2012: 3-7. |
| [9] |
潘志雄.
基于径向基函数的优化代理模型应用研究[J]. 航空工程进展, 2010, 1(3): 242–245.
PAN Zhi-xiong. The application of optimization surrogate model based on radial basic function[J]. Advanced in Aeronautical Science and Engineering, 2010, 1(3): 242–245. |
| [10] |
赵鹏飞, 王丽娟, 陈宗渝, 等.
基于自适应响应面法的车身结构轻量化设计[J]. 南昌大学学报, 2014, 36(3): 247–251.
ZHAO Peng-fei, WANG Li-juan, CHEN Zong-yu, et al. Lightweight design of autobody structures based on adaptive response surface method[J]. Journal of Nanchang University, 2014, 36(3): 247–251. |
| [11] |
周萍. 基于响应面法的车内结构噪声控制研究[D]. 长沙: 湖南大学机械工程系, 2011: 9-10.
ZHOU Ping. Study on interior structure noise control based on response surface methodology[D]. Changsha: Hunan University, School of Mechanical Engineering, 2011: 9-10. |
| [12] |
张勇, 李光耀, 孙光永, 等.
多学科设计优化在整车轻量化设计中的应用研究[J]. 中国机械工程, 2008, 19(7): 877–881.
ZHANG Yong, LI Guang-yao, SUN Guang-yong, et al. Application research on multidisciplinary design optimization of the full vehicle lightweight[J]. China Mechanical Engineering, 2008, 19(7): 877–881. |
| [13] | DAMODARAN P, VÉLEZ-GALLEGO M C. A simulated annealing algorithm to minimize makespan of parallel batch processing machines with unequal job ready times[J]. Expert Systems with Applications, 2012, 39(1): 1451–1458. DOI:10.1016/j.eswa.2011.08.029 |
| [14] |
龙腾, 刘建, WANGG Gary, 等.
基于计算试验设计与代理模型的飞行器近似优化策略探讨[J]. 机械工程学报, 2016, 52(14): 79–105.
LONG Teng, LIU Jian, WANG G Gary, et al. Discussion on approximate optimization strategy of aircraft based on computational experiment design and agent model[J]. Journal of Mechanical Engineering, 2016, 52(14): 79–105. |
| [15] |
张俊红, 朱传峰, 毕凤荣, 等.
基于DOE和MIGA的消声器优化设计[J]. 机械科学与技术, 2016, 35(2): 296–302.
ZHANG Jun-hong, ZHU Chuan-feng, BI Feng-rong, et al. Optimization design of muffler based on DOE and MIGA[J]. Mechanical Science and Technology, 2016, 35(2): 296–302. |
| [16] |
程兵, 于兰峰, 吴永明, 等.
基于响应面法的地坑式架车机轻量化研究[J]. 工程设计学报, 2016, 23(6): 606–611.
CHENG Bing, YU Lan-feng, WU Yong-ming, et al. The research on lightweight design of underfloor lifting system based on response surface method[J]. Chinese Journal of Engineering Design, 2016, 23(6): 606–611. |
| [17] |
丁泉惠, 王森, 黄修长, 等.
基于有限元法和多岛遗传算法的飞轮结构参数优化设计[J]. 噪声与振动控制, 2016, 36(2): 56–60.
DING Quan-hui, WANG Sen, HUANG Xiu-chang, et al. Optimization design of flywheel structural parameters based on finite element analysis and MIGA method[J]. Noise and Vibration Control, 2016, 36(2): 56–60. |
| [18] |
何仕永, 吴晓, 宋伟, 等.
基于响应面法的起重机小车架结构轻量化设计与研究[J]. 现代制造工程, 2013, 34(8): 96–101.
HE Shi-yong, WU Xiao, SONG Wei, et al. Response surface approximation model in optimization design of crane trolley frame[J]. Modern Manufacturing Engineering, 2013, 34(8): 96–101. |



