2. 煤炭资源安全开采与洁净利用工程研究中心, 辽宁 阜新 123000;
3. 矿物加工科学与技术国家重点实验室, 北京 100160
2. Coal Resource Safety Mining and Clean Utilization Engineering Research Center, Fuxin 123000, China;
3. State Key Laboratory of Mineral Processing Science and Technology, Beijing 100160, China
截齿是破岩落煤的刀具,常被应用于煤矿开采、巷道掘进等工程中[1]。煤矿井下开采条件复杂、环境恶劣,会加速截齿磨损,降低截齿使用寿命,使得截齿成为煤矿生产中最易损坏和更换量最大的零件[2-3]。截齿磨损对采煤机的整机性能、工作寿命和开采效率有直接的影响[4-5]。因此,对截齿磨损程度进行监测和识别具有实际的工程研究价值。
近年来,部分专家学者针对截齿相关问题进行了一系列的研究。Dewangan Saurabh等指出了煤岩截割过程中影响截齿寿命的主要因素及原因[6]。刘春生等对截齿截割阻力谱进行实验研究,探究阻力谱分形特征与安装角、切削厚度的关系[7]。陆辉等利用Workbench建立截齿有限元模型,根据仿真结果对截齿结构参数进行优化,得到更加合理的镐形截齿结构[8-9]。姚继权等利用ANSYS软件模拟截齿实际工况,进行力学、模态和热力学分析,得到截齿截割过程中合金头的应力、应变和温度等参数的变化情况[10]。张梦奇等构建了截割试验台,通过截齿截割模拟试验获得截割过程中截齿磨损的变化过程[11]。以上针对截齿的研究方向主要为磨损机理和软件仿真,并没有过多地涉及采煤机截齿磨损程度的监测和识别研究。因此,笔者提出了一种基于多传感特征信号融合的截齿磨损程度在线监测和识别方法,对实验获得的多传感器信号进行时域和频域分析,并构建基于隶属度函数和神经网络的识别模型,实现截齿截割过程中磨损程度的实时监测和精准识别,以期为截齿的监测和识别提供相应的理论和数值依据。
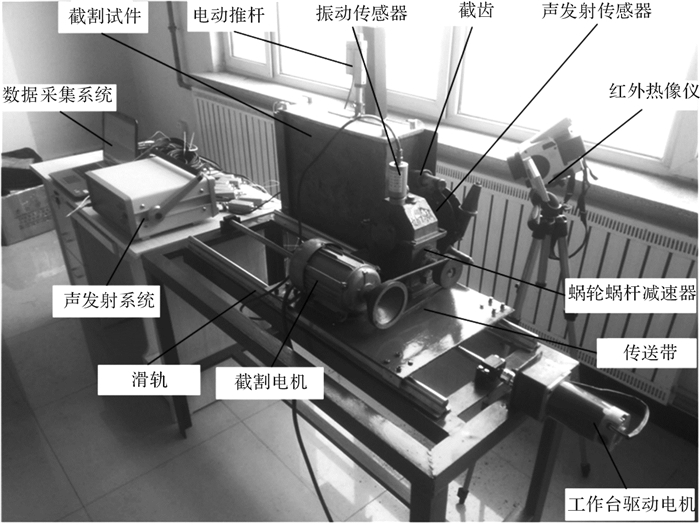
1 截齿磨损实验台为实现截齿磨损程度的识别研究,建立如图 1所示的截齿磨损程度监测实验台,测试、分析不同磨损程度截齿截割过程中的振动加速度信号、声发射信号、红外热像信号和电机电流信号。实验器材选型:U85型截齿;ZXD-YB型三向振动传感器,量程为0~20 mm/s,误差精度为±1%;SAEU3S型声发射系统,频率响应范围为3~2 000 kHz,信号最大幅值为100 dB,误差精度为±3 dB;VCiET780型高热灵敏度检测专家型红外热像仪,光谱范围为7.5~14 μm,热灵敏度可达0.03 ℃;HNC005D型电流传感器,与截割电机的电流输入端相连接,便于电流信号的采集与分析,量程为0~5 A,误差精度为±0.5%;SIRIUS RACK8型数据采集仪,采集截割过程中的多传感器特征信号,并通过数据总线将信号传输至上位机数据采集与分析系统,进行数据存储和分析[12-14]。
|
| 图 1 截齿磨损程度监测实验台 Fig.1 Pick wear degree monitoring experimental station |
测试实验前对截齿进行预处理。为获取5种不同截齿磨损状态,选取全新截齿作为新齿,预处理其余4种截齿的磨损状态,选取截齿合金头尺寸作为不同磨损程度的评价指标。测量新截齿合金头齿尖尺寸参数,并将它四等分,分别对截齿合金头进行相应的打磨预处理,获取中等磨损、中大磨损、严重磨损、截齿失效四种磨损状态的截齿,分别用A1,A2,A3,A4,A5表示。测试时首先将每组待测截齿固定在实验台滚筒上,由于滚筒在截割过程中一直处于旋转运动状态,振动传感器不易固定在截齿滚筒上,故将它安装在与截齿滚筒直接传动连接的减速器壳体上;声发射传感器安装在距截割滚筒最近的减速器壳体上;电流传感器安装在截割电机三相电进线端处;红外热像仪放置方向与滚筒截割方向相一致。
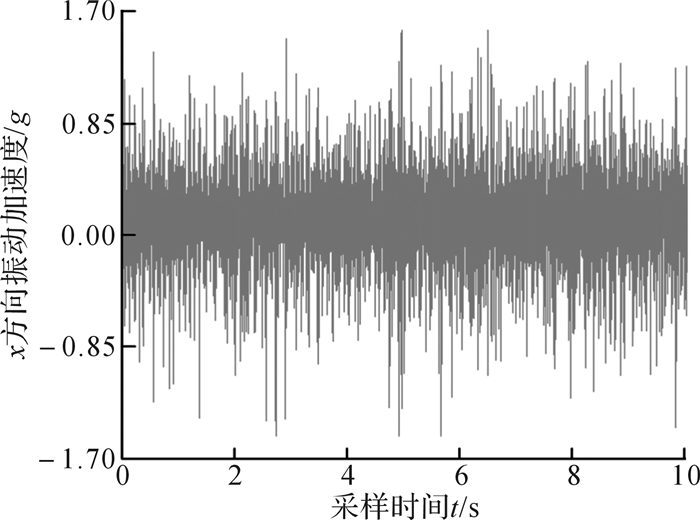
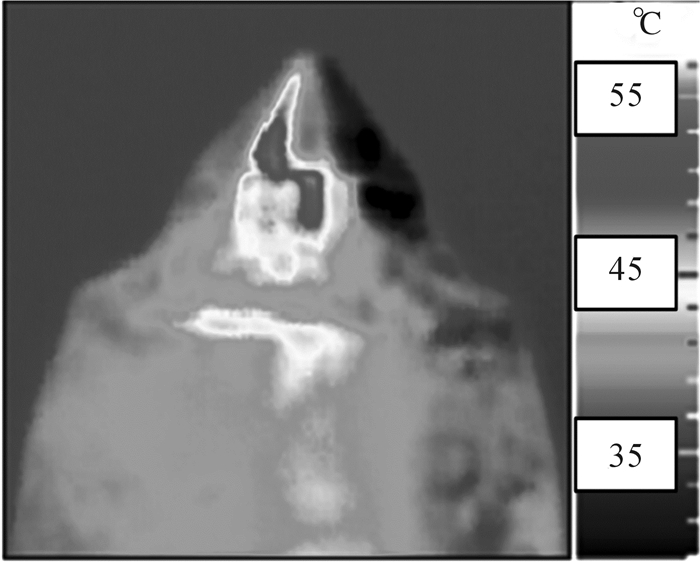
2 截割信号时域分析为实现截齿磨损程度的监测和识别,对截割过程中5种不同磨损程度截齿的振动加速度、声发射信号、电机电流和红外热像的时域信号进行提取和分析,并建立各特征信号的样本数据库。对5种不同磨损程度截齿进行分组实验,首先将滚筒上的齿座全部安装上新截齿,启动实验台工作系统进行截割实验,获取新截齿x方向(滚筒截割前进方向)的振动加速度时域曲线,如图 2所示,每组新截齿进行20组测试实验。测试完新截齿截割特征信号之后,将该组截齿全部换下,安装下一组待测截齿,通过上述方法再依次获取中等磨损、中大磨损、严重磨损、截齿失效等状态下的截齿振动特征信号时域图像,此处不再一一列举。选取每种磨损程度截齿实验中的10组测试信号,提取每组测试信号中的加速度峰值作为特征样本,构建5种不同磨损程度截齿对应的振动加速度峰值特征样本库,如表 1所示。根据上述测试方法,依次获取新截齿截割过程中的声发射信号值时域曲线,如图 3所示,以及5种不同磨损程度截齿对应的声发射信号峰值特征样本库,如表 2所示。新截齿截割时的电机电流时域曲线如图 4所示,5种不同磨损程度截齿对应的电机电流峰值特征样本库如表 3所示。提取新截齿截割中最高温度时的红外热图像,如图 5所示,5种不同磨损程度截齿对应的红外热像信号峰值特征样本库如表 4所示。
|
| 图 2 新截齿截割时的x方向振动加速度时域曲线 Fig.2 Time domain curve of x-direction vibration acceleration during cutting of new pick |
| 组号 | x方向振动加速度峰值/g | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 1.64 | 1.96 | 2.37 | 2.79 | 3.46 |
| 2 | 1.69 | 2.05 | 2.40 | 2.82 | 3.53 |
| 3 | 1.75 | 2.14 | 2.48 | 2.91 | 3.60 |
| 4 | 1.79 | 2.18 | 2.54 | 3.04 | 3.67 |
| 5 | 1.83 | 2.24 | 2.59 | 3.15 | 3.74 |
| 6 | 1.89 | 2.28 | 2.67 | 3.24 | 3.85 |
| 7 | 1.95 | 2.31 | 2.73 | 3.36 | 3.89 |
| 8 | 1.98 | 2.34 | 2.78 | 3.41 | 3.97 |
| 9 | 2.07 | 2.38 | 2.80 | 3.48 | 4.08 |
| 10 | 2.09 | 2.42 | 2.86 | 3.57 | 4.16 |
|
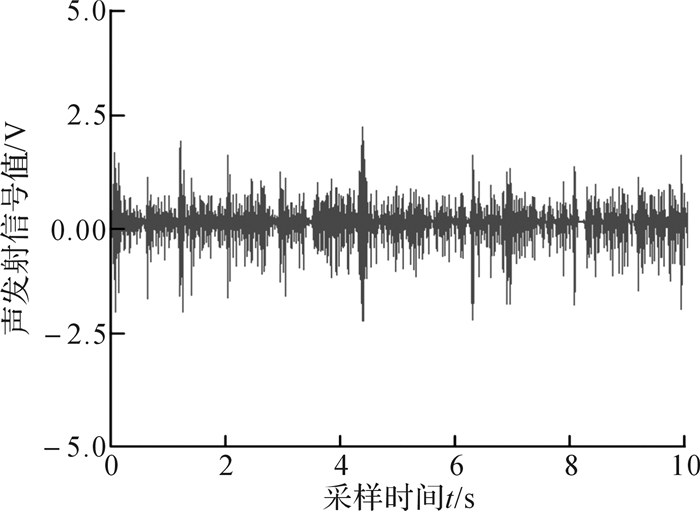
| 图 3 新截齿截割时的声发射信号值时域曲线 Fig.3 Time domain curve of acoustic emission signal value during cutting of new pick |
| 组号 | 声发射信号峰值/V | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 2.42 | 3.16 | 4.02 | 4.81 | 5.83 |
| 2 | 2.51 | 3.23 | 4.13 | 4.95 | 5.96 |
| 3 | 2.62 | 3.39 | 4.24 | 5.14 | 6.12 |
| 4 | 2.72 | 3.46 | 4.37 | 5.19 | 6.27 |
| 5 | 2.83 | 3.57 | 4.46 | 5.27 | 6.41 |
| 6 | 2.89 | 3.68 | 4.51 | 5.38 | 6.58 |
| 7 | 2.96 | 3.81 | 4.65 | 5.49 | 6.71 |
| 8 | 3.12 | 3.92 | 4.72 | 5.62 | 6.84 |
| 9 | 3.17 | 4.13 | 4.91 | 5.87 | 7.08 |
| 10 | 3.26 | 4.19 | 5.04 | 5.96 | 7.17 |
|
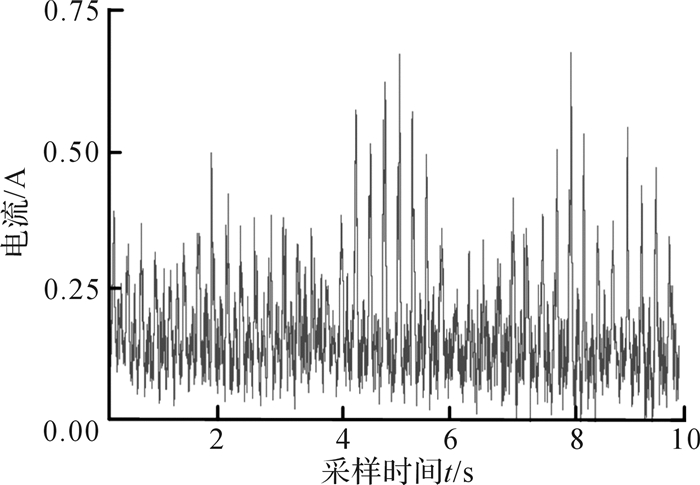
| 图 4 新截齿截割时的电机电流时域曲线 Fig.4 Time domain curve of motor current during cutting of new pick |
| 组号 | 电机电流峰值/A | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 0.64 | 0.95 | 1.36 | 1.84 | 2.36 |
| 2 | 0.68 | 1.04 | 1.41 | 1.90 | 2.43 |
| 3 | 0.72 | 1.12 | 1.47 | 1.97 | 2.48 |
| 4 | 0.76 | 1.18 | 1.53 | 2.06 | 2.54 |
| 5 | 0.84 | 1.22 | 1.61 | 2.13 | 2.59 |
| 6 | 0.86 | 1.24 | 1.67 | 2.21 | 2.64 |
| 7 | 0.92 | 1.28 | 1.72 | 2.27 | 2.68 |
| 8 | 0.96 | 1.32 | 1.79 | 2.33 | 2.73 |
| 9 | 1.02 | 1.38 | 1.85 | 2.38 | 2.79 |
| 10 | 1.10 | 1.44 | 1.92 | 2.45 | 2.85 |
|
| 图 5 新截齿截割中最高温度时的红外热图像 Fig.5 Infrared thermal image at the highest temperature during cutting of new pick |
| 组号 | 温度峰值/℃ | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 58.7 | 54.3 | 49.7 | 44.8 | 40.3 |
| 2 | 58.4 | 53.8 | 49.0 | 44.3 | 39.7 |
| 3 | 57.6 | 52.9 | 48.5 | 43.6 | 39.2 |
| 4 | 56.8 | 52.2 | 47.8 | 43.2 | 38.6 |
| 5 | 56.5 | 51.6 | 47.1 | 42.7 | 38.1 |
| 6 | 55.9 | 51.2 | 46.5 | 42.3 | 37.5 |
| 7 | 55.3 | 50.9 | 45.8 | 41.5 | 37.1 |
| 8 | 54.6 | 50.3 | 45.2 | 40.8 | 36.7 |
| 9 | 54.2 | 49.8 | 44.7 | 40.2 | 36.2 |
| 10 | 53.7 | 49.2 | 44.2 | 39.8 | 35.8 |
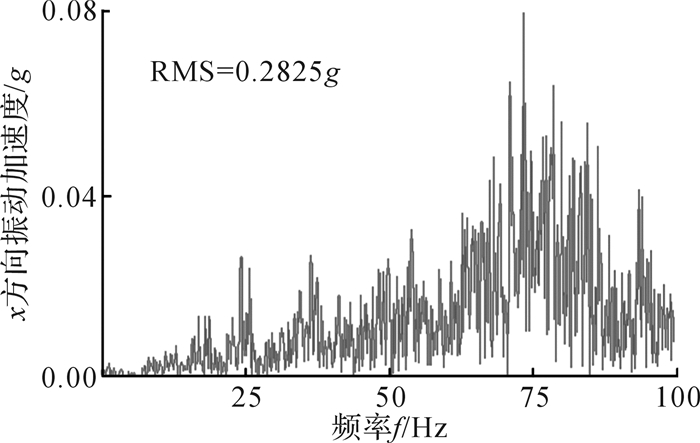
由于振动和声发射的信号峰值较容易受外界环境影响,其最大峰值虽然能反映一定的变化规律,但是其数据具有不确定性和随机性。为了提高识别系统的准确性,降低由于非平稳特征信号导致系统识别精度较低的风险[15-16],对不同磨损程度截齿截割过程中的振动加速度时域图像进行频谱分析,如图 6所示为新截齿截割时的x方向振动加速度频谱图,新截齿A1截割过程中x方向最大振动加速度为0.08g。
|
| 图 6 新截齿截割时的x方向振动加速度频谱图 Fig.6 Frequency spectrum of x-direction vibration acceleration during cutting of new pick |
另外分别计算得到截齿A2,A3,A4,A5截割时的x方向最大振动加速度为0.10g, 0.14g, 0.18g, 0.24g,对比5种截齿振动频谱图的加速度峰值可知,随截齿磨损程度的加剧,其加速度峰值不断增大,但相邻两种磨损程度截齿的加速度峰值变化不是特别明显,因此不能直接选取振动加速度频谱图峰值作为特征信号。将振动加速度频谱图数据导入MATLAB中进行特征数据计算,选取可以直接反映信号强度的均方根作为特征参数,获得5种不同磨损程度截齿振动频谱图的加速度均方根(root mean square,RMS),对应计算得到的一组均方根分别为0.2825g,0.4653g,0.5943g,0.7144g,0.8261g,x方向加速度均方根区别较为明显,因此,可以选取不同磨损程度截齿振动频谱图的加速度均方根作为特征数据样本。每种磨损程度截齿选取10组振动加速度测试信号进行时域信号的频谱分析并求取对应均方根,如表 5所示为不同磨损程度截齿对应的振动频谱图加速度均方根特征样本库。
| 组号 | x方向振动加速度均方根/g | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 0.282 5 | 0.382 7 | 0.457 1 | 0.582 5 | 0.686 5 |
| 2 | 0.291 3 | 0.397 6 | 0.462 0 | 0.591 7 | 0.698 2 |
| 3 | 0.305 4 | 0.405 3 | 0.481 5 | 0.614 2 | 0.712 0 |
| 4 | 0.318 6 | 0.413 1 | 0.497 2 | 0.628 1 | 0.731 5 |
| 5 | 0.325 2 | 0.427 8 | 0.516 7 | 0.641 3 | 0.745 4 |
| 6 | 0.342 9 | 0.435 9 | 0.532 8 | 0.659 7 | 0.762 9 |
| 7 | 0.357 5 | 0.448 4 | 0.541 6 | 0.672 6 | 0.778 2 |
| 8 | 0.376 4 | 0.452 6 | 0.563 2 | 0.684 5 | 0.791 3 |
| 9 | 0.387 3 | 0.459 2 | 0.579 1 | 0.697 2 | 0.805 9 |
| 10 | 0.395 2 | 0.465 3 | 0.594 3 | 0.714 4 | 0.826 1 |
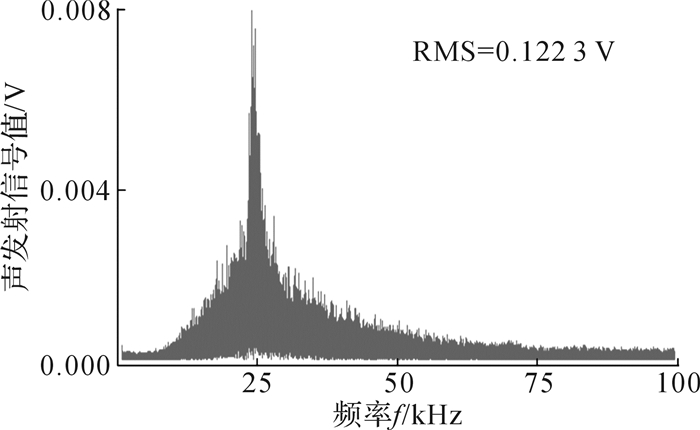
同理对不同磨损状态截齿截割过程中声发射信号值时域图像进行频谱分析。将声发射信号值频谱图数据导入MATLAB中进行特征数据计算,选取可以直接反映信号强度的均方根作为特征参数,获得5种不同磨损程度截齿声发射信号值频谱图数据的均方根,如图 7所示为新截齿截割时的声发射信号值频谱图,对应得到的一组均方根分别为0.122 3,0.326 7,0.429 4,0.527 8,0.634 1 V,均方根区别较为明显,且随着截齿磨损程度的提高,均方根逐渐增大。因此,可以选取不同磨损程度截齿声发射信号值频谱图数据的均方根作为特征数据样本。每种磨损程度截齿选取10组声发射信号值进行时域信号的频谱分析并求取对应均方根,如表 6所示为不同磨损程度截齿对应的声发射信号值频谱图数据的均方根特征样本库。
|
| 图 7 新截齿截割时的声发射信号值频谱图 Fig.7 Frequency spectrum of acoustic emission signal value during cutting of new pick |
| 组号 | 声发射信号值均方根/V | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 | 0.122 3 | 0.198 4 | 0.317 4 | 0.398 1 | 0.508 7 |
| 2 | 0.131 7 | 0.214 7 | 0.325 1 | 0.415 7 | 0.519 2 |
| 3 | 0.145 8 | 0.229 4 | 0.342 7 | 0.427 6 | 0.532 8 |
| 4 | 0.152 6 | 0.241 7 | 0.358 4 | 0.442 3 | 0.548 1 |
| 5 | 0.164 7 | 0.256 3 | 0.372 4 | 0.457 1 | 0.563 6 |
| 6 | 0.179 8 | 0.272 5 | 0.389 6 | 0.471 8 | 0.584 2 |
| 7 | 0.186 7 | 0.293 0 | 0.394 7 | 0.486 9 | 0.592 7 |
| 8 | 0.192 1 | 0.309 7 | 0.401 6 | 0.493 7 | 0.612 5 |
| 9 | 0.201 2 | 0.312 4 | 0.412 9 | 0.516 9 | 0.625 8 |
| 10 | 0.216 4 | 0.326 7 | 0.429 4 | 0.527 8 | 0.634 1 |
对不同磨损程度截齿截割过程中的电机电流时域图像进行频域分析,得到电流的频率—能量图像,图 8所示为新截齿截割时的电机电流能量频谱图。分析实验数据发现,相同频率下不同磨损程度截齿对应的能量差值较小,相邻磨损程度截齿数据样本的模糊性较大,不宜选取电流能量作为特征参数。

|
| 图 8 新截齿截割时的电机电流能量频谱图 Fig.8 Frequency spectrum of motor current energy during cutting of new pick |
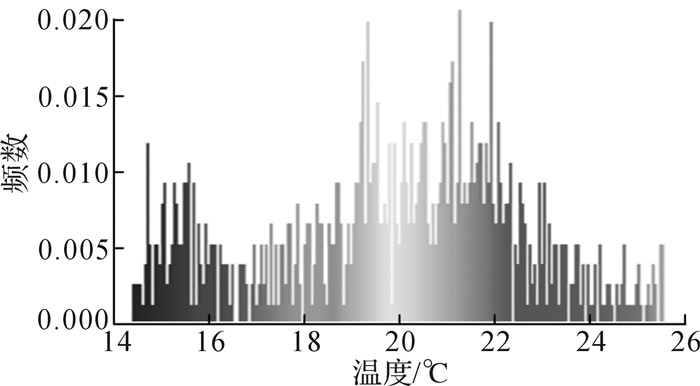
对5种不同磨损程度截齿截割过程中的红外热像信号进行温度—频数曲线分析。图 9所示为新截齿截割时的温度—频数图像,图中最高温度对应的频数较低,经过测试分析,两相邻磨损程度截齿最高温度对应的频数虽然有数值差异,但频数差值较小,相邻磨损程度截齿数据样本的模糊性较大,不宜选取红外热像最高温度的频数值作为特征参数。
|
| 图 9 新截齿截割时的温度—频数图像 Fig.9 Temperature—frequency images during cutting of new pick |
不同磨损程度截齿截割同一煤岩试件过程中,振动加速度信号、声发射信号、电机电流信号以及红外热像信号会受到试件煤岩结构、外界环境和实验台自身振动等因素的影响,导致各传感信号存在一定的随机性和不确定性。由表 3至表 6可知,不同磨损程度截齿的特征信号样本中存在部分数据交集,数据具有一定的模糊性,增大了截齿磨损程度的识别难度。本文针对两相邻磨损程度截齿各特征样本存在数据交集的问题,采用最小模糊度优化模型计算求解各特征信号参数的最优模糊隶属度函数,获取特征样本对应的最大隶属度函数值。选取各特征信号对应的最大隶属度函数值和各特征信号参数数据作为神经网络的输入量,可以更好地对两相邻磨损程度截齿进行区分,从而提高系统识别的准确度。
为了描述数据库样本的模糊性,选取模糊熵作为数据不确定性的评价参数,模糊熵值可以直接表征模糊程度的高低。设模糊集合F={f1, f2, …, fn},隶属度函数为μ(f),则模糊熵的表达式为:
| $ S\left( A \right) = \frac{1}{{n\ln 2}}\sum\limits_{i = 1}^n {\left[ {P\left( {\mu \left( {{f_i}} \right)} \right) + Q\left( {\mu \left( {{f_i}} \right)} \right)} \right]} $ | (1) |
式中:
| $ \left\{ \begin{array}{l} P\left( f \right) = - f\ln f\\ Q\left( f \right) = - \left( {1 - f} \right)\ln \left( {1 - f} \right) \end{array} \right. $ |
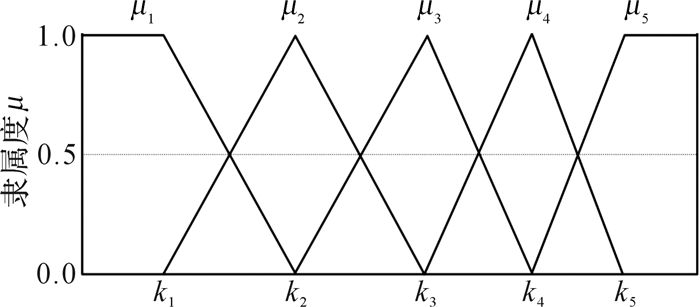
预设的5种不同磨损程度截齿用{M1, M2, M3, M4, M5}的模糊集合表示,所对应的模糊子集的隶属度分别为μ1, μ2, …,μ5,待优化求解的阈值参数分别为k1,k2,…,k5。其隶属度函数图如图 10所示。
|
| 图 10 截齿磨损程度隶属度函数图 Fig.10 Membership function graph of pick wear degree |
选取数据库中数据样本,利用最小模糊度规则对最优阈值进行求解[17]。
| $ \begin{array}{l} {S_{\min }}\left( {{M_1},{M_2},{M_3},{M_4},{M_5}} \right) = \\ \;\;\;\;\;\;\;\frac{1}{{n\ln 2}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^5 {\left[ {P\left( {{\mu _j}\left( {{f_j}} \right)} \right) + Q\left( {{\mu _j}\left( {{f_i}} \right)} \right)} \right]} } \end{array} $ | (2) |
式中:n为集合样本总数;fi为第i个样本数据;j为子隶属函数序列号, j=1, 2, …, 5, 对应的子隶属度函数表达式分别为:
| $ {\mu _1}\left( {{f_i}} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;{f_i} \le {k_1}\\ \frac{{{k_2} - {f_i}}}{{{k_2} - {k_1}}},\;\;\;\;\;{k_1} < {f_i} < {k_2}\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (3) |
| $ {\mu _2}\left( {{f_i}} \right) = \left\{ \begin{array}{l} \frac{{{f_i} - {k_1}}}{{{k_2} - {k_1}}},\;\;\;\;\;{k_1} < {f_i} \le {k_2}\\ \frac{{{k_3} - {f_i}}}{{{k_3} - {k_2}}},\;\;\;\;\;{k_2} < {f_i} < {k_3}\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (4) |
| $ {\mu _3}\left( {{f_i}} \right) = \left\{ \begin{array}{l} \frac{{{f_i} - {k_2}}}{{{k_3} - {k_2}}},\;\;\;\;\;{k_2} < {f_i} \le {k_3}\\ \frac{{{k_4} - {f_i}}}{{{k_4} - {k_3}}},\;\;\;\;\;{k_3} < {f_i} < {k_4}\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (5) |
| $ {\mu _4}\left( {{f_i}} \right) = \left\{ \begin{array}{l} \frac{{{f_i} - {k_3}}}{{{k_4} - {k_3}}},\;\;\;\;\;{k_3} < {f_i} \le {k_4}\\ \frac{{{k_5} - {f_i}}}{{{k_5} - {k_4}}},\;\;\;\;\;{k_4} < {f_i} < {k_5}\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (6) |
| $ {\mu _5}\left( {{f_i}} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;{f_i} \ge {k_5}\\ \frac{{{k_5} - {f_i}}}{{{k_5} - {k_4}}},\;\;\;\;\;{k_4} < {f_i} < {k_5}\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (7) |
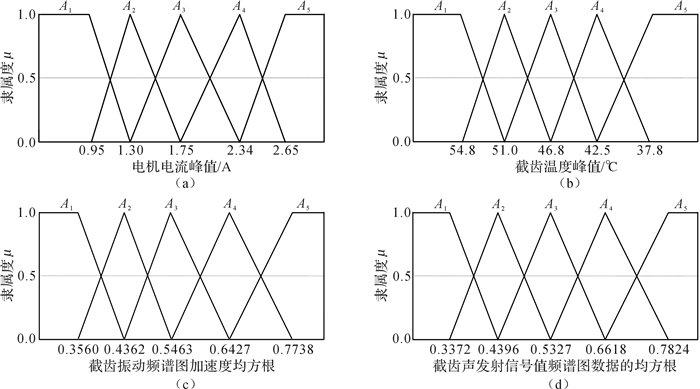
利用MATLAB对式(2)的k值进行优化求解,得到截齿A1,A2,…,A5的特征参数的模糊隶属度函数图,如图 11所示。
|
| 图 11 截齿特征参数的模糊隶属度函数图 Fig.11 Fuzzy membership function diagram for characteristic parameters of picks |
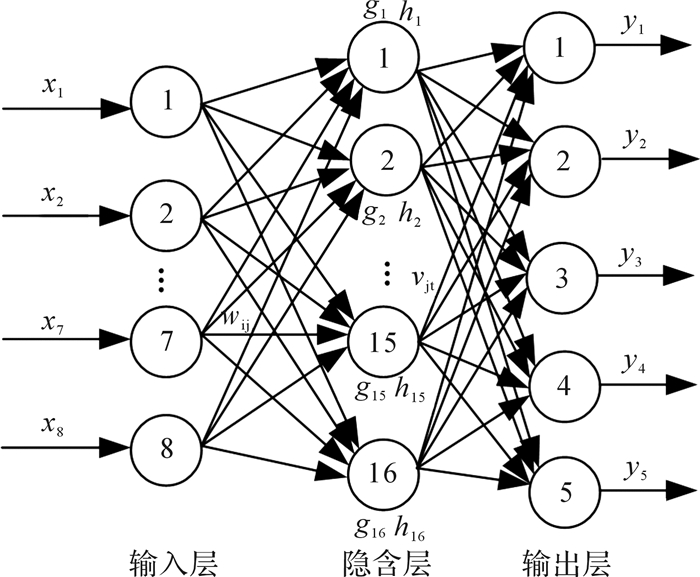
BP神经网络作为多层前馈神经网络, 包括输入层、隐含层、输出层,其特点是信号前向传递,误差反向传播。Hecht-Nielsen证明具有1个隐含层的三层前馈型网络可以逼近任何多变量函数,所以选取三层BP神经网络作为截齿磨损程度的识别模型。如图 12所示为BP神经网络结构图。
|
| 图 12 用于截齿磨损程度识别的BP神经网络结构图 Fig.12 BP neural network structure for recognition of pick wear degree |
选取构建神经网络的特征参数为:电机电流峰值x1、截齿红外热像温度峰值x2、截齿振动频谱图加速度均方根x3、截齿声发射信号值频谱图数据的均方根x4,以及4种特征信号对应的模糊隶属度函数最大值x5,…,x8,故BP神经网络输入层节点个数设置为8个;输出层为5种截齿磨损程度,故输出层设置5个神经元。
隐含层节点数量的估算方法:
1) 根据Kolmogorov定理,确定隐含层节点个数k为:
| $ k = 2x + 1 = 17 $ |
2) 运用最小二乘法对隐含层单元数量进行拟合得到隐含层节点数为:
| $ k = {\left( {x + y} \right)^{\frac{1}{2}}} + a = 13 $ |
式中:x为输入节点个数,y为输出节点个数,a为1~10之间的常数。
本神经网络结构为:输入层为8个神经单元,输出层为5个单元,通过实验数据试错法进行训练,根据表 7所示达到精度0.01时不同神经网络结构对应的训练次数变化情况,选取神经网络隐含层节点数为16个。
| 隐含层节点数 | 13 | 14 | 15 | 16 | 17 | 18 |
| 训练次数 | 46 | 38 | 32 | 26 | 31 | 39 |
BP神经网络中输入层单元的输入向量Xs=(x1, x2,…, xs),输出层单元理想输出向量Oq=(o1, o2,…,oq)。隐含层单元的输入向量Gp=(g1, g2,…,gp),隐含层单元的输出向量Hp=(h1, h2,…,hp)。输出层单元的输入向量Mq=(m1, m2,…,mq),输出层单元实际输出向量Yq=(y1, y2,…,yq)。输入层至隐含层连接权为{Wij},隐含层至输出层连接权为{Vjt},隐含层各单元输出阈值为{θj},输出层各单元输出阈值为{γt},α, β为学习率, 其中i=1, 2,…, s;j=1, 2,…, p;t=1, 2,…, q。
选取的网络响应函数为:
| $ f\left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $ | (8) |
利用输入层单元输入向量Xs=(x1k, x2k, …, xsk)、连接权值{Wij}和阈值{θj}可以计算得到中间层各单元的输入{gj}和中间层各单元的输出{hj}。
| $ {g_j} = \sum\limits_{i = 1}^n {{w_{ij}}} \cdot {i_i} - {\theta _j} $ | (9) |
| $ {h_j} = f\left( {{g_j}} \right) $ | (10) |
利用中间输出{hj}、连接权值{Vjt}和阈值{γt}计算输出层各单元输入{Mj}和输出层各单元的输出{Yt}。
| $ {M_t} = \sum\limits_{j = 1}^p {{v_{jt}}} \cdot {b_j} - {\gamma _t} $ | (11) |
| $ {Y_t} = f\left( {{M_t}} \right) $ | (12) |
通过输出层单元理想输出向量Oq=(o1, o2, …, oq)、网络实际输出{Yj},可以得到输出层各神经单元一般性误差{dtk}。
| $ d_t^k = \left( {o_t^k - {Y_t}} \right) \cdot {Y_t}\left( {1 - {Y_t}} \right) $ | (13) |
进行BP神经网络的学习训练之前,需要对特征数据进行归一化处理,将数据映射到[0, 1]之间的数值,如公式(14)所示:
| $ \mathit{\boldsymbol{y}} = \frac{{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\min }}}}{{{\mathit{\boldsymbol{x}}_{\max }} - {\mathit{\boldsymbol{x}}_{\min }}}} $ | (14) |
式中:x为输入向量,y为输出向量,xmin为输入向量x中的最小值,xmax为输入向量x中的最大值。
4.2.2 BP神经网络训练及验证分析BP神经网络初始权值的选择关系到样本训练的效果,因此初始权值应选为均匀分布的小数经验值,本文选取网络初始权值为[0, 1]之间的随机数[18]。利用sim()函数进行网络模型的仿真和计算:
| $ \mathit{\boldsymbol{y}} = {\rm{sim}}\left( {{\rm{net}},\mathit{\boldsymbol{x}}} \right) $ | (15) |
式中:net为BP神经网络设定参数;sim()为网络仿真函数;x=[x1, x2, …, x8]T为神经网络输入参量;y=[y1, y2, y3, y4, y5]为输出层识别结果,当输出值为[0, 0, 0, 0, 1], [0, 0, 0, 1, 0], [0, 0, 1, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 0, 0]时,对应识别结果分别为新齿、中等磨损、中大磨损、严重磨损、失效截齿。
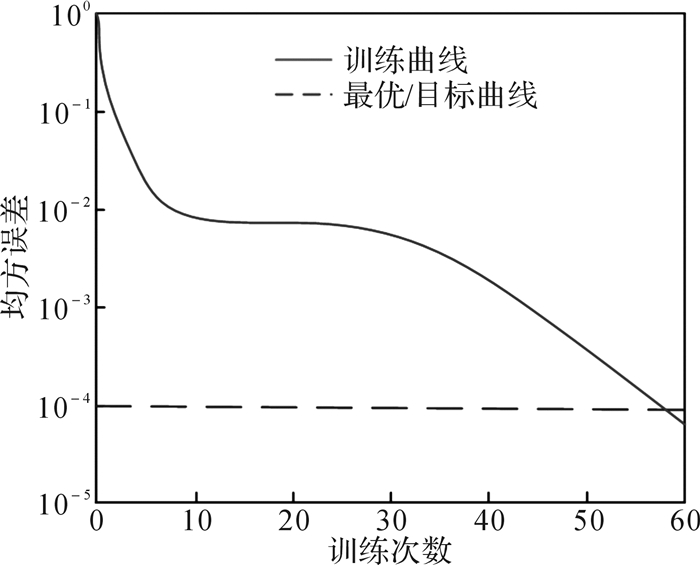
BP网络中隐含层的传递函数为tansig()函数,输出层的传递函数为logsig()函数,隐含层和输出层间激活函数采用Sigmoid()函数,网络初始权值为0, 1之间的随机数,训练步长为1,训练步数为1 000,训练误差为1.0×10-4,其余参数为系统默认值。如图 13所示,若网络的学习误差为1.0×10-4,则训练至第59步己经满足误差目标精度。
|
| 图 13 BP神经网络误差性能曲线 Fig.13 BP neural network error performance curve |
为验证截齿磨损程度在线监测系统的精确性与可靠性,将5种不同磨损程度截齿的各2组检验样本输入己经训练好的BP神经网络,进行截齿磨损程度的验证分析,其网络目标和网络实际输出的结果如表 8所示。从表 8可看出,这10组用于验证的样本能够非常准确地被识别出来,BP神经网络的识别效果良好。经验证实验可知,多特征信号融合识别系统能够对截齿磨损程度类型进行准确识别。
| 组号 | 网络目标 | 网络实际输出 | 截齿状态 | 结果 |
| 1 | [0, 0, 0, 0, 1] | [0.0759, 0.0627, 0.1050, 0.1972, 0.9147] | 新截齿 | 正确 |
| 2 | [0, 0, 0, 0, 1] | [0.1297, 0.0941, 0.0758, 0.1189, 0.9314] | 新截齿 | 正确 |
| 3 | [0, 0, 0, 1, 0] | [0.0834, 0.1259, 0.1036, 0.9349, 0.0875] | 中等磨损 | 正确 |
| 4 | [0, 0, 0, 1, 0] | [0.1256, 0.1142, 0.0972, 0.9172, 0.1124] | 中等磨损 | 正确 |
| 5 | [0, 0, 1, 0, 0] | [0.1394, 0.1142, 0.9054, 0.1062, 0.0817] | 中大磨损 | 正确 |
| 6 | [0, 0, 1, 0, 0] | [0.1052, 0.0964, 0.9136, 0.1123, 0.0821] | 中大磨损 | 正确 |
| 7 | [0, 1, 0, 0, 0] | [0.1223, 0.9252, 0.0852, 0.1157, 0.0932] | 严重磨损 | 正确 |
| 8 | [0, 1, 0, 0, 0] | [0.1334, 0.8915, 0.1364, 0.0924, 0.0852] | 严重磨损 | 正确 |
| 9 | [1, 0, 0, 0, 0] | [0.9175, 0.1064, 0.0928 0.1247, 0.0972] | 失效截齿 | 正确 |
| 10 | [1, 0, 0, 0, 0] | [0.9347, 0.1238, 0.0945, 0.1357, 0.0954] | 失效截齿 | 正确 |
1) 相同截割工况条件下,不同磨损程度截齿截割同一煤岩试件过程中,振动加速度信号、声发射信号、电机电流信号、红外热像信号的变化与不同磨损程度截齿之间存在一定相关性。2)构建基于最小模糊度的隶属度函数模型,获取各特征样本的优化隶属度函数,求解各个样本所对应的最大隶属度值,可以对2种相邻磨损程度截齿进行更好的区别。3)选取8种特征数据样本构建BP神经网络数据库,可以实现截割试件过程中截齿磨损程度的监测和识别研究,为基于多特征信号融合的截齿磨损程度识别研究提供一定的理论和数值依据,为煤炭开采工程中截齿的监测和识别提供解决方案。
| [1] |
付林, 杜长龙, 刘送永, 等.
螺旋钻采煤机钻头截齿载荷特性研究[J]. 中国机械工程, 2013, 24(15): 2020–2024.
FU Lin, DU Chang-long, LIU Song-yong, et al. Research on load characteristics of picks on auger drill miner's aiguille[J]. China Mechanical Engineering, 2013, 24(15): 2020–2024. DOI:10.3969/j.issn.1004-132X.2013.15.007 |
| [2] |
刘浩, 邱大龙, 田冬林, 等.
基于ANSYS采煤机截齿结构改进设计及应力分析[J]. 煤矿机械, 2013, 34(10): 167–169.
LIU Hao, QIU Da-long, TIAN Dong-lin, et al. Structure improvement design and stress analysis of coal winning machine cutting tooth based on ANSYS[J]. Coal Mine Machinery, 2013, 34(10): 167–169. |
| [3] |
朱华, 吴兆宏, 李刚, 等.
煤矿机械磨损失效研究[J]. 煤炭学报, 2006, 31(3): 380–385.
ZHU Hua, WU Zhao-hong, LI Gang, et al. Study on wear failures of mining machinery[J]. Journal of China Coal Society, 2006, 31(3): 380–385. |
| [4] |
张延强, 李秀红, 任家骏, 等.
WK-75型矿用挖掘机斗齿的磨损分析[J]. 工程设计学报, 2015, 22(5): 493–498.
ZHANG Yan-qiang, LI Xiu-hong, REN Jia-jun, et al. Wear analysis on bucket tooth of WK-75 mining excavator[J]. Chinese Journal of Engineering Design, 2015, 22(5): 493–498. |
| [5] |
尚慧岭.
采煤机滚筒截齿失效工况的影响分析及对策[J]. 煤炭科学技术, 2012, 40(8): 75–77.
SHANG Hui-ling. Analysis and countermeasures of pick failure performance influences of cutting drum in coal shearer[J]. Coal Science and Technology, 2012, 40(8): 75–77. |
| [6] | DEWANGAN S, CHATTOPADHYAYA S. Characterization of wear mechanisms in distorted conical picks after coal cutting[J]. Rock Mechanics and Rock Engineering, 2016, 49(1): 225–242. DOI:10.1007/s00603-015-0726-x |
| [7] |
刘春生, 王庆华, 李德根.
镐型截齿截割阻力谱的分形特征与比能耗模型[J]. 煤炭学报, 2015, 40(11): 2623–2628.
LIU Chun-sheng, WANG Qing-hua, LI De-gen. Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J]. Journal of China Coal Society, 2015, 40(11): 2623–2628. |
| [8] |
陆辉, 王义亮, 杨兆建.
采煤机镐形截齿疲劳寿命分析及优化[J]. 煤炭科学技术, 2013, 41(7): 100–102, 106.
LU Hui, WANG Yi-liang, YANG Zhao-jian. Analysis and optimization on fatigue life of pick cutter for cutting drum of coal shearer[J]. Coal Science and Technology, 2013, 41(7): 100–102, 106. |
| [9] |
李祥松.
TRIZ理论在掘进机截割头设计中的应用[J]. 工程设计学报, 2015, 22(3): 219–223.
LI Xiang-song. Application of TRIZ theory in the design of roadheader cutting-head[J]. Chinese Journal of Engineering Design, 2015, 22(3): 219–223. |
| [10] |
姚继权, 李晓豁, 焦丽.
基于Pro/E和ANSYS的镐型截齿有限元分析[J]. 矿山机械, 2008, 36(21): 17–19.
YAO Ji-quan, LI Xiao-huo, JIAO Li. Finite element analysis of pick-shaped cutter based on Pro/ENGINEER and ANSYS[J]. Mining & Processing Equipment, 2008, 36(21): 17–19. |
| [11] |
张梦奇, 郝建生, 马健康.
锥形截齿旋转破岩截割力预测方法试验研究[J]. 煤炭科学技术, 2015, 43(12): 98–103.
ZHANG Meng-qi, HAO Jian-sheng, MA Jian-kang. Experimental study on rock cutting force by rotational moving for coalmining equipment conical pick[J]. Coal Science and Technology, 2015, 43(12): 98–103. |
| [12] |
张强, 王海舰, 李立莹, 等.
基于自适应神经-模糊推理系统模糊信息融合的采煤机截齿磨损在线监测[J]. 中国机械工程, 2016, 27(19): 2607–2613.
ZHANG Qiang, WANG Hai-jian, LI Li-ying, et al. Online monitoring of shearer's pick wear based on ANFIS fuzzy information fusion[J]. China Mechanical Engineering, 2016, 27(19): 2607–2613. DOI:10.3969/j.issn.1004-132X.2016.19.009 |
| [13] |
张强, 王海舰, 王兆, 等.
基于红外热像检测的截齿煤岩截割特性与闪温分析[J]. 传感技术学报, 2016, 29(5): 686–692.
ZHANG Qiang, WANG Hai-jian, WANG Zhao, et al. Analysis of coal-rock's cutting characteristics and flash temperature for peak based on infrared thermal image testing[J]. Chinese Journal of Sensors Actuators, 2016, 29(5): 686–692. |
| [14] |
张强, 刘志恒, 王海舰, 等.
基于BP神经网络的截齿磨损程度在线监测[J]. 中国机械工程, 2017, 28(9): 1062–1068.
ZHANG Qiang, LIU Zhi-heng, WANG Hai-jian, et al. On-line monitoring of pick's wear degrees based on BP neural network[J]. China Mechanical Engineering, 2017, 28(9): 1062–1068. |
| [15] |
张强, 王海舰, 李立莹, 等.
基于多传感特征信息融合的采煤机截齿失效诊断[J]. 中国机械工程, 2016, 27(17): 2334–2340.
ZHANG Qiang, WANG Hai-jian, LI Li-ying, et al. Failure diagnosis of shearer's picks based on information fusion from multi sensors[J]. China Mechanical Engineering, 2016, 27(17): 2334–2340. DOI:10.3969/j.issn.1004-132X.2016.17.011 |
| [16] |
张强, 王海舰, 井旺, 等.
基于模糊神经网络信息融合的采煤机煤岩识别系统[J]. 中国机械工程, 2016, 27(2): 201–208.
ZHANG Qiang, WANG Hai-jian, JING Wang, et al. Shearer's coal-rock recognition system based on fuzzy neural network information fusion[J]. China Mechanical Engineering, 2016, 27(2): 201–208. |
| [17] |
刘晓明, 牟龙华, 张鑫.
基于信息融合的隔爆开关永磁机构储能电容失效诊断[J]. 煤炭学报, 2014, 39(10): 2121–2127.
LIU Xiao-ming, MU Long-hua, ZHANG Xin. Failure diagnosis for storage-capacitor in permanent magnetic actuator of flameproof switchgear based on information fusion[J]. Journal of China Coal Society, 2014, 39(10): 2121–2127. |
| [18] |
秦国华, 谢文斌, 王华敏.
基于神经网络与遗传算法的刀具磨损检测与控制[J]. 光学精密工程, 2015, 23(5): 1314–1321.
QIN Guo-hua, XIE Wen-bin, WANG Hua-min. Detection and control for tool wear based on neural network and genetic algorithm[J]. Optics Precision Engineering, 2015, 23(5): 1314–1321. |


