2. 浙江大学 机械工程学院/浙江省先进制造技术重点实验室, 浙江 杭州 310027;
3. 博世电动工具(中国)有限公司, 浙江 杭州 310052
2. Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province, School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China;
3. BOSCH Power Tools(China) Co., Ltd., Hangzhou 310052, China
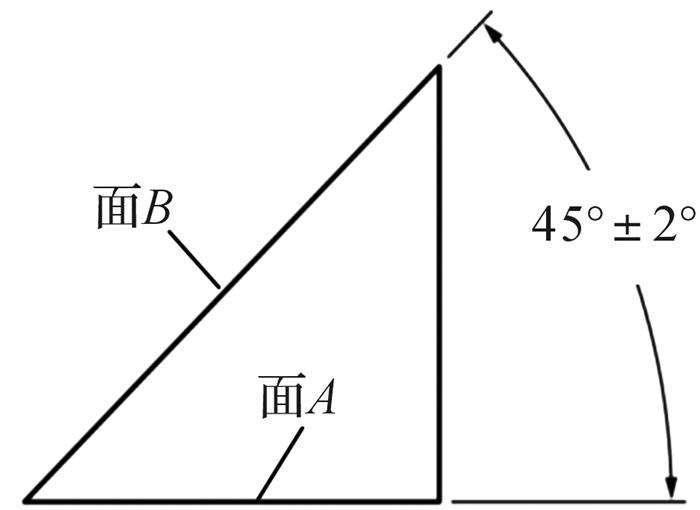
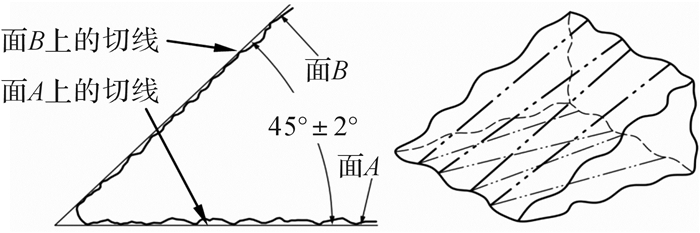
在产品几何技术规范(geometrical product specifications, GPS)标准ISO14405—2中[1],角度尺寸公差定义的“角度”是指线和线之间的角度,如图 1中所标注的“45°±2°”指的是平面A和平面B上某一截面内接触提取要素的2条直线之间的角度,截平面内两直线的方向对应于各自的要素,且保证到各自提取要素线的最大距离为最小[2];如图 2中所标注的“45°±2°”指的是切线和切线之间的夹角及允许的变动范围。可见,角度尺寸公差并不能控制平面A和平面B之间的夹角偏差。
|
| 图 1 角度尺寸公差标注(正/负公差) Fig.1 Indication of angle dimension tolerance (plus-minus tolerance) |
|
| 图 2 非平行平面内角度尺寸公差的释义 Fig.2 Interpretation of angular dimension tolerance in the non parallel planes |
在工程中常需要控制平面与平面之间的夹角偏差,用线与线之间的角度尺寸公差来控制平面与平面之间的角度偏差显然是不合适的。实际上,设计人员可用几何公差来间接控制平面与平面之间的夹角偏差。在GPS标准ISO14405—2中,给出了用方向公差、面轮廓度、理论正确角度来控制平面与平面之间角度的图例,见图 3[1]。几何公差是用几何区域来控制被测要素的几何变动,并不能直接控制平面与平面之间的夹角偏差,对于需要精准控制夹角偏差的场合,须将几何公差换算成角度公差;另外,图 3中未指出被测要素为何种拟合要素,这可能会导致角度偏差失去控制。1)该如何在图样上正确表达平面与平面之间角度公差要求,使得被测要素和基准面的角度偏差被精准地控制在允许的变动范围内;2)如何根据零件图样上的标注来计算角度累积偏差。下面就此进行详细的探讨和分析。

|
| 图 3 ISO14405—2中几何公差控制面-面角度的图例 Fig.3 Examples of angular distance between two integral features controlled by geometric tolerances in ISO14405—2 |
图 4所示为用平行度公差控制零件的上表面相对于底面C的方向关系,若需精确控制被测平面与底面的夹角,其夹角偏差允许的变化范围该如何计算?假想在零件的上表面放置一标准块,且假定标准块的各表面形状及相互之间的方向、位置关系理想,则零件上表面与底面C之间的夹角就转化为标准块上平面(或下平面)和零件底面C之间的夹角,如图 5所示。

|
| 图 4 平行度公差控制平面之间方向关系的图示 Fig.4 Examples of orientation relationship between two planes controlled by parallelism tolerance |

|
| 图 5 被测面与标准块的夹角及接触点 Fig.5 Angle and contact points between measured surface and gage block |
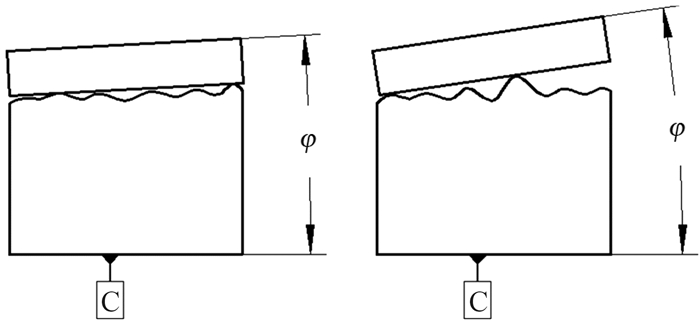
标准块置于零件上表面,可认为与表面发生接触的是一些接触高点,它相对于底面C的夹角完全由表面上的接触高点所决定,接触高点的位置变化将导致标准块相对于基准面C的角度φ也会随之变化,如图 6所示。尽管在图 4中已经采用了方向公差(平行度)来约束接触面,但是由于方向公差(如平行度、垂直度和倾斜度)均不能约束接触高点的位置,从而使得标准块与零件接触形成的夹角失去控制。若因为功能上的需要,要求对标准块上表面和零件底面的夹角进行严格控制,那该如何用几何公差进行有效的约束呢?
|
| 图 6 由接触高点决定的平面之间的夹角 Fig.6 Angle between two contact planes determined by high points |
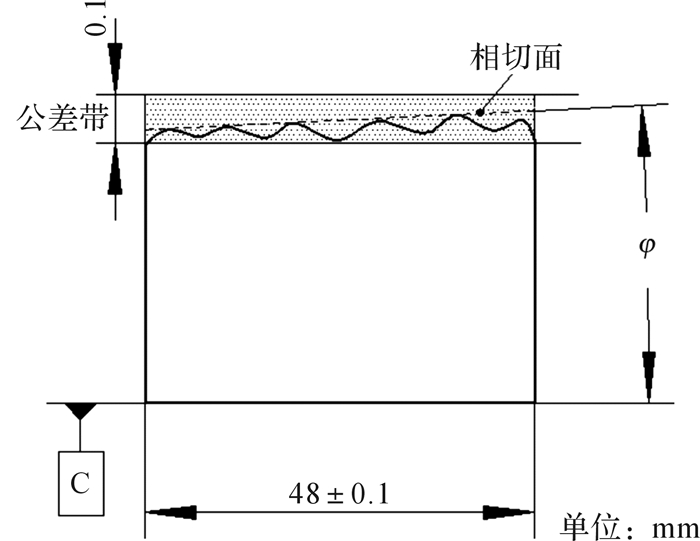
在最新GPS标准ISO_1101_2017中有在几何公差框格内的“公差带、要素和特征规范”部分附加使用的T圈修饰符号[3],GPS中的T圈符号与ASME Y14.5标准中T圈符号含义一致[4],均指被测要素为拟合贴切要素,T圈仅可用于公称直线及平面要素。如图 7中的平行度公差对被测要素附加T圈,它与不附加T圈的平行度公差要求的含义有所不同,附加T圈后约束的对象是被测表面的相切平面,要求零件表面的切平面必须在0.1 mm的公差带范围以内,如图 8所示,即零件上表面切面和基准面C的最大夹角偏差为:
| $ \Delta {\varphi _{{\rm{max}}}} = {\rm{arctan}}\left( {0.1/47.9} \right) \approx 0.002' = 0.12^\circ $ | (1) |

|
| 图 7 被测要素附加贴切拟合要素符号 Fig.7 Toleranced feature with tangent associated feature symbol |
|
| 图 8 使用贴切要素符号的拟合被测要素(相切平面) Fig.8 Associated toleranced feature (tangent plane) using tangent feature symbol |
由图 5可知,零件上表面的相切面与标准块底面是重合的,所以零件上表面的相切面和基准面C的夹角偏差就是标准块底面和基准面C的夹角偏差Δφ,而夹角有顺/逆时针两个方向的变化,故φ=0°±Δφmax=0°±0.12°。
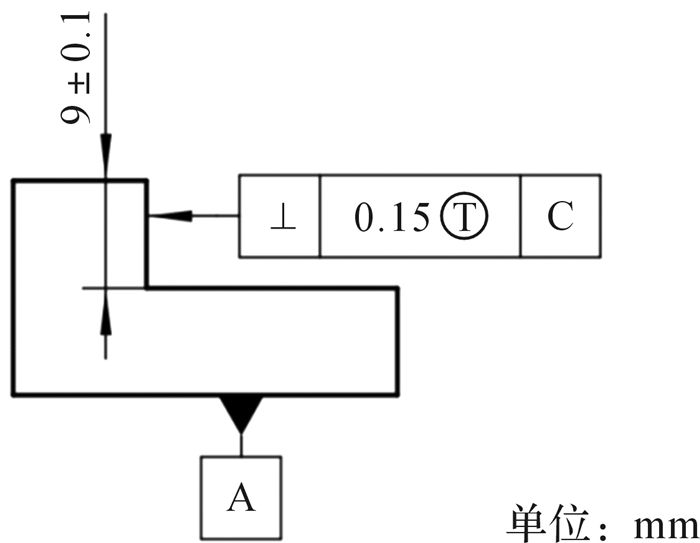
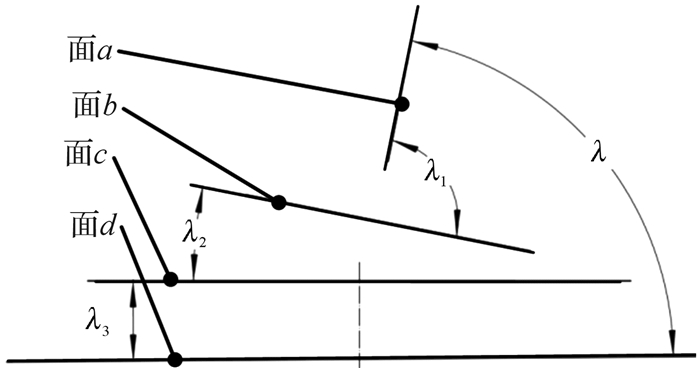
2 几何公差与角度公差的换算及角度偏差累积计算图 9所示的装配体由直角块、锲块和底座装配而成,各零件简图如图 10至图 12所示。因为功能上的需要,要计算控制面d和面a之间夹角λ的角度累积偏差。与计算线性尺寸链类似,计算角度偏差也需要画出角度尺寸链,先将面a、面b、面c和面d画出,再进行处理,如图 13所示。

|
| 图 9 装配体简图 Fig.9 Sketch of assembly |
|
| 图 10 直角块零件简图 Fig.10 Sketch of right angle block part |

|
| 图 11 锲块零件简图 Fig.11 Sketch of wedge block part |

|
| 图 12 底座零件简图 Fig.12 Sketch of base part |
|
| 图 13 装配体角度尺寸链的构建 Fig.13 Construction of angle dimension chain of assembly |
面a与面d之间的夹角λ是角度尺寸链中的封闭环,也就是需要计算的目标环,而λ1,λ2,λ3是该角度尺寸链中的组成环。如果将形成夹角的2条边中的任意一条边平行移动,则该角度的大小不会发生改变。为了方便分析角度尺寸链,将代表面a、面b、面c、面d的4条边平行移动至同一个公共点[5],将封闭环和各组成环组成一个有公共顶点的角度尺寸链,见图 14。

|
| 图 14 带公共顶点的角度尺寸链 Fig.14 Angle dimension chain with common vertex |
将封闭环λ的任意一条边作为起始边,围绕着公共顶点依次旋转到封闭环λ的另外一条边(称为终止边),并将该旋转方向设置成正方向。从面a出发,围绕公共顶点顺时针(正方向)旋转,依次经过面b、面c直至面d,面a与面b夹角λ1为增环(+)、面b与面c夹角λ2为减环(-)、面c与面d夹角λ3为减环(-)[6]。按照上一节给出的方向公差与角度公差换算方法计算出各个特征面与基准面的角度偏差,并进行累积计算,如表 1所示。
| 增/减环 | 角度代号 | 基本角度值 | 角度偏差 |
| + | λ1 | 90° | ±arctan(0.15/8.9)rad |
| - | λ2 | 11° | ±arctan(0.25/43.75)rad |
| - | λ3 | 0° | ±arctan(0.2/81.5)rad |
| 封闭环 | λ | 79° | ±0.025 rad=±1.4° |
如表 1所示,累积的角度偏差为±1.4°,即各个零件在几何公差的控制下,面a和面d之间夹角可在77.6°~80.4°之间变动。此例中的组成环只有3个,用极值法计算较为合理,若组成环数目较多(4个以上),通常应考虑采用统计法计算角度偏差[7-10]。
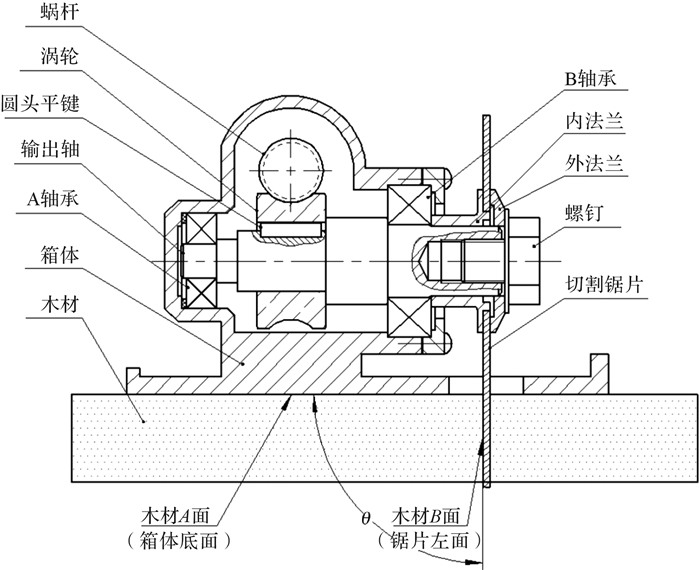
3 工程实例图 15所示为某型号木材切割机(电动工具),它的工作原理是:马达动力通过蜗杆传递给蜗轮,再由蜗轮传递至输出轴,输出轴通过法兰系统传递给切割锯片,从而使得锯片具有旋转切割木材的功能。切割机用户尤其关注木材经过切割后,木材的A面和木材的B面(切割面)之间垂直度误差是否控制在允许的范围内,即要求控制切割机箱体底面和锯片之间的夹角θ的变动值Δθ。而夹角θ与箱体、轴承、输出轴、内法兰和锯片有关,应根据各个零件相关特征的GD & T(geometric dimensioning and tolerancing, 几何尺寸和公差)标注分析零件的相关几何要素的极限位置和角度偏差,并进行角度公差分析和调整。
|
| 图 15 木材切割机装配简图 Fig.15 Assembly sketch of wood cutting machine |
GPS要求公差设计/标注应以满足功能要求为出发点,并保证不同人阅读图纸时不会产生歧义[11-13]。按照GPS这一基本要求,并根据装配定位关系,分3步进行公差设计[14-18]。第1步:定功能,分析产品中各零件是如何装配的,哪些是定位与配合面;第2步:定基准,基准一般选择在零件的装配定位面,根据优先次序定出第1、第2和第3基准;第3步:定公差,选择公差项目类型,设定公差值。根据初步设定的箱体、输出轴、内法兰GD & T标准(轴承和锯片为外购件)进行分析。
3.1 箱体分析图 16是箱体GD & T标注。

|
| 图 16 箱体GD & T标注 Fig.16 GD & T annotation of box part |
从图 16中可看出,采用位置度公差来控制两轴承孔相对于基准面C, D的位置,公差框格后加“SIM”符号表示位置度公差控制的同时性要求,亦能控制A,B两轴承孔间的相对位置关系。A, B两轴承孔在位置度公差约束的情况下(既要保证相对于基准面C, D的位置度公差为Ø0.2 mm,又要保证相对于基准面C的位置度公差为Ø0.02 mm),该两孔轴线分布的极限状态见图 17。图 17所示为箱体轴承孔几何公差带示意图,该公差带是2个同轴的圆柱体,其轴线和基准面C理想平行,直径均为Ø0.2 mm。从图 17中可得出A孔和B孔公共轴线连线和基准面C的最大夹角偏差为:
| $ \Delta {\alpha _{{\rm{max}}}} = {\rm{arctan}}\left( {0.2/55.35} \right) = 0.0036' = 0.207^\circ $ | (2) |

|
| 图 17 箱体轴承孔几何公差带示意图 Fig.17 Diagram of geometric tolerance zone of box bearing hole |
所以,公共轴线A-B和箱体底面C的夹角α为:
| $ \alpha = 0 \pm \Delta {\alpha _{{\rm{max}}}} = 0 \pm 0.207^\circ $ | (3) |
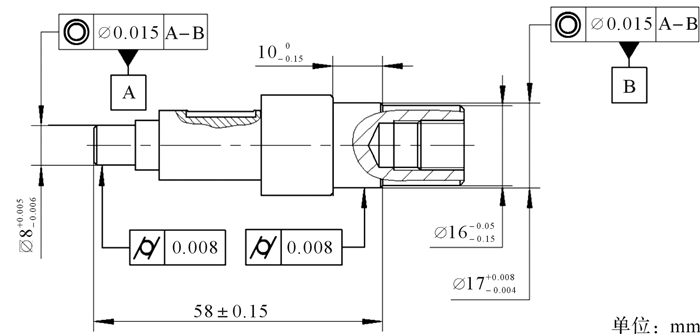
图 18是输出轴GD & T标注。
|
| 图 18 输出轴GD & T标注 Fig.18 GD & T annotation of output shaft |
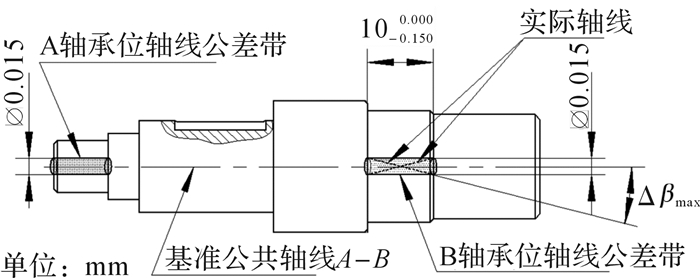
图 19为输出轴上2处轴承位的轴线同轴度的公差带示意图,同轴度公差带形状为共轴的圆柱体,实际轴线分布在圆柱体公差带内。根据图 15中的装配关系,B轴承的端面影响内法兰的方向,故需要计算B轴承位的实际轴线相对于公共基准轴线A-B的夹角。由于A,B两轴承在安装后,内圈与外圈之间的游隙非常小(通常为0~3 μm),可忽略不计,即认为在箱体中两轴承孔基准公共轴线与输出轴两轴承位的公共轴线重合,输出轴两轴承位的公共基准轴线A-B和输出轴的旋转中心是同轴的。故只需计算B轴承位轴线与公共基准轴线A-B的夹角,即B轴承位轴线和旋转中心的夹角。因此,B轴承位实际轴线和公共轴线A-B之间的最大夹角偏差为:
| $ \Delta {\beta _{{\rm{max}}}} = {\rm{arctan}}\left( {0.015/9.85} \right) = 0.00152' = 0.087^\circ $ | (4) |
|
| 图 19 输出轴几何公差带示意图 Fig.19 Diagram of geometric tolerance zone of output shaft |
所以,B轴承位轴线与公共轴线A-B夹角为:
| $ \beta = 0 \pm \Delta {\beta _{{\rm{max}}}} = 0 \pm 0.087^\circ $ | (5) |
轴承的端面决定了法兰的方向,需分析B轴承的端面和B轴承轴线之间的角度偏差,如图 20所示。因为B轴承的内圈和输出轴的B轴承位之间为过盈配合,所以可认为B轴承内圈的轴线和输出轴B轴承位的轴线保持同轴。因为轴承本身的制造精度较高,其本身的制造误差可以忽略不计,故B轴承内圈端面和B轴承内圈轴线之间的夹角最大偏差Δγmax≈0°。所以,B轴承内圈端面与B轴承内圈轴线之间的夹角为:
| $ \gamma = 90^\circ \pm \Delta {\gamma _{{\rm{max}}}} \approx 90^\circ \pm 0^\circ $ | (6) |

|
| 图 20 B轴承公差分析 Fig.20 Tolerance analysis of bear B |
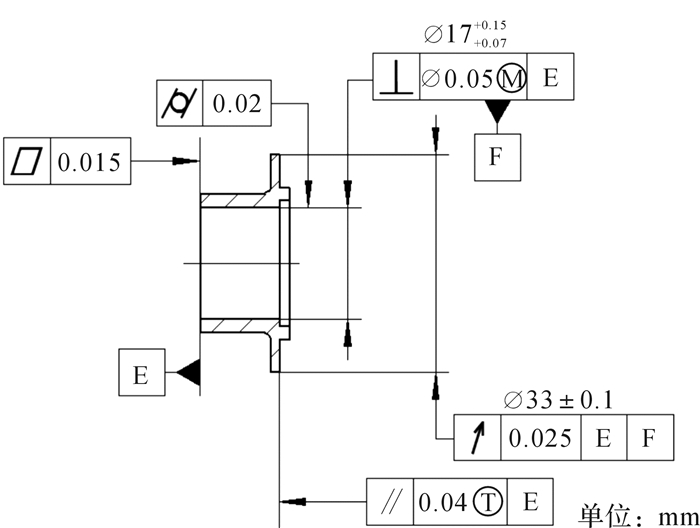
图 21是内法兰GD & T标注。
|
| 图 21 内法兰GD & T标注 Fig.21 GD & T annotation of inner flange |
在内法兰的装配中,其左端面E和B轴承内圈的右端面接触,故用左端面E作为第一基准。内法兰和切割锯片装配接触面为内法兰的Ø33 mm外圆右平面,该圆环状平面决定了切割锯片在空间中的方向,而与切割锯片发生实际接触的是表面上的接触高点,应控制Ø33 mm外圆右平面的切平面,被测要素应为贴切拟合要素,故在图 21中规定内法兰的Ø33 mm外圆右平面相对于基准面E的平行度公差要求时,使用带T圈的修饰符。
由图 22的公差分析示意图可看出,内法兰Ø33 mm外圆右平面相对于基准面E的最大夹角偏差为:
| $ \Delta {\delta _{{\rm{max}}}} = {\rm{arctan}}\left( {0.05/32.9} \right) = 0.0015' = 0.087^\circ $ | (7) |

|
| 图 22 内法兰公差分析 Fig.22 Tolerance analysis of inner flange |
所以,内法兰Ø33 mm外圆右平面相对于基准面E的夹角为:
| $ \delta = 0^\circ \pm \Delta {\delta _{{\rm{max}}}} = 0^\circ \pm 0.087^\circ $ | (8) |
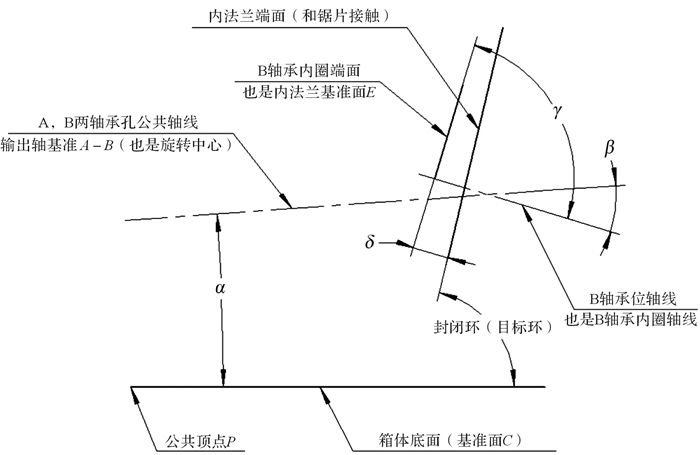
根据各个零件特征上影响角度偏差的公差标注,将相关特征的几何公差转换为角度公差后,接着应进行偏差累积分析。首先,按照第2节的方法将切割机的原始角度尺寸链(如图 23)画成含公共顶点的角度尺寸链,然后确定起始线、终止线以及封闭环(即目标环),设定逆时针方向为正方向。从起始线开始围绕公共顶点依次旋转到终止线,逆时针为正(增环),顺时针为负(减环),如图 24所示。累积分析所需的各角度偏差值见表 2。
|
| 图 23 木材切割机的原始角度尺寸链示意图 Fig.23 Original angle dimension chain diagram of wood cutting machine |

|
| 图 24 木材切割机的带公共顶点的角度尺寸链示意图 Fig.24 Diagram of angle dimension chain with common vertex of wood cutting machine |
| 增/减环 | 角度代号 | 基本角度值/(°) | 角度偏差/(°) |
| + | α | 0 | ±0.207 |
| - | β | 0 | ±0.087 |
| + | γ | 90 | ±0 |
| + | δ | 0 | ±0.087 |
| 封闭环 | θ | 90 | ±0.381(极值法) |
由表 2的计算可知,切割机的底面和切割锯片之间的夹角可在90°±0.381°范围内变化。将此结果和设计目标值进行比较,若不满足功能需求,需调整各组成环所对应特征的几何公差值,再次进行分析,直到最终的计算结果满足设计要求。
4 结语1) 为了有效控制平面之间的角度偏差,在图样上标注几何公差时可在公差框格内“公差带、要素和特征规范”部分附加贴切要素符号。最新的ISO1101和GB/T 1182(征求意见稿)也将T圈纳入标准中;当被测要素使用T圈附加符号后,可控制被测(实际)要素切平面与基准面之间的方向关系(角度)。
2) 在角度偏差累积分析时,应先将图样上标注的各个相关几何公差换算成角度公差,然后借助角度尺寸链进行角度偏差累积计算。几何公差参与角度尺寸链的计算时,需根据实际情况进行相应处理。若累积偏差不满足设计目标,则需要对各个组成环的几何公差进行调整。
3) 木材切割机实例分析中隐含了假设锯片是一个刚性零件,实际上锯片在切割过程中容易发生变形,这需要在设计计算时另作考虑;另外,角度尺寸链实例分析中只针对平面角度尺寸链,空间角度尺寸链的累积分析以及几何公差在控制空间角度累积时的工程实例需进一步研究。
| [1] | International Organization for Standardization. Geometrical product specifications (GPS)-Dimensional tolerancing-Part 2: Dimensions other than linear sizes: ISO 14405-2: 2011(E)[S]. Switzerland: International Organization for Standardization, 2011: 11-12. |
| [2] |
国家质量监督检验检疫总局, 全国产品尺寸与几何技术规范标准化委员会. 产品几何技术规范(GPS)线性和角度尺寸与公差标注: +/-极限规范台阶尺寸、距离、角度尺寸和半径: GB/Z 24638-2009[S]. 北京: 中国标准出版社, 2009: 4-5.
General Administration of Quality Supervision, Inspection and Quarantine of PRC. Geometrical product specifications (GPS)-Linear and angular dimensioning and tolerancing: +/-limit specifications-Step dimensions, distances, angular size and radii: GB/Z 24638-2009[S]. Beijing: Standards Press of China, 2009: 4-5. |
| [3] | International Organization for Standardization. Geometrical product specifications (GPS)-Geometrical tolerancing-Tolerances of form, orientation, location and run-out: ISO_1101_2017(E)[S]. Switzerland: International Organization for Standardization, 2017: 26-28. |
| [4] | American Society of Mechanical Engineers. Dimensioning and tolerancing principles: ASME Y14. 5-2009[S]. New York: ASME Press, 2009: 197. |
| [5] |
张景勘.
平面角度尺寸链(上)[J]. 机械工艺师, 1987(1): 41–42.
ZHANG Jing-kan. Plane angle dimension chain (upper)[J]. Machinery Manufacturing Engineer, 1987(1): 41–42. |
| [6] |
陈穗玉.
尺寸链角度环增减性质的判别[J]. 机械制造, 1989(10): 7–9.
CHEN Sui-yu. Discrimination of the increase and decrease of dimension chain angle ring[J]. Machinery, 1989(10): 7–9. |
| [7] | FISCHER B R. Mechanical tolerance stackup and analysis[M]. 2th ed. New York: CRC Press, 2011: 97-129. |
| [8] | YAN H, CAO Y, YANG J. Statistical tolerance analysis based on good point set and homogeneous transform matrix[J]. Procedia Cirp, 2016, 43: 178–183. DOI:10.1016/j.procir.2016.02.042 |
| [9] | YANG J, WANG J, WU Z, et al. Statistical tolerancing based on variation of point-set[J]. Procedia Cirp, 2013, 10: 9–16. DOI:10.1016/j.procir.2013.08.006 |
| [10] |
FRANK Mannewitz. 复杂公差分析的简单运算[J]. 陈巍, 孙宝寿, 冯革群, 译. 工程设计学报, 2008, 15(4): 237-243.
FRANK Mannewitz. Complex tolerance analyses[J]. Translated by CHEN Wei, SUN Bao-shou, FENG Ge-qun. Chinese Journal of Engineering Design, 2008, 15(4): 237-243. |
| [11] | CAO Y L, MATHIEU L, JIANG J. Key research on computer aided tolerancing[J]. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering), 2015, 16(5): 335–340. |
| [12] | ARMILLOTTA A. A method for computer-aided specification of geometric tolerances[J]. Computer-Aided Design, 2013, 45(12): 1604–1616. DOI:10.1016/j.cad.2013.08.007 |
| [13] | CHENG Y, NI Z, LIU T, et al. An intelligent approach for dimensioning completeness inspection in 3D based on transient geometric elements[J]. Computer-Aided Design, 2014, 53(5): 14–27. |
| [14] | CHAVANNE R, ANSELMETTI B. Functional tolerancing:virtual material condition on complex junctions[J]. Computers in Industry, 2011, 63(3): 210–221. |
| [15] | AMILLOTTA A. A method for computer-aided specification of geometric tolerances[J]. Computer-Aided Design, 2013, 45(12): 1604–1616. DOI:10.1016/j.cad.2013.08.007 |
| [16] |
赵嫚, 茅健.
面向制造过程的装配公差模型研究[J]. 工程设计学报, 2014, 21(6): 529–533.
ZHAO Man, MAO Jian. Research on model of assembly tolerance for manufacturing process[J]. Chinese Journal of Engineering Design, 2014, 21(6): 529–533. |
| [17] |
胡洁, 吴昭同.
计算机辅助形位公差大小的最优分配[J]. 工程设计学报, 2000, 7(4): 28–31.
HU Jie, WU Zhao-tong. Computer aided optimal allocation of geometric tolerance values[J]. Chinese Journal of Engineering Design, 2000, 7(4): 28–31. |
| [18] |
杨将新, 徐旭松, 曹衍龙, 等.
基于装配定位约束的功能公差规范设计[J]. 机械工程学报, 2010, 46(2): 1–8.
YANG Jiang-xin, XU Xu-song, CAO Yan-long, et al. Functional tolerance specification design based on assembly positioning[J]. Journal of Mechanical Engineering, 2010, 46(2): 1–8. |


