近年来,随着石油钻探领域不断扩大,钻探的地层更显复杂[1-2],因此要求钻头具有更好的地层适应性。聚晶金刚石复合片(polycrystalline diamond compact,PDC)钻头在硬地层或者软硬交错的地层中可钻性差,难以满足高效破岩的需求[3-4]。因此设计出同时具有牙轮钻头和PDC钻头的使用特性,并且有较长寿命、较高钻井效率的新型复合钻头是目前石油钻井技术领域急需解决的课题之一。复合钻头可以降低扭转振动以及转矩,提高钻井效率和导向能力,能在致密泥页岩、非均质地层中高效钻进[5-8]。目前国内外学者[9-13]先后提出了不同结构类型的复合钻头及其技术专利,并进行了现场应用。这些复合钻头主要为三牙轮复合钻头。随着深井、超深井以及小井眼钻探数量不断增多,结合单牙轮钻头在复杂地层中工作的优越性,本文设计出一种混合式单牙轮钻头,并通过数值模拟和实验验证的方法对其破岩性能进行分析验证。
1 混合式单牙轮钻头的理论模型 1.1 混合式单牙轮钻头几何学与运动学分析混合式单牙轮钻头与单牙轮钻头有相似的几何结构。如果已知的钻头半径R、牙爪轴倾角β、牙轮上任一点M到牙轮底平面的垂直距离h、M到牙轮轴线的垂直距离r以及牙轮底平面中心到参考水平基准面的初始距离Z0的大小, 则牙轮上任一点M(x, y, z)的绝对坐标值表示为[14]:
| $ \left\{ \begin{array}{l} X = \left( {R - h} \right){\rm{sin}}\;\beta {\rm{cos}}\;\theta + r\left( {{\rm{cos}}\;\alpha {\rm{cos}}\;\beta {\rm{cos}}\;\theta + {\rm{sin}}\;\alpha {\rm{sin}}\;\theta } \right)\\ Y = \left( {R - h} \right){\rm{sin}}\;\beta {\rm{sin}}\;\theta - r\left( {{\rm{sin}}\;\alpha {\rm{cos}}\;\theta - {\rm{cos}}\;\alpha {\rm{cos}}\;\beta {\rm{sin}}\;\theta } \right)\\ Z = {Z_0} - h{\rm{cos}}\;\beta - r{\rm{cos}}\;\alpha {\rm{sin}}\;\beta \end{array} \right. $ | (1) |
式中:θ=ω0t, α=ω1t,ω1,ω0分别为钻头和牙轮的转速。
单牙轮钻头工作时,牙掌围绕自身轴线转动,牙轮围绕牙掌轴线公转,同时沿着牙掌轴线钻进, 所以说牙轮上某定点的运动是复合运动。将式(1)中的θ和α看成时间的函数,则式(1)可转化为牙齿运动方程。
1.2 岩石的本构模型岩石采用砂岩,用高应变、大变形的H-J-C模型进行模拟。H-J-C模型的强度以规范化等效应力描述[15-17]:
| $ {\sigma ^*} = \left[ {A\left( {1 - D} \right) + B{p^{*N}}} \right]\left( {1 + C{\rm{ln}}{{\dot \varepsilon }^{\rm{*}}}} \right) $ |
式中:σ*=σ/fc,为标准化的等效应力,σ为岩石的实际等效应力,fc为岩石的准静态单轴抗压强度;p*=p/fc,为标准化的静水压力;
损伤因子D(0≤D≤1)由等效塑性应变和等效塑性体积应变累加得到:
| $ D = \sum {\frac{{\Delta {\varepsilon _{\rm{p}}} + \Delta {\mu _{\rm{p}}}}}{{\varepsilon _{\rm{p}}^{\rm{f}} + \mu _{\rm{p}}^{\rm{f}}}}} $ |
式中:Δεp为等效塑性应变增量;Δμp为等效塑性体积应变增量;
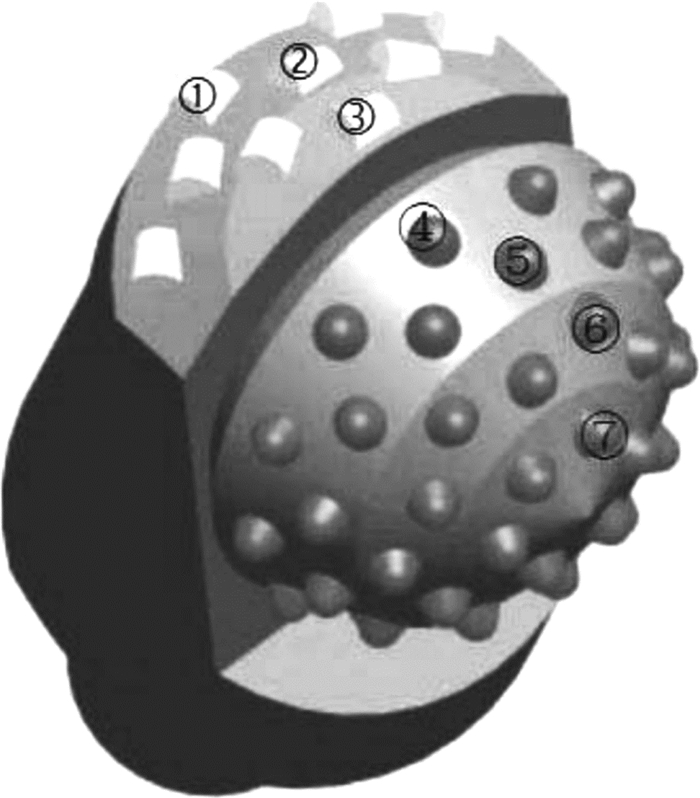
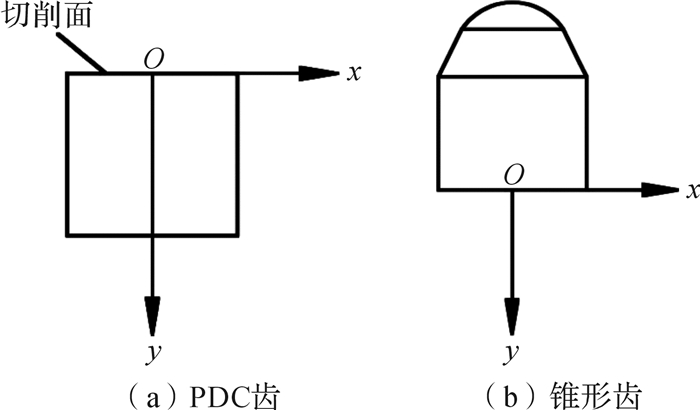
根据研究的重点对钻头模型进行简化。简化后混合式单牙轮钻头由牙掌、牙轮和切削元件构成。通过设计,将牙掌结构与牙轮结构相连接,并且分别在牙轮和牙掌上安装牙齿和切削元件。混合式单牙轮钻头对地层有更好的适应性:牙轮大端通过井底中心,起到提高破岩效率、延缓钻头失效的作用;牙轮小端的锥形齿起保径作用。本文以牙掌和牙轮上分别安装PDC齿和锥形齿为例进行数值模拟。给不同齿圈上的牙齿编号,以研究不同编号牙齿的载荷规律。因为钻头在钻进岩石时,相同齿圈位置的牙齿具有相同的载荷规律,所以取不同齿圈的牙齿,依次编号为1,2,…,7,如图 1所示。通过单独建立牙齿的局部坐标系,来获得牙齿沿规定方向的主切削力。规定牙齿受压方向为y轴的正方向,如图 2所示,要求与台架测试指定牙齿主切削力方向一致。主切削力是指PDC齿对岩石剪切破坏时所受的剪切力和锥形齿对岩石冲击破坏时所受的岩石沿牙齿的轴向反力。
|
| 图 1 混合式单牙轮钻头模型及牙齿编号 Fig.1 Hybrid single cone bit model and teeth number |
|
| 图 2 混合式单牙轮牙齿局部坐标系示意图 Fig.2 Schematic diagram of hybrid single cone bit teeth local coordinate system |
在作有限元分析时,根据混合单牙轮结构设计特点以及合理的数据要求对模型进行简化,并作出如下假设:
1) PDC齿和岩石均为连续、各向同性材料;
2) 在切削过程中不考虑温度场的变化;
3) 钻头不重复破岩;
4) 井眼轴线和钻头旋转中心不发生偏移。
3.2 钻头与岩石相互作用有限元模型的建立数值仿真只研究钻头在钻进过程中不同齿圈牙齿的载荷大小和分布规律。在不考虑牙掌、牙轮形变的情况下,将它们设置为刚体。根据上述假设,在牙掌肩部施加钻压,同时设置牙掌的转速,并给牙掌添加关键字“*PART_INERTIA”,人为指定牙掌的质心在旋转中心线上。牙轮和牙掌通过铰链约束连接,锥形WC硬质合金牙齿和PDC齿分别绑定在牙轮和牙掌上。利用ANSYS/LS-DYNA软件进行模拟分析。首先设置几何模型各个部分的材料参数,然后进行网格划分。由于牙掌和牙轮不是直接参与破岩的部分,同时也不是本文研究的重点,所以采用较粗的网格进行划分。而直接与岩石接触的牙齿则用能描述牙齿几何形状的小尺寸网格进行划分。对于形状规则的岩石,通过映射网格划分方法来提高计算精度。要求对岩石的网格划分尽可能细,但由于网格的减小会引起计算时长呈几何级数增加,所以根据经验将岩石的网格尺寸设置为1.5~2 mm[18]。钻头与岩石相互作用有限元模型如图 3所示。

|
| 图 3 混合式单牙轮钻头与岩石相互作用有限元模型 Fig.3 Finite element model of interaction between hybrid single cone bit and rock |
为了分析牙齿上的载荷,在每一齿圈上选择一个牙齿作为研究对象,在硬质合金牙齿底面和PDC齿端面建立局部坐标系,并使得该坐标系能随牙齿一起运动。根据岩石基本力学参数,结合砂岩三轴围压实验[19]和Hopkinson压杆实验[20-22],给出了武胜砂岩和北碚灰岩的H-J-C本构模型参数,如表 1和表 2所示。
| 参数 | ρ/kg·m-3 | G/MPa | A | B | C | N | fc/GPa | T/GPa | εfmin | Sfmax | pc/GPa | μc | p1/GPa | μ1/GPa | D1 | D2 | K1/GPa | K2/GPa | K3/GPa | |
| 数值 | 2.35 | 5.43 | 0.55 | 1.23 | 0.009 7 | 0.89 | 0.068 | 4.35 | 1.0 | 0.01 | 20 | 0.023 | 1.25×10-3 | 2 | 0.174×10-3 | 0.04 | 1.0 | 39 | -223 | 550 |
| 参数 | ρ/kg·m-3 | G/MPa | A | B | C | N | fc/GPa | T/GPa | εfmin | Sfmax | pc | μc | p1 | μ1 | D1 | D2 | K1值模拟进尺量大于台架测试进尺量,但 | K2值模拟进尺量大于台架测试进尺量,但 | K3值模拟进尺量大于台架测试进尺量,但 | |
| 数值 | 2.69×10-9 | 1.33×104 | 0.73 | 1.9 | 0.007 | 0.98 | 105.95 | 6.76 | 1.0 | 0.01 | 20 | 0.023 | 1.25×10-3 | 2 | 0.174×10-3 | 0.04 | 1.0 | 39 | -223 | 550 |
不可避免的系统误差和随机误差导致了台架实验和数值仿真测得的钻压、钻头轴向力以及牙齿载荷等数据存在噪声。采用Danielson-Lanczos方法进行快速傅里叶变换,将周期函数转换成有限不同频域周期函数叠加,通过阀值滤波滤掉含有随机误差的高频信号,提高统计数据的准确性。
因为PDC齿与岩石连续接触,其载荷波动相对稳定,锥形齿与岩石接触不连续,且接触时间短,所以统计数据值由PDC齿和锥形齿载荷波动平均值和载荷峰值的算数平均值表示。
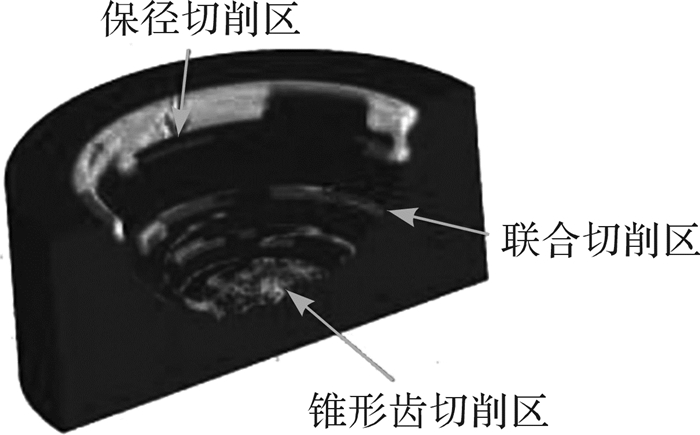
4.2 钻头井底模型图图 4是在给定钻压为25 kN和钻速为60 r/min条件下,混合式单牙轮钻头钻进砂岩后的井底模型图。钻头破岩形式和破岩效果可以通过井底仿真模型直接反映出来。
|
| 图 4 钻进后井底模型图 Fig.4 Model of bottom-hole after drilling |
从图 4中可以看出,井底模型分为3个切削区域:位于井眼最外圈的锥形齿保径切削区、井眼中心周围一定区域内的锥形齿切削区和位于两者之间的PDC齿和锥形齿联合切削区。判断3个区域的依据是:切削齿沿着牙轮和牙掌外轮廓线对称分布于钻头旋转中心线两侧,牙轮上的锥形齿跟随牙掌运动时,由于位置分布关系,牙轮小端起保径作用。剪切破岩为保径切削区域的主要破岩方式,在井底模型中表现为不连续的长距离刮痕。联合切削区域主要破岩方式为冲击和剪切,在井底模型中分别表现为连续刮痕、破碎坑和短距离刮痕。在钻进硬地层时,锥形齿冲击破岩后,PDC齿跟随其后刮削破石,比普通单牙轮钻头破岩效果更好。
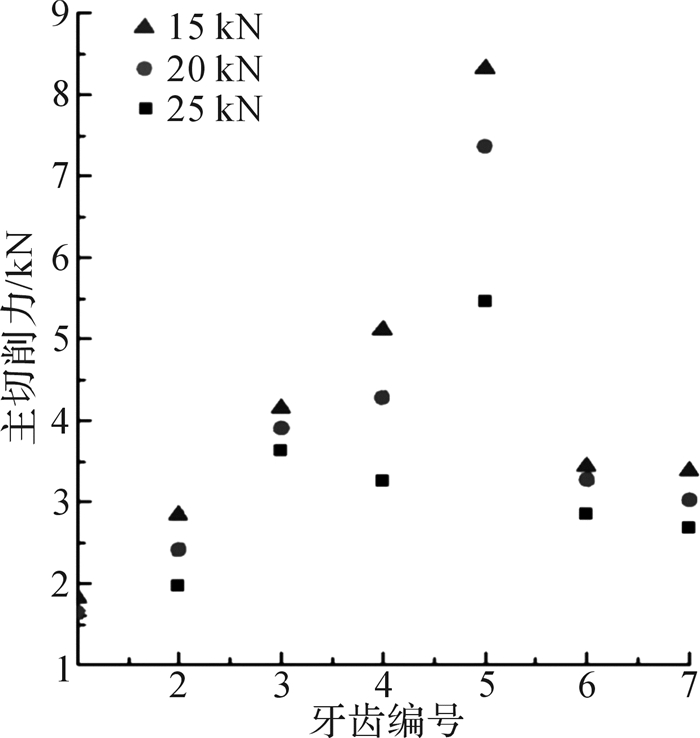
4.3 受力分析 4.3.1 牙齿主切削力图 5是钻压为15,20,25 kN下,混合式单牙轮钻头钻进时各牙齿主切削力的模拟值。如图所示,1至3号PDC齿的主切削力依次增大,这是因为内缘切削齿的切削岩量比外缘切削齿的要大,4至7号锥形齿的主切削力先增大后减小,这是因为5号锥形齿位于牙轮大端且通过井底中心,岩石对它的反作用力较大。说明牙掌底部和牙轮大端的牙齿是主要的切削部位,与钻头结构设计特点相符。牙齿载荷最大值出现在牙轮大端,牙轮大端通过井底中心,因此该区域岩石受到的反作用力相对更大,有利于提高钻头的破岩效率。各齿主切削力随着钻压的升高而增大,另一方面分析得出随着牙齿主切削力增大,切削岩石的效率提高。
|
| 图 5 不同钻压下钻头钻进砂岩时牙齿主切削力模拟值 Fig.5 The main cutting force simulation value of the tooth under different drilling pressure when drilling sandstone |
钻头侧向运动是由不平衡的钻头侧向力引起的,钻头的中心线并不平行于井筒中心线,造成井斜[24-25]。图 6是在钻压为20 kN条件下混合式单牙轮钻头钻进砂岩时侧向力时程模拟曲线,以及不同钻压下侧向力均值大小的对比。从图 6可以看出,侧向力在均值附近波动,产生这一现象是因为钻头与井壁之间的侧向力作用不均, 大小在改变。钻压与侧向力正相关,增大钻压可以提高破岩效率,但同时侧向力也会增大。由于地层的各向异性, 不断变化的钻头侧向力会引起井眼扩大和偏斜。

|
| 图 6 混合式单牙轮钻头钻进时钻头侧向力模拟值 Fig.6 Side force simulation value during drilling of hybrid single cone bit |
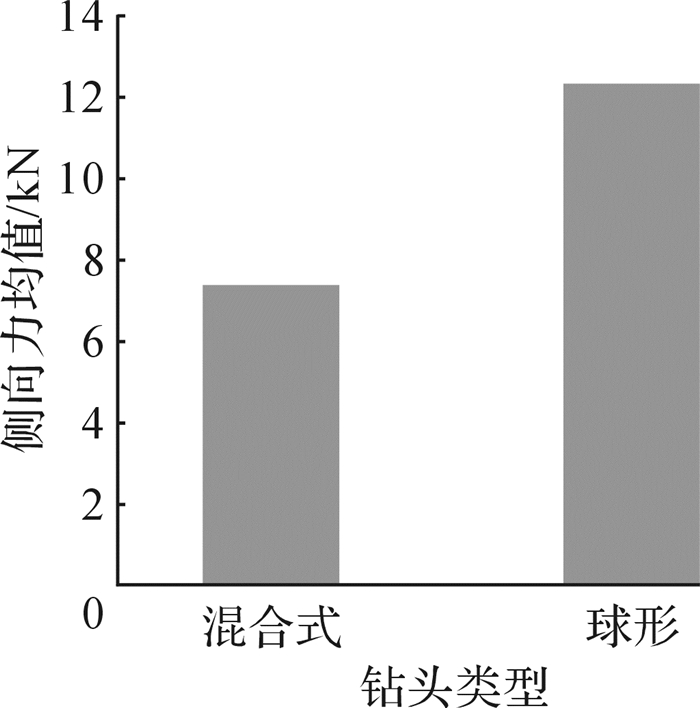
异形单牙轮钻头被广泛应用于石油钻井中,本文对混合式单牙轮钻头和球形单牙轮破岩时的钻头侧向力进行模拟。图 7为在钻压为20 kN和钻速为60 r/min下钻进砂岩时2种钻头侧向力均值对比。从图可以看出:混合式单牙轮钻头侧向力均值明显小于球形单牙轮钻头侧向力均值,前者比后者降低了39.6%。说明与球形单牙轮钻头相比,混合式单牙轮钻头稳定性更好,不易发生井斜。
|
| 图 7 混合式单牙轮钻头与球形单牙轮钻头侧向力模拟均值比较(钻压为25 kN,钻速为60 r/min) Fig.7 Comparison of side force simulation mean value between hybrid single cone bit and spherical single cone bit with drilling pressure of 25 kN and drilling speed of 60 r/min |
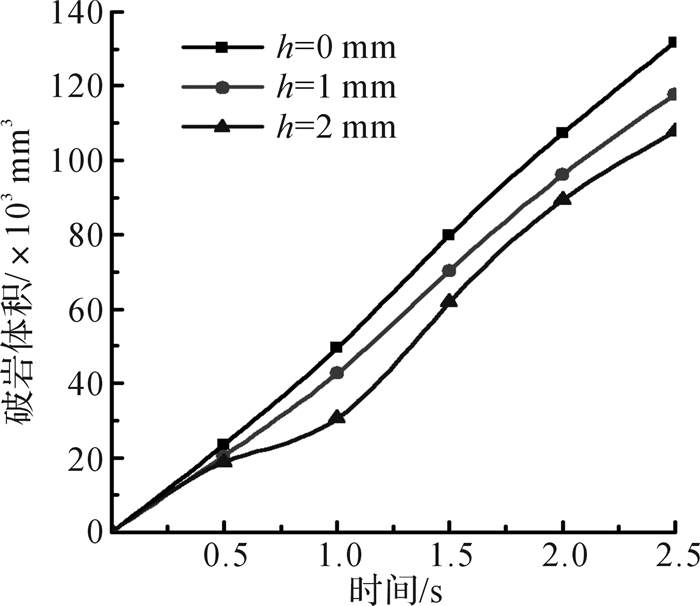
牙掌与牙轮的高度差h会影响破岩效率。当h=0 mm时表明牙掌与牙轮沿钻头的转动中心对称分布,h越大表明牙掌的位置越高。图 8是不同牙掌与牙轮高度差的混合式单牙轮钻头以20 kN钻压和60 r/min钻速钻进砂岩时,钻头破岩体积的时程曲线。
|
| 图 8 不同牙掌与牙轮高度差对混合式单牙轮钻头破岩体积的影响(钻压为20 kN, 钻速为60 r/min) Fig.8 Influence of height different between tooth-palm and roller on the rock breaking volume of hybrid single cone bit with drilling pressure of 20 kN and drilling speed of 60 r/min |
如图 8所示:在第0.5秒之前高度差h对破岩影响较小;之后,随着高度差增大,破岩体积减小。h=0 mm时,牙轮和牙掌上分布的牙齿受力均匀,此时破岩体积最大、破岩效率最高。
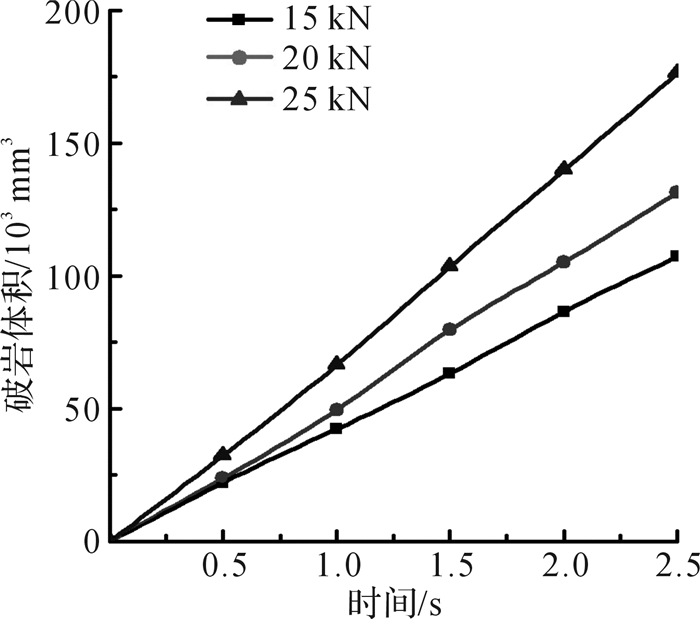
图 9是不同钻压下且h=0 mm时混合式单牙轮钻头破岩体积对比。从图中可以看出:钻压增大,破岩体积随之增大,破岩效率提高但呈非线性增加。
|
| 图 9 不同钻压下混合式单牙轮钻头破岩体积(h=0 mm) Fig.9 Rock breaking volume of hybrid single cone bit at h=0 mm and different drilling pressure |
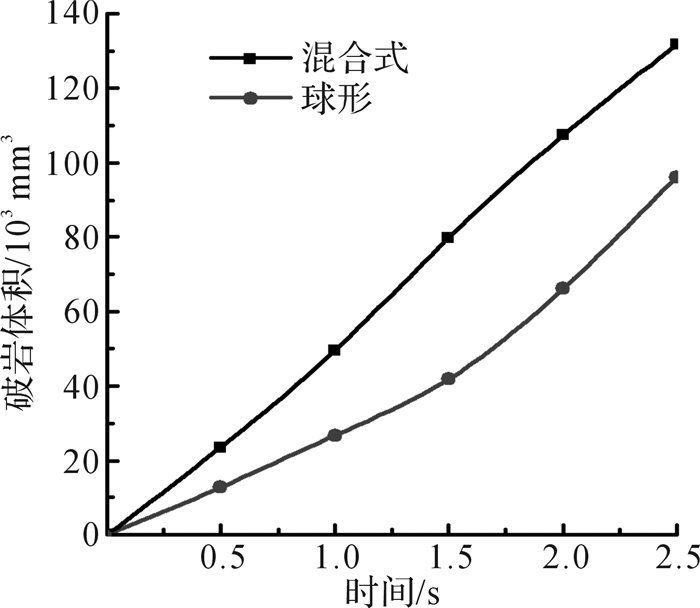
图 10是混合式单牙轮钻头和球形单牙轮钻头以20 kN钻压和60 r/min钻速钻进砂岩时,钻头破岩体积随时间变化的曲线对比。由图可知,球形单牙轮钻头破岩体积随时间积累增加缓慢,混合式单牙轮钻头最终破岩体积比球形单牙轮钻头的提高37%,说明设计的混合式单牙轮的破岩效率较高。
|
| 图 10 混合式单牙轮钻头与球形单牙轮钻头破岩体积模拟值比较(钻压为20 kN,钻速为60 r/min) Fig.10 Comparison of rock breaking volume simulation value between hybrid single cone bit and spherical single cone bit with drilling pressure of 20 kN and drilling speed of 60 r/min |
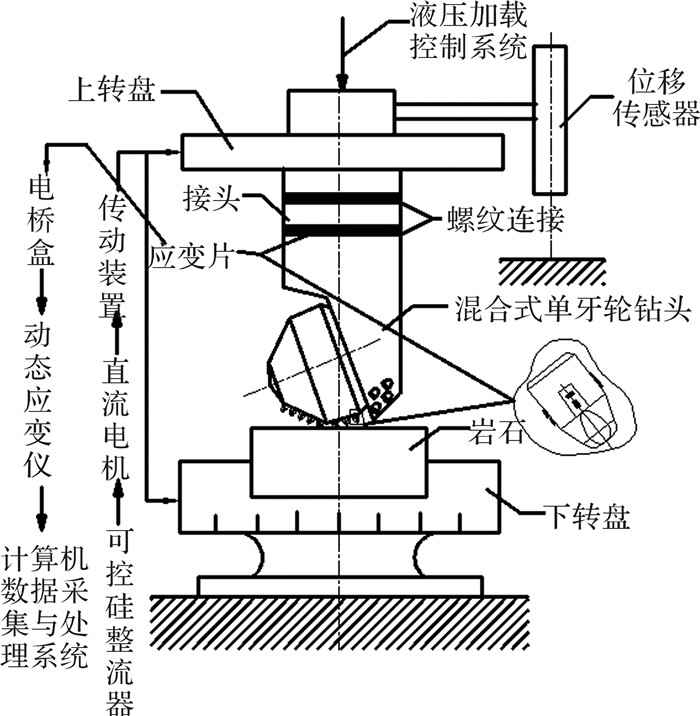
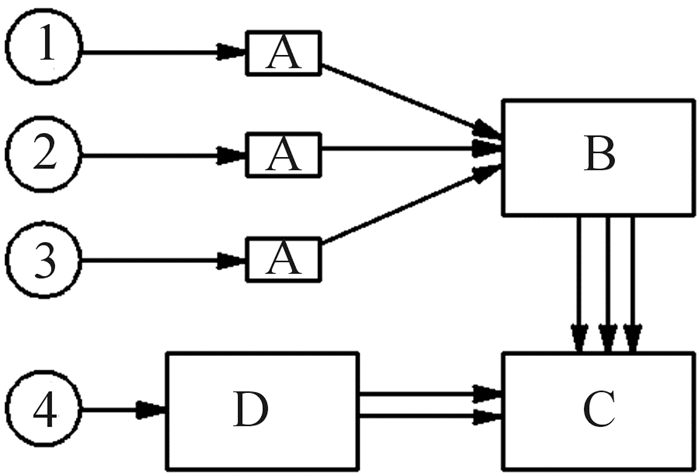
如图 11所示的混合式单牙轮实验台架能够模拟实际工作中给钻头施加钻压和钻速的工作条件。该实验台架有2个转盘,上转盘和下转盘都能实现0~200 r/min内的无级变速。由于应变片导线不能绕钻头扭转,所以通过钻头不动、岩石转动的方法来实现钻头相对岩石转动。实验中岩石转动及钻头转速调整是由直流电动机和传动装置来控制实现的。通过液压系统可加载钻压以及控制钻头的升降。通过不同的传感器测量钻压、钻头轴向力以及钻头进尺量,与计算机连接的动态应变仪用于数据的处理。其数据采集与处理系统示意图如图 12所示[23]。
|
| 图 11 混合式单牙轮钻头实验台架结构 Fig.11 Structure of hybrid single cone bit experiment bench |
|
| A—电桥盒;B—动态应变仪;C—计算机采集与处理系统;D—转速测定仪; 1—测量接头上的钻压信号;2—测量接头上的扭矩信号;3—测量钻头的进尺量信号;4—测量钻头转速信号 图 12 混合式单牙轮钻头实验台数据采集与处理系统示意图 Fig.12 Schematic diagram of data acquisition and processing system for hybrid single cone bit experiment bench |
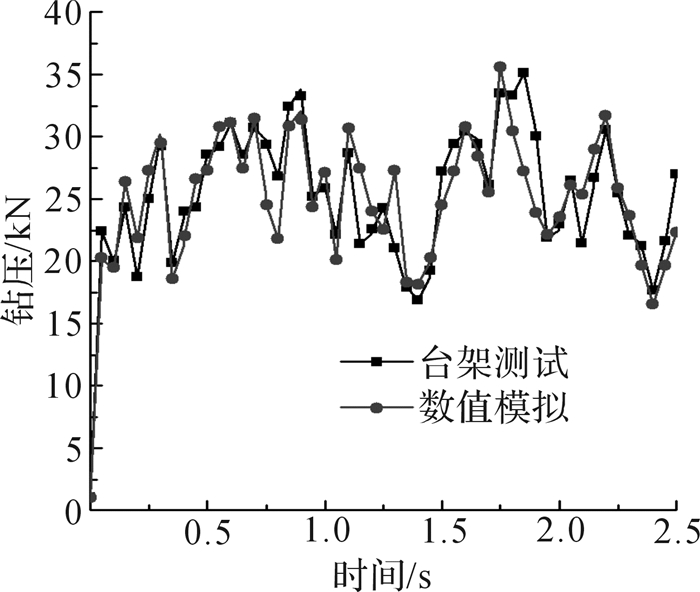
在台架测试中,钻压是通过液压系统加载的,钻压的振荡幅值可以由钻头上方的传感器测得;通过动态应变仪将应变片的应变信号转换为计算机能处理的电压信号来测得钻压。将台架测试测得的钻压的平均值作为数值模拟中的钻压,通过LS-DYNA软件得到钻头轴向力。钻压与钻头轴向力理论上是一对相互作用力,因此可以将轴向力定义为钻头钻压。如图 13是钻头以25 kN加载钻压钻进砂岩时,台架测试和数值模拟得到的钻压时程曲线。
|
| 图 13 混合式单牙轮钻头钻进时钻头钻压时程曲线(加载钻压为25 kN) Fig.13 Time history curve of drilling pressure during drilling of hybrid single cone bit with loading drilling pressure of 25 kN |
由于钻头破岩时,其旋转中心线上下振动,从图 13中看到钻压随时间变化的曲线在某一均值附近上下起伏。有限元分析得到钻头轴向力曲线与台架测试得到的钻压曲线形状相似,数值模拟的均值与台架测试值的相对误差在3%以内。因此数值模拟与台架测试得到的钻压基本相等,证明了数值模拟的可靠性。
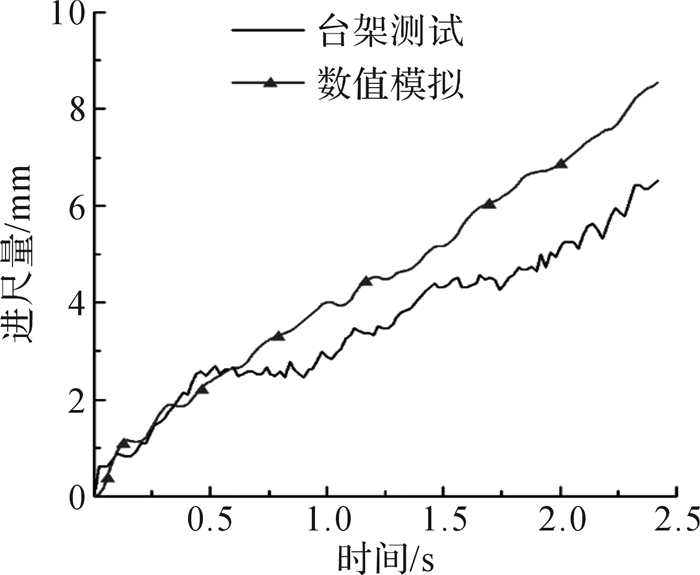
4.5.2 钻头进尺量应变电桥式位移传感器可将位移量转化为电信号,然后用动态应变仪来实现进尺量与电压的转换。在钻压为25 kN和钻速为60 r/min条件下,台架测试和数值模拟得到的钻头在钻进砂岩时的进尺量时程曲线如图 4所示,发现数值模拟进尺量大于台架测试进尺量,但其增加趋势基本一致。由于数值模拟中岩石力学参数与实际存在差异,且施加的钻压和钻速略大于台架测试时施加的钻压和钻速,所以导致数值模拟进尺量较大。
|
| 图 14 混合式单牙轮钻头钻进时钻头进尺量时程曲线(钻压为25 kN,钻速为60 r/min) Fig.14 Time history curve of footage during drilling of hybrid single cone bit with drilling pressure of 25 kN and drilling speed of 60 r/min |
1) 设计了一种新的单牙轮钻头结构,并设计牙掌的结构形式,与牙轮结构相连接,并且分别在牙轮和牙掌上安装锥形齿和PDC齿。分别建立实体模型和数值仿真模型,对台架测试和数值模拟结果作了对比。
2) 台架测试所得混合式单牙轮钻头钻压与进尺量与数值模拟基本一致,证明了数值模拟的可靠性。井底模式分为3个切削区域:锥形齿保径切削区、锥形齿切削区、PDC齿和锥形齿联合切削区。牙掌底部和牙轮大端的牙齿是主要的切削部位,与钻头结构设计特点相符。侧向力随钻压的增加而增大,易造成井斜。
3) 在给定相同钻压和钻速的条件下,与球形单牙轮钻头相比,混合式单牙轮钻头破岩效率提高37%,同时钻头的侧向力减少39.6%。不仅提高了机械钻速,而且大大降低了发生井斜的可能性。牙轮与牙掌的高度差h=0 mm时,钻头在相同时间段内的破岩体积最大,效率最高。
| [1] | ZHU H Y, DENG J G, XIE Y H, et al. Rock mechanics characteristic of complex formation and faster drilling techniques in Western South China Sea oilfields[J]. Ocean Engineering, 2012, 44: 33–45. DOI:10.1016/j.oceaneng.2012.01.031 |
| [2] |
邓金根, 朱海燕, 谢玉洪, 等.
南海西部海域难钻地层特征及破碎机制研究[J]. 岩土力学, 2012, 33(7): 2097–2102.
DENG Jin-gen, ZHU Hai-yan, XIE Yu-hong, et al. Rock mechanical properties and rock breaking mechanism of the complex formation of the western South China Sea oilfields[J]. Rock and Soil Mechanics, 2012, 33(7): 2097–2102. |
| [3] | DE S, MR I. Innovative PDC cutter technology leads to step out performance improvements in diverse applications in shale plays[C]//IADC/SPE Drilling Conference and Exhibition, San Diego, California, Mar. 6-8, 2012. |
| [4] | Al-SAEEDI M J, Al-FAYEZ F A, Al-MUDHAF M N, et al. Solving deep, hard/abrasive 16-in application challenges with new PDC technology saves operator 13 days rig time, kuwait[C]//SPE Project and Facilities Challenges Conference at METS, Doha, Qatar, Feb. 13-16, 2011. |
| [5] | PESSIER R, DAMSCHEN M. Hybrid bits offer distinct advantages in selected roller-cone and PDC-bit applications[J]. SPE Drilling & Completion, 2011, 26(1): 96–103. |
| [6] | DOLEZAL T, FELDERHOFF F C, HOLLIDAY A D, et al. Expansion of field testing and application of new hybrid drill bit[C]//SPE annual technical conference and exhibition, Denver, Colorado, Oct. 30-Nov. 2, 2011. |
| [7] | THOMSON I J, KRASUK R M, SILVA N, et al. Hybrid drill bit improves drilling performance in heterogeneous formations in Brazil[C]//Brasil offshore, Macaé, Jun. 14-17, 2011. |
| [8] |
邓宝, 张青锋, 王德贵, 等.
复合钻头技术及应用[J]. 机械工程师, 2016(1): 76–78.
DENG Bao, ZHANG Qing-feng, WANG De-gui, et al. Analysis and application of hybrid bit technology[J]. Mechanical Engineer, 2016(1): 76–78. |
| [9] | ALLEN J H. Two cone bit with extended diamond cutters: U. S. Patent 4285409[P]. 1981-08-25. |
| [10] | BAKER III W, GARNER L L, HARRIS C R. Hybrid rock bit: U. S. Patent 4343371[P]. 1982-08-10. |
| [11] | SCOTT D E, OLDHAM J T, LYNDE G D, et al. Combination milling tool and drill bit: U. S. Patent 5979571[P]. 1999-11-09. |
| [12] | YANG Y X, CHEN L, LIN M, et al. Combination scraping and impacting drill bit: WO/2013/170788[P]. 2013-11-21. |
| [13] |
胡琴, 刘清友.
复合齿形牙轮钻头及其破岩机理研究[J]. 天然气工业, 2006, 26(4): 77–79.
HU Qin, LIU Qing-you. Study on cone bit with composite tooth and its rock breaking mechanism[J]. Natural Gas Industry, 2006, 26(4): 77–79. |
| [14] |
邓嵘, 杨世良, 喻开安.
单牙轮钻头研究[J]. 西南石油大学学报(自然科学版), 1995, 17(1): 96–100.
DENG Rong, YANG Shi-liang, YU Kai-an. Study on single cone bit[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 1995, 17(1): 96–100. |
| [15] | HOLMQUIST T J, TEMPLETON D W, BISHNOI K D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications[J]. International Journal of Impact Engineering, 2001, 25(3): 211–231. DOI:10.1016/S0734-743X(00)00046-4 |
| [16] |
谢姣. 基于ANSYS/LS-DYNA数值模拟的爆破地震效应影响因素分析[D]. 西安: 长安大学公路学院, 2014: 39-42.
XIE Jiao. The analysis of blasting seismic effect factors based on ANSYS/LS-DYNA numerical simulation[D]. Xi'an: Chang'an University, School of Highway, 2014: 39-42. |
| [17] |
崔玉红, 周世才, 陈蕴生.
非贯通细观裂纹节理介质CT试验的数值模拟及影响参数讨论[J]. 岩石力学与工程学报, 2006, 25(3): 630–640.
CUI Yu-hong, ZHOU Shi-cai, CHEN Yun-sheng. Numerical analysis of meso-crack and meso-damage laws and its influential parameters for non-interpenetrated jointed media based on CT experiment[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 630–640. |
| [18] |
安美. 异形单牙轮钻头牙齿载荷数值模拟与实验验证[D]. 成都: 西南石油大学机电工程学院, 2015: 31-37.
AN Mei. Numerical simulation and experimental verification of tooth load for special-shaped single cone bit[D]. Chengdu: Southwest Petroleum University, School of Mechanical and Electrical Engineering, 2015: 31-37. |
| [19] |
段新伟, 李宝富.
砂岩三轴常规压缩物理和数值实验分析[J]. 河南理工大学学报(自然科学版), 2009, 28(5): 654–657.
DUAN Xin-wei, LI Bao-fu. Analysis of routine triaxial compression physical and numerical test of sandstone[J]. Journal of Henan Polytechnic University (Natural Science), 2009, 28(5): 654–657. |
| [20] |
平琦, 马芹永, 袁璞, 等.
煤矿砂岩SHPB动态压缩力学性能试验与分析[J]. 安徽理工大学学报(自然科学版), 2013, 33(4): 40–44.
PING Qi, MA Qin-yong, YUAN Pu, et al. Dynamic compression properties tests of sandstones from coalmine by SHPB apparatus[J]. Journal of Anhui University of Science & Technology (Natural Science), 2013, 33(4): 40–44. |
| [21] |
平琦.
砂岩动静态拉伸力学性能试验与对比分析[J]. 地下空间与工程学报, 2013, 9(2): 246–252.
PING Qi. Comparative analyses on dynamic and static tensile performances of sandstone[J]. Chinese Journal of Underground Space & Engineering, 2013, 9(2): 246–252. |
| [22] |
陆岳屏, 杨业敏, 寇绍全, 等.
霍布金生压力杆法测定砂岩、石灰岩动态破碎应力和杨氏模量[J]. 岩土工程学报, 1983, 5(3): 28–38.
LU Yue-ping, YANG Ye-min, KOU Shao-quan, et al. An experimental study of determining the dynamic strength and Young's moduli of sandstone and limestone by using the SHPB method[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(3): 28–38. |
| [23] |
邓嵘, 马德坤.
牙轮钻头侧向切削的计算机仿真[J]. 石油矿场机械, 2001, 30(5): 25–28.
DENG Rong, MA De-kun. Computer simulation of cone bit lateral cutting[J]. Oil Field Equipment, 2001, 30(5): 25–28. |
| [24] |
马德坤.
牙轮钻头工作力学[M]. 北京: 石油工业出版社, 2009: 88-92.
MA De-kun. The operational mechanics of the roller bit[M]. Beijing: Petroleum Industry Press, 2009: 88-92. |
| [25] |
彭亚洲. PDC全钻头破岩数值模拟方法研究[D]. 成都: 西南石油大学机电工程学院, 2015: 55-56.
PENG Ya-zhou. Research on numerical simulation method of rock breaking by PDC-full-drill bit[D]. Chengdu: Southwest Petroleum University, School of Mechanical and Electrical Engineering, 2015: 55-56. |


