2. 西南石油大学 石油天然气装备教育部重点实验室, 四川 成都 610500
2. Key Laboratory of Oil & Gas Equipment, Ministry of Education, Southwest Petroleum University, Chengdu 610500, China
随着智能化水平的提高,移动机器人已成为国内外学者研究的热点。作为机器人领域核心研究问题之一——全遍历路径规划,在实际生活生产中有着广泛的应用,如地面清洁、目标搜索、矿产勘查及缺陷检测等[1-5]。移动机器人全遍历路径规划主要需要解决2个问题:1)需遍历工作区域内除障碍物以外的全部区域;2)遍历过程中尽量避免重复遍历[6-10]。迄今为止,针对移动机器人全遍历路径规划的研究已有大量的成果,但都集中于地面移动机器人,对爬壁机器人的研究较少[11-14]。
文献[1]提出了一种全覆盖信度函数路径规划算法。使用不同的函数值表示障碍物、已覆盖栅格和未覆盖栅格;同时引入方向信度函数对栅格信度函数值进行优化;最后,机器人根据栅格信度函数进行遍历路径规划。该方法不仅能实现工作区域的全遍历,并且能够引导机器人快速有效地逃离死区;但该算法未对工作区域分块,对于面积较大的工作环境容易产生累积误差,增大了漏检率。文献[15]提出了一种精确单元分解法。首先,将工作区域分解为一系列子区域;接着,采用旅行商算法找出子区域的遍历顺序;最后,通过迂回运动依次遍历各子区域,直到达到全遍历为止。该方法能实现工作区域的全遍历,但是没有考虑机器人陷入死区的情况,当机器人陷入死区时,其运动路径可能会发生紊乱,加大重复遍历率。
本文根据储罐探伤爬壁机器人(以下简称机器人)工作环境的特殊性,结合单元分解、邻接矩阵及路径选择函数提出了一种基于栅格地图的矩形分解[16]全遍历路径规划算法。首先,建立栅格环境模型,对每个栅格赋予xi值来表示其栅格状态;接着,采用矩形分解法将工作环境划分为若干子区域,通过图的深度优先搜索算法和邻接矩阵确定各子区域的衔接顺序;最后,在子区域的遍历和切换过程中,引入方向函数yi来判断机器人是否陷入死区,结合栅格的xi值提出路径选择函数fi,引导机器人快速逃离死区。
1 储罐壁面简化机器人工作于圆柱形储罐外壁,由于储罐外壁是一个曲面,因此其工作环境是一个三维空间。机器人在储罐外壁工作时的俯视图如图 1所示。

|
| 1—机器人主体;2—储罐外壁;O—储罐圆心;r—储罐半径;B—机器人机身宽度;P—机器人质心;A—机器人左端和O点连线与储罐壁面的交点;α—机器人曲率角 图 1 爬壁机器人在储罐外壁工作的俯视图 Fig.1 Top view of wall climbing robot working on the outer wall of tank |
目前国内外石化行业中常用的圆柱形储罐直径为24.0~40.0 m,高为9.6~16.3 m。本文以储罐直径为24.0 m、高为9.6 m,机器人机身宽度B=300 mm为基础进行计算。
| $ \alpha = \arctan \frac{B}{{2r}} = \arctan \frac{{300}}{{24\;000}} \approx {0.716^ \circ } $ | (1) |
从式(1)可以看出:α的值很小,可忽略不计;并且随着储罐容积的增大,α值呈降低的趋势。因此,可近似看作机器人在竖直平面内工作,即简化为一个二维平面问题。
2 机器人遍历基本路径确定机器人在罐壁工作时可按螺旋式或迂回式覆盖全部工作区域。螺旋式工作时,机器人在壁面的转向次数多且定位比较困难;而迂回式更易于控制和实现机器人对整个罐壁的全覆盖[17-19]。因此,本文选择迂回式作为机器人的全覆盖方式。
本文将机器人视为一个质点,爬壁机器人简化模型如图 2所示。

|
| 1—机器人主体;2—驱动轮;3—超声波传感器;c—机器人质心;B—机器人机身宽度;S—两驱动轮内侧的纵向距离;b,d—驱动轮的宽度和直径;m—驱动轮外侧距机器人前(后)端面的距离;n—超声波传感器距机器人前端面的距离;D—超声波传感器的宽度 图 2 爬壁机器人简化模型 Fig.2 Simplified model of wall climbing robot |
机器人在储罐外壁的遍历运动为匀速直线运动和匀速回转运动两类,本节将根据漏检面积SU分析直线运动及回转运动的遍历效率,以确定遍历基本路径。
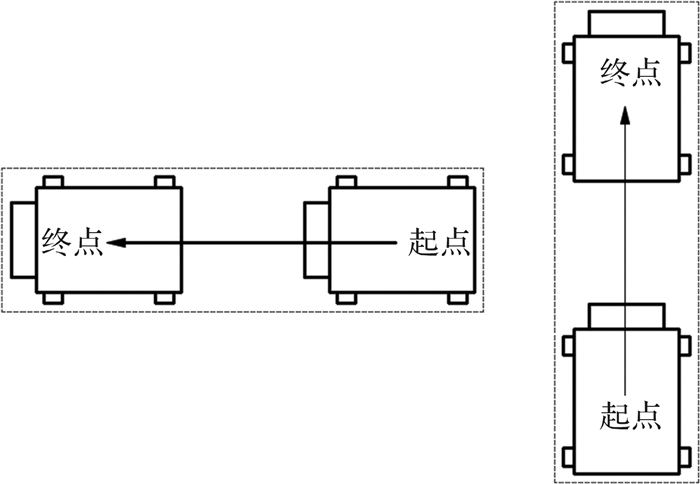
1) 直线运动:机器人以某一恒定速度从起点直线移动到终点,如图 3所示。显然,直线运动漏检面积SUL=0。
|
| 图 3 爬壁机器人直线运动 Fig.3 Linear motion of wall climbing robot |
2) 回转运动:假定机器人超声波传感器的重叠面积为零(即以超声波阵列传感器宽度D的二分之一作为机器人质心c的转弯半径),当机器人传感器扫过的最远处与障碍物边界相切(即如图 4所示距离障碍物边界为I)时进行回转运动。

|
| 图 4 爬壁机器人回转运动 Fig.4 Rotary motion of wall climbing robot |
则:
| $ I = \sqrt {{D^2} + {{\left( {\frac{S}{2} + d + m + n} \right)}^2}} - \left( {\frac{S}{2} + d + m + n} \right) $ | (2) |
回转运动的漏检面积为:
| $ \begin{array}{*{20}{c}} {{S_{{\rm{UR}}}} = \left( {S + 2I + 2n + 2m + 2d} \right)D - }\\ {\frac{{\pi I}}{2}\left( {S + I + 2n + 2m + 2d} \right)} \end{array} $ | (3) |
综上所述,机器人直线运动时不存在漏检,回转运动时存在部分漏检区域。为使漏检面积更小,应减少机器人回转运动次数。
3 基于栅格地图的单元分解全遍历路径规划算法机器人需以尽可能高的覆盖率和尽可能低的重复率覆盖储罐外壁所有可达区域。由于储罐罐壁表面积较大(根据第1节的分析,其表面积为723.8~2 048.3 m2),为了减小定位误差造成的漏检率,本文采用矩形分解法将储罐外壁划分为若干子区域,机器人依次遍历各子区域以完成对罐壁的全覆盖。
3.1 栅格环境建模本文采用栅格地图来表示储罐外壁,方形栅格的大小为机器人前端超声波阵列传感器的宽度D;储罐外壁常见的障碍物有常压人孔、手孔、盘梯、接管及焊缝等。根据栅格是否被障碍物占据,赋予每个栅格一个表示栅格单元状态的xi值,机器人在运动过程中实时更新xi值。xi的取值如公式(4)所示:
| $ {x_i} = \left\{ {\begin{array}{*{20}{l}} { - \blacksquare ,}&{\text{障碍栅格}} \\ {1,}&{\text{自由栅格}} \\ {1 - i\left( {i = 1,2,3, \cdots } \right),}&{{\text{遍历过}}i{\text{次的自由栅格}}} \end{array}} \right. $ | (4) |
定义1:若栅格全部或部分被障碍物占据,则将此栅格定义为障碍栅格;若栅格未被障碍物占据,则将此栅格定义为自由栅格。
建立一个环境模型如图 5所示,其中白色部分为自由区域,黑色部分为障碍物区域;将此环境模型进行栅格化处理后得到栅格地图,如图 6所示。

|
| 图 5 环境模型 Fig.5 Environmental model |

|
| 图 6 栅格地图 Fig.6 Grid map |
采用矩形分块的思想分解目标环境。图 6中,每个栅格可以用(x,y)来表示,x表示栅格所在的列数,y表示栅格所在的行数。矩形分块的具体步骤为:
1) 找出每个障碍物中x值最小的栅格,如果x值最小的栅格不止一个,则找出其中y值最小的栅格并记为M(x1,y1);
2) 找出每个障碍物中x值最大的栅格,如果x值最大的栅格不止一个,则找出其中y值最大的栅格并记为N(x2,y2);
3) 将每个障碍物以其M点和N点虚拟为一个矩形障碍物;
4) 以障碍物的M点为起点沿纵向做割线,直至到达地图边界或障碍物或其他的分割线;
5) 以障碍物的N点为起点沿横向做割线,直至到达地图边界或障碍物或其他的分割线。
将图 6的栅格环境地图进行如上的单元分解后得到的结果如图 7、图 8所示。

|
| 图 7 障碍物矩形化 Fig.7 Rectangular obstacles |

|
| 图 8 栅格地图分块 Fig.8 Several blocks of grid map |
将环境地图分解为若干子区域后,机器人需要做的是按照一定的方式将各子区域进行有效衔接,在最短时间内完成各子区域有序的遍历;同时要满足重复覆盖率小、路径最短的要求。
定义2:分块环境地图中,如果任意2个矩形子区域之间存在公共边或者公共点,定义这2个子区域相邻;反之则不相邻。
最短路径问题是图论的一个重要应用。有序的三元组G=(V, E, ω)称为一个加权无向图,其中:V=(v1, v2, …, vn)为有穷非空集,称为顶点集,文中以每个子区域的中心作为顶点;E称为边集,文中以两相邻顶点间的连线作为无向图的边;ω为权重,文中以两相邻顶点间的距离作为权值。分块环境中各子区域的无向图如图 9所示。

|
| 图 9 分块环境中各子区域无向图 Fig.9 Undirected graph of sub-regions in block environment |
对于有n个顶点的加权无向图,其邻接矩阵A=(aij)n×n,其中:
| $ {{a}_{ij}}=\left\{ \begin{align} &{{\omega }_{ij}},\ \ \ \ 两顶点相邻 \\ &0,\ \ \ \ \ \ \ i=j \\ &\blacksquare ,\ \ \ \ \ 两顶点不相邻 \\ \end{align} \right. $ | (5) |
则加权无向图G的邻接矩阵为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} 0 \hfill \\ 19.24D \hfill \\ \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \end{gathered} &\begin{gathered} 19.24D \hfill \\ 0 \hfill \\ 9.66D \hfill \\ 17.1D \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \end{gathered} &\begin{gathered} 9.66D \hfill \\ 20.5D \hfill \\ 20.5D \hfill \\ 16.8D \hfill \\ 17.1D \hfill \\ \blacksquare \hfill \\ \blacksquare \hfill \\ \end{gathered} &\begin{gathered} \blacksquare \hfill \\ 17.1D \hfill \\ 0 \hfill \\ 0 \hfill \\ 20.5D \hfill \\ 12.18D \hfill \\ 20.11D \hfill \\ \end{gathered} &\begin{gathered} \blacksquare \hfill \\ \blacksquare \hfill \\ 16.8D \hfill \\ 20.5D \hfill \\ 0 \hfill \\ \blacksquare \hfill \\ 12.18D \hfill \\ \end{gathered} &\begin{gathered} \blacksquare \hfill \\ \blacksquare \hfill \\ 17.1D \hfill \\ 12.18D \hfill \\ \blacksquare \hfill \\ 0 \hfill \\ 20.5D \hfill \\ \end{gathered} &\begin{gathered} \blacksquare \hfill \\ \blacksquare \hfill \\ \blacksquare \blacksquare \hfill \\ 20.11D \hfill \\ 12.18D \hfill \\ 20.5D \hfill \\ 0 \hfill \\ \end{gathered} \end{array}} \right] $ |
定义3:在无向图G中,仅经过每个顶点一次且权重最小的路径,称为最优全遍历路径。
按深度优先搜索算法可找出无向图G的最优全遍历路径,其过程如图 10所示。首先用加权邻接矩阵表示子区域无向图,任意设置一个起点,并置访问标志;然后扫描加权矩阵里起点所在的行,搜索与起点距离最近且未被访问过的顶点,并置访问标志;接着扫描加权矩阵里上一顶点所在的行,搜索与上一顶点距离最近且未被访问过的顶点,并置访问标志。若顶点存在,则继续向后扫描;若顶点不存在,则返回上一顶点重新搜索;重复以上步骤,直到所有顶点都被访问过,输出此顶点序列。按照这种算法,假设机器人从顶点①出发,则最优全遍历路径为:①→③→②→④→⑥→⑦→⑤。

|
| 图 10 图深度优先搜索算法流程 Fig.10 The process of graph depth-first search algorithm |
本文采用迂回式规划遍历各子区域,根据第2节的分析,为减小机器人的漏检面积,应尽量减少爬壁机器人回转运动的次数。
定义4:当机器人周边的相邻区域均为边界、障碍物或者是已覆盖过的栅格时,爬壁机器人陷入死区。
如图 11所示,当机器人陷入死区后,为了让机器人以尽可能短的路径逃离死区,本文以机器人当前所在栅格位置与距离最近且未遍历栅格位置和下一步可能移动到的栅格位置的角度差作为移动的方向向导,引导机器人快速逃离死区。引入方向函数yi,其定义为:
| $ {y_i} = \cos \Delta {\varphi _i} $ | (6) |

|
| 图 11 机器人陷入死区 Fig.11 A robot falling into the dead zone |
其中移动方向角之差Δφi为:
| $ \Delta {\varphi _i} = {\varphi _{\text{T}}} - {\theta _i} = \arctan \left| {\frac{{{y_{{\text{U}}i}} - {y_{{\text{p}}i}}}}{{{x_{{\text{U}}i}} - {x_{{\text{p}}i}}}}} \right| - \arctan \left| {\frac{{{y_{{\text{N}}i}} - {y_{{\text{p}}i}}}}{{{x_{{\text{N}}i}} - {x_{{\text{p}}i}}}}} \right| $ | (7) |
式中:Δφi是机器人当前栅格位置和下一步可能移动到的栅格位置连线与机器人当前栅格位置和最近未覆盖栅格位置连线的夹角,Δφi∈(0, π);(xpi, ypi)是机器人当前所在栅格位置坐标;(xNi, yNi)是机器人下一步可能移动到的栅格位置坐标;(xUi, yUi)是距离机器人当前位置最近未遍历的栅格位置坐标;φT是机器人当前所在位置和最近未覆盖栅格位置之间连线与横坐标之间的夹角;θi是机器人当前栅格位置与下一步可能移动到的栅格位置之间连线与横坐标之间的夹角。
机器人移动方向函数如图 12所示。

|
| 图 12 机器人移动方向函数示意图 Fig.12 Schematic diagram of robot movement direction function |
为了使机器人避开障碍物并以尽可能短的路径逃离死区,本文根据栅格的xi值和方向函数yi,定义一个路径选择函数fi,路径选择的原则是机器人始终向着路径函数值最大的方向运动。其定义为:
| $ {f_i} = {x_i} + t{y_i} $ | (8) |
| $ {U_i} \Leftarrow {f_{{U_i}}} = \max \left\{ {{f_i} = {x_i} + t{y_i},i = 1,2, \cdots ,k} \right\} $ | (9) |
式(9)中:Ui表示机器人下一个位置;t是一个权值常数,0 < t < 1;k是与当前栅格相邻的栅格个数。以图 11中机器人陷入死区时为算例,结合路径选择函数fi(设置权值常数t=0.5)分析机器人逃离死区的具体路径。根据公式(4)计算机器人在死区位置时其周围栅格的xi值,如图 13(a)所示;根据公式(6)和公式(7)计算机器人在死区位置时其周围栅格的方向函数值yi,如图 13(b)所示;根据公式(8)计算机器人在死区位置时其周围栅格的路径选择函数值fi,如图 13(c)所示。

|
| 图 13 机器人陷入死区时的路径选择分析 Fig.13 Path selection analysis of robot falling into the dead zone |
由于机器人始终向着路径选择函数fi值最大的方向移动以逃离死区,因此机器人下一步的移动位置为机器人正下方的栅格。进一步分析机器人陷入死区时每一步的逃离路径,表 1列出了图 11中机器人逃离死区过程中每走一步其周围栅格的路径选择函数值,以图 11左下角为起点,每个栅格的大小为D。图 14显示了爬壁机器人逃离死区并继续遍历当前子区域的过程,图中黑粗色线段表示爬壁机器人逃离死区的路径。
| 邻近位置 | 当前位置 | |||
| (3D,10D) | (3D,9D) | (3D,8D) | (3D,7D) | |
| (x+D, y+D) | - | -∞ | -∞ | -∞ |
| (x+D, y) | -∞ | -∞ | -∞ | -∞ |
| (x+D, y-D) | -∞ | -∞ | -∞ | 2 |
| (x, y+D) | - | -1.475 | -1.445 | -1.355 |
| (x, y-D) | 0.485 | 0.475 | 0.445 | 0.355 |
| (x-D, y+D) | - | -0.445 | -0.475 | -1 |
| (x-D, y) | -0.12 | -0.16 | -0.225 | -0.355 |
| (x-D, y-D) | 0.255 | 0.225 | 0.16 | 0 |
| 下一步位置 | (3D,9D) | (3D,8D) | (3D,7D) | (4D,6D) |

|
| 图 14 机器人逃离死区时的移动路径 Fig.14 Moving path of robot escaping from the dead zone |
机器人完成当前子区域的遍历以后,需依次切换到下一相邻子区域进行遍历。本文为每个子区域设置4个关联栅格,以得到更短的切换路径,如图 15所示。4个关联栅格按逆时针顺序排列。假设爬壁机器人的工作环境被划分为z个子区域。

|
| 图 15 子区域关联栅格 Fig.15 Correlation grid of sub-region |
定义5:当前子区域遍历起始栅格为子区域进入栅格ci_in;当前子区域遍历结束栅格为子区域出口栅格ci_out。
根据机器人遍历各子区域所需转向次数的奇偶性,子区域进入栅格和出口栅格有以下不同的关系:
| $ \left\{ \begin{gathered} {c_{i1}} \Leftrightarrow {c_{i2}},{c_{i3}} \Leftrightarrow {c_{i4}},\;\;\;\;转向次数为奇数 \hfill \\ {c_{i1}} \Leftrightarrow {c_{i4}},{c_{i2}} \Leftrightarrow {c_{i3}},\;\;\;\;转向次数为偶数 \hfill \\ \end{gathered} \right. $ | (10) |
其中子区域进入栅格和出口栅格分别位于“⇔”的两侧;如果进入栅格确定了,则出口栅格随之确定。
定义6:当前子区域遍历完成以后,以与当前子区域出口栅格欧式距离dij最短的相邻子区域的关联栅格作为该子区域的进入栅格。
| $ {d_{ij\_\min }} = \min d\left( {{c_{i\_{\text{out}}}},{c_{j\_{\text{in}}}}} \right)\;\;\;\;i,j \in \left( {1,z} \right) $ | (11) |
相邻子区域的切换有以下2种情况:
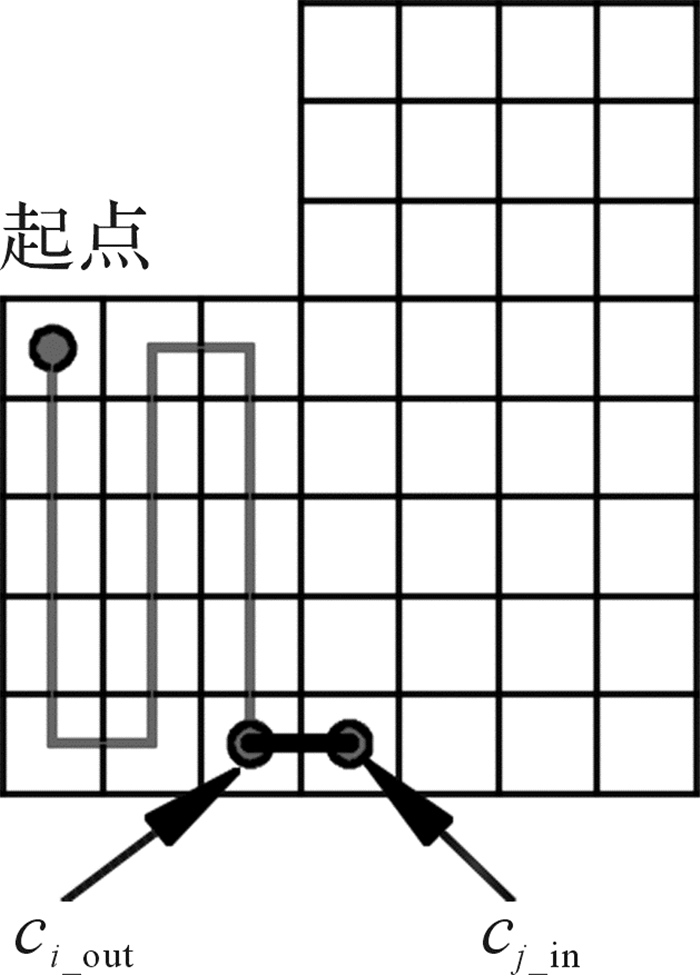
1) ci_in和cj_out之间无障碍物阻隔。此种情况下,当前子区域遍历结束以后, 机器人根据dij_min确定下一相邻子区域的进入栅格,然后匀速直线运动到此栅格后开始下一子区域的遍历。无障碍物阻隔时机器人的移动路径如图 16所示。
|
| 图 16 无障碍物阻隔时机器人的移动路径 Fig.16 Movement path of robot without barriers obstructing |
2) ci_in和cj_out之间有障碍物阻隔。此种情况下,机器人首先根据dij_min确定下一相邻子区域的进入栅格;其次,根据公式(8)计算出机器人当前位置周围栅格的路径选择函数值fi,以确定机器人从当前子区域的出口栅格运动到下一子区域进入栅格的路径,对于方向函数yi,以相邻子区域的进入栅格坐标(xj_in, yj_in)替换掉公式(7)中距离机器人当前位置最近的未遍历栅格坐标(xUi, yUi)进行计算即可。有障碍物阻隔时机器人的移动路径如图 17所示。

|
| 图 17 有障碍物阻隔时机器人的移动路径 Fig.17 Movement path of robot with barriers obstructing |
本文提及的算法是在栅格地图中对机器人进行路径规划研究,因此需对工作区域构建栅格地图。仿真实验工作区域设置为30D×30D的栅格地图,其中随机分布着各种形状的障碍物,如图 18所示。首先对仿真环境中的障碍物进行矩形化处理,结果如图 19。接下来根据矩形分块思想对环境进行分块,整个栅格环境被分解为9个大小不同的子区域,结果见图 20,建立表示各子区域重心间距离的邻接矩阵并以图的深度优先搜索算法确定各子区域的最优连接顺序为:①→③→⑤→⑦→⑨→⑧→⑥→④→②。为了讨论路径规划算法效果,将机器人视为质点,同时假设爬壁机器人是可以全方位运动的,所有的仿真实验设置参数t=0.5。机器人全遍历路径规划化仿真结果如图 21所示。

|
| 图 18 栅格仿真环境地图 Fig.18 The map of grid simulation environment |

|
| 图 19 仿真环境中的矩形化障碍物 Fig.19 Rectangular obstacles in simulation environment |

|
| 图 20 仿真环境的栅格地图分块 Fig.20 Several blocks of grid map in simulation environment |

|
| 图 21 机器人全遍历路径规划仿真结果 Fig.21 Simulation results of robot complete coverage path planning |
定义7:机器人按规划完成遍历后,已遍历面积Sc与可达区域面积Sv之比为遍历面积百分率Jc,即Jc=Sc/Sv;所有遍历重叠面积之和So与可达区域面积Sv之比为重复遍历率Jo,即Jo=So/Sv。
从图 21中可以得出机器人的遍历面积百分率及重复遍历率, 如表 2所示。
| 评价指标 | 量值 |
| 漏检栅格 | 13块 |
| 重复遍历栅格 | 31块 |
| 可达栅格 | 742块 |
| 遍历面积百分率Jc | 98.25% |
| 重复遍历率Jo | 4.18% |
由仿真结果分析:提出的全遍历路径规划方法基本实现了对环境的全遍历,虽存在重复遍历情况,但重复遍历率较低且重复部分为机器人逃离死区的移动路径。
6 结论本文采用矩形分解法将储罐罐壁划分为若干子区域,在环境拓扑图中找到了一种最优的子区域连接顺序;同时结合路径选择函数找出了爬壁机器人陷入死区时的最优逃离路径。仿真实验证明本文所提算法能够能够引导机器人以低重复率及高覆盖率实现工作区域的全覆盖,且能快速有效地逃离死区。
| [1] |
曹翔, 俞阿龙.
移动机器人全覆盖信度函数路径规划算法[J]. 智能系统学报, 2017, 12(3): 1–12.
CAO Xiang, YU A-long. Complete coverage path planning algorithm of mobile robot based on belief function[J]. Journal of Intelligent Systems, 2017, 12(3): 1–12. |
| [2] | LI Y, CHEN H, MENG J E, et al. Coverage path planning for UAVs based on enhanced exact cellular decomposition method[J]. Mechatronics, 2011, 21(5): 876–885. DOI:10.1016/j.mechatronics.2010.10.009 |
| [3] | ZHANG H, WANG W, ZHAO W, et al. A topological area coverage algorithm for indoor vacuuming robot[C]//IEEE International Conference on Automation and Logistics, Jinan, Aug. 18-21, 2007. |
| [4] | JANCHIV A, BATSAIKHAN D, KIM G H, et al. Complete coverage path planning for multi-robots based on[C]//International Conference on Control, Automation and Systems, Kintex, Gyeonggi-do, Oct. 26-29, 2011. |
| [5] |
王俭, 陈卫东, 赵鹤鸣, 等.
移动机器人全覆盖路径规划优化方法[J]. 计算机工程, 2005, 31(22): 162–163.
WANG Jian, CHEN Wei-dong, ZHAO He-ming, et al. Full coverage path planning optimization method for mobile robot[J]. Computer Engineering, 2005, 31(22): 162–163. DOI:10.3969/j.issn.1000-3428.2005.22.056 |
| [6] |
简毅, 张月.
移动机器人全局覆盖路径规划算法研究进展与展望[J]. 计算机应用, 2014, 34(10): 2844–2849.
JIAN Yi, ZHANG Yue. Research progress and prospect of global coverage path planning algorithm for mobile robot[J]. Journal of Computer Applications, 2014, 34(10): 2844–2849. DOI:10.11772/j.issn.1001-9081.2014.10.2844 |
| [7] | MICHEL D, MCISAAC K. New path planning scheme for complete coverage of mapped areas by single and multiple robots[C]//International Conference on Mechatronics and Automation, Chengdu, Aug. 5-8, 2012. |
| [8] | DENG Y, YANG G W, CUI X M, et al. Application of improved back propagation neural network in mowing robot's path planning[J]. Applied Mechanics & Materials, 2014, 602-605: 916–919. |
| [9] | OH J S, CHOI Y H, PARK J B, et al. Complete coverage navigation of cleaning robots using triangular-cell-based map[J]. IEEE Transactions on Industrial Electronics, 2008, 51(3): 718–726. |
| [10] | HU G, HU Z, WANG H. Complete coverage path planning for road cleaning robot[C]//International Conference on Networking, Sensing and Control, Chicago, IL, Apr. 10-12, 2010. |
| [11] |
李开生, 张慧慧, 费仁元, 等.
具有遍历特性的移动机器人规划方法的研究[J]. 机器人, 2001, 23(6): 486–492.
LI Kai-sheng, ZHANG Hui-hui, FEI Ren-yuan, et al. Research on path planning of mobile robot with coverage-path feature[J]. Robot, 2001, 23(6): 486–492. |
| [12] |
邱雪娜, 刘士荣, 宋加涛, 等.
不确定动态环境下移动机器人的完全遍历路径规划[J]. 机器人, 2006, 28(6): 586–592.
QIU Xue-na, LIU Shi-rong, SONG Jia-tao, et al. Complete coverage path planning for mobile robots in uncertain dynamic environments[J]. Robot, 2006, 28(6): 586–592. |
| [13] | CHOSET H. Coverage for robotics:a survey of recent results[J]. Annals of Mathematics & Artificial Intelligence, 2001, 31(1/4): 113–126. |
| [14] |
张赤斌, 王兴松.
基于蚁群算法的完全遍历路径规划研究[J]. 中国机械工程, 2008, 19(16): 1945–1949.
ZHANG Chi-bin, WANG Xing-song. Complete coverage path planning based on ant colony algorithm[J]. China Mechanical Engineering, 2008, 19(16): 1945–1949. DOI:10.3321/j.issn:1004-132X.2008.16.013 |
| [15] | HUANG W H. Optimal line-sweep-based decompositions for coverage algorithms[C]//IEEE International Conference on Robotics and Automation, Seoul, May 21-26, 2001. |
| [16] |
田春颖, 刘瑜, 冯申坤, 等.
基于栅格地图的移动机器人完全遍历算法——矩形分解法[J]. 机械工程学报, 2004, 40(10): 56–61.
TIAN Chun-ying, LIU Yu, FENG Shen-kun, et al. Complete traversal algorithm of mobile robot based on grid map-rectangular decomposition method[J]. Chinese Journal of Mechanical Engineering, 2004, 40(10): 56–61. DOI:10.3321/j.issn:0577-6686.2004.10.012 |
| [17] |
陈卫平. 全区域覆盖自主移动机器人路径规划与避障的研究[D]. 南京: 南京理工大学电子工程与光电技术学院, 2004: 10-33.
CHEN Wei-ping. Research on path planning and obstacle avoidance for full area coverage autonomous mobile robot[D]. Nanjing: Nanjing University of Science and Technology, School of Electronic and Optical Engineering, 2004: 10-33. |
| [18] |
刘松, 李志蜀, 李奇, 等.
机器人全覆盖最优路径规划的改进遗传算法[J]. 计算机工程与应用, 2009, 45(31): 245–248.
LIU Song, LI Zhi-shu, LI Qi, et al. Improved genetic algorithms optimal area covering path planning for family robot[J]. Computer Engineering and Applications, 2009, 45(31): 245–248. DOI:10.3778/j.issn.1002-8331.2009.31.073 |
| [19] |
刘淑华, 夏菁, 孙学敏, 等.
已知环境下一种高效全覆盖路径规划算法[J]. 东北师大学报(自然科学版), 2011, 43(4): 39–43.
LIU Shu-hua, XIA Jing, SUN Xue-min, et al. An efficient complete coverage path planning in known environments[J]. Journal of Northeast Normal University (Natural Science Edition), 2011, 43(4): 39–43. |


