2. 中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033
2. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China
随着非相干光光栅剪切相位衬度成像方法的诞生,以及近年来国内大面积硬X射线曲面光栅研制日趋成熟,相位衬度成像推广至人体检测逐渐成为可能[1-2]。为此,笔者研制了一台基于垂直转轴的相位衬度CT(computed tomography, 计算机断层扫描)样机,用于验证相位衬度成像原理、曲面光栅性能及图像重构算法等。为体现相位衬度成像的优势,样机重构的断层图像空间分辨率设计指标要求优于0.1 mm。CT机轴系误差会影响扫描过程中X射线拍摄样品各帧之间的对准,容易造成运动伪影,进而影响重构图像的分辨率[3]。对该CT样机的要求:在旋转中心∅200 mm视野内,被测样品与扫描系统的相对径向偏移误差需小于5 μm,轴向偏移误差需小于10 μm。此外,相位衬度成像系统比常规医用CT机多3块曲面光栅参与X射线成像,光栅在扫描过程中位置的不稳定性也会影响成像效果。
大型单轴精密转台的轴系设计以光电经纬仪的垂直轴系最为典型,杜俊峰、李松等较早地对光电经纬仪的轴系精度指标和误差分析方法作了阐述[4-5];毛雨辉等对光电经纬仪轴系精度的影响因素进行了分析[6];类成华、伞晓刚等对光电经纬仪的轴系结构进行了优化设计,实现了轻量化[7-8];丁晓东、任顺清等介绍了垂直轴系晃动误差的测量、分析和数据处理方法[9-10]。
本文针对CT成像物理需求,设计了大直径精密转台,进行了轴系结构设计与分析、轴系精度指标分解以及轴系关键组件误差分配和精度综合,最后对实际样机的轴系精度进行了检测,以验证该转台轴系结构满足相位衬度成像要求。
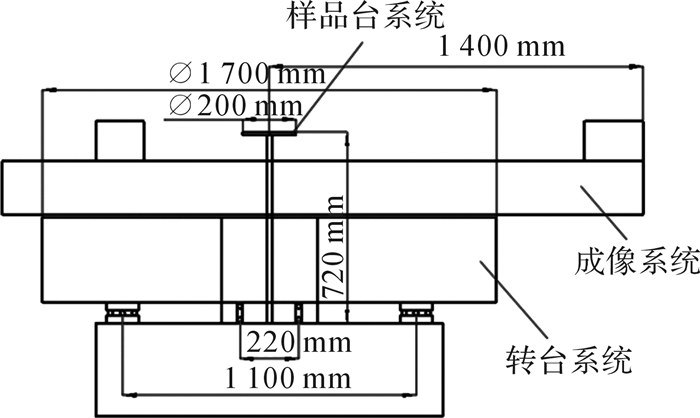
1 相位衬度CT样机转台轴系结构设计如图 1所示,相位衬度CT样机主要由转台系统、成像系统和样品台系统组成,其中成像系统光学半径为1 400 mm。为有效承托成像系统,并考虑到滑环尺寸及整机重量等因素,转台台面外径最终确定为1 700 mm。
|
| 图 1 相位衬度CT样机系统布局图 Fig.1 Layout of phase contrast CT prototype system |
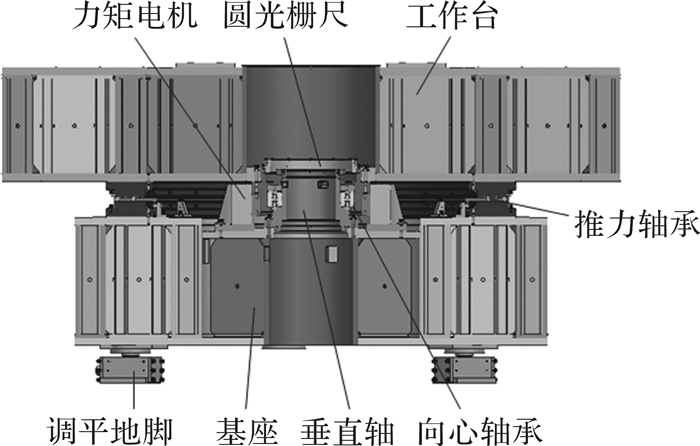
转台系统由轴系、工作台、基座、垂直轴、力矩电机、圆光栅组件、调平地脚及其他零部件组成,如图 2所示。轴系关键部件为密珠轴承,由推力密珠轴承和向心密珠轴承组成,前者负责承载,同时控制轴系角晃动误差,后者起定心作用,控制轴系的径向偏摆。向心密珠轴承的内外圈(内外轴承环)为圆柱形轴和孔,推力密珠轴承上下座圈(上下轴承环)为2个圆环平面,轴承环之间密布滚珠,实现工作台相对基座的旋转运动。相比一般滚动轴承,密珠轴承的特点在于[11]:1)轴承内各元件的局部误差在密珠平均效应作用下对轴系精度影响比较小;2)密珠轴承内外环设计时预留一定的过盈量,可提高主轴的回转精度和刚度。
|
| 图 2 相位衬度CT样机转台系统结构组成 Fig.2 Structure composition of phase contrast CT prototype turntable system |
密珠轴系设计及工艺加工过程中,需严格控制轴承环、滚珠及配合件的几何形状误差,表面粗糙度和滚珠球径误差,并根据负载大小,合理排布滚珠数量、位置以及过盈量。
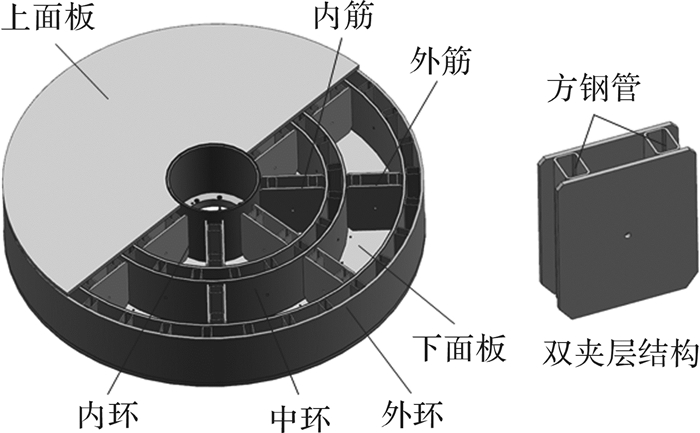
轴系组件的高刚度是获得轴系高精度的前提。工作台外径达1 700 mm,采用焊接结构,如图 3所示,转台为封闭箱体型式,由Q235板料焊接而成,内部由8组辐射筋条连接内环、中环和外环。其中,内外筋、中环和外环模块均采用了双夹层结构(双侧钢板中间焊接方钢管),增大了结构截面的惯性矩,有效提高了模块的抗弯和抗扭刚度。基座的结构形式与工作台类似,不再赘述。采用焊接结构,相比铸造的优点在于[12]:焊接用钢的弹性模量约为铸铁的1.5~2倍,比刚度大,容易实现轻量化;焊接结构内部布筋、改型更灵活;焊接结构件可以采用完全封闭的箱型结构,不需要留出沙口;焊接工艺相对简单,加工周期短。
|
| 图 3 转台系统工作台结构形式 Fig.3 Structure form of turntable system worktable |
转台焊接过程中通过焊接工装保证各零件、模块的位置精度,充分利用对称焊、多道焊、间歇焊和塞焊等焊接工艺,保证焊后变形尽量小。各零部件焊后要进行必要的退火和振动时效处理,使得焊接应力充分释放,以保证较高的尺寸稳定性[13]。
推力轴承环平均直径达1 100 mm,厚度为50 mm,其本体刚度较低,难以获得极高的平面度。因此,工艺实施时,先刮研轴承环和工作台(基座)的安装面,以获得较高的接触刚度,再将两者组合连接,组合件的刚度远远高于轴承环本体,再依次对轴承环工作面进行精加工、磨削、研磨工序,容易获得极高的平面度。与之类似,向心轴承环与垂直轴组件同轴组合后加工,容易获得极高的圆柱度。
轴承环材料选用GCr15SiMn,淬火后硬度达58~62 HRC,滚珠的数量与球径基于赫兹接触应力公式计算获得,推力轴承环密布了4排共480颗球直径为12 mm的双零级滚珠,向心轴承密布了3排共60颗球直径为12 mm的双零级滚珠。
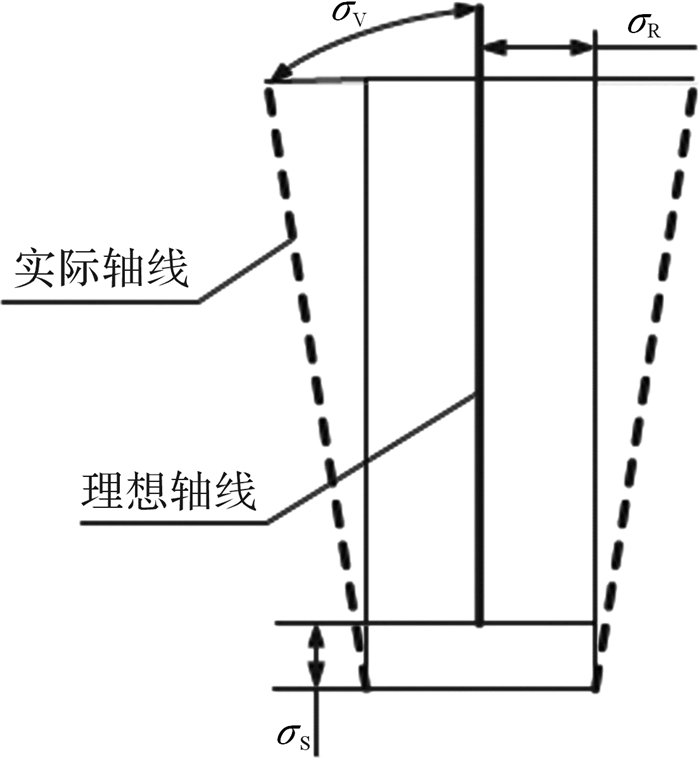
2 转台轴系精度指标分析 2.1 转台轴系精度评价指标分解精密机械轴系精度一般用主轴轴线的位置变动量来表征[4-5],可分为3个独立的分量,如图 4所示,分别为纯轴向窜动误差σS、纯角度摆动误差σV和纯径向移动误差σR。
|
| 图 4 主轴运动误差示意图 Fig.4 Schematic diagram of spindle motion error |
主轴回转精度评价指标主要包括以下三方面:
1) 轴向窜动误差σS:主轴回转误差的轴向分量,反映轴系的轴向回转精度。
2) 晃动误差σV:主轴实际回转轴线相对转轴理论轴线的纯角度摆动量,即定向误差,表明主轴实际回转轴线相对给定方向的偏离程度。
3) 置中误差σH:在主轴旋转的任一轴向位置上,主轴实际回转轴线的纯径向位移与轴线角度摆动引起的主轴轴心的径向偏移之和,表征主轴上某点相对理想轴线的综合径向偏移程度。
| $ {\sigma _{\text{H}}} = {\sigma _{\text{R}}} + {l_{\text{i}}}{\sigma _{\text{V}}} $ | (1) |
式中li为主轴到摆动角顶点的轴向距离。
2.2 转台轴系精度指标要求如图 1所示,本文设计的转台直径大,轴系摆角顶点近似位于轴承圆心处。扫描过程中,样品与转台之间的运动误差为相对值,为简化分析,可假设转台轴系静止不动,样品台作旋转运动。样品台相对主轴晃动摆角顶点距离为720 mm,要求在旋转中心∅200 mm视野内被测样品与转台系统的相对径向偏移误差小于5 μm,轴向偏移误差小于10 μm。
因此,主轴的轴向窜动误差要求小于10 μm;主轴置中误差小于5 μm;根据式(1)取纯径向移动量小于1.5 μm,轴系晃动误差小于1″。
相位衬度CT样机转台轴系的精度指标分解结果如表 1所示。
| 精度指标 | 量值 |
| 轴向窜动误差 | ≤10 μm |
| 置中误差 | ≤5 μm |
| 晃动误差 | ≤1″ |
转台上承载相位衬度成像系统总成,负载总质量约为1 200 kg,呈矩形状分布,对转台的静态变形情况以及动力学性能进行分析,研究转台系统结构刚度,可在结构设计过程中比较准确地确定轴系刚度和谐振频率的数值,避免设计的盲目化[7]。
在有限元前处理环境下对板材结构抽取中面后划分面网格,对网格赋予厚度和材料属性。为提高计算精度,面网格尽量划分为四边形网格,体网格尽量划分为六面体网格。有限元模型中,根据实际连接方式采用合适的模拟单元装配。
3.1 静态分析静态分析主要研究转台在重力场静力环境下的变形情况。约束转台调平地脚支撑处节点自由度,将模拟负载质量块安装在转台工作台上,设置重力加速度g的大小和方向,求解计算,结果如图 5所示。
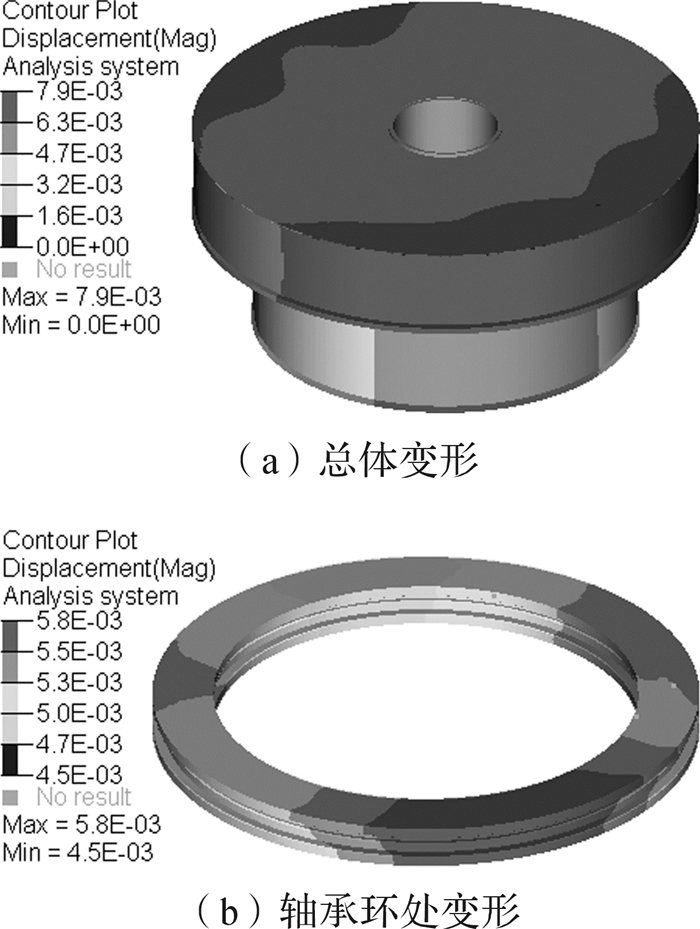
|
| 图 5 转台静态变形云图 Fig.5 Turntable static deformation nephogram |
从图 5可以看出,转台在负载重力作用下,整体呈下沉趋势,最大变形位于工作台边缘位置,变形量为7.9 μm,推力轴承环表面相对变形量仅为1.3 μm,平面误差小,说明工作台和基座的静态刚度设计合理。
3.2 动力学分析相位衬度成像旋转扫描时需要转台有良好的稳定性,不能出现扭动或变形,结构应具备对外界或自身内部振动的抵抗能力,避免产生共振或疲劳。转台的动力学分析从两方面进行:一是惯性释放分析,研究转台启动和停车阶段在力矩电机驱动下作近似匀加(减)速运动时结构内部的变形情况;二是模态分析,研究转台结构的固有振动特性,即固有频率和振型,据此对转台的动态性能进行评价。
1) 惯性释放分析。
惯性释放分析是先计算不平衡外力作用下的结构运动(加速度),通过惯性力构造平衡力系,以计算准静态结构响应。忽略刚体运动成分,只关注结构本身的变形[14]。
将负载质量块安装在工作台上,工作台与电机转子的连接法兰节点通过RBE3单元与中心主节点连接,对主节点施加驱动力矩(300 Nm),设置INREL参数值为-2,开启惯性释放分析,分析结果如图 6所示。

|
| 图 6 工作台变形云图 Fig.6 Worktable deformation nephogram |
从图 6可以看出,工作台最大变形位于与力矩电机连接法兰处,但也仅为0.2 μm,表明加减速阶段工作台结构稳定性非常好。
2) 模态分析。
为反映转台真实应用工况,研究负载状态下转台的模态特性,便于发现转台结构动力学特性的缺陷[15],进行了有限元模态分析,结果如表 2所示。
| 阶数 | 固有频率/Hz | 模态振型 | 振型描述 |
| 1 | 104 |  |
整体基于约束脚座绕x轴旋转 |
| 2 | 117 | 整体基于约束脚座绕y轴旋转 | |
| 3 | 189 | 基准平台两侧悬臂段弯曲 |
从表 2可知,转台连同负载的固有频率高于100 Hz时,其振型光滑,无局部刚度过低引起的突变。
该精密转台工作时受到的激励来源于环境和力矩电机的振动。外界环境振动通过独立地基隔振后,高频振动成分得到有效衰减,一般只有20 Hz以下的低频振动会传递至转台,力矩电机转速不超过30 r/min,工作频率也很低。因此,结合转台的模态特性可以看出,第1阶固有频率比外界激励频率大很多,结构本身不会出现谐振现象,结构动力学性能良好。
4 轴系精度分析与误差分配相位衬度CT样机转台轴系误差会影响扫描过程中X射线拍摄样品各帧之间的对准,容易造成运动伪影,进而影响重构图像的分辨率。转台轴系的误差主要有如下几种:
1) 转台调平误差。
地面的不平度会造成转台轴线相对铅垂位置的倾斜,负载偏心在转动过程中会产生交变载荷。调平误差可借助精密水平仪来检测,通过松紧3个调平地脚的螺栓实现转台调平,保证转动一周这3点的位置水平仪示值相同,通常情况下,调平误差不大于0.2″。
不同于光电经纬仪对外部目标的绝对捕捉和跟踪,相位衬度CT样机样品台系统与转台基座是固接的,调平误差不影响样品与成像系统之间的相对误差。
2) 轴向窜动误差。
推力轴承密珠的均化效应使得滚珠的误差对轴向精度几乎没有影响,主轴的轴向窜动误差可忽略不计。
但由于轴系晃动摆角会引起∅200 mm视野区边缘的轴向偏移,以晃动误差为1″进行计算,轴向偏移误差也仅为0.5 μm,满足指标要求(≤10 μm)。
3) 轴系晃动误差。
平面轴系是靠滚珠和上下推力轴承的滚道平面支撑和定向的,故轴系晃动与滚珠、上下推力轴承的平面误差有关。由于密珠的均化效应,滚珠的不圆度误差很难复现,可以忽略不计。因此轴系晃动误差主要取决于轴承滚道平面的平面度误差[4-5]。晃动误差的最大值由式(2)近似计算[16]:
| $ {\sigma _{{{\text{V}}_{1\max }}}} = \rho K\Delta y/D $ | (2) |
式中:Δy为推力轴承环平面度误差;D为推力轴承的中径,设计值为1 100 mm;K为负载系数,一般取0.4~0.96;ρ为弧度转化为角秒值的系数,为206 265。
该误差服从均匀分布(置信因子为
| $ {\sigma _{{{\text{V}}_1}}} = {\sigma _{{{\text{V}}_{1\max }}}}/\sqrt 3 $ | (3) |
垂直轴系随机晃动误差σV2由推力轴承环平面度误差和转动时基座刚度变化引起的轴承环平面变形决定,该误差服从反余弦分布(置信因子为
| $ {\sigma _{{{\text{V}}_2}}} = \rho \sqrt {{{\left( {\frac{1}{{\sqrt 2 }}\frac{{\Delta y}}{D}} \right)}^2} + {{\left( {\frac{1}{{\sqrt 2 }}\frac{\sigma }{D}} \right)}^2}} $ | (4) |
式中δ为基座刚度变化引起的轴承环平面变形,由静态分析结果得δ=1.3 μm。
因此,转台轴系的综合晃动误差为:
| $ {\sigma _{\text{V}}} = \sqrt {\sigma _{{{\text{V}}_1}}^2 + \sigma _{{{\text{V}}_2}}^2} $ | (5) |
由此可见,轴承环平面度误差是最关键的设计参数,通过试算,确定最终推力轴承环的平面度误差为5 μm,轴系晃动误差σV≤0.72″~0.86″,满足指标要求。
4) 轴系置中误差。
转台轴系置中误差反映为样品台相对成像系统的径向偏移量,是轴线纯径向位移和角度晃动合成结果。由于向心轴承内外环配作,有5~10 μm的过盈量,不存在间隙引起的偏移,轴线径向偏移量主要由内外轴承环圆柱度误差引起,该误差服从均匀分布,计算公式如下[17]:
| $ {\sigma _{\text{R}}} = \sqrt {{{\left( {\frac{{\Delta {x_1}}}{{\sqrt 3 }}} \right)}^2} + {{\left( {\frac{{\Delta {x_2}}}{{\sqrt 3 }}} \right)}^2}} $ | (6) |
式中Δx1,Δx2为内、外轴承环的圆柱度误差。
因此,相位衬度CT样机转台轴系相对样品台的置中误差为:
| $ {\sigma _{\text{H}}} = {\sigma _{\text{R}}} + l{\sigma _{\text{V}}}/\rho $ | (7) |
式中:l为样品台至主轴晃动摆角顶点距离,为720 mm。
通过推算,确定最终向心轴承环的圆柱度误差为2 μm,转台轴系置中误差σH≤4.1~4.6 μm,满足指标要求。
5 样机检测转台轴系组件经三坐标测量机或千分表检验,其形状误差和方向误差合格后,与力矩电机、圆光栅尺、滑环等一起装配,装配完成的样机实物如图 7所示。

|
| 图 7 转台样机实物图 Fig.7 Turntable prototype diagram |
根据轴系精度指标要求,样机检测项目包括3项:轴系晃动误差σV、轴向窜动误差σS和置中误差σH,前两者直接测量,置中误差σH根据式(7)计算而得。
轴系的晃动误差采用精密电子水平仪(青岛前哨SDS11型,精度为0.2″)进行检测,将水平仪沿径向放置在转台上,如图 8所示,调节底部调平地脚,转动转台,使水平仪圆周三点示值相等。从0°到360°旋转2周后再反转2周以消除双周误差,每间隔30°测量一次,共取12个测点,得到4组数据,采用傅里叶谐波分析法对测试数据进行处理[10]。

|
| 图 8 精密电子水平仪及测点位置 Fig.8 Precision electronic level instrument and point position |
主轴轴向窜动误差测点位置为圆光栅座的上端面,其表面经过精研后,平面度误差不超过2 μm。为了准确测量主轴纯径向移动误差,测点位置取靠近向心轴承上方法兰座的内孔,被测孔经过精研后,利用三坐标测量机进行检测,要求其圆柱度误差不超过2 μm。
经检测,轴系晃动误差为0.7″,主轴轴向窜动误差为4 μm,主轴纯径向移动误差为4 μm,根据式(7)计算后得转台轴系相对样品台的置中误差为4.4 μm,均优于精度指标值。
6 结束语本文根据X射线相位衬度CT扫描成像的物理需求,设计了基于密珠轴系的大直径精密转台,转台采用焊接结构,具有质量轻、转动阻力小、回转精度高的特点。
文中讨论了轴系精度的评价指标,结合转台尺寸参数和成像视野区允许的运动误差对转台轴系精度指标进行了分解。研究了转台结构的静动态性能,静态分析、惯性释放分析和模态分析结果验证了结构刚度是合理的。通过精度分析对轴系关键组件的几何误差进行了分配。最终装配样机的轴系晃动误差为0.7″,验证了转台轴系结构设计、误差分配是合理的,满足相位衬度CT高分辨率、高稳定性成像要求。
| [1] | PFEIFFER F, WEITKAMP T, BUNK O, et al. Phase retrieval and differential phase-contrast imaging with low brilliance X-ray sources[J]. Nature Physics, 2006, 2(4): 258–261. DOI:10.1038/nphys265 |
| [2] |
朱佩平, 吴自玉.
X射线相位衬度成像[J]. 物理, 2007, 36(6): 443–451.
ZHU Pei-ping, WU Zi-yu. X-ray phase contrast imaging[J]. Physics, 2007, 36(6): 443–451. |
| [3] | TAPFER A, BECH M, PAUWELS B, et al. Development of a prototype gantry system for preclinical X-ray phase-contrast computed tomography[J]. Medical Physics, 2011, 38(11): 5910–5914. DOI:10.1118/1.3644844 |
| [4] |
杜俊峰, 李正周.
GD-220光电经纬仪轴系的精度分析[J]. 光学精密工程, 2002, 10(4): 416–419.
DU Jun-feng, LI Zheng-zhou. Accuracy analysis of GD-220 photoelectric theodolite shafting[J]. Optics and Precision Engineering, 2002, 10(4): 416–419. |
| [5] |
李松, 张立平.
空间相机偏流调整旋转轴系的设计与精度分析[J]. 光学精密工程, 2004, 12(2): 141–145.
LI Song, ZHANG Li-ping. Design and accuracy analysis for drift adjusting rotary axes of space camera[J]. Optics and Precision Engineering, 2004, 12(2): 141–145. |
| [6] |
毛雨辉, 张进, 李国华.
大型光电经纬仪跟踪架水平轴系的结构设计[J]. 机械设计, 2014, 31(12): 49–53.
MAO Yu-hui, ZHANG Jin, LI Guo-hua. Structural design of tracking-mount horizontal axis for large photoelectric theodolite[J]. Journal of Machine Design, 2014, 31(12): 49–53. DOI:10.3969/j.issn.1001-3997.2014.12.013 |
| [7] |
类成华, 王守印.
光电经纬仪垂直轴系优化设计[J]. 工程设计学报, 2008, 15(4): 278–282.
LEI Cheng-hua, WANG Shou-yin. Optimization design of theodolite's vertical shaft[J]. Chinese Journal of Engineering Design, 2008, 15(4): 278–282. |
| [8] |
伞晓刚, 王晶, 薛育.
大型光电经纬仪转台的一种轻量化设计[J]. 长春理工大学学报(自然科学版), 2010, 33(4): 31–35.
SAN Xiao-gang, WANG Jing, XUE Yu. A method of lightweight design for turntable of large photoelectric theodolite[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2010, 33(4): 31–35. |
| [9] |
丁晓东, 王智平, 郑见灵, 等.
经纬仪垂直轴系晃动误差的测量和分析[J]. 四川兵工学报, 2010, 31(6): 138–141.
DING Xiao-dong, WANG Zhi-ping, ZHENG Jian-ling, et al. Measurement and analysis of the sway error of theodolite's vertical shaft system[J]. Journal of Sichuan Ordnance, 2010, 31(6): 138–141. |
| [10] |
任顺清, 王俊柱.
用水平仪测试倾角回转误差的数据处理[J]. 哈尔滨工业大学学报, 2006, 38(6): 837–839.
REN Shun-qing, WANG Jun-zhu. Data processing method of calculating wobble error with level instrument[J]. Journal of Harbin Institute of Technology, 2006, 38(6): 837–839. |
| [11] |
徐峰, 李庆祥.
精密机械设计[M]. 北京: 清华大学出版社, 2005: 379-384.
XU Feng, LI Qing-xiang. Precision machinery design[M]. Beijing: Tsinghua University Press, 2005: 379-384. |
| [12] |
张怀凤.
焊接结构件的机床大件[J]. 机械, 2011, 38(S1): 91–93.
ZHANG Huai-feng. Welding structural parts of the machine tool[J]. Machinery, 2011, 38(S1): 91–93. |
| [13] |
王顺俊, 朱昌宏.
薄板箱体的焊接变形及其控制[J]. 焊接技术, 2015, 44(3): 82–84.
WANG Shun-jun, ZHU Hong-chang. Welding deformation and control of sheet metal box[J]. Welding Technology, 2015, 44(3): 82–84. |
| [14] |
曹萍, 王卫英.
基于惯性释放的微型客车车身强度分析[J]. 机械设计, 2011, 28(7): 46–49.
CAO Ping, WANG Wei-ying. Strength analysis of a minibus body based on inertia relief[J]. Journal of Machine Design, 2011, 28(7): 46–49. |
| [15] |
谭启檐, 高云国, 王小庆, 等.
激光转台芯部结构动态特性研究与优化[J]. 工程设计学报, 2010, 17(3): 186–189.
TAN Qi-yan, GAO Yun-guo, WANG Xiao-qing, et al. Dynamic analysis and optimization of inner supporting structure for laser emission turntable[J]. Chinese Journal of Engineering Design, 2010, 17(3): 186–189. |
| [16] |
费业泰.
误差理论与数据处理[M]. 北京: 机械工业出版社, 2000: 58-81.
FEI Ye-tai. The theory of error and data processing[M]. Beijing: China Machine Press, 2000: 58-81. |
| [17] |
李玉和, 郭阳宽.
现代精密仪器设计[M]. 2版. 北京: 清华大学出版社, 2010: 77-82.
LI Yu-he, GUO Yang-kuan. Modern precision instrument design[M]. 2th ed. Beijing: Tsinghua University Press, 2010: 77-82. |
| [18] |
马宏, 王金波.
仪器精度理论[M]. 2版. 北京: 北京航空航天大学出版社, 2014: 41-59.
MA Hong, WANG Jin-bo. Instrument accuracy theory[M]. 2th ed. Beijing: Beihang University Press, 2014: 41-59. |



