2. 上海振华重工(集团)股份有限公司, 上海 200125
2. Shanghai Zhenhua Port Machinery Company Limited, Shanghai 200125, China
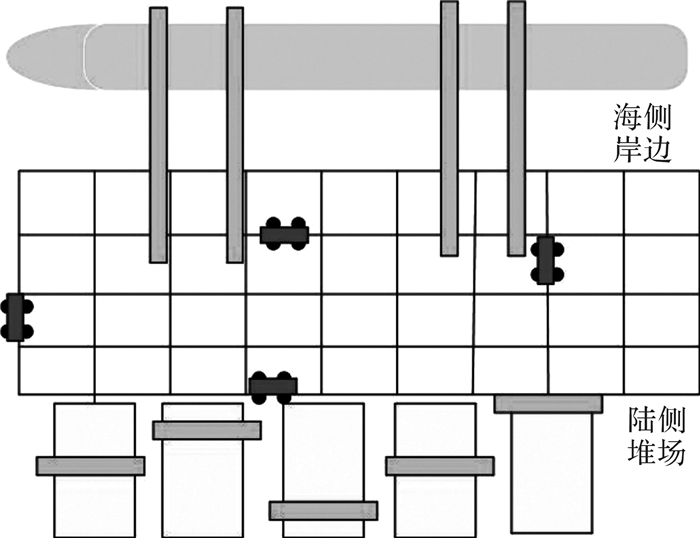
目前集装箱码头自动化是码头发展新趋势,自动化码头相对于传统码头最明显的区别是自动化码头的布局是垂岸式的,垂岸是指堆场的布局垂直于码头前沿。自动化集装箱码头的布局如图 1所示。
|
| 图 1 自动化集装箱码头布局图 Fig.1 Automated container terminal layout |
自动化码头包括两大系统:装卸系统和水平运输系统。装卸系统中包含两大设备:在岸边装卸集装箱的岸桥和在堆场装卸集装箱的场桥。水平运输工具主要是自动导引车(automated guided vehicle,AGV)。
AGV是一种无人驾驶的水平运输工具, 已经在物流、汽车等行业得到了广泛的应用[1]。在自动化集装箱码头中,AGV作为集装箱码头的水平运输工具, 承担着岸边和堆场之间的集装箱运输任务。在集装箱码头自动化进程中,水平运输工具的自动化是其中重要的一环。但是AGV的路径规划不当会使得AGV相互冲突,此时不但无法提高码头的运作效率,反而阻碍码头顺畅运作。因此,AGV路径规划是亟待解决的问题。
国内外学者对AGV路径规划问题作了不少研究[2-4]。Nishi等[5]提出用分层算法求解AGV调度和无冲突路径问题,使得任务的总延迟时间最短,最后用仿真验证了方法的有效性。Xin等[6]以装卸集装箱的总完工时间最短为目标,利用线性混合整数规划模型实现了码头AGV避碰路径规划。冯双海[7]对多AGV调度和路径规划问题进行了研究,采用A*算法求解AGV最短路径,结合多指标调度理论进行AGV调度,并基于有向图进行AGV路径规划并进行了仿真验证,为AGV管理系统的设计和实现提供理论基础。蓝志坤等[8]主要研究了多AGV动态路径规划问题,采用全局规划和动态局部调整相结合的方法,解决AGV死锁、冲突问题,实现AGV系统运行时间最短。苏霞等[9]研究了柔性制造系统的AGV路径规划问题,通过在AGV路径节点上注册和删除信息来更新模型,并利用改进的A*算法规划路径,对潜在的冲突进行检测、分类,再进行针对性的避碰,以此来搜索最短路径。
此外,国内外学者对基于时间窗的AGV路径规划问题也进行了研究[8-11]。贺丽娜等[12]利用时间窗规划路径,提出一种基于先验决策的无碰撞路径规划方法,该方法是根据Dijkstra算法对每台AGV规划出最短路径,再结合时间窗原理进行AGV的无碰撞规划。胡彬等[13]提出一种基于时间窗的动态路径规划方法,先求出基于最短路径的备选路径,利用备选路径排出理想状况下的时间窗,然后对时间窗重叠部分进行计算和更新。张铮炜等[1]提出一种基于时间窗改进Dijkstra的动态路径规划算法,各AGV路径规划的先后顺序由任务优先级和地图中的先验信息决定,利用图论法规划AGV路径,更新地图中时间窗信息,并结合最新时间窗信息,规划顺序靠后的AGV路径,实现AGV避碰。Smolic-Rocak等[14]提出一种多AGV运行的动态路径规划方法,AGV的路径规划取决于运行中的AGV当前任务量以及任务优先级,为了解决动态路径最短问题,提出利用时间窗约束的路径规划方法,但该方法需要进行窗口重叠测试,以实现AGV避碰。
综上所述,目前相关的研究普遍采用一定的方法先规划路径[15],再进行AGV避碰调整[16-17],最后用仿真验证其有效性,也存在采用考虑时间窗约束的AGV路径规划方法。尽管这些文献考虑了最短路径以及利用各个路段上的时间资源来规划路径,但是仅在最短路径上直接进行调整,或是在最短路径上基于时间的变化调整该路径的后续路段,都未曾考虑在最短路径之外的路径上进行规划。本文提出的方法是在给AGV下派任务的基础上,以AGV的最短路径为目标设置各路段的时间窗,并按备选路径转折次数来确定其优先级,实现各路段无时间窗重叠即各AGV之间没有冲突。对于时间窗重叠的路段,采用在原路径上插入时间窗或者在备选路径上插入时间窗的方法,调整各路段时间窗后再进行时间窗重叠测试,若仍存在重叠,则继续调整至最终实现多AGV的无冲突路径规划。最后通过实例验证方法的有效性。
1 AGV工作环境和任务分配自动化集装箱码头中AGV的运输场地布局有2种类型:一种是循环布局,另一种是交叉布局[1]。相对于循环布局,交叉布局下的AGV具有更高的运作效率,并且目前国内建成和在建的自动化集装箱码头多选用交叉布局。
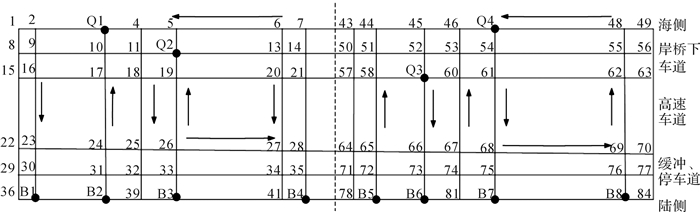
为避免AGV在码头上运行时偏离方向,将地下的磁钉作为导引,本文中AGV的路径规划也基于此。图 2是本文采取的自动化码头路径网络,图中一共有84个节点以模拟磁钉点。岸桥和箱区所在的位置在图 2中以黑点表示,它们占据的节点编号如表 1所示。图 2中线段为有向线段,外围线段为逆时针方向,中间的相邻纵向线段方向相反。
|
| 图 2 自动化集装箱码头路径网络图 Fig.2 Automated container terminal path network diagram |
| 箱区 | 节点 | 箱区 | 节点 | 岸桥 | 节点 | ||
| B1 | 37 | B5 | 79 | Q1 | 3 | ||
| B2 | 38 | B6 | 80 | Q2 | 12 | ||
| B3 | 40 | B7 | 82 | Q3 | 59 | ||
| B4 | 42 | B8 | 83 | Q4 | 47 |
为了便于对AGV路径进行研究,还需要对自动化集装箱码头的路径网络和AGV作如下规定:1)只考虑集装箱卸箱任务,不考虑装箱任务;2)AGV车道为单向,不会出现相向碰撞的情况;3)AGV匀速行驶,不考虑加减速、转折以及空重箱对AGV速度的影响;4)任意行驶路段仅允许1台AGV行驶;5)多台AGV对应多台岸桥,且不固定服务于某台岸桥;6)每个任务由1台AGV完成,每辆AGV只能装1个集装箱;7)岸桥下有中转平台,不考虑岸桥对AGV的等待,但是考虑AGV等待岸桥;8)AGV的起始点在岸桥侧。
自动化集装箱码头上现有20个集装箱卸箱任务,已知完成任务的AGV以及任务的起终点[18],具体任务分配如表 2所示。以图 2中虚线为界将作业区分为左右两个,各作业区分别配备2个岸桥、4台AGV、4个堆场以及10个任务。AGV的速度为5 m/s,每个岸桥完成一个集装箱任务的时间为120 s。
| AGV | 任务 | 路径 | 任务最早开始时间 |
| 1 | 4, 10, 18 | Q2-B1-Q1-B2-Q2-B4 | 第0秒,第240秒, 第480秒 |
| 2 | 8, 17 | Q1-B1-Q2-B4 | 第120秒,第360秒 |
| 3 | 6, 14, 16 | Q1-B3-Q2-B3-Q1-B2 | 第0秒,第240秒, 第480秒 |
| 4 | 9, 11 | Q2-B3-Q1-B1 | 第120秒,第360秒 |
| 5 | 3, 19 | Q3-B5-Q4-B8 | 第120秒,第360秒 |
| 6 | 2, 5, 20 | Q4-B7-Q3-B8-Q4-B5 | 第0秒,第240秒, 第480秒 |
| 7 | 1, 13, 15 | Q3-B6-Q4-B7-Q3-B6 | 第0秒,第240秒, 第480秒 |
| 8 | 7, 12 | Q4-B6-Q3-B5 | 第120秒,第360秒 |
据表 2可知,如1号AGV按照分配需要依次完成3个卸箱任务,任务编号分别为4,10,18。任务4的起终点是岸桥2到箱区1,即Q2-B1,最早开始时间为第0秒;任务10的起终点是Q1-B2,最早开始时间为第240秒;任务18的起终点是Q2-B4,最早开始时间为第480秒。所以1号AGV的路径为Q2-B1-Q1-B2-Q2-B4。
针对任务, 首先根据码头路径布局和任务的分配确定岸桥到箱区的路径,再利用最优路径数学模型求得岸桥到箱区的最短路径(由于路径的单向性,从岸桥到箱区与箱区到岸桥的最短路径不同)。在最短路径有数条的情况下,以“路径转折数较少, 则优先级较高”为原则选择最短路径;若只有1条最短路径,用路径搜索法选出备选路径,也以路径转折数确定优先级。再根据最短路径设置各路段的时间窗,若各路段不存在时间窗重叠,则各AGV之间无冲突路径,规划完成。若存在重叠,对AGV进入该路段的时间进行调整,并调整后续路段的时间窗,或者采用在备用路径插入时间窗的方法,再进行时间窗重叠的检测,在2种方案中选择通过时间窗检测且任务完成时间较短的方案,仍存有冲突的话,继续调整至路段时间窗无重叠。
2 基于最优路径的数学模型建立 2.1 符号说明1) 集合。
Q:岸桥所在的节点集合。
B:场桥所在的节点集合。
N={1, 2, …, n}:路径网络中的节点集合。
E={e21, e18, …, eij}:路径网络中的路段的集合,其中eij={i→j,i, j∈N},表示节点i与节点j之间的距离。
w={w21, w18, …, wij}:路段的权重,其中
K:AGV的集合。
D:需要排序的最短路径和备选路径的集合。
D1:需要排序的具有相同长度的最短路径和备选路径的集合。
d:一条路径中路段的集合。
2) 参数。
v:AGV的速度。
T:一条路径的转折数。
nd:路径中路段的个数。
3) 决策变量。
| $ {X_{ijk}} = \left\{ \begin{array}{l} 1,第\;k\;辆车依次通过节点\;i\;和节点\;j\\ 0,其它 \end{array} \right. $ |
| $ {Z_{ij}} = \left\{ \begin{array}{l} 1,选择从节点\;i\;到节点\;j\;的路径\\ 0,其它 \end{array} \right. $ |
由于路径网络的单向性,对于相同的岸桥和箱区,从岸桥到箱区与从箱区到岸桥所经过的节点是不同的。建立数学模型用于求解各岸桥到各箱区的最短路径,改变式(1)和式(2)中的起终点就可以得到箱区到岸桥的最短路径。
| $ s = \min \left( {\sum\limits_{i \in N} {{Z_{qi}}{e_{qi}}} + \sum\limits_{i,j \in N} {{Z_{ij}}{e_{ij}}} + \sum\limits_{j \in N} {{Z_{jb}}{e_{jb}}} } \right) $ | (1) |
| $ \begin{array}{l} {\rm{s}}.{\rm{t}}\\ \sum\limits_{i \in N} {{Z_{qi}}} = \sum\limits_{j \in N} {{Z_{jb}}} ,q \in Q,b \in B \end{array} $ | (2) |
| $ {Z_{ij}} \le {X_{ijk}},i,j \in N,\forall k \in K $ | (3) |
| $ \sum\limits_{i,j \in N} {{X_{ijk}} \le n - 1} ,\forall k \in K $ | (4) |
| $ {Z_{ij}} = \left\{ {0,1} \right\},i,j \in N $ | (5) |
各AGV需要完成多个任务时, 其路径是由几段小路径组成。如AGV1要完成所分配的任务, 需用数学模型求解Q1-B1,B1-Q2,Q2-B4这3条小路径各自的最短路径。若根据上述模型得到的最短路径只有1条,则采用路径搜索法获得备选路径。路径搜索方法是在最短路径的基础上,寻找符合路段方向、相同起终点以及转折少的路径,但是其总长度长于最短路径。备选路径的排序按“转折数较少,则优先级较高”原则进行。
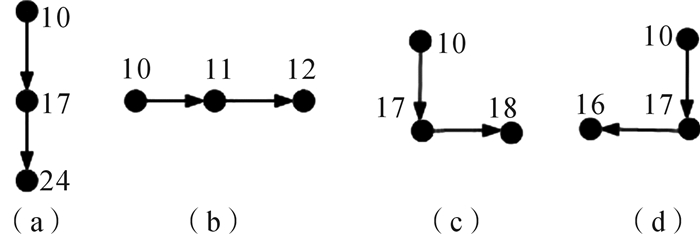
路径的走向大致分为2类:一类是按照原有方向前进,如图 3(a),(b);另一类是改变了原来的方向前进,如图 3(c),(d)。找到连续的3个点,通过判断点与点之间的位置关系确定路径在该路段是否改变方向。
|
| 图 3 AGV路径上3个节点之间的位置关系 Fig.3 The position relationship between three nodes on the AGV path |
| $ S = \mathop {\arg }\limits_d \min \left( {{T_d}} \right) $ | (6) |
| $ \begin{array}{l} {\rm{s}}.{\rm{t}}\\ c = \mathop {\arg }\limits_y \left\{ {\left[ {\sum\limits_{i,j \in N} {j\left( {{Z_{ij}}{{\left( y \right)}_d}} \right)} - \sum\limits_{t = 1}^{{n_d}} {\sum\limits_{i,j \in N} {i\left( {{Z_{ij}}{{\left( t \right)}_d}} \right)} } } \right] = 0,} \right.\\ \;\;\;\;\;{Z_{ij}}{\left( y \right)_d} = 1,{Z_{ij}}{\left( t \right)_d} = 1,\forall y \in \left( {1,2, \cdots ,{n_d}} \right),\\ \;\;\;\;\;\left. {\forall d \in {D_1}} \right\} \end{array} $ | (7) |
| $ \begin{array}{l} \left\{ {{t_{\left( {{Z_{ij}}{{\left( c \right)}_d}} \right)}}\left| {\left[ {\left| {i\left( {{Z_{ij}}{{\left( c \right)}_d} - j\left( {{Z_{ij}}{{\left( c \right)}_d}} \right)} \right.} \right| - } \right.} \right.} \right.\\ \left. {\left. {\left| {i\left( {{Z_{ij}}{{\left( {c + 1} \right)}_d} - j\left( {{Z_{ij}}{{\left( {c + 1} \right)}_d}} \right)} \right.} \right| \ne 0} \right]} \right\} = 1,\forall i,j \in N \end{array} $ | (8) |
| $ {T_d} = \sum\limits_{c = 1}^{{n_d}} {{t_{\left( {{Z_{ij}}{{\left( c \right)}_d}} \right)}}} ,\forall d \in {D_1} $ | (9) |
式(6)为目标函数,表示在路径长度相同的一组路径中取转折最少的一条路径;式(7)表示判断一条路径上的3个点是否连续; 式(8)表示等式成立1次则路径转折1次,其中t(Zij(c)d)表示路径d上的第c个路段的节点j处有1次转折,否则不转折;式(9)表示一条路径的总转折次数。
采用最优路径数学模型和路径搜索方法确定各岸桥与箱区之间的路径,依据转折数确定优先级来确认最短路径和备选路径。根据表 2的AGV任务分配,可知AGV1完成各任务的最短路径和第1备选路径如表 3所示。
| 任务起终点 | 最短路径 | 路径权重/s | 转折数 | 第1备选路径 | 路径权重/s | 转折数 |
| Q2-B1 | Q2-11-10-9-16-23-30-B1 | 120 | 1 | Q2-11-10-9-8-15-22-29-36-B1 | 140 | 2 |
| B1-Q1 | B1-B2-31-24-17-10-Q1 | 110 | 1 | B1-B2-39-B3-33-26-19-Q2-5-4-Q1 | 150 | 2 |
| Q1-B2 | Q1-2-9-16-23-30-B1-B2 | 130 | 2 | Q1-2-1-8-15-22-29-36-B1-B2 | 150 | 2 |
| B2-Q2 | B2-39-B3-33-26-19-Q2 | 100 | 1 | B2-31-24-25-26-19-Q2 | 100 | 2 |
| Q2-B4 | Q2-11-18-25-32-39-B3-41-B4 | 140 | 2 | Q2-11-18-25-32-33-34-41-B4 | 140 | 4 |
同理可以得出其余7台AGV的最短路径及其备选路径。
2.3 时间窗约束下路径规划的实现针对每个集装箱任务m,都需规划出一条最短路径,而每台AGV的最短路径由各任务的最短路径组成。已知的AGV k在(tin, ij, tout, ij)期间占据特定节点i, j之间的路段eij。Twm, ij=(k, m, rm, eij, tin, m, ij, tout, m, ij),其中rm, eij表示为完成任务m的当前可行最短路径中路段eij的排位序号,tin, m, ij是为完成任务m的AGV k开始占用路段eij的时间,tout, m, ij是完成任务m后AGV k不再占用路段eij的时间。任务m在路段eij的权重为:
| $ {w_{m,ij}} = {t_{{\rm{out}},m,ij}} - {t_{{\rm{in}},m,ij}} $ | (10) |
| $ {t_{{\rm{in}},m,ij}} = \left\{ \begin{array}{l} {t_{{\rm{st}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;{r_{m,{e_{ij}}}} = 1\\ {t_{{\rm{out}},{r_{m,{e_{ij}}}} - 1}},\;\;\;\;\;{r_{m,{e_{ij}}}} > 1 \end{array} \right. $ | (11) |
式(11)表示若路段eij是任务m的起始路段,最早开始时间tst大于AGV离开上一个路段的时间,即进入路段eij的时间为tst,若不是,则进入路段eij的时间为AGV离开上一个路段的时间。
通过式(10)和(11)计算得到AGV在各路段的进入时间和各路段新权重,若最后的迭代结果为各路段eij无时间窗重叠,则AGV无碰撞,路径规划完成;否则,需进行调整。
在实际应用中,路段eij被各AGV分时占用,路段eij上会有一系列时间窗Twm, ij=(k, m, rm, eij, tin, m, ij, tout, m, ij), 从而形成Twij, Twij表示在路段eij上,各任务占用的时间窗,以及完成任务的AGV在路段eij上的进入和退出时间,表示为:
| $ {\mathit{\boldsymbol{T}}_{{w_{ij}}}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_{{w_{1,ij}}}}}&{{\mathit{\boldsymbol{T}}_{{w_{2,ij}}}}}& \cdots &{{\mathit{\boldsymbol{T}}_{{w_{m,ij}}}}} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{t}}_{{\text{in}},ij}} = {\left[ {\begin{array}{*{20}{c}} {{t_{{\text{in}},1,ij}}}&{\;{t_{in,2,ij}}}&{\;\; \cdots }&{\;\;\;{t_{{\text{in}},m,ij}}} \end{array}} \right]^{\text{T}}} $ |
| $ {\mathit{\boldsymbol{t}}_{{\text{out}},ij}} = {\left[ {{t_{{\text{out}},1,ij}}\;\;\;\;{t_{{\text{out}},2,ij}}\;\;\; \cdots {t_{{\text{out}},m,ij}}} \right]^{\text{T}}} $ |
向量的维度为任务的数量,随着时间变化任务数量会改变。若任务m不占用路段eij时间窗,则时间窗Twij的分量为零,同时tin, ij, tout, ij的分量为▍。
若在路段eij上有时间窗的重叠,将各重叠时间窗的重叠开始时间进行降序排列,选取开始时间最小的时间窗,选择该时间窗中以最小时间为进入时间的任务m作为调整对象,方法如下:
步骤1:在产生重叠时间窗的原路径上调整时间窗。在原路径冲突路段eij后加入时间窗,需要满足条件:路段eij连续的空闲时间窗空隙大于AGV通过路段所需时间(路段eij的权重wij)。
步骤2:在备选路径中加入时间窗。
在备选路径中加入时间窗,需要满足以下3个条件:
1) 进入各路段的时间必须不小于各路段上一个任务的离开时间;
2) 进入各路段的时间必须不小于AGV离开上一个路段的时间;
3) 进入路段后路段连续的空闲时间窗空隙大于AGV通过路段eij所需时间。
任务m在备选路径上进行时间窗检测和安排。全部a个任务中有p个任务在路段eij上,任务m的第1备选路径包含路段eij。在路段eij上插入新的时间窗前,路段eij上有p个任务占据路段eij的时间窗,时间窗如下式所示:
| $ {\mathit{\boldsymbol{T}}_{{w_{ij}}}} = \left[ {{\mathit{\boldsymbol{T}}_{{w_{1,ij}}}},{\mathit{\boldsymbol{T}}_{{w_{2,ij}}}},{\mathit{\boldsymbol{T}}_{{w_{3,ij}}}} \cdots {\mathit{\boldsymbol{T}}_{{w_{p,ij}}}}} \right],p < a $ |
路段eij上可以插入的时间窗空隙满足:
| $ \begin{array}{l} C = \arg \mathop {\min }\limits_l \left\{ {{{\left( {{t_{{\rm{in}},ij}}} \right)}_l};\left[ {{{\left( {{t_{{\rm{in}},ij}}} \right)}_{l + 1}} - \max \left( {{{\left( {{t_{{\rm{out}},ij}}} \right)}_l},} \right.} \right.} \right.\\ \left. {\left. {\left. {{t_{{\rm{out}},{r_{m,{e_{ij}}}} - 1}}} \right)} \right] > {w_{ij}},l = 1,2, \cdots ,p} \right\} \end{array} $ | (13) |
则任务m进入路段eij的时间为:
| $ {t_{{\rm{in}},m,ij}} = \max \left( {{{\left( {{t_{{\rm{out}},ij}}} \right)}_{C - 1}},{t_{{\rm{out}},{r_{m,{e_{ij}}}} - 1}}} \right) $ | (14) |
式中C表示在路段eij上第l个任务时间窗,任务m在路段eij上的时间窗是第l+1个任务时间窗。
任务m的离开路段eij的时间为:
| $ {t_{{\rm{out}},m,ij}} = \max \left( {{t_{{\rm{in}},m,ij}} + {w_{m,ij}},{t_{{\rm{in}},{r_{m,{e_{ij}}}} + 1}}} \right) $ | (15) |
若路段eij上的p个任务的时间窗排布紧密,无法再插入时间窗,便在已有时间窗的最后插入时间窗,即:
| $ \left\{ \begin{array}{l} {t_{{\rm{in}},m,ij}} = {\left( {{t_{{\rm{out}},ij}}} \right)_p}\\ {t_{{\rm{out}},m,ij}} = {t_{{\rm{in}},m,ij}} + {w_{m,ij}} \end{array} \right. $ | (16) |
路段eij上的时间窗更新后,基于式(14)至(16)对任务m所选路径的后续路段进行时间窗更新。在任务m所选路径的各路段时间窗重新安排后,需要进行重叠检查。
| $ \begin{array}{*{20}{c}} {\left\{ {{{\left( {{t_{{\rm{in}},ij}}} \right)}_l};\left[ {{{\left( {{t_{{\rm{in}},ij}}} \right)}_{l + 1}} - {{\left( {{t_{{\rm{out}},ij}}} \right)}_l}} \right] < 0,} \right.}\\ {\left. {l = 1,2,3, \cdots ,p - 1} \right\} = \varphi } \end{array} $ | (17) |
若检查结果符合式(17),则无重叠时间窗,即AGV之间无碰撞,路径规划完成。若不符合,则存在重叠时间窗,需重复上述过程进行调整。
最终路径选择取决于所得路径的权重大小,选取权重最小的路径作为最优路径。
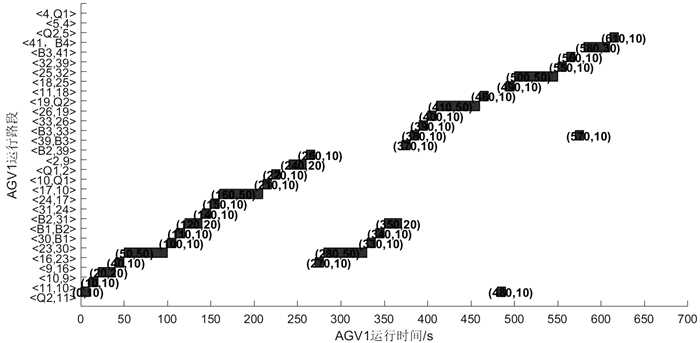
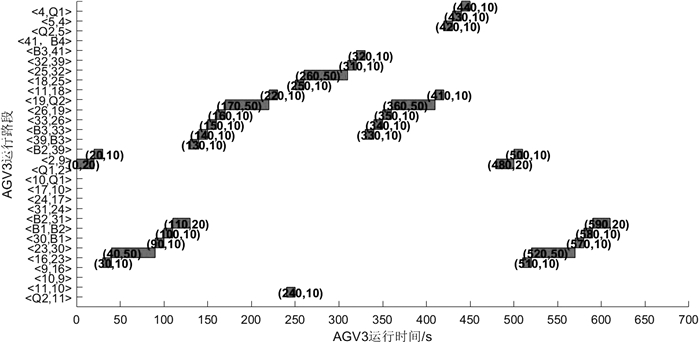
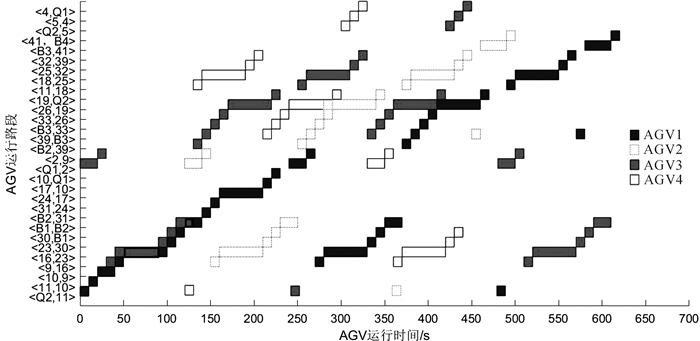
3 实例验证为验证基于路段时间窗的AGV路径规划方法的有效性,以图 2所示的AGV路径网络为基础,以安全避碰和各AGV耗时为评价标准,对多台AGV的路径规划进行测试。具体的任务安排如表 2所示。图 4和图 5分别为最短路径下AGV1,AGV3的路径时间窗分布图。图 6是AGV1至AGV4在最短路径下的路径时间窗分布图。从图 4可知,AGV1完成任务4, 10, 18需要经过的路段为Q2-11-10-9-16-23-30-B1-B2-31-24-17-10-Q1-2-9-16-23-30-B1-B2-39-B3-33-26-19-Q2-11-18-25-32-39-B3-41-B4,AGV1在路段 < Q2, 11>的第1个时间窗(0, 10)表示AGV1开始占用路段 < Q2, 11>的时间为第0秒,占用的时长为10 s,即结束占用的时间为第10秒。图 6中路段 < 16, 23>,< B1, B2>存在冲突,冲突时间窗在图 6中已用黑框标示出,冲突时间窗数据如表 4所示。
|
| 图 4 最短路径情况下AGV1路径时间窗分布图 Fig.4 The distribution of the AGV1 path time window under the shortest path |
|
| 图 5 最短路径情况下AGV3路径时间窗分布图 Fig.5 The distribution of the AGV3 path time window under the shortest path |
|
| 图 6 最短路径情况下多AGV路径时间窗分布图 Fig.6 The distribution of AGVs path time window under the shortest path |
| 冲突对象 | 冲突路段 | 冲突开始时间 | 冲突结束时间 |
| AGV1,AGV3 | < 16, 23> | 第50秒 | 第90秒 |
| < B1, B2> | 第120秒 | 第130秒 |
对于2台相冲突的AGV,选择调整对象的原则是选择冲突开始时进入该路段的AGV,也就是后进入冲突路段的AGV。对冲突AGV进行延迟通过和采用在备选路径上插入时间窗的方法,其结果如表 5所示。
| s | |||
| AGV | 理想状态下 | 延迟通过 | 备选路径 |
| AGV1 | 620 | 660 | 640 |
| AGV2 | 500 | 500 | 500 |
| AGV3 | 610 | 610 | 610 |
| AGV4 | 440 | 440 | 440 |
从表 5可知,按照原则,采用上述2种方法对AGV1进行调整,都达到了很好的效果。调整后,AGV1与AGV3路径冲突解除,两者都能在理想状态下通过各路段,而且也没有因为AGV1的调整使原本没有冲突的AGV2和AGV4产生新的冲突。在案例中,选择在备选路径上插入时间窗的方法都相对优于延迟通过,采用备选路径的AGV花费的总时间更少。原因有以下几点:路径的选择是基于最短路径,最短路径的某些路段是被选择的高频路径,发生冲突的路段也是这些高频路段,这些路段上往往AGV流量高,路段时间窗占用得多,不容易安排新的时间窗,并且延迟通过占用上一路段更多的时间,也会使交通拥堵。而备选路径上的AGV流量相对于最短路径要小,反而在更短的时间内完成任务,提高了AGV的利用率。
4 结语本文研究的是只考虑卸箱任务的自动化集装箱码头多AGV路径规划问题,通过将最优路径数学模型、路径搜索方法和时间窗相结合,提出了一种基于路段时间窗的自动化集装箱码头多AGV路径规划方法。该方法能够通过时间窗重叠测试来预测各AGV按规划运行时是否有冲突,若有,则可检测出冲突路段、冲突发生时间以及相互冲突的AGV。在时间窗重叠时选择在原路径或备选路径上插入时间窗的方法来调整设置时间窗至AGV无冲突。通过实例验证了该方法的有效性,结果表明该方法能实现多AGV无冲突的路径规划,并且任务完成时间短,提高了AGV的工作效率。本文在研究过程中没有考虑AGV自身长度等因素,因此今后在研究集装箱码头AGV无冲突路径规划过程中可以考虑加入该因素。
| [1] |
张峥炜, 陈波, 陈卫东.
时间窗约束下的AGV动态路径规划[J]. 微型电脑应用, 2016, 32(11): 46–49.
ZHANG Zheng-wei, CHEN Bo, CHEN Wei-dong. Dynamic routing of automated guided vehicles with time window[J]. Microcomputer Application, 2016, 32(11): 46–49. DOI:10.3969/j.issn.1007-757X.2016.11.014 |
| [2] | DUINKERKEN Mark B, LODEWIJKS Gabriel. Routing of AGVs on automated container terminals[C]//2015 IEEE 19th International Conference on Computer Supported Cooperative Work in Design, Calabria, May 6-8, 2015. http://ieeexplore.ieee.org/document/7230993/ |
| [3] | SONG Li-qin, HUANG Shell-ying. A hybrid metaheuristic method for dispatching automated guided vehicles in container terminals[C]//2013 IEEE Symposium on Computational Intelligence in Scheduling (SCIS), Singapore, Apr. 16-19, 2013. https://www.researchgate.net/publication/243964438_A_Hybrid_Metaheuristic_Method_for_Dispatching_Automated_Guided_Vehicles_in_Container_Terminals |
| [4] |
霍凯歌, 张亚琦, 胡志华.
自动化集装箱码头多载AGV调度问题研究[J]. 大连理工大学学报, 2016, 56(3): 244–251.
HUO Kai-ge, ZHANG Ya-qi, HU Zhi-hua. Research on scheduling problem of multi-load AGV at automated container terminals[J]. Journal of Dalian University of Technology, 2016, 56(3): 244–251. DOI:10.7511/dllgxb201603004 |
| [5] | NISHI T, HIRANAKA Y, GROSSMANN I E. A bilevel decomposition algorithm for simultaneous production scheduling and conflict-free routing for automated guided vehicles[J]. Computers and Operations Research, 2011, 38(5): 876–888. DOI:10.1016/j.cor.2010.08.012 |
| [6] | XIN Jian-bin, NEGENBORN R R, CORMAN F, et al. Control of interacting machines in automated container terminal using a sequential planning approach for collision avoidance[J]. Transportation Research Part C:Emerging Technologies, 2015: 60, 377–396. |
| [7] |
冯海双. AGV自动运输系统调度及路径规划的研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2013: 1-73.
FENG Hai-shuang. Research on scheduling and path planning of AGV automatic transport system[D]. Harbin: Harbin Institute of Technology, School of Mechatronics Engineering, 2013: 1-73. http://www.doc88.com/p-4039058190987.html |
| [8] |
蓝志坤, 蓝志环.
多AGV系统的动态路径规划算法[J]. 公路交通科技, 2012(10): 121–125.
LAN Zhi-kun, LAN Zhi-huan. Algorithm of dynamic path planning for multiple AGV system[J]. Highway Traffic Technology, 2012(10): 121–125. DOI:10.3969/j.issn.1002-0268.2012.10.021 |
| [9] |
苏霞, 李伟光.
FMS中自动导引车路径规划[J]. 机械设计与制造, 2015(1): 201–203.
SU Xia, LI Wei-guang. Path planning of automated guided vehicles in FMS[J]. Mechanical Design and Manufacturing, 2015(1): 201–203. |
| [10] |
乔岩, 钱晓明, 楼佩煌, 等.
基于改进时间窗的AGVs避碰路径规划[J]. 计算机集成制造系统, 2012, 18(12): 2683–2688.
QIAO Yan, QIAN Xiao-ming, LOU Pei-huang, et al. Improved time window based conflict-free automated guided vehicle system routing[J]. Computer Integrated Manufacturing Systems, 2012, 18(12): 2683–2688. |
| [11] |
朱龙彪, 王辉, 王景良, 等.
基于动态时间窗的泊车系统路径规划研究[J]. 工程设计学报, 2017, 24(4): 440–448.
ZHU Long-biao, WANG Hui, WANG Jing-liang, et al. Research on path planning of parking system based on dynamic time window[J]. Chinese Journal of Engineering Design, 2017, 24(4): 440–448. |
| [12] |
贺丽娜, 楼佩煌, 钱晓明, 等.
基于时间窗的自动导引车无碰撞路径规划[J]. 计算机集成制造系统, 2010, 16(12): 2630–2634.
HE Li-na, LOU Pei-huang, QIAN Xiao-ming, et al. Conflict-free automated guided vehicles routing based on time window[J]. Computer Integrated Manufacturing Systems, 2010, 16(12): 2630–2634. |
| [13] |
胡彬, 王冰, 王春香, 等.
一种基于时间窗的自动导引车动态路径规划方法[J]. 上海交通大学学报, 2012, 46(6): 967–971.
HU Bin, WANG Bing, WANG Chun-xiang, et al. Dynamic routing of automated guided vehicle based on time window[J]. Journal of Shanghai Jiaotong University, 2012, 46(6): 967–971. |
| [14] | SMOLIC-ROCAK N, BOGDAN S, KOVACIC Z, et al. Time windows based dynamic routing in multi-AGV systems[J]. Transactions on Automation Science and Engineering, 2010, 7(1): 151–155. DOI:10.1109/TASE.2009.2016350 |
| [15] | FAZLOLLAHTABAR H, SAIDI-MEHRABAD M, BALAKRISHNAN J. Mathematical optimization for earliness/tardiness minimization in a multiple automated guided vehicle manufacturing system via integrated heuristic algorithms[J]. Robotics and Autonomous Systems, 2015, 72: 131–138. DOI:10.1016/j.robot.2015.05.002 |
| [16] | LEHMANN M, GRUNOW M, GUNTHER H O. Deadlock handling for real-time control of AGVs at automated container terminals[J]. OR Spectrum:Quantitative Approaches in Management, 2006, 28(4): 631–657. |
| [17] | PARK J H, KIM H J, LEE C. Ubiquitous software controller to prevent deadlocks for automated guided vehicle systems in a container port terminal environment[J]. Journal of Intelligent Manufacturing, 2009, 20(3): 321–325. DOI:10.1007/s10845-008-0212-3 |
| [18] |
杨勇生, 崔佳羽, 梁承姬, 等.
基于软时间窗的自动化集装箱码头AGV路径规划[J]. 广西大学学报(自然科学版), 2017, 42(5): 1793–1801.
YANG Yong-sheng, CUI Jia-yu, LIANG Cheng-ji, et al. Research on the routing of AGV in automated container terminal based on soft time window[J]. Journal of Guangxi University (Natural Science Edition), 2017, 42(5): 1793–1801. |


