2. 成都飞机工业(集团)有限责任公司, 四川 成都 610065;
3. 四川大学 制造科学与工程学院, 四川 成都 610065
2. Chengdu Aircraft Industrial(Group) Co., Ltd., Chengdu 610065, China;
3. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China
导弹在实施打击任务过程中飞行的高度和速度在短时间内剧烈变化, 使得其工作环境温度和气动加热等急剧变化而导致整流罩蒙皮温度和热载荷也随之变化[1]。而导引头电子设备是射频微波高密度集成装置[2], 它对目标进行探测, 并导引导弹飞向目标, 对导弹的作战性能有着重大影响, 其热可靠性关系到整个导弹系统作战任务的成败[3]。因此,为保证弹载电子设备的工作正常,使它满足战术导弹命中精度和作用距离的要求,在导弹设计阶段应精确地计算出弹载电子设备的稳态和瞬态热载荷以及预测因热载荷变化而引起的导引头内的环境温度变化,从而准确分析影响天线测向精度及设备工作稳定性的主要因素。然而,由于无法获取在导弹脱靶飞行后打靶弹在高空高速环境下的实测数据,而地面试验又无法模拟高空环境下高速气动加热对中段探测装置的电气性能和中制导段调姿的影响,所以如何准确模拟高空高速环境下弹体气动加热的实际工况,复现出相应导引头测向变化的故障问题,成为急需解决的重点难题[4]。
弹载电子设备在高速运行过程中的瞬态热载荷变化是一个流场和结构场相互联系、相互作用的流固耦合(fluid structure interaction,FSI)问题,该问题是一直是众多科研人员关注和研究的热点[5-7]。目前,解决流固耦合问题的方法主要有直接耦合式解法(monolithic approach)和分离方法(partitioned approach)[8-10]。高展等根据Tonti图将离散几何法应用于三维集成电路中TSV阵列的电-热-力场的耦合问题, 并将计算结果与基于有限元法的商业软件COMSOL的结果进行对比,提高了多物理场耦合问题上的计算精度[11]。吴泽玉等为了解决流-固耦合动力学求解效率和精度低等问题, 提出了一种增维精细积分法[12]。张健等利用热流固耦合的数值模拟方法,研究了在均匀加热状态下三维方形管道的瞬态传热问题[13]。郭崇志等利用数值模拟方法,得出了流场分析得到的不均匀温度无法准确地作为结构分析的温度载荷的结论[14]。卢燕等结合CFD和FEM方法对精密离心机的热变形进行流-热-固多场耦合计算,采用流固耦合换热整场求解法计算离心机温度场[15]。基于现有研究,本文提出了一种基于流固耦合的弹载电子设备瞬态热仿真分析与计算方法。结合理论计算的气动加热数据、地面试验环境下模拟数据及流固耦合模型中的参数进行对比修正,从而获得较为精确的整流罩表面在任意飞行时刻的热流密度分段函数,并结合该型号导弹的实际结构尺寸,将其整流罩表面分割的大量结构微元与热流密度分段函数相对应,运用MATLAB软件计算拟合出每块结构微元对应的瞬态功率曲线分段函数,有效地将气动能量转化为针对导弹外壳壁面微元随时间变化的功率加热模块。最后,运用热仿真软件模拟导弹在高空高速环境下中段制导探测装置所处的热环境工况,并根据相应热环境工况的加载,计算出整个弹载电子设备在任意飞行时刻的热场分布云图,从云图中直观预测出整个弹载电子设备的工作温度及其环境温度的瞬态变化情况,从而为弹载电子设备的热防护及其热设计提供有效的支持。
1 气动加热物理模型和计算方法 1.1 气动加热计算理论模型高速飞行的导弹附近的流场为典型的湍流流场,并带有各种复杂的换热过程[16]。为简化问题,忽略流动过程中的辐射换热效应,以S-A湍流模型描述流动过程,其控制方程包括:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0 $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j} + p} \right) = \frac{\partial }{{\partial {x_j}}}\left[{{{\left( {{\tau _{ij}}} \right)}_{{\rm{eff}}}}} \right] $ | (2) |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left[{{u_i}\left( {\rho E + p} \right)} \right] = \\ \frac{\partial }{{\partial {x_j}}}\left[{{u_i}{{\left( {{\tau _{ij}}} \right)}_{{\rm{eff}}}}} \right] + \frac{\partial }{{\partial {x_j}}}\left[{{k_{{\rm{eff}}}}\left( {\frac{{\partial T}}{{\partial {x_j}}}} \right) + \sum {{h_{\rm{s}}}{J_{\rm{s}}}} } \right] \end{array} $ | (3) |
式中:ρ为密度,p为压强,(τij)eff为有效应力,ui,uj为速度,T为温度,E为总能量,keff为扩散热系数,hs为体积膨胀系数,Js为熵通量。
对于固相的传热过程,采用无热源的热传导方程描述:
| $ {\rho _p}{C_p}\frac{{\partial {T_p}}}{{\partial t}} = \frac{\partial }{{\partial {x_i}}}\left( {{\lambda _p}\frac{{\partial {T_p}}}{{\partial {x_i}}}} \right) $ | (4) |
式中:ρp为固体密度,Cp为固体比热,Tp为头罩温度, λp为导热系数。
1.2 流固耦合热传导求解方法气相和固相的交界面是热交换的耦合壁面,对于气相采用湍流的壁面函数法计算,固相表面温度和热流量基于与气相通过热流相等的条件进行耦合计算。
为了考虑通过壁面进行的热传递, 必须给出壁面的材料特性、壁面的厚度以及壁面的热生成率等参数。从流体单元到固体壁面的热通量通过下式计算:
| $ q = {h_{\rm{f}}}\left( {{T_{\rm{w}}}-{T_{\rm{f}}}} \right) + {q_{{\rm{rad}}}} $ | (5) |
式中:hf为对流换热系数,Tw为固体壁面温度,Tf为壁面流体温度,qrad为辐射热通量。
在高速可压缩流体中, 由于黏性耗散加热的影响, 靠近壁面区域的温度分布与亚音速流中的情况有非常大的不同, 所以在计算高速可压缩流体靠近壁面区域的温度分布时一定要加入黏性耗散加热的影响。壁面边界定律具有如下组成形式:
| $ \begin{array}{l} {T^*} = \frac{{\left( {{T_{\rm{w}}}- {T_{\rm{f}}}} \right)\rho {C_p}C_\mu ^{1/4}k_P^{1/2}}}{q} = \\ \left\{ {\begin{array}{*{20}{c}} {{P_{\rm{r}}}{y^*} + \frac{1}{2}\rho {P_{\rm{r}}}\frac{{C_\mu ^{1/4}k_P^{1/2}}}{q}U_P^2}&{{y^*} < y_T^*}\\ {{P_{{\rm{rt}}}}\left[{\frac{1}{k}\ln \left( {E{y^*}} \right) + P} \right] + }&{}\\ {\frac{1}{2}\rho \frac{{C_\mu ^{1/4}k_P^{1/2}}}{q}\left[{{P_{{\rm{rt}}}}U_P^2 + \left( {{P_{\rm{r}}}-{P_{{\rm{rt}}}}} \right)U_C^2} \right]}&{{y^*} > y_T^*} \end{array}} \right. \end{array} $ | (6) |
其中P由Jayatilleke给出的公式计算得出:
| $ P = 9.24\left[{{{\left( {\frac{{{P_{\rm{r}}}}}{{{P_{{\rm{rt}}}}}}} \right)}^{3/4}}-1} \right]\left[{1 + 0.28{{\rm{e}}^{-0.007\frac{{{P_{\rm{r}}}}}{{{P_{{\rm{rt}}}}}}}}} \right] $ | (7) |
固体区域的能量方程为:
| $ \frac{\partial }{{\partial t}}\left( {\rho {C_p}{T_p}} \right) + {▋_g}\left( {V\rho {C_p}{T_p}} \right) = {▋ _g}\left( {k\;\;\;▋ T} \right) + S $ | (8) |
式中:T*为流固耦合区壁面温度,Pr为普朗特常数,Prt为湍流普朗特常数, P为流固耦合区壁面压力,UC为流固耦合区壁面平均速度,y*为流固耦合区壁面距离,kP为湍流功能系数,S为内热源。
1.3 计算方法计算前应明确导弹整体气动参数及其结构形式,本文所讨论的某型反辐射导弹的热防护结构如下:
1) 整流罩(天线罩):复合石英天线罩,罩体厚度为6 mm;
2) 天线罩内防热罩:聚芳基乙炔,厚度为1.5 mm;
3) 天线罩连接环:6 mm罩体与殷钢粘接;
4) 导引头舱:3 mm玻璃钢+3 mm 2Cr13;
5) 战斗部舱:3 mm玻璃钢+3 mm 35号钢;
6) 控制舱:3 mm玻璃钢+3 mm TC4;
7) 空气舵:钼渗铜材料。
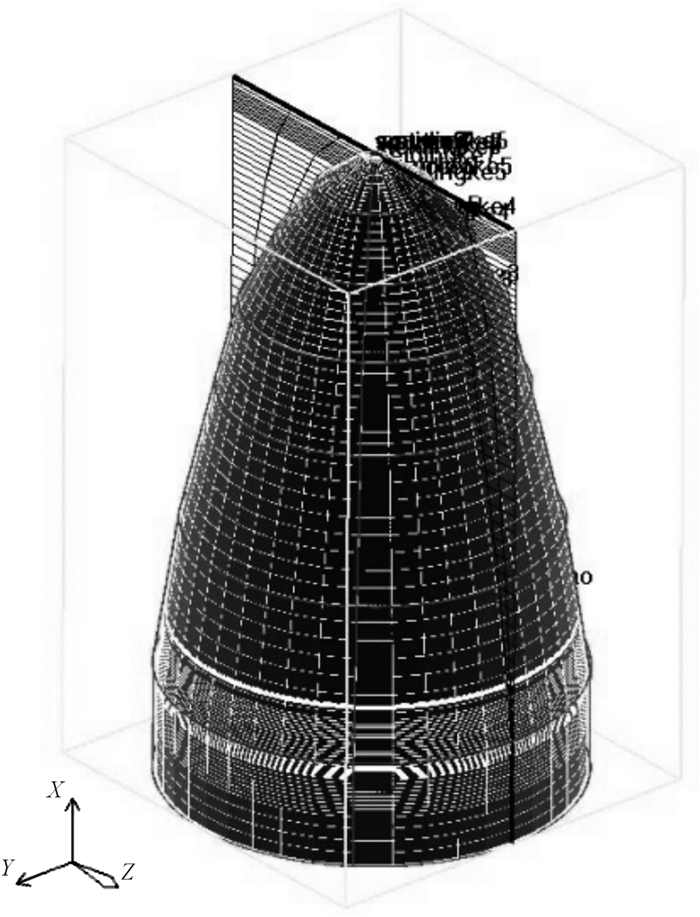
采用有限体积法对导弹结构进行实体划分,运用上述讨论的流固耦合法对划分后的单元模块进行瞬态求解。对于整个控制方程组,由于计算流场为超音速流场,故采用耦合求解格式,计算时采用TVD二阶格式。为减小计算量,对计算区域进行了简化。结合实际工程需求,主要针对导引头部分进行热分析与数值求解。导引头网格划分如图 1所示。
|
| 图 1 导引头网格划分 Fig.1 The grid division of seeker |
本文所讨论的某型导弹从升空到击中目标,总飞行时间为48 s。这里将网格划分后的整流罩表面近似看作一个个面积平整的微元,运用上面的计算公式,便可以将气动加热的能量与整流罩表面微元结合,从而计算出随时间变化的热流密度函数。
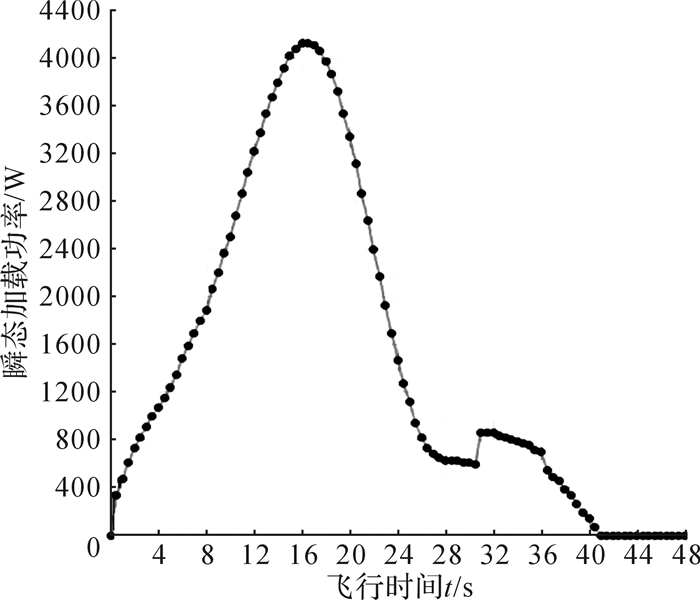
2 弹载电子设备的瞬态热分析 2.1 热流密度函数的修正与转化通过流固耦合算法得出的与整流罩表面微元对应的热流密度函数与实际情况可能会存在一定的误差,这会影响后期整弹热分析的求解精度。通过结合静态热模拟试验和电弧加热包罩试验所得的大量数据与流固耦合模型中的参数进行对比修正,获得较为精确的整流罩表面在任意飞行时刻的热流密度分段函数。结合该型号导弹的实际结构尺寸,可将其整流罩表面分割的大量结构微元与求得的热流密度分段函数相对应,运用MATLAB软件计算拟合出每块结构微元对应的瞬态功率曲线分段函数[17]。这样可有效地将气动加热的能量转化为针对导弹外壳壁面微元随时间变化的功率加热模块。其中一块微元的瞬态功率曲线分段函数如图 2所示。
|
| 图 2 整流罩表面某一微元的瞬态功率曲线分段函数 Fig.2 Transient power curve piecewise function of a certain microelement on the surface of fairing |
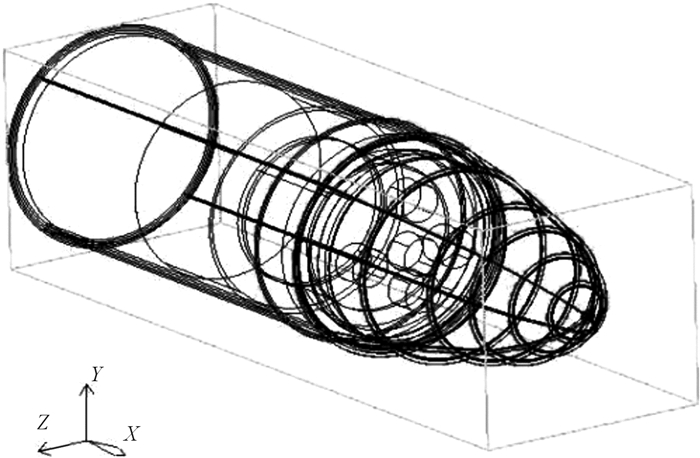
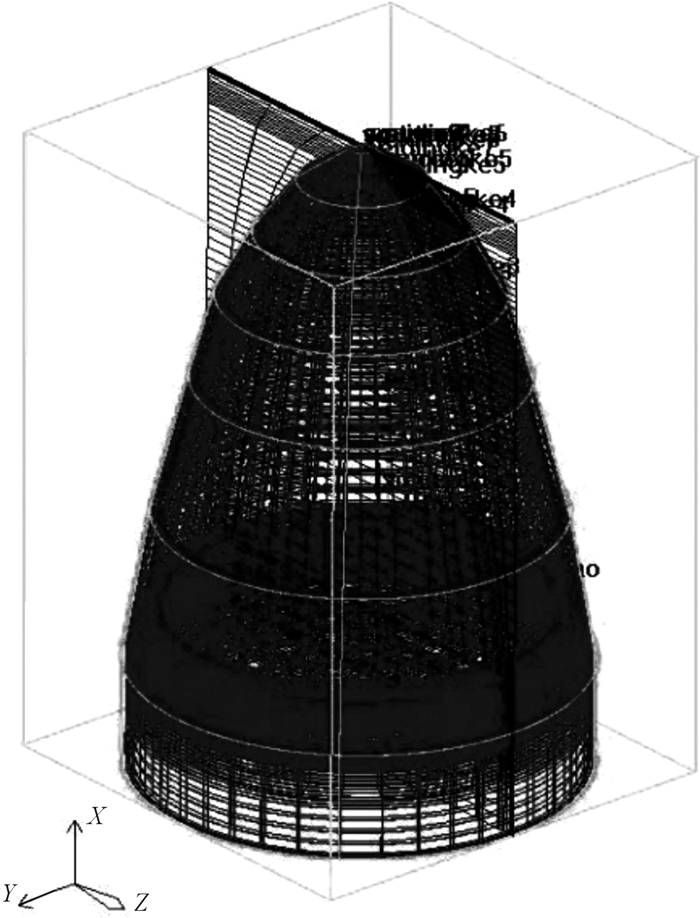
运用Fluent[18]结合该型导弹及其内装弹载设备的实际结构物性参数建立热仿真计算模型,如图 3所示。结合实际工程需求运用GMBIT网格划分软件,对导引头及其弹载电子设备进行有限元网格划分,如图 4所示。
|
| 图 3 某型导弹热分析简化模型 Fig.3 Simplified thermal analysis model of a certain missile |
|
| 图 4 导引头及其弹载电子设备网格划分 Fig.4 The grid division of seeker and its missile-borne electronic equipment |
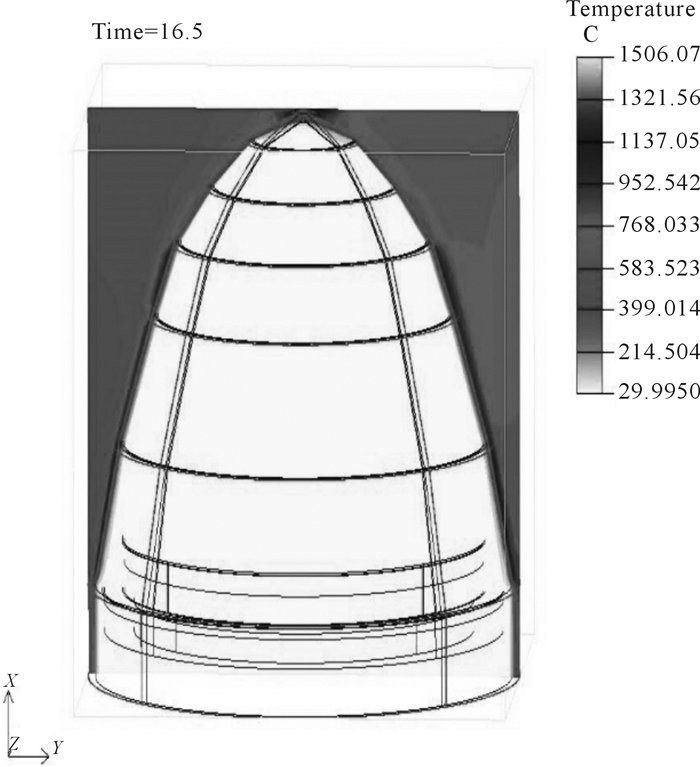
导引头由整流罩(天线罩)、天线罩内防热罩、隔热板、吸波板、柱螺旋天线阵、连接环及微波器件组成。其中柱螺旋天线阵是关系到整个导弹系统制导精度的关键器件,因此对工作环境有一定要求,且对整个天线阵的温度梯度有较高标准要求,柱螺旋天线间的温度梯度直接影响其测向精度,所以导引头在整个飞行过程中内部热场的分布至关重要。本文将流固耦合计算修正转化后的功率分段函数加载到Fluent的热分析模型中,得到导引头及其弹载电子设备在任意飞行时刻的热场分布云图,如图 5至图 7所示。
|
| 图 5 t=16.5 s时导引头及其弹载电子设备瞬态轴向温度云图 Fig.5 Transient axial temperature nephogram of seeker and its missile-borne electronic equipment at t=16.5 s |
|
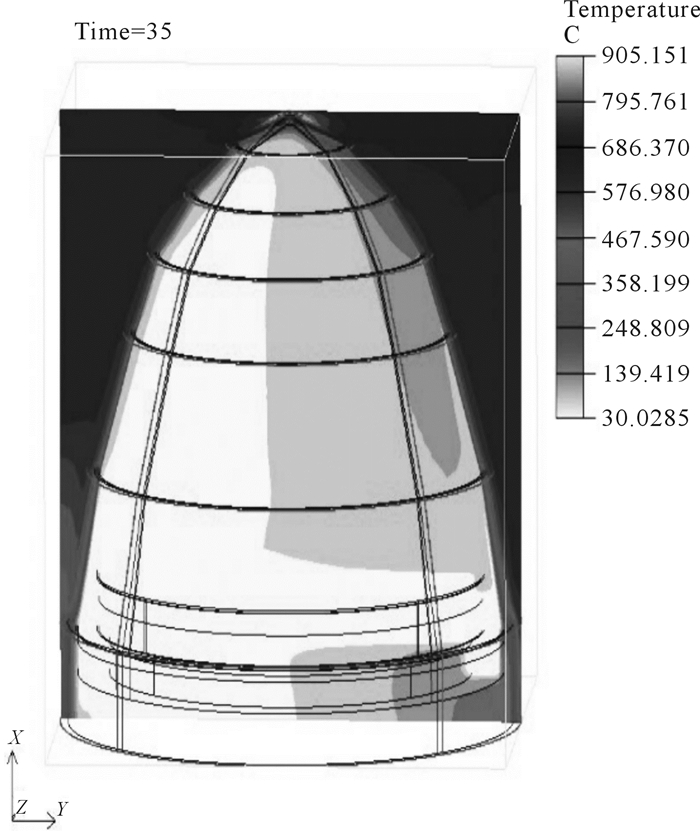
| 图 6 t=35 s时导引头及其弹载电子设备瞬态轴向温度云图 Fig.6 Transient axial temperature nephogram of seeker and its missile-borne electronic equipment at t=35 s |
|
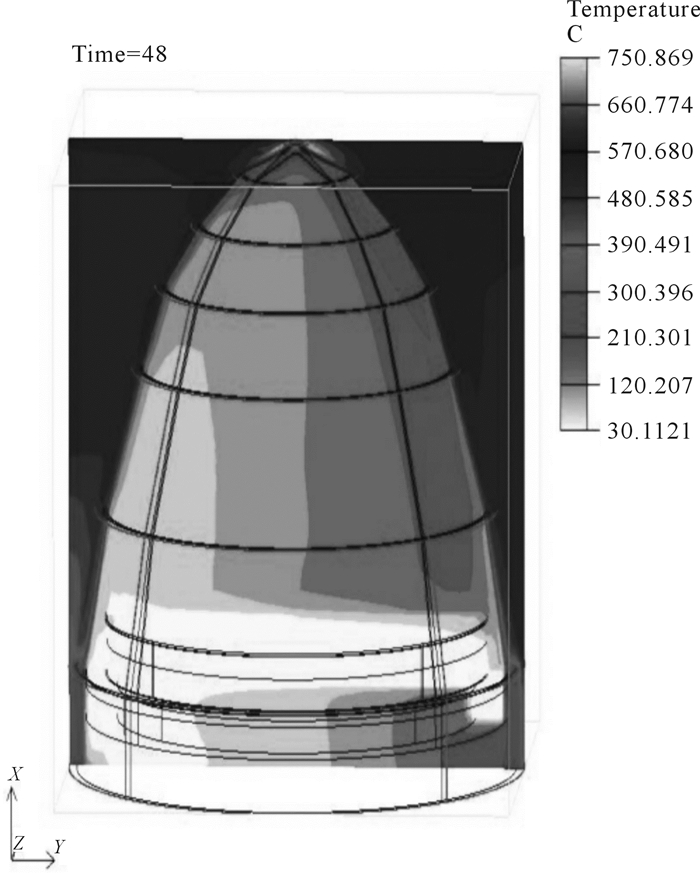
| 图 7 t=48 s时导引头及其弹载电子设备瞬态轴向温度云图 Fig.7 Transient axial temperature nephogram of seeker and its missile-borne electronic equipment at t=48 s |
|
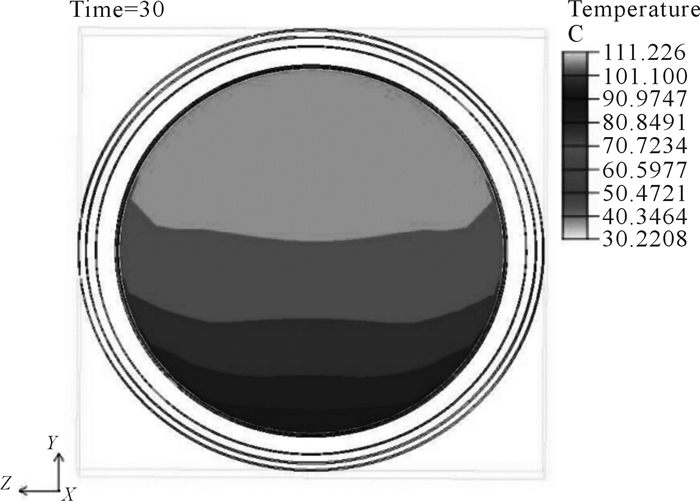
| 图 8 t=30 s时隔热板瞬态温度云图 Fig.8 Transient temperature nephogram of insulation board at t=30 s |
|
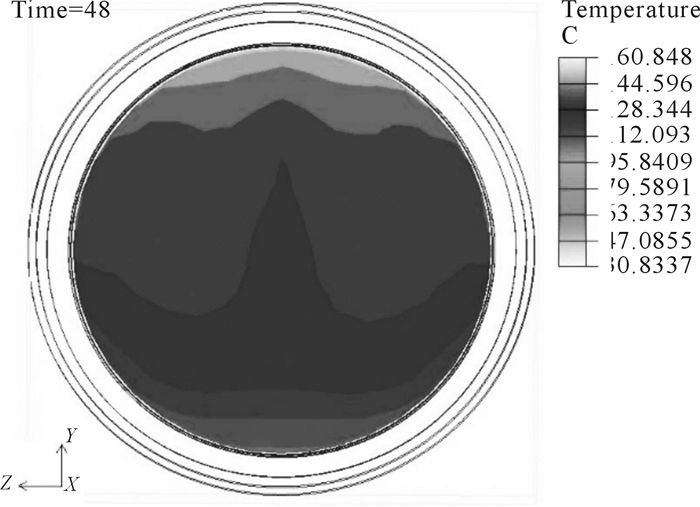
| 图 9 t=48 s时隔热板瞬态温度云图 Fig.9 Transient temperature nephogram of insulation board at t=48 valign="top" |
|
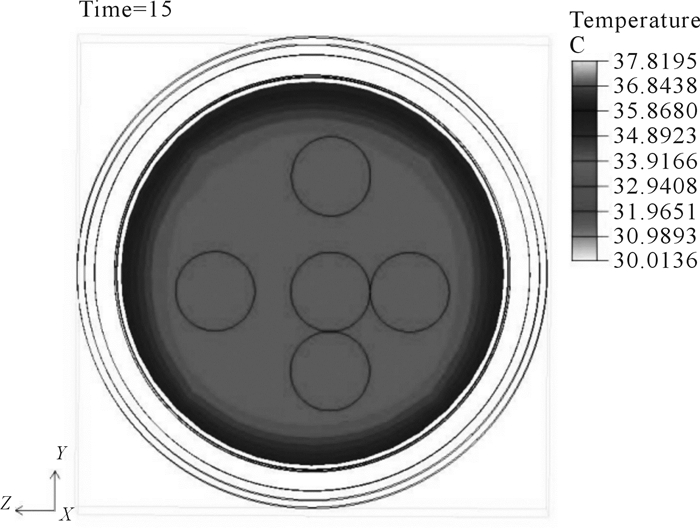
| 图 10 t=15 s时吸波板瞬态温度云图 Fig.10 Transient temperature nephogram of absorbing board at t=15 s |

|
| 图 11 t=48 s时吸波板瞬态温度云图 Fig.11 Transient temperature nephogram of absorbing board at t=48 s |
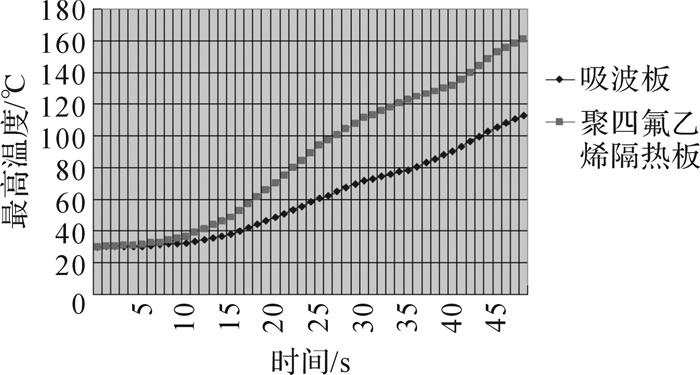
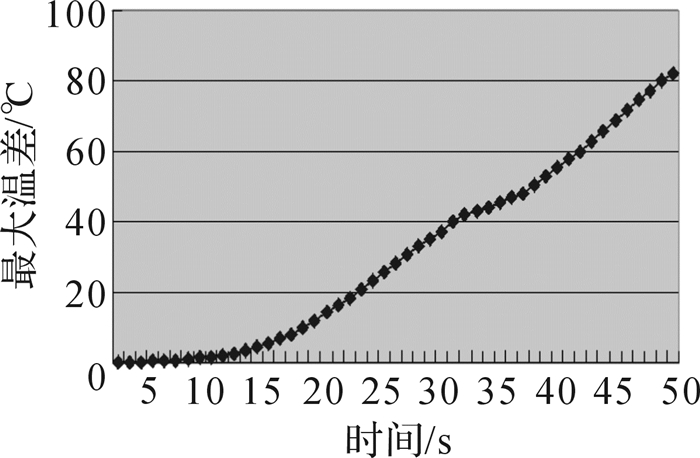
通过仿真计算出整个飞行过程中吸波板、隔热板的温度最大值和吸波板内最大温差,如图 12至图 13所示。
|
| 图 12 吸波板、隔热板温度最大值 Fig.12 Maximum temperature of absorbing board and insulation board |
|
| 图 13 吸波板内最大温差 Fig.13 Maximum temperature difference of absorbing board |
通过观察各温度云图,可看出导弹在高空高速飞行过程中由于受到气动加热作用,其导引头壁面最高温度高达上千摄氏度。同时由于导弹飞行姿态的影响,其飞行过程中有一定攻角,而攻角会将弹体分为迎风面与背风面,从而引起气动加热的不均匀,导致整个弹载电子设备温度场的不均匀。从图 12可知,吸波板体内温度最大值为82.4 ℃,结合仿真及后期实测可知,天线阵面表面温度差值为15~27 ℃。而这样的温度梯度对天线的测向精度会有一定的影响,因此在弹载电子设备及其柱螺旋天线基材选择上要有一定热设计的要求。
3 结论本文针对某型反辐射导弹建立了流固耦合模型并进行了非定常数值模拟计算,并结合Fluent进行了导引头及其弹载电子设备的热仿真分析,从而有效地预测出整个弹载电子设备任意飞行时刻的热场分布云图,这对导引头及其弹载电子设备的热防护设计与评估具有一定的指导意义。
| [1] |
王真, 高凤岐, 高敏, 等.
导引头稳定平台的新型自抗扰控制器设计研究[J]. 电光与控制, 2016, 23(9): 84–89.
WANG Zhen, GAO Feng-qi, GAO Min, et al. On design of auto-disturbance rejection controller for seeker stabilized platform[J]. Electronics Optics & Control, 2016, 23(9): 84–89. |
| [2] |
余建祖.
电子设备热设计及分析技术[M]. 北京: 北京航空航天大学出版社, 2000: 25-26.
YU Jian-zu. Thermal design and analysis techniques of electronic equipment[M]. Beijing: Beihang University Press, 2000: 25-26. |
| [3] |
张志英, 陈雨琪, 张宏军, 等.
基于动态故障树的导弹驾驶仪系统可靠性分析[J]. 南京理工大学学报, 2013, 37(4): 543–550.
ZHANG Zhi-ying, CHEN Yu-qi, ZHANG Hong-jun, et al. Reliability analysis of missile autopilot system based on dynamic fault tree[J]. Journal of Nanjing University of Science and Technology, 2013, 37(4): 543–550. |
| [4] |
陈鑫, 王浩丞, 唐勇, 等.
多径环境中被动雷达导引头测向性能分析[J]. 电子信息对抗技术, 2011, 26(4): 1–4.
CHEN Xin, WANG Hao-cheng, TANG Yong, et al. Angle characteristic analysis of PRS in multipath environment[J]. Electronic Information Warfare Technology, 2011, 26(4): 1–4. |
| [5] |
钱若军, 董石麟, 袁行飞, 等.
流固耦合理论研究进展[J]. 空间结构, 2008, 14(1): 3–15.
QIAN Ruo-jun, DONG Shi-lin, YUAN Xing-fei, et al. Advances in research on fluid-structure interaction theory[J]. Spatial Structures, 2008, 14(1): 3–15. |
| [6] | XING J T, PRICE W G, CHEN Y G. A numerical method to simulate nonlinear fluid-rigid structure interaction problems[J]. Acta Mechanica Solida Sinica, 2005, 26(4): 373–383. |
| [7] |
杨林. 非线性流固耦合问题的数值仿真方法研究[D]. 青岛: 中国海洋大学工程学院, 2011: 3-5.
YANG Lin. Numerical simulation method research of the nonlinear fluid-solid interaction problems[D]. Qingdao: Ocean University of China, College of Engineering, 2011: 3-5. http://t.docin.com/p-1096464837.html |
| [8] |
陈锋, 王春江, 周岱, 等.
流固耦合理论与算法评述[J]. 空间结构, 2012, 18(4): 55–63.
CHEN Feng, WANG Chun-jiang, ZHOU Dai, et al. Review of theory and numerical methods of fluid-structure interaction[J]. Spatial Structures, 2012, 18(4): 55–63. |
| [9] |
朱洪来, 白象忠.
流固耦合问题的描述方法及分类简化准则[J]. 工程力学, 2007, 24(10): 92–99.
ZHU Hong-lai, BAI Xiang-zhong. Description method and simplified classification rule for fluid-solid interaction problems[J]. Engineering Mechanics, 2007, 24(10): 92–99. DOI:10.3969/j.issn.1000-4750.2007.10.017 |
| [10] |
高双武, 强洪夫, 周伟, 等.
流固耦合数值模拟方法及其在分段式SRM的应用[J]. 弹箭与制导学报, 2012, 32(1): 111–113.
GAO Shuang-wu, QIANG Hong-fu, ZHOU Wei, et al. Fluid structure interaction method and its application in SRM with segments[J]. Journal of Projectiles Rockets Missiles and Guidance, 2012, 32(1): 111–113. |
| [11] |
高展, 徐小宇, 闫帅, 等.
基于离散几何法的多物理场耦合问题研究[J]. 电子设计工程, 2017, 25(1): 166–170.
GAO Zhan, XU Xiao-yu, YAN Shuai, et al. Study of multiphysics problem based on discrete geometric method[J]. Electronic Design Engineering, 2017, 25(1): 166–170. |
| [12] |
吴泽玉, 王东炜, 汪志昊, 等.
流-固耦合问题的精细积分求解法[J]. 上海交通大学学报, 2017, 51(6): 756–760.
WU Ze-yu, WANG Dong-wei, WANG Zhi-hao, et al. Precise integration method for solving fluid-soild coupling problems[J]. Journal of Shanghai Jiaotong University, 2017, 51(6): 756–760. |
| [13] |
张健, 黄晨光.
三维瞬态方形管流的热流固耦合数值模拟[J]. 工程力学, 2010, 27(6): 232–239.
ZHANG Jian, HUANG Chen-guang. Numerical simulation of 3-D transient thermo-fluid-solid coupled flow in a rectangular channel[J]. Engineering Mechanics, 2010, 27(6): 232–239. |
| [14] |
郭崇志, 肖乐.
换热器流固传热边界数值模拟温度场的顺序耦合方法[J]. 化工进展, 2010, 29(9): 1615–1619.
GUO Chong-zhi, XIAO Le. A sequence coupling method for numerical simulation of temperature field in liquid-solid heat transfer boundary of a heat exchanger[J]. Chemical Industry and Engineering Progress, 2010, 29(9): 1615–1619. |
| [15] |
卢燕, 王珏, 凌明祥, 等.
精密离心机热变形多物理场耦合数值计算[J]. 工程设计学报, 2016, 23(1): 49–53.
LU Yan, WANG Yu, LING Ming-xiang, et al. Numerical simulation of multi-physics coupling for the thermal deformation of precision centrifuge[J]. Chinese Journal of Engineering Design, 2016, 23(1): 49–53. |
| [16] |
王正裕, 李孝伟.
基于动态嵌套网格技术的飞行器导弹发射的数值模拟[J]. 上海大学学报(自然科学版), 2008, 14(2): 173–176.
WANG Zheng-yu, LI Xiao-wei. Simulation of air launched missile based on moving chimera grid[J]. Journal of Shanghai University (Natural Science), 2008, 14(2): 173–176. |
| [17] |
王静, 高效伟.
热辐射问题的边界元算法[J]. 导弹与航天运载技术, 2011(1): 46–53.
WANG Jing, GAO Xiao-wei. A boundary element method for solving heat radiation problems[J]. Missiles and Space Vehicles, 2011(1): 46–53. |
| [18] |
白洁, 陈皓, 廖选平, 等.
导弹末制导状态亚声速流场数值模拟[J]. 导弹与航天运载技术, 2014(4): 23–27.
BAI Jie, CHEN Hao, LIAO Xuan-ping, et al. Numerical simulation on the subsonic flow of terminal guiding missile[J]. Missiles and Space Vehicles, 2014(4): 23–27. |



