风能作为一种可再生能源,有着良好的发展前景,是未来能源结构的重要组成部分之一[1-2]。风机叶片作为捕获风能的装置,其性能直接影响风电系统的运行和效率。静态检测可以检测叶片出厂后到服役前存在的各种缺陷,它是保证叶片工作性能的关键,因而显得格外重要[3]。
目前,风电叶片的静态无损检测方法主要有X射线、红外热成像和超声波检测技术等,其中:X射线检测技术由于受叶片尺寸的限制,还未广泛地应用于叶片的全尺寸检测;红外热成像检测技术虽然操作简单,但光线的照射以及叶片表面温差较小等因素都会对其检测结果造成不利影响,对于缺陷的检出和定性分析有一定难度;超声波检测技术因具有检测对象范围广、检测深度大、缺陷定位准确、速度快以及便于现场使用等特点,已成为国内外应用最广泛、使用频率最高且发展较快的一种无损检技术[4-5]。
现有的检测装置一般是由纯刚性金属组成框架,且装置搭载大型超声检测探头,存在体积、重量大,成本较高,局部检测效率低,运动不灵活[6]等缺陷。本文提出的风电叶片检测装置,是在刚性杆的基础上引入绳牵引结构,构成索杆混联驱动,使得末端工作空间扩大、惯性变小、易拆卸、可重组、运动更加灵活,同时,该装置可进行叶片全尺寸检测,也可根据需要对局部区域进行单独检测。在末端运动平台上搭载便携式超声检测仪,大大降低了整体设备的成本,独特的联轴器、减速电机、万向球设计则保证了装置稳定性。整个检测装置可通过自动化控制来实现风电叶片表面的无损检测,提高检测效率。
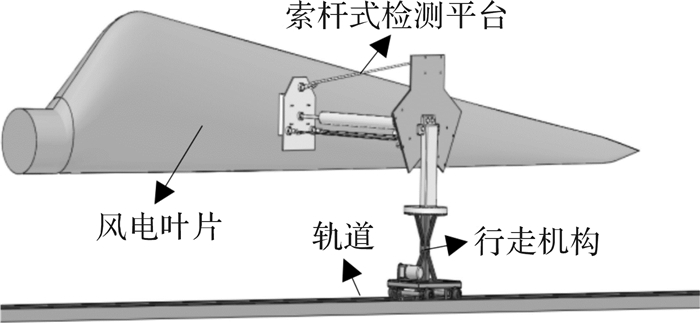
1 索杆式风电叶片检测装置总体结构索杆式风电叶片检测装置由索杆式检测平台、行走机构以及控制器组成,行走机构置于轨道之上,带动固连于其顶部的检测平台水平移动。风电叶片检测装置的总体结构如图 1所示。
|
| 图 1 索杆式风电叶片检测装置总体结构示意图 Fig.1 The overall structure diagram of the detection device of cable-link wind turbine blades |
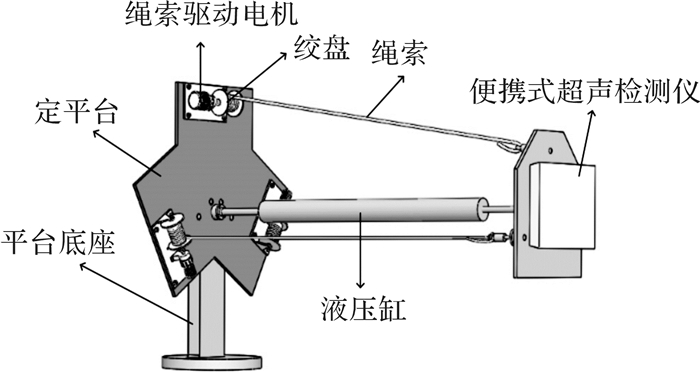
索杆式检测平台上搭载便携式超声检测仪,它是整个检测装置的核心部分,其结构如图 2所示。该平台由平台底座、位于平台底座上的定平台、与定平台相对的动平台以及便携式超声检测仪组成。定平台和动平台通过1个液压缸和3条绳索相连接,绳索的一端缠绕在绞盘上,被首尾相接的3个减速电机驱动,另一端通过球铰连接于动平台上对应的端部位置。液压缸的两端分别通过球铰连接于定平台和动平台上。位于最上方的绳索强度大于下方的2条绳索,最上方绳索对应的绳索驱动电机的功率大于下方2条绳索对应的绳索驱动电机的功率。
|
| 图 2 索杆式检测平台的结构 Fig.2 The structure of the cable-link detection platform |
绳索驱动电机和绞盘转轴通过联轴器连接, 绞盘在转动的同时进行移动, 使得绳索与绞盘之间的接触点位置保持不变,保证了绳索的位移精度和稳定性。带动检测平台水平移动的行走机构由减速电机驱动,并在与轨道内壁接触处设置了万向球结构,防止侧翻,确保了装置整体的稳定性。
检测平台在行走机构的带动下到达待检测区域,通过4条支链的驱动使动平台(即超声检测仪)进行多自由度运动,与风电叶片表面进行贴合,完成超声无损检测。根据数据接收端得到的波形数据,可确定对应的缺陷。
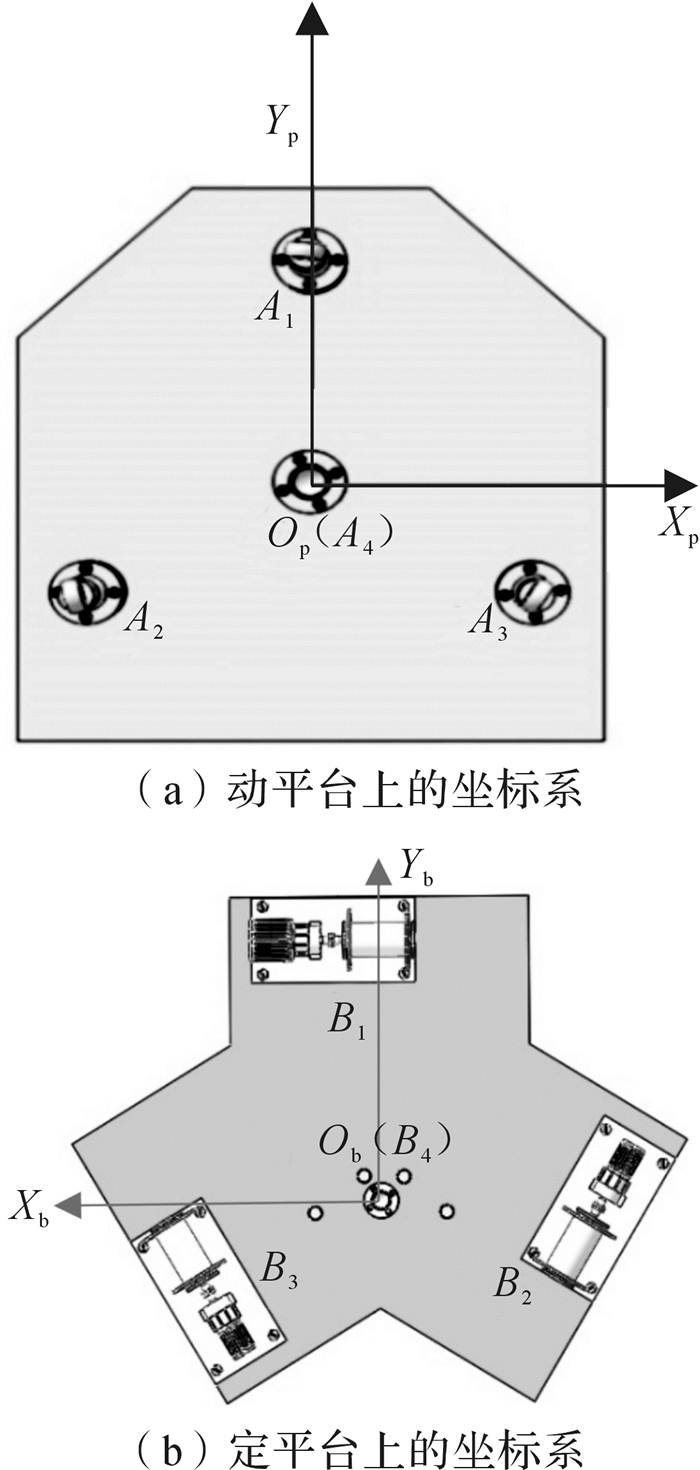
2 索杆式检测平台的运动特性分析 2.1 坐标系的建立在建模过程中,假定3条绳索始终处于紧张状态,无弹性并且忽略绳索的重力。分别在动平台与定平台中建立动坐标系Op-YpYpZp、定坐标系Ob-XbYbZb,如图 3所示,动坐标系原点Op为液压缸与动平台的固连球铰的中心A4,定坐标系原点Ob为液压缸与定平台的固连球铰的中心B4。3条绳索与动平台相接的3个球铰中心间的距离相等且球铰按等边三角形的形式排布在3个顶点位置,顶点为Ai(i=1, 2, 3)。3个绞盘与各自绳索的接触点按等腰三角形的形式排布在3个顶点位置,顶点为Bi(i=1, 2, 3)。检测平台处于初始位置时(如图 4所示),定平台与动平台板面平行,2个坐标系的各坐标轴方向相一致,液压缸轴线垂直于2个平台的平面。设pai为Ai在动坐标系中的位置矢量, bbi为Bi在定坐标系中的位置矢量, pRb表示动坐标系相对于定坐标系的姿态变换矩阵, 定坐标系原点Ob指向动坐标系原点Op的矢量为pPb,绳索矢量Li=BiAi(i=1, 2, 3),液压缸矢量可以表示为L4=pPb=ObOp=B4A4。
|
| 图 3 定平台与动平台上的坐标系 Fig.3 The coordinate system on the fixed platform and moving platform |

|
| 图 4 检测平台初始位置俯视图 Fig.4 The top viewport of initial position of the detection platform |
动平台的姿态表示方法有很多种,此处采用Z-Y-X欧拉角描述。动坐标系相对定坐标系转动方式为:先绕X轴旋转α,再绕Y轴旋转β,最后绕Z轴旋转γ,则机构的末端运动姿态可表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{R}}\left( {Z,\gamma } \right)\mathit{\boldsymbol{R}}\left( {Y,\beta } \right)\mathit{\boldsymbol{R}}\left( {X,\alpha } \right) = \\ \;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} \begin{array}{l} {\rm{c}}\gamma {\rm{c}}\beta \\ {\rm{s}}\gamma {\rm{c}}\beta \\ - {\rm{s}}\beta \end{array}&\begin{array}{l} {\rm{c}}\gamma {\rm{s}}\beta {\rm{s}}\alpha - {\rm{s}}\gamma {\rm{c}}\alpha \\ {\rm{s}}\gamma {\rm{s}}\beta {\rm{s}}\alpha + {\rm{c}}\alpha {\rm{c}}\gamma \\ {\rm{c}}\beta {\rm{s}}\alpha \end{array}&\begin{array}{l} {\rm{c}}\gamma {\rm{s}}\beta {\rm{c}}\alpha + {\rm{s}}\alpha {\rm{s}}\gamma \\ {\rm{s}}\gamma {\rm{s}}\beta {\rm{c}}\alpha - {\rm{c}}\gamma {\rm{s}}\alpha \\ {\rm{c}}\beta {\rm{c}}\alpha \end{array} \end{array}} \right) \end{array} $ | (1) |
式中:s, c分别代表sin, cos,R(X, α)表示动平台绕X轴旋转α得到的旋转矩阵,R(Y,β)表示动平台绕Y轴旋转β得到的旋转矩阵,R(Z,γ)表示动平台绕Z轴旋转γ得到的旋转矩阵。
2.3 位置反解位置反解为已知动平台的位姿为(x, y, z, α, β)T,求解3根绳索的长度l1, l2, l3和液压缸的长度l4。动坐标系中固连在动平台的4个球铰的中心Ai(i=1, 2, 3, 4)在定坐标系中的位置矢量bai可表示为:
| $ ^{\rm{b}}{\mathit{\boldsymbol{a}}_i} = {}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} $ | (2) |
由于结构和受力因素的影响,检测平台(动平台)没有沿Z轴方向转动,所以姿态变换矩阵可以简化为:
| $ ^{\text{p}}{\mathit{\boldsymbol{R}}_{\text{b}}} = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {\cos \beta } \\ 0 \\ { - \sin \beta } \end{array}}&{\begin{array}{*{20}{l}} {\sin \alpha \sin \beta } \\ {\cos \alpha } \\ {\cos \beta \sin \alpha } \end{array}}&{\begin{array}{*{20}{l}} {\cos \alpha {\text{sin}}\beta } \\ { - \sin \alpha } \\ {\cos \alpha \cos \beta } \end{array}} \end{array}} \right) $ | (3) |
在定坐标系中,根据向量之间的运算关系,可得:
| $ {\mathit{\boldsymbol{L}}_i} = {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{A}}_i}{ = ^{\rm{b}}}{\mathit{\boldsymbol{a}}_i}{ - ^{\rm{b}}}{\mathit{\boldsymbol{b}}_i},i = 1,2,3,4 $ | (4) |
在已知检测平台位姿的情况下,绳索的长度l1, l2, l3和液压缸的长度l4可以表示为:
| $ {l_i} = \left\| {{\mathit{\boldsymbol{L}}_i}} \right\| = \left\| {{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{A}}_i}} \right\| $ | (5) |
位置正解为已知3条绳索的长度l1, l2, l3和液压缸的长度l4,求动平台的位姿(x, y, z, α, β)T。由于采用解析法很难求得方程的根,且多含有虚根[7-9],本文采用Newton-Raphson迭代法进行求解,将非线性方程组线性化[10-11]。Newton-Raphson迭代法的求解过程如下。
根据式(5)定义误差函数:
| $ {G_i}\left( \mathit{\boldsymbol{X}} \right) = \left\| {{\mathit{\boldsymbol{L}}_i}} \right\| - {l_i},i = 1,2,3,4 $ | (6) |
式中:X为机构动平台的位姿,即(x, y, z, α, β)T, li(i=1, 2, 3, 4)为所求位姿对应的支链长度。
根据Newton-Raphson迭代法可得:
| $ {\mathit{\boldsymbol{X}}_{n + 1}} = {\mathit{\boldsymbol{X}}_n} + \Delta \mathit{\boldsymbol{X}} $ | (7) |
式中:
| $ \Delta \mathit{\boldsymbol{X}} = - \frac{{{G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{{{G'}_i}\left( \mathit{\boldsymbol{X}} \right)}} $ | (8) |
| $ {\mathit{\boldsymbol{F}}_i}\Delta \mathit{\boldsymbol{X}} = - {G_i}\left( \mathit{\boldsymbol{X}} \right) $ | (9) |
式中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_i} = {{G'}_i}\left( \mathit{\boldsymbol{X}} \right) = {{\left( {\frac{{\partial {G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial x}}\frac{{\partial {G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial y}}\frac{{\partial {G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial x}}\frac{{\partial {G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial \alpha }}\frac{{\partial {G_i}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial \beta }}} \right)}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{F}}_i} \in {\mathit{\boldsymbol{R}}_{1 \times 5}},i = 1,2,3,4} \end{array} $ | (10) |
设机构的位姿偏导数矩阵为:
| $ \mathit{\boldsymbol{F}} = {\left( {{\mathit{\boldsymbol{F}}_1},{\mathit{\boldsymbol{F}}_2},{\mathit{\boldsymbol{F}}_3},{\mathit{\boldsymbol{F}}_4}} \right)^{\rm{T}}} $ | (11) |
误差函数矩阵为:
| $ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{X}} \right) = {\left( {{G_1}\left( \mathit{\boldsymbol{X}} \right),{G_2}\left( \mathit{\boldsymbol{X}} \right),{G_3}\left( \mathit{\boldsymbol{X}} \right),{G_4}\left( \mathit{\boldsymbol{X}} \right)} \right)^{\rm{T}}} $ | (12) |
则式(9)可以改写成:
| $ \mathit{\boldsymbol{F}}\Delta \mathit{\boldsymbol{X}} = - \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{X}} \right) $ | (13) |
由于偏导数矩阵F不是方阵,想要求解ΔX,需要得到F的广义逆矩阵F-1,因F为列满秩矩阵,则:
| $ {\mathit{\boldsymbol{F}}^{ - 1}} = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}} $ | (14) |
则式(13)可以表示为:
| $ \Delta \mathit{\boldsymbol{X}} = - {\mathit{\boldsymbol{F}}^{ - 1}}\mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{X}} \right) $ | (15) |
设定初始值X0,对式(15)进行迭代计算,反复迭代直到满足‖ΔX‖ < δ(在本文中,误差限δ=10-6),便可得到该机构位置正解的近似值。
2.5 机构的速度分析机构的速度雅克比矩阵表示机构关节空间速度与末端速度的传动比,在本机构中表示动平台的速度与4条驱动支链长度变化的一种变换关系[12-13]。本文采用几何方法推导机构的速度雅克比矩阵。
由机构的位置反解可知,4条驱动支链的矢量:
| $ {\mathit{\boldsymbol{L}}_i} = {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{A}}_i},i = 1,2,3,4 $ | (16) |
由数量积的运算法则可知:
| $ l_i^2 = {\left( {{\mathit{\boldsymbol{L}}_i}} \right)^{\rm{T}}}{\mathit{\boldsymbol{L}}_i} $ | (17) |
将式(17)两边同时对t求导可得:
| $ \begin{array}{l} 2{l_i}{{\dot l}_i} = {\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}} - {}^{\rm{b}}{{\mathit{\boldsymbol{\dot b}}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} - {}^{\rm{b}}{\mathit{\boldsymbol{b}}_i}} \right) + \\ \;\;\;\;\;\;\;\;\;{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} - {}^{\rm{b}}{\mathit{\boldsymbol{b}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}} - {}^{\rm{b}}{{\mathit{\boldsymbol{\dot b}}}_i}} \right) \end{array} $ | (18) |
由建立的坐标系可知bbi为定值,其导数值为0,则式(18)可以简化为:
| $ \begin{array}{l} 2{l_i}{{\dot l}_i} = {\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} - {}^{\rm{b}}{\mathit{\boldsymbol{b}}_i}} \right) + \\ \;\;\;\;\;\;\;\;\;{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} - {}^{\rm{b}}{\mathit{\boldsymbol{b}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}}} \right) \end{array} $ | (19) |
由向量间的运算关系进一步将式(19)化简为:
| $ 2{l_i}{{\dot l}_i} = 2{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{P}}_{\rm{b}}} - {}^{\rm{b}}{\mathit{\boldsymbol{b}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}}} \right) $ | (20) |
将式(4)代入并化简得:
| $ {l_i}{{\dot l}_i} = {\left( {{\mathit{\boldsymbol{L}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{{\mathit{\boldsymbol{\dot P}}}_{\rm{b}}}} \right) $ | (21) |
定义速度和角速度矢量:
| $ {}^{\rm{p}}{\mathit{\boldsymbol{v}}_{\rm{b}}} = {\left( {\begin{array}{*{20}{c}} {{v_x}}&{{v_y}}&{{v_z}} \end{array}} \right)^{\rm{T}}} $ | (22) |
| $ {}^{\rm{p}}{\omega _{\rm{b}}} = {\left( {\begin{array}{*{20}{c}} {{\omega _x}}&{{\omega _y}}&{{\omega _z}} \end{array}} \right)^{\rm{T}}} $ | (23) |
| $ \mathit{\boldsymbol{\dot X}} = \left( \begin{array}{l} {}^{\rm{p}}{\omega _{\rm{b}}}\\ {}^{\rm{p}}{\mathit{\boldsymbol{v}}_{\rm{b}}} \end{array} \right) $ | (24) |
定义角速度矩阵:
| $ \mathit{\boldsymbol{S}}\left( \omega \right) = \left( {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ {\omega _z}\\ {\omega _y} \end{array}&\begin{array}{l} - {\omega _z}\\ 0\\ {\omega _x} \end{array}&\begin{array}{l} {\omega _y}\\ - {\omega _x}\\ 0 \end{array} \end{array}} \right) $ | (25) |
| $ {}^{\rm{p}}{{\mathit{\boldsymbol{\dot R}}}_{\rm{b}}} = \mathit{\boldsymbol{S}}{\left( \omega \right)^{\rm{p}}}{\mathit{\boldsymbol{R}}_{\rm{b}}} = {}^{\rm{p}}{\omega _{\rm{b}}} \times {}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}} $ | (26) |
将式(26)代入式(21),化简得:
| $ {l_i}{{\dot l}_i} = {\left( {{\mathit{\boldsymbol{L}}_i}} \right)^{\rm{T}}}\left( {{}^{\rm{p}}{\omega _{\rm{b}}} \times {}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} + {}^{\rm{p}}{\mathit{\boldsymbol{v}}_{\rm{b}}}} \right) $ | (27) |
本文中ωz=0。
由向量运算关系:a(b×c)=(c×a)b, 化简式(27)可得:
| $ {l_i}{{\dot l}_i} = {\left( {{\mathit{\boldsymbol{L}}_i}} \right)^{\rm{T}}}{}^{\rm{p}}{\mathit{\boldsymbol{v}}_{\rm{b}}} + \left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_i} \times {\mathit{\boldsymbol{L}}_i}} \right){}^{\rm{p}}{\omega _{\rm{b}}} $ | (28) |
定义矩阵:
| $ \mathit{\boldsymbol{\dot l}} = {\left( {\begin{array}{*{20}{c}} {{{\dot l}_1}}&{{{\dot l}_2}}&{{{\dot l}_3}}&{{{\dot l}_4}} \end{array}} \right)^{\rm{T}}} $ | (29) |
| $ {\mathit{\boldsymbol{J}}_l} = {\rm{diag}}{\left( {\begin{array}{*{20}{c}} {{l_1}}&{{l_2}}&{{l_3}}&{{l_4}} \end{array}} \right)^{\rm{T}}} $ | (30) |
| $ {\mathit{\boldsymbol{J}}_x} = \left( {\begin{array}{*{20}{c}} {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_1} \times {\mathit{\boldsymbol{L}}_1}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{L}}_1}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_2} \times {\mathit{\boldsymbol{L}}_2}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{L}}_2}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_3} \times {\mathit{\boldsymbol{L}}_3}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{L}}_3}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_4} \times {\mathit{\boldsymbol{L}}_4}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{L}}_4}^{\rm{T}}} \end{array}} \right) $ | (31) |
则式(28)为:
| $ {\mathit{\boldsymbol{J}}_l}\mathit{\boldsymbol{\dot l}} = {\mathit{\boldsymbol{J}}_x}\mathit{\boldsymbol{\dot X}} $ | (32) |
由于Jl为对角矩阵,且4条驱动支链的长度都大于0,所以矩阵Jl可逆, 则可得:
| $ \mathit{\boldsymbol{\dot l = \dot JX}} $ | (33) |
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{J}}_l^{ - 1}{\mathit{\boldsymbol{J}}_x} $ | (34) |
| $ \mathit{\boldsymbol{J}} = \left( {\begin{array}{*{20}{c}} {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_1} \times {\mathit{\boldsymbol{u}}_1}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{u}}_1}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_2} \times {\mathit{\boldsymbol{u}}_2}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{u}}_2}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_3} \times {\mathit{\boldsymbol{u}}_3}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{u}}_3}^{\rm{T}}}\\ {{{\left( {{}^{\rm{p}}{\mathit{\boldsymbol{R}}_{\rm{b}}}{}^{\rm{p}}{\mathit{\boldsymbol{a}}_4} \times {\mathit{\boldsymbol{u}}_4}} \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{u}}_4}^{\rm{T}}} \end{array}} \right) $ | (35) |
式中ui为4条驱动支链的单位矢量,方向与各条支链的矢量相同,ui可表示为:
| $ {\mathit{\boldsymbol{u}}_i} = \frac{{{\mathit{\boldsymbol{L}}_i}}}{{{l_i}}},i = 1,2,3,4 $ | (36) |
矩阵J即为机构的速度雅克比矩阵,求出雅克比矩阵后,便得出了4条驱动支链的速度与机构末端速度之间的关系式[14]。
3 具体数值计算及运动学仿真 3.1 索杆式检测平台结构参数的设定设定索杆式检测平台的结构参数,如表 1所示。
| 机构参数 | 量值/mm |
| pa1 | (0, 380, 0)T |
| pa2 | (-329.089 7, -190, 0)T |
| pa3 | (329.089 7, -190, 0)T |
| bb1 | (0, 580, 0)T |
| bb2 | (-502.294 7, -190, 0)T |
| bb3 | (502.294 7, -190, 0)T |
Newton-Raphson迭代法中,将反解过程中由3组位姿求得的绳索和液压缸的长度作为迭代初始值, 进行位置正解。利用MATLAB编程求得平台的位姿,则位置反解与正解结果如表 2和表 3所示。
| 参数 | 位置反解计算结果 | ||
| x/mm | 237.513 2 | 215.318 5 | 85.459 1 |
| y/mm | 501.276 5 | 767.129 3 | 152.247 1 |
| z/m | -803.317 7 | -678.333 7 | -778.203 4 |
| α/rad | 0.273 2 | 0 | 0.412 4 |
| β/rad | 0 | 0.231 5 | 0.154 8 |
| l1/m | 793.719 7 | 910.018 9 | 642.055 4 |
| l2/m | 1 075.822 0 | 1 053.441 2 | 857.642 7 |
| l3/m | 996.413 1 | 1 076.044 7 | 925.490 5 |
| l4/m | 976.222 3 | 1 046.415 8 | 797.548 1 |
| 参数 | 位置正解计算结果 | ||
| l1/m | 793.719 7 | 910.018 9 | 642.055 4 |
| l2/m | 1 075.822 0 | 1 053.441 2 | 857.642 7 |
| l3/m | 996.413 1 | 1 076.044 7 | 925.490 5 |
| l4/m | 976.222 3 | 1 046.415 8 | 797.548 1 |
| x/m | 237.713 9 | 215.151 9 | 85.379 0 |
| y/m | 500.901 0 | 767.629 4 | 152.390 4 |
| z/m | -802.714 3 | -678.731 5 | -777.598 1 |
| α/rad | 0.273 0 | 0 | 0.412 7 |
| β/rad | 0.000 1 | 0.231 4 | 0.154 9 |
将正解计算结果与反解计算结果进行对比可知,当误差限δ=10-6时,机构位置坐标的误差小于0.65 mm, 姿态旋转角度的误差小于0.000 5 rad,二者的相对误差都小于0.1%,在误差允许的范围内。证明了当求解机构位置正解时,采用Newton-Raphson数值迭代法是可行的。
3.3 运动学仿真根据推导出的速度雅克比矩阵, 通过MATLAB可以计算出索杆式检测平台从初始位姿(0,0,-600,0,0)T开始绕X轴以恒定角速度ωx=0.07 rad/s转动4 s过程中4条驱动支链的运动情况, 结果如图 5所示。

|
| 图 5 绳索与液压缸速度变化曲线 Fig.5 The velocity variation curve of cables and hydraulic cylinder |
由图 5可知, 当机构在规定的运动过程中, 绳索1缩短的速度逐渐增大, 绳索2与绳索3运动趋势相同,伸长的速度不断减小, 且减小的速率小于绳索1速度增大的速率, 液压缸静止不动,所有驱动支链的速度变化曲线是平滑连续的, 证明了该机构在运动过程中是稳定连续的。
4 总结1) 针对现有的风电叶片检测装置的缺点,设计了一种由索杆混联结构驱动的风电叶片检测装置。该装置惯性小,易拆卸,可重组,运动灵活且稳定性和安全性高,可完成全尺寸检测和局部检测,避免了现有纯刚性结构检测装置运动不灵活、不易控制、成本高等缺点。
2) 简述了检测装置的组成及其工作原理,对该装置的索杆式检测平台进行运动学分析,通过在平台上建立坐标系,对机构进行了正反解分析,得到了机构的位置反解模型,用Newton-Raphson迭代法求解了机构的位置正解模型,并推导出了机构的速度雅克比矩阵,从而得到机构的运动速度模型。
3) 通过MATLAB编程,在给定检测平台具体结构参数的情况下,对正反解模型进行验证,结果证明Newton-Raphson迭代法得到的位置正解误差低,结果精确,并通过运动学仿真证明了该机构在运动过程中是稳定连续的。
| [1] |
程启明, 程尹曼, 王映斐, 等.
风力发电系统技术的发展综述[J]. 自动化仪表, 2012, 33(1): 1–8.
CHENG Qi-ming, CHENG Yin-man, WANG Ying-fei, et al. Overview of the development of control technique for wind power generation[J]. Process Automation Instrumentation, 2012, 33(1): 1–8. |
| [2] |
李军军, 吴政球, 谭勋琼, 等.
风力发电及其技术发展综述[J]. 电力建设, 2011, 32(8): 64–72.
LI Jun-jun, WU Zheng-qiu, TAN Xun-qiong, et al. Review of wind power generation and relative technology development[J]. Electric Power Construction, 2011, 32(8): 64–72. |
| [3] |
周伟, 张洪波, 马立辉, 等.
风电叶片复合材料结构缺陷无损检测研究进展[J]. 塑料科技, 2013, 38(12): 84–86.
ZHOU Wei, ZHANG Hong-bo, MA Li-hui, et al. Advances in non-destructive testing of structure defects for wind turbine blade computer material[J]. Plastics Science and Technology, 2013, 38(12): 84–86. |
| [4] |
羊森林, 赵萍, 王峰, 等.
大型风电叶片缺陷及其无损检测技术研究[J]. 东方汽轮机, 2012(1): 26–34.
YANG Sen-lin, ZHAO Ping, WANG Feng, et al. Study on the defects of large-scale wind turbine blades and the non-destructive testing techniques[J]. Dongfang Turbine, 2012(1): 26–34. |
| [5] | STENSGAARD T H, KIM B, PETER B, et al. Distribution of defects in wind turbine blades and reliability assessment of blades containing defects[J]. Engineering Structures, 2011, 33(1): 171–180. DOI:10.1016/j.engstruct.2010.10.002 |
| [6] |
方文平, 刘日明. 风电叶片超声无损检测装置: CN106226013A[P]. 2016-12-14.
FANG Wen-ping, LIU Ri-ming. Ultrasonic non-destructive detection device of wind turbine blades: CN106226013A[P]. 2016-12-14. |
| [7] | WANG Ke-yi, ZHANG Li-xun, MENG Hao. Driving properties of plane wire-driven robot[J]. Journal of Central South University, 2013, 20(1): 56–61. DOI:10.1007/s11771-013-1459-1 |
| [8] |
李巍, 赵志刚, 石广田, 等.
多机器人并联绳牵引系统的运动学及动力学解[J]. 浙江大学学报(工学版), 2015, 49(10): 1916–1923.
LI Wei, ZHAO Zhi-gang, SHI Guang-tian, et al. Solution of kinematics and dynamics for parallel cable-driven system with multi-robots[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(10): 1916–1923. |
| [9] | BEHZADIPOUR S. Kinematics and dynamics of a self-stress cartesian cable-driven mechanism[J]. Journal of Mechanical Design, 2009, 131(6): 061005. DOI:10.1115/1.3125206 |
| [10] | HE J H. Improvement of Newton iteration method[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2000, 1(3): 239–240. |
| [11] | ABBASBANDY S. Improving Newton-Raphson method for nonlinear equations by modify adomian decomposition method[J]. Applied Mathematics & Computation, 2003, 145(2/3): 887–893. |
| [12] |
张彦斌, 吴鑫, 刘宏昭, 等.
一种新兴并联机器人机构的运动分析及完全各向同性研究[J]. 中国机械工程, 2008, 19(2): 213–216.
ZHANG Yan-bin, WU Xin, LIU Hong-zhao, et al. Kinematics analysis and fully-isotropic design of a novel parallel robotic manipulator[J]. China Mechanical Engineering, 2008, 19(2): 213–216. |
| [13] | SHI Zhong, HUANG Xue-xiang, HU Tian-jian, et al. Weighted augment Jacobian matrix with a variable coefficient method for kinematics mapping of space teleoperation based on human-robot motion similarity[J]. Advanced in Space Research, 2016, 58(7): 1401–1416. DOI:10.1016/j.asr.2016.06.015 |
| [14] |
杨尹, 顾寄南, 郭林.
基于ADAMS的4-RUPaR高速搬运并联机器人轨迹规划与运动学仿真[J]. 工程设计学报, 2013, 20(5): 375–382.
YANG Yin, GU Ji-nan, GUO Lin. Trajectory planning and kinematics simulation of the 4-RUPaR high-speed handling parallel robot based on ADAMS[J]. Chinese Journal of Engineering Design, 2013, 20(5): 375–382. |


