2. 中国石油集团东方地球物理勘探有限责任公司, 河北 涿州 072750
2. Bureau of Geophysical Prospecting INC., China National Petroleum Corporation, Zhuozhou 072750, China
随着地球物理勘探技术的发展,具有安全可控、绿色环保等特点的各类非爆炸震源得到了广泛的应用[1]。以液压式震源为代表的大型人工震源设备在地表平坦、远离人烟的地区已取得较好的勘探效果[2],但在人口密集、森林覆盖率较高的区域以及丘陵山地,急需一种结构简单、运移方便且有较大输出力的小型震源装置来弥补这一空白。精密可控震源是20世纪末发展起来的一种新型震源,其结构简单、易于拆装,噪音小且无尾气排放,不仅符合目前各国绿色探勘对震源设备的要求[3],同时也十分适合在大型震源无法进入的特殊地区进行勘探作业。缘于精密可控震源本身结构特点,它激发的扫描信号具有重复性好、频率低、传播距离远等优点,为石油、天然气探勘开发提供了一条新路径[4-7]。
震源装置信号激发是地震勘探的第一个环节,为提升地质反演资料的分辨率,以期最大程度地将振动器产生的相干振动能量传入地下,且尽量减少输出信号的畸变[8],从而更加准确地推断地下油气资源分布规律。由于精密可控震源压重通过隔振系统与平板连接在一起,在实际激振作业过程中,激振器带动平板以及大地表层振动的同时不可避免地使压重产生振动。由于压重本身的质量较大,它产生的振动不仅会削减输出信号的能量,同时会产生干扰噪声,降低震源输出信号质量。不合理的隔振系统参数会导致压重振幅过大,甚至产生共振。
目前针对动力机械上部隔振系统已有了不少研究:2001年牛军川等基于能量传递观点分析了橡胶隔振器对旋转机械的隔振效果[9];2009年邓东等针对振动器阀控系统建立了动力学模型并求解,寻找最优阻尼比以改善扫描起始段信号质量[10];2013年李兆锋等采用有限元方法分析了双层浮筏隔振系统在振动筛中的隔振效果[11];2014年李淑清等针对液压式可控震源低频段设计了混合隔振系统[12];2015年王永芳等通过有限元分析了隔振参数对液压式可控震源上装部件的影响规律[13]。但是这些研究往往忽略了大地对上部结构振动特性的影响,所求得的结论可能会与实际情况有所偏差。因此,在分析隔振系统参数对精密可控震源压重振动情况影响规律时,考虑大地对震源振动性能的影响,寻找到符合实际的最优参数,从而减小压重振动对震源输出能量的影响,实现提升精密可控震源下传信号能量和信噪比的目的,对于该震源的推广应用具有十分重要的意义。
1 精密可控震源大地频变动力学系统为研究隔振系统参数对压重振动幅值的影响规律,建立精密可控震源系统动力学模型并进行相关分析计算。
1.1 精密可控震源工作原理CASS-10国产移动式精密可控震源实物见图 1,它主要由压重、立柱、电机、偏心质量块、激振箱体以及平板组成,2个偏心质量块分别由2个电机直接带动作同步反向旋转,从而产生周期变化的激振力[14]。

|
| 图 1 CASS-10国产移动式精密可控震源实物图 Fig.1 CASS-10 domestic mobile ACROSS physical map |
压重提供的重力作用于平板,保证精密可控震源在受到由偏心质量块旋转产生的周期变化的激振力作用时仍与地面保持良好的耦合,避免输出信号发生畸变,且压重质量可根据震源出力要求在一定范围内调节。隔振系统位于立柱和平板之间,一般采用矩形橡胶隔振器。
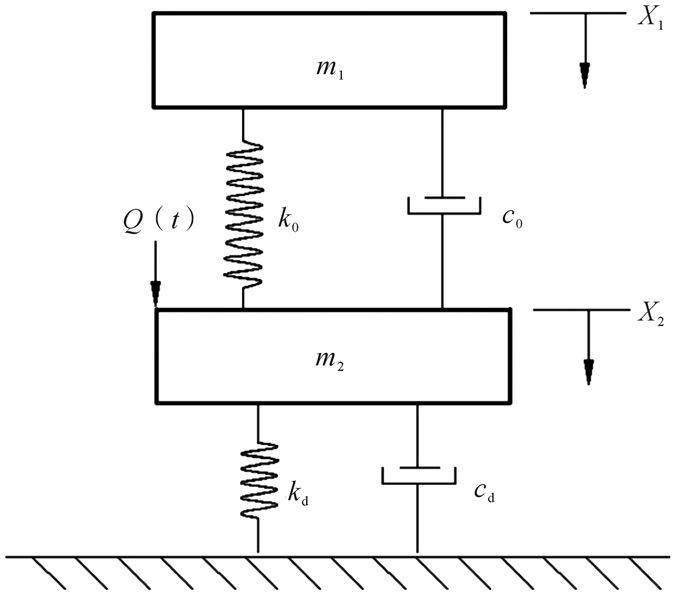
1.2 基于半无限空间的精密可控震源大地频变动力学模型根据精密可控震源激振作业的工作原理,可将它转化为两自由度的动力学模型,如图 2所示,图中Q(t)为激振力,m1为压重的质量,m2为平板以及激振箱体质量,k0,c0是压重与振动平板之间隔振系统的刚度及阻尼,kd,cd为耦合地面的刚度及阻尼。
|
| 图 2 精密可控震源大地动力学模型 Fig.2 ACROSS-ground dynamics model |
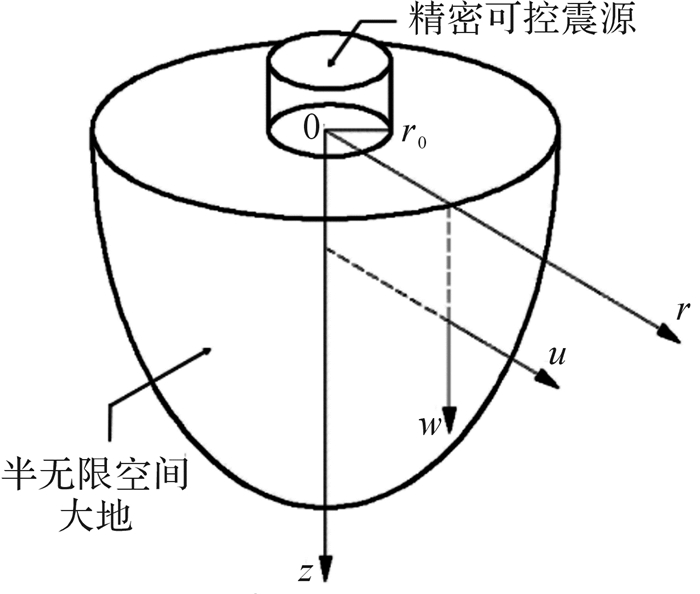
振动器产生的激振力作用于大地表面,而现有研究常将基础当作刚体[9, 11, 13],作这样假设的计算结果往往与实际有较大的偏差。如图 3所示,实际激振时震源与大地相互作用,大地会影响可控震源的动力学性能,因此基于半无限空间理论开展精密可控震源-大地系统动力学分析。
|
| 图 3 基于半无限空间理论的精密可控震源大地激振模型 Fig.3 The excitation model of ACROSS-ground based on semi-infinite space theory |
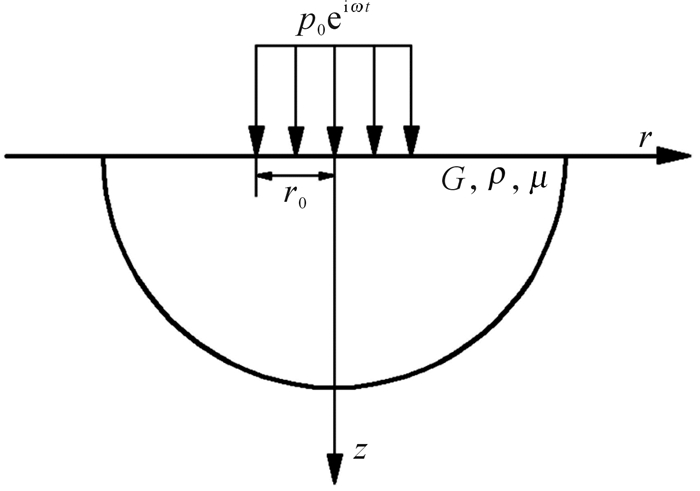
为简化数学模型,对平板和大地相互作用力进行合理假设:平板变形很小,振动过程中平板与大地不发生脱耦。此时振动器平板对大地的作用力p0eiωt近似为均布于半径为r0的圆面积内的周期力,如图 4所示。
|
| 图 4 均布周期力作用下的半无限空间理论模型 Fig.4 Semi-infinite space theory model under uniform-periodic force |
根据半无限空间理论,大地表面受周期扰力p0eiωt作用下,Sung以基底中心r=0处的位移w(r, 0, t)近似作为基底位移, 得到了如下结论[14]:
| $ w\left( t \right) = - \frac{{{p_0}{{\rm{e}}^{{\rm{i}}\omega t}}}}{{G{r_0}}}\left( {{f_1} + {\rm{i}}{f_2}} \right) $ | (1) |
式中:
| $ {f_1} = - 0.238\;733 + 0.059\;683a_0^2 - 0.004\;163a_0^4 + \cdots $ |
| $ {f_2} = 0.148\;594{a_0} - 0.017\;757a_0^3 + 0.000\;808a_0^5 - \cdots $ |
| $ {a_0} = \omega {r_0}\sqrt {\rho /G} $ |
| $ G = E/2\left( {1 + \mu } \right) $ |
其中:ρ, E, μ分别为大地质量密度、弹性模量和泊松比;f1和f2为无量纲频率a0的函数,且随着力的分布不同而变化。
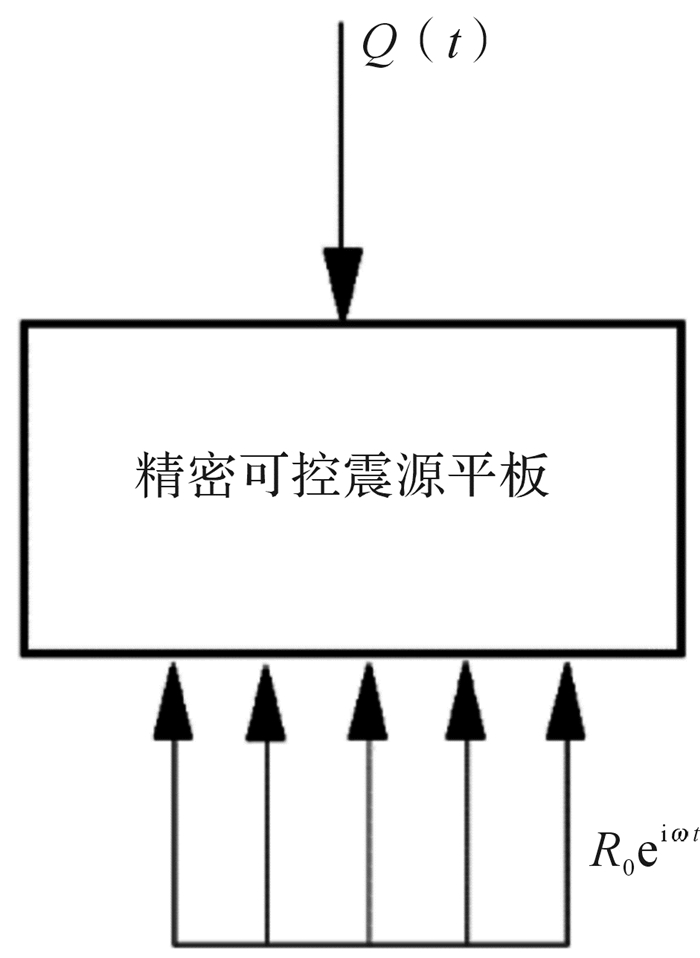
将图 3所示的振动模型中振动装置部分单独分离出来进行分析,如图 5所示,其中R0eiωt为大地作用于精密可控震源的反力,Q(t)为激振力。
|
| 图 5 精密可控震源平板受力情况 Fig.5 The force condition of the ACROSS plate |
据公式(1)可知,大地波动反力为:
| $ R = {R_0}{{\rm{e}}^{{\rm{i}}\omega t}} = {p_0}{{\rm{e}}^{{\rm{i}}\omega t}} = - \frac{1}{{\left( {{f_1} + {\rm{i}}{f_2}} \right)}}G{r_0}w\left( t \right) $ | (2) |
对振动装置部分建立动平衡方程:
| $ m\ddot \omega \left( t \right) + {R_0}{{\rm{e}}^{{\rm{i}}\omega t}} = Q\left( t \right) $ | (3) |
式中:m为平板质量,ω(t)为块式平板的位移响应。
将方程(2)代入式(3)即有:
| $ m\ddot \omega \left( t \right) + \left[ { - \frac{1}{{\left( {{f_1} + {\rm{i}}{f_2}} \right)}}G{r_0}w\left( t \right)} \right] = Q\left( t \right) $ | (4) |
对于谐和振动ω(t),由于iωw(t)=
| $ \begin{array}{l} m\ddot \omega \left( t \right) + \left[ {\frac{{{f_2}}}{{\left( {f_1^2 + f_2^2} \right){a_0}}}\sqrt {G\rho } r_0^2} \right]\dot \omega \left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left( { - \frac{{{f_1}}}{{f_1^2 + f_2^2}}G{r_0}} \right)\omega \left( t \right) = Q\left( t \right) \end{array} $ | (5) |
令
| $ m\ddot \omega \left( t \right) + \left( {\sqrt {G\rho } r_0^2{F_2}} \right)\dot \omega \left( t \right) + \left( {G{r_0}{F_1}} \right)\omega \left( t \right) = Q\left( t \right) $ | (6) |
式(6)即是按半无限空间理论模型建立的平板竖直振动形式解。可知半无限空间理论模型中对应耦合地面的刚度系数和阻尼系数表达式分别为:
将kd,cd的表达式代入图 2所示的动力学模型中,根据达朗贝尔原理,得到精密可控震源-大地系统频变动力学方程:
| $ \mathit{\boldsymbol{M}}\left\{ {\mathit{\boldsymbol{\ddot x}}} \right\} + \mathit{\boldsymbol{C}}\left\{ {\mathit{\boldsymbol{\dot x}}} \right\} + \mathit{\boldsymbol{K}}\left\{ \mathit{\boldsymbol{x}} \right\} = \mathit{\boldsymbol{Q}} $ | (7) |
其中:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0\\ 0&{{m_2}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{c_0}}&{ - {c_0}}\\ { - {c_0}}&{{c_{\rm{d}}} + {c_0}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{k_0}}&{ - {k_0}}\\ { - {k_0}}&{{k_{\rm{d}}} + {k_0}} \end{array}} \right] $ |
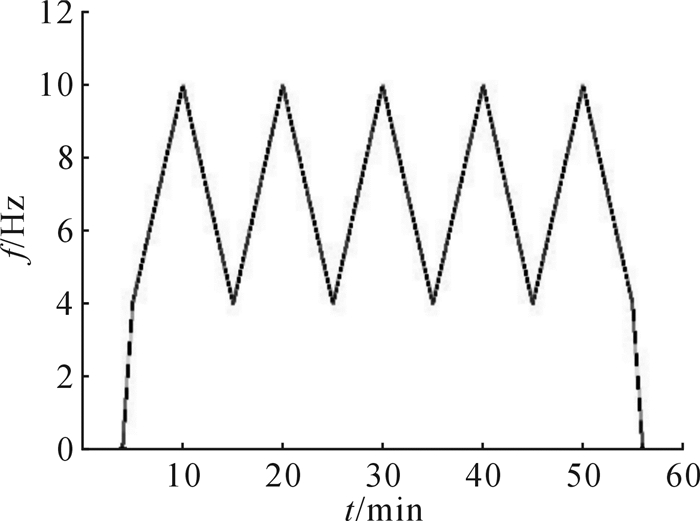
系统外力等于震源激振力,根据精密可控震源实际工作的扫描模式,ω(t)线性扫描信号如图 6所示[15]。
|
| 图 6 精密可控震源扫描信号 Fig.6 The sweep signal of ACROSS |
则1个周期内激振频率表达式为:
| $ \omega \left( t \right) = \left\{ \begin{array}{l} {\omega _1} + \frac{{2t\left( {{\omega _2} - {\omega _1}} \right)}}{T},\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le t \le \frac{T}{2}\\ {\omega _2} - \frac{{\left( {2t - T} \right)\left( {{\omega _2} - {\omega _1}} \right)}}{T},\;\;\;\;\;\;\frac{T}{2} < t \le T \end{array} \right. $ |
式中:ω1,ω2分别为扫描频宽的下限值和上限值,T为扫描周期。
据精密可控震源出力原理[15],激振力表示为:
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} 0\\ {2mr{\omega ^2}\left( t \right)\cos \left( {\omega \left( t \right) \times t} \right)} \end{array}} \right] $ |
虽然K,C均为时间t的函数,式(7)属于参变系统方程[16],但在震源扫描模式(图 6)下激振频率变化率很小,仅为0.02 Hz/s,而由式(6)可知,kd,cd均为ω的函数,为简化计算,在每个时刻将该方程近似看作不变系统方程, 仍按照线性振动系统进行求解。设方程特解(即系统响应)为:
| $ \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_1}{{\rm{e}}^{{\rm{i}}\omega t}}}\\ {{B_2}{{\rm{e}}^{{\rm{i}}\omega t}}} \end{array}} \right] $ |
其中B1,B2为平板与压重的振动幅值,则易得:
| $ \mathit{\boldsymbol{\dot x}} = {\rm{i}}\omega \mathit{\boldsymbol{x}},\mathit{\boldsymbol{\ddot x}} = - {\omega ^2}\mathit{\boldsymbol{x}} $ |
同理可得:
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} 0\\ F \end{array}} \right]{{\rm{e}}^{{\rm{i}}\omega t}} $ |
式中F=2mrω2(t)=Aω2(t), 为激振力幅值范围。
将各表达式代入式(7)并化简可得:
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{B_1}}\\ {{B_2}} \end{array}} \right] = {\mathit{\boldsymbol{Z}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} 0\\ F \end{array}} \right] = \frac{F}{{\left| \mathit{\boldsymbol{Z}} \right|}}\left[ \begin{array}{l} {k_0} + {\rm{i}}\omega {c_0}\\ {k_0} + {\rm{i}}\omega {c_0} - {m_1}{\omega ^2} \end{array} \right] $ |
其中:
| $ \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} {k_0} + {\rm{i}}\omega {c_0} - {m_1}{\omega ^2}\\ - {k_0} - {\rm{i}}\omega {c_0} \end{array}&\begin{array}{l} - {k_0} - {\rm{i}}\omega {c_0}\\ {k_{\rm{d}}} + {k_0} + {\rm{i}}\omega {c_{\rm{d}}} + {\rm{i}}\omega {c_{\rm{0}}} - {m_2}{\omega ^2} \end{array} \end{array}} \right] $ |
由于B1,B2均含复数,对它取模即得到精密可控震源压重及平板的幅值表达式。
为了更好地研究精密可控震源压重振动幅值,引入平板受静力下的位移B0=F/kd,令:
| $ \begin{array}{l} {\beta _1} = {B_1}/{B_0} = {\left[ {{\alpha ^4} + {{\left( {2{\xi _0}\alpha \lambda } \right)}^2}} \right]^{\frac{1}{2}}} \times \left\{ {\left[ {\left( {{\alpha ^2} - {\lambda ^2}} \right)} \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\left( {1 - {\lambda ^2}} \right) - {\mu _{\rm{r}}}{\lambda ^2}{\alpha ^2} - 4{\xi _0}{\xi _{\rm{d}}}\alpha {\lambda ^2}} \right]^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {2{\xi _{\rm{d}}}\lambda \left( {{\alpha ^2} - {\lambda ^2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {{{\left. {2{\xi _0}\alpha \lambda \times \left( {1 - {\mu _{\rm{r}}}{\lambda ^2} - {\lambda ^2}} \right)} \right]}^2}} \right\}^{ - \frac{1}{2}}} \end{array} $ |
式中:
β1为压重振幅放大系数,其物理意义为任意时刻压重振幅与平板静位移的比值,该值越大则表示系统对压重振幅放大作用越明显,本文将它作为压重振动剧烈程度的评价指标。
2 隔振参数对评价指标影响规律分析及优化计算为减少压重对精密可控震源输出信号的影响,需要使振幅放大系数β1尽可能减小。为此分析隔振参数与β1之间的关系,以寻找最优的参数组合。精密可控震源与大地各参数如表 1、表 2所示。
| 参数 | 平板及激振 箱体质量/kg |
平板等效 直径/m |
原隔振系统刚 度/kN·mm-1 |
原隔振系 统阻尼比 |
| 数值 | 2 600 | 1 | 10 | 0.04 |
将各参数代入β1的表达式,通过MATLAB软件计算震源扫描频率范围内压重振幅放大系数β1随各参数的变化规律。
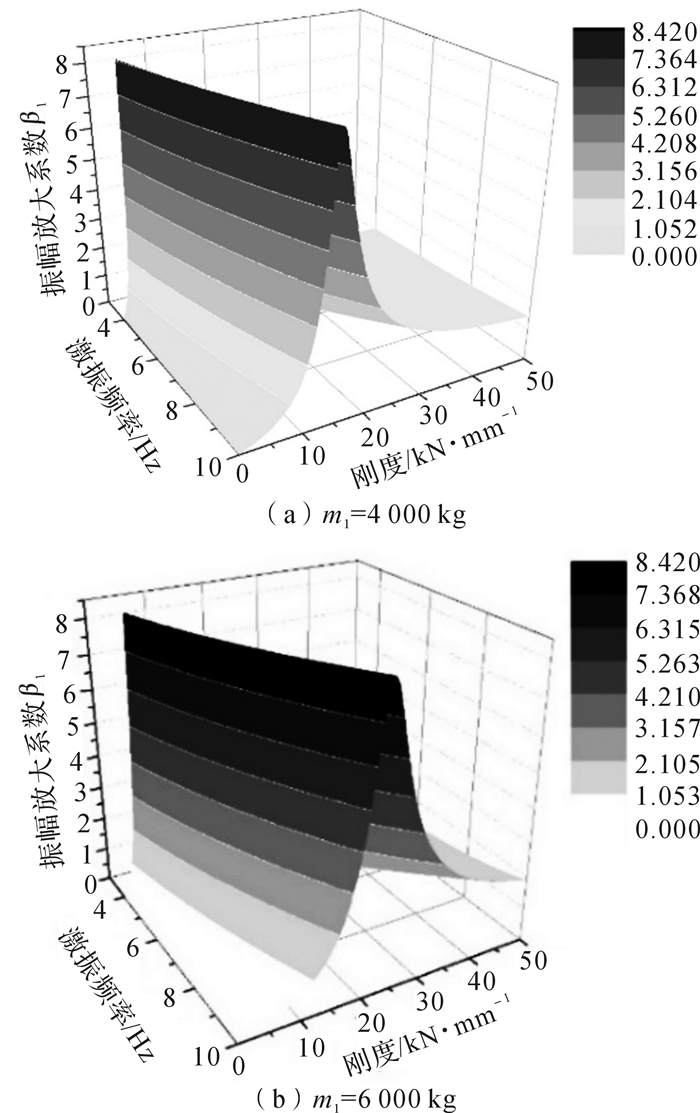
2.1 隔振系统刚度k0对β1影响规律分析压重质量m1需根据出力以2 000 kg为递增单元在2 000~8 000 kg范围内进行调节。分别计算4 000,6 000 kg压重质量下β1随k0的变化情况,结果如图 7所示,其中刚度变化范围参考橡胶隔振器的特性,取k0=0.1~50 kN·mm-1[17]。
|
| 图 7 β1随隔振系统刚度k0的变化规律 Fig.7 Change regulation of β1 with vibration isolation system stiffness k0 |
由图 7(a)可知:1)不同激振频率下压重振幅放大系数极大值所对应的刚度数值并不相同,但均处于5~15 kN·mm-1这样一个较小的区间内,且频率越高,β1的极大值时所对应的刚度越大;2)不同激振频率下压重振幅放大系数随隔振系统刚度变化趋势均为先迅速上升后缓慢下降,极小值为0.05,极大值为8.42;3)随着激振频率增大,压重振幅放大系数变化速度变缓。
对比图 7(a)和(b)可知,当压重质量m1变化时,β1随k0的变化规律同样发生改变:1)出现压重振幅放大系数极大值的刚度区间扩大为5~22 kN·mm-1;2)β1随刚度变化上升和下降的趋势均变缓。
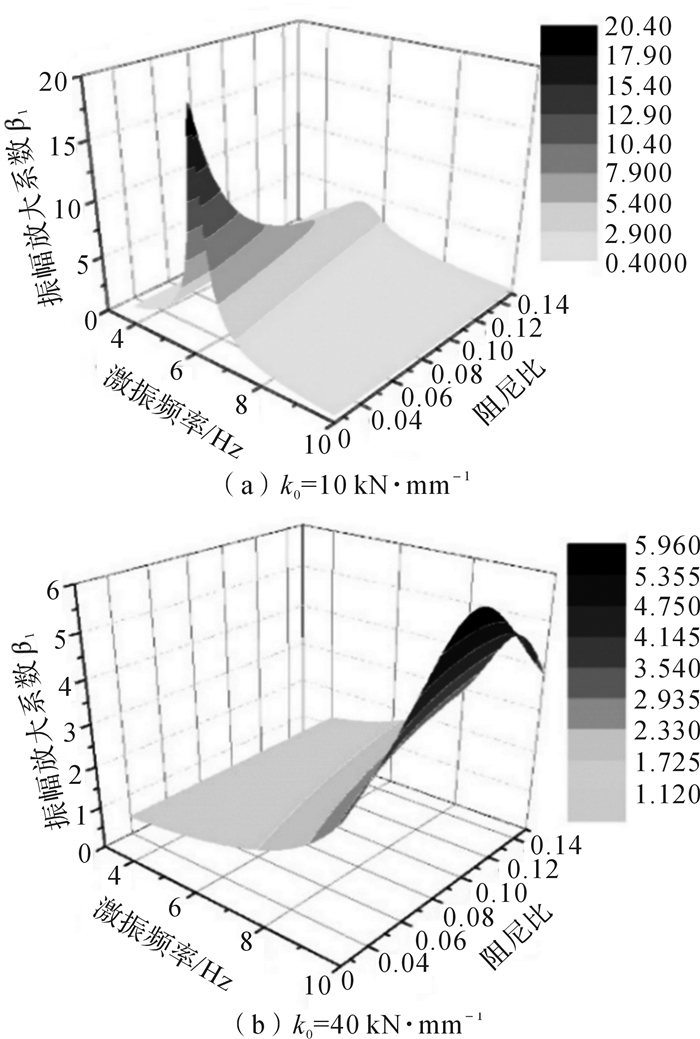
2.2 隔振系统阻尼比ξ0对β1影响规律分析为了同时表征刚度的影响,分别计算10,40 kN·mm-1刚度下压重振幅放大系数β1随阻尼比ξ0的变化情况,压重质量m1=6 000 kg,结果如图 8所示,其中阻尼比ξ0=0.025~0.15[17]。
|
| 图 8 β1随隔振系统阻尼比ξ0的变化规律 Fig.8 Change regulation of β1 with vibration isolation system damping ratio ξ0 |
由图 8(a)可知:1)随着阻尼比的增大,β1极大值逐渐减小,且减小趋势逐渐放缓; 2)β1随着激振频率的增加先上升后下降,在6 Hz处出现极大值,为20.4,在10 Hz处出现极小值,为0.4。
对比图 8(a)和图 8(b)可知,当系统刚度k0变化时,β1随ξ0的变化规律同样发生改变:1)β1极大值出现在10 Hz处,极大值减小为5.96;2)影响β1的因素主要为激振频率,而阻尼比对它的影响不明显。
2.3 不同压重质量下隔振系统最优参数组合由上述分析可知,精密可控震源压重和平板之间的隔振系统的刚度、阻尼比对振幅影响很大,且随着压重质量、激振频率变化时所呈现的动力学规律也有着很大区别。
为得到精密可控震源隔振系统的最优参数组合,基于坐标轮换法设计了优化算法[18],其中设计变量为隔振系统刚度k0和阻尼比ξ0,以整个频宽范围内平均振幅放大系数β1最小为优化目标,兼顾系统动力学性能的稳定性和隔振系统的经济性,设立约束条件为:
| $ \left\{ \begin{array}{l} 0.1 \le {k_0} \le 50\;{\rm{kN}} \cdot {\rm{m}}{{\rm{m}}^{ - 1}}\\ 0.025 \le {\xi _0} \le 0.15\\ \left| {\frac{{{{\bar \beta }_1}\left( {{{k'}_0} + 1\% \Delta {k_0},{{\xi '}_0}} \right) - {{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}}{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}}} \right| \le 5\% \\ \left| {\frac{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0} + 1\% \Delta {\xi _0}} \right) - {{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}}{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}}} \right| \le 5\% \\ \frac{{{{\bar \beta }_1}\left( {{{k'}_0} + 1\% \Delta {k_0},{{\xi '}_0}} \right)}}{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}} \le 99\% \\ \frac{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0} + 1\% \Delta {{\xi '}_0}} \right)}}{{{{\bar \beta }_1}\left( {{{k'}_0},{{\xi '}_0}} \right)}} \le 99\% \end{array} \right. $ |
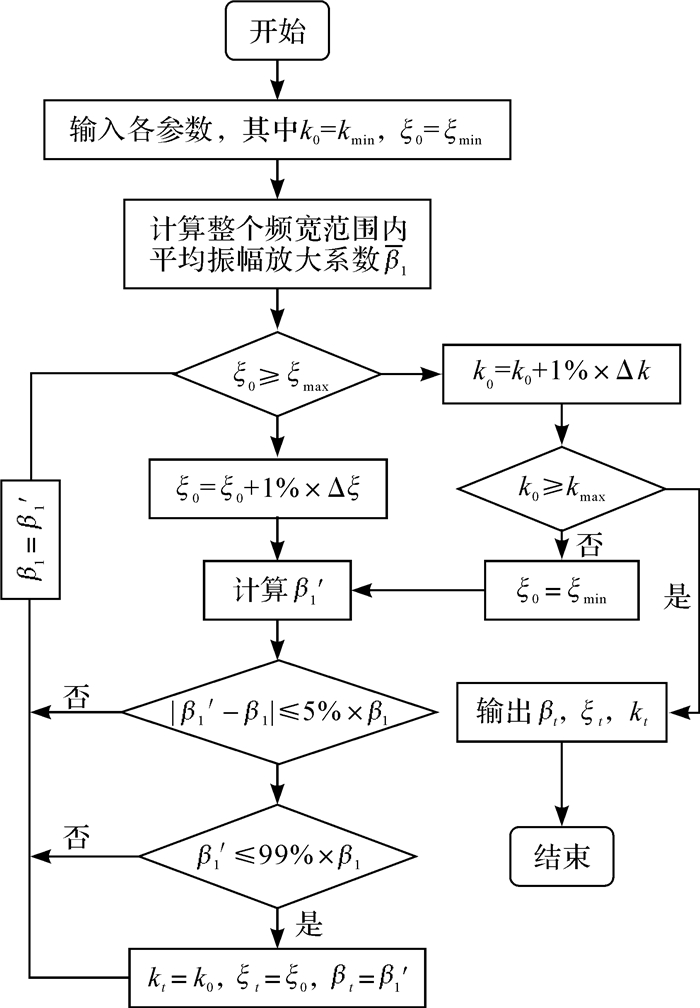
利用MATLAB进行优化计算,其计算逻辑如图 9所示,优化后结果见表 3。
|
| 图 9 刚度和阻尼比优化计算逻辑图 Fig.9 The optimization calculation logic diagram for stiffness and damping ratio |
| 压重质量/kg | 隔振系统最优刚 度/kN·mm-1 |
隔振系统最 优阻尼比 |
平均压重振 幅放大系数 |
| 2 000 | 11.2 | 0.235 | 1.547 |
| 4 000 | 22.1 | 0.243 | 1.541 |
| 6 000 | 33.6 | 0.210 | 1.572 |
| 8 000 | 44.6 | 0.225 | 1.557 |
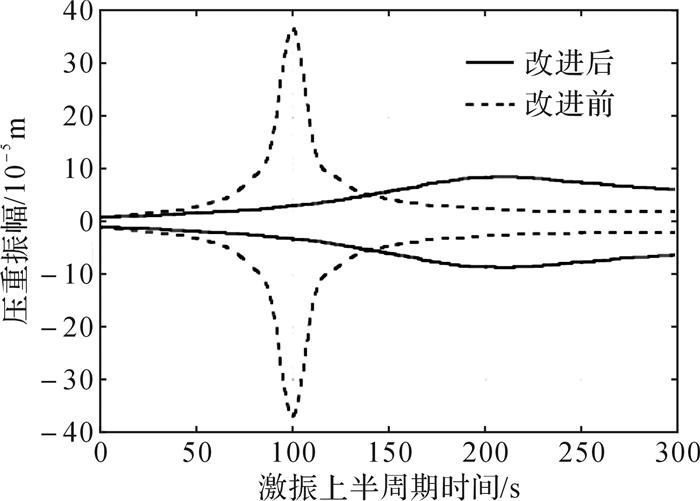
为检验优化效果,以m1=6 000 kg为例,求解方程(7),绘制震源扫描信号上半周期(下半周期规律相似)压重振幅的包络线,如图 10所示。
|
| 图 10 优化前后压重振幅对比 Fig.10 Comparison of weight amplitude before and after optimization |
从图中可知,改进前隔振系统在振动过程中压重振幅发生较大的变化,有明显的共振现象发生;改进后压重在震源扫描信号上半周期内振幅变化平缓,且压重振幅极大值较改进前减小了75%。
3 结论1) 精密可控震源振动动力学性能不仅与自身机械系统参数有关,震源激振频率、近地表地层的弹性模量以及泊松比等物理参数也对它有较大影响。
2) 计算表明不合理的隔振系统参数组合会导致压重发生剧烈振动,整个扫描周期内的压重质量、隔振系统刚度以及阻尼比均对压重振动幅值有较大影响,通过合理设计能有效避免共振现象发生。
3) 通过优化计算得到不同压重质量下,精密可控震源在4~10 Hz扫描频宽范围内的最优刚度及阻尼比参考值,可减小激振作业时压重的振动幅值,以达到削减输出信号干扰、提升与地层之间的能量传递率的目的。
4) 在压重质量为6 000 kg时,经过对隔振参数的优化计算,整个激振周期内优化后的压重振动幅值变化较优化前更加平缓,且振幅极大值下降了75%。
| [1] |
王宝善, 葛洪魁, 王彬, 等.
利用人工重复震源进行地下介质结构及其变化研究的探索和进展[J]. 中国地震, 2016, 32(2): 168–179.
WANG Bao-shan, GE Hong-kui, WANG Bin, et al. Practices and advances in exploring the subsurface structure and its temporal evolution with repeatable artificial sources[J]. Earthquake Research in China, 2016, 32(2): 168–179. |
| [2] |
佟训乾, 林君, 姜弢, 等.
陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912–1921.
TONG Xun-qian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Progress in Geophysics, 2012, 27(5): 1912–1921. DOI:10.6038/j.issn.1004-2903.2012.05.011 |
| [3] |
田建军, 胡建华, 庞超烈, 等.
在地震勘探作业中实施"绿色勘探"[J]. 油气田环境保护, 2007, 17(3): 37–40, 61.
TIAN Jian-jun, HU Jian-hua, PANG Chao-lie, et al. Carrying out "the green exploration" in seismic exploration[J]. Environmental Protection of Oil & Gas Fields, 2007, 17(3): 37–40, 61. |
| [4] |
杨微, 王宝善, 葛洪魁, 等.
精密控制机械震源特征及信号检测方法[J]. 中国石油大学学报(自然科学版), 2013, 30(1): 50–55, 69.
YANG Wei, WANG Bao-shan, GE Hong-kui, et al. Characteristics and signal detection method of accurately controlled routinely operated signal system[J]. Journal of China University of Petroleum (Edition of Natural Science), 2013, 30(1): 50–55, 69. |
| [5] |
王洪体, 庄灿涛, 薛兵, 等.
精密主动地震监测[J]. 地球物理学报, 2009, 52(7): 1808–1815.
WANG Hong-ti, ZHUANG Can-tao, XUE Bing, et al. Precisely and actively seismic monitoring[J]. Chinese Journal of Geophysics, 2009, 52(7): 1808–1815. |
| [6] |
崔仁胜, 周银兴, 陈阳, 等.
我国精密可控震源主动探测研究进展[J]. 防灾科技学院学报, 2016, 18(4): 21–29.
CUI Ren-sheng, ZHOU Yin-xing, CHEN Yang, et al. Research progress in active monitoring of the controlled accurately seismic source in China[J]. Journal of Institute of Disaster Prevention, 2016, 18(4): 21–29. |
| [7] |
董一兵, 胡斌, 杨锐, 等.
河北赤城可控震源主动监测实验[J]. 华北地震科学, 2015, 33(4): 6–13.
DONG Yi-bing, HU Bin, YANG Rui, et al. Active monitoring experiment in Chicheng using precision seismic vibrator[J]. North China Earthquake Science, 2015, 33(4): 6–13. |
| [8] |
姜弢, 林君, 陈祖斌, 等.
相控震源对水平层状地下介质的高信噪比检测[J]. 仪器仪表学报, 2006, 27(11): 1369–1372.
JIANG Tao, LIN Jun, CHEN Zu-bin, et al. High signal-to-nosie ratio detection of horizontal layer underground medium with phased-array vibroseis[J]. Chinese Journal of Scientific Instrument, 2006, 27(11): 1369–1372. DOI:10.3321/j.issn:0254-3087.2006.11.002 |
| [9] |
牛军川, 田国会, 宋孔杰.
旋转机械主动隔振研究Ⅰ:功率流传递特性[J]. 山东工业大学学报, 2001, 31(4): 301–305.
NIU Jun-chuan, TIAN Guo-hui, SONG Kong-jie. Study on active isolation vibration partⅠ:transmission property of power flow[J]. Journal of Shandong University of Technology, 2001, 31(4): 301–305. |
| [10] |
邓东, 马红伟, 吴伟, 等.
KZ-34可控震源振动性能的研究与改进[J]. 物探装备, 2009, 19(S1): 15–20.
DENG Dong, MA Hong-wei, WU Wei, et al. Research and improvement about the vibration performance of KZ-34 type vibrator[J]. Equipment for Geophysical Prospecting, 2009, 19(S1): 15–20. |
| [11] |
李兆锋, 刘士杰, 李超超.
振动筛双层隔振系统的设计研究[J]. 煤矿机械, 2013, 34(8): 45–47.
LI Zhao-feng, LIU Shi-jie, LI Chao-chao. Double layered isolation of linear vibration screener system design and research[J]. Coal Mine Machinery, 2013, 34(8): 45–47. |
| [12] |
李淑清, 王亮亮, 陶知非, 等.
KZ-28型可控震源高精度隔振系统研究[J]. 天津科技大学学报, 2014, 29(3): 58–62.
LI Shu-qing, WANG Liang-liang, TAO Zhi-fei, et al. Research on precision vibration isolation system of KZ-28 vibroseis[J]. Journal of Tianjin University of Science & Technology, 2014, 29(3): 58–62. |
| [13] |
王永芳, 季颖, 朱登杰, 等.
可控震源空气弹簧隔振系统分析及动力学仿真[J]. 物探装备, 2015, 25(4): 215–218.
WANG Yong-fang, JI Ying, ZHU Deng-jie, et al. Dynamic simulation of air spring in vibration isolation system of vibrator[J]. Equipment for Geophysical Prospecting, 2015, 25(4): 215–218. |
| [14] | SUNG T Y. Vibration in semi-infinite solids due to periodic surface loading[M]. Philadelphia: ASTM Special Technical Publication, 1953: 10-13. |
| [15] |
林君, 陈鹏程, 姜弢, 等.
浅层地震探测的可控震源信号设计[J]. 地球物理学进展, 2004, 19(4): 807–811.
LIN Jun, CHEN Peng-cheng, JIANG Tao, et al. The signal design of electrodynamic vibroseis for subsurface imaging[J]. Progress in Geophysics, 2004, 19(4): 807–811. |
| [16] |
刘延柱, 陈立群.
非线性振动[M]. 北京: 高等教育出版社, 2001: 152-176.
LIU Yan-zhu, CHEN Li-qun. Nonlinear vibration[M]. Beijing: Higher Education Press, 2001: 152-176. |
| [17] |
成大先.
机械设计手册:机械振动·机架设计[M]. 北京: 化学工业出版社, 2010: 15-34.
CHENG Da-xian. Machine design handbooks:mechanical vibration·rack design[M]. Beijing: Chemical Industry Press, 2010: 15-34. |
| [18] |
濮良贵.
机械优化设计[M]. 西安: 西北工业大学出版社, 1991: 118-119.
PU Liang-gui. Mechanical optimal design[M]. Xi'an: Northwestern Polytechnical University Press, 1991: 118-119. |


